Positive cooperativity without domains or subunits in a monomeric membrane channel

Abstract

The monomeric VDAC channel shows an accelerated pH titration of its transport properties with a Hill coefficient of about 2. This manifests itself as a sharp peak in conductance noise as well as a fast change in channel selectivity with pH. On the basis of the known structure of this channel, we propose that this cooperativity arises from a mechanically linked mobile pair of ionizable groups. Concerted movement of these groups between two states changes the distance from nearby electrostatic charge to influence the pK of the groups. This model of pH-dependent motion produces positive cooperative behavior that fits the observations without need for subunits or identifiable domains within the protein. The mathematical formalism has never required such domains, but these are generally considered an essential part of cooperative behavior in proteins. The present proposal reduces the size of a cooperative unit to a minimum, extending the limits of what is perceived to be possible. Together with large-scale conformational transitions, these subtle cooperative structural changes may allow proteins to adapt, with high sensitivity, to changes in their environment. They might also be relatively easy to engineer into a protein.

Oxygen uptake by hemoglobin (1, 2) is the classical example of cooperative phenomena in proteins. The advantage gained by responding with greater than linear sensitivity to changes in the concentration of substances in the environment no doubt led to the widespread evolution of cooperative behavior in many biological systems, including ion channels (3–5). The concentration dependence of the proton effect on ion transport or on enzyme function is usually characterized in terms of the Hill formalism (2, 6, 7). A steep dependence of conductance on pH with Hill coefficient n_H ∼ 3 was found with a number of different channels, including the inwardly rectifying (8) and ATP-sensitive (9) K channels and Cl channels (10). Invariably, high Hill coefficients are attributed to the presence of subunits in protein structure. Reported cooperativity in monomeric proteins, such as recoverin (11), arises from the interaction of distinct binding domains in the protein that behave as functional subunits. Here we propose cooperativity arising in a far more subtle way.

In this study we find cooperativity in the pH dependence of ion transport through the monomeric (12, 13) VDAC channel isolated from Neurospora crassa. This voltage-dependent anionic channel of the outer membrane of mitochondria is composed of one 30-kDa polypeptide molecule. Although no atomic resolution crystal structure is available, studies on two-dimensional crystals, circular dichroism measurements, and extensive functional studies show that VDAC forms a simple single-walled aqueous pore with an ∼2.4- to 2.8-nm inner diameter (14–16). The wall is almost exclusively composed of β-strands in an antiparallel configuration. VDAC's ion selectivity is primarily determined by the estimated net +3 charge that lines its aqueous pore (17). We report that the medium pH influences the single-channel conductance, selectivity, and current noise with a quadratic power dependence (Hill coefficient of 2).

Materials and Methods

Noise and Single-Channel Conductance Measurements.

VDAC channels were isolated and purified from N. crassa mitochondria (18, 19). Planar membranes were formed by the monolayer method (20, 21) across a 70-μm-diameter hole in a 15-μm-thick Teflon partition using diphytanoyl phosphatidylcholine. The solution contained 1 M KCl, 1 mM CaCl₂, and 5 mM Hepes. The pH was adjusted by adding HCl or KOH and was monitored during the experiment with a microelectrode (Orion 9810). The details of noise analysis of a single VDAC channel were described earlier (21). Measurements were made at T = (23 ± 1.5)°C.

Selectivity Measurements on Multichannel Membranes.

Multichannel planar membranes used the same source of VDAC and phospholipid as above. The solution contained 500 mM KCl cis and 100 mM KCl trans with 5 mM CaCl₂/5 mM Mes on both sides. Initially the pH was 4.8, but this was slowly raised by infusing both sides with 0.5 mM glycylglycine, pH 12. The pH was monitored continuously (Beetrode; World Precision Instruments, Sarasota, FL; corrected for response time), as was the current in the presence of alternatively +18 mV and −15 mV from which the conductance and reversal potentials were calculated.

Results and Discussion

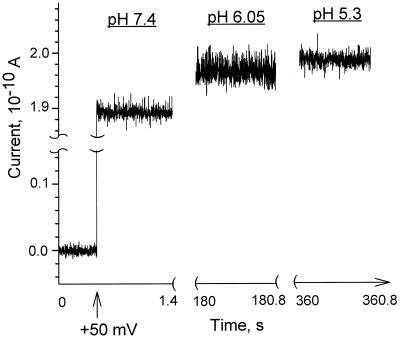
The properties of the VDAC channel depend on the media acidity in several respects. Fig. 1 demonstrates two of them. First, the mean current through the channel slightly increases when pH is decreased from 7.4 to 6; second, there is a significant difference in characteristic noise at the three different pH values. This current noise reflects dynamic changes in ion flow through the channel resulting from protonation/deprotonation of particular residues. The records correspond to the same open channel. The channel was inserted at pH 7.4, and then the pH was decreased by adding HCl to the aqueous solutions. The nonmonotonic behavior of the current noise is clearly seen: the noise track at pH 6.05 is wider compared with the tracks at pH 7.4 and 5.3.

Figure 1.

Ionic currents through a single VDAC channel show dependence on pH. Recordings were made on the same channel (left to right) at pH 7.4 by using 0 mV and +50 mV applied potential, and at pH 6.05 and pH 5.3 by using +50 mV. Note a small increase in the mean current induced by decreasing the pH of the bathing solution from 7.4 to 6 and an excess current noise evident at intermediate pH values. The solution contained 1 M KCl, 1 mM CaCl₂, and 5 mM Hepes. Current recordings were filtered by an eight-pole Bessel filter at 1.2 kHz.

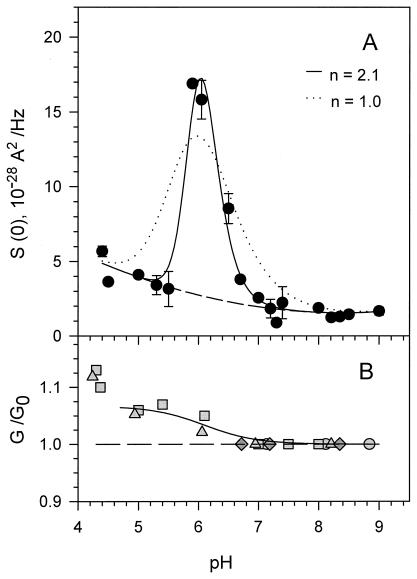
A pronounced and clearly defined peak of current noise around pH 6 is shown in Fig. 2A. The amplitude of the noise from the open channel at pH 6 exceeds that of the background by an order of magnitude, whereas at a pH higher than 7, it is close to the background. The base of the peak is not symmetrical and at a pH lower than 5.5 the noise level is more than double of that at pH values between 7 and 9. The relative pH-induced changes in the conductance of a single VDAC channel are shown in Fig. 2B. Decrease in bathing solution pH increases single-channel conductance by about 5% of its initial value at high pH. This increase happens over a narrow pH range in the vicinity of pH 6. It should be noted that this 5% increase is within the variability of single-channel conductance: in our experiments, channel conductance in 1 M KCl buffered between pH 7.0 and 9.0 was 4.2 ± 0.3 nS. Therefore, the single-channel conductance measured after the pH change was normalized by the value measured when the channel first inserted (pH between 7.0 and 9.0). Fig. 2B presents the results of four experiments where the single-channel conductance was measured after consecutive additions of HCl. In this way, the small conductance changes were resolved. Over the pH scale investigated, these changes were reversible within the accuracy of our measurements.

Figure 2.

The “accelerated titration” is seen in the pH-dependent current fluctuations (A), accompanied by the change in the relative channel conductance (B). Each point of the low-frequency current spectral density, S(0), represents an average over the frequency range 100 < f < 1,000 Hz at +50 mV with the background (that is, spectral density of channel noise at 0 mV) subtracted. For a first-order protonation reaction of a single residue with equilibrium constant K and dissociation constant, k_off, S(0) is given by (22, 23): 4(Δi_max)²10^pK−pH/k_off (1 + 10^pK−pH)³, where Δi_max is the change in the channel current between the states of fully protonated and unprotonated forms of the residue. The corresponding ionization-induced change in the average current through a single channel is a monotonic function of pH: Δi(pH) = Δi_max 10^pK−pH/(1 + 10^pK−pH). Fitting Δi(pH) to the experimental data in B yields Δi_max = 1.34 × 10⁻¹¹ A. Using this value in the spectral density equation and fitting to the data, we obtain pK = 5.7 and k_off = 1.0 × 10⁵ s⁻¹ (dotted line). Formally introducing cooperativity by replacing pK − pH with n_H(pK − pH) and refitting the data yields n_H = 2.1, pK = 5.9, and k_off = 7.3 × 10⁴ s⁻¹ (solid line). The single-channel conductance shown in B at different pH values is given as a ratio to the single-channel conductance at the pH indicated to that at pH 7 to pH 9 (dashed line) at which the VDAC channel was initially inserted. Each symbol corresponds to a different experiment.

A comparison of Fig. 2 A and B reveals that the pH at which the peak of low-frequency open-channel noise was observed correlates very well with the pH at which the change in single-channel conductance was detected. As previously proposed for the α-toxin channel (22, 23), the reversible binding of protons to ionizable residues inside the channel could be responsible for channel current noise and changes in its mean current. Binding of a proton to a single residue induces a change in the electrostatic potential profile in the channel, causing a stepwise increase in the current carried by the electrolyte. Applying this model to the VDAC channel (see legend of Fig. 2), we obtain the dotted line in Fig. 2A as the best fit with parameters pK = 5.7 and proton dissociation constant k_off = 1.0 × 10⁵ s⁻¹. Thus, the model (22, 23) describes the nonmonotonic behavior of the current noise, but does not account for the sharpness of the experimental peak. To account for the sharpness of the noise peak, we formally introduce the effect of cooperativity through the Hill coefficient n_H. The corresponding fit (see legend for equations) is shown in Fig. 2A as a solid line and gives n_H = 2.1, pK = 5.9, and k_off = 7.3 × 10⁴ s⁻¹.

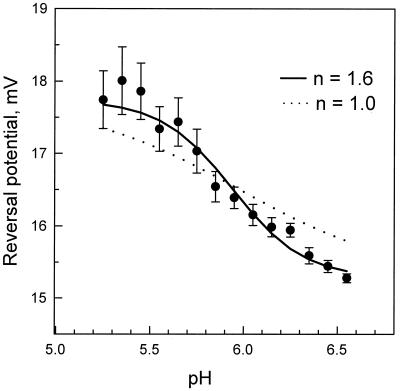
The pH-induced change in the electrostatic potential profile of the channel should be reflected in the change of its ionic selectivity. If the salt concentration is different on the two sides of the membrane, the ions will diffuse down their gradient. The more permeant ion will carry more charge, resulting in a net current. Thus the voltage needed to bring this current to zero (the reversal potential) is a measure of ion selectivity. Fig. 3 illustrates pH-dependent reversal potentials that were obtained as averages from multichannel membranes separating 500 and 100 mM KCl solutions. The reversal potential decreased by 2.5 mV as the pH was increased from 5.3 to 6.6. This result is consistent with the titration of one group in this pH range (15) and a reduction in anion selectivity. A least-squares fit just in the 2.5-mV range yields a Hill coefficient of 2. However, to avoid bias, a fit that allowed all parameters to vary was used. It yielded a Hill coefficient of 1.6 (solid line). If this coefficient is put equal to 1.0 then systematic deviations for several points exceed three standard errors (dotted line).

Figure 3.

The dependence of the reversal potential on bathing solution acidity at pH values around the conductance noise peak (Fig. 2A) supports conclusions about cooperative titration. The means of seven experiments are illustrated along with standard errors. The theoretical curves fitted to the data use the form Ψ(pH) = Ψ_min + ΔΨ/[1 + 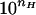^(pH−pK)], where first, all parameters were set free (solid line, n_H = 1.6; Ψ_min = 15.2 mV; ΔΨ = 3.1 mV; pK = 5.86), and second, the Hill coefficient was put equal to 1.0 (dotted line). A much better fit is seen for n_H = 1.6.

A rigorous quantitative analysis of the three pH-induced effects reported in this study—peak in the low-frequency noise spectral density, change in the single-channel conductance, and variation of the reversal potential—requires detailed structural information concerning not only the overall channel architecture but also the exact position of the residues in question. Nevertheless, even in the absence of such information our results clearly demonstrate the presence of cooperative behavior found in a single-domain monomeric ion channel.

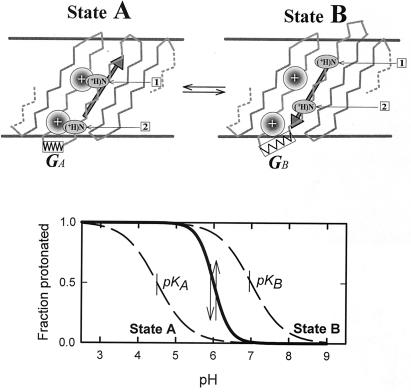
In the spirit of the analysis by Tanford (24, 25) to explain cooperativity in systems that have rearrangement of subunits, we propose a mechanism with concerted motion of several ionizable residues between protein regions that change the pK of the residues. One possible model is illustrated in Fig. 4. Note that simpler models, involving interaction between charged groups but lacking “concerted motion” of groups, did not yield positive cooperativity. Here, two ionizable residues (1 and 2) are linked mechanically (e.g., belong to the same strand of a β-sheet that lines the pore) and can hop between two positions (A and B) that differ in the local electric fields experienced by the residues. When the residues are uncharged, the low-energy state (A) is the one in which the residues are close to the local high positive charge density. When the residues are charged, the electrostatic repulsion between the residue and the local charge favors the other state (B). This causes a stress in the protein depicted as a change in the structural pattern and an extended spring. We are interested in the pH dependence of the protonation of the residues.

Figure 4.

Schematic model that explains cooperativity without subunits. (Upper) A portion of the polypeptide chain of a protein contains two titratable residues (1 and 2) separated sufficiently so as not to affect each other's charge state. In state A, the residues are close to positively charged regions of the protein, whereas in B they are moved away from these regions. The structural change induces a reduction in the electrical potential felt by each residue but introduces a stress in the protein depicted by the stretched spring. When the sites are unprotonated, state A is the low-energy conformation with the pK value of the residue reduced by the positive charge. Protonation increases the positive charge of the residue and the resulting electrostatic repulsion (upward arrow) favors state B. Stress of this state is shown here as an extended spring that acts in the opposite direction (downward arrow). (Lower) Origin of accelerated titration as a transition from the titration curve of state A to the titration curve of state B as proton concentration and, consequently, the charge of the residues are decreased.

The model uses five parameters. Four pK_I (I = A1, A2, B1, B2) that are −log K_I of the four dissociation constants related to partial protonations α_I

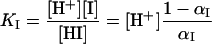for each group (1, 2) in each state (A, B), and the change in free energy for this transition when the residues are uncharged, ΔG. In the model of Fig. 4 the changes in the dissociation constants upon A-to-B transition are related to the changes in local potentials experienced by the residues in positions 1 and 2, ΔΨ₁ and ΔΨ₂. In this case pK_1B − pK_1A = eΔΨ₁/(kT ln 10) and pK_2B − pK_2A = eΔΨ₂/(kT ln 10).

The degree of protonation depends on the fraction f_A and f_B of protein in states A and B so that the total number of protons bound is

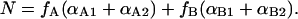Hill coefficient in this case is defined as a maximum of the following derivative

where we solve for f_A and f_B as a function of ΔG and pH by the equations of detailed balance.

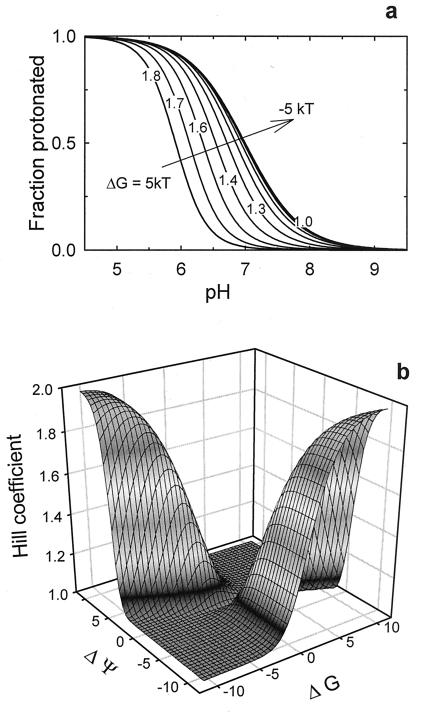
Fig. 5A shows Hill coefficients up to 2.0, using ΔpK₁ = ΔpK₂ = 2.8 (ΔΨ₁ = ΔΨ₂ = −6.5 kT), pK_1B = pK_2B = 7.0, and a given range of ΔG. This accelerated titration reflects titration-driven changes in f_A and f_B. The change in free energy of each state with a change in pH is itself proportional to the sums (α_A1 + α_A2) and (α_B1 + α_B2). In direct proportion to the degree of protonation, titration speeds up conversion to the state that has higher affinity. An appropriate combination of ΔG and ΔΨ is required to achieve the steep pH dependence (Fig. 5B).

Figure 5.

The model describes a steep pH dependence of the protonation state of residues on the protein. (a) Conditions closely corresponding to the observations on VDAC (apparent pK of 5.9 and n_H = 1.8) were achieved by using the following parameters for the leftmost curve: electrical potential changes felt by the residue of −6.5 kT in going from state A to state B; an intrinsic pK (pK_1B = pK_2B) of 7; a conformational free energy difference of 5 kT. The rest of the curves show a transition to “normal” titration as the free energy difference goes down. (b) The Hill coefficient of the titration (A) as a function of electrostatic potential difference, ΔΨ = ΔΨ₁ = ΔΨ₂, and interstate free energy change ΔG at equal pK values.

Fig. 5A demonstrates a shift of pK by 1.1 pH units (from 7.0 to 5.9) and significant sharpening of the titration curve for ΔG = 5 kT. The Hill coefficient equals 1.82. It should be noted that while the first feature (the pK shift) can be observed even in the case of independent residue titration, the second one (the transition sharpening) is a direct consequence of titration coupling through the mechanical link. Thus, the concerted motion of titratable residues caused by a single strand translocation (Fig. 4) describes our findings well. This translocation represents only a minor change in the protein structure as compared to the channel transition between open and closed states (26). A model with three or more residues produces Hill coefficients of 3 and higher and, therefore, can explain a number of empirical observations of “accelerated titration” that go well beyond the experimental results discussed above.

It is worth reemphasizing that while mathematically our description does not differ from that developed for the well-known models of subunits undergoing a concerted conformational change, our model reduces the scale of cooperative rearrangement to a minimum of one mobile chain with a pair of ionizable residues.

As yet, the cooperativity reported here cannot be linked to any known physiological function. The pH-dependent changes in VDAC channel properties are small. However, our findings demonstrate that the complexity of protein structure per se can result in cooperative behavior without any cooperative rearrangements among subunits of subunit-like domains within the protein. Clearly, cooperativity in oligomeric proteins may also arise from interactions that have nothing to do with the oligomeric structure itself. We conclude that a “cooperative behavior” is not restricted to a scenario of interactions between “functional” subunits within a protein.