Like-charge attraction between polyelectrolytes induced by counterion charge density waves

Abstract

Electrostatics in aqueous media is commonly understood in terms of screened Coulomb interactions, where like-charged objects, such as polyelectrolytes, always repel. These intuitive expectations are based on mean field theories, such as the Poisson–Boltzmann formalism, which are routinely used in colloid science and computational biology [Israelachvili, J. (1992) Intermolecular and Surface Forces (Academic, London), 2nd ed.]. Like-charge attractions, however, have been observed in a variety of systems [Gelbart, W. M., Bruinsma, R. F., Pincus, P. A. & Parsegian, V. A. (2000) Phys. Today 53, 38–44]. Intense theoretical scrutiny over the last 30 years suggests that counterions play a central role, but no consensus exists for the precise mechanism. We have directly observed the organization of multivalent ions on cytoskeletal filamentous actin (a well defined biological polyelectrolyte) by using synchrotron x-ray diffraction and discovered an unanticipated symmetry-breaking collective counterion mechanism for generating attractions. Surprisingly, the counterions do not form a lattice that simply follows actin's helical symmetry; rather, the counterions organize into “frozen” ripples parallel to the actin filaments and form 1D charge density waves. Moreover, this 1D counterion charge density wave couples to twist distortions of the oppositely charged actin filaments. This general cooperative molecular mechanism is analogous to the formation of polarons in ionic solids and mediates attractions by facilitating a “zipper-like” charge alignment between the counterions and the polyelectrolyte charge distribution. We believe these results can fundamentally impinge on our general understanding of electrostatics in aqueous media and are relevant to a wide range of colloidal and biomedical processes.

All proposed theoretical explanations for like-charge attraction (1–10) introduce some form of positional counterion correlations within a condensed layer of oppositely charged counterions (11). Dynamic “van der Waals”-like correlations of long-wavelength ion fluctuations have been suggested (2–5). Static mechanisms consisting of ion correlations along the axis of the polyelectrolyte rods in the form of a Wigner lattice have also been considered (7–10). All extant theories, however, use highly idealized models for the polyelectrolytes, such as infinitely thin lines or “smooth” rods. The present experimental work examines the extent to which these predictions survive in a real polyelectrolyte system and provides a point of contact between the two extreme viewpoints above. The general form of the counterion mechanism we observe here, which involves a coupling between counterion correlation and polyelectrolyte deformation (Fig. 1), is applicable to a wide range of colloidal and biomedical processes that depend on controlling interactions between macroions dispersed in fluid suspensions.

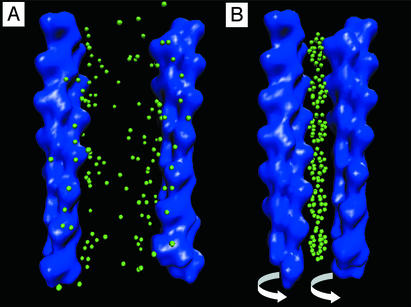
Fig. 1.

Schematic representations of uncondensed and condensed F-actin. (A) At low multivalent ion concentrations, two F-actin filaments maintain their native 13/6 symmetry and are unbound. (B) At high multivalent ion concentrations, the ions collectively form a CDW and bundle F-actin filaments. Moreover, the CDW forms a coupled mode with torsional distortions of the F-actin and has overtwisted it by 3.8° per monomer to a new 36/17 symmetry. The representations of F-actin are low-resolution density maps generated by using situs software (http://situs.biomachina.org).

Materials and Methods

Diffraction features generated by counterion correlations are expected to be weak compared with those generated by biopolymer organization. To detect positional correlations in counterion distributions on the surface of a charged polymer with small angle x-ray scattering (SAXS), a number of experimental strategies have been used. Filamentous actin (F-actin) has been chosen as a model system because it is a rigid polyelectrolyte (persistence length ξ_A ≈10 μm) with a large diameter (D_A ≈ 75 Å) (12, 13), so that correlated counterion “lattices” can have the potential to form large domains, and thereby generate sharp, detectable peaks. Because the number of atoms that comprise the charged biopolymer is large compared with the number of counterions, high Z counterions (Ba^2–) have been used to improve the Z-contrast between counterion scattering and protein scattering. Finally, to further highlight the diffraction features that are generated by the counterions, we have compared the SAXS patterns from F-actin that has been condensed nonelectrostatically (no added multivalent ions, prepared by progressive ultracentrifugation and water removal) with F-actin that has been condensed electrostatically by using multivalent ions. Unlike nonelectrostatically condensed samples, multivalent ion condensed biopolymer samples typically exhibit poor alignment, because of the existence of strong attractions and the resultant precipitation of the biopolymer. We mitigated this problem by using a small (300 × 300 μm²) synchrotron x-ray beam on a sheared sample.

Monomeric actin (G-actin) (molecular weight, 43,000) was prepared from a lyophilized powder of rabbit skeletal muscle purchased from Cytoskeleton (Denver). The nonpolymerizing G-actin solution contained a 5 mM Tris buffer at pH 8.0, with 0.2 mM CaCl₂, 0.5 mM ATP, 0.2 mM DTT, and 0.01% NaN₃. G-actin (2 mg/ml) was polymerized into F-actin (linear charge density λ_A ≈ –1e/2.5 Å at pH 7) with the addition of salt (100 mM KCl). Human plasma gelsolin (Cytoskeleton) was used to regulate the F-actin length. The filaments were then treated with phalloidin (molecular weight 789.2) to prevent actin depolymerization. F-actin gels were ultracentrifuged at 100,000 × g to pellet the filaments. After the removal of the supernatant buffer solution, the F-actin was resuspended to a final concentration of 10 mg/ml by using Millipore H₂O (18.2 MΩ). Electrostatically condensed samples were prepared by mixing with MgCl₂ or BaCl₂ salt solutions. All samples were sealed in 1.5-mm-diameter quartz capillaries. SAXS experiments were performed at Beamline 4-2 of the Stanford Synchrotron Radiation Laboratory. The x-ray energy was monochromatized to 8.98 KeV by using a double-bounce Si(111) crystal.

Results and Discussion

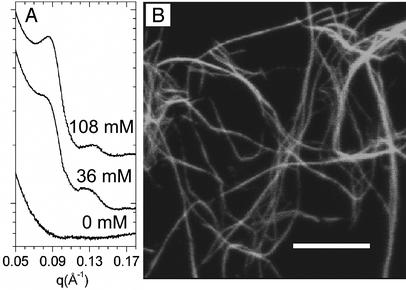
The basic supramolecular structure of the biopolymer component of the composite counterion-biopolymer system can be seen in the progressive formation of F-actin bundles with increasing multivalent ion concentrations. SAXS measurements of F-actin condensed with Ba^2– (Fig. 2A) indicate an actin-actin close-packing peak characteristic of the bundled phase appears at q = 0.089 Å^–1. These F-actin bundles can also be imaged in real space by using laser-scanning confocal fluorescence microscopy (Fig. 2B). The F-actin filaments were labeled with phalloidinated Alexa Fluor 488 (Molecular Probes). A Leica SP-2 confocal microscopy system (Beckman Institute, Urbana, IL) was used to image the dilute F-actin solutions in sealed sample cells at different ionic strengths. The observed thickness of bundles in the image indicates that each bundle is comprised of thousands of filaments.

Fig. 2.

(A) SAXS profiles of F-actin (≈2 μm long) condensed by Ba^2– ions. At 0 mM Ba^2– concentration, F-actin is in an uncondensed isotropic phase. At high Ba^2– concentrations (36 and 108 mM), F-actin condenses into close packed bundles with a correlation peak at q = 0.089 Å^–1, indicating the existence of an attraction. A weak higher-order reflection can also be observed at q = 0.136 Å^–1, which deviates slightly from the position expected from an exact hexagonal lattice. (B) A confocal image of a dilute (0.03 mg/ml) solution of bundles of F-actin (≈10 μm) at 72 mM global Ba^2– concentration. (Scale bar, 8 μm.)

A direct comparison between the 2D SAXS patterns of F-actin condensed osmotically without using divalent ions and of F-actin condensed electrostatically with divalent ions is made in Fig. 3. Fig. 3A is a 2D SAXS pattern of partially aligned F-actin at 90 mg/ml in the absence of divalent ions. The F-actin rods are aligned along the q_z axis and are powder-averaged in the plane perpendicular to the q_z axis. For the analysis of the 2D SAXS patterns (Fig. 3 A and D), cuts along q_r and q_z are produced by integrating the 2D SAXS image over 40° wedges in χ, centered about the q_r and q_z axes, where q_r ≡ qcosχ, q_z ≡ qsinχ, q = (4π/λ)sinθ, and 2θ is the Bragg angle. The three equatorial peaks (a–c) in Fig. 3B correspond to the first-order, 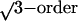, and second-order peaks expected from local hexagonal coordination. The two strong, partially orientationally averaged peaks (d and e) along the meridional direction (Fig. 3C) are the well known sixth- and seventh-layer lines characteristic of 13/6 symmetry (13 monomers in 6 full turns) (14), in agreement with the known structure of F-actin. To account for the sample mosaic and the effects of integration on layer lines, we partially powder-averaged (π/2 ≥ χ ≥ π/4) theoretical 2D diffraction patterns. The resulting modeled peak positions have been optimized by varying the monomer spacing in 0.1-Å increments. These peak positions and combined full width at half-maximum are well described (to within 1%) by a Fourier transform of the standard four-sphere model (15) for the actin filament, using the Holmes coordinates (14), combined with Gaussian layer line profiles (16).

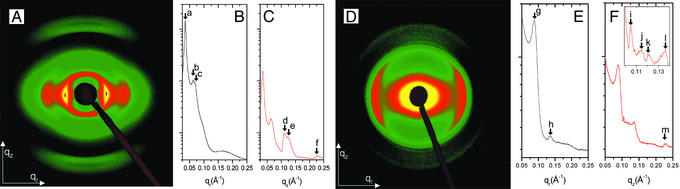
Fig. 3.

(A) A 2D SAXS pattern of nonelectrostatically condensed F-actin. The procedure for generating Integrated cuts along q_r (B) and along q_z (C) are described in the text. Peak positions for all observed layer lines (6th, 7th, and 13th) agree with the native 13/6 actin model to within <1%. (D) 2D SAXS of Ba^2– condensed F-actin. Cuts along q_r (E) and q_z (F) are performed the same way. The data indicate the formation of a counterion 1D CDW and an induced 3.8° overtwist of F-actin (see text). The peak positions are 0.035 Å^–1 (a), 0.062 Å^–1 (b), 0.07 Å^–1 (c), 0.111 Å^–1 (d), 0.123 Å^–1 (e), 0.225 Å^–1 (f), 0.089 Å^–1 (g), 0.136 Å^–1 (h), 0.105 Å^–1 (i), 0.115 Å^–1 (j), 0.120 Å^–1 (k), 0.136 Å^–1 (l), and 0.227 Å^–1 (m). (Inset) A magnification of the CDW peak (i) and neighboring layer line scattering (j and k).

The diffraction pattern for multivalent ion condensed F-actin bundles differs dramatically from that of the nonelectrostatically condensed F-actin. Fig. 3D is a 2D SAXS pattern of a partially aligned sample of F-actin at 7.5 mg/ml condensed with 60 mM Ba^2–. The filaments are oriented parallel to q_z on average as in the nonelectrostatically condensed sample above. The most salient difference between the two diffraction patterns (between Fig. 3 A and D and between Fig. 3 C and F) is the appearance of a sharp diffraction feature at q_z = 0.105 Å^–1 in the electrostatically condensed case (Fig. 3F, peak i). This finding is surprising because the sample alignment is weaker for the electrostatically condensed actin compared with the nonelectrostatically condensed actin, and weaker alignment can only broaden and weaken existing peaks, but never produce new ones. It is in fact not possible to generate this new peak by using the F-actin helix. This peak, which only occurs for multivalent ion condensed samples and is aligned along the q_z-axis, corresponds to “ripples” of multivalent ion density along the filament axis, analogous to a classical 1D charge density wave (CDW). Compared to any of the F-actin layer line peaks in this region of reciprocal space, this peak is symmetrical, significantly sharper, and more intense. This peak is consistent with the diffraction from a new 1D periodic charge distribution with a finite in-plane width and azimuthal symmetry. Its diffraction signal is proportional to the modulus squared of its Fourier transform, which is the product of a periodic arrangement of Bragg sheets multiplied by 0th-order Bessel functions centered on the q_z axis, which suppress the off-axis Bragg sheet intensity. Unlike the higher-order Bessel function peaks from the F-actin helix, which are shifted and broadened along q_z by the large mosaic distribution of bundle orientations within the sample volume, this peak remains sharp along q_z even after such orientational averaging. Because we observe a single peak, the counterion CDW is dominated by one Fourier component and is approximately described by a simple sinusoidal density variation with a spatial period of 59.8 Å, which is comparable to the spacing between monomer ridges on the surface of one side of an F-actin filament (approximately two times the monomer spacing). Because of the weak diffraction signal of the CDW, we cannot rule out the possibility of higher harmonics. Our results, however, suggest that the dominant Fourier component of the CDW is the one at q_z = 0.105 Å^–1, which implies that the counterion distribution can be approximated by a “frozen” 1D sinusoidal ripple along the polyelectrolyte.

This simple picture, however, is incomplete. For example, why do the counterions follow a new 1D symmetry rather than the full helical symmetry of the charge distribution on F-actin? A close examination of the diffraction pattern from the multivalent ion-condensed F-actin reveals that the 1D CDW has enforced a change in the native F-actin symmetry and overtwisted the F-actin helix by 3.8° per monomer. This can be seen by the direct comparison of Fig. 3D with the nonelectrostatically condensed actin in Fig. 3A. The equatorial peak positions (g and h) deviate slightly from those expected from an exact hexagonal lattice and indicate that the bundled filaments are tightly packed (Fig. 3E). Along the meridional direction, the Bessel function peaks of the native 13/6 layer lines of the nonelectrostatically condensed sample (Fig. 3C) have been replaced by a cluster of weaker peaks (j–l) in the multivalent ion condensed sample (Fig. 3F). The peak at 0.136 Å^–1 (l) is clearly caused by the mosaic smearing of the strong transverse inter-rod correlation at the same q-value along the equatorial direction, and the intensity agrees well with calculations accounting for the mosaic distribution. The remaining peaks can be completely explained by overtwisting F-actin to a new 36/17 symmetry. Experimentally, F-actin is known to exhibit a range of twists states (13, 17, 18), an observation that is consistent with its low torsional rigidity, as measured with single-molecule techniques (19). We consider changes in the F-actin helical twist away from its native symmetry by starting with the standard four-sphere model in the 13/6 helix and monomer spacing of 28.7 Å (the value extracted from the measurement of actin in Fig. 3A) and twisting the filament over a range of ±10° per monomer in increments of 0.05°. Long repeat helical symmetries up to the 108/51 range have been checked for the appearance of new intense layer lines, and none were found. The measured peaks at q = 0.115 and 0.120 Å^–1 agree well with the l = 17 and 19 layer lines of the overtwisted 36/17 symmetry (calculated peaks at q = 0.113 and 0.120 Å^–1 after adding mosaic smearing). Even the higher-order feature at q = 0.227 Å^–1 is reproduced.

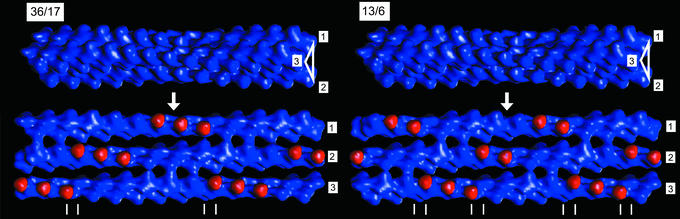
Why does the composite polyelectrolyte-counterion system choose the overtwisted 36/17 symmetry? The angle between adjacent monomers on a 13/6 helix is given by –6*2π/13, or –166.2°. By contrast, the angle per monomer on a 36/17 helix is –170°, which indicates an additional twist of –3.8° per monomer. An examination of the local environment around a 1D CDW reveals why the 36/17 symmetry is favored. Consider a simple columnar hexagonal array of F-actin filaments decorated by parallel 1D CDWs. The most elementary unit of this structure is a three-filament bundle, which defines a “channel” of triangular cross section, threaded by a 1D CDW of ions. Fig. 4 depicts the negative charge distribution within such a three-filament bundle. The red-colored regions on each filament correspond to subdomain-1s (sd-1s) of the actin monomers that face the inside of the channel. These subdomains are the most highly negatively charged and the most protrusive regions on the surface of F-actin. To lower the electrostatic energy, these domains should ideally be positioned adjacent to the maxima of the oppositely charged 1D CDW. However, because F-actin is a helix, the highly charged sd-1 will process in and out of this central channel and will not always be in register with the CDW. If we examine the “unwrapped” three-filament bundle and follow sd-1 from monomer to monomer and filament to filament along the bundle, we find that no matter how the initial relative phases of the F-actin are chosen, a large number of defects will occur for the native 13/6 symmetry, in which sd-1s of adjacent filaments are in very close proximity to one another, which is electrostatically and sterically unfavorable. Given that F-actin is a helix, defects of this kind are unavoidable, unless the helix was completely unwound. However, the spatial frequency of these defects is dramatically reduced if the F-actin filament is overtwisted to a 36/17 symmetry. The 36/17 symmetry provides long regions with evenly spaced negative-charge patches with a period equal to twice the monomer spacing on a single filament, d = 57.4 Å, which is quite close to 59.8 Å, our measured period for the 1D CDW of multivalent ions. In fact, this observed organization of multivalent ions into a classical CDW may be related to the occurrence of these defects.

Fig. 4.

For the 36/17 and 13/6 symmetries, a schematic representation of a three-filament bundle with the central triangular tunnel highlighted (Upper) and the same bundle in its unwrapped form, showing the interior charge distribution of the tunnel (Lower). The red-colored regions correspond to the highly charged sd-1s of the actin monomers facing the interior of the bundle. Double lines mark the location of the electrostatic/steric defects where sd-1s from adjacent filaments are in close proximity. Overtwisting the 13/6 helix to a 36/17 helix dramatically reduces the density of these defects and generates long regions of evenly spaced charged patches to match with the periodic counterion CDW.

Does optimizing the electrostatic interactions in a single interstitial channel necessarily do so for all of the interstitial channels? The answer to this question leads to one other important advantage in changing the actin twist state from 13/6 to 36/17. There are 36 monomers in the crystallographic repeat of twisted F-actin in the 36/17 configuration. Thirty-six is divisible by 6, whereas 13, the number of monomers in the native crystallographic repeat of F-actin, is not. In the limit of 6-fold coordination of 36/17 F-actin rods into a columnar arrangement, it can be shown that all of the interstitial channels can be optimized simultaneously, because all channels within a periodic unit cell can be optimized (only one of the two possible channel types are shown in Fig. 4), whereas the same is not true for 13/6 F-actin.

The torsional modulus of F-actin has been measured, and the energetic cost of twisting the filament by 3.8° is relatively small (E_twist = ½κ Δθ²d^–1 = 1.6 kT, κ ≈ 8 × 10^–26 Nm²) (19). By using the measured value for the torsional modulus and the equipartition theorem, the rms twist of F-actin at room temperature just from thermal fluctuations is ≈3°.

The possibility of coupling between the CDWs in neighboring tunnels deserves comment. There is not sufficient dynamic range in the diffraction signal to detect inter-CDW coupling, by discriminating between true long-range order (LRO), which is expected if the CDWs in different channels are coupled, and quasi-LRO (QLRO), which is expected from a 1D system (20). In fact, the peaks are expected to be sharp for both LRO and QLRO, and the differences are detected usually in the asymptotic behavior of the correlation peaks (ref. 21 and references therein).

Conclusions

We have experimentally examined the mechanism for like-charge attraction in cytoskeletal F-actin and found evidence for counterion correlations. The microscopic mechanism involves a coupled mode between a counterion CDW and the polyelectrolyte twist. (The counterion CDW cannot exist without the polyelectrolyte twist and vice versa.) Because most polyelectrolytes are more flexible than F-actin, variations of these coupled cooperative distortions that facilitate counterion ordering and like-charge attraction are likely to occur in a wide range of polyelectrolyte systems. This molecular mechanism is analogous to the formation of polarons in ionic solids, in which an electron drags a “cloud” of longitudinal optic phonons and acquires a large effective mass (22, 23). In the present polyelectrolyte system, fluctuating counterions drag along soft helical distortions of the polyelectrolyte, and consequently freeze into a static correlation, thus providing a transition between the extreme viewpoints of dynamic and static counterion correlations. The effect is analogous to superconductivity, in which a lattice distortion mediates an attraction between two like-charged particles; in the polyelectrolyte system, charged particles mediate an attraction between two like-charged distorted lattices. In a broader context, similar collective compromises between F-actin twist and crosslinking of F-actin by actin binding proteins may influence the hierarchy of existing interactions (24) and have important thermodynamic consequences for cytoskeletal regulation. Another general issue is the role of ion multivalence in like-charge attraction, because different polyelectrolytes require ions of different valences to condense. An experimentally motivated criterion for the degree of ion multivalence required for generating attractions has been recently proposed (25), and a systematic study of collective counterion dynamics for different ion valences is under way.