Shape bistability of a membrane neck: A toggle switch to control vesicle content release

Abstract

Shape dynamics and permeability of a membrane neck connecting a vesicle and plasma membrane are considered. The neck is modeled by a lipid membrane tubule extended between two parallel axisymmetric rings. Within a range of lengths, defined by system geometry and mechanical properties of the membrane, the tubule has two stable shapes: catenoidal microtubule and cylindrical nanotubule. The permeabilities of these two shapes, measured as ionic conductivity of the tubule interior, differ by up to four orders of magnitude. Near the critical length the transitions between the shapes occur within less than a millisecond. Theoretical estimates show that the shape switching is controlled by a single parameter, the tubule length. Thus the tubule connection can operate as a conductivity microswitch, toggling the release of vesicle content in such cellular processes as “kiss-and-run” exocytosis. In support of this notion, bistable behavior of membrane connections between vesicles and the cell plasma membrane in macrophages is demonstrated.

The interior of a eukaryotic cell is highly compartmentalized. For leak-proof intercompartment exchange, lipid membranes surrounding intracellular organelles undergo structural rearrangements and commonly form membrane tubules. Transient tubule connections form when a membrane vesicle pinches off or fuses to a target membrane (1–3). Recent data suggest that tubule connections may also be quite long-lived structures involved in intracellular transport (4, 5). Material exchange between vesicles connected by membrane tubules occurs in artificial lipid systems (6). The efficiency of this exchange depends on average tubule permeability, which is a function of tubule shape and stability. Although stable configurations and shape transformations of lipid membrane tubules have been studied extensively (7–9), the interrelation between shape dynamics and tubule permeability and the relevance of tubule shape transformations to biological processes remain unknown.

To investigate these phenomena, we studied shape dynamics and permeability of both purely lipidic and cellular membrane tubules. The system, originally developed in classical experiments on soap-film bridges (10, 11), is composed of a tubule formed from a bilayer lipid membrane (BLM) extended between two parallel coaxial end-rings (Fig. 1A) (11, 12). One of the rings was a stationary orifice in a Teflon partition, and the other one was a tip of a patch pipette mounted on a piezo-driven micromanipulator. Moving the pipette along the neck axis changed the tubule length, and changes in tubule shape and permeability were monitored. The tubule permeability was assessed as electrical conductance (i.e., ionic permeability, “conductance” here-after) of the tubule interior between left and right solutions (Fig. 1 A). This BLM system is related to those successfully used to study membrane properties in tether-pulling experiments (13–15). Tethers are usually pulled out by the point force application (holding a small patch of the large membrane and pulling it away from the membrane), mimicking the action of cellular motor proteins (16). As the boundary parameters of cellular membrane necks are unknown, we scanned a wide range of end-ring sizes in our system.

Fig. 1.

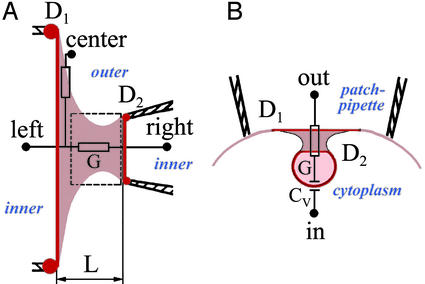
Experimental systems for studies of BLM tubule and cell membrane neck. (A) A BLM tubule (beige) is extended between two end-rings; the left one is the Teflon orifice of diameter D₁, and the right one is the patch pipette with an opening of diameter D₂. D₁ varied from 100 to 200 μm; D₂ varied from 1 to 100 μm. L is the length of the tubule. Lipid reservoirs are shown by red dots. Electrical conductance of the tubule G is measured by using left and right electrodes. The tubule wall conductance (leakage through the wall) is measured by using right and center electrodes. The rectangular outline shows the area from which fluorescent images (Fig. 2B) were taken. (B) A vesicle pinching off from a patch of cell membrane inside the patch pipette. The neck (beige) connects two rings (D₁ and D₂), formed presumably by protein coat on the vesicle and proteins associated with plasma membrane (dark red). Electrical conductance of the neck G and the vesicle capacitance C_v were calculated from changes of electrical admittance measured with in and out electrodes.

To characterize the dynamic behavior of cell membrane tubules, we examined the macrophage cell line IC-21. The permeability of cell membrane necks (also referred to as “fission pores”) has been studied only in a few systems (17–20). One of the most intriguing findings is the pore “flicker,” fluctuations of the pore conductance between high and low level (17, 19–21). IC-21 cells, capable of endocytosis and phagocytosis (22, 23), can form relatively large endocytic granules, close in size to the smallest end-ring in the BLM system. On IC-21 cells, a small (several micrometers in diameter) patch of the plasma membrane of an individual cell was electrically isolated inside a micropipette (Fig. 1B). The fusion and fission of vesicles to and from this membrane patch was monitored as changes in patch electrical admittance, giving the dynamics of the electrical conductance of single connections between a vesicle and plasma membrane of the IC-21 macrophages.

We demonstrate that the BLM tubule has two stable shapes that can be approximated by catenoids and cylinders, the known stationary shapes of cylindrically symmetrical membranes (12, 24–27). We found that the conductance of each stable tubule shape depends on model parameters; the conductance of each of the two tubule shapes can differ by four orders of magnitude. We estimated theoretically the range of parameters where the two shapes coexist, and we confirmed experimentally that within this range the membrane tubule is shape bistable. We demonstrate that the membrane connection between a vesicle and the cell membrane in macrophages exhibits a similar bistable behavior.

Materials and Methods

BLM Tubule Formation and Extension. Solvent-free membranes were formed from diphytanoyl phosphatidylcholine (DPhPC), dinervonoyl phosphatidylcholine (DNPC), or 1:1:2 mixtures of oleoyl phosphatidylcholine (OPC), oleoyl phosphatidylethanolamine (OPE), and cholesterol (Chol) in squalane, as described (28). In some experiments, fluorescent lipid probe (rhodaminedioleoyl phosphatidylethanolamine, Rh-DOPE, 5 mol %) was added. Membrane thickness, as membrane specific electrical capacitance, corresponded to that of a single lipid bilayer (≈4 nm). BLM lateral tension (σ) was set at a fixed value by maintaining excess lipid reservoirs on the end-rings (12, 29), and bilayer bending rigidity was determined by lipid composition.

Membrane tubules were made by patch-clamping a planar phospholipid bilayer membrane formed on a Teflon orifice (30). A fire-polished glass pipette was pressed against the planar BLM and, after the formation of a high-resistance seal, the patch of the membrane within the pipette was ruptured by applying a pulse of negative pressure. Thus a tubule of zero length (a planar membrane ring with outer diameter D₁ and inner diameter D₂) was formed. A membrane tubule was elongated by pulling the pipette away from the planar membrane. The end-rings (the circular attachments of the tubule to the pipette tip and Teflon orifice) formed a coaxial pair. The BLM separated the inner and outer electrolyte solutions (Fig. 1 A). In our experiments, 100 mM KCl solution was routinely used [viscosity μ ≈ 1 centipoise (cP; 1 cP = 10^–3 Pa·s)]; in some experiments, 100 mM KCl was supplemented with sucrose (50% wt/wt; μ = 15.4 cP). The hydrostatic pressure difference between inner and outer solutions was controlled (usually to zero). Membrane tubule length (L) was varied by accurate micromanipulations by using a sensitive calibrated piezo-manipulator (Newport, Irvine, CA; 30-μm travel). Tubule geometry was monitored by fluorescent microscopy. The qualitative behavior of BLM tubules of different lipid compositions was similar. Unless otherwise indicated, the results shown are for DPhPC.

Ionic conductivity through the tubule and across the tubule wall was measured by using the voltage clamp technique (Fig. 1 A). To monitor tubule conductance, currents flowing through the tubule at a given voltage difference applied on the tubule ends (10–20 or 100 mV between left and right electrodes; Fig. 1 A) were recorded. To estimate the leakage through the tubule wall, a voltage difference of 10–50 mV was applied between the right and center electrodes and the current evoked was measured (Fig. 1 A) by using patch-clamp amplifiers (EPC-7, List Electronics, Darmstadt, Germany). Data were digitized online by using L-Card ADC (L-305, L-Card, Moscow).

On-Cell Measurements of Exo- and Endocytic Events. Mouse peritoneal macrophages (line IC-21) were cultured by using standard procedures recommended by the American Type Culture Collection. The electrical admittance of a small patch of the IC-21 plasma membrane was measured as described (31). Briefly, a single cell was patch-clamped by using 1–3 MΩ Sylgard-coated (SYLG184) glass pipettes filled with PBS. After the formation of a tight contact between the pipette and the cell membrane (Fig. 1B), a 5-kHz 60-mV peak-to-peak amplitude sine-wave potential was superimposed with a 20-mV holding potential. The resulting current flowing through the membrane patch was integrated by using either software [browse software (32) on PC-44 ADC (Digital Instruments, Santa Barbara, CA); 0.3-fF background noise] or a hardware-based lock-in amplifier (NF Instruments, Yokohama, Japan; 0.1-fF background noise). The imaginary (Im) and real (Re) parts of the patch integral admittance were obtained online. The capacitance changes (ΔC) and membrane neck conductance (G) were calculated offline according to formulae: ΔC = (ΔRe² + ΔIm²)/(ΔIm·2πf) and G = (ΔRe² + ΔIm²)/ΔRe (where f is the sine wave frequency) (3, 24). Vesicle diameters, estimated by capacitance changes, varied from 150 to 425 nm. The fusion/fission events were selected as described (31, 33).

Results

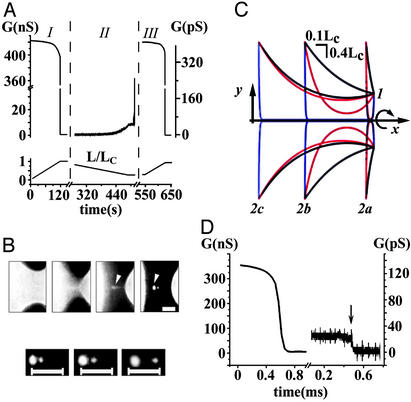
Shape Transformations of a BLM Tubule. Experiments on the BLM began from the formation of a tubule at L = 0 (see Materials and Methods). When L was gradually increased, tubule conductance started to decline slowly (Fig. 2A, I). Fluorescent microscopy demonstrated that with each elongation step, the tubule relaxed to a catenoidal shape (the first image in Fig. 2B Upper) with a progressively thinner waist (11, 12). Fig. 2C shows the calculated contours of this shape at different L (black curves). At some length (close to a critical length L_c, see Appendix), a spontaneous change of the tubule shape occurred: the waist of the tubule dramatically narrowed and the tubule seemed to vanish (Fig. 2B Upper). Concurrently, the tubule conductance decreased abruptly by more than four orders of magnitude (Fig. 2D). The system appeared as two separate membranes on the end-rings; several satellite lipid vesicles were often seen near the tubule axis (34) (Fig. 2B Upper, arrowheads). Phenomenologically, this process strongly resembles the collapse of a soap-film bridge (10, 11, 34). However, in contrast to a soap-film bridge, connections between lipid membranes on the end-rings were preserved, as the satellite lipid vesicles followed the motion of the supporting end-rings (Fig. 2B Lower). Additionally, electrical recordings revealed a significant residual conductance after the tubule shape change (Fig. 2D). Without external perturbation, this conductance was constant for tens of minutes, suggesting formation of a stable structure rather than the viscous retardation of waist narrowing. We call this structure narrow tubule (NT) to distinguish it from the original wide tubule (WT). Fig. 2C shows the calculated contours of NT at different L (blue curves). NT could be ruptured by a sufficient mechanical disturbance; the NT breakdown was detected as an abrupt drop in conductance (Fig. 2D, arrow) and a disappearance of the satellite vesicles (data not shown).

Fig. 2.

Shape transformations of a lipid membrane tubule. (A) The tubule conductance as a function of L. D₁/D₂ ≈ 50, D₂ ≈ 2 μm, μ = 1 cP. The left G-axis corresponds to I and III and the right G-axis corresponds to II. (B) Fluorescent microscopy of the tubule; D₁/D₂ ≈ 3.2, D₂ ≈ 60 μm, μ = 15.4 cP. (Upper) An example of the tubule shape transition. The first image corresponds to the catenoidal tubule at L ≈ L_c, and the next frames were taken at +30, +60, and +90 ms. To visualize the membranes on the end-rings after the tubule shape transformation, a small positive pressure between the tubule exterior and interior was applied; this pressure did not significantly alter the catenoidal shape. (Lower) The satellite vesicles (arrowheads in Upper) move with the increase of the length between the end-rings. (Bars, 20 μm.) (C) The calculated contours of WT (black curves), NT (blue curves), and unstable catenoid (red curves; see Appendix); 1 designates the right end-ring, and 2a, 2b, and 2c designate the left end-ring at different L (1.1l_c, 0.6L_c, and 0.9L_c, respectively). The 3D shapes are constructed by rotation of the contours around the x-axis as shown by the arrow. End-rings with similar diameters were chosen for clarity (D₁/D₂ = 1/3, d = 0.1D₁). (D) The drop of the tubule conductance (G)at constant L ≈ L_c, tubule parameters as in A; the break in time axis is for ≈76 s. The arrow indicates the tubule rupture by a mechanical disturbance.

Decreasing the distance between end-rings led to a backward transformation of the tubule. The conductance of the NT grew slowly (Fig. 2 A, II). At a certain tubule length (near l_c, see Appendix) the conductance jumped up, again by almost four orders of magnitude, to the value characteristic of WT (Fig. 2 A, III). It was possible to switch from WT to NT and back to WT several times (Fig. 2 A).

Our analysis indicates that shape transformations occur when WT (at L_c) or NT (at l_c) approaches the unstable catenoidal shape (red curves in Fig. 2C). Near each critical length an ambient disturbance triggers the instability and the tubule changes its shape along the pathway, thus lowering tubule energy (see Appendix). If L is bigger than L_c, only NT exists; equally, for L smaller than l_c, only WT remains. Thus we described a hysteretic cycle of tubule transformations within the tubule length excursions between L_c and l_c. Within this length range the BLM tubule is shape bistable.

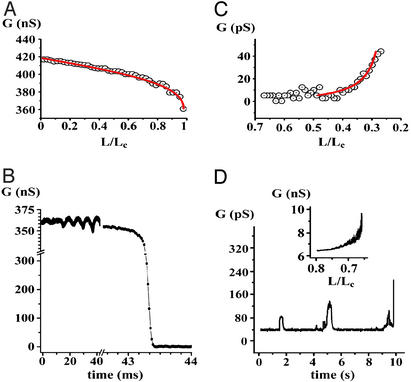
The Conductance of WT and NT in Stationary Regime and at Critical Points. The catenoidal shape of the WT was confirmed by fitting the measured tubule conductance to that calculated for an appropriate catenoid (Fig. 3A). Before L_c (see Appendix) was reached, elongation-induced changes of the WT shape and conductance were reversible; i.e., upon returning one step back, the tubule shape and conductance were restored. Near L_c (within ≈5%), the WT conductance decreased either abruptly (Fig. 2D) or after a period of oscillations (“ringing”; Fig. 3B). The oscillations were always observed in experiments with OPC/OPE/Chol membrane, and only rarely (in 8% of the trials) with other lipid compositions. For the typical tubule geometry used in our experiments (D₁/D₂ ≈ 50, D₂ ≈ 2 μm), the final conductance decline occurred within less than a millisecond in a 1-cP solution [15.4-cP solution was used to slow down the process for fluorescent microscopy visualization (Fig. 2B)]. The characteristic time of the WT-to-NT transition, normalized to the initial conductance of the tubule, was 2.2 ± 0.2 μs/nS (mean ± SD, 18 trials, DPhPC tubule).

Fig. 3.

The behavior of the tubule conductance during the full cycle of the shape transformations; D₁/D₂ ≈ 50, D₂ ≈ 1 μm. (A) The decrease in conductance measured during the WT elongation (as in I in Fig. 2 A). Initial conductance corresponds to the patch-pipette resistance (see Fig. 2 A). Circles indicate averaged experimental data, and the red line shows the calculated conductance of the catenoid. The fitting procedure allowed us to determine L_c with ≈5% precision. (B) The conductance decrease during the WT-to-NT transformation at fixed L ≈ L_c; conductance “ringing” oscillations are seen. (C) The NT conductance growth during the decrease of L (as in II in Fig. 2 A). Circles indicate averaged experimental data, and the red line shows the hyperbolic fit to the data. (D) Small conductance fluctuations preceding the NT-to-WT transformation and the final increase of the conductance (as in II in Fig. 2 A). (Inset) The behavior of the NT conductance during the decrease of L, OPC/OPE/Chol membrane tubule.

After the WT conductance drop corresponding the WT-to-NT transformation, residual conductance was detected either at L_c (Fig. 2D) or at L < L_c (Figs. 2 A and 3C). In total, the WT-to-NT transformation was observed 93 times, and the WT membrane broke during the tubule narrowing 32 times (Table 1). The occurrence of NT formation depended on lipid composition (Table 1). The NT conductance depended inversely on L, as if the end-rings were connected by a cylinder with a fixed diameter (Fig. 3C). This is consistent with the NT structure predicted theoretically (see Appendix). The slow stepwise decrease of NT length down to a fraction of L_c led to the transformation of NT back to WT (Figs. 2 A and 3D). This event occurred spontaneously in 72 of 93 trials. In 21 trials, the complete reopening of the tubule was achieved by the application of a small positive hydrostatic pressure difference across the NT wall (Table 1). The NT length at which the transformation occurred varied from 0.05 to 0.3 of L_c for DPhPC and DNPC membranes, and was as high as 0.6L_c in the case of the OPC/OPE/Chol membranes. This length was frequently greater than the second critical length l_c, estimated theoretically (see Appendix); thus l_c defines only the lower limit of the NT length. The NT conductance at this length varied significantly (tens of picosiemens for the DPhPC and the DNPC membranes, and several nanosiemens for OPC/OPE/Chol membranes; compare Fig. 3C and Fig. 3D Inset). Fluctuations of the NT conductance usually preceded the final NT opening (Fig. 3D). No change in the tubule wall conductivity (i.e., no leakage through the tubule wall) was detected during the shape transformations (data not shown).

Table 1. Occurrence of WT-to-NT and NT-to-WT transformations.

Lipid	No. of experiments	NT formations	NT-to-WT transitions
DPhPC	54	40	36 (17*)
DNPC	64	38	36 (4*)
OPC/OPE/Chol	15	15	15 (0*)

^*With pressure application.

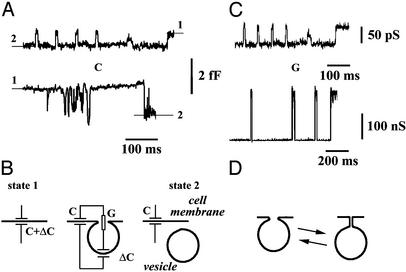
The Conductance of a Cell Membrane Tubule. The conductance of individual membrane connections that emerge during membrane vesicle detachment or fusion (18–20, 31, 33, 35) was monitored by using on-cell admittance measurement technique (35). On-cell recordings of the admittance of a small patch of IC-21 plasma membrane revealed stepwise changes of capacitance reflecting fusion (Fig. 4A Upper) or pinching-off (Fig. 4A Lower) of small membrane vesicles (Fig. 4B). Fig. 4A shows that in IC-21 cells, both upward and downward capacitance changes were often reversible; i.e., the capacitance “flickered” (17, 19–21, 33). The occurrence of such oscillations was ≈15% of all detected fusion/fission events (50 of 346 total). The characteristic time between adjacent capacitance jumps (Fig. 4A) was much smaller than the mean time between two irreversible events (fusion or fission). The amplitudes of the jumps in a sequence were very close (Fig. 4A), hence the oscillations correspond to reversible fusion or fission of a single vesicle rather than to a consecutive fusion and fission of two different vesicles (31). The changes of the vesicle neck conductance G corresponding to the capacitance flicker are shown in Fig. 4C Upper. The conductance switches between two fixed levels, similar to the switching of the BLM tubule conductance upon its length variation (Fig. 2 A). Moreover, in five trials, OPC/OPE/Chol membranes demonstrated spontaneous oscillations of the tubule conductance at L near L_c. Fig. 4C Lower shows an example of such oscillations of the lipid tubule conductance. Properly scaled, the lipid tubule oscillations mimic the conductance fluctuations of the cell vesicle neck (compare Upper and Lower in Fig. 4C). Fig. 4D illustrates the changes of the neck shape that presumably account for the observed oscillations of the neck conductance.

Fig. 4.

Bistability of the membrane neck connecting a vesicle to cell plasma membrane: on-cell admittance measurements (31) on cultured macrophages IC-21. (A) An example of the capacitance change (ΔC) from level 2 to level 1 during fusion (Upper) or from level 1 to level 2 during fission (Lower) of vesicles to/from a small patch of IC-21 cell membrane; reversible changes of the capacitance (capacitance flicker) are seen in both traces. (B) The cartoon shows the changes of the equivalent electrical circuit of the patch during pinching off (from state 1 to state 2 in A) or fusion (from state 2 to state 1 in A) of a vesicle to a cell membrane (see also Fig. 1B). (C) The oscillations of the membrane neck conductance (Upper) during the capacitance flicker. Lower shows the oscillations of the BLM tubule conductance during the WT-to-NT transitions. The BLM was formed from the OPC/OPE/Chol mixture. (D) The cartoon illustrates the reversible changes of the neck shape that can account for the conductance oscillations.

Discussion

Surface Tension and Shape Bistability. The shape of a liquid tubule neck, such as a liquid bridge, soap film, or BLM tubule, is controlled by interfacial forces. Often, surface tension is a single dominating force-factor (10, 11, 36). This force, minimizing interfacial area, causes necking instability: two droplets connected by a small neck either coalesce or split apart (36), and soap-film necks collapse at L_c (10, 11). Other force factors, such as the interfacial bending moment, can stabilize necks. Lipid membranes in water can form fairly complex equilibrium structures in which stable tubular necks connect membrane compartments (6, 8, 9, 37). Usually, neck formation is directed purely by minimization of membrane-bending energy (27, 37, 38). The scenario in which tension and bending moments compete for control over neck stability and geometrical parameters has attracted less attention. Cylindrical tethers, the diameters of which are established by the balance between the two forces, are the most widely studied of different experimental systems (6, 9, 13–16). It has been suggested that other examples of equilibrium shape would include other members of the Delaunay shape family (26). Tension variations can direct tubule shape transformations. Application of tension to a relaxed tubule triggers peristaltic instability: the tubule transforms into a chain of interconnected “pearls” (39). The tubule restores its shape when the tension decreases. We extended these results further, showing that a lipid membrane tubule under tension can have several stationary shapes under simple two-ring boundary conditions. Our model is unlikely to describe the whole set of stationary shapes connecting the rings. Moreover, many factors, such as the exact type of the boundary conditions imposed on the end-rings (29, 40, 41) or membrane asymmetry [e.g., introduction of spontaneous curvature (41)], can affect the tubule behavior. Nevertheless, our data demonstrate that if tension is applied, the membrane neck can be shape bistable.

Bistability of Cell Membrane Tubules. In cells, mixing and separation of compartment content requires breaking or forming a connection between compartments. Our data suggest the existence of a mechanism ensuring transient opening of the neck: the vesicle neck permeability can be toggled by neck shape transformations (Fig. 4D). This mechanism may operate during “kiss-and-run” exocytosis (42, 43). Specifically, large increases of the permeability quickly achieved by shape toggling can account for substantial release of content during transient pore openings (44), in accord with structural evidence of neck dilation reversibility (45). The shape transformations of a neck, according to our scheme, are based on the interplay between lateral tension and bending rigidity. There are many indications that cellular membrane necks could be transiently under tension (41, 46, 47). Factors controlling this tension and the geometry of cellular necks remain to be studied. We suggest that the two-ring model reflects geometrical restrictions imposed by a vesicle protein coat and cytoskeleton (see Fig. 1B and ref. 41), whereas neck tension can be set by protein–lipid interactions (48). Our study indicates that the breakdown of the membrane connection would need an additional strong perturbation to break the nanotubule (Fig. 2D, arrow), perhaps the dedicated function of cell “pinchase” proteins (41, 49).

Our measurements of the cell membrane neck conductance reveal stepwise repetitive changes of the conductance, similar to those obtained on the BLM tubule. In retrospect, we found a qualitatively similar behavior in the conductance between fusing or fissioning compartments in data on various cell systems (17, 19–21, 33). Overall, the seemingly common ability of a cell membrane connection to switch between two states with high and low permeability substantiates the hypothesis of shape bistability of cellular necks.

In conclusion, mechanical factors governing the distance between two compartments, such as action of cytoskeletal proteins (50), may regulate the conductivity of a membrane tubule connecting the compartment. The operation of such a conductivity switch is based on the interplay between membrane lateral tension and bending rigidity. The tubule-based conductivity switch satisfies the important physiological criterion: preservation of the compartmentalization of the cell interior, as the tubule wall remains nonleaky during the shape transformations. Formation of a bilayer lipid tubule and its functionalization by proteins can be the key processes determining the dynamics of cellular membrane networks.

Appendix

Tubule Shape Bistability. Tubule stationary shapes were found by minimizing the Gibbs free energy functional E = ∫(σ + 2k(H)²)dA (24), where A is surface area, k is the bilayer bending modulus, and H is the mean curvature of the tubule surface. The model assumes that (i) the tubule connects two rings with fixed diameters D₁ and D₂; (ii) zero mean curvature (24) boundary conditions are imposed on the rings; and (iii) the hydrostatic pressure difference across the tubule membrane is zero. Instead of explicitly solving the variational equation δE = 0, we assumed that the WT and NT shapes could be approximated by a combination of catenoids and cylinders (29, 40).

Catenoid, the minimal surface of revolution (Fig. 2C, black and red contours), is an established stationary shape for soap-film bridges (11, 34) and, in certain cases, for tubule lipid membranes (27, 29). Catenoid is generated by revolution of a catenary: y_c(x) = a·cosh((x – x₀)/a) (Fig. 2C); two parameters, a (the radius of the catenoid waist) and x₀, completely determine the shape of the catenoid. The catenary satisfies the variational equation under our boundary conditions (δE(y_c(x)) ≡ 0). The parameters a and x₀ of a catenoid connecting two end-rings of diameters D₁ and D₂ were calculated numerically for each distance L between the end-rings by using the system of equations:

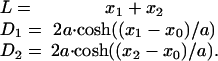[1]

It is known that this system has two solutions if L is less than the critical length L_c determined as L_c(D₁, D₂) = max(L(D₁, D₂, a), a varied from 0 to D_sm/2); where D_sm is the smaller diameter and L(D₁, D₂, a) = a·arccosh(D₂/2a) + arccosh(D₁/2a)). These two catenoidal solutions differ by the waist radius a; when bending rigidity is negligible (as in soap films), the catenoid with wider waist (Fig. 2C, black contour) is stable, and the one with narrower waist (Fig. 2C, red contour) is unstable (11, 12). If bending factor cannot be neglected, the wider catenoid remains stable, as any small deformation will increase both its surface and H. The narrow catenoid can still be destabilized by a small variation of a (not shown). Thus the WT shape is the wide stable catenoid. Eq. 1 shows that the shape parameters and hence the conductance of WT are completely determined by the end-ring diameters, D₁ and D₂, and by the catenoid length L.

The NT structure can be approximated by two catenoidal “wings” connected by a narrow cylindrical nanotubule, also termed the tether (Figs. 2C, blue contour, and 5A) (9, 13–15). The diameter d of a stable tether is determined by a balance between the membrane lateral tension and bending rigidity: d = 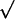2k/σ (9, 15, 24, 26); if k = 25 k_BT and σ = 1 dyn/cm, d is ≈10 nm. Catenoidal wing is a catenoid smoothly (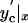 = 0 at the point of connection with the cylinder) connecting an end-ring having the diameter D₁ or D₂ and a cylinder having the diameter d. These boundary conditions uniquely determine (independently on L) the lengths l₁ and l₂ of the catenoidal wings (Fig. 5A). The wing lengths remain constant and only l_cyl changes when the tubule length L is varied. Each of three parts of the NT shape satisfies (independently) variational equation (δE = 0), if at the connection points (x_c) the following conditions are imposed: (i) d = 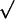2k/σ; and (ii) 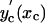= 0. Density of surface energy E_d = σ + 2k(H)² is constant (as the chemical potential is assumed to be constant over the tubule surface), thus σ depends on H (51): in the cylindrical region of NT, σ is half as large as in the wings. Note that this is the condition for lateral force balance at the catenoid–cylinder junction (51). In this simplified description of NT, we neglect the catenoid–cylinder transition zone (14, 29, 40). However, by using surface evolver software (52), we found that at L slightly greater than L_c, the tubule converges to a stationary shape reasonably close to the catenoid–cylinder model (results not shown; see also refs. 29 and 40). If l_cyl ≫ l₁, l₂, the NT conductance primarily depends on d and L, and thus, in distinction from the WT conductance, depends on material parameters of the BLM.

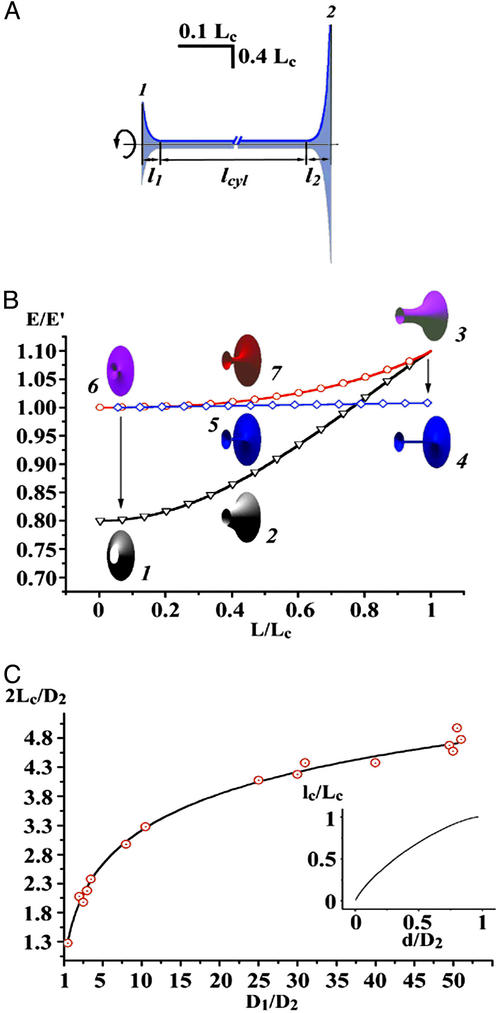
Fig. 5.

Theoretical calculations of the tubule shape and energy (D₁/D₂ = 1/3, d = 0.1D₁). (A) The contours of NT (blue) connecting the end-rings 1 and 2 separated by L = 0.6L_c; two catenoidal “wings” (l₁ and l₂) and the cylindrical tether (l_cyl) are seen. (B) Energy (E) of WT (black curve, triangles), NT (blue curve, diamonds), and unstable catenoid (red curve, circles). The energy is normalized to the total energy of two circular planar bilayer membranes covering end-rings (E′). Calculated 3D images of WT (shapes 1, 2, and 3), NT (shapes 4, 5, and 6), and unstable catenoid (shapes 6, 7, and 3) are shown for l_c, 0.4L_c and L_c. Note that WT at L_c is an unstable catenoid (shape 3); NT at l_c is also an unstable catenoid (shape 6). Arrows indicate transitions between WT and NT. (C) The dependence of L_c on the end-ring diameters (D₁ and D₂); circles, experiment; line, theory. (Inset) The dependence of the l_c on d for D₁/D₂ = 50.

After the shape parameters of the tubule had been found, the energy (E) and conductance of the tubule were calculated. Fig. 5B illustrates the calculated dependence of tubule shapes and energies on tubule lengths in the range from 0 to L_c. Elongation of WT leads to an increase of the energy (black curve in Fig. 5B) and thinning of the waist (see also Fig. 2C). In contrast, elongation of the NT causes the increase of the tether length (see also Fig. 2C), but does not alter either the tether diameter or the lengths of the catenoidal wings; the NT energy (blue curve in Fig. 5B) increases only slightly. Arrows on Fig. 5B indicate the WT-to-NT and NT-to-WT transitions. These transitions are energetically favorable: the tubule moves along the pathway lowering tubule energy (Fig. 5B).

The shape transitions occur when WT or NT gets close to the unstable catenoid (red curves in Figs. 2C and 5B). WT reaches the unstable shape at the catenoidal critical length (Figs. 2C and 5B). Thus, the WT critical length L_c is the catenoidal critical length (12, 13). NT reaches the unstable shape when the tether length approaches zero (Figs. 2C and 5B). Hence, l_c is approximately a sum of the lengths of two catenoidal wings. The critical lengths mark the boundaries of the shape bistability region. In the frameworks of our description L_c and l_c are completely determined by three parameters of the tubule: D₁, D₂, and d. As shown in Fig. 5C, L_c is a function of D₁ and D₂ only, whereas l_c depends also on d, a parameter dependent on the membrane lateral tension and material properties (9, 13, 15). Notably, as L_c and l_c scale with ring diameters (Fig. 5C), the tubule shape transformations can be induced not only by changing L but also by changing any ring diameter at fixed tubule length.

Interestingly, the l_c, estimated for a tubule made from the OPC/OPE/Chol mixture, was close to the L_c (Fig. 5C Inset). In this situation, the instability zones might overlay, resulting in oscillations between the NT and WT shapes (as in Fig. 4C). As NT and WT approximations work only if d is considerably smaller than D₂ (and thus l_c is smaller than L_c; Fig. 5C), the modeling of these oscillations requires further study of the tubule shape behavior at arbitrary d/D₂.