The speed of the flagellar rotary motor of Escherichia coli varies linearly with protonmotive force

Abstract

A protonmotive force (pmf) across the cell's inner membrane powers the flagellar rotary motor of Escherichia coli. Speed is known to be proportional to pmf when viscous loads are heavy. Here we show that speed also is proportional to pmf when viscous loads are light. Two motors on the same bacterium were monitored as the cell was slowly deenergized. The first motor rotated the entire cell body (a heavy load), while the second motor rotated a small latex bead (a light load). The first motor rotated slowly and provided a measure of the cell's pmf. The second motor rotated rapidly and was compared with the first, to give the speed–pmf relation for light loads. Experiments were done at 24.0°C and 16.2°C, with initial speeds indicating operation well into the high-speed, low-torque regime. Speed was found to be proportional to pmf over the entire (accessible) dynamic range (0–270 Hz). If the passage of a fixed number of protons carries the motor through each revolution, i.e., if the motor is tightly coupled, a linear speed–pmf relation is expected close to stall, where the work done against the viscous load matches the energy dissipated in proton flow. A linear relation is expected at high speeds if proton translocation is rate-limiting and involves multiple steps, a model that also applies to simple proton channels. The present work shows that a linear relation is true more generally, providing an additional constraint on possible motor mechanisms.

The flagellar rotary motor of an Escherichia coli bacterium couples proton flux across the inner cell membrane to motor rotation. Protons move down an electrochemical gradient through specific MotA/B protein complexes anchored to the cell wall. As a result, these complexes, known as torque-generating units, step along the rotor, causing it to rotate. At heavy viscous loads and low speeds, motor torque is approximately constant (and efficiencies are high), whereas at light viscous loads and high speeds, motor torque declines rapidly (and efficiencies become small). For a review of motor structure and function, see ref. 1. Fung and Berg (2) found that when the motor operates in the low-speed regime near stall (<10 Hz), its speed is proportional to the voltage applied across the inner cell membrane. The experiments reported here extend these measurements well into the motor's high-speed regime. In this regime, the speed–protonmotive force (pmf) relation will depend explicitly on the mechanochemical cycle of the motor; therefore, its characterization puts new restrictions on possible motor mechanisms.

Methods

Cells of E. coli strain KAF95, a strain with sticky filaments that rotate exclusively counterclockwise (3), were inoculated from frozen stocks, grown in Luria broth [1% tryptone (Difco)/0.5% yeast extract (Difco)/0.5% NaCl] at 30°C until mid-exponential phase, and then sheared by using syringes with 26-gauge needles connected by 0.58-mm i.d. polyethylene tubing, producing cells with short flagellar stubs. These cells were tethered by allowing the culture to settle onto an ethanol-rinsed glass coverslip within a flow cell (4). Temperature was controlled to within ±0.1°C by a Peltier system similar to that described previously (5) and checked with a small thermocouple. After ≈20 min, growth medium and loose cells were flushed from the system with motility medium [10 mM potassium phosphate/0.1 mM EDTA/1 mM l-methionine/0.05% (vol/vol) lactic acid, pH 7.0]. Latex beads (0.4-μm diameter, ≈0.5% solids in motility medium; Bangs Laboratories, Fishers, IN) then were introduced and allowed to settle onto the tethered cells for 5–10 min before being flushed out. Usually, each preparation contained a few candidate cells, with one flagellum tethered to the coverslip and another to a latex bead. Cells with irregular body rotation, presumably due to intermittent sticking between the cell body and glass coverslip, were easily identified by eye and excluded. It was more difficult to avoid poorly rotating beads, because their high rates of rotation did not allow for immediate identification of intermittent sticking. Such beads showed wildly varying and inconsistent responses to changes in pmf. The addition of small amounts of neutral detergents reduced the occurrence of such events, and cleaning the flow cell with ethanol between experiments eliminated the problem. Suitable cells were imaged onto a pinhole in front of a photomultiplier tube with a ×40 phase-contrast objective (6), and the output was band-pass filtered, recorded, and analyzed by using labview (National Instruments, Austin, TX). Sodium azide (175–250 μM) or carbonylcyanide m-chlorophenylhydrazone (CCCP, 5–7.5 μM) was introduced for 30–60 s. After a delay of 1–2 min, the cells gradually slowed down, stopping 5–10 min later. Power spectra were computed for successive 5-s intervals. The low-frequency peak was large, so it could be found automatically by identifying the point of maximum power over the full spectrum. The high-frequency peak was smaller, but it could be found automatically by identifying the point of maximum power above a threshold set at a frequency ≈20–50 Hz below the high-frequency peak. Sometimes, noise peaks of lower frequency were picked instead, generating points that clustered near the threshold. These were edited out by hand.

Results

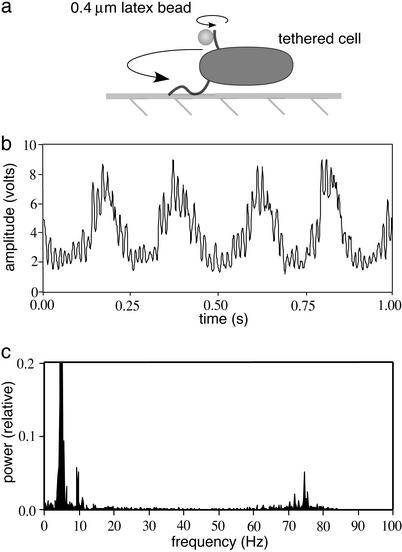
The motor's speed–pmf relation was measured by comparing two motors on the same bacterium, one operating at low speed and the other at high speed. One flagellar filament was tethered to a glass coverslip and the other was tethered to a 0.4-μm-diameter latex bead, as shown in Fig. 1a. The motor driving the first filament rotates the entire cell body and thus operates under heavy load. The motor driving the second filament rotates the bead and thus operates under light load. The rotation rates of both motors were monitored simultaneously by aligning the phase-contrast image of the rotating cell with a pinhole in front of a photomultiplier tube (6), giving signals of the sort shown in Fig. 1b. Power-spectral analysis of these signals gave peaks corresponding to both rates (Fig. 1c).

Fig. 1.

(a) Flagella of a single bacterium were tethered to a glass coverslip and to a small, 0.4-μm-diameter latex bead, respectively. One flagellum rotated slowly because of the large viscous load of the entire bacterium. The other rotated rapidly because of the small viscous load of the latex bead. (b) The rotation speeds of both flagella were monitored simultaneously by aligning the image with a pinhole in front of a photomultiplier tube. As the bead and cell rotated past the pinhole, they generated a signal that contained both the low- and high-frequency components of the compound movement. (c) The power spectrum of this signal taken from a 5-s window revealed the two rotation rates (≈5 and ≈75 Hz, respectively). The rotation axis of the tether for the body of this cell was off center, so that whereas the long end of the cell spanned the full width of the pinhole, the short end did not. This asymmetry generated a low-amplitude peak at twice the rotation frequency (at ≈10 Hz), which was ignored. The power at ≈5 Hz is off scale on the plot shown here.

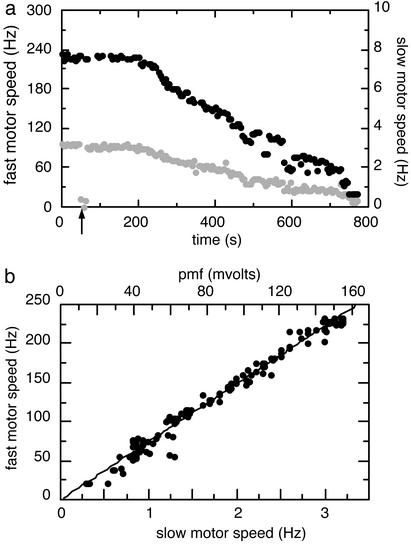
Each cell was monitored over the course of 5–15 min, with results of the sort shown in Fig. 2a. The initial rotation rates of the two motors of the fully energized cell were measured for ≈40 s, and then sodium azide (a respiratory poison) or carbonylcyanide m-chlorophenylhydrazone (CCCP, an uncoupler) was added to the surrounding medium (Fig. 2a, arrow). After a delay, the cell gradually ran out of energy, and both motors slowed down. The rotation speeds of the fast and slow motors of Fig. 2a are plotted against one another in Fig. 2b. This plot shows that the fast motor speed is proportional to the slow motor speed. Because both motors run off the same pmf, this relationship is insensitive to short-term variations in pmf, and because the rotation speed of the slow motor is known to be proportional to pmf (2), the slow motor speed (lower x axis) can be rescaled to show the pmf of the cell (upper x axis), thus generating the speed–pmf plot for the fast motor. Here we assume that the fully energized cell has a pmf of ≈150 mV (7).

Fig. 2.

(a) Data for two motors on the same bacterium at 24.0°C are shown. The fully energized bacterium was monitored for ≈40 s, and then sodium azide (187 μM) was added (arrow). The cell gradually deenergized. Black points represent the speed of the latex bead (scale on the left), and gray points represent the speed of the cell body (scale on the right). (b) The data from a are plotted with fast motor speed vs. slow motor speed. Because the slow motor speed (lower x axis) is proportional to pmf, it can be rescaled to give the pmf of the cell (upper x axis). The regression line was constrained to pass through the origin.

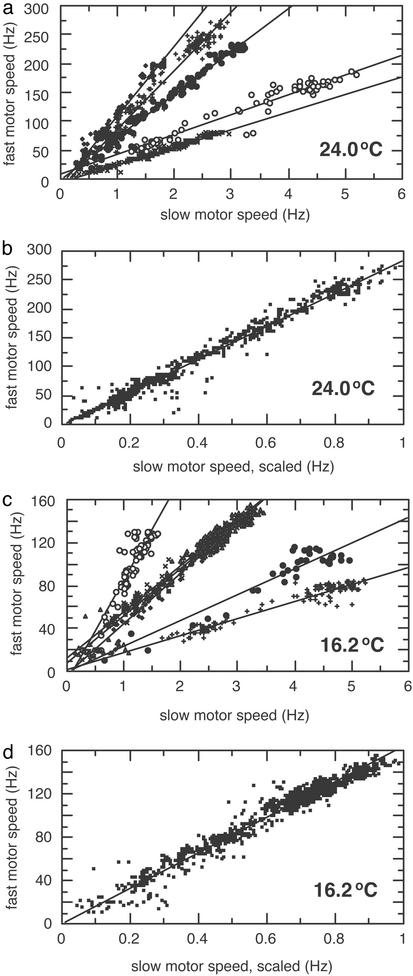
Data were collected from a number of cells over a wide range of speeds and at two different temperatures, as shown in Fig. 3. Raw data for individual cells are plotted in Fig. 3 a and c, and cumulative displays are shown in Fig. 3 b and d. The regression lines for individual cells all pass close to the origin. The cumulative displays were constructed from data from individual cells by rescaling the slow-speed axes (effectively scaling the frictional drag coefficient of the cell body) to match slopes. The fast-speed axes were not rescaled, so they still reflect the actual speeds of the latex beads. These plots are accurately fit with regression lines constrained to pass through the origin, thus demonstrating the proportionality between the rotation rates of the paired motors at all speeds.

Fig. 3.

(a) Data from five bacteria at 24.0°C were plotted on the same graph and marked with different symbols (with the data for the cell of Fig. 2 shown as filled circles). The regression lines were not constrained. The initial speeds of the cell bodies were 2.7, 4.7, 1.8, 3.1, and 2.8 Hz, and the initial speeds of the beads were 80, 175, 201, 233, and 271 Hz, respectively. (b) Data from the bacteria in a were plotted cumulatively by scaling the slow-speed axis to match slopes; see the text. The regression line was constrained to pass through the origin. (c) Data from six bacteria at 16.2°C were plotted on the same graph and marked with different symbols. The regression lines were not constrained. The initial speeds of the cell bodies were 5.0, 4.6, 2.6, 1.5, 2.8, and 3.2 Hz, and the initial speeds of the beads were 83, 110, 121, 130, 136, and 151 Hz, respectively. (d) Data from the bacteria in c were plotted cumulatively by scaling the slow-speed axis to match slopes. The regression line was constrained to pass through the origin.

The torque generated by the motor falls gradually from a maximum at stall to ≈90% of that value at a transition region called the “knee,” and then it falls more rapidly, reaching zero at the “zero-torque speed.” With a fully energized motor at 24.0°C, the knee and the zero-torque speed occur at ≈180 and ≈380 Hz, respectively, whereas at 16.2°C, the knee and the zero-torque speed occur at ≈80 and ≈180 Hz, respectively (3). Therefore, from the maximum fast motor speeds indicated in Fig. 3 a and c, we can tell whether the load was light enough to put the operating point in the high-speed regime. Because the knee speed is substantially lower at lower temperatures, the high-speed regime was easier to reach at 16.2°C than at 24.0°C. At 24.0°C, the initial speeds ranged from 80 to 270 Hz, from well below to well above the knee, whereas at 16.2°C they ranged from 80 to 150 Hz, mostly above the knee. In all cases, the rotation rates of the two motors on each cell were proportional to one another, thus extending the results of Fung and Berg (2) and indicating that the motor's speed is proportional to pmf in both its low- and high-speed regimes.

The reason that we could probe motor response over such a wide range of initial speeds is that the frictional drag coefficients for beads attached to flagellar stubs vary appreciably with stub geometry and with bead rotational eccentricity. The frictional drag coefficients for tethered cells vary, in turn, with cell size and tethering geometry. Frictional drag coefficients, f, are proportional to viscosity, η, and to a geometrical factor, for example, for a sphere of radius a rotating about its center, f = 8πηa³. At low Reynolds number, the torque required to spin an inert object at angular velocity ω is proportional to its frictional drag coefficient, N = fω. On a torque–speed plot, this relationship appears as a load line of slope f.

Discussion

In tightly coupled models of the bacterial flagellar motor, the proton flux through MotA/B complexes is strictly proportional to the rate of rotation. At low speeds, near stall, such models operate close to thermodynamic equilibrium, at unit efficiency (8). For each revolution, the work done equals the energy dissipated: 2πN = neΔp, where n is the number of protons per revolution, e is the charge on a proton, and Δp is the pmf. Therefore, the torque is independent of temperature and proportional to pmf, as observed experimentally (2, 5). At high speeds, above the knee in the torque–speed curve, the motor runs far from equilibrium, and its efficiency drops. Our measurements show that, for a given viscous load, the motor's rotation rate remains proportional to the cell's pmf regardless of speed. They do not, however, discern between the electrical and chemical components of the pmf (which are initially about Δψ = –115 mV and –59ΔpH = 35 mV respectively, given an external pH of 7.0 and a cytoplasmic pH of 7.6) (9, 10). Experiments varying the external pH of the cell and, thus, the magnitude of chemical and electrical potentials across the membrane demonstrate a similar minimal effect on motor speed at both high and low loads (11). In both regimes, the motor apparently responds to the entire pmf rather than either component, thus making the pmf dependence the essential measurement. However, this is not the case if the internal pH is lowered substantially (12).

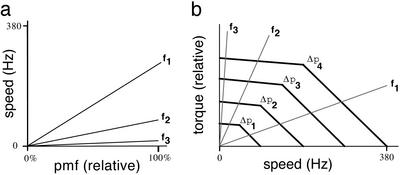
If speed is proportional to pmf along a given load line, then ω = α(f)Δp, where α(f) is a constant that depends on the frictional drag coefficient, f. Because N = fω, we have N = fα(f)Δp. This results in a linear scaling of the torque–speed curve with pmf, as shown in Fig. 4. The motor runs at the speed at which the load line intersects the torque–speed curve, i.e., at a speed at which the torque required to spin the load is balanced by the torque generated by the motor. As pmf decreases, the speeds or torques observed along two load lines remain in proportion to one another. For example, for load lines f₁ and f₃ (Fig. 4), the ratios ω₁/ω₃ = α(f₁)/α(f₃) and N₁/N₃ = f₁α(f₁)/f₃α(f₃) do not depend on Δp. This result is possible only if the torque–speed curve retains its shape as it shifts with pmf. A tightly coupled motor (i.e., with the number of protons per revolution, n, constant) will maintain constant efficiency along any given load line. As noted above, the energy output of such a motor is 2πN per revolution, and the energy input is neΔp. Therefore, for any given load line, efficiency equals energy output divided by energy input, or 2πN/neΔp = 2πfα(f)Δp/neΔp = 2πfα(f)/ne, which is independent of Δp. A tightly coupled motor also has a constant resistance along any given load line. The current, i, through the motor is proportional to the rotation rate ω: i = neω/2π.So i = neα(f)Δp/2π = Δp/R, where R = 2π/neα(f) is the motor's resistance, which is constant for any given f.

Fig. 4.

(a) Speeds observed for objects with different frictional drag coefficients, f₁ < f₂ < f₃, shown as a function of relative pmf. f₁ and f₂ span the range of frictional drag coefficients observed at 24°C with different beads, and f₃ approximates the frictional drag coefficient observed with different cells. (b) Idealized torque–speed curves of a flagellar motor at four different relative pmfs, Δp₁–Δp₄ = 25%, 50%, 75%, and 100%, respectively. Load lines are shown for the same three frictional drag coefficients represented in a. Because the motor runs at the speed at which the torque generated matches the viscous drag on the object spun, i.e., at the speed corresponding to the intersection of the torque–speed curve and the specified load line, the linearity of the speed curves plotted in a demands that the torque–speed curves scale linearly with pmf, as shown in b.

In its high-speed, light-load regime, the flagellar motor behaves much like an open voltage-gated proton channel. Previous experiments have shown for this regime that speed depends strongly on temperature, strongly on exchange of ²H₂O for H₂O, and weakly on pH, all of which are characteristic of voltage-gated proton channels (11, 13). If we assume tight coupling, the speed–pmf relation measured here demonstrates a simple ohmic current–pmf relation, also indicative of such channels. If (i) two protons are used per mechanical step of a single torque-generating unit (1), (ii) each one travels through a separate channel (14), (iii) there are ≈50 such steps per revolution (rev) (15), and (iv) the motor spins at 380 Hz at zero load (3), then the flux through each channel is ≈50 H⁺/rev × 380 Hz = 1.9 × 10⁴ H⁺/s. This result is about the same as the current through an open, ≈30-fS voltage-gated proton channel (13): 4.5 fA (at 150 mV) ≈ 2.8 × 10⁴ H⁺/s. Both of these fluxes are much smaller than those observed in other ion channels.

It is not yet known how the motor generates torque. The membrane-spanning MotA/B proteins have resisted crystallization, so we do not have an atomic structure. What we do know has been pieced together from genetics, biochemistry, and physiology (1). Kinetic and biochemical analyses suggest that the motor's unique torque–speed curve results from a power-stroke mechanism, in which the majority of the work done and the majority of the electrochemical energy dissipated occur during one step in the motor's cycle (16, 17). At high speeds, where the motor operates far from equilibrium, it is not obvious that the work done by a power-stroke will remain proportional to pmf. In contrast, the high-speed characteristics of the flagellar motor are similar to those of an open voltage-gated proton channel, where protons are thought to cross the membrane by moving along a chain of hydrogen bonds. In this scheme, energy is dissipated in series of small hops resulting in an ohmic pmf dependence. Mechanisms linking proton translocation through such hydrogen-bonded chains to conformational changes in channel proteins have been suggested (18, 19). However, it is not clear how any of these changes could be used to generate torque. It seems more likely that, at high speeds, the rate-limiting steps occur in a proton channel that is effectively in series with the torque-generating machinery and that the latter exhibits a relatively low impedance. In any event, at high speeds, where little useful work is done, the motor appears to operate as a simple proton channel.

Comparable studies have been made of the sodium-driven polar flagellar motor of Vibrio alginolyticus (20), which, over a limited range of external Na⁺ concentrations, shows speeds for a given load that increase with sodium-motive force, and a family of torque–speed curves similar to those shown in Fig. 4b. However, the torque–speed curves for Vibrio appear to be more narrowly spaced at high loads than at low loads. Given that one can replace MotA and all but the C-terminal part of MotB with homologous components from Vibrio and produce motors in E. coli that run on Na⁺ (21), the channels might differ, but the rest of the machinery must be similar.