Establishing a grassland signature in veins: ¹⁸O in the leaf water of C₃ and C₄ grasses

Abstract

We show that ¹⁸O evaporative enrichment of bulk leaf water in grass species can be significantly more enriched than predicted by the Craig–Gordon model, with C₄ grasses considerably more enriched than C₃ grasses. Our results suggest that the unanticipated ¹⁸O leaf water enrichment of grasses is attributable to the progressive evaporative enrichment along parallel veins (a function of both leaf length and interveinal distance), a pattern that does not occur in Dicotyledonous species. We propose that the differential ¹⁸O enrichment of grasses will result in distinct C¹⁸O¹⁶O biospheric signals from grassland and forest ecosystems, allowing for further partitioning of terrestrial carbon fluxes.

The evaporative isotopic enrichment of ¹⁸O in surface waters (such as lakes) was described by Craig and Gordon (1) more than three decades ago and was later applied to leaves, which also undergo an isotopic enrichment during transpiration (2–5). Application of the Craig–Gordon model to leaves from trees and herbs has been shown experimentally to be robust over a wide range of environmental conditions (4, 6–7). Capitalizing on this established relationship, Farquhar and colleagues (8) showed that the equilibration of ¹⁸O between CO₂ and leaf water could be used to partition the gross fluxes of CO₂ from vegetation on a global basis.

Previous studies showed that there were no differences in bulk leaf water ¹⁸O enrichment of Dicotyledonous plants possessing either the C₃ or C₄ photosynthetic pathways and that leaf water behaved similarly to predictions of the Craig–Gordon model (4, 6). Based on these consistent results, global modeling efforts have used the Craig–Gordon model for estimates of leaf water δ¹⁸O [δ¹⁸O_wl, Standard Mean Ocean Water (SMOW) scale throughout] values that are needed to calculate the C¹⁸O¹⁶O retrodiffusing from terrestrial ecosystems to the atmosphere (8–11). However, the Craig–Gordon model of evaporative leaf-water enrichment has remained untested on grasses and other Monocotyledonous species. A fundamental difference between monocots and dicots that hinted that δ¹⁸O_wl might be different is the veinal structure of leaves, with monocot leaves having parallel veins whereas dicot leaves primarily have a reticulate veinal structure. We hypothesized that grass leaves will exhibit a leaf-water ¹⁸O evaporative enrichment pattern that is not consistent with the commonly used single-water-source version of the Craig–Gordon model, because the nature of water movement along parallel veins in a grass leaf is more analogous to movement of water through a sequence of pools in series.

We investigated possible ¹⁸O differences in leaf water enrichment with a variety of C₃ and C₄ grasses, because grasses with different photosynthetic pathway are known to have different interveinal differences (12, 13). Our hypotheses were (i) leaf water ¹⁸O enrichment of grasses should be greater than observed in dicots and (ii) leaf water ¹⁸O enrichment of C₄ grasses (narrower interveinal distances) should be greater than leaf water ¹⁸O enrichment of C₃ grasses (wider interveinal distances).

Methods

Plant Material and Growth Conditions.

In our pilot experiment, we grew Lolium multiflorum (C₃ grass), Muhlenbergia wrightii (C₄ grass), and Helianthus annuus (C₃ dicot) (n = 6 for each species) from seed under identical environmental conditions with an average midday relative humidity of 40%. In our survey experiment we used five C₃ grasses and five C₄ grasses (species listed in Table 1). For the survey experiment, n = 3 for each species and average midday relative humidity was 35%. The growth conditions and experimental protocol were identical for both experiments except where specified below.

Table 1.

Observed and predicted values of δ¹⁸O_wl for bulk leaf water

Plant	Observed δ18Owl, ‰	Craig–Gordon-predicted δ18Owl, ‰
Agropyron desertorum (C3)	7.7  ± 1.6	7.8
Agrostis stolonifera (C3)	9.2  ± 2.8	8.1
Alopecurus pratensis (C3)	8.3  ± 3.6	7.6
Bromus inermis (C3)	8.2  ± 1.7	7.6
Lolium multiflorum (C3)	8.0  ± 1.2	7.8
Andropogon gerardii (C4)	15.1  ± 3.7	8.0
Bouteloua curtipendula (C4)	12.7  ± 0.3	7.6
Eragrostis curvula (C4)	12.4  ± 4.2	8.0
Leptochloa dubia (C4)	14.2  ± 2.8	7.8
Muhlenbergia wrightii (C4)	9.0  ± 2.6	8.1
C3 mean	8.3  ± 0.5a	7.8
C4 mean	12.6  ± 3.2b	7.8

Each value represents a mean of three plants and the associated standard deviation. C₃ and C₄ means are significantly different at P < 0.01. Predicted δ¹⁸O_wl values (SMOW scale) are based on a single-water-source Craig–Gordon model. Sample conditions were: δ¹⁸O_{atm w vapor} = −27‰; relative humidity = 35%; air temperature = 25°C; leaf temperatures varied but were not significantly different from the mean of 27°C. Sample conditions for pilot experiment (data in text): δ¹⁸O_{atm w vapor} = −24‰; δ¹⁸O_source = −15.6‰; relative humidity = 40%; air temperature = 35°C; leaf temperatures were C₃ dicot = 34°C, C₃ grass = 35°C, and C₄ grass = 37°C. 

Plants for all experiments were grown in the greenhouse in a manner that kept the root systems completely submerged in an isotopically constant water source, whereas the aerial portions of the plants experienced greenhouse conditions. Plants were grown from germination in 1-liter pots in a sterilized soil/perlite/vermiculite (1:1:1) mixture, and the pots were placed in 190-liter open-top plastic chambers (stock tanks; Rubbermaid, Wooster, OH). To avoid evaporative enrichment and to keep source water constant, a flow-through system was developed in which the chambers were fitted with water entry and exit ports. Tap water was gravity fed to the chambers by a system of hoses from a 658-liter buffer tank. Closed-cell foam was placed at water level to further assure that no evaporative enrichment of source water occurred. The water level within the chambers was kept constant and at a level that submerged all but the top 1 cm of soil in each pot. Source water was oxygenated by two aquarium pumps, with the air flow separated to ten diffusers distributed evenly throughout the bottom of the chambers. A nutrient solution was supplied to the plants once a week by addition to the large buffer tank. Oscillating fans were placed next to the chambers to mitigate the propagation of leaf boundary layer differences between species. Wet bulb/dry bulb thermocouples were situated at plant height to measure air temperature and relative humidity throughout the experiments. A light sensor (Li-Cor, Lincoln, NE) was placed at plant height to measure irradiance, which averaged approximately 500 μmol⋅m⁻²⋅s⁻¹ in the pilot experiment and 1,000 μmol⋅m⁻²⋅s⁻¹ in the survey experiment, both for a 16-h photoperiod. Thermocouples and light sensor readings were recorded at 15-min intervals with a datalogger (model 21X;Campbell Scientific, Logan, UT).

Sample Collection.

Immediately before sampling leaf material, water samples of inlet and outlet water were taken to ensure no evaporative enrichment was occurring within the chambers. During this time, water vapor in air was collected by drawing air through an ethanol dry ice trap. Leaf temperature was measured before sampling leaf material. In the pilot experiment, samples were taken for leaf water δ¹⁸O once per week for a 3-week period. In the survey experiment, leaf water was sampled at one time period. With the exception of Fig. 2, all leaf water δ¹⁸O values represent the entire leaf blade from ligule to tip.

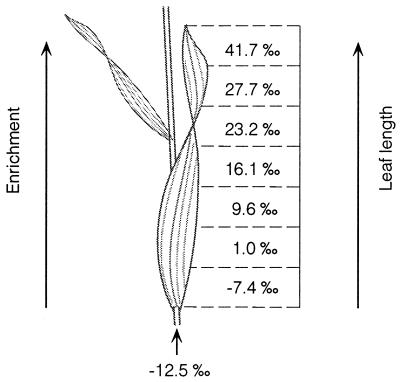
Figure 2.

Representative distribution of bulk leaf water δ¹⁸O_wl values of grass leaf sections for greenhouse-grown plants. For this specific grass blade (Miscanthus sinensis), the stem source water δ¹⁸O value was −12.5‰; all other sampling parameters were the same as in Table 1. All grass species mentioned in this study were sampled in the same manner and showed similar results.

Anatomical Measurements.

Immediately before sampling for leaf water in the survey experiments, leaf blade length was measured. Using a second set of leaves, measurements of interveinal distance were made by excising the whole, fully expanded leaves of three plants per species and removing the middle, widest portion of the leaf. The middle portions were free-hand sectioned into 1-mm sections and placed in Petri dishes filled with a H₂O/Clorox solution (80:20) for ≈1 h until fully cleared. Sections were mounted in glycerol, and interveinal distance was measured with a light microscope coupled with a drawing tube and bit pad (Donsanto Microplan II, Natuck, MA).

Isotope Analysis.

Leaf water was extracted by cryogenic distillation as detailed in Ehleringer and Osmond (14). For δ¹⁸O analysis of all water samples the equilibration technique of Socki et al. (15) was used with the following modifications. Water (20–500 μl) was introduced by syringe into a 6-ml headspace vial and sealed with a 20-mm Hycor Septum (Alltech, Deerfield, IL). Before injection of water, the headspace vial was evacuated and backfilled to atmospheric pressure (measured at the time of vial preparation) with air of 9:1, N₂:CO₂. The CO₂ and water samples were allowed to equilibrate for 48–72 h within the headspace vials. A 250-μl gas-tight lockable syringe (VICI Precision Sampling, Baton Rouge, LA) was used to inject 50–150 μl of air from the headspace vial into the helium carrier stream of a Varian GC (model 3300) through a split/splitless on-column injector (approximately a 1:10 split). The sample was carried through a 50-m plot column (Porapak-Q) and on through a 1:2 fixed-post column split interface to the MS (model 252; Finnigan-MAT, San Jose, CA) in continuous flow mode. Before injection of the sample into the column, the syringe was filled and evacuated with a “presample” to purge the syringe. After purging the syringe with the presample, the syringe was filled with a sample and overpressurized to ensure that the needle dead space volume was cleansed before injection. After every 10 samples, we analyzed one each of two laboratory standards. The two laboratory water standards were analyzed in volumes from 10 to 500 μl with this modified H₂O:CO₂ equilibration headspace vial technique and showed no significant variation related to water volume. Precision for all isotope analysis was 0.2‰.

Results and Discussion

In applying the Craig–Gordon model to leaves, two primary assumptions are made: (i) the leaf represents a single well-mixed pool into which water enters from the petiole and from which water exits solely by evapotranspiration, and (ii) the leaf is at isotopic steady-state, where the isotopic composition of the transpiration stream is identical to the water entering the leaf through the petiole. The isotopic composition of water in the leaf is then a function of known fractionation factors that are controlled by leaf temperature, the evaporative gradient, the leaf boundary layer, and the isotopic composition of atmospheric water vapor. All previous studies using the Craig–Gordon model to predict leaf water δ¹⁸O have shown the model to work well, or in some cases the predicted δ¹⁸O_wl was more enriched than what was actually observed (4–7, 16, 17). The explanation for the latter observation is that the leaf does not represent a perfectly mixed pool and that some contribution of unenriched vein water in bulk leaf water tends to decrease the observed ¹⁸O enrichment. If the primary assumptions are met and accurate measures of all parameters necessary to calculate predictions are made, the δ¹⁸O of leaf water cannot exceed predictions of the Craig–Gordon model.

After several weeks of growth in the pilot experiment, we sampled bulk leaf water (from ligule to leaf blade tip in the grasses) δ¹⁸O values and other source and atmospheric parameters necessary to evaluate the Craig–Gordon model (7) 1 day a week for 3 successive weeks. The δ¹⁸O_wl value for the C₄ grass (14.7 ± 3.0‰) was significantly and consistently more enriched than that of the C₃ grass (7.2 ± 2.0‰; P < 0.01), which was significantly more enriched than the C₃ dicot (3.9 ± 1.0‰; P < 0.01) under midday growth conditions. The observed δ¹⁸O_wl values for the dicot leaves were consistent with predictions of the Craig–Gordon model (4.1‰). However, the observed δ¹⁸O_wl values in both grasses were consistently more enriched than those predicted by the Craig–Gordon model: 7.2‰ versus 4.7‰ for the C₃ grass, and 14.7‰ versus 6.1‰ for the C₄ grass. The differences in predicted values among plants reflected measured differences in leaf temperatures.

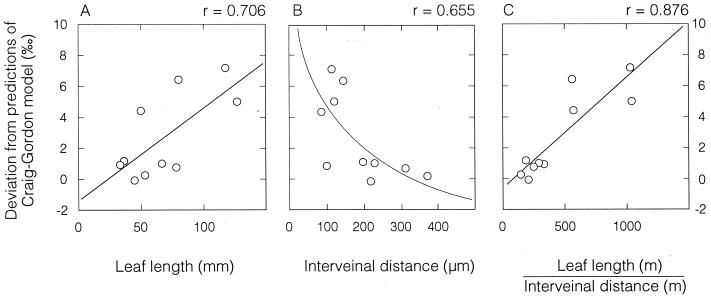
After 6 weeks of growth in the survey experiment, we sampled bulk leaf water δ¹⁸O values and all other parameters as detailed above. The patterns observed were similar to those of the pilot experiment: Whole-leaf δ¹⁸O_wl values of all C₄ grasses were >4‰ more enriched than all C₃ grasses, and the observed whole-leaf δ¹⁸O_wl of all but one grass species were more enriched than predicted Craig–Gordon values (Table 1). In analyzing the residuals (observed minus predicted values or deviations from a single-source-water version of the Craig–Gordon model), we observed a significant positive correlation with leaf length and a significant negative correlation with interveinal distance (Fig. 1 A and B; P < 0.01). When the residual was plotted versus leaf length divided by interveinal distance (Fig. 1C), there was a highly significant correlation that explained most of the deviation of the bulk grass blade δ¹⁸O_wl from the Craig–Gordon model (r = 0.876; P < 0.001).

Figure 1.

The relationships between δ¹⁸O_wl residuals (difference between the observed and predicted δ¹⁸O_wl values) versus grass leaf morphological characteristics. (A) Residual versus leaf length (P < 0.01). (B) Residual versus interveinal distance (P < 0.01). (C) Residual versus leaf length divided by interveinal distance (P < 0.001). Each point represents a different grass species and is the mean of three plants.

To assess the pattern of ¹⁸O enrichment in grasses, whole grass blades were collected and sectioned from base to tip, and the δ¹⁸O_wl value was measured in each section. A large and distinct progressive δ¹⁸O_wl enrichment was observed along the length of the grass leaf (Fig. 2). The base-to-tip δ¹⁸O_wl difference for this grass blade was 49‰. All grass species analyzed exhibited a similar pattern of progressive enrichment, with some base-to-tip differences exceeding 50‰. Such large and distinct ¹⁸O enrichment patterns did not occur in dicot leaves (17).

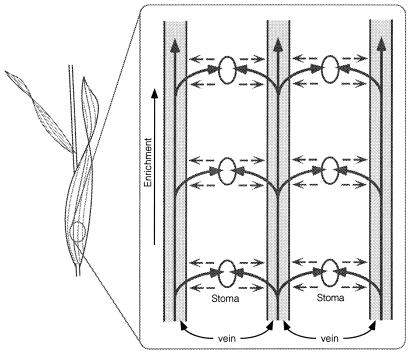
We propose a simple explanation that accounts for both the progressive enrichment and the effect of interveinal distance on grass δ¹⁸O_wl (Fig. 3). As water moves out of leaf veins and toward the stomatal apertures, leaf water becomes evaporatively ¹⁸O-enriched. As a result, an ¹⁸O gradient develops between the stomatal complex (region of evaporatively enriched water) and vein (water source) as expected by the Craig–Gordon model. Despite the large advective transpirational flux toward the stoma, back diffusion of ¹⁸O-enriched leaf water toward the vein should occur [Peclet effect (18)] and any back diffusion ultimately enriches vein water. This enriched vein water travels up the leaf providing source water to the next stomatal complex, and the vein water is further enriched (explaining the observation in Fig. 2). We also expect that at any particular point along a grass blade, the extent to which vein water mixes with water from evaporative sites should be a function of the distance from the vein to the evaporative site (back diffusion path length). If interveinal distances are short, there is more mixing, and the vein water enrichment should be greater for every leaf segment. Interveinal distances are known to be significantly shorter in C₄ grasses than in C₃ grasses (12, 13). Consistent with this pattern, we observed that δ¹⁸O_wl values were more enriched in C₄ grasses.

Figure 3.

Schematic of progressive ¹⁸O enrichment of leaf water as expected in grass leaves. As source water (solid arrowed lines) exits a vein and moves toward a stoma, it becomes evaporatively enriched in ¹⁸O. This enrichment process creates a concentration gradient of enriched water at the stoma relative to water in the vein, which results in a back diffusion of enriched water (dashed arrowed lines). The mixing of the isotopically distinct water pools results in a slight enrichment of vein water, which then influences ¹⁸O enrichment of leaf water in the next leaf segment, where the process occurs again further enriching vein water.

The patterns of leaf water enrichment we describe here require successively enriched pools in contrast to the Craig– Gordon model, which considers only one pool. Our hypothesis for grass blade enrichment is analogous to the string-of-lakes model developed by Gat and Bowser (19):

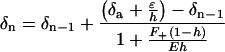1

where δ_a and δ_n refer to the δ¹⁸O of atmospheric water vapor and water entering an evaporating surface (i.e., stoma), respectively. F₊ represents the flux into a segment, and E represents the evaporative flux out of a segment. Humidity is represented by h, and ɛ = ɛ_eq + (1 − h)ɛ_k, where ɛ_eq and ɛ_k represent the equilibrium and kinetic fractionation factors.

If one assumes that E is the same for all leaf segments, then the mean δ¹⁸O value of water from all segments has the same value as predicted by the single-water-source Craig–Gordon model. Under this assumption, we do predict progressive ¹⁸O enrichment along the leaf for successive leaf segments, but the predicted δ¹⁸O values of each segment do not match observed values (Table 2). Actual E along a grass blade is known to vary (20). When we fitted E values of leaf segments to match the δ¹⁸O_wl data, we obtained close agreement (Table 2). There was not a fitted value of E that accurately predicted δ¹⁸O in the terminal segment. We believe this observation is because the water volume in a leaf decreases as the leaf tapers toward the tip, a phenomenon not incorporated into the model. Note that by varying E between segments, the predicted whole-leaf water δ¹⁸O_wl value is considerably more enriched than that predicted by the single-water-source Craig–Gordon model, without violating steady-state assumptions. As it stands, the Gat–Bowser model assumes complete mixing within each segment (e.g., interveinal distance of 0), but if we relax this assumption in accordance with known C₃/C₄ anatomical differences, species-specific differences can be incorporated into the model.

Table 2.

Observed and predicted leaf water δ¹⁸O values of leaf segments

Leaf segment	Observed δ18O, ‰	Craig–Gordon model-predicted δ18O, ‰	Gat–Bowser model
			Nonvariable E		Fitted E
			E, mmol⋅m−2⋅s−1	Predicted δ18O, ‰	E, mmol⋅m−2⋅s−1	Predicted δ18O, ‰
Base 1	−7.4	11.0	7.14	−7.5	7.40	−7.4
2	1.0	11.0	7.14	−2.4	12.25	1.0
3	9.6	11.0	7.14	3.2	10.60	9.6
4	16.1	11.0	7.14	9.4	6.05	16.1
5	23.2	11.0	7.14	16.4	5.70	23.2
6	27.7	11.0	7.14	24.6	2.40	27.7
Tip 7	41.7	11.0	7.14	35.3	5.60	37.3
Mean	16.0	11.0	7.14	11.3	7.14	15.4

δ¹⁸O_source was −12.5‰, and all other environmental parameters were as mentioned in Table 1. In the Gat–Bowser model, the mean value of E for the entire leaf remains constant. However, the proportion of E within a segment was either held constant (nonvariable E) or was varied (fitted E). The calculated variations in fitted E across the length of the leaf are less than those of sugarcane (20). 

The ¹⁸O differences in leaf water should affect C¹⁸O¹⁶O values of gross photosynthetic CO₂ fluxes, because carbonic anhydrase assures rapid equilibration of ¹⁸O in leaf water and CO₂ (8). Hence, ¹⁸O leaf water differences should be reflected in the δ¹⁸O values of retrodiffused CO₂ leaving the leaf and from the ecosystem. Farquhar et al. (8) showed that most of the latitudinal variation in global C¹⁸O¹⁶O is a direct result of leaf water enrichment in terrestrial vegetation and implied that C¹⁸O¹⁶O values could be used to further distinguish terrestrial from oceanic CO₂ fluxes. Our observations suggest that C₃-dominated grasslands and C₃ forests should be different in δ¹⁸O_wl. Consequently, the discrimination value of C¹⁸O¹⁶O fluxing from these ecosystems should differ according to the theory developed by Farquhar and colleagues (8). Discrimination against C¹⁸O¹⁶O in C₄ plants is distinguishable from C₃ plants based on the inherent differences of [CO₂] in the air spaces of the leaf (8). However, based on the correlations shown here between δ¹⁸O_wl and leaf anatomy, the C¹⁸O¹⁶O discrimination values of major grasslands, such as the short-grass and tall-grass C₄-dominated prairies, may be distinct because of the large differences in leaf length and interveinal distance of the dominant species in these grasslands. Furthermore, the vast difference in C¹⁸O¹⁶O discrimination between C₃ and C₄ grasses, along with δ¹³C information from CO₂, may allow for separation of seasonal activity shifts in C₃/C₄ dominance within these grasslands.

Grass-dominated ecosystems comprise nearly one-fourth of total global vegetated land area (21) and are among the most productive ecosystems. Yet there can be more than a 4-fold difference in primary productivity on a year-to-year basis (22). Given that the ¹³CO₂ discrimination by C₄ grasslands is nearly indistinguishable from oceanic discrimination (23), partitioning of the global carbon flux into grassland versus oceanic carbon sinks is difficult. The higher δ¹⁸O_wl and C¹⁸O¹⁶O discrimination values predicted for grassland ecosystems might be an approach for distinguishing grassland from oceanic productivity in the global ¹³C¹⁸O¹⁶O flask observations.