Resolving the question of color naming universals

Abstract

The existence of cross-linguistic universals in color naming is currently contested. Early empirical studies, based principally on languages of industrialized societies, suggested that all languages may draw on a universally shared repertoire of color categories. Recent work, in contrast, based on languages from nonindustrialized societies, has suggested that color categories may not be universal. No comprehensive objective tests have yet been conducted to resolve this issue. We conduct such tests on color naming data from languages of both industrialized and nonindustrialized societies and show that strong universal tendencies in color naming exist across both sorts of language.

Do languages categorize colors similarly, or does color categorization vary freely across languages? This question pits two contrasting views of linguistic meaning against each other. In one view, meaning is constrained by universally shared aspects of perception, cognition, or the environment; in the other, it is determined principally by the arbitrary linguistic conventions of a particular language. For this reason, the question of color naming universality has attracted considerable attention (1–5) and generated considerable controversy (6–13). Curiously, however, the core empirical question of whether there are genuine universal tendencies in color naming has never been put to objective test, and it remains contested (6–10). Our goal is to resolve this issue.

In 1969 Berlin and Kay (BK) (1) advanced the hypothesis that “a total universal inventory of exactly 11 basic color categories exists from which the 11 or fewer basic color terms of any given language are always drawn.” They supported this hypothesis with color naming data from 20 languages. In subsequent work, the specific hypothesis of 11 universal basic color categories was generalized to the hypothesis that there exist universal constraints on cross-language color naming related to these 11 basic color percepts, particularly to the six Hering opponent primaries, black, white, red, yellow, green, and blue (14–17). This hypothesis, which we refer to as the universality hypothesis, has gained considerable acceptance over the years (2–5).

However, it has also encountered considerable resistance (6–10). A central concern has been the absence of any objective test of the hypothesis (7). Color naming data have typically been analyzed in an intuitive fashion, by determining through visual inspection whether color categories from different languages tend to cluster together in color space. A serious problem with this means of analysis is that humans sometimes incorrectly perceive clustering in points that are randomly distributed (18). Thus, it is possible that the perceived clustering of color terms, on which the claim of universality rests, is spurious.

Another concern is that the BK language sample (1) was small and skewed: 17 of the 20 languages studied were written languages of industrialized societies. Thus, even if the results had rested on an objective test, it is unclear how well they would generalize to other sorts of languages. The results leave open the possibility that color naming is similar primarily across those languages that are linked to each other through the global process of industrialization (6, 11, 12). There are also further reasons to question the representativeness of the original data of BK (1): no more than a single speaker was tested for most languages, the data were gathered in the San Francisco Bay area rather than in the native locale of the language, and all of the speakers tested also spoke English (6, 7, 11–13).

The most damaging evidence against the universality hypothesis is that there are languages that appear not to fit the proposed universal pattern. Interestingly, these tend to be unwritten languages of nonindustrialized societies, consistent with the idea that similarities in color naming may be limited in cross-linguistic scope. Most such languages do not have separate color terms for green and blue but rather use a single term to cover these regions of color space (17). Others, such as Hanunóo (19) and Zuni (7), have color terms that have been interpreted as reflecting extra-chromatic concepts such as dryness and freshness rather than the proposed universal color categories (ref. 7, but see also ref. 20). Another proposed counterexample is Berinmo, a Papua New Guinea language with color term boundaries that disagree with comparable boundaries in English (8, 9).

Significantly, these cross-linguistic differences in color naming are sometimes correlated with differences in color cognition, calling into question the idea of a fixed cognitive bedrock underlying linguistic universals. Specifically, Berinmo speakers exhibit enhanced color discrimination from memory across Berinmo category boundaries, but not across English boundaries, whereas English speakers show the reverse pattern (8, 9). Similar results have been obtained comparing English with Tarahumara (21). These findings have been taken by some to suggest that linguistic color categories may be largely arbitrary constructs of specific languages, constrained only loosely by very general principles, such as the principle that no single color category may cover unconnected regions of color space (8).

Given this, are there genuine cross-linguistic universals in color naming or not? To resolve this issue, we conducted statistical tests on a comprehensive body of color naming data.

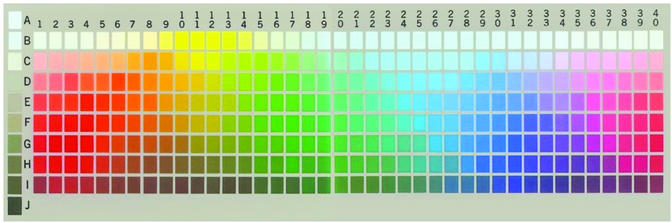
The central empirical focus of our study was the color naming data of the Word Color Survey (WCS). The WCS was undertaken in response to the above-mentioned shortcomings of the BK data (1): it has collected color naming data in situ from 110 unwritten languages spoken in small-scale, nonindustrialized societies, from an average of 24 native speakers per language (mode: 25 speakers), insofar as possible monolinguals. Speakers were asked to name each of 330 color chips produced by the Munsell Color Company (New Windsor, NY), representing 40 gradations of hue at eight levels of value (lightness) and maximal available chroma (saturation), plus 10 neutral (black-gray-white) chips at 10 levels of value. Chips were presented in a fixed random order for naming. The array of all color chips is shown in Fig. 1. (The actual stimulus colors may not be faithfully represented there.) In addition, each speaker was asked to indicate the best example(s) of each of his or her basic color terms. The original BK study used a color array that was nearly identical to this, except that it lacked the lightest neutral chip. The languages investigated in the WCS and BK are listed in Tables 1 and 2.

Fig. 1.

Color array from the WCS. For the Munsell notations of the colors in this stimulus array see ref. 1.

Table 1. Languages in the WCS.

Index	Language	Where spoken	No. of subjects
1	Abidji	Ivory Coast	25
2	Agarabi	Papua New Guinea	24
3	Agta	Philippines	25
4	Aguacatec	Guatemala	25
5	Amarakaeri	Peru	06
6	Ampeeli	Papua New Guinea	27
7	Amuzgo	Mexico	25
8	Angaatiha	Papua New Guinea	25
9	Apinaye	Brazil	30
10	Arabela	Peru	25
11	Bahinemo	Papua New Guinea	25
12	Bauzi	Indonesia	25
13	Berik	Indonesia (Irian Jaya)	25
14	Bete	Ivory Coast	25
15	Bhili	India	25
16	Buglere	Panama	25
17	Cakchiquel	Guatemala	30
18	Campa	Peru	25
19	Camsa	Columbia	25
20	Candoshi	Peru	11
21	Cavineña	Bolivia	25
22	Cayapa	Ecuador	24
23	Chácobo	Bolivia	25
24	Chavacano (Zamboangueño)	Philippines	25
25	Chayahuita	Peru	25
26	Chinantec	Mexico	25
27	Chiquitano	Bolivia	25
28	Chumburu	Ghana	25
29	Cofán	Ecuador	20
30	Colorado	Ecuador	25
31	Cree	Canada	25
32	Culina	Peru, Brazil	25
33	Didinga	Sudan	25
34	Djuka	Surinam	25
35	Dyimini	Ivory Coast	25
36	Ejagam	Nigeria, Cameroon	25
37	Ese Ejja	Bolivia	25
38	Garifuna (Black Carib)	Guatemala	28
39	Guahibo	Colombia	25
40	Guambiano	Columbia	27
41	Guarijío	Mexico	25
42	Guaymí (Ngäbere)	Panama	25
43	Gunu	Cameroon	25
44	Halbi	India	25
45	Huastec	Mexico	25
46	Huave	Mexico	25
47	Iduna	Papua New Guinea	25
48	Ifugao (Keley-i)	Philippines	25
49	Iwam (Sepik)	Papua New Guinea	25
50	Jicaque	Honduras	10
51	Kalam	Papua New Guinea	25
52	Kamano-Kafe	Papua New Guinea	25
53	Karajá	Brazil	19
54	Kemtuik	Indonesia (Irian Jaya)	25
55	Kokni (Kokoni)	India	25
56	Konkomba	Ghana	25
57	Kriol	Australia	25
58	Kuku-Yalanji	Australia	20
59	Kuna	Panama	25
60	Kwerba	Indonesia (Irian Jaya)	25
61	Lele	Chad	15
62	Mampruli	Ghana	24
63	Maring	Papua New Guinea	25
64	Martu Wangka	Australia	25
65	Mawchi	India	25
66	Mayoruna	Peru	25
67	Mazahua	Mexico	25
68	Mazatec	Mexico	25
69	Menye	Papua New Guinea	25
70	Micmac	Canada	25
71	Mikasuki	United States	25
72	Mixtec	Mexico	25
73	Mundu	Sudan	18
74	Múra Pirahá	Brazil	25
75	Murle	Sudan	25
76	Murrinh-Patha	Australia	25
77	Nafaanra	Ghana	29
78	Nahuatl	Mexico	06
79	Ocaina	Peru	25
80	Papago (O'odham)	United States, Mexico	25
81	Patep	Papua New Guinea	24
82	Paya	Honduras	20
83	Podopa	Papua New Guinea	14
84	Saramaccan	Surinam	25
85	Seri	Mexico	25
86	Shipibo	Peru	25
87	Sirionó	Bolivia	25
88	Slave	Canada	24
89	Sursurunga	Papua New Guinea	26
90	Tabla	Indonesia (Irian Jaya)	25
91	Tacana	Bolivia	08
92	Tarahumara (Central dialect)	Mexico	09
93	Tarahumara (Western dialect)	Mexico	06
94	Tboli	Philippines	25
95	Teribe	Panama	26
96	Ticuna	Peru	25
97	Tifal	Papua New Guinea	25
98	Tlapanec	Mexico	25
99	Tucano	Colombia	25
100	Vagla	Ghana	25
101	Vasavi	India	25
102	Waorani (Auca)	Ecuador	25
103	Walpiri	Australia	25
104	Wobé	Ivory Coast	25
105	Yacouba	Ivory Coast	27
106	Yakan	Philippines	25
107	Yaminahua	Peru	25
108	Yucuna	Colombia	25
109	Yupik	United States	25
110	Zapotec	Mexico	25

Table 2. Languages studied by BK (1).

Index	Language	Where spoken
1	Arabic (Lebanese colloquial)	Lebanon
2	Bahasa Indonesia	Indonesia
3	Bulgarian	Bulgaria
4	Cantonese	China
5	Catalan	Spain
6	(American) English	United States
7	Hebrew	Israel
8	Hungarian	Hungary
9	Ibibio	Nigeria
10	Japanese	Japan
11	Korean	Korea
12	Mandarin	China
13	(Mexican) Spanish	Mexico
14	Pomo	United States
15	Swahili	Tanzania
16	Tagalog	Philippines
17	Thai	Thailand
18	Tzeltal	Mexico
19	Urdu	Pakistan
20	Vietnamese	Vietnam

Data reported from one subject per language

We approach the issue of whether there are universal tendencies in color naming by asking two questions:

1. Do color terms from different languages in the WCS cluster together in color space to a degree greater than chance?

2. Do WCS color terms, all from unwritten languages of nonindustrialized societies, fall near color terms of written languages from industrialized societies, as represented by the BK sample?

To test for clustering, we represented color terms as points in color space, and then tested for clustering of those points. Because the idea of clustering depends essentially on the concept of distance, we required a color space in which psychologically meaningful distances can be calculated. Consequently we transformed our 330 color stimuli from Munsell space, which lacks such a distance metric, to CIEL^*a^*b^* space, which has one (22). CIEL^*a^*b^* is a 3D color space, in which the L^* dimension represents lightness, and the two remaining dimensions, a^* and b^*, define a plane orthogonal to L^*, such that angle in that plane represents hue, and radius represents saturation. We represented each color term T in each language L by its centroid in this space. This was computed by first finding, for each speaker of L who used term T, the centroid in CIEL^*a^*b^* space of the chips named T by that speaker. These speaker centroids were then averaged together to yield an overall term centroid for T. Finally, that term centroid was coerced back to the chip most similar to it in the stimulus array, so that our overall representation of the term resided within the set of points out of which it was constructed. This coercion was done by first selecting that row of the array with L^* value nearest that of the centroid [L^* values are constant within each value (i.e., lightness) row of the stimulus array]. We then examined two chips, the chromatic (colored) chip in that row with hue angle in the a^*b^* plane closest to the centroid, and the neutral chip in that row, and selected the one that had hue radius in the a^*b^* plane closest to the average radius of the chips represented by the centroid. This selected chip was our point representation of the color term.

Given such point representations of all color terms, we tested whether these points were more clustered across languages than would be expected by chance, through a Monte Carlo test. This required first a measure of color-term clustering and then an indication of how clustered one might expect color terms to be by chance.

We defined a measure D of the dispersion of the terms in the WCS data set: for each color term c in each language l, we found the closest term c^* in each other language l^*, and added up those distances. Distance between terms was defined as CIEL^*a^*b^* distance between their point representations.

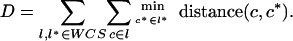Because D is a measure of dispersion, low values of D indicate clustering.

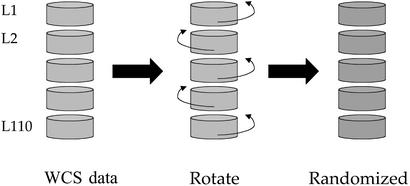
To determine how much dispersion one would expect by chance, we created a set of randomized hypothetical datasets through computer simulation and measured dispersion in them. Our randomization method was informed by the observation that general principles of categorization operating within a given language can be expected to produce a certain amount of dispersion in any natural system of categories. We wanted to be certain that our randomized data sets obeyed such within-language principles of categorization. To this end, we started with the actual WCS data set and rotated each language's term centroids in the a^*b^* (hue) plane by a random amount, the same random amount for all terms within a language, but different random amounts for different languages, as shown in Fig. 2. These rotated centroids were then coerced back to the WCS color array in the manner described above. This process produced one hypothetical data set, which preserved within-language structure while randomizing cross-language structure, appropriately, as the latter is the central focus of this study.

Fig. 2.

Creating a randomized data set.

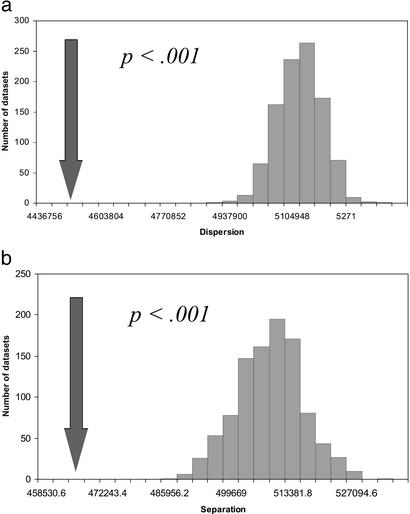
The process creating a randomized data set was repeated independently 1,000 times, and the D dispersion measure was calculated for each hypothetical data set. Fig. 3a shows the distribution of D in the 1,000 hypothetical data sets compared with D in the actual WCS data. The actual WCS D value is well below the lower boundary of the hypothetical distribution. Thus, the WCS data show significantly less dispersion, that is, more clustering, than expected by chance, P < 0.001.

Fig. 3.

Monte Carlo tests. (a) Clustering within the WCS. The distribution of dispersion values shown in gray was obtained from 1,000 randomized data sets. The arrow indicates the dispersion value obtained from the WCS data. (b) Comparing the WCS with BK. The distribution of separation values shown in gray was obtained from 1,000 randomized data sets. The arrow indicates the separation value obtained by comparing the WCS data with BK data (1).

Our second question is whether the WCS color naming data (from unwritten languages of nonindustrialized societies) bear greater than chance similarity to the BK color naming data (1) (primarily from written languages of industrialized societies.) To test this, we used another Monte Carlo test in which 1,000 hypothetical data sets were created from the WCS data by using the same random hue angle rotation technique as before (see Fig. 2). However, this time, rather than measuring dispersion within a single data set, we measured distances across data sets, yielding an overall measure S of the separation between the WCS data (either real or hypothetical) and the BK data. Specifically, for each color term c in each language l in the WCS data set (either real or hypothetical), we found the closest term c^* in each language l^* in the BK data set and added up those distances to obtain the sum S.

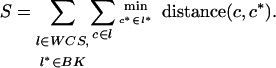[2]

Comparing the value for S observed in the WCS data set to the distribution of values obtained in 1,000 hypothetical randomizations of that data set, Fig. 3b shows that the value of S for the actual WCS data is well below the lower limit of the hypothetical distribution. Thus, the WCS data are significantly closer to the BK data than expected by chance, P < 0.001. We then removed from the BK data set the only unwritten languages of nonindustrialized societies in that data set (Ibibio, Pomo, and Tzeltal), reran this test, and obtained the same qualitative result, P < 0.001. This finding indicates a similarity in color naming across languages of industrialized and nonindustrialized societies.

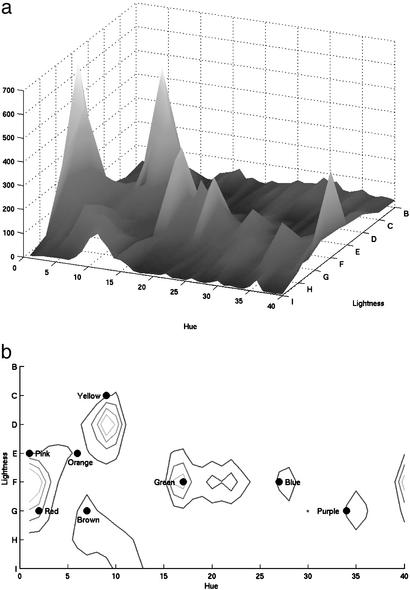
These universal tendencies are shown in Fig. 4a. The floor plane of this display corresponds to the 320 chromatic (non-neutral) colors in the stimulus array of Fig. 1, and the height of the surface at each position represents the number of WCS speaker centroids falling at that point in color space [MacLaury (23) displays a comparable histogram, restricted to the hue dimension]. This distribution of color terms from nonindustrialized languages is shown from above in the contour plot of Fig. 4b, compared with naming centroids for English color terms (24). The English terms blue, green, purple, and brown fall at or very near peaks of the WCS distribution, whereas yellow, orange, pink, and red fall in the neighborhood of WCS peaks. There is also a WCS peak between English green and blue. This peak may reflect the fact that the majority of the languages in the WCS span green and blue with a single term, whose naming centroid would be expected to fall between those for green and blue (17). Similarly, the apparent deviation of the English red and yellow naming centroids from the closest WCS centroid peaks is plausibly attributable to the fact that almost all WCS languages lack terms for pink and orange; instead, they include pink with red in a single broader term and orange with yellow. A term spanning yellow and orange would be expected to have a naming centroid somewhere between yellow and orange and a term spanning red and pink would be expected to have a naming centroid somewhere between red and pink, as may be observed with regard to the relevant centroid peaks in Fig. 4b.

Fig. 4.

Distribution of color terms from nonindustrialized languages. (a) The floor plane corresponds to the chromatic (non-neutral) portion of the color stimulus array. The height of the surface at each point in the plane denotes the number of speaker centroids in the WCS data set that fall at that position in color space. (b) The distribution of a is viewed from above by a contour plot. The outermost contour represents a height of 100 centroids, and each subsequent contour represents an increment in height of 100 centroids. English color terms fall near the peaks of the WCS distribution.

Do more WCS centroids fall at the 11 positions named by these English color terms, together with black, gray, and white, than would be expected by chance? We defined the “location” of an English color term to be that cell of the stimulus array on which its centroid fell and found that the mean number of WCS centroids per cell falling on these 11 English-named locations (M = 153.3) was more than the corresponding number falling on the remaining 319 cells of the stimulus array (M = 61.4), t(328) = 3.7, P < 0.0005. Thus, although languages vary considerably in the number of major color terms they contain (1) and can also vary significantly in the location of the boundaries between terms (8, 9), certain privileged points in color space appear to anchor the color naming systems of the world's languages, viewed as a statistical aggregate, and these universally privileged points are reflected in the basic color terms of English.

The application of statistical tests to the color naming data of the WCS has established three points: (i) there are clear cross-linguistic statistical tendencies for named color categories to cluster at certain privileged points in perceptual color space; (ii) these privileged points are similar for the unwritten languages of nonindustrialized communities and the written languages of industrialized societies; and (iii) these privileged points tend to lie near, although not always at, those colors named red, yellow, green, blue, purple, brown, orange, pink, black, white, and gray in English.