Compliant leg behaviour explains basic dynamics of walking and running

Abstract

The basic mechanics of human locomotion are associated with vaulting over stiff legs in walking and rebounding on compliant legs in running. However, while rebounding legs well explain the stance dynamics of running, stiff legs cannot reproduce that of walking. With a simple bipedal spring–mass model, we show that not stiff but compliant legs are essential to obtain the basic walking mechanics; incorporating the double support as an essential part of the walking motion, the model reproduces the characteristic stance dynamics that result in the observed small vertical oscillation of the body and the observed out-of-phase changes in forward kinetic and gravitational potential energies. Exploring the parameter space of this model, we further show that it not only combines the basic dynamics of walking and running in one mechanical system, but also reveals these gaits to be just two out of the many solutions to legged locomotion offered by compliant leg behaviour and accessed by energy or speed.

1. Introduction

In his seventeenth century volume ‘De motu animalium’, Borelli discussed walking as vaulting over stiff legs using a pair of compasses and noted the importance of rebounding on compliant legs in running (Borelli 1685). From that early account up to the present, walking and running have been treated as different mechanical paradigms, and the two corresponding models, the inverted pendulum model for walking (Alexander 1976; Mochon & McMahon 1980) and the spring-mass model for running (Blickhan 1989; McMahon & Cheng 1990), have developed into the conceptual basis for our understanding and technical realization of legged locomotion. The models motivate the changes of kinetic and potential energies that are observed in each gait (Cavagna et al. 1964, 1977; Dickinson et al. 2000), give insights into the remarkable universal speed dependency that describes the walk–run transition (Alexander 1989; Kram et al. 1997; Minetti 2001) and reveal the importance of self-stability for legged systems (Garcia et al. 1998; Kuo 1999; Seyfarth et al. 2002; Ghigliazza et al. 2003) inspiring the construction of walking (McGeer 1990; Collins et al. 2005) and running machines (Raibert 1986; Saranli et al. 2001; Cham et al. 2004).

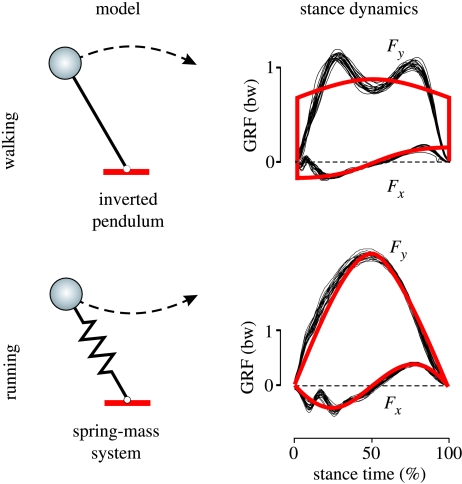
However, these models also show that, whereas rebounding on compliant legs explains well the basic mechanics of running, vaulting over stiff legs cannot truly reproduce that of walking (Full & Koditschek 1999). For instance, instead of the large vertical amplitudes suggested by vaulting over stiff legs, the upper body shows comparably small vertical amplitudes during walking (Weber & Weber; Lee & Farley 1998). This discrepancy is also reflected in the forces acting on the centre of mass (COM; Marey 1894; Fischer 1899). For example, in stance, the vertical ground reaction force (GRF) is characteristically M-shaped: it has one early and one late peak separated by a minimum around midstance, which the inverted pendulum model cannot reproduce (figure 1; Pandy 2003).

Figure 1.

Standard conceptual models of legged locomotion and their predictive power with respect to walking and running dynamics. The inverted pendulum and the spring–mass system are the standard models for walking and running. The model-predicted stance dynamics (red lines) fit experimental data (black traces recorded from human treadmill walking at 1.2 m s⁻¹ and running at 4.0 m s⁻¹) only for the spring–mass model for running. Note that, in the inverted pendulum dynamics, delta functions appear at 0 and 100% stance time if one adds collision and push-off models imitating double support. F_x,y, horizontal and vertical ground reaction force (GRF) normalized to body weight (bw).

To account for these differences, more complex models of walking use more detailed representations of the leg components, including springs and dampers, multi-segments or neuromuscular structures (Siegler et al. 1982; Gurp et al. 1987; Pandy & Berme 1988; Neptune et al. 2001; Pandy 2003; Zajac et al. 2003). Although these models describe the dynamics of walking much closer than an inverted pendulum can, and indicate compliant leg behaviour to be relevant in walking, they are too complex to serve as conceptual models. Hence, despite being inaccurate, the stiff-legged motion remains the mechanical paradigm for the walking gait (Dickinson et al. 2000; Srinivasan & Ruina 2005).

We argue that not stiff but compliant legs are fundamental to the walking gait. Hereto, we first introduce the bipedal spring–mass model, which adds a second leg to the known running model and represents the simplest walking model using compliant legs. We then look for stable locomotion of this model and show that its resulting steady-state patterns reproduce those observed in walking. Finally, we generalize the model and suggest that walking and running are just two out of the many solutions to legged locomotion offered by compliant leg behaviour and accessed by energy or speed.

2. The bipedal spring–mass model

The model represents the body as point mass m at the COM and describes the legs as two massless, linear springs of equal rest length ${\ell }_0$ and stiffness k (figure 2). Both springs act independently and influence the model dynamics only during stance when the spring force opposes the gravitational force. On the contrary, in swing, the respective spring has no physical meaning, but describes a kinematic touchdown condition $y_{\text{TD}}={\ell }_0\text{sin}{\alpha }_0$, given by the rest length ${\ell }_0$ and the fixed leg orientation α₀ with respect to gravity. The transition from swing to stance occurs when the swing-leg strikes the ground, whereas that from stance to swing occurs when the spring reaches its rest length during lengthening. To compare the model dynamics with that of human walking, we fix the parameters mass, rest limb length and gravitational acceleration to m=80 kg, ${\ell }_0=1\text{m}$ and g=9.81 m s⁻², respectively.

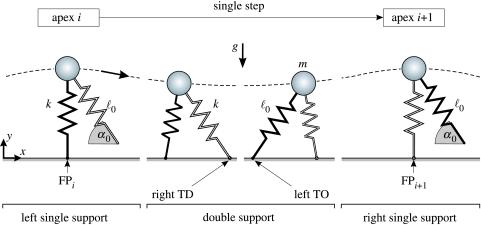
Figure 2.

The bipedal spring–mass model. The model has two independent, massless spring legs attached to a point mass m. Both springs have stiffness k, rest length ${\ell }_0$ and, in their swing phases, a constant orientation α₀ with respect to gravity (g, gravitational acceleration). A single step is shown that starts at the highest COM position in left leg single support (apex i), includes the double support ranging from right leg touchdown (right TD) to left leg take-off (left TO), and ends at the next apex in right leg single support (apex i+1). FP, foot point position in single support.

To obtain steady-state solutions of this model, we investigate a single step, which is defined as the interval between two subsequent apex events marking the highest points of the COM trajectory. For example, in figure 2, the model starts at the ith apex with the left spring (black) in single support and the right spring (white) describing the swing-leg. Since the gravitational force exceeds the opposing spring force, the left spring shortens while rotating forward and the COM height decreases (dotted line). When the right leg touches the ground (‘right TD’), the model enters the double-support phase. The additional push of the right stance-spring reverses the vertical and decelerates the horizontal COM motion. Owing to sufficient momentum, the forward progression continuous to extend the left spring until it reaches its rest length. At this instant, the left spring takes off (‘left TO’) and the system enters the single support phase of the right spring in which the (i+1)th apex is reached when the upward COM motion stops (vertical COM velocity $\dot{y}=0$), completing the step. Owing to the parametric symmetry between both springs, one step represents a basic gait cycle and its identical repetition, the steady-state locomotion.

3. Walking solutions reproducing experimental data

Depending on the chosen parameter values, the model may take off in single support or stumble and fall down; however, it also shows, and converges to, steady-state locomotion. By searching for stable locomotion using the return map of a single step (for details on the stability analysis see appendix Aa–c), we find three characteristic steady-state solutions A–C of the model, which have in common that their stance-phase patterns resemble those observed in animal and human walking (figure 3). The horizontal GRF shows the observed change from negative to positive values and the vertical axis, the double peak that distinguishes the walking gait (F_x and F_y, first row of subplots). Correspondingly, as in animals and humans (Lee & Farley 1998; Gard et al. 2004), the COM oscillates around its landing height in the vertical GRF with a smaller increase in height during stance than that of the inverted pendulum motion (Δy, second row). Moreover, closer than the inverted pendulum, the bipedal spring–mass model describes the out-of-phase changes in the forward kinetic and the gravitational potential energies that occur in walking (ΔE_k,x and ΔE_p, third row).

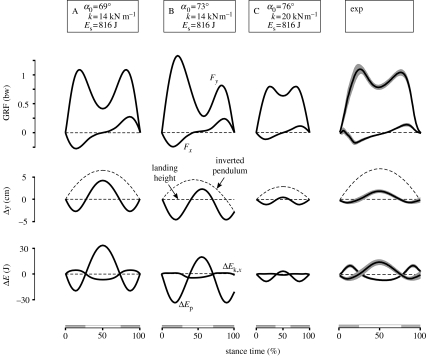
Figure 3.

Stance-phase patterns of walking at about 1.2 m s⁻¹. (A–C) Examples of three characteristic steady-state solutions of the bipedal spring–mass model are compared with (exp) experimental results (mean and s.d. shown as line and shaded area) of five subjects (mean±s.d. of mass: 81±3.5 kg, leg length: 1.07±0.03 m) walking on a treadmill (Adal3D, TecMachine, France; with force sensors recording horizontal and vertical GRFs). The subplots show horizontal and vertical GRFs, F_x and F_y; vertical displacement, Δy; and changes in forward kinetic and gravitational potential energies, ΔE_k,x and ΔE_p. The vertical displacement is compared with that of an inverted pendulum (dashed line). The shaded segments at the time-scales denote double supports. The depicted lengths of the time-scales reflect the absolute stance times.

The stance-phase patterns of the three example solutions A–C not only share general features of animal and human walking, but also have differences that reflect those observed in walking at different speeds. First, the patterns differ in their symmetry with respect to midstance (50% of stance time). They are symmetric in A and C, but asymmetric in B. For instance, in A and C, the vertical GRF has two equal peaks that lead to the known M-shape. On the contrary, in B, the vertical force has a first peak that is clearly higher than the second one (F_y, first row). Furthermore, the patterns differ in their amplitudes, which are large in A and B, but only small in C. For instance, although for all three solutions A–C, the vertical displacement of the COM is smaller than that of an inverted pendulum, in C, the COM remains close to the landing height throughout stance (Δy, second row). Similar differences in symmetry and amplitude can be found in animal and human walking when considering different speeds (Keller et al. 1996). For slow walking, symmetric stance-phase patterns with small amplitudes are observed that compare to the patterns in C. For faster walking, patterns with larger amplitudes are observed that compare to the patterns in A or B.

To investigate how the solutions A–C depend on the specific parameters chosen, we scan the physiologically plausible range of angle of attack α₀, spring stiffness k and system energy E_s for stable locomotion of the model. (Dimensional analysis shows that the model has only three independent parameters: angle of attack α₀, dimensionless spring stiffness $\tilde{k}=k{\ell }_0/(mg)$ and dimensionless system energy ${\tilde{E}}_{\text{s}}=E_{\text{s}}/(mg{\ell }_0)$, where E_s is the constant system energy of the conservative model. Without loss of generality, we can use their dimensional counterparts α₀, k and E_s, since we fixed the remaining parameters m, g and ${\ell }_0$.) We find that the parameter adjustments leading to solutions, which describe animal- and human-like patterns similar to A–C, form a whole domain in this three-dimensional parameter space (figure 4a, walking domain indicated by double force-peak icon). This domain splits into three sub-domains (slice through this domain at E_s=816 J shown in figure 4b), which correspond to the three characteristic solutions A–C. Within these sub-domains, the model is robust with respect to changes in swing-leg orientation and spring stiffness. Although different angles α₀ or stiffness values k lead to different steady-state solutions, their stance-phase patterns show the same characteristics. Across the three sub-domains, the model still tolerates changes in its leg parameters, but assumes characteristically different steady-state solutions. For instance, at a system energy of E_s=816 J, which corresponds to an average walking speed of about 1.2 m s⁻¹ in the model, solutions with small amplitudes, such as in C, are obtained for steep angles and stiff-leg springs $({\alpha }_0>75°,k>17\text{kN}{\text{m}}^{-1})$; solutions with larger amplitudes, such as in A or B, result from flatter angles and more compliant leg springs $({\alpha }_0<75°,k<17\text{kN}{\text{m}}^{-1})$. Here, the leg stiffness predicted for walking is so low that it approaches values reported for running (Farley et al. 1993).

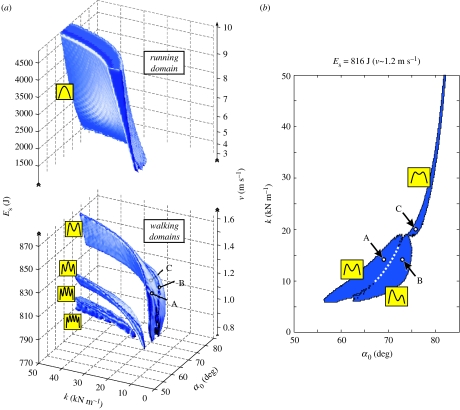
Figure 4.

Parameter domains for stable walking and running. (a) Combinations of angle of attack α₀, spring stiffness k and system energy E_s leading to stable locomotion are shown. Related to E_s, the locomotion speed v is shown, which is the average speed of all solutions that belong to one system energy (maximum deviation 0.1 m s⁻¹ at E_s=800 J). The model finds stable walking at low energies or slow speeds (walking domains): next to the domain with double-peak patterns of the vertical GRF, domains with multi-peak patterns exist (small icons). Owing to the limited scan resolution, only domains with up to five peaks are resolved, and the four- and five-peak domains seem to overlap. Circles indicate the parameter sets of the examples A–C shown in figure 3. In addition to walking, the model finds stable running with single-peak vertical GRF above an energy or speed gap of about 500 J or 1.5 m s⁻¹ (running domain). Note the different scales of system energy at the walking domains and the running domain. (b) A slice at E_s=816 J (v∼1.2 m s⁻¹) through the walking domain with double-peak patterns is shown. Three sub-domains of parameters exist that lead to three qualitatively different steady-state patterns (small icons) exemplified by the three solutions A–C (compare figure 3).

4. Walking solutions unknown from experiments

For lower system energies or slower speeds, the model discovers new domains of parameters for stable locomotion, which lead to steady-state walking patterns unknown from experiments (figure 4a, walking domains indicated by multiple force-peak icons). For instance, the vertical GRF patterns show more than two force peaks. In fact, toward small system energies, the number of force peaks increases with each new domain; and although our limited scan resolution resolves only domains with up to the five-peak force pattern, their number grows incessantly.

The simple analogue of a vertical spring that is loaded by a mass m helps us to understand these multi-peak patterns. Owing to the mass, this spring has a compressed rest position ${\ell }_0^{*}={\ell }_0-(mg/k)$, where k and ${\ell }_0$ are the spring's stiffness and normal rest length. Any small deflection causes this system to oscillate around ${\ell }_0^{*}$ in the vertical GRF with a defined period $T=2\pi \sqrt{m/k}$, and the oscillation results in the peaks and valleys of the GRF measured underneath the spring. If the loaded spring remains in the vertical, the oscillation goes on incessantly and an unlimited number of force peaks is recorded. However, if the spring rotates forward additionally, the oscillation is limited as it falls down; the faster it rotates, the lesser are the number of force peaks recorded.

The natural spring oscillation and its limitation by forward rotation also apply to the bipedal spring–mass model; however, its double support (which is neglected in the inverted pendulum model) adds a crucial component to obtain multi-peak patterns in walking. The second leg not only prevents the COM from falling during locomotion, but also gradually increases and decreases the effective load that acts on the other spring leg in its early and late stance. This ‘load sharing’ allows a stance spring to start from its initial rest length ${\ell }_0$, oscillate around the length ${\ell }_0^{*}$ without completely relaxing in single support, and finally resume its rest length ${\ell }_0$ at the end of stance. The stance spring oscillation and the gradual transition of support by the opposite leg require a precise timing, which is met only by distinct sets of parameters that form the separate parameter domains for stable locomotion of the model.

5. Walking and running mechanics combined in one model

Earlier, we mentioned that, the bipedal spring–mass model may also take off in single support. This happens if the stance spring produces too large a rebound in single-support and relaxes completely, even though it is fully loaded by the mass. For our simple analogue of a vertical spring–mass system, the same happens if the deflection from the compressed rest position ${\ell }_0^{*}$ is too large and the system energy is too high. Although the spring still oscillates around ${\ell }_0^{*}$ in the vertical, it has intermittent flight phases and, in the stance phases, produces only a single rebound with one force peak of the vertical GRF—a behaviour related to bouncing gaits. Consequently, the bipedal spring–mass model cannot only walk, but also run (see also appendix Ad).

As a result, the bipedal model unifies both gaits with one mechanical concept and extending the systematic parameter scan to higher system energies additionally reveals the domain of parameters that lead to stable running of the model (figure 4a, running domain indicated by single force-peak icon). This domain has already been described in an earlier study on spring–mass running (Seyfarth et al. 2002). It requires a minimum locomotion speed of about 3 m s⁻¹, which introduces a speed gap of about 1.5 m s⁻¹ between the two gaits. A similar speed gap, albeit not as large, is found in experiments on the human gait transition. Even though humans prefer to switch from walking to running at one speed of about 2.3 m s⁻¹ when they are instructed to walk or run at different speeds on a treadmill (Thorstensson & Roberthson 1987; Hreljac 1993), they immediately switch from walking at about 1.8 m s⁻¹ to running at about 2.3 m s⁻¹ during spontaneous overground progression (Minetti et al. 1994), which more closely resembles the natural situation.

6. Discussion

Our results suggest that the two fundamental gaits of walking and running are much less different than generally assumed; with the same compliant stance-leg behaviour found in running, a bipedal spring–mass model could reproduce the stance dynamics observed in walking (figure 3). Thus, it seems that, rather than a stiff-legged inverted pendulum gait, walking is, like running, a bouncing gait. Here, the sequence of single and double support in walking replaces that of flight and stance in running. Moreover, the identified multi-peak patterns show that walking and running are just two out of the many stable solutions to legged locomotion of the same mechanical system. Each of these multi-peak solutions occupies a separate domain in the parameter space (figure 4a). In particular, the walking and running domains are isolated by a gap in system energy or locomotion speed, which could explain why both gaits are perceived as such distinct gaits in animal and human locomotion, even though they represent the same mechanical concept that is based on compliant leg behaviour.

The results also challenge the view that the walking efficiency depends on how close the COM motion resembles that of an inverted pendulum. Classically, walking efficiency is quantified by the percentage recovery, a parameter that determines how much of the stride energy is recovered using the inverted pendulum's compensating exchange of gravitational potential and kinetic energies (Cavagna et al. 1977; Mochon & McMahon 1980; Dickinson et al. 2000). For an ideal stiff-legged walk, the percentage recovery would be 100%, yet walking experiments show that it reaches at best 70% in bipeds and only 35–50% in quadrupeds (Cavagna et al. 1977; Minetti et al. 1999). The difference is mostly related to the double supports in which reversing the COM in the vertical disturbs the motion of consecutive inverted pendulum arcs (Alexander 1976, 1991; McGeer 1990). However, the bipedal spring–mass model shows that double supports are crucial to obtain the walking dynamics and also demonstrates that a resulting low percentage recovery (15–35% for examples A–C) does not imply inefficient walking. By transiently storing in the leg springs the energy that would otherwise be lost during double support, the model recovers 100% of the stride energy. Recent experimental findings support such an elastic contribution (Fukunaga et al. 2001). Thus, walking efficiency seems to depend less on how close the COM trajectory follows inverted pendulum arcs, but more on how much of the stride energy can be stored elastically when redirecting the COM in double support.

The bipedal spring–mass model is a very simple model of legged locomotion, which in contrast to more complex representations (Pandy 2003; Zajac et al. 2003) includes only two essential features: bipedalism and leg compliance. Yet, this model explains the basic dynamics of walking and running, and unites both gaits within one consistent mechanical framework. It may therefore serve in future as a general gait template (Full & Koditschek 1999) that guides more complex models in exploring, and technical systems in realizing, legged locomotion from walking to the walk–run transition to running.

Appendix A

(a) Model equations and simulation environment

For a single step from one apex (i) to the next (i+1, compare figure 2), the equations governing the motion of the COM are $m\ddot{x}=Px$ and $m\ddot{y}=Py-mg$ in the initial left leg single support, $m\ddot{x}=Px-Q(d-x)$ and $m\ddot{y}=Py+Qy-mg$ in the intermittent double support, and $m\ddot{x}=-Q(d-x)$ and $m\ddot{y}=Qy-mg$ in the final right leg single support, where $P=k({\ell }_0/\sqrt{x^2+y^2}-1)$, $Q=k({\ell }_0/\sqrt{{(d-x)}^2+y^2}-1)$ and $d={\text{FP}}_{i+1,x}-{\text{FP}}_{i,x}$ with FP denoting the foot point of a stance spring. The model is implemented in the Matlab/Simulink environment (Rel. 14, Mathworks, Inc., Natick, MA, USA) and simulations are run using the embedded variable step integrator ode113 (maximum step size: 10⁻³, absolute and relative error tolerance: 10⁻⁶).

(b) Apex return map

During a walking step that starts at apex i, the simulation aborts if the model turns backward, takes off in single support or stumbles and falls down (y_i+1<y_TD). The simulation otherwise stops if the model reaches the next apex i+1. The relationship between the initial system state at apex i and the resulting system state at apex i+1 defines the apex return map, whose fixed points identify the steady-state locomotion of the model. At any apex (index ‘apex’), the system state simplifies to only two independent variables: the horizontal distance between COM and foot point of the stance spring (FP; figure 2), $\mathrm{\Delta }{x}_{\text{apex}}=x_{\text{apex}}-{\text{FP}}_{\text{apex},x}$, and the apex height, y_apex. This simplification holds since Δx_apex accounts for the influence of x_apex on the dynamics of a step, ${\dot{x}}_{\text{apex}}=\sqrt{2E_{\text{s}}/m-k/m{({\ell }_0-{\ell }_{\text{apex}})}^2-2g{y}_{\text{apex}}}$, where E_s is the constant system energy of the conservative spring–mass model and ${\ell }_{\text{apex}}=\sqrt{\mathrm{\Delta }{x}_{\text{apex}}^2+y_{\text{apex}}^2}$, and ${\dot{y}}_{\text{apex}}=0$ by definition of the apex event. Consequently, the apex return map is defined as R:(Δx, y)_i→(Δx, y)_i+1. A fixed point R satisfies the condition (Δx, y)_i+1=(Δx, y)_i and corresponds to steady-state locomotion of the walking model (we investigate only period-one limit cycles). A stable fixed point additionally satisfies that, in its neighbourhood, the eigenvalues λ_1,2 of the Jacobian matrix

$$D{R}_{ab}=\left(\begin{array}{cc}\frac{\partial \mathrm{\Delta }{x}_{i+1}}{\partial \mathrm{\Delta }{x}_i}& \frac{\partial \mathrm{\Delta }{x}_{i+1}}{\partial y_i}\\ \frac{\partial y_{i+1}}{\partial \mathrm{\Delta }{x}_i}& \frac{\partial y_{i+1}}{\partial y_i}\end{array}\right)$$

lie within the unit circle (|λ_1,2|<1) (Strogatz 2001). A stable fixed point does not require that the fixed-point condition be met exactly when computing R, as the model converges to the steady-state trajectory also from slightly disturbed apex states.

(c) Numerical return map analysis

We exploit the convergence to stable fixed points to find the steady-state locomotion of the model using the apex return map. Instead of computing R from single-step simulations of an extensive grid of initial apex states, we investigate only 50 such states (see below), but for each of them, iterate the step simulation. If any of these states lies in the basin of attraction of a stable fixed point, the model converges to the steady-state trajectory during iteration. For practical reasons, however, we stop after 99 steps and verify that an identified fixed point is a stable one by checking λ_1,2 in a small neighbourhood of it.

The 50 initial apex states are 50 equally distributed apex heights y_i ranging from $y_{\text{min}}={\ell }_0\text{sin}{\alpha }_0$ (landing condition of swing leg) to $y_{\text{max}}={\ell }_0$ (take-off condition of stance leg) with the initial horizontal position fixed to Δx_i=0. This restriction to vertical spring positions as initial apex states assumes that they cover the basin of attraction of stable solutions. The assumption is justified for symmetric steady-state trajectories (examples A and C in figure 3) as they correspond to fixed points with Δx_apex=0, but it may be wrong for asymmetric steady-state trajectories (example B in figure 3) as they correspond to fixed points with Δx_apex≠0. However, preliminary tests that compared this simplified search algorithm with extensive return map scans, including asymmetric start positions x_Δ,i≠0, showed no substantial differences in finding stable asymmetric, as well as symmetric, steady-state solutions.

(d) Extension to running

Running needs no different model, but two formal changes in the simulation. First, we enable flight phases. Starting at apex i, the former sequence of single–double–single support phase now can be paralleled by a sequence of flight–stance–flight phase. Reaching apex i+1 in the second flight phase completes a step. The apex return map simplifies to R:y_i→y_i+1 (Seyfarth et al. 2002). Its analysis remains the same as described earlier. Second, to avoid hopping with two parallel legs, we ensure that only one leg can land at a time.