An experimental study into the acousto-mechanical effects of invading the cochlea

Abstract

The active and nonlinear mechanical processing of sound that takes place in the mammalian cochlea is fundamental to our sense of hearing. We have investigated the effects of opening the cochlea in order to make experimental observations of this processing. Using an optically transparent window that permits laser interferometric access to the apical turn of the guinea-pig cochlea, we show that the acousto-mechanical transfer functions of the sealed (i.e. near intact) cochlea are considerably simpler than those of the unsealed cochlea. Comparison of our results with those of others suggests that most previous investigations of apical cochlear mechanics have been made under unsealed conditions, and are therefore likely to have misrepresented the filtering of low-frequency sounds in the cochlea. The mechanical filtering that is apparent in the apical turns of sealed cochleae also differs from the filtering seen in individual auditory nerve fibres with similar characteristic frequencies. As previous studies have shown the neural and mechanical tuning of the basal cochlea to be almost identical, we conclude that the strategies used to process low frequency sounds in the apical turns of the cochlea might differ fundamentally from those used to process high frequency sounds in the basal turns.

1. Introduction

The cochlea, which is the acoustic portion of the inner ear, converts sound waves into meaningful patterns of neural activity. In the mammalian cochlea, much of the sound processing that accompanies this conversion is accomplished mechanically: tuned accessory structures (including the basilar membrane; BM in figure 1) split the sound into its various spectral components, and active (i.e. force generating) processes that originate in the motile outer hair cells of the organ of Corti amplify the sound (for a recent review, see Robles & Ruggero 2001). This active cochlear mechanical processing is the subject of intense medical and scientific interest, because it underlies both the frequency selectivity and the sensitivity of the entire auditory system. The processing seems to change in nature from the base of the cochlea, where the highest frequency components of a sound are processed, to the apex, where the lowest frequencies are analysed (Cooper & Rhode 1998; Robles & Ruggero 2001). The present study focuses on one aspect of cochlear mechanics which has been overlooked in many previous studies, but which could explain some significant differences between previous studies of the basal (i.e. high frequency) versus apical (low frequency) regions of the mammalian cochlea.

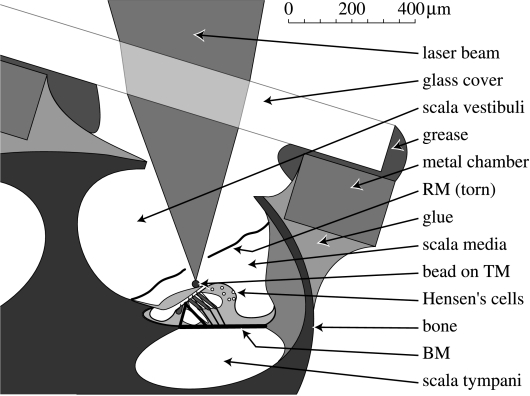
Figure 1.

The interferometric approach to the apical turn of the guinea-pig cochlea, showing schematic details of the artificial chamber that permits the apical cochlea to be sealed and unsealed. The laser interferometer is shown focused on a reflective bead that has been deposited on the tectorial membrane (TM) via a small tear in Reissner's membrane (RM). Recordings from the naturally reflective lipid droplets (white circles) in the Hensen's cell region were made both before and after the RM was torn (see §2 for details). BM, basilar membrane.

One of the most striking differences between the mechanics of the basal and apical cochlea concerns the number of peaks in their frequency tuning characteristics. Acousto-mechanical transfer functions for each location in the basal cochlea peak at only one frequency, whereas those for locations in the apical cochlea are commonly reported to have two peaks, separated by a distinct ‘mid-band sensitivity notch’ (Khanna et al. 1989; Cooper & Rhode 1995, 1996; Cooper 1996; Gummer et al. 1996). Furthermore, while the shapes of the single peaks in the basal turn transfer functions closely match the shapes of the tuning curves for auditory nerve fibres with appropriate ‘best’ or ‘characteristic’ frequencies (BF/CF; e.g. see Narayan et al. 1998), the shapes of the apical turn transfer functions differ both quantitatively and qualitatively from those observed at the level of the auditory nerve (Cooper & Rhode 1995, 1998). Mid-band sensitivity notches do occur in the threshold tuning curves of single auditory nerve fibres in the apical turns of the cochlea (e.g. as highlighted for CFs of below approx. 1 kHz by Kiang et al. 1986), but the location(s) of these notches differs from those observed in the mechanical experiments: two notches are often seen in each auditory nerve fibre, one above CF and one below CF, whereas the mechanical notches are commonly seen only above CF. (Multiple notches have also been observed recently in mechanical experiments at high sound pressure levels in the basal cochlea (e.g. Rhode in press), but these are not apparent in the near-threshold tuning characteristics.)

Two groups of hypotheses have been proposed to account for the sensitivity notches that are seen in the apical cochlea. The first group associates the notches with a loading effect of the tectorial membrane (TM). The TM has been hypothesized to act as an independent mechanical resonator that can modify the mechanical tuning seen both at and beyond the level of the BM (Zwislocki & Kletsky 1979; Allen 1980; Zwislocki 1980). Resonant TM hypotheses have received experimental support from some in vitro mechanical measurements (e.g. Gummer et al. 1996; Hemmert et al. 2000b), but appear to be inconsistent with other measurements, including those made in vivo (e.g. Cooper & Rhode 1995, 1998; Ulfendahl et al. 1995; Rhode & Cooper 1996; Dong & Cooper 2002).

The second group of hypotheses attributes the mechanical notches to the destructive interference that can occur between two types of fluid-borne wave in the cochlea, and argues that this interference only becomes problematical (i.e. gives rise to a mid-band notch) when the cochlea is invaded, or ‘unsealed’ (as it has been in most of the mechanical studies that have been carried out to date). The two-wave hypotheses do not account for the notches that can be seen in neural tuning curves, but they do put strong constraints on their likely origins. If the macro-mechanical movements of the cochlear partition do not contain mid-band notches (in an intact cochlea), while the neural tuning curves do, then the neural notches are likely to be either ‘micro-mechanical’ or electrical in origin (e.g. as in the models of Zwislocki & Kletsky 1979; Allen 1980; Zwislocki 1980; Hubbard 1993).

The first type of wave in most two-wave hypotheses is a compressional wave that propagates at a speed close to that of sound in water (i.e. approx. 1500 m s⁻¹). The compressional wave is often considered to invade all regions of the cochlea instantaneously, such that it can be treated (mathematically) as a ‘common-mode’ wave. This type of wave has become known as the ‘P+’ wave of cochlear mechanics (after Peterson & Bogert 1950), and is ignored in most modelling studies because (by definition) it cannot move the BM. The second type of wave in the cochlea is a travelling pressure-difference wave, which was denoted ‘P−’ by Peterson & Bogert (1950), and which has been studied extensively ever since the pioneering works of Békésy (1960) and Zwislocki (1948). The travelling wave is dispersive, and propagates much more slowly than the compressional wave, because it depends on interactions between the fluid pressure-differences and the flexible mechanical elements of the cochlear partition (the most important of these being the BM, see Lighthill 1981 for review). Direct recordings of both the P+ and the P− waves have recently been provided in detailed studies of the fluid pressure distributions in the scalae of living cochleae (e.g. Olson 1998, 1999, 2001; Dong & Olson 2005).

In order to further our understanding of the cochlea's mechanics, we have sought to test the hypothesis that mid-band sensitivity notches result from the interaction between the two types of wave discussed above. Our approach involved comparisons between the sound-evoked vibrations observed in individual cochleae under ‘sealed’ and ‘unsealed’ conditions, and our results demonstrate that mid-band sensitivity notches are artefacts of the unsealed cochlea. Perhaps more importantly, our findings in sealed cochleae open up the possibility that substantial differences exist between the mechanical and neural tuning properties of the mammalian cochlea, especially in its apical-most region.

2. Methods

Sound-evoked vibrations were recorded from Hensen's cells (HCs) and from the TM in the apical turn of the cochlea in deeply anaesthetized guinea-pigs. All of the experiments were conducted on a vibration-isolated table inside a sound-isolated chamber. The experimental techniques were similar to those used in previous studies (Cooper & Rhode 1995, 1996), with all procedures performed in accordance with UK Home Office guidelines on the operation of the Animals (Scientific Procedures) Act of 1986. Young, pigmented guinea-pigs (weight range 320–800 g) were anaesthetized using combinations of sodium pentobarbitone (30 mg kg⁻¹) and Hypnorm (0.6 ml kg⁻¹). Anaesthesia was monitored by testing the pedal withdrawal reflex at intervals of no more than 30 min, with supplementary doses of the anaesthetics being given to eliminate this reflex throughout all in vivo procedures. Lethal overdoses of pentobarbitone were administered at the end of the in vivo recordings. The animals' core temperatures were maintained at 37–38 °C using a thermostatic heating blanket monitored by a rectal probe thermistor. A tracheotomy was performed and artificial ventilation was used to maintain end-tidal CO₂ concentrations around 4.5%.

The right ear canal was exposed and resected, the postero-lateral and ventral aspects of the right auditory bulla were exposed and opened, and the dorsal surface of the skull was fixed into a combined head-holder and ear-piece using bone-screws and dental cement. A closed-field sound-system was used to deliver acoustic stimuli into the ear canal, and sound pressure levels (measured in decibels re: 20 μPa, i.e. dB SPL) were calibrated within 3 mm of the eardrum using a probe tube microphone.

Sound-evoked compound action potential (CAP) recordings were made from a silver wire electrode attached to a bony niche within approximately 1 mm of the round window. CAP threshold audiograms (Johnstone et al. 1979) were used to monitor the cochlea's condition at key points during the experiment, including: (i) immediately after the initial exposure of the cochlea; (ii) after opening a small hole (approx. 400×600 μm) at the apex of the cochlea; (iii) after tearing Reissner's membrane (RM); and (iv) near the end of the in vivo recordings. As reported elsewhere (Dong & Cooper 2001), the only procedure to have a consistent and significant effect on the low-frequency (e.g. 0.3–1 kHz) CAP thresholds (typically in the form of a 10–20 dB sensitivity loss) was the tearing of the RM.

An artificial chamber with a removable glass cover-slip was constructed to allow HC and TM recordings to be made under ‘sealed’ and ‘unsealed’ cochlear conditions, as illustrated in figure 1. The metal body of the chamber was glued to the apex (using cyanoacrylate adhesive) before the cochlea was opened. The cochlear opening measured between 200 μm×200 μm and 600 μm×400 μm, and was made at a position approximately 17 mm from the base of the basilar membrane according to Békésy's map of the guinea-pig cochlea (see fig. 12–21 of Békésy 1960). Care was taken to avoid damaging the underlying RM at this stage in the experiment. The glass cover-slip was held on top of the chamber by a thin layer of high-vacuum grease, which was smeared onto both the glass and metal surfaces before the cochlea was opened. A fluid-tight seal between the cover-slip and the grease was a pre-requisite for recording under sealed conditions, but this seal was rarely maintained for long (in vivo): in healthy animals, the static intra-cochlear fluid pressure tended to rupture the seal after between 5 and 20 min. Recordings of the responses under unsealed conditions were made after the seal had been ruptured, while the cover-slip was still ‘in place’ but with fluid leaking out of the chamber. Recordings were discontinued whenever the fluid dislodged the glass cover to such an extent that the optical field of view and/or the interferometer's alignment (see below) became unsatisfactory.

Measurements of sound-evoked vibrations were made using a displacement-sensitive heterodyne laser interferometer (Cooper 1999). Responses were measured either from the HCs, or from gold-coated polystyrene microbeads (25 μm diameter, 1.05 g cm⁻³; Polysciences, Inc.) that had been deposited on the TM after the RM had been torn (as illustrated in figure 1). The HCs were the only natural structures in the apex of the cochlea that reflected enough light for our interferometer to work with a high signal-to-noise ratio. The recordings from the HCs could be collected both before and after the RM was torn, whereas those from the TM could only be made after tearing the RM (a process which abolishes the endocochlear potential, and allows perilymph and endolymph to mix together, etc.).

Response waveforms were digitized and averaged across multiple presentations of a given acoustic stimulus (e.g. a click, or a short tone burst of a given frequency and intensity) before being stored to disk for off-line analysis. Recordings of the sound-evoked vibrations of the ossicles in the middle ear (typically on the lenticular process of the incus) were used to normalize the cochlear data.

3. Results

Due to the difficulties of re-sealing the cochleae after the initial openings, only 10 cochleae provided convincing data on the mechanical effects of opening the apical turn. Data from five of the best experiments are highlighted in this study, with the quality of the experiments being judged by: (i) the acoustic sensitivity of the preparation; (ii) the presence of sound-evoked shifts in the baseline position of the cochlear partition before the RM was ruptured; and (iii) the availability of clean, stable data recorded in quick succession under both sealed and unsealed conditions.

3.1 Effects on responses to tone bursts: in the time domain

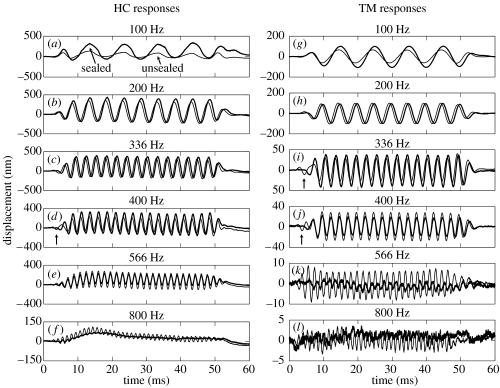
In vivo responses to four series of 80 dB SPL tone bursts at six frequencies are presented for one animal (wub92) in figure 2. The responses were measured from a single HC (left panels, before the RM was torn) and from a reflective bead that had settled on the TM (right panels, after the RM was torn). The thick lines in figure 2 show the responses under sealed conditions, and the thin lines show those under unsealed conditions. All of the responses have measurable sinusoidal components under both sealed and unsealed conditions. There are visible levels of harmonic distortion in the low-frequency HC responses, but the distortion disappears once the RM has been torn (e.g. as illustrated by the TM responses). Baseline position shifts are also evident in the HC recordings (when the RM was intact), but these are not the focus of the present report (cf. Cooper & Dong 2000, 2003). Below approximately 200 Hz, the responses from the sealed cochlea are larger than those from the unsealed cochlea: e.g. the amplitudes of the HC vibrations fall by 9 dB at 100 Hz (figure 2a) and those of the TM fall by 4 dB at 100 Hz (figure 2g) when the cochlea is unsealed. Above the preparation's BF of approximately 200–300 Hz, the response amplitudes are lower in the sealed cochlea than in the unsealed cochlea: e.g. there are 4 dB increases at 566 Hz for the HC (figure 2e) and at 400 Hz for the TM (figure 2j) when the cochlea is unsealed. The hydraulic state of the cochlea also affects the timing of the responses: slight phase-leads occur at most frequencies when the apex becomes unsealed, and distinct ‘onset responses’ and/or phase reversals occur at some frequencies under unsealed conditions (e.g. at 400 Hz on the HC, and at 366 and 400 Hz on the TM, see arrows in figure 2d,i,j).

Figure 2.

HC and TM responses to tone bursts in one cochlea (wub92). Bold and thin lines depict responses under sealed and unsealed conditions, respectively. (a–f) HC responses recorded before the RM was torn to expose the TM. (g–l) TM responses recorded after tearing the RM. Arrows in (d), (i) and (j) point out ‘early onset’ and ‘phase-reversed’ response components observed under unsealed conditions (as described in text). Stimulus level=80 dB SPL. Responses averaged 16×.

3.2 Effects on responses to tone bursts: in the frequency domain

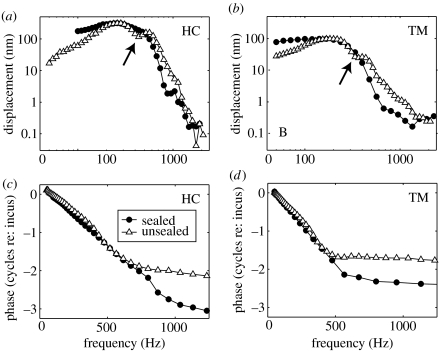
Figure 3 shows the tuning characteristics derived from HC and TM responses like those shown in figure 2. The variation in vibration amplitude as a function of stimulus frequency is shown in figure 3a,b, while the phase accumulation with frequency is shown in figure 3c,d (re: the middle-ear responses measured from the incus). Under sealed conditions (filled circles in figure 3), the tuning curves are relatively flat below the preparation's BF (approx. 250 Hz for the HC, before tearing the RM, and approx. 200 Hz for the TM, after tearing the RM). Above the BF, the tuning curves decrease at rates which increase with increasing frequency until approximately 600–800 Hz. Under unsealed conditions (open triangles in figure 3), however, the tuning curves look more like bell-shaped band-pass filters with a significant mid-band sensitivity notch (at approx. 430 Hz for the HC and 350 Hz for the TM—see arrows in figure 3a,b, respectively). The BFs under unsealed conditions are similar to those in the sealed cochleae, but the shapes of the tuning curves are different. The phase accumulation in the unsealed cochlea is less than that in the sealed cochlea over much of the frequency range, as shown in figure 3c,d.

Figure 3.

Tuning characteristics derived from HC and TM responses to tone bursts in one cochlea (wub92). (a, b) Response amplitudes evoked by 80 dB SPL stimuli under sealed and unsealed conditions (filled circles and open triangles, respectively). Arrows point to mid-band sensitivity notches observed under unsealed conditions. (c, d) Corresponding phase data, expressed relative to the incus responses in the same ear.

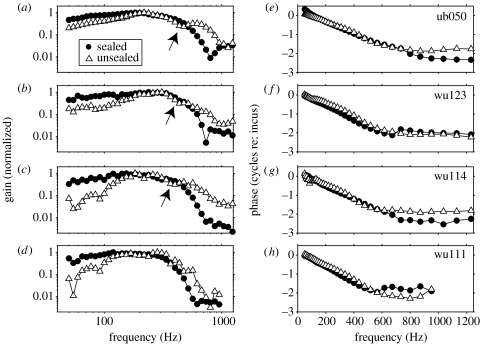
Figure 4 shows amplitude and phase transfer functions derived from four other cochleae under sealed and unsealed conditions. Filled circles depict responses under sealed conditions, and open triangles show those under unsealed conditions. Each transfer function is shown after normalization by the relevant middle-ear data. In order to compensate for any magnitude differences that might result from between-condition differences in the recording positions used in each preparation, the amplitude transfer functions in figure 4a–d have also been normalized by their peak values (this normalization reduced the variation across the experiments shown by a factor of approx. 4). Unsealing the cochlea decreases the transfer function gain below each preparation's BF, but increases it at higher frequencies (e.g. above 600 Hz in figure 4a–d). In addition, there is some evidence of a mid-band sensitivity notch in three out of the four cochleae under unsealed conditions (see arrows in figure 4a–c), but not under sealed conditions. The hydraulic condition has relatively little effect on the phase transfer functions, although slight phase-leads occur at most mid-band frequencies (e.g. 100–500 Hz) when the cochlea becomes unsealed.

Figure 4.

Transfer functions derived from HC responses to 80 dB SPL tone bursts in four cochleae. Filled circles and open triangles show responses observed under sealed and unsealed conditions, respectively. All of the responses have been normalized by the incus responses observed in the same ears, and response amplitudes are expressed with respect to their peak values (i.e. normalized to a peak ‘gain’ of 1; see text).

3.3 Effects on responses to clicks: in the time domain

Previous studies (e.g. Cooper 1996; Cooper & Rhode 1996) have suggested that mid-band sensitivity notches, such as those described above, arise from interactions between two types of waves in the cochlea: a fast ‘longitudinal’ compression wave, which would not normally drive the cochlear partition directly, and a slow ‘transverse’ wave, which is driven by pressure differences across the cochlear partition (between the scala vestibuli/media and the scala tympani). This possibility can be explored further by studying the cochlea's responses to transient stimuli, which should permit the ‘fast’ and ‘slow’ features of the responses to be separated (in the time domain) and characterized almost independently.

Figure 5b–f shows HC responses to condensation and rarefaction clicks in one cochlea under various hydraulic conditions. The responses of the incus in the same ear are plotted in figure 5a for comparison. The incus responses consist of a short, almost unidirectional pulse, consistent with the relatively untuned, wide-band nature of middle-ear vibrations. The condensation clicks (right column) cause the incus to push the oval window inwards, while the rarefaction clicks (left column) pull the oval window outwards with respect to the cochlea.

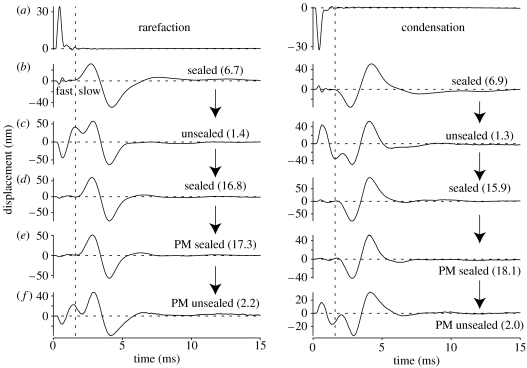
Figure 5.

Responses to rarefaction and condensation clicks in one cochlea (ub050). (a) Responses recorded from the incus. (b–f) Responses from a small cluster of HCs under different hydraulic and physiological conditions. The apical cochlea was initially (b) sealed, (c) became unsealed and (d) was re-sealed using a new cover-slip. Post-mortem (PM) measurements were then made under (e) sealed conditions before the cover-slip was dislodged manually to obtain the final (f) unsealed waveforms. The vertical dashed lines mark the onset of the major HC response component under sealed cochlear conditions. These lines serve as a boundary to separate the ‘fast’ and ‘slow’ components of each response, despite the fact that the components overlap when the cochlea is unsealed (see text). The numbers in parentheses alongside each waveform indicate the ratio of the peak-to-peak amplitudes of the response components occurring on either side of the vertical line (i.e. the slow component's peak-to-peak amplitude divided by the fast component's peak-to-peak amplitude). Peak-equivalent stimulus levels=80 dB SPL. Responses averaged 250×. The RM was intact during all measurements.

The HC responses to the clicks can be divided into two more-or-less distinct components in the time domain. The first component (labelled ‘fast’ in figure 5b) is smaller than the second, and begins within 30 μs of the incus vibrations. This component is particularly small, short-lived, and easy to distinguish in the well-sealed cochlea (as illustrated in figure 5b,d,e), but it becomes larger, more prolonged, and impossible to separate from later components when the cochlea is unsealed (as illustrated in figure 5c,f). The second component of the responses (labelled ‘slow’ in figure 5b) begins around 1.5 ms after the onset of the incus vibrations, and is larger in amplitude and longer in duration than the first component (oscillating for at least 6 ms in most preparations). The two components can be distinguished (i.e. separated) quite well in the time domain when the cochlea is sealed (e.g. figure 5b,d,e), but they merge together under unsealed conditions (figure 5c,f).

The fast and slow components of the cochlea's responses to a click differ in two fundamental respects. First, the amplitude (and shape) of the fast component varies considerably with the hydraulic condition of the cochlea, whereas that of the slow component does not. The second difference relates to the polarities of the two components. In response to a condensation (rarefaction) click, the fast component initially deflects the cochlear partition towards the scala vestibuli (scala tympani), whereas the slow component deflects it towards the scala tympani (scala vestibuli) before the scala vestibuli (scala tympani).

Since the fast component of the click responses is at its smallest when the cochlea is sealed, we suggest that the ratio of the slow component's amplitude to the fast component's amplitude can be used to assess the ‘quality’ of the chamber's seal. Based on the data from this study (e.g. figures 5 and 6), we suggest that slow/fast component amplitude ratios below 5 indicate that the cochlea is not well sealed, while those above 10 indicate that it is well sealed.

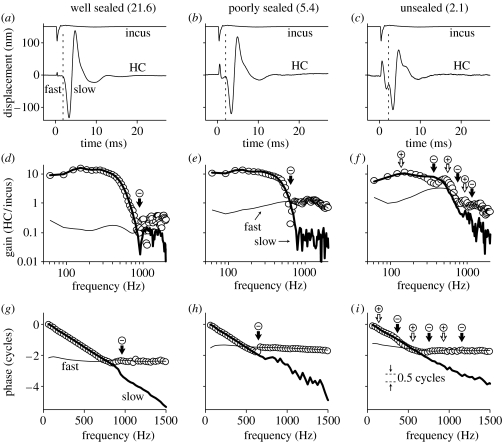
Figure 6.

Frequency-dependent interactions between ‘fast’ and ‘slow’ response components in one cochlea (wu126). (a–c) HC and incus responses to rarefaction clicks under three different sealing conditions, as labelled. Vertical dashed lines are used to separate each HC response into fast and slow components. The numbers in parentheses above each panel indicate the ratio of the peak-to-peak amplitudes of the fast and slow HC response components (i.e. the slow component's peak-to-peak amplitude divided by the fast component's peak-to-peak amplitude). (d–f) Amplitude transfer functions derived from data in (a–c), respectively. The fast and slow components (thin and bold solid lines, respectively) were analysed after separating the responses in the time-domain using a 720 μs wide raised-cosine ramp function centred on the dashed lines in (a–c). The transfer functions for the complete time-domain responses are shown as open circles. (g–i) Corresponding phase transfer functions. The fast component phases have been offset by either 1.0 or 2.0 cycles to facilitate their comparison with the complete phase transfer functions (open circles). The arrows in (d–i) indicate a selection of frequencies where the fast and slow components occur exactly in-phase (+, open arrows) or in anti-phase (−, solid arrows). Peak-equivalent stimulus levels=80 dB SPL. Responses averaged 250×. The RM was intact during all measurements.

3.4 Frequency-dependent interactions between fast and slow components of the click-evoked responses

Figure 6 explores the spectral consequences of the interactions that take place between the fast and slow components of the cochlea's response to a transient stimulus. Figure 6a–c shows the responses of a single HC to rarefaction clicks under three different conditions: in figure 6a, the cochlea was well sealed; in figure 6b, the seal was just about to rupture (although no fluid could be seen leaking from the chamber at the point that this recording was made); and in figure 6c, the seal had ruptured. The fast response component grows considerably larger (and wider) from figure 6a to c, whereas the slow component becomes slightly smaller (see §4, and note the decrease in the slow component/fast component amplitude ratio, from 21.6, through 5.4, to 2.1, in figure 6a–c).

The spectral composition of each of the time-domain responses shown in figure 6a–c is examined in figure 6d–f (in terms of amplitude), and g–i (in terms of phase), respectively. The open circles in these figures show the magnitudes and phases of the fast Fourier transforms of the raw (i.e. complete) response waveforms (each expressed relative to the incus responses). In the well-sealed cochlea, the ‘complete’ amplitude transfer function (shown by the circles in figure 6d) resembles a low-pass filter that is similar to those observed using tone burst stimuli in sealed cochleae (e.g. figures 3 and 4). In the data from the unsealed cochlea (figure 6f), however, the complete transfer function is more complex, with at least one mid-band sensitivity notch (cf. the black arrow at approx. 400 Hz in figure 6f).

The spectral contributions made by the fast and slow components of the responses are shown by the bold and thin lines in figure 6d–f and g–i. The slow component's spectrum is similar under all conditions (bold lines in figure 6d–f; the amplitude of the slow component falls by less than 6 dB from figure 6d to f). The slow component has a low-pass transfer function, varying very little below approximately 400 Hz, but then cutting off rapidly to approach a high-frequency plateau where the responses are around 40 dB lower in amplitude (giving gains of around 0.1 above roughly 1 kHz). The stability of the slow component's spectrum across the various conditions confirms our impression that sealing has little effect on the slow component in the time domain. In contrast, the fast component's spectrum changes considerably with the condition of the cochlear seal (thin lines in figure 6d–f). Under well-sealed conditions, the amplitude gain of the fast component is around 0.1–0.4, which is almost 40 dB lower than the gain of the slow component at frequencies below approximately 400 Hz. The fast component becomes comparable in size to the slow component at approximately 800 Hz, and it dominates the overall response above approximately 1000 Hz (figure 6d). Just before the seal ruptured (as shown in figure 6e), the fast component grows by a factor of between 3 and 10 (i.e. 10–20 dB) at all but the lowest frequencies, and it dominates the overall response above approximately 800 Hz. After the seal had ruptured, the fast component grows by a further 10–20 dB, becoming comparable to the slow component at around 400 Hz, and larger than the slow component above approximately 600 Hz.

With reference to the main aim of this paper, it is noteworthy that neither the fast component nor the slow component of the click responses shows any hint of a 400 Hz notch in its transfer function. We can therefore imply that the 400 Hz notch in the ‘complete’ transfer function (open circles in figure 6f) is a result of interference between the fast and slow components. The phase transfer functions for the fast and slow components (as shown in figure 6f–h) lend strong support to this hypothesis. The phase transfer functions for each component can be well approximated by a straight line, with the rate of change of phase with frequency being slow for the fast component, and fast for the slow component. Since the slow component accumulates almost two cycles of phase below the approximately 600 Hz cut-off of its transfer function, while the fast component accumulates virtually no phase, there are two ‘mid-band’ frequencies where the two components occur in anti-phase to one another. Frequencies where the fast and slow components occur in anti-phase are marked by the black arrows in figure 6f,i, and these coincide almost perfectly with the notches in the ‘complete’ amplitude transfer function (open circles in figure 6f). The notches in the complete transfer functions are therefore entirely consistent with those that can be predicted from knowledge of the underlying fast and slow response components.

It is also noteworthy that the destructive interference does not disappear completely even when the cochlea is well sealed: all that happens is that there is a decrease in the amplitude of the fast response component, and a corresponding increase in the frequency at which the amplitudes of the fast and slow components becomes comparable. The notches that separate the main pass-band of the ‘complete’ transfer functions from the plateau region in a sealed cochleae (cf. the black arrows in figure 6d,e) occur at frequencies where the fast and slow response components occur exactly in anti-phase (cf. the black arrows in figure 6g,h). We can therefore conclude that whenever the fast and slow components of a response occur in anti-phase (and have comparable amplitudes), they interfere destructively to cause a notch.

4. Discussion

Experimental investigations of cochlear mechanics almost invariably involve the invasion of the cochlear labyrinth, but the effects of this invasion are rarely taken into account. The present study shows that alterations in the hydraulic state of the apical turn of the cochlea substantially affect its acousto-mechanical response properties: the sensitivity of the cochlear partition is decreased at low frequencies (below the BF) and increased at high frequencies (above the BF) when the scala vestibuli becomes ‘unsealed’. The partition's low-pass tuning characteristics are hence artificially transformed into a more band-pass form. A mid-band sensitivity notch is also ‘created’ by unsealing the cochlea. This notch appears similar in both form and underpinning to the notch that separates the main envelope of the cochlea's travelling wave from the ‘plateau’ response region (at the foot of the transfer function's steep high-frequency cut-off region). The only difference seems to be that the plateau responses are exaggerated in the unsealed cochlea, such that they can interfere with the travelling wave (either constructively or destructively) even in the BF region.

Previous investigations into the effects of sealing and/or unsealing the cochlea lend support to all of our findings: the effects on the low-frequency cut-off slope of the transfer function were first noted by Ulfendahl et al. (1991), and those on the ‘fast’ plateau responses were reported in the mid-1990s (e.g. Cooper 1996; Cooper & Rhode 1996). The idea that destructive interference between the fast and slow response components could lead to the creation of mid-band sensitivity notches in the unsealed cochlea was proposed by Cooper & Rhode (1996), and subsequently supported by others (e.g. Hemmert et al. 2000a,b; Zinn et al. 2000). The origin of the fast response components has remained a somewhat controversial issue: Cooper & Rhode (1996) suggested that the fast responses were driven directly by the fluid-borne compressional wave, and were artefacts of opening the apical cochlea (in effect, they suggested that Peterson & Bogert's (1950) P+ wave became distorted in unsealed cochleae, such that it coupled some sound-energy almost instantaneously into an abnormal P− wave in the immediate vicinity of the cochlear opening). This hypothesis was backed up by the demonstration that the fast responses depended on the hydraulic state of the cochlea. However, Cooper & Rhode were unable to seal the cochlea particularly well, or to seal and unseal it repeatedly, and their findings were hence viewed with scepticism (see, for example, Zinn et al. 2000, who preferred to interpret both the fast responses and the mid-band sensitivity notches as evidence of a resonance in the TM). The findings of the present report (e.g. as shown in figure 5) lend considerable support to Cooper & Rhode's interpretation, by showing that the fast response components become smaller and the mid-band notches disappear in well-sealed cochleae (the hydraulic condition of the apical cochlea would not be expected to affect the function of the TM, of course).

4.1 Do ‘fast’ responses exist in the intact cochlea?

Based on their observations in reasonably well-sealed cochleae, Cooper & Rhode (1996) suggested that fast response components might disappear entirely in fully intact cochleae. However, even the best sealed of the preparations in the present report had measurable fast responses. While this might well indicate that the preparations were not fully intact, a comparison with data obtained in other regions of the cochlea suggests another possibility: perhaps finite levels of fast response exist even in fully intact cochleae. The levels of fast response that we observe (under optimal, even if not perfect conditions) amount to roughly 1% of the responses at the peak of the slow travelling wave. This is very similar to the level observed in the plateau regions of transfer functions measured from the passive BM in the basal turns of the cochlea (e.g. Rhode 1971, 1978, 1980; Wilson & Evans 1983; Robles et al. 1986; Cooper & Rhode 1992; Ruggero et al. 1997). All of these studies have involved opening the cochlea, of course, but this has been done on the opposite side of the cochlear partition than in the present report (i.e. opening the scala tympani, rather than the scala vestibuli) and at the other end of the cochlea (the base, rather than the apex), where any effects on the cochlea's hydrodynamics should be minimized by the presence of the round window (cf. Dancer & Franke 1980; Nedzelnitsky 1980; Olson 1998). Indeed, the recent studies of Narayan et al. (1998; Ruggero et al. 2000) can be used to prove that the effects of opening the basal turn's scala tympani are negligible from a sound processing point of view: these authors recorded tuning curves from individual auditory nerve fibres in the same preparations that they used to make BM recordings from, and found neural tuning which was indistinguishable from normative data (collected from perfectly intact cochleae). What is more, the BM data from these cochleae showed clear evidence of a plateau response region, whereas the neural data did not. The simplest interpretation of these data is that fast responses are a normal feature of the cochlea's hydrodynamic response to a sound, but that (unlike the slow travelling wave responses) they do not lead to excitation of the auditory nerve.

4.2 Comparisons between mechanical and neural tuning

Perhaps the most important new observation to be made in the present report is that the transfer functions recorded from the apical turn of a well-sealed cochlea are almost low-pass in nature. The mechanical tuning therefore differs considerably from the tuning of single auditory nerve fibres with similar CFs, which is more band-pass in nature, with cut-off slopes of between 10 and 20 dB per octave below CF, and over 20 dB per octave above CF (Kiang et al. 1965, 1986; Evans 1972; Cooper & Rhode 1995). The high-frequency cut-off slopes of the mechanical tuning curves in sealed cochleae agree fairly well with the neural data (except for the plateau region), but the low-frequency cut-off is insufficient to explain the neural tuning. The absence of mid-band sensitivity notches in the mechanical tuning of a well-sealed cochlea also contrasts with the neural data, which frequently show at least one sharp notch in their tuning characteristics (e.g. Kiang et al. 1986; Cooper & Rhode 1995).

The discrepancy between the cut-off slopes of the mechanical and neural tuning in the apical turn of the cochlea is highly reminiscent of that which was thought to exist in the basal turn about 30 years ago (cf. Evans 1972; Evans & Wilson 1975). Our understanding of the mechanics in the basal turns of the cochlea has developed significantly over the past 30 years, however, and the mechanical and neural tuning of the basal turns are now known to be almost identical (cf. Narayan et al. 1998; Ruggero et al. 2000). What was discovered during the 1970s and 1980s was that the basal cochlea's mechanics were physiologically vulnerable (e.g. Rhode 1978), and that sharp mechanical tuning in the base of the cochlea depends on the active and nonlinear amplification by the cochlear partition's outer hair cells (see Robles & Ruggero 2001 for a recent review). More recent observations suggest that the sound processing that occurs in the apex of the cochlea is also active and nonlinear (e.g. Rhode & Cooper 1996; Hao & Khanna 2000; Zinn et al. 2000; Cooper & Dong 2003). There is little indication that the frequency selectivity of the apical turn changes substantially with physiological condition, however, because the nonlinearities appear to be either weak (Cooper & Rhode 1995; Hao & Khanna 2000; Zinn et al. 2000; Cooper & Dong 2003) or uniformly distributed over a fairly wide frequency range (Rhode & Cooper 1996).

As most of the cochleae considered in the present study exhibited some evidence of physiologically-vulnerable nonlinearity in their mechanics (before tearing the RM; e.g. figure 2a–f), we consider it unlikely that their tuning could be sharpened up substantially by a ‘cochlear amplifier’ of the type apparent in the more basal cochlea. We therefore suggest (i) that substantial differences exist between the mechanical and neural tuning properties of the apical mammalian cochlea and (ii) that the strategies used to process low frequency sounds in the apical turns of the cochlea differ fundamentally from those used to process high frequency sounds in the basal turns.