Abstract
What type of connectivity structure are we seeing in protein–protein interaction networks? A number of random graph models have been mooted. After fitting model parameters to real data, the models can be judged by their success in reproducing key network properties. Here, we propose a very simple random graph model that inserts a connection according to the degree, or ‘stickiness’, of the two proteins involved. This model can be regarded as a testable distillation of more sophisticated versions that attempt to account for the presence of interaction surfaces or binding domains. By computing a range of network similarity measures, including relative graphlet frequency distance, we find that our model outperforms other random graph classes. In particular, we show that given the underlying degree information, fitting a stickiness model produces better results than simply choosing a degree-matching graph uniformly at random. Therefore, the results lend support to the basic modelling methodology.
Keywords: protein–protein interaction networks, network models, network properties
1. Introduction and model
A protein–protein interaction (PPI) network is commonly viewed as an unweighted, undirected graph. Each node in the graph represents a protein and an edge between a pair of nodes indicates that these proteins have been observed to interact physically (Ito et al. 2000; Uetz et al. 2000; Giot et al. 2003; Li et al. 2004; Rual et al. 2005; Stelzl et al. 2005). The types of connectivity patterns that arise are neither completely random, in the classical Erdös–Rényi sense (henceforth denoted by ‘ER’), nor completely deterministic (Grindrod & Kibble 2004).
In an attempt to understand and describe the PPI connectivities, a number of models, i.e. formulae for generating edges in some probabilistic sense, have been proposed and tested against observed networks (Jeong et al. 2001; Maslov & Sneppen, 2002; Barabási et al. 2003; Pržulj et al. 2004; de Silva & Stumpf 2005). Many works have focused on matching degree distributions and recovering a scale-free law (Jeong et al. 2001; Maslov & Sneppen 2002; Barabási et al. 2003; Salathé et al. 2005), although whether PPI networks are really scale-free is still the subject of debate (Pržulj et al. 2004; Han et al. 2005; Dupuy et al. 2006; Friedel & Zimmer 2006; Khanin & Wit 2006). Our aim here is to present a new, pared-down, but biologically motivated model that simplifies previous work to the extent that fitting parameters and comparing local and global graph properties become meaningful and revealing.
Among the few existing models that incorporate some biological justification are those of Caldarelli et al. (2002), Thomas et al. (2003) and Deeds et al. (2006). These related models have in common the idea that proteins interact because they share complimentary physical aspects, a concept that is consistent with the underlying biochemistry. Following Thomas et al. (2003), we will refer to these physical aspects as binding domains. The approach in these papers is to generate graphs by assigning binding domain information to the nodes at random and then inserting links probabilistically according to some pairwise matching criterion. The aim is then to reproduce properties observed in real PPI networks, most notably the degree distribution. We also mention that a refined ‘lock-and-key’ version of the model from Thomas et al. (2003) has been used to extract protein-level detail from real datasets (Morrison et al. 2006), further justifying the modelling approach.
Presently, it would be a very challenging task to infer the number and distribution of distinct binding domains from a real PPI network (Bateman 2002; Deng et al. 2002), not least because the networks are known to be noisy (Sprinzak et al. 2003). For this reason, it is difficult to decide whether the models from (Caldarelli et al. 2002; Thomas et al. 2003; Deeds et al. 2006) are being tested under realistic parameter ranges. Therefore, we propose a simplified model that attempts to summarize the abundance and popularity of binding domains on a protein as a single number based on its normalized degree; we call this number the stickiness index. The model has the benefit of being tunable to the given degree structure of a PPI network. In this way, a benchmark model that captures the essence of Caldarelli et al. (2002), Deeds et al. (2006), Thomas et al. (2003) can be tested.
Our work can be motivated by two main assumptions.
Assumption 1. Having a high degree implies that a protein has many binding domains and/or its binding domains are commonly involved in interactions.
Assumption 2. A pair of proteins is more likely to interact (share complementary binding domains) if both have high stickiness indices, and correspondingly less likely to interact if one or both have a low stickiness index. Thus, we take the product of the two stickiness indices to define the probability of interaction—this borrows from the concept of an AND gate in Boolean logic (Ben-Ari 2001) and the idea of a rank-one approximation in dimension reduction (Eldén 2006).
The following pseudocode defines our model.
input , list of degrees of N nodes
output , adjacency matrix from model
- for i=1 to N
end
Initialize all wij=0
- for i=1 to N
- for j=1 to N
- compute a uniform (0, 1) sample, r
- if r≤θiθj
- wij=1 and wji=1
- end if
- end for
end for
This choice of stickiness index θi ensures that the ith node in the model has the expected degree degi. Moreover, under assumption 2, this definition of stickiness in terms of degree is the only one that captures the correct expected degree. Details are given in appendix A.
Our stickiness index coincides with the concept of fitness in Caldarelli et al. (2002), with a notable distinction that fitness in Caldarelli et al. (2002) is assigned at random, with a focus on the resulting degree distribution, whereas stickiness above is assigned deterministically, based on the unique choice that matches the expected degrees. Since we do not require any other parameter fitting, this approach allows us to perform a ‘proof of principle’ test of the basic idea that links can be modelled via mutual compatibility.
Note that high-degree proteins in the present PPI networks may not necessarily contain a plenty of binding domains, as implied by our assumption 1. Instead, their high connectivities may be artefacts of technical false positives, auto-activators or ‘sticky’ proteins, or owing to biological false positives, as some PPIs can occur in the experimental procedure, but not in vivo because protein pairs are not expressed at the same time, in the same sub-cellular compartment, or in the same tissue (Han et al. 2005). Thus, our assumption 1 may be a severe oversimplification for some proteins in the present PPI datasets. Nevertheless, as PPI detection biotechnologies improve to produce cleaner, higher-confidence PPI data, assumption 1 will become more descriptive of the observed networks.
A multitude of random graph models that reproduce scale-free degree distributions have been proposed, although the relevance of scale-freeness to PPI networks has been questioned (Pržulj et al. 2004; Han et al. 2005; Dupuy et al. 2006; Friedel & Zimmer 2006; Khanin & Wit 2006). The most notable such models are those based on biologically motivated gene duplication and mutation network growth principles (Vazquez et al. 2001; Pastor-Satorras et al. 2003; Wagner 2003; Goh et al. 2004). In these models, networks grow by duplication of nodes (genes), and as a node gets duplicated, it inherits most of the neighbours (interactions) of the parent node, but gains some new neighbours as well. Thus, a hybrid model having properties of both the gene duplication–mutation model and the stickiness index-based model is a promising future direction. In such a model, a duplicated gene would inherit the parent's stickiness index along with many of the parent's neighbours, as in a gene duplication–mutation model and it would gain new neighbours in proportion to its inherited stickiness index and stickiness indices of the nodes already in the network, as in our stickiness index-based model.
We remark that early tests on low confidence data in (Maslov & Sneppen 2002) suggest that PPI networks have a bias against connections between high-degree proteins. This is potentially at odds with the models in Caldarelli et al. (2002), Deeds et al. (2006), Thomas et al. (2003), where sets of proteins that share matching and commonly occurring (high fitness) physical aspects will interact and all have high degree. In our simple model, we assign edges independently, but it would be possible to add a post-processing stage in which the links were rewired in order to test various types of correlation. Hence, a further application of our model is in studying correlation effects in PPI network topology.
2. Experiments and results
Comparing large real-world networks is computationally intensive as it involves an NP-complete subgraph isomorphism problem (West 2001). Thus, simple heuristics measuring global and local network properties have been used. The most commonly examined global network properties are the degree distribution, clustering coefficient and network diameter (see Newman (2003) for a detailed survey). More recently, bottom-up local approaches to study a network structure have been proposed (Milo et al. 2002; Shen-Orr et al. 2002; Pržulj et al. 2004). Analogous to sequence motifs, network motifs have been defined as subgraphs that recur in a network at frequencies much higher than those found in randomized networks (Milo et al. 2002; Shen-Orr et al. 2002; Milo et al. 2004); they were used to uncover basic functional units in various real-world networks. To account for frequencies of occurrence of all small subgraphs rather than for only the over-represented ones, graphlets were defined as small connected non-isomorphic induced subgraphs of a large network and their relative frequencies were used to define a new distance measure between two networks (Pržulj et al. 2004).
To examine the fit of our new stickiness index-based model of PPI networks, we use all these standard global and local network parameters. The relative graphlet frequency distance is the most demanding network similarity measure, imposing 29 different constraints on the networks being compared (details in Pržulj et al. 2004); hence, we use it as our main comparison tool. We compared 14 large publicly available PPI networks with sample networks from five models, including the stickiness model.
We used PPI networks of the following eukaryotic organisms: yeast Saccharomyces cerevisiae; fruitfly Drosophila melanogaster; nematode worm Caenorhabditis elegans; and human. Several different datasets are available for yeast and human, so we analysed five yeast PPI networks of different confidence levels obtained from three different high-throughput studies (Ito et al. 2000; Uetz et al. 2000; von Mering et al. 2002), as well as five human PPI networks obtained from the two recent high-throughput studies (Rual et al. 2005; Stelzl et al. 2005) and three curated databases (Zanzoni et al. 2002; Bader et al. 2003; Peri et al. 2004). We denote by ‘YHC’ the high-confidence yeast PPI network from von Mering et al. (2002), by ‘Y11K’ the yeast PPI network defined by the top 11 000 interactions in the von Mering et al. classification (von Mering et al. 2002), by ‘YIC’ the Ito et al. ‘core’ yeast PPI network (Ito et al. 2000), by ‘YU’ the Uetz et al. yeast PPI network (Uetz et al. 2000), and by ‘YICU’ the union of YIC and YU yeast PPI networks (we combined them as in (Han et al. 2005) to increase coverage). ‘FE’ and ‘FH’ denote the fruitfly D. melanogaster entire and high-confidence PPI networks from (Giot et al. 2003). Similarly, ‘WE’ and ‘WC’ denote the worm C. elegans entire and ‘core’ PPI networks from (Li et al. 2004). Finally, ‘HS’, ‘HR’, ‘HB’, ‘HH’ and ‘HM’ stand for human PPI networks from yeast two-hybrid (Y2H) screens by Stelzl et al. (Stelzl et al. 2005) and Rual et al. (Rual et al. 2005) and from curated databases BIND (Bader et al. 2003), HPRD (Peri et al. 2004) and MINT (Zanzoni et al. 2002), respectively, (BIND, HPRD and MINT data were downloaded from OPHID (Brown & Jurisica 2005) on 10 February 2006). Note that YHC and Y11K networks are mainly coming from tandem affinity purifications (Gavin et al. 2002) and high-throughput mass spectrometric protein complex identification (Ho et al. 2002), while YIC, YU, YICU, FE, FH, WE, WH, HS and HR are yeast two-hybrid, and HB, HH, and HM are a result of human curation (BIND, HPRD and MINT). Thus, we are using PPI networks of different confidence levels that come from a range of high-throughput PPI detection biotechnologies as well as from human curation.
We compared these PPI networks with the following five model networks: ER random graphs (Erdös & Rényi 1959, 1960); random graphs with exactly the same degree distribution as that of a PPI network (Bender & Canfield 1978; Newman 2002) (denoted ‘R-SF’ for ‘random scale-free’); Barabasi–Albert scale-free networks (Barabási & Albert 1999) (denoted by ‘BA-SF’); three-dimensional geometric random graphs (Penrose 2003) (denoted by ‘GEO-3D’); and the stickiness model networks described previously (denoted by ‘STICKY’).
For each of the 14 PPI networks and for each of the five models, we compared the PPI network with 25 samples from the model. Each sample matched the number of nodes and edges in the corresponding PPI network.
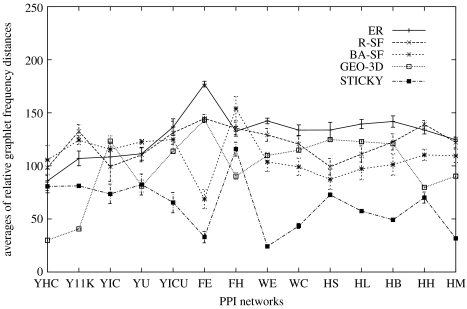
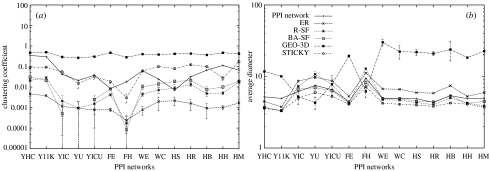
Average relative graphlet frequency distances between the PPI and the corresponding model networks for each of the five network models are presented in figure 1. The stickiness model shows an improved fit over all other network models with respect to relative graphlet frequency distances in 10 out of 14 tested PPI networks (filled squares in figure 1); it fits as well as the GEO-3D model (open squares in figure 1) in one and is outperformed by the GEO-3D model in three PPI networks. In addition, this model reproduces global network properties, such as the degree distribution (see appendix A), the clustering coefficients (open circles in figure 2a) and the average diameters of PPI networks (open circles in figure 2b).
Figure 1.
Relative graphlet frequency distances (y-axis) between the 14 PPI networks (x-axis) and their corresponding model networks. The lower the number, the better the fit. Averages of distances between 25 sample networks and the corresponding PPI network are presented for each random graph model and each PPI network. Points are joined only for clarity. The error bar around a point spans one standard deviation above and below (in some cases, error bars are barely visible, since they are of the size of the point). Labels on the horizontal axis are described in the text.
Figure 2.
(a) Clustering coefficients of 14 PPI networks and averages of clustering coefficients of 25 model networks corresponding to a PPI network. (b) Average diameters of the 14 PPI networks and averages of average diameters of 25 model networks corresponding to a PPI network. Error bars and labels are as described in the legend of figure 1.
It is of particular note that the R-SF model does not perform as well as the stickiness model. This means that, given the degree distribution of a PPI network,
simply drawing a network uniformly at random from the class of all networks that match the degree distribution is less successful in capturing the underlying substructure than
enhancing this degree information by using the simple modelling insights summarized in assumptions 1 and 2.
3. Conclusions
Overall, the stickiness framework produces a convenient, parameter-free random network that is motivated by transparent modelling arguments and may be regarded as a simplified, testable distillation of more sophisticated models. The results give further justification for the modelling approaches in (Caldarelli et al. 2002; Thomas et al. 2003; Deeds et al. 2006). Since the model accurately reproduces all widely used quantitative measures, it also provides a benchmark against which others may be compared.
Acknowledgments
We thank the referees for their valuable feedback.
Appendix A
Suppose is the PPI network adjacency matrix, then aij=aji=1 if proteins i and j are connected and aij=aji=0 otherwise. We are using to denote the degree of protein i.
Suppose that some function of the degree, f[i](degi), defines the stickiness index of protein i, then under assumption 2 (and independently for each distinct pair of proteins),
where i↔j denotes the event that i and j are connected.
In order to match the PPI network degree with the expected degree from the model, we require
Let . Then, the formula above tells us that degi=Cf[i](degi), and thus
Summing over i shows that . We conclude that
confirming that our stickiness index, θi, is uniquely defined under our assumptions.
We note that for all probabilities to be in the range [0, 1], we require θiθj≤1 for all i,j. (Assuming that all proteins have at least one interaction, a sufficient condition is that the product of the two largest degrees is bounded by N.) This property holds for all networks considered here.
As discussed in (Caldarelli et al. 2002), an intuitively reasonable alternative to the multiplicative model is the additive version
However, copying the same style of analysis leads to the conclusion that
so that
Since many proteins have degree less than half the network average, this model breaks down owing to the assignment of negative probabilities.
References
- Bader G.D, Betel D, Hogue C.W.V. BIND: the biomolecular interaction network database. Nucleic Acids Res. 2003;31:248–250. doi: 10.1093/nar/gkg056. doi:10.1093/nar/gkg056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási A.-L, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–12. doi: 10.1126/science.286.5439.509. doi:10.1126/science.286.5439.509 [DOI] [PubMed] [Google Scholar]
- Barabási, A.-L., Dezso, Z., Ravasz, E., Yook, Z.-H. & Oltvai, Z. N. 2003 Scale-free and hierarchical structures in complex networks. In Modeling of complex systems: Seventh Granada Lectures. AIP Conference Proceedings, vol. 661, p. 1–16. College Park, MA: AIP.
- Bateman A, et al. The pfam protein families database. Nucleic Acids Res. 2002;30:276–280. doi: 10.1093/nar/30.1.276. doi:10.1093/nar/30.1.276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Ari M. Springer; Berlin, Germany: 2001. Mathematical logic for computer science. [Google Scholar]
- Bender E.A, Canfield E.R. The asymptotic number of labeled graphs with given degree sequences. J. Comb. Theor. A. 1978;24:296–307. doi:10.1016/0097-3165(78)90059-6 [Google Scholar]
- Brown K, Jurisica I. Online predicted human interaction database. Bioinformatics. 2005;21:2076–2082. doi: 10.1093/bioinformatics/bti273. [DOI] [PubMed] [Google Scholar]
- Caldarelli G, Capocci A, De Los Rios P, Munoz M.A. Scale-free networks from varying vertex intrinsic fitness. Phys. Rev. Lett. 2002;89:258702-1-4. doi: 10.1103/PhysRevLett.89.258702. doi:10.1103/PhysRevLett.89.258702 [DOI] [PubMed] [Google Scholar]
- de Silva E, Stumpf M.P.H. Complex networks and simple models in biology. J. R. Soc. Interface. 2005;2:419–430. doi: 10.1098/rsif.2005.0067. doi:10.1098/rsif.2005.0067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deeds Eric J, Ashenberg Orr, Shakhnovich Eugene I. A simple physical model for scaling in protein–protein interaction networks. Proc. Natl Acad. Sci. 2006;103:311–316. doi: 10.1073/pnas.0509715102. doi:10.1073/pnas.0509715102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng M, Mehta S, Sun F, Chen T. Inferring domain–domain interactions from protein–protein interactions. Genome Res. 2002;12:1540–1548. doi: 10.1101/gr.153002. doi:10.1101/gr.153002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupuy D, Bertin N, Cusick M.E, Han J.-D.J, Vidal M. Reply to toward the complete interactome. Nat. Biotechnol. 2006;24:615–615. doi:10.1038/nbt0606-615a [Google Scholar]
- Eldén, L. 2006 Matrix methods in data mining and pattern recognition SIAM, PA.
- Erdös P, Rényi A. On random graphs. Publicationes Mathematicae. 1959;6:290–297. [Google Scholar]
- Erdös P, Rényi A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960;5:17–61. [Google Scholar]
- Friedel C.C, Zimmer R. Toward the complete interactome. Nat. Biotechnol. 2006;24:614–615. doi: 10.1038/nbt0606-614. doi:10.1038/nbt0606-614 [DOI] [PubMed] [Google Scholar]
- Gavin A.C, et al. Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature. 2002;415:141–147. doi: 10.1038/415141a. doi:10.1038/415141a [DOI] [PubMed] [Google Scholar]
- Giot L, et al. A protein interaction map of drosophila melanogaster. Science. 2003;302:1727–1736. doi: 10.1126/science.1090289. doi:10.1126/science.1090289 [DOI] [PubMed] [Google Scholar]
- Goh, K.-I., Kahng, B. & Kim, D. 2004 Hybrid network model: the protein and the protein family interaction networks. See http://arxiv.org/abs/q-bio.MN/0312009
- Grindrod P, Kibble M. Review of uses of network and graph theory concepts within proteomics. Expert Rev. Proteomics. 2004;1:89–98. doi: 10.1586/14789450.1.2.229. doi:10.1586/14789450.1.2.229 [DOI] [PubMed] [Google Scholar]
- Han J.D.H, Dupuy D, Bertin N, Cusick M.E, Vidal M. Effect of sampling on topology predictions of protein–protein interaction networks. Nat. Biotechnol. 2005;23:839–844. doi: 10.1038/nbt1116. doi:10.1038/nbt1116 [DOI] [PubMed] [Google Scholar]
- Ho Y, et al. Systematic identification of protein complexes in saccharomyces cerevisiae by mass spectrometry. Nature. 2002;415:180–183. doi: 10.1038/415180a. doi:10.1038/415180a [DOI] [PubMed] [Google Scholar]
- Ito T, Tashiro K, Muta S, Ozawa R, Chiba T, Nishizawa M, Yamamoto K, Kuhara S, Sakaki Y. Toward a protein–protein interaction map of the budding yeast: a comprehensive system to examine two-hybrid interactions in all possible combinations between the yeast proteins. Proc. Natl Acad. Sci. USA. 2000;97:1143–1147. doi: 10.1073/pnas.97.3.1143. doi:10.1073/pnas.97.3.1143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong H, Mason S.P, Barabási A.-L, Oltvai Z.N. Lethality and centrality in protein networks. Nature. 2001;411:41–42. doi: 10.1038/35075138. doi:10.1038/35075138 [DOI] [PubMed] [Google Scholar]
- Khanin R, Wit F. How scale-free are gene networks? J. Comput. Biol. 2006;13:810–818. doi: 10.1089/cmb.2006.13.810. doi:10.1089/cmb.2006.13.810 [DOI] [PubMed] [Google Scholar]
- Li S, et al. A map of the interactome network of the metazoan c. elegans. Science. 2004;303:540–543. doi: 10.1126/science.1091403. doi:10.1126/science.1091403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maslov S, Sneppen K. Specificity and stability in topology of protein networks. Science. 2002;296:910–913. doi: 10.1126/science.1065103. doi:10.1126/science.1065103 [DOI] [PubMed] [Google Scholar]
- Milo R, Itzkovitz S, Kashtan N, Levitt R, Shen-Orr S, Ayzenshtat I, Sheffer M, Alon U. Superfamilies of evolved and designed networks. Science. 2004;303:1538–1542. doi: 10.1126/science.1089167. doi:10.1126/science.1089167 [DOI] [PubMed] [Google Scholar]
- Milo R, Shen-Orr S.S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U. Network motifs: simple building blocks of complex networks. Science. 2002;298:824–827. doi: 10.1126/science.298.5594.824. doi:10.1126/science.298.5594.824 [DOI] [PubMed] [Google Scholar]
- Morrison J.L, Breitling R, Higham D.J, Gilbert D.R. A lock-and-key model for protein–protein interactions. Bioinformatics. 2006;22:2010–2019. doi: 10.1093/bioinformatics/btl338. doi:10.1093/bioinformatics/btl338 [DOI] [PubMed] [Google Scholar]
- Newman M.E.J. Random graphs as models of networks. In: Bornholdt S, Schuster H.G, editors. Handbook of graphs and networks. Wiley-VHC; Berlin, Germany: 2002. [Google Scholar]
- Newman M.E.J. The structure and function of complex networks. SIAM Rev. 2003;45:167–256. doi:10.1137/S003614450342480 [Google Scholar]
- Pastor-Satorras R, Smith E, Sole V. Evolving protein interaction networks through gene duplication. J. Theor. Biol. 2003;222:199–210. doi: 10.1016/s0022-5193(03)00028-6. doi:10.1016/S0022-5193(03)00028-6 [DOI] [PubMed] [Google Scholar]
- Penrose M. Oxford Univeristy Press; Oxford, UK: 2003. Geometric random graphs. [Google Scholar]
- Peri S, et al. Human protein reference database as a discovery resource for proteomics. Nucleic Acids Res. 2004;32:1362–4962. doi: 10.1093/nar/gkh070. doi:10.1093/nar/gkh070 Database issue:D497-501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pržulj N, Corneil D.G, Jurisica I. Modeling interactome: scale-free or geometric? Bioinformatics. 2004;20:3508–3515. doi: 10.1093/bioinformatics/bth436. doi:10.1093/bioinformatics/bth436 [DOI] [PubMed] [Google Scholar]
- Rual J.-F, et al. Towards a proteome-scale map of the human protein–protein interaction network. Nature. 2005;437:1173–178. doi: 10.1038/nature04209. doi:10.1038/nature04209 [DOI] [PubMed] [Google Scholar]
- Salathé M, May R.M, Bonhoeffer S. The evolution of network topology by selective removal. J. R. Soc. Interface. 2005;2:533–536. doi: 10.1098/rsif.2005.0072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen-Orr S.S, Milo R, Mangan S, Alon U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002;31:64–68. doi: 10.1038/ng881. doi:10.1038/ng881 [DOI] [PubMed] [Google Scholar]
- Sprinzak E, Sattath S, Margalit H. How reliable are experimental protein–protein interaction data? J. Mol. Biol. 2003;327:919–923. doi: 10.1016/s0022-2836(03)00239-0. doi:10.1016/S0022-2836(03)00239-0 [DOI] [PubMed] [Google Scholar]
- Stelzl U, et al. A human protein–protein interaction network: A resource for annotating the proteome. Cell. 2005;122:957–968. doi: 10.1016/j.cell.2005.08.029. doi:10.1016/j.cell.2005.08.029 [DOI] [PubMed] [Google Scholar]
- Thomas A, Cannings R, Monk N.A.M, Cannings C. On the structure of protein–protein interaction networks. Biochem. Soc. Trans. 2003;31:1491–1496. doi: 10.1042/bst0311491. [DOI] [PubMed] [Google Scholar]
- Uetz P, et al. A comprehensive analysis of protein–protein interactions in Saccharomyces cerevisiae. Nature. 2000;403:623–627. doi: 10.1038/35001009. doi:10.1038/35001009 [DOI] [PubMed] [Google Scholar]
- Vazquez A, Flammini A, Maritan A, Vespignani A. Modeling of protein interaction networks. ComPlexUs. 2001;1:38–44. [Google Scholar]
- von Mering C, Krause R, Snel B, Cornell M, Oliver S.G, Fields S, Bork P. Comparative assessment of large-scale data sets of protein–protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. doi:10.1038/nature750 [DOI] [PubMed] [Google Scholar]
- Wagner A. How the global structure of protein interaction networks evolves. Proc. R. Soc. B. 2003;270:457–466. doi: 10.1098/rspb.2002.2269. doi:10.1098/rspb.2002.2269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- West D.B. 2nd edn. Prentice Hall; Upper Saddle River, NJ: 2001. Introduction to graph theory. [Google Scholar]
- Zanzoni A, Montecchi-Palazzi L, Quondam M, Ausiello G, Helmer-Citterich M, Cesareni G. Mint: a molecular interaction database. FEBS Letters. 2002;513:135–140. doi: 10.1016/s0014-5793(01)03293-8. doi:10.1016/S0014-5793(01)03293-8 [DOI] [PubMed] [Google Scholar]