Quantal transmission at mossy fibre targets in the CA3 region of the rat hippocampus

Abstract

Recent anatomical evidence that inhibitory interneurones receive approximately 10 times more synapses from mossy fibres than do principal neurones (Acsády et al. 1998) has led to the re-examination of the extent to which interneurones are involved in CA3 network excitability. Although many of the anatomical and physiological properties of mossy fibre–CA3 interneurone synapses have been previously described (Acsády et al. 1998; Tóth et al. 2000), an investigation into the quantal nature of transmission at this synapse has not yet been conducted. Here, we employed variance–mean (VM) analysis to compare the release probability, quantal size (q) and number of release sites (n) at mossy fibre target neurones in CA3. At six of seven interneurone synapses in which a high concentration of Ca²⁺ was experimentally imposed, the variance–mean relationship could be approximated by a parabola. Estimates of n were 1–2, and the weighted release probability in normal Ca²⁺ conditions ranged from 0.34 to 0.51. At pyramidal cell synapses, the variance–mean relationship approximated a linear relationship, suggesting that release probability was significantly lower. The weighted quantal amplitude was similar at interneurone synapses and pyramidal cell synapses, although the variability in quantal amplitude was larger at interneurone synapses. Mossy fibre transmission at CA3 interneurone synapses can be explained by a lower number of release sites, a broader range of release probabilities, and larger range of quantal amplitudes than at CA3 pyramidal synapses. Finally, quantal events on to interneurones elicited spike transmission, owing in part to the more depolarized membrane potential than pyramidal cells. These results suggest that although mossy fibre synapses on to pyramidal cells are associated with a larger number of release sites per synapse, the higher connectivity, higher initial release probability, and larger relative impact per quantum on to CA3 interneurones generate strong feedforward inhibition at physiological firing frequencies of dentate granule cells. Given the central role of CA3 interneurones in mossy fibre synaptic transmission, these details of mossy fibre synaptic transmission should provide insight into CA3 network dynamics under both physiological and pathophysiological circumstances.

GABAergic stratum lucidum interneurones are uniquely positioned within the hippocampus to provide feedforward inhibition to CA3 pyramidal neurones (Gulyás et al. 1992; Spruston et al. 1997; Vida & Frotscher, 2000). The axons of dentate gyrus granule cells, the so-called mossy fibres, innervate their principal cell and interneurone targets via anatomically (Acsády et al. 1998) and functionally (Maccaferri et al. 1998; Tóth et al. 2000) distinct synapse types. Mossy fibre–principal cell synapses are formed by the well-described large complex ‘mossy’ terminals that comprise large numbers of release sites (Chicurel & Harris, 1992). In contrast, interneurones of the CA3 stratum lucidum are innervated by small en passant or filopodial mossy fibre synapses which possess numerous anatomical properties distinct from synapses on to principal cells (Acsády et al. 1998). Unlike the giant mossy fibre terminals that form up to 35 active zones (Chicurel & Harris, 1992; Henze et al. 2000), these synapses typically form one or a few release sites on to interneurones (Acsády et al. 1998). However, interneurones in the hilus and CA3 have been shown to receive approximately 10 times more synapses from mossy fibres than do principal neurones (Acsády et al. 1998), casting doubt on the classical view of the mossy fibre pathway as solely an excitatory relay within a trisynaptic circuit (Anderson et al. 1969).

While anatomical analyses can provide information regarding the potential number of release sites and size of the postsynaptic density, many physiological parameters must also be known to ascertain the comparative ‘strength’ of a synapse. These parameters not only include presynaptic properties such as the release probability, quantal amplitude, and short-term plasticity dynamics, but also postsynaptic properties such as input resistance, membrane time constant and resting membrane potential (Trussell, 1998; Carter & Regehr, 2002). In this study, we provide quantitative comparisons for the quantal parameters of mossy fibre targets using multiple probability fluctuation analysis (Silver et al. 1998), also known as variance–mean analysis (Reid & Clements, 1999; Clements & Silver, 2000). Variance–mean analysis has potential advantages over some of the more traditional approaches to quantal analysis in that it requires fewer free parameters in fitting equations and potentially fewer total samples. However, one caveat to this method is that it has difficulty estimating the maximum release probability or number of release sites unless the release probability can be varied over a sufficiently large range (Silver et al. 1998; Clements & Silver, 2000). For this reason, variance–mean analysis has been especially useful at elucidating quantal parameters at large, high probability synapses such as the cerebellar climbing fibre–Purkinje cell synapse (Silver et al. 1998) and calyx of Held (Oleskevich et al. 2000; Meyer et al. 2001), but less so at perforant path synapses that apparently cannot achieve such high release probabilities (Reid & Clements, 1999).

In a previous study, we found that mossy fibre transmission on to CA3 interneurones was associated with a limited degree of facilitation compared to transmission on to pyramidal cells (Tóth et al. 2000). Moreover, in contrast to CA3 pyramidal cells, most mossy fibre–CA3 interneurone synapses displayed short-term depression in the presence of high Ca²⁺ solutions, suggesting that relatively high release probabilities can be imposed experimentally at these synapses. In this paper, we perform variance–mean analysis at CA3 interneurone and pyramidal cell synapses. Furthermore, studies conducted up to this point have not attempted to evoke EPSCs from single mossy fibres. Here, we extract quantal parameters from mossy fibre inputs while attempting to stimulate a minimal number of fibres. To complete our description of quantal transmission at these synapses, we examine mossy fibre-evoked spike transmission at interneurone and pyramidal cell synapses.

Methods

Hippocampal slice preparation

Sprague-Dawley rats ranging from 15 to 19 days old were used in this study. This age range of animals was chosen because mossy fibre expansions are close to their mature form (Amaral & Dent, 1981; Lei & McBain, 2002). Rats were deeply anaesthetized with isoflurane, and the brains were dissected in ice-cold saline solution that contained (mm) 130 NaCl, 24 NaHCO₃, 3.5 KCl, 1.25 NaHPO₄, 1.0 CaCl₂, 5.0 MgCl₂, 10 glucose, saturated with 95% O₂/5% CO₂, pH 7.4, as previously described (Tóth & McBain, 1998). In more recent experiments, the saline solution was a partial sucrose solution that contained (mm) 87 NaCl, 25 NaHCO₃, 25 glucose, 75 sucrose, 2.5 KCl, 1.25 NaH₂PO₄, 0.5 CaCl₂ and 7 MgCl₂, and was incubated at 36°C for up to 1 h (Geiger & Jonas, 2000). Transverse hippocampal slices (300 μm) were obtained using a VT-1000S vibratome (Leica Microsystems, Bannockburn, IL, USA) equipped with a sapphire knife (DDK, Wilmington, DE, USA). CA3 interneurones located within the stratum lucidum were visualized with a ×60 water immersion objective (Olympus) using infrared video microscopy (Infrapatch; Luigs and Neumann, Ratingen, Germany). All animal procedures conformed to the National Institutes of Health animal welfare guidelines.

Electrophysiology

Unless stated otherwise in the text, all recordings were performed in an extracellular solution with the following composition: (mm) 130 NaCl, 24 NaHCO₃, 3.5 KCl, 1.25 NaHPO₄, 2.5 CaCl₂, 1.25 MgCl₂, 10 glucose, saturated with 95% O₂/5% CO₂, pH 7.4. All experiments were carried out in the presence of 100 μmdl-2-amino-5-phosphonovaleric acid (dl-APV) and 5 μm SR-95531 (Sigma; St Louis, MO, USA) to block NMDA and GABA_A receptors, respectively. Whole-cell patch clamp recordings were made using an Axopatch 200B amplifier (Axon Instruments, Union City, CA, USA). Data were acquired with pClamp8 software (Axon Instruments) at an acquisition rate of 20 kHz and filtered at 3 kHz with a Bessel filter (Frequency Devices, Haverhill, MA, USA). Recordings were made at room temperature (∼24°C). Recording electrodes fabricated from borosilicate glass (World Precision Instruments, Sarasota, FL, USA) had resistances between 2.2 and 4.0 MΩ when filled with a solution containing (mm) 100 gluconic acid, 100 CsOH, 10 EGTA, 5 MgCl₂, 8 NaCl, 2 Na₂ATP, 0.3 NaGTP, 31 Hepes, pH 7.3. For current clamp experiments, electrodes were filled with a potassium gluconate-based solution containing (mm) 135 potassium gluconate, 20 KCl, 0.1 EGTA, 2 MgCl₂, 2 Na₂ATP, and 10 Hepes, pH 7.3. In current clamp experiments, membrane potentials were corrected for an estimated 12 mV junction potential. Series resistance was monitored online by use of a –5 mV hyperpolarizing voltage step of 12 ms length occurring near the end of each recorded episode. Synaptic responses were evoked by low intensity stimulation (100–130 μs duration, 10–70 μA intensity) in the dentate gyrus, the hilus or the stratum lucidum of the hippocampal CA3 region via a constant current isolation unit (A360, World Precision Instruments) connected to a patch electrode that was filled with a 1 m NaCl solution (Jonas et al. 1993). For initial searching for fibres that elicited EPSCs, stimulation occurred at 30–80 μA at a frequency of 1 Hz (Jonas et al. 1993). Once evoked EPSCs were detected, the stimulation frequency was reduced to 0.67 Hz. For strontium experiments, to produce enough asynchronous events to overcome the basal frequency of spontaneous events, it was necessary to stimulate more than one mossy fibre synapse. In this case, the stimulus intensity was adjusted until EPSCs could be evoked reliably. The membrane potential was held at –60 mV unless stated otherwise.

Identification of putative single mossy fibre inputs

For identification of single fibres, previous studies have used plots of stimulus intensity (or duration) versus average EPSC amplitude (Jonas et al. 1993; Silver et al. 1998; Bekkers & Clements, 1999). The observation of a sharp increase in the average evoked EPSC amplitude to a steady, invariant amplitude, rather than a gradual increase in average EPSC amplitude with increasing stimulus intensity, has been argued as evidence for the stimulation of single fibres (Jonas et al. 1993; Silver et al. 1996, 1998; Bekkers & Clements, 1999; Oleskevich et al. 2000). We acquired blocks of 10–30 EPSCs, collected at each stimulus intensity at a rate of 0.67 Hz, gradually increasing the stimulation intensity in increments of 5 μA after each block. In considering this approach, we were concerned that measuring the average EPSC amplitude did not take into account the possibility of a different proportion of conduction failures at different stimulus intensity settings. For this reason, failures and successes were not averaged together at each stimulus intensity setting. Instead, measures of both average peak amplitude of the successes (hereafter referred to as potency) and failure rate were generated and plotted against stimulus intensity (Fig. 1B). The stimulation intensity setting for the experiment was selected based on a range in which the failure rate was the lowest possible while the potency remained stable. The stimulus electrode was repositioned if there was an obvious increase in potency as the stimulus intensity was increased. Occasionally, we observed circumstances in which the failure rate was reduced with increasing stimulation intensity while the average EPSC potency remained relatively stable (Fig. 1). One potential explanation for this reduction of failure rate is that one or more additional synapses were recruited that had similar quantal amplitudes. However, one would expect that under such conditions this effect would result in an increased potency, on average, due to the increased likelihood of multivesicular release upon stimulation. An alternative explanation for the reduced failure rate without a change in potency is that as the stimulation intensity was increased, the fibre was stimulated more reliably. To increase the likelihood of stimulating fibres reliably, we chose a stimulation intensity setting over which both the potency and proportion of failures were stable (arrow in Fig. 1). This procedure was used prior to the acquisition of each variance–mean experiment conducted.

Figure 1. Stimulus–response relationship for identification of putative single-fibre inputs.

A, representative successes (black) and failures (grey) at each stimulus intensity (5–30 μA, in increments of 5 μA). B, average potency (filled circles) and failure rate (open circles) at each stimulus intensity. The arrow indicates a stimulus intensity setting typically used for variance–mean experiments.

Group II metabotropic glutamate receptors are selectively expressed on presynaptic mossy fibre terminals but not at CA3 collateral synapses (Shigemoto et al. 1997). Activation of these receptors by the agonists DCG-IV or ACPD inhibits mossy fibre-mediated synaptic transmission (Manzoni et al. 1995; Kamiya et al. 1996; Maccaferri et al. 1998; Tóth et al. 2000), allowing a convenient method for determining the presynaptic identity of the synapse. Typically 50 consecutive traces were averaged before and after a 5 min application of DCG-IV (Tocris), and the composite EPSCs were superimposed for comparison. Inputs were classified as DCG-IV-sensitive if there was greater than 50% inhibition of the EPSC amplitude. Inputs had to be fairly resistant to DCG-IV to be accepted as a CA3 collateral (CL; <20% DCG-IV inhibition). EPSCs that showed an intermediate range of DCG-IV inhibition (∼20–50%), which might reflect a mixture of mossy fibre and CL inputs, were discarded.

Data analysis and detection of evoked events

Data were analysed using modified versions of ‘plug-in’ programs originally written in C or Pascal by John Clements (John Curtin School of Medical Research, Australia National University, Canberra, Australia) for use in Axograph 4.6.3 or 4.7 (Axon Instruments). Stimulus artifacts were subtracted as previously described (Bekkers & Clements, 1999), interpolated, or deleted. Traces were then digitially filtered at 1 kHz prior to event detection.

Evoked EPSCs were detected automatically with the use of a sliding template algorithm (Bekkers & Clements, 1999) as previously described for spontaneous events (Clements & Bekkers, 1997) and implemented in Axograph. This event detection algorithm has been previously demonstrated to be more selective and sensitive than other detection algorithms (Clements & Bekkers, 1997). Briefly, the template, which included a 1–2 ms baseline region, was constructed from the approximate middle of the range of rise and decay times of 5–10 well-resolved EPSCs initially detected manually. This template was then slid along each data point in a 5–8 ms region 0.5 ms after the onset of the stimulus artifact. For evoked events, the detection threshold, a term derived from the optimum scale factor and quality of the fit of the template to the data, was set to four times the standard deviation of the noise, a setting that has been shown through simulations to detect virtually no false positives and at least 95% of well-resolved synaptic events (Clements & Bekkers, 1997; see also Fig. 3D). The amplitudes of the evoked events were measured as previously described, except that the region over which the peak was measured was 0.5 ms. Traces in which an event was not detected in this region were treated as failures, which were measured as previously described (Clements & Bekkers, 1997). After successes were aligned at the onset, successes and failures were intercalated in their original episodic order and inspected manually. Traces that showed errors in the baseline due to contamination by spontaneous EPSCs or obvious inflections in their rising phase were excluded from further analysis. To avoid an underestimation of the proportion of successes, detected EPSCs that rose smoothly to a clear peak but were contaminated by events on the decay phase were accepted (i.e. Wall & Usowicz, 1998). However, for the analysis of EPSC decay kinetics, only events with smooth rise and decay time courses that returned to baseline were accepted.

Figure 3. Automated determination of event detection threshold.

Events were detected by use of an optimally scaled sliding template algorithm implemented in Axograph (Clements & Bekkers, 1997, 1999). The positive template (P) was generated from the waveform of the average synchronous event in the presence of strontium (A, inset). The inverse of this template served to detect false positives (FP; A, inset). The detection criterion reaches a peak when the template is optimally scaled to the synaptic event (B, inset). Number of events and false positive events for a range of detection threshold settings (A). The optimal threshold was achieved when the false positive ratio first fell below 5% (B, arrow).

Variance–mean analysis

Means and variances of peak amplitudes were calculated for each release probability condition. The baseline noise variance was subtracted from the variance obtained in each condition. The relationship between variance (σ²) and mean (x¯) was fit with the following equation (Clements & Silver, 2000):

(1)

where q is the quantal amplitude, CV is the intrasite coefficient of variation and n is the number of release sites. In cases in which the variance–mean plot approximated a linear relationship, the variance–mean plot was fit with the equation:

(2)

The CV is a minor adjustment term that affects q by ∼5–15%. On the basis of our own initial observations (i.e. Fig. 4), as well as the assertion that the range of 0.2–0.4 is typical (Clements & Silver, 2000), we chose to fix the CV at 0.3. The maximum release probability (p_max) was calculated with the equation:

(3)

where x¯_max is the mean EPSC amplitude in the highest release condition and q and n are values derived from the fit.

Figure 4. Properties of putative single mossy fibre-CA3 interneurone EPSCs.

Fifteen representative traces and the corresponding amplitude histogram for EPSCs collected in the presence of 2.5 mm Ca²⁺/1.25 mm Mg²⁺ (A and B) and 1 mm Ca²⁺/3 mm Mg²⁺ conditions (C and D). Noise bin size: 0.5 ms; success bin size: 1.5 ms. Failure percentages (24 versus 9%) are indicated in the corresponding histograms. E and F, latency and rise time distributions in 2.5 mm Ca²⁺ and 1.25 mm Mg²⁺, respectively. F (inset), average of 234 EPSCs selected for smooth decays.

Variance–mean simulations

To estimate the quantal parameters associated with mossy fibre synapses, we utilized a variation of variance–mean analysis developed previously (Silver et al. 1998; Reid & Clements, 1999). Most mossy fibre–CA3 interneurone synapses display paired-pulse depression in the presence of high Ca²⁺ concentrations (Tóth et al. 2000), raising the possibility that the release probability can be varied over a range in which the variance–mean plot ‘rolls over’ (the variance in the high Ca²⁺ condition was similar to or lower than the variance in the normal Ca²⁺ condition), allowing a parabolic, rather than linear, fit and subsequent extraction of the number of release sites using eqn (1). One uncertainty not directly addressed in previous reports is that of the minimum number of conditions and/or samples within a condition needed to achieve a rigorous variance–mean analysis result. Previous variance–mean analyses have not explicitly considered sampling errors associated with either the number of conditions or the number of samples within a condition. In the present series of experiments, the finite duration of electrophysiological recordings, as well as the necessity for pharmacological identification of the synapse (Tóth & McBain, 1998), puts practical limitations on the total number of samples and release conditions that can be attained during the course of a recording. In a previous study, we were able to achieve three different extracellular Ca²⁺ concentration exchanges, followed by pharmacological identification of the synapse (Tóth et al. 2000). To address whether this experimental design could yield sufficiently meaningful variance–mean estimates, we first performed variance–mean simulations given the limited number of release conditions and sample sizes using automated versions of programs originally written in Axograph 4.7 by John Clements. Lists of synaptic amplitudes were generated based on user-defined quantal parameters, quantal coefficient of variation, and noise. The program generates theoretical synaptic amplitude and noise distributions based on binomial statistics, draws random samples from the amplitude and noise distribution, and returns an amplitude time series. On the basis of preliminary observations (i.e. Fig. 4), EPSC event amplitudes were randomly generated for the following conditions: a single release site, a quantal amplitude of 20 pA with a CV of 0.3, three release probability conditions (0.27, 0.53 and 0.8), and 1 pA standard deviation of the noise. Each condition contained 100 events (Fig. 2A). Variances and means were obtained for each condition and plotted in Fig. 2B. The fit yielded values of q= 22.4 pA, n= 0.83 and p_max= 0.87. In contrast, fitting amplitude histograms from the same simulation using traditional quantal analysis yielded values of n between 1 and 6, depending on the release condition. To address errors associated with both the limited number of samples and conditions, we developed two approaches. In the first approach, means and variances of 20 ‘balanced’ bootstrap replications for each condition were obtained by concatenating 20 copies of the original data set (z samples), shuffling them, calculating the mean and variance of successive blocks of z until all data points were used up (Efron & Tibshirani, 1993; Fig. 2C), then plotting means and variances. The 95% confidence interval associated with the fit was used as a measure of the error due to sampling (Fig. 2D). The error associated with p_max was calculated from eqn (3).

Figure 2. Variance–mean bootstrapping and running variance–mean simulations.

A, event amplitudes were generated for the following conditions: n= 1, q= 20 pA (CV = 0.3), three release probability conditions (0.27, 0.53 and 0.8), 1 pA s.d. of the noise and 100 samples per condition. B, variance–mean plot using variances and means obtained from A. C, balanced bootstrap replications for each condition obtained by random resampling. D, bootstrapped variance–mean plot obtained by resampling 20 times for each condition, as in C. The 95% confidence interval associated with the fit (dashed lines in D) was used as a measure of the error due to sampling. E, events from each condition in A were concatenated. Means and variances were then averaged in a 20-point window, then slid down by one point (1–20–2–21, etc.) and repeated, yielding a variance–mean plot (F) which was then binned (G; 2.5 pA bins). The quantal parameters extracted from the parabolic fit to this variance–mean relationship were similar to that using three static release conditions (compare D and G).

To address errors associated with the limited number of release conditions, a ‘running’ mean–variance plot was constructed. Events from each condition were combined together such that transitions between release conditions were blurred to mimic non-stationary intermediate probabilities achieved during solution changes (Fig. 2E). Means and variances were then averaged in a 20-point window, then slid down by one point (1–20, 2–21, etc.) and repeated. The following procedure yielded a mean–variance plot (Fig. 2F). The plot was then binned (in this case in 2.5 pA bins) and fit using eqn (1). The quantal parameters extracted from this fit were comparable to simulations where only three release conditions were employed (Fig. 2B). Similar quantal parameters were also obtained when a 20–40 event sample, which gradually ramped up release probability, was inserted between transitions (data not shown). The correspondence of the values between the original mean–variance plot and the running mean–variance plot is remarkable, suggesting that errors associated with the non-stationarity of release probability during transitions were minimal and that limiting the original mean–variance plot to three conditions did not overly compromise the accuracy of the results. These results indicate that the experimental design of three release conditions should allow extraction of meaningful quantal parameters using variance–mean analysis. Data presented in the results are means ±s.e.m.

Detection of strontium-induced asynchronous events

For the detection of asynchronous events, the detection criterion was determined empirically (Fig. 3). We took advantage of the fact that strontium reduces the release probability of the synchronous component, a condition likely to produce synchronous events similar to uniquantal asynchronous events. The positive template was therefore constructed from the approximate midrange of rise times and decay times of 5–10 of the smallest synchronous events in the presence of strontium (P; Fig. 3A, inset). The inverse of this template served to detect false positives (FP; Fig. 3A, inset). Both templates were then passed through the spontaneous portion of the data set (0–1 s prior to the stimulus artifact) at a range of detection threshold settings (Fig. 3B, inset). The number of detected events and false positives was calculated at each detection threshold setting (Fig. 3A). We then used the criterion of 5% false positives to determine the optimal threshold setting (Fig. 3B). Asynchronous events were then captured 5–1000 ms after the stimulus artifact at the detection threshold reached empirically. Because the CA3 region is highly interconnected and prone to relatively high spontaneous activity (∼2–5 Hz) that could interfere with the collection of asynchronous events, we took additional steps to reduce the contribution of contaminating spontaneous events. We considered simply increasing the detection threshold to provide a more stringent match to the waveform of the evoked event, but this procedure reduces the sensitivity of the detection algorithm to small events. To achieve sufficient selectivity without losing sensitivity, we instead sorted asynchronous events by ±2 ×s.d. of the average rise time of the synchronous events following event detection. After event selection, detected events were aligned at the onset and inspected manually, similarly to evoked events.

Results

Properties of putative single mossy fibre–CA3 interneurone EPSCs

Anatomical studies indicate that at the ultrastructural level, mossy fibres from en passant boutons or filipodial extensions are typically associated with a single active zone (Acsády et al. 1998). We sought to test this hypothesis using physiological means. We first hypothesized that if it were possible to stimulate a single mossy fibre, we would expect to observe a fixed quantal amplitude that is independent of release probability due to the all-or-none nature of release at single site synapses (Silver et al. 1996). A typical experiment is illustrated in Fig. 4. EPSCs were collected in the presence of 2.5 mm Ca²⁺ and 1.25 mm Mg²⁺ (‘normal’) conditions. Shown are 15 representative events and the corresponding amplitude histogram (Fig. 4A and B). The amplitude histogram was fit with a binomial to yield n= 1 ± 0, p_max= 0.27 ± 0.02, q= 14.9 ± 0.4 pA and q_CV= 0.41 ± 0.03. Events were then collected in the presence of 1 mm Ca²⁺ and 3 mm Mg²⁺ conditions (Fig. 4C). For the low Ca²⁺ condition, the quantal parameters were: n= 1 ± 1, p_max= 0.12 ± 0.03, q= 19.8 ± 1.1 and q_CV= 0.36 ± 0.08. The release probability was reduced to 12% in the low Ca²⁺ conditions, consistent with the idea that the EPSCs represented quantal amplitudes in both normal and low Ca²⁺ conditions. However, a statistical comparison of the EPSC amplitude distributions in normal and low Ca²⁺ conditions indicated that average amplitude was larger in the low Ca²⁺ conditions (P < 0.01), which may indicate some degree of Ca²⁺ unblock of Ca²⁺-permeable AMPA receptors in low Ca²⁺ conditions. The coefficient of variation of successes, between the two conditions was similar (0.41 versus 0.36, respectively), consistent with the idea that this variability reflected primarily intrasite rather than intersite quantal variability. Figure 4E is the latency distribution in normal Ca²⁺. The mean latency for this cell occurred at 2.4 ± 0.8 ms, consistent with the EPSCs arising from a monosynaptic connection. For a population of 11 cells, the mean latency was 2.7 ± 0.2 ms. Finally, the rise time distribution is plotted for normal Ca²⁺ (Fig. 4F). Even after digital filtering at 1 kHz, the mean 20–80% rise time was 300 ± 90 μs, suggesting a relatively proximal synapse. To explore EPSC kinetics, we averaged a subset of EPSCs selected for smooth decays and omitted the 1 kHz filtering step (Fig. 4F inset). The 20–80% rise time of the average EPSC was 117 μs, suggesting a connection as proximal as found at mossy fibre–dentate basket cell synapses (Geiger et al. 1997). The exponential fit of EPSC decay (Fig. 4F inset; τ_fast= 1.4 ms (79%), τ_slow= 4.7 ms (19%)) suggested a time course similar to the conductance time course measured via the voltage jump method (∼1.5 ms), suggesting minimal dendritic filtering (Walker et al. 2002). For the population, the mean 20–80% rise time was 575 ± 60 μs (n= 11), reflecting mossy fibre inputs arriving at variable proximal electrotonic locations on the dendrites, in accordance with values reported previously (Tóth et al. 2000; Walker et al. 2002). The mean EPSC decay of the population was 3.7 ± 0.4 ms (expressed as a weighted mean; n= 11), also similar to previous observations (Tóth et al. 2000; Walker et al. 2002).

Variance–mean analysis at mossy fibre–CA3 interneurone synapses

Figure 5 illustrates an experiment in which minimally evoked EPSCs were acquired in three different release conditions: low (1 mm Ca²⁺ and 3 mm Mg²⁺), normal (2.5 mm Ca²⁺ and 1.25 mm Mg²⁺) and high (3.8 mm Ca²⁺ and 0.8 mm Mg²⁺). Fifteen representative traces, overlaid for each condition, are displayed in Fig. 5A. Note the decrease in the proportion of failures (grey traces) with increasing release conditions. Plotted to the right of the traces are peak amplitudes that were sequentially acquired in each condition, from which mean and variance measurements were calculated. A variance–mean relationship, constructed from each release conditions in Fig. 5A, is plotted in Fig. 5B. The average quantal amplitude was calculated to be 27.4 pA. Due to the fact that the variance–mean relationship rolls over, it was possible to fit the data with eqn (1), which allows an estimate of the number of release sites and maximum release probability. In this case, the number of release sites was close to 1 and the maximum release probability was estimated to be 0.76. The bootstrapped and running variance–mean plots, which estimate sampling error in the experiment, are shown in Fig. 5C and D. The quantal parameters estimated from both plots corroborate the estimates calculated in Fig. 5B. To determine whether a decrease in the proportion of failures could account for the increase in release probability, the release probability for each condition (calculated from the mean–variance plot by use of eqn (2)) was compared to the success ratio for the same condition (Fig. 5E). From the variance–mean plot, the release probabilities for low, normal and high Ca²⁺ conditions were 0.19, 0.49 and 0.76, respectively. The corresponding percentages of successes from each condition were 0.22, 0.41 and 0.80, respectively, confirming that the change in release probability could be adequately explained by the change in failure rate. These results are expected of a synapse with only a single release site, as simulated in the model above (Fig. 2). Similarly, a uniquantal response should have a fixed quantal amplitude throughout the entire range of release conditions. We calculated the potency (average quantal amplitude of the successes) for each release condition. The average potencies for low, normal and high Ca²⁺ were 19.2, 26.9 and 21.5 pA, respectively. The quantal content was calculated from the potency in normal Ca²⁺ divided by the potency in low Ca²⁺ (Table 1), which was 1.4. While there was an approximately 30% difference in quantal amplitude between normal and low Ca²⁺ that may suggest a few, rather than one, release sites, on the whole, the correspondence in quantal amplitudes in low versus high Ca²⁺, the correspondence between failure rate and calculated release probability, the similarities in the potencies and the quantal amplitude calculated from variance–mean analyses, and the estimation of the number of release sites of ∼1 all provide evidence that the behaviour of this mossy fibre synapse is most likely to be explained by a single release site. Table 1 lists an additional five cells in which the release probability could be varied over a sufficient range to estimate the number of release sites through variance–mean analysis. Estimates of n varied between 1 and 2, the quantal amplitude varied from 12.1 to 48.2 pA and p_max varied from 0.44 to 0.78. Moreover, with the exception of one cell, the quantal content was also near 1, providing independent corroboration that the behaviour of most synapses could be sufficiently explained by a single release site. Also listed in Table 1 is p_norm, the release probability in normal Ca²⁺ solutions, as extracted from the variance–mean relationship. These values ranged from 0.34 to 0.51. Five other cells are also listed in which only the quantal amplitude could be measured. While the number of release sites could not be measured for this subset due to either low release probability or having only two experimental release probability conditions, the quantal content was also near 1. A comparison of mean potency was made in normal and low Ca²⁺ for the entire data set. There was no significant difference between the mean potency in the presence of normal or low Ca²⁺ (29.0 ± 5.3 versus 26.0 ± 4.6, P= 0.15, n= 11). These results offer evidence that on the whole, the physiology indicates a single release site, in accordance with the anatomical literature (Acsády et al. 1998).

Figure 5. Variance-mean analysis of mossy fibre-CA3 interneurone synapses.

A, left, overlay of 15 representative traces acquired during three different release conditions: low (1 mm Ca²⁺ and 3 mm Mg²⁺), normal (2.5 mm Ca²⁺ and 1.25 mm Mg²⁺) and high (3.8 mm Ca²⁺ and 0.8 mm Mg²⁺). A, right, amplitudes for each condition from which mean and variance measurements were calculated. Simple (B), bootstrapped (C) and running (D) variance–mean plots, constructed from amplitudes in A, right. E, the release probability for each condition obtained from variance–mean analysis (filled circles) compared to the success ratio for the same condition (open circles).

Table 1.

Quantal parameters at mossy fibre-CAB interneurone synapses

Cell	Ca2+/Mg2+	Samples	qc	uEPSC (pA)	q (pA)	n	pnorm	pmax
1	2/1	146	1.4	19.2	29.0 ± 1.5	1 ± 0.06	0.51 ± 0.08	0.78 ± 0.08
	1/3	244
	3.5/0.5	276
2	2/1	191	1.1	9.0	12.1 ± 1.4	1 ± 0.4	0.34 ± 0.08	0.52 ± 0.16
	1/3	199
	3.5/0.5	142
3	2/1	193	1.2	41.2	40.0 ± 3.4	1 ± 0.1	0.34 ± 0.10	0.45 ± 0.12
	1/33.5/0.5	100
	3.5/0.5	179
4	2/1	179	1.2	34.8	48.2 ± 4.1	1 ± 0.2	0.38 ± 0.07	0.63 ± 0.13
	1/3	169
	3.5/0.5	84
5	2/1	40	2.2	7.8	13.0 ± 1.9	2 ± 0.4	0.36 ± 0.14	0.61 ± 0.28
	1/3	49
	PP	19
6	2/1	46	1.0	22.3	22.8 ± 9.6	2 ± 1.0	0.34 ± 0.20	0.44 ± 0.25
	1/3	126
	PP	16
7	2/1	414899	0.8	25.0	21.4 ± 0.9	–	–	–
	PP	48
	1/3	99
8	2/1	148	1.3	16.8	16.4 ± 0.8	–	–	–
	1/3	395
9	2/1	89	1.3	30.2	31.1 ± 0.8	–	–	–
	1/3	298
10	2/1	182	1.3	61.0	69.6 ± 1.6	–	–	–
	1/3	189
11	2/1	1344	0.7	19.8	13.2 ± 0.7	–	–	–
	1/3	727

qc, Quantal content; uEPSC, unitary EPSC measured in low Ca²⁺ conditions; n, the number of release sites rounded to the nearest integer; q quantal size; p_max maximum release probability; p_norm release probability in normal Ca²⁺ solutions; PP, paired-pulse with 50 ms interval.

Variance–mean analysis at mossy fibre–CA3 pyramidal cell synapses

A comparison of quantal transmission at mossy fibre interneurone synapses with that at pyramidal cell synapses attained in a previous study (Jonas et al. 1993; von Kitzing et al. 1994) suggests major differences in the nature of quantal transmission at these two synapses types. At pyramidal cell synapses, the number of release sites was estimated to be between 8 and 21, while at interneurone synapses we estimate 1–2 release sites. Furthermore, the mean release probability for a subset of interneurone synapses is 0.34–0.51, while at pyramidal cell synapses it was estimated to be between 0.20 and 0.28 (von Kitzing et al. 1994). Finally, the quantal amplitude at pyramidal cell synapses was 6.3–11.0 (mean 8.0) pA (Jonas et al. 1993; current calculated from conductance at –60 mV, assuming a linear current–voltage relationship) whereas at interneurone synapses we estimated it to be 12.1–69.6 (mean 31.3) pA. However, these measurements may not be directly comparable due to differences in experimental conditions and analytical techniques between the two studies. To provide a more direct comparison of the quantal parameters at interneurone and pyramidal cell synapses, we performed variance–mean analysis at pyramidal cell synapses under exactly the same experimentally imposed release probability conditions as in the interneurone experiments. Based on the quantal parameters previously attained through traditional amplitude fitting (Jonas et al. 1993), we hypothesized the variance–mean relationship for pyramidal cell synapses would be approximately linear due to the lower release probability suggested at these synapses; moreover, we expected that the quantal amplitude derived from the slope of this relationship would be similar to that attained with traditional quantal analysis. Figure 6 illustates a typical experiment in which mossy fibre–pyramidal neurone synaptic currents were acquired in three different release probability conditions. Note the much larger synaptic currents in high Ca²⁺ that is reminiscent of the large dynamic range seen by varying release probability through frequency-dependent facilitation (Fig. 6A; Salin et al. 1996; Tóth et al. 2000). The variance–mean relationship was fit with a straight line, indicating that release probability remained low even in high Ca²⁺ concentrations (Fig 6C and D). The slope of the variance–mean relationship indicated a quantal amplitude of 29.9 pA (bootstrap 30.8 ± 1.2 pA). In the presence of low Ca²⁺ solutions, in which failures comprised 63% of evoked responses, EPSCs of ∼30 pA amplitude were represented, suggesting that many quantal amplitudes in low Ca²⁺ represented unitary quantal events (Fig. 6B; continuous line indicating q value attained through variance–mean analysis). In six of seven cells, the variance–mean relationship was linear, indicating a low release probability (<0.3) synapse even under high Ca²⁺ conditions. In one cell, the variance–mean relationship was approximated by a parabola. The quantal parameters extracted from this fit were q= 23.6 pA, p_norm= 0.60 and n= 11, consistent with the large number of release sites observed in the anatomical literature. As a population of seven cells, the mean quantal amplitude was 29.4 ± 1.5 pA, an amplitude not significantly different than that at interneurone synapses (P = 0.8). As in the interneurone experiments, the identity of the input was confirmed to be of mossy fibre origin by applying DCG-IV (81.9 ± 5.3% inhibition, n= 7).

Figure 6. Variance-mean analysis at mossy fibre-CA3 pyramidal cell synapses.

A, mossy fibre–pyramidal cell synaptic transmission in three release probability conditions. B, magnification of low release probability condition in A(above) To facilitate comparison of EPSC amplitudes with the quantal amplitude derived from variance–mean analysis (C), the line indicates an amplitude of ∼30 pA. D, balanced bootstrap plot of the variance–mean analysis.

Quantal amplitude of mossy fibre–CA3 interneurone synapses in strontium-containing solutions

Historically, an independent measure of quantal amplitude can be obtained by recording miniature events in the presence of tetrodotoxin (Del Castillo & Katz, 1954). The average miniature event is assumed to represent synapses that are relatively homogeneous in their properties. However, stratum lucidum interneurones receive multiple types of afferents that are associated with different pre- and postsynaptic characteristics (Tóth & McBain, 1998; Tóth et al. 2000; Walker et al. 2002). Moreover, due to considerable electrotonic overlap in the distribution of CA3 collateral and mossy fibre synapses on to these interneurones (Walker et al. 2002), using kinetic criteria to infer the presynaptic origin of mEPSCs (Jonas & Spruston, 1994) is limited. While it could be argued that spontaneous EPSCs possessing decay kinetics approaching that of the rapid mossy fibre conductance time course (∼1.5 ms; see Walker et al. 2002) are most likely to arise from mossy fibre terminals (Fig. 4), mossy fibre mEPSCs occurring at longer electrotonic locations along the dendrite would not be well represented. Moreover, it is unclear whether this experimental design is conducive to pharmacological identification with DCG-IV.

To provide independent verification of quantal amplitude, we therefore used strontium-containing solutions to promote release of asynchronous synaptic events (Abdul-Ghani et al. 1996; Silver et al. 1998; Bekkers & Clements, 1999). Synchronous and asynchronous events are thought to originate from the same set of active synapses (Dodge et al. 1969; Goda & Stevens, 1994; Oliet et al. 1996; Otis et al. 1996), the asynchronous events representing unitary quantal currents (Bekkers & Clements, 1999). A representative experiment is illustrated in Fig. 7. Events in the presence of 2.5 mm Ca²⁺ and 1.25 mm Mg²⁺ (Fig. 7A, upper traces) or 8 mm strontium and 0 mm Mg²⁺ (Fig. 7A, lower traces) are shown. In Fig. 7B, the frequency of asynchronous events was plotted 5–1000 ms after the onset of synaptic stimulation (open columns). For this recording, the average frequency of spontaneous events, calculated to be 1.0 Hz, was determined from a 1 s region prior to the stimulus artifact and then subtracted from the histogram, leaving the asynchronous events (Fig. 7B, hatched columns). These events rose to a peak frequency of 12.5 Hz and decayed exponentially (τ= 45 ms) to a level similar to the spontaneous frequency (represented by the steady-state component of the exponential fit). However, even with the spontaneous component subtracted, the probability that a particular event in a bin will be a spontaneous event was quite high for bins that had similar frequency to that of the baseline spontaneous frequency. We therefore only accepted events in bins in which the probability of contamination by spontaneous events was <20% (Abdul-Ghani et al. 1996). These bins are illustrated as filled bins in the lower histogram. Thirty consecutive traces of these accepted events are demonstrated in Fig. 7C and the corresponding amplitude histogram associated with filled bins in Fig. 7B is illustrated in Fig. 7D, showing a large variability in quantal amplitudes. Note that some of the asynchronous events are relatively large amplitude (∼80 pA). The average quantal amplitude obtained from this experiment was 28.9 pA. After a period of asynchronous event collection, the bath was switched back to normal saline and the synapse was confirmed as mossy fibre in nature with the use of DCG-IV. DCG-IV blocked the EPSC by 52.7%. In a total of four experiments, the average quantal amplitude of asynchronous events was 24.5 ± 3.6 pA (n= 4). The average level of DCG-IV inhibition in this data set was 66.0 ± 4.6%, indicating that the events were of mossy fibre origin. This average quantal amplitude from asynchronous events was not significantly different than the average unitary EPSC amplitude (26.0 ± 4.6 pA, P= 0.81, n= 11) or the quantal amplitude from VM analysis (31.3 ± 5.6, P= 0.33). Inputs identified as CA3 collaterals had an average quantal amplitude of 20.3 ± 5.6 pA and were blocked 16.2 ± 3.1% by DCG-IV (n= 3).

Figure 7. Quantal amplitude of mossy fibre-CA3.

A, evoked events in the presence of 2.5 mm Ca²⁺ and1.25 mm Mg²⁺ (upper traces) or 8 mm strontium (lower traces). B, open bars, latency histogram for asynchronous events 5–1000 ms after the onset of synaptic stimulation. Hatched bars, latency histogram with average spontaneous frequency subtracted. Asynchronous events rise to a peak frequency of 12.5 Hz and decay exponentially to a level not significantly different than the spontaneous frequency. Filled bars, latency bins in which the probability of contamination by spontaneous events is <20%. Thirty consecutive traces (C) and corresponding amplitude histogram (D) associated with the filled latency bins in B. Amplitude bin width: 2 pA; noise bin width: 0.1 pA. D, inset, average quantal event. E, comparison of average quantal amplitude measured in the presence of strontium, through the unitary quantal amplitude in the presence of low Ca²⁺ solutions, or extracted from variance–mean analysis. The amplitudes were not significantly different across all three conditions.

Facilitation at mossy fibre–interneurone synapses is not associated with a change in potency

We have shown previously that many mossy fibre–CA3 interneurone synapses exhibit paired-pulse facilitation, especially in normal or low Ca²⁺ solutions (Tóth et al. 2000). Since most forms of short-term plasticity are thought to involve dynamic changes in presynaptic release probability (Zucker & Regehr, 2002), we sought to exploit this mechanism as an alternative means of changing release probability. At synapses with the capacity for multivesicular release, either through multiple release sites or multivesicular release from a single site, facilitated currents are likely to reflect the summation of multiple quanta. One would expect, then, that multivesicular synapses should be associated with an increased potency upon facilitation. However, at synapses that have a single release site in which multivescular release does not occur, facilitation should produce only a transient increase in the probability that a single vesicle will fuse. In this case, the potency should remain constant regardless of whether or not the synapse is facilitated (Silver et al. 1996).

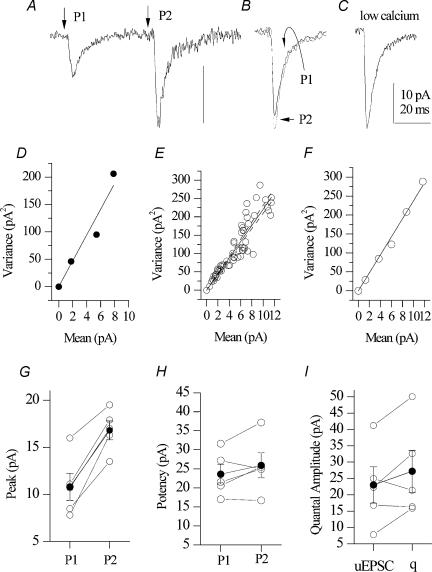
In the next series of experiments, we tested these alternatives by evoking pairs of single-fibre synaptic responses separated by a 50 ms interval. One typical experiment is illustrated in Fig. 8A. The average peak amplitude of the initial synaptic response (P1) was 7.8 pA, which increased to 16.3 pA in peak amplitude upon synaptic stimulation of the second synaptic response (P2) 50 ms later, indicating facilitation of the synapse. Breaking down synaptic responses on the basis of successes and failures revealed that the failure percentage was reduced from 61.9% in P1 to 35.3% in P2. However, the average potencies for both P1 and P2 were similar (21.5 versus 24.9 pA; Fig. 8B). These values were comparable to the average potency at the same synapse recorded in the presence of low Ca²⁺ solutions (25.0 pA) that should yield a reliable estimation of the unitary EPSC. Moreover, in the same recording, a variance–mean relationship obtained in the presence of normal, low and high Ca²⁺ conditions revealed an average quantal amplitude of 21.6 pA (bootstrap: 20.3 ± 1.0 pA; running variance–mean: 21.8 pA; Fig. 8D–F), consistent with the idea that the recorded EPSCs represent quantal events. Thus, in this experiment, facilitation appears to involve an increase in release probability without an increase in potency.

Figure 8. Facilitation of mossy fibre-interneurone synapses is not associated with a change in potency.

A, average of 20 trials in which pairs of single-fibre synaptic responses were evoked, separated by a 50 ms interval. B, average success for both P1 and P2. C, average success in the presence of low calcium solutions. D, variance–mean relationship obtained in the same recording as in A–C(q= 21.6 pA). E and F, bootstrapped, running variance–mean plots, respectively (q= 20.3 ± 1.0 pA, q= 21.8 pA, respectively). G, P1 and P2 peak amplitudes (including failures) for a population of five synapses (10.8 ± 1.4 to 16.8 ± 1.0 pA (P = 0.002; n= 5). H, comparison of P1 and P2 potencies (23.6 ± 2.6 versus 25.9 ± 3.3 pA, P= 0.21) for the same population. I, comparison of average unitary quantal amplitude obtained in the presence of low Ca²⁺ (22.6 ± 5.5 pA) and the quantal amplitude extracted from variance–mean analysis (27.2 ± 6.4 pA; P= 0.17).

As a population, mossy fibre synapses facilitated from 10.8 ± 1.4 to 16.8 ± 1.0 pA (Fig. 7G; P= 0.002; n= 5), the failure percentage decreased from 53.4 ± 4.5 to 35.9 ± 5.8% (P = 0.02) without a significant decrease in the peak P1 and P2 EPSCs (Fig. 8H; 23.6 ± 2.6 versus 25.9 ± 3.3 pA, P= 0.21). Moreover, there was no significant difference between the average unitary quantal amplitude obtained in the presence of low Ca²⁺ (22.6 ± 5.5 pA) and the quantal amplitude extracted from variance–mean analysis (27.2 ± 6.4 pA; P= 0.17). Thus, we observe that mossy fibre–CA3 interneurone synapses facilitate without involving a significant change in potency, consistent with a transient increase in release probability at a single site synapse.

Quantal amplitude of mossy fibre–CA3 interneurone synapses in the presence of DCG-IV

Despite its widespread use, several questions regarding the action of DCG-IV remain unresolved. Previous observations have indicated that DCG-IV rarely blocks transmission fully at mossy fibre–interneurone synapses (Doherty & Dingledine, 1998; Tóth & McBain, 1998; Walker et al. 2002). Due in part to the fact that previous studies had not attempted to stimulate a single mossy fibre, it is not clear whether the DCG-IV-insensitive component represents contamination by CA3 collaterals or simply an incomplete block of mossy fibre synaptic transmission. If mossy fibre synapses on to CA3 interneurones are indeed mediated by a single release site, presynaptic inhibition should entail an increase in failure rate without a change in quantal amplitude.

Using the criterion for separating failures from successes (see Methods), we calculated both the failure percentage and potency (quantal amplitude without failures) before and after application of DCG-IV at the end of each experiment (Fig. 9). Figure 9A demonstrates a typical experiment in which a period of 50 events was acquired in a baseline region, then DCG-IV was washed in. In the absence of DCG-IV, the mean EPSC amplitude was 13.0 pA. In the presence of DCG-IV, despite the fact that the mean EPSC amplitude fell to 4.4 pA, representing a 66.4% inhibition of transmission, the average quantal amplitude remained the same (Fig. 9B). Thus, virtually all of the effect of the inhibition was due to an increase in the percentage of failures, increasing from 41 to 86% in the presence of DCG-IV. Finally, the average EPSC waveforms in both conditions were nearly identical, suggesting that the DCG-IV-insensitive component did not merely reflect spurious contamination of other evoked events, presumably mediated by CA3 collaterals, but reflected a true incomplete block of mossy fibre synaptic transmission by DCG-IV.

Figure 9. Presynaptic inhibition of mossy fibre-interneurone synapses by DCG-IV is associated with an increase in failure percentage without a change in potency.

A, plot of amplitude versus event for 50 events acquired during a baseline region and then in the presence of DCG-IV. B, average traces attained in the absence (black traces in B from black bar in A) and presence (grey traces in B from grey bar in A) of DCG-IV (left, failures included; right, failures excluded). C, comparison of the percentage of failures in control and DCG-IV-containing solutions (53.3 ± 5.1 versus 83.6 ± 3.3%; P= 0.0003, n= 7). D, comparison of the average potency in control and DCG-IV-containing solutions (27.3 ± 6.0 versus 24.5 ± 6.1 pA, P= 0.20).

Failure percentages and potencies from seven experiments are illustrated in Fig. 9C and D. As a population, DCG-IV increased the failure percentage from 53.3 ± 5.1 to 83.6 ± 3.3% (P = 0.0003, n= 7) without a significant change in the potency (27.3 ± 6.0 versus 24.5 ± 6.1 pA, P= 0.20; mean DCG-IV block: 69.7 ± 4.9%), consistent with the expected presynaptic action of DCG-IV at the level of a single release site.

Mossy fibre spike transmission at CA3 targets

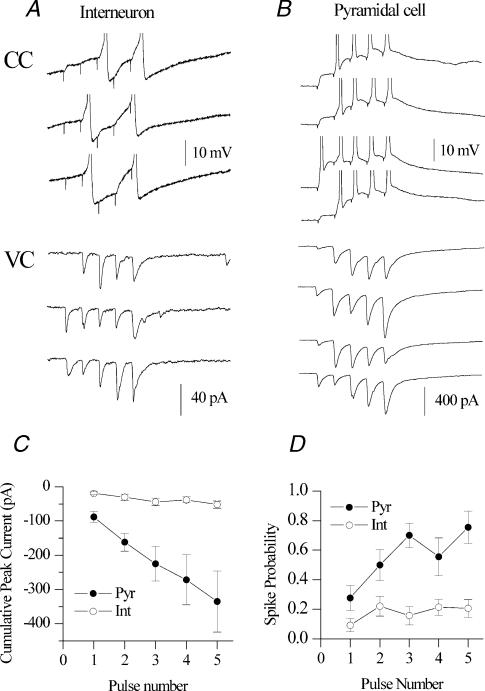
In a study of mossy fibre synaptic transmission in vivo, Henze and coworkers detected extracellular action potentials in CA3 pyramidal cell and interneurone targets in response to firing of a single granule cell (Henze et al. 2002). However, it is unclear whether the quantal amplitudes generated by mossy fibre transmission on to interneurones trigger sufficient depolarization to drive spike transmission. We explored quantal mechanisms underlying mossy fibre-induced spike transmission at both pyramidal and interneurone targets. First, in an initial 2 min period, we monitored the resting potential and spontaneous firing frequency of CA3 pyramidal cells and interneurones. Seven of nine (78%) of pyramidal neurones recorded during this initial period were quiescent, giving no action potentials. In two pyramidal cells, action potentials were occasionally seen, occurring irregularly at an average frequency of <1 Hz. The average resting membrane potential for the population of pyramidal cells was –70.6 ± 2.0 mV. In contrast, six of seven (86%) of interneurones fired spontaneously with an average firing frequency of 2.8 ± 0.8 Hz, consistent with the literature reporting in vivo results (Henze et al. 2002). The initial resting membrane potential of interneurones was more depolarized than that of pyramidal cells (–56.1 ± 1.3 versus–70.6 ± 2.0 mV, P < 0.001). Cells were then voltage clamped at –60 mV and a train of mossy fibre EPSCs was evoked. A train of five EPSCs at 40 Hz was chosen because it was in the frequency range in which dentate granule cells fire action potentials when the cell enters its place field (Henze et al. 2002). Figure 10A and B illustrates the response of a representative interneurone and pyramidal cells to mossy fibre stimulation at 40 Hz in both voltage clamp and current clamp mode. In voltage clamp (VC), mossy fibre stimulation on to interneurones elicited small, all-or-none quantal amplitudes approximately 20–40 pA (Fig. 10A) in the range of unitary EPSCs described above. The average EPSC amplitude ranged from 19.5 to 40.9 pA and did not significantly differ in average amplitude over the course of the train (Fig. 10C, open circles, P > 0.05). However, in pyramidal cells, mossy fibre EPSCs underwent dramatic short-term facilitation (Fig. 10B, VC). As a population, the average pyramidal cell EPSC amplitude increased from 87.8 ± 16.1 to 242.9 ± 65.3 pA over the course of the 40 Hz train (Fig. 10C, filled circles). We then switched to current clamp (CC) mode and assessed the ability of mossy fibre EPSCs to generate action potentials at each cell's resting membrane potential. The larger initial EPSC amplitude (87.8 ± 16.1 versus 19.5 ± 4.1 pA, P= 0.003) in pyramidal cells generated three times larger initial EPSPs in pyramidal cells than in interneurones (3.2 ± 0.5 versus 1.1 ± 0.3 mV, P= 0.004). Despite the much larger average EPSP amplitude generated in pyramidal cells, the probability that the initial EPSP elicited action potentials was only 0.28 ± 0.08, indicating that activation of the giant mossy fibre bouton does not always cause action potential firing or ‘detonation’ in CA3 pyramidal cells (Jonas et al. 1993; Henze et al. 2002). However, a train of five EPSPs at 40 Hz caused spike transmission in both interneurones and pyramidal cells (Fig. 10A and B, CC). Although the initial spike probability was not significantly different between pyramidal cells and interneurones (0.09 ± 0.04 versus 0.28 ± 0.08, P= 0.07), over the course of the 40 Hz stimulation, spike probability increased in both interneurone (0.09 ± 0.04 to 0.22 ± 0.07, P= 0.01) and pyramidal cells (0.28 ± 0.08 to 0.76 ± 0.11, P= 0.006), consistent with the in vivo data (Henze et al. 2002). Finally, the mossy fibre nature of the synaptic inputs was confirmed by application of DCG-IV at the end of the experiment. Interneurone and pyramidal cell inputs were inhibited 90.8 ± 3.1% (n= 9) and 81.9 ± 6.0% (n= 6), respectively. These data directly demonstrate that mossy fibre quantal events are capable of generating action potentials in stratum lucidum interneurones.

Figure 10. Mossy fibre spike transmission at CA3 targets.

Representative current clamp (CC) and voltage clamp (VC) traces to repetitive activation of mossy fibre input (5 pulses at 20 Hz) for stratum lucidum interneurone (A) and CA3 pyramidal cell (B) recordings. C, plot of cumulative peak EPSC current versus pulse number in the train for both interneurones (open circles) and pyramidal cells (closed circles). D, plot of spike probability versus pulse number in the train for both interneurones (open circles) and pyramidal cells (closed circles).

Discussion

Quantal parameters at mossy fibre–CA3 interneurone synapses: comparison with pyramidal cell synapses

In this paper, we have demonstrated several lines of evidence that indicate that mossy fibre synapses on to CA3 stratum lucidum interneurones comprise a small number of functional release sites (∼1–2). First, the mean potency (mean EPSC amplitude in the absence of failures) in the presence of normal and low Ca²⁺ was not significantly different (Silver et al. 1996), indicating that changes in failure rate underlie differences between release probability conditions. In addition, alternative means of changing release probability, such as paired-pulse facilitation or the application of the mGluR agonist, DCG-IV, also did not significantly change the mean potency. Second, variance–mean analysis indicated a low number of release sites (1–2). Finally, the average quantal amplitude in the presence of extracellular strontium was not significantly different from that of the evoked unitary quantal amplitude measured in the presence of low Ca²⁺. These findings are remarkably consistent with electron microscopic data indicating that mossy fibres typically innervate CA3 interneurones with a single active zone (Acsády et al. 1998). In cases where either the quantal content or number of release sites extracted from variance–mean analysis suggested more than a single release site, there are a number of possibilities why this may be so, including the possibility of perforated synapses, the possibility of more than one filopodial/en passant bouton innervating a single CA3 interneurone, multivesicular release from a single release site and/or the failure to stimulate a single fibre.

Consistent with exhibition of depression in the presence of high Ca²⁺ (Tóth et al. 2000), we found that moderate to high release probability could be attained at mossy fibre–interneurone synapses. Moreover, the release probability was in the low–mid range (0.1–0.5) of release probabilities in the presence of near-physiological levels of external Ca²⁺. On the basis of quantal analysis (Jonas et al. 1993; von Kitzing et al. 1994) and the large quantal content revealed by near maximal activation (Salin et al. 1996; Geiger & Jonas, 2000; Tóth et al. 2000), pyramidal cell synapses have been thought to possess a low initial release probability. We also confirmed that mossy fibre–pyramidal cell synapses achieve low release probability even in high Ca²⁺ conditions due to the fact that the variance–mean relationship was linear. For practical considerations, we chose to stimulate pyramidal cell synapses at a frequency of 0.67 Hz, a frequency that induces significant short-term facilitation (Salin et al. 1996; Tóth et al. 2000).

In this study, we found that the mean unitary quantal amplitude at mossy fibre–interneurone synapses was 27.2 ± 6.4 pA (range 12–69 pA). Previous work at mossy fibre–CA3 pyramidal synapses indicated that the unitary quantal amplitude, derived from the first peak in amplitude histograms, was 7–12 pA, measured using driving forces 10–30 mV larger than those used in this study (Jonas et al. 1993; von Kitzing et al. 1994). However, in our hands, the mean quantal amplitude, as calculated from variance–mean analysis, was 29.4 ± 1.5 pA, similar to that at interneurone synapses. In an attempt to reconcile our measure of q with that shown previously, we considered the possibility that sources of spurious variance may have inflated our measure of quantal amplitude. Although we had attempted to stimulate a single fibre, the weighted quantal amplitude should be independent of the number of fibres stimulated (Reid & Clements, 1999). We also considered polysynaptic activity as an additional source of variance, given that high Ca²⁺ conditions would be expected to elicit substantial spike transmission. However, the variance measurement in high Ca²⁺ was proportional to the mean and fell along the same line as the low and normal Ca²⁺ conditions (Fig. 6C). Inspection of the quantal amplitudes in low Ca²⁺ conditions did reveal some small, 7–12 pA EPSCs similar to those found in a previous study (Fig. 6B; Jonas et al. 1993; von Kitzing et al. 1994). However, EPSCs of amplitudes similar to the value of q from variance–mean analysis were also represented (Fig. 6B). Significant intersite quantal variability at some mossy fibre–pyramidal cell synapses may reconcile the larger weighted q measured here than the q measured via traditional quantal analysis. The larger range of quantal amplitudes at interneuronal synapses is consistent with the longer and more variable postsynaptic densities that are apposed to filopodial extensions and en passant boutons (Acsády et al. 1998). It appears likely that substantial intersite variability exists between mossy fibre synapses on to the same interneurone as well, as suggested by the broad range of asynchronous amplitudes present in the presence of strontium when multiple fibres are stimulated (Fig. 7C and D). It is possible that larger quantal events reflect synaptic transmssion at filopodial extensions, which are generally associated with longer postsynaptic densities than en passant boutons at interneurone synapses or the short postsynaptic densities found at large pyramidal cell synapses (Acsády et al. 1998).

Mossy fibre-induced spike transmission in CA3 interneurones

In a recent article, intracellularly recorded dentate granule cells were driven to fire trains of action potentials while recording single units from CA3 targets in vivo (Henze et al. 2002). In response to initial spikes from granule cells, putative CA3 pyramidal cells did not always elicit monosynaptic action potentials, confirming that despite the large number of release sites of mossy fibre terminals, the initial release probability is low. However, the probability of spike transmission increased during the train of action potentials. This observation is expected, given the high degree of facilitation and summation of mossy fibre EPSPs known to occur at these synapses in vitro. Interestingly, a significant increase in the probability of spike transmission occurring at putative CA3 interneurones was also observed. This observation is striking, given that the postsynaptic spikes were supposedly generated from the summation of unitary quantal events, as well as the limited degree of facilitation at this synapse. Can a train of quantal events trigger action potentials in the postsynaptic CA3 interneurone? We tested this hypothesis directly by activating a mossy fibre synapse first in voltage clamp mode to measure the quantal EPSCs, then in current clamp to assess the effect of the EPSCs on spike generation. One additional difference was that stratum lucidum interneurones possessed a more depolarized resting potential than pyramidal cells (–56.1 ± 1.3 versus–70.6 ± 2.0 mV). Many interneurones fired spontaneously at frequencies similar to in vivo spontaneous firing frequency of stratum lucidum (SL) intereurones (2.8 Hz in vitroversus 3.4 Hz in vivo; Henze et al. 2002). Thus, despite the much smaller size of interneurone EPSCs, mossy fibre quantal events generate sufficient excitatory drive to trigger interneurone firing (Carter & Regehr, 2002).

Implications for CA3 network excitability

Despite the sparse number of interneurones in CA3 relative to that of pyramidal cells, there is a growing realization of the relative importance of stratum lucidum interneurones in both physiological and pathophysiological states in the hippocampus; their importance in the CA3 network stems directly from the density and strength of their connections. In contrast to a single dentate granule cell axon contacting approximately 10–18 CA3 pyramidal cells via the large mossy fibre boutons (Acsády et al. 1998), each granule cell is also associated with 25–35 filopodial extensions and an additional 12–17 small en passant terminals, both of which synapse exclusively on to SL interneurones (Acsády et al. 1998). In all, the number of mossy fibre boutons on to interneurones outnumber those of pyramidal cells by as much as 4:1 in CA3 alone, rising to 10:1 when the mossy fibre terminals in the hilus are included. Coupled with the higher probability of release and higher potency of each release site in driving spike transmission, the extensive interconnectivity of mossy fibre synapses should excite many more interneurones than pyramidal cells at low (<0.5 Hz) in vivo discharge rates of dentate granule cells (Jung & McNaughton, 1993). Moreover, SL interneurones form a dense network of inhibitory terminals with pyramidal cell dendrites in stratum pyramidale and stratum lucidum. SL interneurone activation results in large, fast IPSCs to CA3 pyramidal cells (Vida & Frotscher, 2000). Taken together, the anatomical and physiological evidence points to a strong feedforward network resulting in a net inhibition in CA3, a concept underscored by the paradoxical observation that synchronous activation of dentate granule cells in vivo during dentate spikes results in a net inhibition of CA3 pyramidal cell firing (Bragin et al. 1995a,b; Penttonen et al. 1997).

Although the higher release probability of mossy–interneurone inputs, coupled with the higher interneurone innervation, will tend to favour feed-forward inhibition at low firing frequencies of dentate granule cells, both in vivo and in vivo experiments suggest that the relative release dynamics will change at higher dentate granule cell firing frequencies. When the animal moves into the dentate granule cell's place field, it is capable of short, high frequency bursts during the in-field discharge (Henze et al. 2002). During this time, the higher frequency-dependent facilitation at mossy fibre–pyramidal cell synapses than at mossy fibre–interneurone synapses will temporarily shift the dynamics of excitation and inhibition within CA3, allowing relief from inhibition and focal discharge of pyramidal cells. Thus, the dynamics of excitation and inhibition within CA3 will shift depending on the firing frequency of the dentate granule cell.