The mechanism of the force response to stretch in human skinned muscle fibres with different myosin isoforms

Abstract

Force enhancement during lengthening of an active muscle, a condition that normally occurs during locomotion in vivo, is attributed to recruitment of myosin heads that exhibit fast attachment to and detachment from actin in a cycle that does not imply ATP splitting. We investigated the kinetic and mechanical features of this cycle in Ca²⁺ activated single skinned fibres from human skeletal muscles containing different myosin heavy chain (MHC) isoforms, identified with single-fibre gel electrophoresis. Fibres were activated by using a new set-up that allows development of most of the tension following a temperature jump from 0–1°C to the test temperature (∼12°C). In this way we could prevent the development of sarcomere non-uniformity and record sarcomere length changes with a striation follower in any phase of the mechanical protocol. We found that: (i) fibres with fast MHC isoforms develop 40–70% larger isometric forces than those with slow isoforms, as a result of both a larger fraction of force-generating myosin heads and a higher force per head; (ii) in both slow and fast fibres, force enhancement by stretch is due to recruitment of myosin head attachments, without increase in strain per head above the value generated by the isometric heads; and (iii) the extent of recruitment is larger in slow fibres than in fast fibres, so that the steady force and power output elicited by lengthening become similar, indicating that mechanical and kinetic properties of the actin–myosin interactions under stretch become independent of the MHC isoform.

When a muscle is stretched during an active contraction, a condition that normally occurs during locomotion in vivo, the increase in force is much higher than that expected on the basis of a smooth continuation of the force-shortening velocity curve (Katz, 1939), a feature that makes the muscle an efficient braking system under stretch. It is known that during stretch the ATP consumption decreases below the isometric level (Infante et al. 1964; Curtin & Davies, 1973; Linari et al. 2003), but at the same time there is evidence that force enhancement by stretch is due to an increase in the number of myosin heads attached to actin (Linari et al. 2000). These results have been explained assuming that during lengthening the actin–myosin interaction exhibits a different kinetics with respect to the isometric condition or during shortening: the attached myosin head under strain is prevented from completing the conventional cycle (Lymn & Taylor, 1971) and detaches from actin through a step that does not involve ATP splitting (Piazzesi et al. 1992; Huxley, 1998). Myosin heads detached in this way reattach with a rate much higher than the rate of attachment in the isometric condition or during shortening, so that, even during fast lengthening, attachment does not become the rate-limiting step and the number of attached heads remains high (Lombardi & Piazzesi, 1990).

In vertebrates and mammalian muscles the performance of a muscle fibre contracting in isometric conditions or actively shortening exhibits a large variability: parameters such as unloaded shortening velocity, maximum power output and ATPase activity, which are expressions of the myosin–actin interaction kinetics, vary from one muscle fibre to the other in relation to their myosin heavy chain (MHC) isoform composition (see for reviews Schiaffino & Reggiani, 1996; Bottinelli & Reggiani, 2000). Are the kinetic and mechanical features of myosin heads cycling during steady lengthening different in muscle fibres containing different MHC isoforms? We investigated this question in Ca²⁺ activated single skinned fibres dissected from human muscles and containing different MHC isoforms, identified with single-fibre gel electrophoresis. Fibres were activated by using a set-up that allows development of most of the tension following a temperature jump between a low-temperature activating solution (0–1°C) and the test temperature activating solution (∼12°C). This method, first used by Pate et al. (1994), prevents the development of sarcomere non-uniformities, due to the diffusion-limited time of activation across the fibre, and allows us to record sarcomere length changes by a striation follower (Huxley et al. 1981) in any phase of the mechanical protocol. We found that force enhancement by stretch is due to recruitment of myosin head attachments, without an increase in strain per head above the value generated by the isometric heads. The extent of recruitment is larger in slow fibres, where the isometric force is smaller than in fast fibres, so that steady forces and power output elicited by lengthening are similar in slow and fast fibres independently of the MHC isoform.

Methods

Muscle biopsy and fibre preparation

The muscle fibres used in this study were obtained from the vastus lateralis of five young healthy subjects (20–40 years old) in the Hospital of Pavia (Italy). The study was approved by the ethical committee of the University of Pavia and conformed to the standards set by the Declaration of Helsinki (last modified in 2000). After the subjects were fully informed of the goal of the experiments and of the risks involved in the biopsy procedure, written informed consent was obtained.

The biopsy samples were immersed in ice-cold skinning solution (Bottinelli et al. 1996; Stienen et al. 1996), separated into small bundles (70–150 fibres, ∼10 mm long) and stored in skinning solution, containing 50% glycerol, at –20°C for 3–4 weeks. For the experiments, a bundle of fibres was transferred to a Petri dish with a Silgard (Dow Corning Limited, UK) covered base and kept at 4–6°C. Single fibres were dissected under a stereomicroscope and pinned down on the Silgard surface at both ends. Fibres were treated with relaxing solution (Table 1) containing Triton X-100 (1%, v/v) for 30–40 min at 2–4°C to ensure complete removal of the sarcolemma and sarcoplasmic reticulum. A segment 5–6 mm long was cut from the fibre and T-shaped aluminium clips were mounted at its extremities for attachment to transducers.

Table 1.

Composition of solutions used for human skinned muscle fibres

Solution	TES (mM)	Na2ATP (mM)	MgCl2 (mM)	EGTA (mM)	HDTA (mM)	CaEGTA (mM)	Na2CP (mM)	GLH (mM)
Relaxing	100	5.4	7.7	25	–	–	19.1	10
Pre-activating	100	5.5	6.9	0.1	24.9	–	19.5	10
Activating	100	5.5	6.8	–	–	25	19.5	10

TES, N-tris[hydroxymethyl]methyl-2-aminoethanesulphonic acid; ATP, adenosine 5′-triphosphate; EGTA, ethylene glycol-bis-(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid; HDTA, 1,6 diaminohexane-N,N,N′,N′-tetraacetic acid; CP, N-[Imino(phosphonoamino)methyl]-N-methylglycine; GLH, glutathione. 1 mg ml⁻¹ creatine phosphokinase, 10-μm trans-epoxysuccinyl-l-leucylamido-(4-guanidino)butane (E-64) and 20 μg ml⁻¹ leupeptin were added to all solutions. pH of all solutions, 7.10 at 12°C (adjusted with KOH, 2–12 × 10⁻³m). Ionic strength: 200 mm. HDTA was obtained from Fluka (Buchs, Switzerland). All other chemicals were obtained from Sigma.

Experimental set-up

The fibre segment was mounted in a drop of relaxing solution between the lever arms of a loudspeaker motor (Lombardi & Piazzesi, 1990) and a force transducer. The force transducers used were either strain gauge force transducers (AE 801 SensorNor, Horten, Norway, resonant frequency 2.0–2.3 kHz and sensitivity 100–200 V N⁻¹) or capacitance force transducers (resonant frequency 40–50 kHz, sensitivity 80–200 V N⁻¹, Huxley & Lombardi, 1980). A rapid solution exchange system driven by a stepper motor (speed 15 mm s⁻¹), similar to that previously described by Linari et al. (1993), allowed continuous recording by a striation follower (Huxley et al. 1981) from a selected population of sarcomeres (800–1000). Before starting the experiment the fibre was transferred from relaxing solution to rigor solution (0–1°C), then the fibre ends were first fixed with a rigor solution containing glutaraldehyde (5%, v/v) and then glued to the aluminium clips with shellac dissolved in ethanol (for more details see Linari et al. 1998).

The system used in these experiments was modified from the previous one (Linari et al. 1998) to allow rapid change of temperature of the bathing solution. The volume of the drops (∼70 μl) was delimited by top and bottom coverglass pieces of size 8 × 3 mm, and separated by 3 mm. The pedestals carrying the coverglass pieces were placed on two aluminium plates that could be maintained at two different temperatures by means of two separated servocontrolled thermoelectric modules. Each plate carried two pedestals. The pedestals of the first plate were used to transfer the fibre from preactivating solution to activating solution at the same low temperature. The transition from low-temperature to high-temperature activating solution occured by moving the fibre from the second drop carried by the low-temperature plate to the first drop carried by the high-temperature plate. Since the stepper motor moved to transfer the fibre to the next drop, the sarcomere length could be measured by the striation follower as soon as the optic axis passed beyond the end of the pedestal made by aluminium (shadow zone) and entered the part of the pedestal made by coverglass. This occured ∼30 ms after the fibre had entered into the next drop. Thus, following the transfer to the high-temperature activating solution, the sarcomere length could be monitored by the striation follower for most of the force development (see Fig. 2, later).

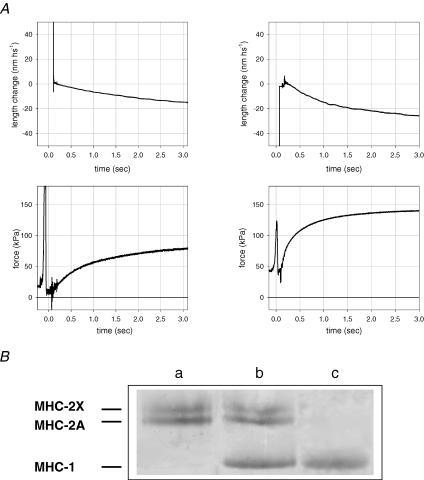
Figure 2. Force development following a T-jump (from 1 to 12°C) in slow (left column) and fast (right column) fibres and identification of fibre types.

A, traces indicate segment length change (upper panel), force response and zero force (lower panel). The artefact before the striation follower signal is due to the fibre travelling in air and within the shadow zone. Slow fibre (type 1 isoform): fibre length, 2.10 mm; segment length under the striation follower, 1.00 mm; average segment sarcomere length, 2.58 μm; CSA, 5200 μm². Fast fibre (type 2A/2X isoform): fibre length, 2.45 mm; segment length under the striation follower, 0.87 mm; average segment sarcomere length, 2.52 μm; CSA, 9000 μm². B, MHC isoform identification in single fibres by SDS-PAGE. The areas of migration of MHC-1, MHC-2A and MHC-2X are indicated on the left. Lane a: a single fibre containing MHC-2A and MHC-2X, i.e. a fast, type 2AX, fibre; lane b: a sample from vastus lateralis muscle containing all three adult MHC isoforms; lane c: a single fibre containing MHC-1, i.e. a slow, type 1, fibre.

Experimental protocol

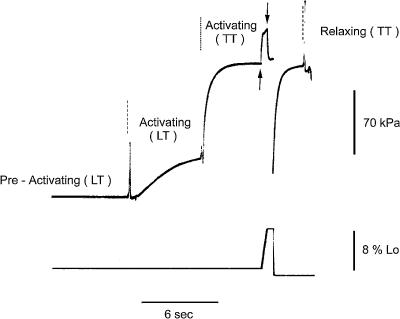
The sarcomere length, width (w) and height (h) in the central 2–4 mm segment of the fibre were measured at 0.5-mm intervals with a 40× dry objective (NA 0.60, Zeiss) and an 8× or 25× eyepiece while the fibre was in relaxing solution. The sarcomere length in the relaxed fibre was set to 2.40–2.65 μm. The cross-sectional area (CSA) was determined assuming the fibre cross-section to be elliptical (CSA =whπ/4). The fibre was transferred from relaxing solution at 12°C to preactivating solution at 1°C and then to activating solution at 1°C. At saturating pCa, force rose to a steady value of 1/4–1/5 the isometric force developed at the test (12°C) temperature (Fig. 1). Then the fibre was transferred to activating solution at the test temperature. This procedure allows the development of tension at the test temperature when Ca²⁺ is already uniformly distributed around the myofilaments. In this way it is possible to prevent the development of sarcomere length inhomogeneity across the fibre which occurs when the fibre is directly activated at the test temperature. Once the force attained the plateau value, a ramp shortening or lengthening (<8% of the fibre length or <100 nm per half-sarcomere, hs) was imposed by the motor. The lengthening velocities used were always <1 μm s⁻¹ hs⁻¹ in order to minimize the possibility of inducing inhomogeneous responses to stretch from the sarcomeres along the fibre (Lombardi & Piazzesi, 1990). The fibre was kept in the activating solution at the test temperature for 4–8 s, and then transferred to relaxing solution at the test temperature. With our temperature jump (T-jump) activation procedure, at 12°C the striation pattern remained homogeneous for several (12–15) activation–relaxation cycles. The experiment ended when the signal from the striation follower became unreliable or when the force response started to exhibit a continuous rise even beyond the extent of lengthening necessary to attain the peak or angle of force (Edman et al. 1978; Colomo et al. 1988; Lombardi & Piazzesi, 1990). Attempts to perform the experiments at a higher temperature (24°C, closer to physiological conditions) were frustrated by the reduced number of activations during which the striation pattern remained ordered.

Figure 1. Slow-time-base record from a fast fibre to show the experimental protocol.

Upper trace, force; lower trace, motor position. The dashed lines mark the time when the solution was changed; the dotted line marks the time of transition from low temperature (LT) to test temperature (TT). Arrows indicate the time during which a ramp lengthening (8% of fibre length) at a velocity of 0.09 μm s⁻¹ hs⁻¹ was imposed on the fibre before returning to relaxing solution. A large release (10% of fibre length) is imposed on the fibre to measure the force baseline (not resolved in the force record since the trace is from the chart recorder). Fibre length, 3.03 mm; average sarcomere length, 2.53 μm; CSA, 8900 μm². Low temperature (LT), 1.0°C; test temperature (TT), 11.5°C. Fibre characterization indicates that the MHC isoform is 2A/2X type.

At the end of the experiment the fibre was cut free from clips and placed in a capillary glass tube containing sample buffer (Laemmli, 1970) for subsequent electrophoretic determination of myosin isoform composition.

To record the isometric force development or the force response to ramp shortening or lengthening, the strain gauge force transducer was used. In stiffness experiments, small step length changes complete in about 110 μs (range from +3 to –3 nm hs⁻¹) were imposed on the activated fibre both in isometric conditions and during the steady-state force response to ramp lengthening. The stiffness was calculated from the ratio between the force change and the hs length change, as measured by the striation follower. In these experiments the 50-kHz capacitance force transducer was used to attain adequate time resolution. This transducer is intrinsically sensitive to changes in temperature but at the time when the step was imposed, 3–5 s after the fibre was transferred to the test-temperature solution, the thermal drift was negligible. To determine the baseline tension at this time, a large step release was applied 200 ms after the small step length change.

All experimental determinations were carried out during activations at saturating pCa (4.50), with the exception of a series of experiments where steady force and stiffness were measured at different pCa (ranging between 6.00 and 4.50) to determine the dependence of stiffness on isometric force and thus estimate the contribution of myofilaments to hs compliance (Blangéet al. 1985; Jung et al. 1992; Martyn et al. 2002).

Data recording and analysis

Force, motor position and sarcomere length signals were recorded with a sampling interval of 0.5 ms via an A/D card (Computerscope EGAA, RC Electronics) on a 386/33 MHz PC. In experiments where stiffness was measured, the same signals were also recorded on a digital oscilloscope (Nicolet ProSystem 20) with a sampling interval of 5–10 μs. The responses were measured directly on the PC with the EGAA software and on the digital oscilloscope with its internal reading system. Force and motor position were continuously monitored also on a chart recorder (Multitrace 2 Recorders 5022, Lectromed). The data are expressed as mean ± s.e.m.

Myosin isoform identification

The fibre type was defined on the basis of MHC isoforms used as molecular markers. The MHC isoform composition of each fibre was determined by means of 6% polyacrylamide gel electrophoresis after denaturation in sodium dodecyl sulphate (SDS-PAGE, Fig. 2B). The electrophoretic method used is described in detail by Bottinelli et al. (1996). Three major bands in the region of MHC isoforms, corresponding to MHC-1, MHC-2A and MHC-2X, were separated. According to this analysis, 46% of the 35 fibres used in this work contain the MHC-1 isoform, 17% contain MHC-2A and 37% contain MHC-2A/2X. We will refer to fibres containing MHC-1 as slow fibres and to fibres containing MHC-2A and MHC-2A/2X as fast fibres.

As shown in the results, the characteristics of the force response to either shortening or lengthening suggested a further distinction within slow fibres, even if we could not find any difference with gel electrophoresis. Therefore in the section concerning force velocity experiments slow fibres appear separated into two categories: slow fibres 1 (sf-1) and slow fibres 2 (sf-2).

Myosin light chain (MLC) separation was performed as previously described (Bottinelli et al. 1994) on 10–20% linear polyacrylamide gradient slab gels. Two regulatory MLC isoforms, the slow isoform MLC-2s and the fast isoform MLC-2f, and three alkali MLC isoforms, the slow MLC-1s and the two fast isoforms MLC-1f and MLC-3f, could be separated.

Solutions

The composition of the solutions, reported in Table 1, was calculated with a computer program kindly provided by Philip Brandt (see Brandt et al. 1972). The concentrations of multivalent ionic species were calculated after solving the equilibria of two metals (Ca and Mg) and two ligands (EGTA and ATP). According to a suggestion by M. Kellermayer (University of Pecs, Hungary), two inhibitors of proteases were added to all solutions to preserve lattice proteins and thus sarcomere homogeneity: 10-μmtrans-epoxysuccinyl-L-leucylamido-(4-guanidino) butane (E-64, Sigma), a cysteine protease inhibitor, and 20 μg ml⁻¹ leupeptin (Sigma), a serine and cysteine protease inhibitor.

Results

Force development following T-jump to 12°C

When the fibre was transferred from the preactivating solution to the low-temperature activating solution, force rose to a steady state value of 1/4–1/5 the force developed in the test-temperature activating solution (Fig. 1). The force development at low temperature was slower in slow fibres than in fast fibres; the half-time of force development (t_1/2) was 5.8 ± 0.7 s in slow fibres (n = 6) and 2.1 ± 0.3 s in fast fibres (n = 8). The plateau force at low temperature, relative to the force developed at the test temperature (T₀), was 0.18 ± 0.06 in slow fibres and 0.22 ± 0.09 in fast fibres. Once the plateau value was attained, the fibre was transferred to the activating solution at the test temperature. Figure 2A shows force and sarcomere length changes with the T-jump activation protocol applied to a slow fibre (left column) and to a fast fibre (right column). There was no change in force during the ∼100 ms while the fibre remained in air after leaving the low-temperature drop (see also Fig. 1). Then, as soon as the fibre went into the drop of activating solution at the test temperature, the force started to increase abruptly. t_1/2 was 580 ± 20 ms in the slow fibres (n = 7), 235 ± 12 ms in the fast fibres containing MHC-2A isoform (2A fibres, n = 5) and 150 ± 22 ms in the fast fibres containing MHC-2A/2X isoform (2A/2X fibres, n = 5). The shortening per hs during force development was 15.5 ± 0.6 nm in the slow fibres, 16.9 ± 6.1 nm in the 2A fibres and 20.8 ± 8.3 nm in the 2A/2X fibres. Thus in these experiments the end compliance was consistently about 2% of fibre length per T₀. T₀ was 66 ± 4 kPa (CSA 6500 ± 1700 μm², mean ± s.d.) in the slow fibres, 84 ± 10 kPa (CSA 5200 ± 1600 μm²) in the fast 2A fibres and 118 ± 13 kPa (CSA 10 780 ± 5100 μm²) in the fast 2A/2X fibres. These values agree with those determined previously with similar bathing solutions, taking into account the different temperature: Stienen et al. (1996) at 20°C found 115 kPa (slow fibres), 135 kPa (type 2A fibres) and 167 kPa (type 2A/2X fibres).

Force responses to steady shortening and lengthening

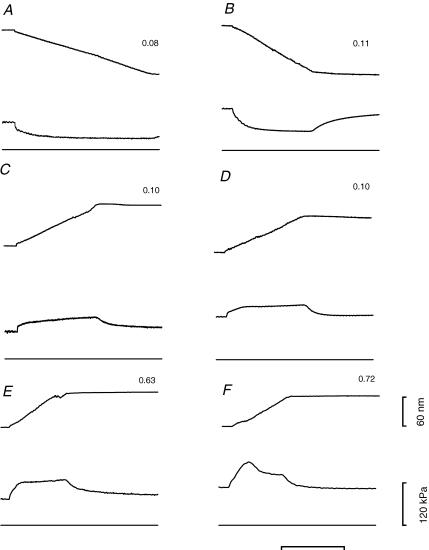
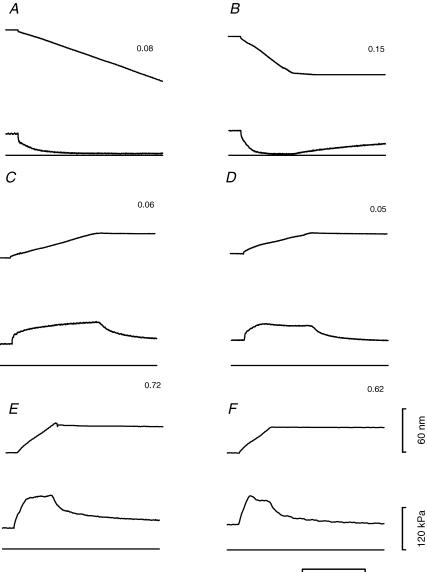
Force responses to steady sarcomere shortening and lengthening are shown in Fig. 3 for two fast fibres and in Fig. 4 for two slow fibres. In fast fibres, the shortening speed necessary to reduce the force to ∼0.5T₀ was 0.08 μm s⁻¹ hs⁻¹ in 2A fibres and 0.11 μm s⁻¹ hs⁻¹ in 2A/2X fibres (Fig. 3A and B). In slow fibres, similar shortening speeds reduced the force to <0.1T₀. Actually, slow fibres showed a large variability in their shortening speed which, together with a difference in the transitory response to stretch shown below, suggested a separation into two groups, even if no differences have been found by gel electrophoresis in their MHC and MLC isoforms. In five out of the thirteen slow fibres, defined as sf-1, a shortening velocity of 0.08 μm s⁻¹ hs⁻¹ reduced the force to ∼0.05T₀. In the remaining eight slow fibres, defined as sf-2, the same value of steady force was obtained with twice the shortening velocity (Fig. 4A and B). During lengthening, force rose and settled to an almost steady-state value that depended on the lengthening velocity in the same way for both slow and fast fibres. At low lengthening velocity (<0.1 μm s⁻¹ hs⁻¹, C and D in Figs 3 and 4), force rose monotonically up to a constant value. At lengthening velocities >0.1 μm s⁻¹ hs⁻¹ in fast 2A/2X fibres and in slow sf-2 fibres (Figs 3F and 4F), but not in fast 2A fibres (Fig. 3E) and in slow sf-1 fibres (Fig. 4E), force attained a peak before settling to a steady value. This is a phenomenon already described both in intact frog fibres (Edman et al. 1978; Lombardi & Piazzesi, 1990) and in skinned rabbit psoas fibres (Stienen et al. 1992; Getz et al. 1998). The plot of peak of force versus lengthening speed does not show a give, but rather shows an almost linear dependence on the lengthening speed (filled circles in Fig. 5), in agreement with previous experiments in frog muscle fibres (Lombardi & Piazzesi, 1990). The extent of lengthening necessary to attain the peak of force was similar in both slow and fast fibres and independent of lengthening velocity. Pooled data for lengthening velocities larger than 0.2 μm s⁻¹ hs⁻¹ give values of 13.56 ± 0.90 nm hs⁻¹ (velocity 0.49 ± 0.09 μm s⁻¹ hs⁻¹) for the slow fibres and 14.26 ± 0.55 nm hs⁻¹ (velocity 0.50 ± 0.07 μm s⁻¹ hs⁻¹) for the fast fibres.

Figure 3. Force response to steady shortening (A and B) and lengthening (C–F) imposed on activated fast fibres.

Left column: 2A type; right column: 2A/2X type. Figures close to the records indicate the velocity (μm s⁻¹ hs⁻¹) during the steady-state force response. In each row, force responses obtained at similar velocities are compared. In each frame, from top to bottom, traces indicate: sarcomere length change, force response and zero force. The time-scale is 400 ms (A–D) or 100 ms (E–F). 2A fibre: fibre length, 2.25 mm; segment length, 0.98 mm; average sarcomere length in the segment, 2.71 μm; CSA, 6700 μm², temperature, 11.8°C. 2A/2X fibre: fibre length, 3.03 mm; segment length, 0.85 mm; average sarcomere length in the segment, 2.52 μm; CSA, 8900 μm², temperature, 11.5°C. The two fibres are from vastus lateralis muscle of two different subjects.

Figure 4. Force response to steady shortening (A and B) and lengthening (C–F) imposed on activated slow fibres. Left column: sf-1 type; right column: sf-2 type.

Figures close to the records indicate the velocity (μm s⁻¹ hs⁻¹) at the steady state of force response. In each row, force responses obtained for similar velocities are compared. In each frame, from top to bottom, traces indicate: sarcomere length change, force response and zero force. The time-scale is 400 ms (A–D) or 100 ms (E–F). sf-1 fibre: fibre length, 1.96 mm; segment length, 1.05 mm; average sarcomere length in the segment, 2.51 μm; CSA, 7000 μm², temperature, 11.8°C. sf-2 fibre: fibre length, 2.10 mm; segment length, 1.0 mm; average sarcomere length in the segment, 2.58 μm; CSA, 5200 μm², temperature, 11.8°C. The two fibres are from vastus lateralis muscle of the same subject.

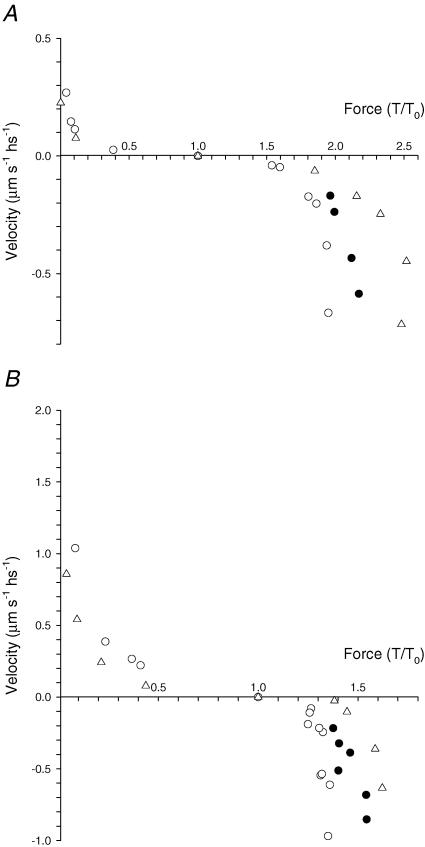
Figure 5. Force–velocity relations in two slow fibres (A) and in two fast fibres (B). Negative velocity refers to lengthening.

Open symbols, steady force; filled circles, peak of force during lengthening. A, triangles (sf-1) and circles (sf-2) refer to the same slow fibres as in Fig. 4. B, triangles: 2A fast fibre (same fibre as in Fig. 3); circles: 2A/2X fast fibre (fibre length, 3.40 mm; segment length under the striation follower, 1.20 mm; average segment sarcomere length, 2.64 μm; CSA, 12 400 μm²; temperature, 11.6°C; isometric force, 170 kPa). Filled circles show the relation between the peak of force and the lengthening velocity during the corresponding phase of force response for the sf-2 and 2A/2X fibres.

Figure 5 shows the force–velocity relations for the two types of slow fibres (A) and fast fibres (B). The mean force–velocity relations from all the fibres of each type are shown in Fig. 6. The lines represent Hill's equation (Hill, 1938) fitted to the force–shortening velocity points from each fibre type:

where a/T₀, b and V_max (speed of unloaded shortening) are free parameters. V_max of slow sf-2 fibres is about twice that of slow sf-1 fibres but ∼6 times smaller than that of fast 2A/2X fibres (Table 2 and see Bottinelli et al. 1996). Force–lengthening velocity relations show that in both slow and fast fibres the maximum value of steady force does not increase for velocities larger than 0.3 μm s⁻¹ hs⁻¹. Note that in fast fibres, in agreement with the data from twitch frog fibres (Lombardi & Piazzesi, 1990), this velocity is 10 times lower than V_max, while in slow fibres it is similar to V_max (Table 2). Thus the force at which the fibre exhibits the phenomenon of give, T_G (Katz, 1939), is attained in all cases at a velocity <0.3 μm s⁻¹ hs⁻¹. T_G/T₀ is 2.39 ± 0.06 in slow sf-1 fibres, 1.99 ± 0.02 in slow sf-2 fibres, 1.62 ± 0.03 in fast 2A fibres and 1.36 ± 0.02 in fast 2A/2X fibres. Consequently the stretch-dependent potentiation of steady force is larger the smaller the isometric force. In fact, when expressed in kPa (Fig. 6B), T_G is similar (140–160 kPa) for all fibre types.

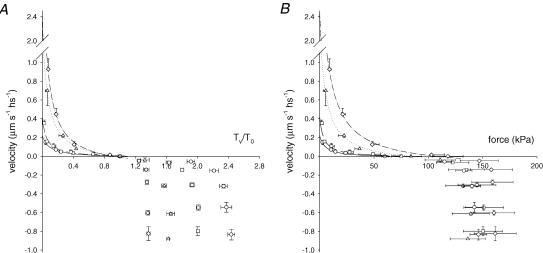
Figure 6. Mean force–velocity relations in slow and fast fibres.

A, force relative to the isometric value. B, force in kPa. Negative velocities refer to lengthening. Circles: sf-1, n = 8; squares, sf-2, n = 5; triangles: 2A, n = 6; diamonds: 2A/2X, n = 11. Bars are ± s.e.m.. Data are grouped in classes of velocity. The sample number in each class varies between 2 and 14. Lines are Hill's equations fitted to the pooled force–shortening velocity data. Continuous lines, sf-1; dashed lines, sf-2; dotted lines, 2A; dot–dashed lines, 2A/2X.

Table 2.

Relevant parameters of the force–velocity experiments for slow and fast fibres

	T0 (kPa)	Vmax (μm s−1 hs−1)	Wmax (mW m−2 hs−1)	Vopt (μm s−1 hs−1)	Tv/T0
Slow fibres
(sf-1) (n = 8)	60 ± 3	0.219 ± 0.014	0.669	0.046	2.39 ± 0.06
(sf-2) (n = 5)	75 ± 9	0.422 ± 0.033	1.024	0.072	1.99 ± 0.02
Fast fibres
2A (n = 6)	84 ± 10	1.459 ± 0.106	4.716	0.281	1.62 ± 0.03
2A/2X (n = 11)	118 ± 13	2.482 ± 0.933	9.303	0.464	1.36 ± 0.02

Power output during steady shortening and lengthening

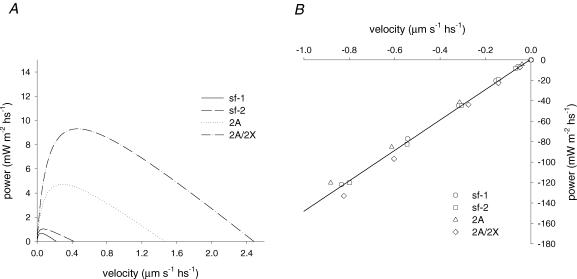
Figure 7A shows the power–shortening velocity relation for sf-1 (continuous line), sf-2 (dashed line), 2A (dotted line) and 2A/2X fibres (dot–dashed line) calculated from the parameters of Hill's equation in Fig. 6A. The relevant parameters are reported also in Table 2. For slow fibres the maximum power output (W_max) was 0.669 mW m⁻² hs⁻¹ (sf-1) and 1.024 mW m⁻² hs⁻¹ (sf-2). The shortening velocity for the maximum power (V_opt) was 0.046 and 0.072 μm s⁻¹, respectively. For fast fibres W_max was 4.716 mW m⁻² hs⁻¹ (2A) and 9.303 mW m⁻² hs⁻¹ (2A/2X); V_opt was 0.281 and 0.464 μm s⁻¹, respectively. Thus also for W_max and V_opt there is roughly a factor of 2 difference between the two subtypes of slow fibres. During steady lengthening the amount of power absorbed per hs by either slow or fast fibres was similar. The power was linearly related to the velocity (Fig. 7B) as a consequence of the constant value of steady force response in the range of velocity used. The linear regression equation fitted to the pooled data indicates a slope of about 150 kPa.

Figure 7. Relations between power and velocity during steady shortening (A) and lengthening (B).

Lines in A were obtained from Hill's equation fitted to the relative force–shortening velocity curves of Fig. 6. The points in B represent the mean values obtained from the points for lengthening in Fig. 6, and the line represents the linear regression (slope, 148.9 ± 2.9 kPa; ordinate intercept, 0.81 ± 1.31 mW m⁻² hs⁻¹) fitted to the pooled data.

Stiffness during isometric contraction of fibres activated with different pCa

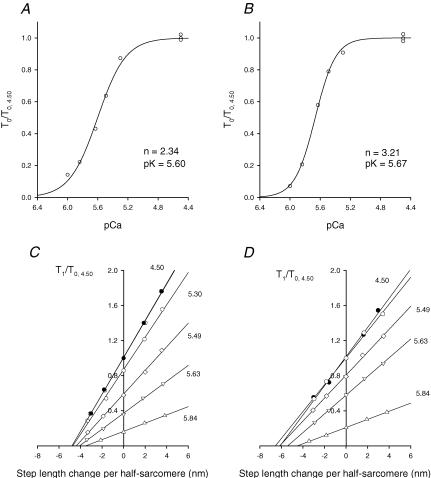
Force response to stretch can be accounted for by an increase in either strain or number of attached myosin heads or by a combination of the two mechanisms. Which mechanism it is can be established by determining the changes in fibre stiffness during stretch, if the fractional contribution of the various structures (myofilaments and attached myosin heads) to hs compliance is known. For this we used the method of Blangéet al. (1985) (see also Martyn et al. 2002) by determining the change in stiffness with the steady isometric force induced by different concentrations of Ca²⁺ in the activating solution (Figs 8 and 9). To measure the stiffness, small steps (range +3 to –3 nm hs⁻¹) were superimposed on the steady force developed at each pCa. The stiffness (e₀) was calculated by the slope of the relation between the force attained at the end of the step and the step size (Fig. 9C and D, T₁ relation, Huxley & Simmons, 1971). The number of activation–relaxation cycles with good sarcomere signal was limited to 12–15, so that stiffness measurements at different pCa (range 6.0–4.50) were performed on a group of fibres different from those used to determine the stiffness during stretch. Typical records at different pCa are shown in Fig. 8 for a slow fibre. The T₁ relation at any Ca²⁺ concentration could be fitted with a linear regression equation (continuous lines in Fig. 9C and D), the slope of which (the stiffness) increased with T₀, but not in proportion, as shown by the increase in the intercept on the length axis, Y₀. At saturating pCa (4.50) Y₀, which measures the extension of the hs elasticity in the isometric conditions preceding the step (Huxley & Simmons, 1971), was 5.17 ± 0.31 nm hs⁻¹ (T_0,S= 72 ± 5 kPa) in three slow fibres and 6.53 ± 0.05 nm hs⁻¹ (T_0,S= 106 ± 4 kPa) in two fast 2A/2X fibres. Figure 10 shows the relation between Y₀ and the isometric force for different Ca²⁺ concentrations in slow and fast 2A/2X fibres. In both fibre types Y₀ increases linearly with force. The slopes and the ordinate intercepts of the straight lines fitted to either sets of data are 0.021 ± 0.005 nm kPa⁻¹ and 3.58 ± 0.28 nm for the slow fibres (open symbols), and 0.023 ± 0.005 nm kPa⁻¹ and 4.29 ± 0.36 nm for the fast 2A/2X fibres (filled symbols). The slope of the relations is an estimate of the compliance of the elastic component in series to the force generators, due mainly to the elasticity of actin and myosin filaments (Huxley et al. 1994; Wakabayashi et al. 1994; Dobbie et al. 1998). The finding that, independently of the fibre type, the slopes of the two relations are practically the same (0.022 nm kPa⁻¹) is in turn a strong support for the idea that this contribution to hs compliance is due to passive elastic components, like the actin and myosin filaments, that are expected to have identical mechanical properties in either fibre type. Under these conditions the ordinate intercepts represent an estimate of the strain in the isometric force generators, the myosin heads, which appears 20% larger in fast fibres than in slow fibres. Considering that T_0,S is ∼50% larger in fast fibres (see Fig. 9 legend), it is evident that the strength of the attachment is only one of the factors responsible for the difference in isometric force between slow and fast fibres.

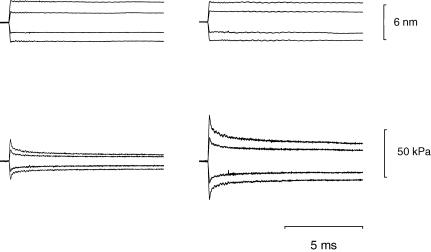
Figure 8. Superimposed tension responses to length steps of different size in a slow fibre activated at different pCa.

Left column, pCa = 5.63; right column, pCa = 4.50. Upper panels, length change per hs; lower panels, force response. Fibre length, 3.15 mm; segment length, 1.05 mm; average sarcomere length in the segment, 2.40 μm; CSA, 5800 μm²; temperature, 12.1°C; isometric force at pCa = 4.50, 66 kPa.

Figure 9. Isometric force–pCa relation (A and B) and T₁ relations at different pCa (C and D) in a slow fibre (A and C) and a fast fibre (B and D).

The continuous lines in A and B are calculated from Hill's equation: T₀/T_0,4.50= 1/[1 + 10^n(pK–pCa)], where n, the Hill coefficient, expresses the slope and pK is pCa at which T₀= 0.5T_0,4.50. The best-fitting parameters, obtained with the nonlinear least-squares method (SigmaPlot, Jandel Scientific), are listed in the figure close to the graphs. T₁ curves in C and D are obtained by plotting the extreme tension attained at the end of the length step (T₁, relative to T₀ at pCa = 4.50, T_0,S) against the step amplitude. Different symbols refer to different pCa as indicated by the figure close to the corresponding relation. Circles refer to full activation before (open circles) and after (filled circles) the series at larger pCa. The lines represent the linear regressions fitted to the experimental points at each pCa. A and C, same fibre as in Fig. 8. B and D, fast (2A/2X) fibre: fibre length, 3.51 mm; segment length, 1.03 mm; average sarcomere length in the segment, 2.45 μm; CSA, 9500 μm²; temperature, 12.1°C; T_0,S, 109 kPa. Mean values (± s.e.m.) of the isometric force (T₀) and stiffness (e₀) at full activation are as follows. Slow fibres (3 fibres): T₀= 72 ± 5 kPa; e₀= 13.97 ± 2.36 kPa nm⁻¹; fast fibres (2 fibres): T₀= 106 ± 4 kPa; e₀= 16.15 ± 0.93 kPa nm⁻¹.

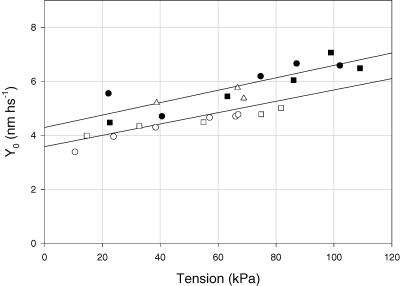
Figure 10. Relation of hs extension (Y₀) versus T₀ at different pCa values.

Open symbols: slow fibres; filled symbols: fast 2A/2X fibres. Different symbols refer to different fibres. The continuous lines were obtained by linear regression on the pooled data for either slow or fast fibres.

Change in stiffness during lengthening

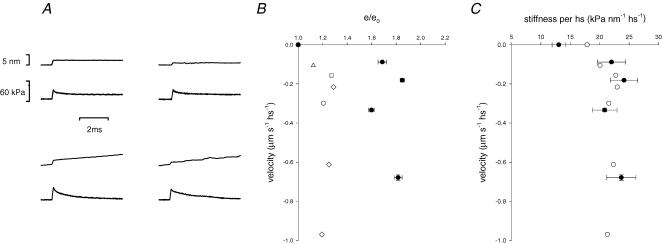
Changes in stiffness induced on maximally activated fibres by steady lengthening are summarized in Fig. 11 and Table 3. Data were obtained from four fast (2A/2X) fibres, and nine slow fibres (including both sf-1 and sf-2 fibres) activated at saturating pCa. Steps were imposed at the plateau of either the isometric force or the steady force response to lengthening (Fig. 11A). In both fibre types the stiffness during steady lengthening (e_v) is larger than in the corresponding isometric contraction (e₀). In fast fibres with an isometric force ∼75% larger than in slow fibres, e₀ is ∼35% larger. As shown in Fig. 11B, the increase in stiffness is independent of lengthening velocity (Lombardi & Piazzesi, 1990) and is much larger in slow fibres (∼65%, filled circles) than in 2A/2X fibres (∼20%, open symbols). Since the isometric force in fast fibres is 75% greater than in slow fibres, during lengthening the stiffness per hs in kPa nm⁻¹ is the same independently of fibre type (Table 3 and Fig. 11C).

Figure 11. Stiffness during steady lengthening in slow and fast fibres.

A, sample records of force responses to step length changes imposed on the active fibre either in isometric conditions (upper row) or during steady force response to lengthening at about 0.65 μm s⁻¹ hs⁻¹ (lower row) in a slow fibre (left column) and in a fast 2A/2X fibre (right column). In each panel, the upper trace is length change per hs; the lower trace is the force response. Slow fibre: fibre length, 3.35 mm; segment length, 1.07 mm; average sarcomere length in the segment, 2.51 μm; CSA, 4500 μm²; temperature, 12.1°C; T₀, 67 kPa; T_v/T₀, 2.48. 2A/2X fibre: fibre length, 3.4 mm; segment length, 1.2 mm; average sarcomere length in the segment, 2.64 μm; CSA, 12 400 μm²; temperature, 11.6°C; T₀, 170 kPa; T_v/T₀, 1.32. B, relation of stiffness versus lengthening velocity. Stiffness is relative to that measured in isometric conditions. Filled circles are mean values (± s.e.m.) for slow fibres (nine fibres; data contributing to each class between 5 and 15). Open symbols are for fast fibres (four fibres; each symbol refers to a different fibre). C, relation of the stiffness measured in kPa nm⁻¹ hs⁻¹versus lengthening velocity for the same data as in B.

Table 3.

Mean values (± s.e.m.) of isometric force (T₀), isometric stiffness (e₀), force (T_v) and stiffness (e_v) during steady lengthening in different fibre types

	T0 (kPa)	e0 (kPa nm−1)	Tv (kPa)	ev (kPa nm−1)
Slow fibres (n = 9)	68 ± 7	13.04 ± 1.13	148 ± 16	21.77 ± 2.08
Fast 2A/2X fibres (n = 4)	120 ± 28	17.85 ± 3.64	166 ± 38	21.78 ± 4.46

Discussion

The experiments reported in this paper show that different types of human skeletal muscle fibres respond to forcible lengthening, during maximal Ca²⁺ activation, producing the same force and stiffness and absorbing the same power. The diversity determined by the presence of distinct MHC isoforms, which is detectable during an isometric contraction (tension, ATPase activity) and active shortening (V_max and maximum power output), cannot be observed during steady-state lengthening. The experiments furthermore provide an explanation of the difference of isometric force in different fibre types, by estimating the difference in the strain of attached myosin heads. These results are obtained by applying for the first time high-resolution mechanics to the study of permeabilized human muscle fibres with identified composition in myosin isoforms. The implementation of a new protocol for fibre activation at low temperature has been instrumental for preservation of the sarcomere pattern so that sarcomere length changes could be recorded by a striation follower during shortening or lengthening manoeuvres.

The isometric force in slow and fast fibres

As shown in Table 4, which collects data from force–pCa experiments and force–velocity experiments, at 12°C the isometric tension is larger in fast fibres than in slow fibres by 47–76%. Similarly, the stiffness is 15–37% larger in fast fibres. A greater isometric tension of human fast fibres compared with slow has already been reported in previous studies (Stienen et al. 1996; He et al. 2000). The difference can find a quantitative explanation in terms of either the fraction of attached heads or the force per attached head, as reported below. Among fast fibres only 2A/2X fibres are considered, since this is the type of fast fibres for which the contribution of the myofilaments and the attached myosin heads to the hs compliance has been determined by force– and stiffness–pCa relations. Figure 10 shows that the compliance of the passive structures in series with force-generating myosin heads is ∼0.022 nm kPa⁻¹. This value can be used to determine the compliance of the myosin cross-bridges, from the compliance of the hs, according to eqns (A10) of Ford et al. (1981) and (A1) of Linari et al. (1998). At full overlap and assuming that the compliance of the Z line is zero and the compliance in series to myosin cross-bridges is due to actin and myosin filaments, these equations can be reduced to

(1)

where C is the hs compliance, C_f is the myofilament equivalent compliance and βɛ₀, the reciprocal of the compliance of the cross-bridges, is the cross-bridge stiffness, given by the product of the stiffness of myosin heads if all heads are attached (ɛ₀) and the fraction of attached myosin heads (β).

Table 4.

Summary of relevant mechanical parameters (mean values) from the two kinds of experiments (force–pCa experiments and force–velocity experiments) in slow and fast 2A/2X fibres

					Force–velocity experiments
Force–pCa experiments					Isometric					Steady lengthening
Y0 (nm)	F0/e0 (nm)	βe0 (kPa nm−1)	T0 (kPa)	e0 (kPa nm−1)	Y0 (nm)	F0/e0 (nm)	βe0 (kPa nm−1)	Tv (kPa)	ev (kPa nm−1)	Yv (nm)	Tv/βve0 (nm)	βve0 (kPa nm−1)	T0 (kPa)	e0 (kPa nm−1)
Slow
5.17	3.58	20.11	68	13.04	5.21	3.71	18.33	148	21.77	6.80	3.54	41.80	106	16.15
Fast
72	13.97	6.53	4.29	24.71	120	17.85	6.72	4.08	29.41	166	21.78	7.62	3.97	41.81

The parameters are: force in isometric conditions, T₀, and during steady lengthening, T_v; stiffness in isometric conditions, e₀, and during steady lengthening, e_v; hs strain in isometric conditions, Y₀, and during steady lengthening, Y_v; average strain per cross-bridge in isometric conditions, F₀/ɛ₀, and during steady lengthening, T_v/β_vɛ₀; stiffness of the cross-bridges in isometric conditions, βɛ₀, and during steady lengthening, β_vɛ₀.

According to the results in Fig. 10 and to previous results in the literature (Kraft & Brenner, 1997; Jung et al. 1992; Martyn et al. 2002), pCa influences the fraction of myosin heads in the strong bound force generating state. Thus for either slow or fast fibres the strain per head remains constant independently of pCa and is estimated by the ordinate intercept of the relation between the hs strain, Y₀( =CT₀), and the isometric force (T₀). Under these conditions and using eqn (1), the linear equation fitted to the data in Fig. 10 can be rewritten as

(2)

If the strain and thus the force per myosin head is constant and independent of pCa,

(3)

where F₀ is the isometric force exerted by the hs if all the heads are attached. Using this definition, eqn (2) becomes

(4)

where F₀/ɛ₀ is the ordinate intercept of the relations in Fig. 10 and represents the average strain per attached myosin head. Assuming that, for an equal number of attached heads, the compliance of the heads (1/ɛ₀) is the same in both fibre types, the larger strain of fast fibre heads reflects an increase in F₀, that is, an increase in the force exerted by each myosin head. Note that, using the value of C_f estimated from the Y₀:T₀ relations in force–pCa experiments, F₀/ɛ₀ can be calculated also for the data from force–velocity experiments (Table 4). F₀/ɛ₀ is 20% (force–pCa experiments) to 10% (force–velocity experiments) larger in fast than in slow fibres (Table 4), and this explains only a part of the larger T₀ of fast fibres at saturating pCa (47–76%). A substantial contribution to the increase in T₀ must be attributed to the different fraction of attached force-generating heads, β (=T₀/F₀). β is 22% (force–pCa experiments) to 60% (force–velocity experiments) larger in fast than in slow fibres. The conclusion that the fraction of interacting heads is higher in fast than in slow fibres is in agreement with our previous observations (He et al. 2000), based on comparison of the ATPase activity–tension relations determined in slow and fast fibres during ramp shortening. It is worth noting that also a smaller density of myofibrils in slow fibres would produce a parallel reduction of both force and stiffness. However, this possibility is not sustained by structural evidence (Eisenberg, 1983 and references therein) and, in any case, is contradicted by the finding that the stiffness becomes similar in both fibre types during constant-velocity stretch (Fig. 11C and Table 3).

The large variability of F₀/ɛ₀ and βɛ₀ for the same class of fibres in the two experiments (Table 4) reflects the variability of T₀ and Y₀. The reliability of the estimate of filament compliance can be tested by comparison with current estimates of the compliances of actin and myosin filaments obtained with much better resolution from frog intact muscle fibres. For the comparison it must be considered that the force per CSA in this work is underestimated by a factor of 1.44 because of the increase in fibre diameter by 20% produced by skinning (Godt & Maughan, 1981; Metzger & Moss, 1987; Linari et al. 1998), and a ratio 3 : 1 of actin over myosin filament compliance must be assumed (Wakabayashi et al. 1994; Huxley et al. 1994; Dobbie et al. 1998; Piazzesi et al. 2003). Equations described by Linari et al. (1998) allow us to calculate the average strain of actin and myosin filaments from their compliances, and the values obtained (0.26% $T_0^{-1}$ for the actin filament and 0.17% $T_0^{-1}$ for the myosin filament) are in agreement with the values estimated in frog muscle from mechanical and X-ray diffraction experiments (Wakabayashi et al. 1994; Huxley et al. 1994; Dobbie et al. 1998).

The nature of force response to lengthening

Forcible lengthening of maximally activated fibres produces increases in steady force and stiffness that are much larger in slow than in fast fibres. The force increase is ∼120% in slow fibres and ∼40% in fast fibres, while the stiffness increase is ∼65% in slow fibres and ∼20% in fast fibres (Table 3). Two clear and important features derive from these results: the first is that during lengthening both force and stiffness of slow and fast fibres become similar; the second is that in either fibre type the stretch-dependent increase in force is twice the stretch-dependent increase in stiffness.

The finding that the stretch-dependent increase in force is larger in slow (less isometric force-generating) fibres is in agreement with all the work in frog and mammalian muscle, showing that the stretch-dependent increase in force is larger when the isometric force is depressed by different interventions like hypertonicity (Mansson, 1994; Piazzesi et al. 1994), fatigue (Curtin & Edman, 1994), increase in phosphate concentration (Dantzig et al. 1990; Stienen et al. 1992) and decrease in temperature (Piazzesi et al. 2003). Recently a larger increase in force by stretch when isometric force is depressed by fatigue and by reduction in temperature has been demonstrated also in human skeletal muscle in situ (De Ruiter & De Haan, 2001). All these data are consistent with the idea, developed from the theory of Huxley & Simmons (1971), that cross-bridges under strain are prevented from going through the force-generating transition and accumulate in an early strongly bound state (Lombardi & Piazzesi, 1990; Piazzesi et al. 1992). The farther from the initial low force-generating state is the equilibrium distribution in the isometric condition (the higher the isometric force), the larger will be the strain-dependent backward redistribution that partially neutralizes the force increase due to the imposed strain (and thus the smaller the steady force enhancement by stretch).

Among the factors responsible for the force enhancement during lengthening, the increase in strain of an elastic component in parallel to cross-bridges, like titin, is likely to be not relevant under the conditions of our experiments. In fact virtually no resting tension is developed at the starting sarcomere length (2.4–2.65 μm) with elongations below 100 nm hs⁻¹. In the range of sarcomere lengths and elongations utilized in this study, the response of titin-based parallel elasticity might become evident only under conditions that favour the development of sarcomere inhomogeneity, when the weak sarcomeres yield and take all of the lengthening imposed on the fibre, until the parallel elastic component stress–strain relation equilibrates the force of stronger sarcomeres in series (Morgan, 1990). The characteristics of intrinsically inhomogeneous fibres are: (i) a reduced force enhancement during the initial phase of the stretch; (ii) a continuous rise of force (creep) even beyond the break-point or angle of force increase; and (iii) a long-lasting force enhancement after the stretch ends (Edman et al. 1978, 1982; Colomo et al. 1988; Edman & Tsuchiya, 1996). This behaviour is favoured by conditions such as when the stretch is applied on tetani in the descending limb of the length–tension relation (Edman et al. 1982) or high-velocity lengthening is repeatedly imposed on successive tetani (Lombardi & Piazzesi, 1990). Our protocol is specifically devised to minimize development of inhomogeneity between sarcomeres during stretch, by limiting the stretch speed to <1 μm s⁻¹ hs⁻¹ and alternating shortening and lengthening contractions. In our experiments (see Figs 3 and 4) the creep of force during lengthening beyond the point of the peak or angle of force is absent or small, providing evidence for excluding a significant contribution of a parallel elastic component to the response to stretch. Eventually the larger force enhancement of slow fibres with respect to fast fibres cannot be explained by a different contribution of a parallel elastic component like titin, since slow fibres are known to develop less passive tension in response to elongation (Wang et al. 1991; Horowits, 1992), a feature which might be related to the greater length of the titin isoform expressed in slow compared with fast fibres (Labeit & Kolmerer, 1995). A recent study in frog fibres elongated under special conditions like 2,3-butanedione monoxime (BDM) depressed contraction (Bagni et al. 2002) has revealed the contribution of a not yet identified, non cross-bridge related parallel elastic component of the order of 5% of the isometric tetanic force: a 5% contribution of this component to our responses cannot be excluded.

The factors that, under our conditions, are relevant for explaining the force response to stretch and the different responses of slow and fast fibres have to be found in the mechanical and kinetic properties of cross-bridges. To determine if there is a substantial contribution of changes in the fraction of attached myosin heads, it is necessary to analyse the stretch-dependent changes in the hs stiffness in terms of the fractional contribution of cross-bridges and myofilaments.

Assuming that myofilament compliance behaves in a linear way also at forces larger than the active isometric force (Linari et al. 2000), the cross-bridge strain can be calculated for the steady response to lengthening, by using the observed hs strain during steady lengthening (Y_V, the abscissa intercept of the T₁ relation during lengthening) and the myofilament compliance determined from force–pCa experiments (C_f= 0.022 nm kPa⁻¹). In fact, adapting eqn (2) to the steady lengthening response,

(5)

where β_V is the fraction of myosin heads attached during lengthening. From eqn (5) the average strain per cross-bridge during lengthening, T_V/(β_Vɛ₀), can be calculated and is 3.54 nm for slow fibres and 3.97 nm for fast fibres (Table 4). These values are not very different from the corresponding values during isometric contraction, 3.71 and 4.08 nm, respectively. Consequently the stiffness of cross-bridges during lengthening, β_Vɛ₀, is increased by almost the same amount as the force, ∼130% (slow fibres) and ∼40% (fast fibres), attaining a similar value in either fibre type (Table 4).

According to this analysis, the force enhancement by stretch is fully explained by the increase in the number of attached heads, while their strain remains similar, although passive, to that actively generated in the isometric contraction.

A requirement to make the response to stretch adequate to the task of resisting sudden increases in load beyond the isometric force without a large strain in the attached heads is that the recruitment of new attachments is very rapid. Actually in intact fibres from the frog it has been found that the increase in stiffness following a step stretch is complete within 0.5 ms or so (Lucii et al. 2001a,b). The mechanism that could explain such a fast recruitment could be that even small increases in strain of the force-generating heads, as soon as the attached actin monomer moves away from the M line, favour the attachment of the second (partner) head of the same myosin molecule on the next actin monomer closer to the M line (Linari et al. 2000). Alternatively, in isometric conditions there could be a fraction of myosin heads in a weak binding state and ready for the transition to strong binding as soon as the actin monomer, sharing the weak interaction, moves away from the M line (see also Getz et al. 1998). The evidence, from these experiments, that the recruitment of cross-bridges by lengthening can increase the fraction of attached heads up to more than twice the isometric fraction (the case of slow fibres) supports the second hypothesis. This argument suggests in turn that slow fibres, which exhibit a lower isometric force and have a smaller fraction of strongly attached force-generating heads with respect to fast fibres, have a larger fraction of myosin heads in the weak binding state, ready to be recruited by lengthening.

In conclusion, the MHC isoform determines the isometric force developed by the activated fibre by modulating the force per head and the fraction of strong bound force-generating heads, but, at the same time, provides the fibre with the same resistance to stretch, irrespective of the fibre type, by exhibiting the same strong bond during lengthening for all the myosin heads that can interact with actin.

In contrast to the mechanical properties during steady lengthening, different fibre types show different characteristics during force rise at the beginning of lengthening. For lengthening speeds >0.1 μm s⁻¹ hs⁻¹ the force rises smoothly to the steady value in the sf-1 subgroup of slow fibres and 2A fibres, while in the sf-2 subgroup of slow fibres and 2A/2X fibres the force passes through a peak larger than the steady-state value. Actually, also in the fibres with a smooth transition to steady force, a transient peak in force should be generated by a sufficiently high lengthening speed. The lack of evidence for a peak in the full range of velocities used (0.1–0.8 μm s⁻¹ hs⁻¹) could be due to the fact that, as the lengthening speed is increased, the degree of inhomogeneity in the redistribution of lengthening among the sarcomeres increases to an extent sufficient to prevent the development of the transient peak (Colomo et al. 1988; Lombardi & Piazzesi, 1990). In any case, the presence/absence of the peak of force at velocities slightly greater than 0.1 μm s⁻¹ hs⁻¹ further supports the separation in subclasses within both slow and fast fibres.

The peak of force during high-speed lengthening has been explained by the time taken by the attached heads responsible for the isometric force before the start of lengthening to redistribute toward lower force-generating states (A₂→A₁ transition in Lombardi & Piazzesi, 1990). According to this idea there should be no peak of force if there is enough time for the state redistribution before a great proportion of high force-generating A2 heads can be strained or, alternatively, the rate constant for the reversal of the force-generating transition (k₋₂ in Lombardi & Piazzesi, 1990) is large enough to provide a fast re-equilibration during lengthening. The first argument explains the absence of the peak of force for lengthening speeds below 0.1 μm s⁻¹ hs⁻¹. The second argument could explain the absence of the peak in sf-1 fibres and 2A fibres even at speeds >0.1 μm s⁻¹ hs⁻¹. In fact in these two fibre types T₀ is lower than in the corresponding types that show the force peak (sf-2 and 2A/2X). In conclusion, a larger k₋₂ could explain both the lower fraction of high force-generating cross-bridges and the absence of a force peak during lengthening.

Molecular basis of the diversity of the mechanical response

A large body of evidence supports the view that the energetic parameters (ATP consumption rate, tension cost) and the mechanical parameters (shortening velocity, power output) of the contractile response of skeletal muscle fibres are primarily determined by MHC isoform composition with a contribution of the alkali MLC isoform (see for a review Schiaffino & Reggiani, 1996; Bottinelli & Reggiani, 2000). The results of this study show that all MHC isoforms, when exposed to an external work pulling actin filaments away from the centre of the sarcomere, behave in the same way in spite of the structural diversity which is responsible for their specific kinetic and mechanical properties in isometric contraction and during shortening. An interesting finding is the heterogeneity observed inside the group of slow fibres (i.e. fibres expressing MHC-1) without any obvious explanation in terms of myosin isoform. Slow fibres have been divided into two subgroups, sf-1 and sf-2, on the basis of both a bimodal distribution of the force response to a ramp shortening and the transitory response to lengthening. The fibres identified as sf-2 exibit V_max, W_max and V_opt larger by a factor of 2 and T₀ larger by ∼25% with respect to sf-1 fibres (Table 2); they also show a transient peak before the force reaches a steady value during lengthening, and the increase of relative force (T/T₀) during lengthening is lower in sf-2 than in sf-1. However, between sf-2 fibres and fast 2A fibres there are differences of factors of 4–6 in V_max, W_max and V_opt and of 10–20% in T₀ (Table 2 and Figs 6 and 7). A first element to take into account to explain the difference is the presence in sf-2 fibres of a small fraction of MHC-2A which might be undetected by gel electrophoresis. The resolution of single-fibre gel electrophoresis is about 1% (Bottinelli et al. 1994). Owing to the non linear interaction between a slow and a fast myosin isoform as regards shortening capability (Harris et al. 1994), the effect of the slower isoform is predominant and thus the presence of 1% of MHC-2A should not be sufficient to increase the shortening velocity significantly. A contribution of MLC isoform composition can be excluded, as both alkali and regulatory MLC isoforms have been found to be slow in all slow fibres examined. The presence of more than one slow MHC isoform in skeletal muscle fibres is matter of debate. Three slow MHC isoforms have been distinguished on the basis of antibody reactivity in rat muscles (Hughes et al. 1993). In rabbit muscle a second MHC isoform was found in a sub-population of slow fibres and has been identified as MHC-alpha cardiac (Galler et al. 1997). Moreover, a second MHC isoform has been separated from MHC-1 in rat soleus muscle (Fauteck & Kandarian, 1995); such extra MHC, which did not co-migrate with MHC-alpha cardiac, was not identified further. None of the above findings has been confirmed in human skeletal muscle. Although a very recent study of mRNAs coding for MHC isoforms in human muscles following strength training has suggested the up-regulation of MHC-alpha slow mRNA, such an isoform has not been identified at single-fibre level (Liu et al. 2003). The most likely explanation of the functional difference between fibres identified as type 1 by gel electrophoresis is in our view represented by post-translational modifications, which have been shown to occur under special conditions (ageing) in MHC-slow (Bottinelli, 2001; Hook et al. 1999), but might be more frequent than until now suspected.

In conclusion, the results of the present study significantly contribute to the understanding of the diversity among myosin isoforms. The higher isometric tension developed by fast compared with slow fibres is explained both by higher force and strain per myosin head and by a greater fraction of attached heads, reflecting both a shift of the balance towards strongly attached heads and a shift of strongly attached heads to higher force-generating states. Further studies are required to explain in molecular terms these two aspects, particularly the higher strain and force in fast myosin during isometric contraction. From the physiological point of view, the main finding is that all myosin isoforms exhibit the same stress under strain, contributing in the most efficient way to generate the high resistance of muscle to forcible lengthening.