Modulation of excitation–contraction coupling by isoproterenol in cardiomyocytes with controlled SR Ca²⁺ load and Ca²⁺ current trigger

Abstract

Cardiac Ca²⁺ transients are enhanced by cAMP-dependent protein kinase (PKA). However, PKA-dependent modulation of ryanodine receptor (RyR) function in intact cells is difficult to measure, because PKA simultaneously increases Ca²⁺ current (I_Ca), SR Ca²⁺ uptake and SR Ca²⁺ loading (which independently increase SR Ca²⁺ release). We measured I_Ca and SR Ca²⁺ release ± 1 μm isoproterenol (ISO; isoprenaline) in voltage-clamped ventricular myocytes of rabbits and transgenic mice (expressing only non-phosphorylatable phospholamban). This mouse model helps control for any effect of ISO-enhanced SR uptake on observed release, but the two species produced essentially identical results. SR Ca²⁺ load and I_Ca were adjusted by conditioning. We thus evaluated PKA effects on SR Ca²⁺ release at constant SR Ca²⁺ load and I_Ca trigger (with constant unitary I_Ca). The amount of SR Ca²⁺ release increased as a function of either I_Ca or SR Ca²⁺ load, but ISO did not alter the relationships (measured as gain or fractional release). This was true over a wide range of SR Ca²⁺ load and I_Ca. However, the maximal rate of SR Ca²⁺ release was ∼50% faster with ISO (at most loads and I_Ca levels). We conclude that the isolated effect of PKA on SR Ca²⁺ release is an increase in maximal rate of release and faster turn-off of release (such that integrated SR Ca²⁺ release is unchanged). The increased amount of SR Ca²⁺ release normally seen with ISO depends primarily on increased I_Ca trigger and SR Ca²⁺ load, whereas faster release kinetics may be the main result of RyR phosphorylation.

Cardiac manifestations of adrenergic stimulation (inotropy, chronotropy and lusitropy) were already under investigation by 1900 (Elliott, 1905). Via protein kinase A (PKA) activation, β-adrenergic receptor (β-AR) activation promotes phosphorylation of at least four cellular targets which have key roles in the control of excitation–contraction coupling (ECC) and Ca²⁺-induced Ca²⁺ release (CICR). PKA-dependent phosphorylation of: (1) troponin-I (TnI) reduces myofilament Ca²⁺ sensitivity (Zhang et al. 1995), (2) L-type Ca²⁺ channels increases Ca²⁺ current (I_Ca, due mainly to increased open probability; Bean et al. 1984), (3) phospholamban (PLB) enhances SR Ca²⁺-ATPase activity and SR Ca²⁺ load (by disinhibiting SR Ca²⁺-ATPase; Lindemann et al. 1983), (4) ryanodine receptor/Ca²⁺ release channels (RyR) can alter function as described below (Yoshida et al. 1992; Marx et al. 2000). Since non-subtype-selective β-AR agonists like isoproterenol (ISO) normally phosphorylate all these targets simultaneously, the balance of effects on ECC in the intact cell is complex. This study evaluates how PKA-dependent RyR phosphorylation affects RyR behaviour during ECC, independently of effects on I_Ca, TnI or PLB.

In cardiac RyRs in isolation in lipid bilayers (in steady state), PKA activation led to enhanced open probability (P_o) and appearance of submaximal conductance states, with a net increase in integrated Ca²⁺ flux (Marx et al. 2000,2001). These PKA effects were correlated with unbinding of the FK-506 binding protein (FKBP-12.6) from the RyR, where FKBP-12.6 bound to RyR normally stabilizes and coordinates RyR gating, minimizing substate occurrence and SR Ca²⁺ leak (Marx et al. 2001; Prestle et al. 2001). On the other hand, Valdivia et al. (1995) showed that PKA decreased steady-state RyR P_o in bilayers, but enhanced the transient peak P_o in response to a rapid rise in activating [Ca²⁺] (meant to simulate what happens in ECC). Extrapolating these disparate RyR bilayer results to intact cells, we might or might not expect enhanced SR Ca²⁺ release with PKA (for a given I_Ca trigger and SR Ca²⁺ load).

Li et al. (2002) studied PKA effects on resting Ca²⁺ sparks in intact and permeabilized ventricular myocytes, thereby retaining RyR in a more physiological local environment. Ca²⁺ sparks reflect the stochastic resting openings of clusters of RyRs and are probably the main route of Ca²⁺ leak from the SR (Cheng et al. 1993; Bers, 2001). PKA greatly stimulated Ca²⁺ spark frequency in these myocytes, but only when PLB could be phosphorylated (which caused SR Ca²⁺ load to increase). In mice that either lack PLB or express only a mutant PLB which lacks both the Ser¹⁶ and Thr¹⁷ regulatory phosphorylation sites (the latter used also in the present study), Ca²⁺ spark frequency and characteristics were unchanged, despite direct evidence of RyR phosphorylation. Evidently, PKA activation does not affect RyR leak much during rest. However, the situation could be quite different during ECC where I_Ca triggers RyR opening. Intact stimulated cells are required to assess this.

With β-AR stimulation, larger and faster relaxing [Ca²⁺]_i transients are routinely observed in cardiac myocytes (Callewaert et al. 1988), and the typical bell-shaped dependence of [Ca²⁺]_i transients on membrane voltage usually becomes flat-topped (Hussain & Orchard, 1997). However, in these studies, both the I_Ca trigger and SR Ca²⁺ load increased simultaneously with ISO. Since both load and trigger strongly affect ECC/CICR independently of β-AR modulation (Bassani et al. 1995b; Shannon et al. 2000), these studies do not reveal how intrinsic RyR function is altered independently of I_Ca or SR Ca²⁺ load changes.

β-AR stimulation led to more spatially organized and time-synchronized depolarization-induced Ca²⁺ release in rat ventricular myocytes (Song et al. 2001) and post-infarct border zone rabbit myocytes (Litwin et al. 1998). The former reported a decrease of ECC gain with ISO, but in that study most I_Ca triggers with ISO were large, a possibly saturating condition where we see ECC gain to be at its lowest with or without ISO (note that ECC gain is usually some function of Ca²⁺ release/I_Ca). In contrast, Viatchenko-Karpinski & Györke (2001) found increased ECC gain with ISO, but only when both intra- and extracellular Na⁺ were present (implying a role of Na⁺–Ca²⁺ exchange, which can alter the spatial properties and stability of the Ca²⁺ trigger; Sham, 2000). delPrincipe et al. (2001) also detected an ISO-mediated increase in ECC gain, especially near threshold. They used a controlled flash-photolytic Ca²⁺ trigger (rather than I_Ca), in cells at constant SR load. While this technique offers close control of the Ca²⁺ trigger, it is less physiological than I_Ca. Taken together, these disparate results indicate that Ca²⁺ release in active cells is strongly dependent on specifics of the trigger and SR Ca²⁺ load.

A unique feature of our experiments is that we compared fractional SR Ca²⁺ release (and ECC gain) ± ISO over a broad range of controlled I_Ca triggers and SR Ca²⁺ loads. We used steady-state pre-inactivation of I_Ca to control I_Ca (rather than test membrane potential (E_m) or external [Ca²⁺]). This helped us adjust triggers with ISO over a wide range, including moderate non-saturating values expected during APs. In fact ISO versus control comparisons were made at comparable macroscopic I_Ca and identical unitary I_Ca amplitude, test voltage and external [Ca²⁺]. We used varying conditioning pulses to obtain overlapping SR Ca²⁺ loads (± ISO). This extends our previous strategy (Li et al. 1997) where we showed that calmodulin-dependent protein kinase II (CaMKII) activation profoundly enhanced SR Ca²⁺ release for a given I_Ca and SR Ca²⁺ load (over a range of I_Ca triggers).

Further, although we used mainly rabbit ventricular myocytes, we also used a recently developed mouse model expressing only mutant PLB where both phosphorylation sites (Ser¹⁶ and Thr¹⁷) are mutated to Ala. This mutant PLB was reintroduced in the PLB knockout (Luo et al. 1994) background. The SR Ca²⁺-ATPase in this model has a Ca²⁺ affinity comparable to wild-type mice, but cannot be stimulated by ISO (Brittsan et al. 2003). This made it both easier to control SR Ca²⁺ loading ± ISO, and also prevented the acceleration of [Ca²⁺]_i decline seen in ISO (which could complicate Ca²⁺ release analysis).

Here we find, as expected, that under fixed conditions (either control or ISO), increasing I_Ca or SR Ca²⁺ load enhance fractional SR Ca²⁺ release (and enhanced SR Ca²⁺ load enhances ECC gain). For comparable I_Ca and SR Ca²⁺ load, ISO had little effect on either SR fractional release or ECC gain, but did cause a significant increase in the SR Ca²⁺ release rate.

Methods

Cell preparation

All cells were isolated using species-specific protocols approved by Loyola University's Institutional Animal Care and Use Committee (IACUC). The nominally Ca²⁺-free cell isolation solution was either Tyrode solution (mm: NaCl 140, KCl 4, MgCl₂ 1, and Hepes 10; pH 7.2) or Dulbecco's minimal essential medium gassed with 95% O₂–5% CO₂ (DMEM; Type 22300, Gibco/Invitrogen, USA). Rabbits were anaesthetized with sodium pentobarbital (50 mg kg⁻¹i.v.) and deep anaesthesia verified (complete absence of reflex on repeated corneal touch and foot pinch). Hearts were excised (at which time the animal died of exsanguination), rinsed in ice-cold Ca²⁺-free solution, and retrogradely perfused at 37°C, at either constant flow (30–36 ml min⁻¹) or preferably constant pressure (80 mmHg). After 5 min of perfusion with Ca²⁺-free solution, collagenase (0.3–0.7 mg ml⁻¹; Yakult Corporation, Japan or Boehringer Mannheim, Germany) and Ca²⁺ (10–20 μm) were added. After 15–25 min, perfusion was stopped and ventricles were minced into ∼2 mm³ size pieces. Optionally the pieces were incubated for 5–20 min in fresh enzyme. Finally, enzyme activity was stopped with DMEM solution containing bovine serum albumin (BSA; 0.5–1%), and tissue was agitated or triturated to liberate single cells. These were washed and stored in DMEM solution adjusted to [Ca²⁺]= 150 μm.

Mice were anaesthetized (inhalation of 2–3% isoflurane in 100% O₂), tracheotomized and mechanically ventilated. Upon verifying total insentience (complete absence of reflex on repeated corneal touch and foot pinch), we opened the chest cavity, injected cold high-K⁺ cardioplegia solution into the vena cava, quickly excised the heart (at which time the mouse died of exsanguination), and transferred it to our gravity-driven (80 mmHg) apparatus for perfusion at 37°C. The initial flow rate, ∼3 ml min⁻¹, increased during digestion, and this increase was a criterion for ending perfusion. After enzyme perfusion the mouse hearts were further treated as described above for rabbit. All mice were the PLB double mutants described in the introduction.

Fluorescent measurement of [Ca²⁺]_i

Cells were plated on single-use laminin-coated glass cover slips and mounted on an epifluorescence microscope. We loaded rabbit cells with 10 μm indo-1 AM, applied externally for 22–27 min at 23°C, and allowed an equal time for washing and de-esterification. Indo-1 was excited at 365 ± 5 nm and emitted fluorescence (405 ± 10 nm and 485 ± 10 nm) was recorded at 100 Hz bandwidth. The background-subtracted ratio (R) of fluorescence at 405 nm versus 485 nm was converted to [Ca²⁺]_i using [Ca²⁺]_i=K_dβ(R−R_min)/(R_max−R) (Grynkiewicz et al. 1985). R_min, R_max, and β were determined and K_d was taken as 844 nm (Bassani et al. 1995a).

Mouse (and some rabbit) myocytes were loaded with fluo-3 AM for 25–40 min, with a comparable de-esterification time. Cells were excited at 480 ± 5 nm, and emission was recorded at 535 ± 20 nm [Ca²⁺]_i, was determined using (Cheng et al. 1993):

where R was emitted fluorescence divided by resting emitted fluorescence, each after background subtraction. [Ca²⁺]_rest was taken as 100 nm, and K_d= 1100 nm was used to calculate [Ca²⁺]_i. No difference in results was evident between the two indicators.

Solutions and recording conditions

I_Ca was recorded in perforated patch whole cell voltage clamp (120 μg ml⁻¹ amphotericin-B) to prevent rundown. Capacitance was cancelled and series resistance was compensated as needed. Cells were recorded in a modified Tyrode solution containing (mm: NaCl 140, CsCl 4, MgCl₂ 1, CaCl₂ 1 (for mouse) or 2 (for rabbit), and Hepes 10; pH 7.4 at 23°C) with niflumate (30 μm) included to block Cl⁻ currents. ISO was freshly made (<1.5 h before use) and added at 0.3–1 μm. This same solution with caffeine (10 mm) added was rapidly applied for SR Ca²⁺ load measurements. The pipette solution contained 40 mm CsCl and 80 mm of either caesium methanesulphonate or caesium glutamate, Hepes 10 mm (pH 7.2), 1 mm MgCl₂ and 1 mmKCl, the latter to ensure a counter-ion supply for SR Ca²⁺ release (Litwin et al. 1998). The liquid junction potential (13 mV, pipette negative) was corrected. We kept the pipette solution Na⁺ free and I_Na inactivated (see below) to minimize subsarcolemmal [Na⁺] and avoid Ca²⁺ influx via outward Na⁺–Ca²⁺ exchange current (I_NaCaX). These solutions assured that all depolarization-activated current was I_Ca and that all Na⁺–Ca²⁺ exchange current flowed as post-pulse inward tail current (Trafford et al. 1997).

Measurement of SR Ca²⁺ load

SR Ca²⁺ content was measured relative to non-mitochondrial cell volume as described (Ginsburg et al. 1998). [Ca²⁺]_i at rest and at peak during caffeine application were each converted to total cytosolic Ca²⁺ considering Ca²⁺ binding at high and low affinity sites and by the fluorophore ([Ca]_T=[Ca²⁺]_i+ 203 μm/(1 + 420 nm/[Ca²⁺]_i) + 703 μm/(1 + 79000 nm/[Ca²⁺]_i) + 50 μm/(1 + 1000 nm/[Ca²⁺]_i; Hove-Madsen & Bers, 1993; Bers, 2001), and the difference (Δ[Ca]_T) was taken as the SR Ca²⁺ load. In most cells, caffeine-induced I_NaCaX was recorded and fitted, and the fit was integrated (Varro et al. 1993), for an additional confirmatory measure of SR Ca²⁺ content.

Recording protocols

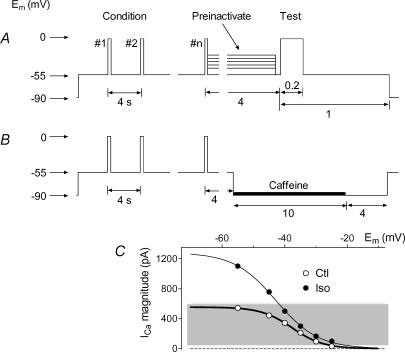
Figure 1A shows the protocol used in all experiments except those in Fig. 2 to condition the SR to a particular load and then evoke twitch responses. SR loading was adjusted by changing the number of pulses (n= 15) at 0.25 Hz, their depolarization level and/or duration as needed. After a conditioning series, one of usually six different test trigger amplitudes was applied. The trigger strength was adjusted by pre-inactivation of I_Ca at various holding potentials (V_hold) levels for 4 s after the conditioning, but all test triggers were depolarizations to 0 mV. As shown by example in Fig. 1C (with both sets of I_Ca from the same cell), trigger strength could be adjusted over a similar range ± ISO (grey background), by shifting the range of pre-inactivating E_m. Cells were held at −90 mV between trials to promote inward I_NaCaX and thereby minimize SR reloading independently of the applied conditioning, but in order to keep I_Na inactivated, V_hold was never negative of −55 mV during a trial. As shown in Fig. 1B, after the six sequences of conditioning–test twitch we applied a final identical conditioning series followed by caffeine (10 mm) to measure the corresponding SR load.

Figure 1. Experimental protocol.

A, voltage clamp protocol to evoke twitch contractions with various sized I_Ca in a cell whose SR was repeatedly loaded with the same conditioning regime. Pre-inactivation followed by depolarization, always to 0 mV, was used to vary I_Ca without changing unitary Ca²⁺ flux. B, immediately after the protocol shown in A, the same conditioning was repeated, followed by application of 10 mm caffeine, to measure the conditioned load. C, example showing substantially overlapping (grey background) I_Ca magnitudes attained ± ISO by adjusting pre-inactivation voltage (all traces from same cell).

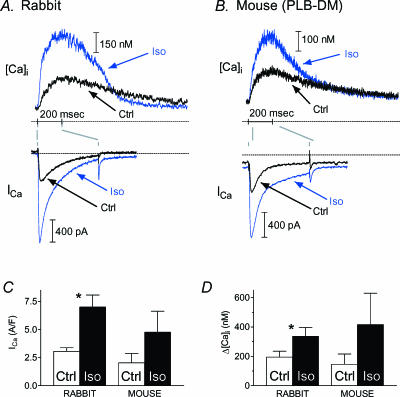
Figure 2. ISO effects with uncontrolled I_Ca trigger and SR Ca²⁺ load.

In cells stimulated infrequently (≤ 0.05 Hz) to maximize I_Ca recovery, but otherwise without specific control of trigger and load, I_Ca and [Ca²⁺]_i increased on adding ISO (blue traces) in both rabbit (A) and DM mouse (B). [Ca²⁺]_i transient decay accelerated in rabbit but not in DM mouse. C and D, average I_Ca density and [Ca²⁺]_i transient size in rabbit (n= 10; *P≤ 0.05, Student's t test) and mouse (n= 3; not tested).

Data treatment

Peak [Ca²⁺]_i and time to peak were found directly from the traces for both twitch- and caffeine-induced transients. We determined other features of [Ca²⁺]_i by fitting, which overcomes subjectivity and variation due to noise. The decaying portions of all [Ca²⁺]_i transients in a given series (sharing one SR load) were fitted to establish the decay time constant τ, with all sharing a common asymptote for that series. This fitted asymptote was taken as the baseline, to make maximum use of the data and avoid bias in case [Ca²⁺]_i did not decay quite fully within a record. Twitch amplitude was the difference between peak and asymptotic values. After all decays were fitted, rising phases of twitch [Ca²⁺]_i were fitted to a Boltzmann sigmoidal function:

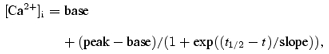to establish the maximum rate of rise and its time of occurrence.

Peak I_Ca and time to peak were found directly from the traces. To establish ΔI_Ca and a baseline for integration, I_Ca decay post peak was fitted to a weighted sum of two exponentials with asymptote. Only the depolarized region of I_Ca (always at 0 mV) was fitted, so no leak correction was needed. All I_Ca values in a given series (sharing one SR load) were readily fitted with a common asymptote (prediction for 0 mV at t=∞). Using the long decaying portion of I_Ca to determine a common baseline minimized uncertainty, especially for smaller I_Ca which may be critical in assessing ECC gain changes. Recorded current often shifted outward with ISO (presumably due to unsuppressed CFTR Cl⁻ channel current), but by defining I_Ca as peak minus fitted baseline (all at 0 mV) we removed any influence of this shift. All I_Ca in Figs 2–5 were adjusted for plotting so that the fitted asymptote fell on the dotted line. Error bars in figures are ±s.e.m.

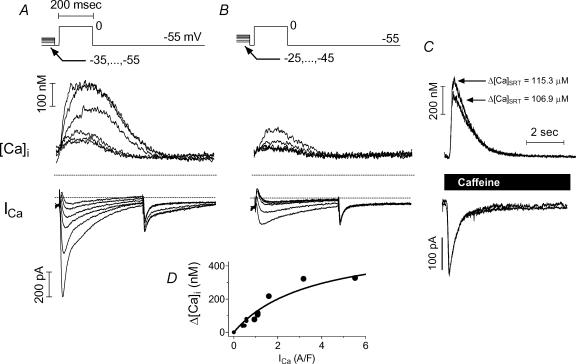
Figure 5. Free Ca²⁺ release increased in graded then saturating fashion with increasing trigger strength at constant SR load.

A, [Ca²⁺]_i transients and I_Ca in a larger series generated by pre-inactivating with V_h=−55, −47, −42, −39, −36, −33 mV. B, [Ca²⁺]_i transients and I_Ca in a smaller series generated by pre-inactivating with V_h=−45, −40, −34, −31, −28, −25 mV. C, SR loads in the two series matched closely according to [Ca²⁺]_i transient and I_NaCaX. Rabbit cell during ISO treatment. Cell responded robustly on application of ISO (not shown). D, both sets of release followed the same functional dependence on I_Ca.

Results

We obtained 105 sets of (normally 6) trigger I_Ca–SR release Δ[Ca²⁺]_i couples with a corresponding SR load from 37 cells (28 rabbit, 9 mouse). This resulted in 664 individual trigger–release couples. We combined rabbit and mouse data, because there were no discernible differences (except where specifically noted below; Fig. 12B) when they were analysed separately.

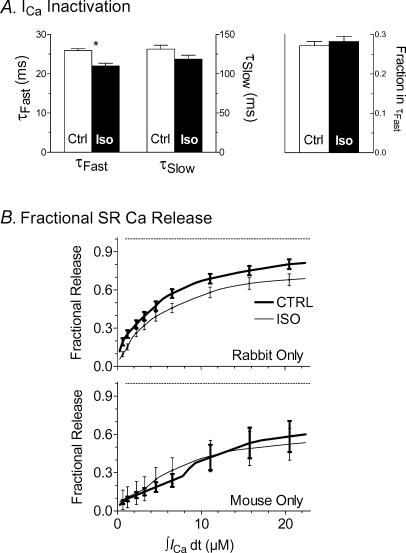
Figure 12. I_Ca inactivation and species dependence of fractional SR Ca²⁺ release.

A, I_Ca decline was fitted to a biexponential function; the fast decay time constant τ_fast shortened with ISO, but τ_slow and the proportion of amplitude in the fast component did not change. B, fractional SR Ca²⁺ release data from Fig. 9, separated by species (including all SR Ca²⁺ load groups), shows constancy of release ± ISO in mouse.

Canonical ISO effects

Figure 2 shows that both I_Ca and the [Ca²⁺]_i transient from a rabbit (A) and a mouse (B) cell increased on ISO addition (blue traces). In these records we did not specifically control trigger or SR Ca²⁺ loading. Instead of using the protocol in Fig. 1, we depolarized cells infrequently (≤ 0.05 Hz) to promote maximal I_Ca availability. In rabbit, but not mouse (lacking phosphorylatable PLB), the [Ca²⁺]_i transient decayed faster with ISO (note crossover of traces in rabbit). Uncontrolled I_Ca–[Ca²⁺]_i pairs were obtained from most cells with paired control–ISO data (including washout, not shown, in some cases), to confirm that ISO produced its expected effects in our situation, and also that the cells did not run down. C and D in Fig. 2 show, respectively, that both I_Ca and [Ca²⁺]_i amplitude increased substantially in rabbit. As expected, the time constant (τ) for monoexponentially fitted [Ca²⁺]_i decay decreased in rabbit by 53% (from 700 ± 128 to 329 ± 64 ms; n= 10 cells; P < 0.05, not shown). Similar increases in I_Ca and [Ca²⁺]_i amplitude occurred, but decay τ was less affected, as expected in the PLB mutant mouse (see Fig. 2B). An ISO-mediated increase of I_Ca and [Ca²⁺]_i without any change in decay kinetics has been verified previously in this model (Brittsan et al. 2003).

Ca²⁺ release with matched triggers and SR loads

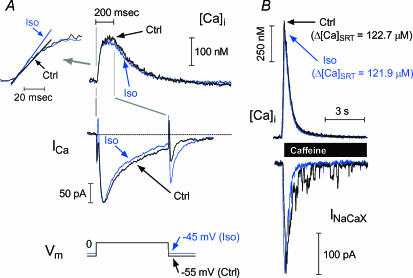
Figure 3A shows twitch [Ca²⁺]_i and I_Ca recorded ± ISO using the protocol in Fig. 1. Traces were selected where the trigger I_Ca and SR Ca²⁺ load (Fig. 3B) were very closely matched. An appropriate range of I_Ca triggers was obtained by pre-inactivating at −45 mV in ISO versus−55 mV in control. In this example, from a DM mouse myocyte, the Ca²⁺ transients ± ISO are virtually identical. There is a minor increase in I_Ca decay rate with ISO (a point we will consider below). This would suggest that ISO has only very minor effects on overall RyR behaviour during ECC, but as shown in the inset (Fig. 3A, left) the maximal rate of rise of [Ca²⁺]_i also increased discernibly.

Figure 3. ISO response with I_Ca trigger and SR Ca²⁺ load held constant.

Example records of [Ca²⁺]_i and I_Ca (A) with closely matched I_Ca amplitude, from one DM mouse myocyte, in control (black traces) and ISO (blue traces). [Ca²⁺]_i transient amplitude was unaffected by ISO, but inset (A, left) shows that maximum rate of rise of [Ca²⁺]_i increased. B, caffeine-evoked [Ca²⁺]_i and inward Na⁺–Ca²⁺ exchange currents show that SR Ca²⁺ loading was well matched.

Statistical testing for differences in Ca²⁺ release and ECC gain ± ISO would ideally be based on directly paired records like those in Fig. 3. However, it was difficult to match both trigger and load precisely in a record pair, and as we show next, independently of ISO, Ca²⁺ release depends profoundly on both. Accordingly we developed release/gain functions which describe each record. These functions were then compared over corresponding trigger and load ranges.

Ca²⁺ release was strongly affected by trigger and SR load

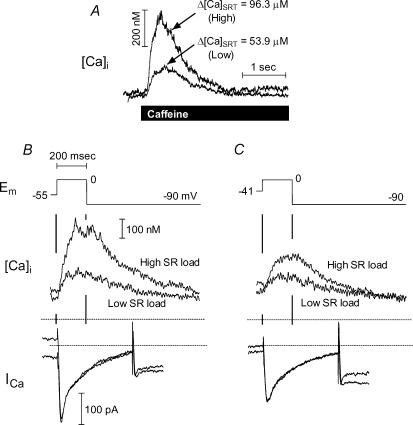
Figure 4, shows that, independently of ISO, increasing SR Ca²⁺ load increased twitch Ca²⁺ release when trigger I_Ca was held constant. Figure 4A shows larger and smaller SR loads, while Fig. 4B and C shows twitch [Ca²⁺]_i and I_Ca for two different trigger strengths at the respective loads. The rabbit cell in these records was not treated with ISO, but later gave a robust ISO response (not shown). Because the I_Ca trigger was constant in both B and C in Fig. 4, the different transient amplitudes indicate a load-dependent change in ECC gain.

Figure 4. E–C coupling gain increased with SR Ca²⁺ load at constant trigger strength.

A, Caffeine-induced [Ca²⁺]_i transients showing high and low SR loads. Below are responses at the two loads to two trigger strengths, set with either minimal (B; V_h=−55 mV) or substantial (C; V_h=−41 mV)I_Ca pre-inactivation. Rabbit cell, control only. This cell subsequently responded robustly to ISO (not shown).

Figure 5 (from another rabbit cell) shows that (independently of ISO) SR Ca²⁺ release increased with increasing I_Ca trigger strength. The larger amplitude I_Ca series (A) graded Ca²⁺ release over a larger range than the smaller I_Ca series (B), while the SR Ca²⁺ loading was nearly constant (106.9 μmol (l cytosol)⁻¹ for the large trigger series versus 115.3 for the small series). All traces in this example were recorded with ISO. It is notable that pre-inactivation in the range of −45 to −25 mV produced small graded responses, despite the presence of ISO and despite the slightly higher SR Ca²⁺ loading in the pre-inactivated series (i.e. any sensitization of Ca²⁺ release by ISO should be apparent with these small triggers). For these two twitch series, release as a function of peak I_Ca trigger fell along a single saturating function (inset, upper left). Twitches due to fully activated I_Ca (not shown) recorded before and after these two series showed that this cell was strongly responsive to ISO and did not run down.

Ca²⁺ release and gain functions at constant SR load

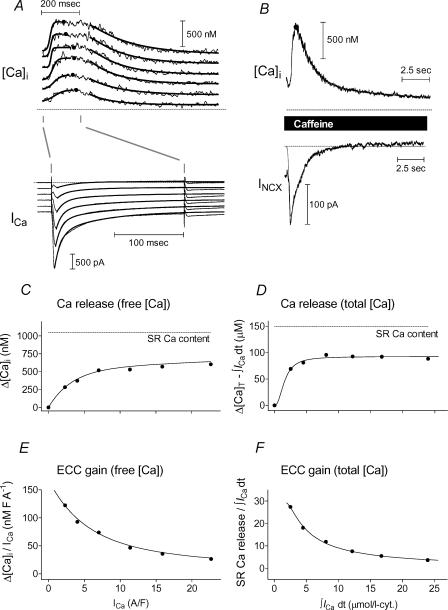
Figure 6 shows how we obtained one Ca²⁺ release and one ECC gain function for free [Ca²⁺], along with corresponding functions for total [Ca²⁺], as well as a maximum rate of rise and time to maximum rate of rise (not shown) from each set of six twitches (Fig. 6A) with a corresponding SR load (Fig. 6B). Figure 6A shows curves fitted separately for rise and decay segments of [Ca²⁺]_i transients and I_Ca decay.

Figure 6. Release and gain functions.

A, top, [Ca²⁺]_i transients and I_Ca from a set of 6 twitches associated with a particular conditioned SR Ca²⁺ load. Traces shown separated by 200 pA (I_Ca) and 200 nm ([Ca²⁺]_i), respectively, for clarity. [Ca²⁺]_i peaks and times of peak were found by examination (dots). Maximum rates of rise (with times of occurrence), half-decay times, and a common asymptotic baseline were all found by fitting (bold lines). A, bottom, I_Ca was similarly fitted with a common asymptote serving as a baseline for amplitude and integral calculations. B, corresponding caffeine-evoked [Ca²⁺]_i (top) and I_NaCaX (bottom) were also fitted (same baseline as the twitch [Ca²⁺]_i in A) to establish SR Ca²⁺ load. C, Ca²⁺ release data (peak – asymptotic [Ca²⁺]_i) are fitted to allow interpolation or extrapolation to I_Ca values not specifically measured. Dotted line indicates SR Ca²⁺ load. D, same as C, but peak and asymptotic free Ca²⁺ were first converted to total [Ca] and subtracted, and then Ca²⁺ influx (I_Ca integral) was removed to find net change in total [Ca]. E and F, same as C and D, respectively, with all data converted to gain by expressing release/influx.

Figure 6B shows fits for the decay of the caffeine-evoked free [Ca²⁺]_i transient (top, biexponential) and the entire Na⁺–Ca²⁺ exchange current (bottom, sigmoidal rise/exponential decay), used to determine SR Ca²⁺ loads.

To allow a comparison of responses among twitch sets over useful ranges of peak I_Ca and Ca²⁺ influx values, we fitted each set of Ca²⁺ release data to a three-parameter saturating function, e.g. sigmoidal, piecewise linear, etc., as shown in Fig. 6C (points: data; curve: fit) for free Δ[Ca²⁺]_i and Fig. 6D for total calcium. Total calcium release was defined as twitch Δ[Ca]_T−∫I_Cadt (the change in total [Ca²⁺] due to release with the cumulated Ca²⁺ influx removed), with ∫I_Cadt measured with respect to the I_Ca common asymptote. Integration was started when inward-going I_Ca first crossed the asymptotic value and carried out as far as the time of the corresponding peak twitch [Ca²⁺]_i transient (dots on traces in Fig. 6A).

Fractional SR release was calculated by normalizing fitted predictions to the measured SR Ca²⁺ content (dotted lines in Fig. 6C and D). Figure 6E and F show corresponding ECC gain functions (obtained as slopes of the data and curves in Fig. 6C–D).

The ordinate in Fig. 6C has units of nm, while that in Fig. 6D is in μm. Thus the gain function in Fig. 6E is in nm× F × A⁻¹, while that in Fig. 6F is dimensionless.

Ca²⁺ release in virtually every record increased with increasing trigger in a saturating manner, indicating a decreasing gain (for both free and total [Ca]). Release/gain functions from data like those in Figs 4 and 5 showed very clear systematic changes due to SR Ca²⁺ loading and trigger, respectively (independently of ISO). Thus our method of parameterizing Ca²⁺ release/gain is well suited to detecting any changes due to ISO.

Range and grouping of I_Ca and SR loads in control and ISO

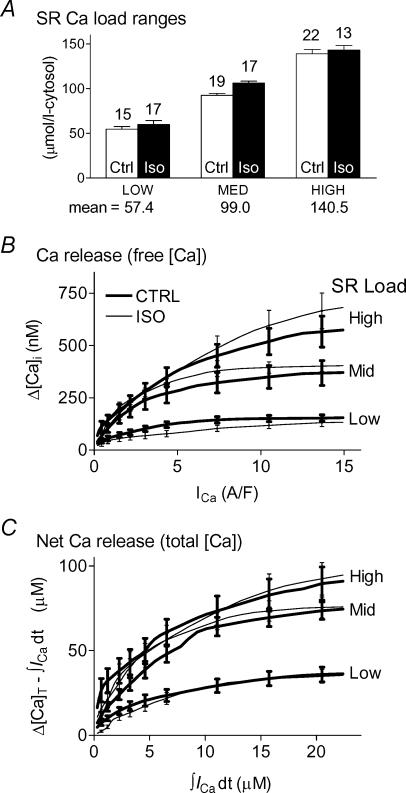
As shown in Fig. 7A, we grouped attained SR Ca²⁺ loads in three ranges (± ISO), to match their means and to put comparable numbers of functions in each group (see Fig. 7 for values). We might expect Ca²⁺ release to be enhanced with ISO (see Introduction), but this could be obscured if SR loading decreased with ISO. To avoid this possible pitfall, we built the SR load groups so that the mean load in each group was at least as high + ISO as without ISO. Trigger I_Ca influxes (peak I_Ca) were studied over the range 0.2–15 A F⁻¹ while corresponding I_Ca integrals were examined over the range 0.3–22 μm (respective x-axes in Fig. 6C and D). These ranges extend well below and above the typical I_Ca peak influx (∼4 A F⁻¹) during action potentials, which would be of the most physiological interest (Yuan et al. 1996).

Figure 7. Ca²⁺ release amplitude did not change with ISO.

A, classification of SR load data in three overlapping ranges ± ISO. Load group boundaries were set to give comparable mean values and numbers of observations in each group. B and C, Ca²⁺ release functions expressed as free Δ[Ca²⁺]_i (B) and total Δ[Ca]_T (C) increased with trigger in saturating fashion, and also increased with SR load. ISO affected free Ca²⁺ release minimally and unsystematically, especially compared with effects of trigger and load themselves. Each trace is the average of predictions made for the available data in a given load range (n shown in Fig. 7A). Error bars (±s.e.m.) were placed at visually convenient intervals.

Amplitude-based Ca²⁺ release and gain were minimally affected by ISO

In Fig. 7 we also show Ca²⁺ transient amplitude (B) and total SR Ca²⁺ release (C) in the three SR load ranges, for control (thick lines) and ISO (thin lines). Each curve is the average of n curves (n shown in Fig. 7A) for the corresponding load and condition. All release functions saturated, but saturation appeared at higher influxes when SR load was higher. Release increased systematically with increasing load or increasing trigger, and these changes were greater than any change in release ± ISO within a given load range. The small changes seen with ISO were unsystematic; i.e. for either free or total [Ca], release could be slightly reduced, increased, or unaffected by ISO.

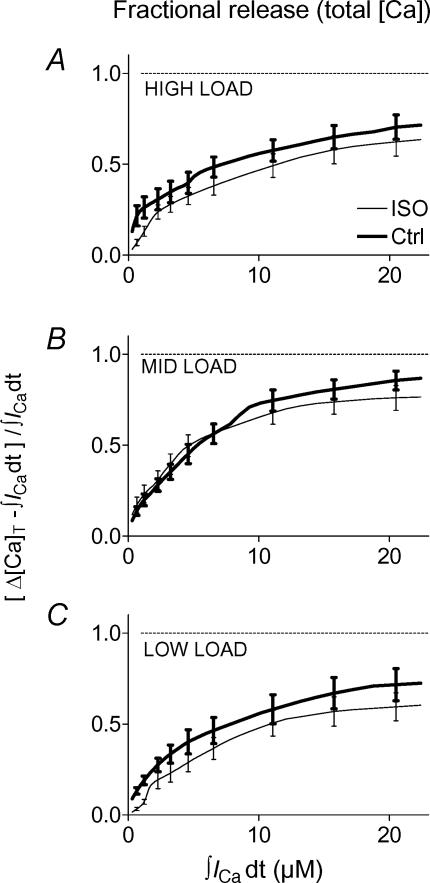
Figure 8 shows fractional SR Ca²⁺ release based on total calcium for high (A), medium (B) and low (C) SR load ranges. Release functions were averaged as in Fig. 7, but each release datum was normalized to its corresponding SR load before being included in the average. Because fractional release overcomes small cell-to-cell variations in SR load and is constrained between 0 and 1, it might reveal ISO effects more sensitively. Fractional release, like absolute increase, saturated at higher influxes with higher SR load, but the fraction at saturation was quite constant near 0.6–0.8 in all cases. Fractional release was either slightly reduced or unaffected by ISO (see also Fig. 12B).

Figure 8. Fractional Ca²⁺ release did not change with ISO.

The predictions of Fig. 7B for total calcium release are shown converted to a fraction of the SR Ca²⁺ load released, to help separate the ISO effect from the load-dependent effect. Under either condition (control or ISO), fractional release saturated near 0.7.

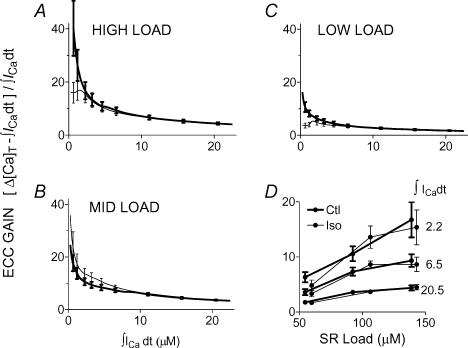
Figure 9 shows ECC gain for high (A), medium (B) and low (C) SR load ranges. As expected for saturating Ca²⁺ release, gain was highest for the smallest triggers and decreased toward a limiting value as the trigger increased. This limiting gain increased with increasing SR load. For the smallest triggers in each load range, there was more variation in gain ± ISO. The greater scatter at low I_Ca or influx is intrinsic to the definition of the gain (small denominator). Throughout the modest-to-large trigger range gain predictions were unchanged ± ISO. In order to show more clearly how ECC gain depended on SR Ca²⁺ load but not on ISO, Fig. 9D shows data from A, B, and C replotted at selected I_Ca.

Figure 9. ECC gain did not change with ISO.

The predictions of Fig. 7C have been converted to gain and are shown separately for high (A), medium (B) and low (C) SR load ranges. Each release datum was divided by the corresponding influx. At very large triggers, saturation of release left gain at its smallest and least sensitive to modulation, while small and unsystematic effects are seen in the smallest trigger ranges. D, predictions at three selected Ca²⁺ influxes are replotted to show that gain increased with increasing SR Load.

Rate of Ca²⁺ release was faster with ISO

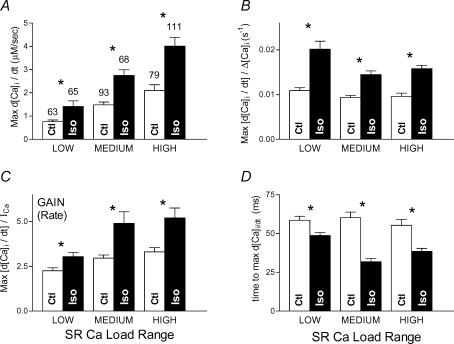
Figure 10A shows maximal rates of rise (in μm s⁻¹, mean ±s.e.m., with n as shown) for twitches whose rising phase was fitted (as in Fig. 6A). With ISO, the maximal rate of rise was ∼50% faster versus control in each SR load group (all P < 0.05). The maximum rate of rise was faster with increasing SR load (control or ISO). We surmised that this was implicit in larger Δ[Ca²⁺]_i transients rising faster. In Fig. 10B, we show that the maximal rate of [Ca²⁺]_i rise normalized to Δ[Ca²⁺]_i was relatively constant versus SR load, yet was still ≥ 50% faster with ISO.

Figure 10. Temporal properties of Ca²⁺ transients with ISO.

A, maximal rate of rise of [Ca²⁺]_i transients was substantially faster with ISO. Maximal rate of rise was also faster with increased SR loading, but this may be explained by the larger sizes of [Ca²⁺]_i transients, as shown in B (data of A normalized to [Ca²⁺]_i amplitude). C, ‘Rate gain’, i.e. maximal rate of rise normalized to I_Ca peak influx rate, was also higher with ISO. D, time at which maximal rate of rise (A) occurred was earlier with ISO. All comparisons: *P < 0.05.

We also expected larger I_Ca to produce faster rising Δ[Ca²⁺]_i transients. In Fig. 10C we plot a ‘rate gain’ measure (d[Ca²⁺]_i/dt_max/(I_Ca), which also shows that release was faster with ISO. For this figure, to re-express free d[Ca²⁺]_i/dt_max as total, we scaled it up by the approximate cytosolic buffering power for rabbit myocytes (×110; Delbridge et al. 1996). Thus, the rate gains here, like the total calcium-based gains in Fig. 9, are dimensionless and amount to small whole numbers, as expected for Ca²⁺-induced Ca²⁺ release. Finally, in Fig. 10D we show that the time from depolarization to maximum release rate was also earlier with ISO. The time-to-peak of I_Ca (not shown) did not shorten with ISO and so probably does not explain the faster Δ[Ca²⁺]_i.

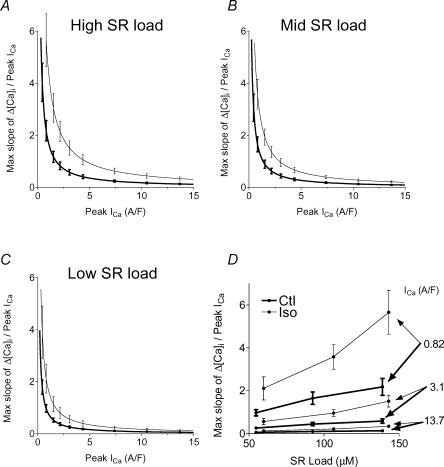
In Fig. 11 appear functions (analogous to the gain functions of Fig. 9) to show how rate gain depended on I_Ca for the high (A), medium (B) and low (C) SR load ranges. Rate gain increased systematically with ISO at any SR load, and with increasing load regardless of ISO. Figure 11D replots data in A, B, and C at selected I_Ca, to show that rate gain increased dramatically for small I_Ca, increased somewhat with increasing SR load, and increased systematically with ISO.

Figure 11. Ca²⁺ release normalized to influx was faster with ISO.

‘Rate gain’, i.e. maximal rate of rise normalized to I_Ca peak influx rate, increased with increasing SR load (A, B and C), and decreased with increasing Ca²⁺ influx, but was systematically higher with ISO. D, predictions at three selected Ca²⁺ influxes are replotted to show that rate gain increased with increasing SR load and decreased dramatically with increasing trigger.

Rates of I_Ca and [Ca²⁺]_i decline with ISO

Faster SR Ca²⁺ release should accelerate I_Ca inactivation (Bers, 2001). Figure 12A shows that ISO slightly but significantly accelerated the fast component of I_Ca decay rate, without affecting the slow component or the relative strength of the components. Faster I_Ca inactivation could contribute to faster shut-off of SR Ca²⁺ release in ISO, an implicit conclusion in our results (i.e. faster Ca²⁺ release rate, but with same integral).

Faster SR Ca²⁺ uptake with ISO could also curtail the peak of the Ca²⁺ transient, resulting in an underestimation of the total SR Ca²⁺ release in ISO (Bassani et al. 1994). Indeed [Ca²⁺]_i decay was faster with ISO in rabbit, though much less so in mouse (Figs 2 and 3), even if we studied only similar-sized Δ[Ca²⁺]_i and I_Ca± ISO to remove intrinsic effects of amplitude on τ (Bers & Berlin, 1995; not shown). In Fig. 8, fractional SR Ca²⁺ release + ISO for large triggers fell slightly below release without ISO. This might represent a slight snubbing of peak [Ca²⁺]_i by faster SR Ca²⁺ uptake, particularly when released [Ca²⁺] was large. To test this we plotted fractional SR Ca²⁺ release data (all SR loads) separately for rabbit and mouse (Fig. 12B). Indeed, fractional SR Ca²⁺ release was slightly lower with ISO in rabbit but not in mouse, where SR Ca²⁺ uptake was not affected (Brittsan et al. 2003) consistent with our conclusion that SR Ca²⁺ release amplitude is stable ± ISO.

Discussion

Rationale

The inotropic effect of sympathetic stimulation of the heart is mediated mainly by β-AR and PKA activation (Bers, 2001). There are four main PKA targets affecting ECC: I_Ca, PLB, TnI and RyR. There is extensive and compelling evidence that PKA increases I_Ca and SR Ca²⁺-ATPase activity (via PLB phosphorylation), and that these two mechanisms contribute centrally to PKA-induced cardiac inotropy.

The functional role of RyR phosphorylation by PKA is more controversial. It has been difficult to isolate RyR function in the cellular environment where I_Ca and SR Ca²⁺ load critically determine RyR behaviour and are both altered by PKA. Indeed PKA effects on ECC consistent with increased, decreased and unchanged RyR activation by Ca²⁺ have all been reported in myocyte studies (Viatchenko-Karpinski & Györke, 2001; Song et al. 2001; delPrincipe et al. 2001; Li et al. 2002). Even for isolated RyRs in lipid bilayers, results of PKA phosphorylation are mixed (Valdivia et al. 1995; Marx et al. 2000; Jiang et al. 2002).

Summary of outcome

This study addressed the above problem by comparing SR Ca²⁺ release (± 1 μm ISO) where both I_Ca and SR Ca²⁺ load were controlled and measured over a broad range. We found that for any given SR Ca²⁺ load and I_Ca, the amount of SR Ca²⁺ release was not significantly affected by ISO (Figs 3,7 and 9), despite clearly demonstrated ISO effects in the same cells when I_Ca and load were not controlled (Fig. 2). This was true whether release amplitude was measured using free Ca²⁺ (Δ[Ca²⁺]_i; Fig. 7B), total calcium (Δ[Ca]_T; Fig. 7C and 9), or fractional SR Ca²⁺ release (Fig. 8), and whether expressed directly (Figs 7B and C) or using ECC gain functions (SR Ca²⁺ released–integrated I_Ca; Fig. 9). In contrast, I_Ca and SR Ca²⁺ load specifically and strongly affected Ca²⁺ release and gain, independently of ISO (Figs 4 and 5).

Despite not altering the overall amount of Ca²⁺ released, ISO did systematically increase the maximal rate of SR Ca²⁺ release for a given I_Ca and SR Ca²⁺ load (Figs 10 and 11). Since release amplitude was constant, some means must also hasten the turn-off of Ca²⁺ release when ISO is present.

Control of I_Ca and SR Ca²⁺ uptake and loading

Increasing either I_Ca or SR Ca²⁺ load increases SR Ca²⁺ release (Fabiato, 1983; Bers, 2001; Figs 4 and 5). The ability of I_Ca to control SR Ca²⁺ release (at constant SR Ca²⁺ load) in graded fashion is at the heart of the CICR mechanism. At the same time, the relationship between SR Ca²⁺ load and SR Ca²⁺ release is very steep, so that small changes in SR Ca²⁺ load can greatly alter SR Ca²⁺ release. To accomplish the required control of both I_Ca and SR Ca²⁺ load (measured almost cotemporally with each set of twitches), several options were available.

We varied I_Ca by altering Ca²⁺ channel availability (Fig. 1), rather than test E_m or [Ca²⁺]_o. ISO enhances macroscopic I_Ca mostly by increasing channel open probability. Our use of pre-inactivation with ISO present compensated properly for this by reducing the number of channels available. Indeed, if we had altered test E_m or [Ca²⁺]_o, we would have altered single channel I_Ca and latency (with consequent effects on ECC gain; see below). We believe that single channel I_Ca would not vary in our protocol.

Despite this, ISO also can promote long (mode 2) L-type Ca²⁺ channel openings (Yue et al. 1990). For a given macroscopic I_Ca, if mode 2 openings occur, then fewer channels must be active. If the initial part of an I_Ca opening is what triggers SR Ca²⁺ release, Ca²⁺ admitted later during prolonged openings would be largely wasted, appearing to decrease ECC gain, i.e. there would be less SR Ca²⁺ release for a given I_Ca. Indeed, Ca²⁺ channel agonists such as BayK-8644 (Tsien et al. 1986) or FPL-64176 (Janczewski et al. 2000), which strongly promote mode 2 behaviour, do reduce Ca²⁺ release and intrinsic ECC gain (McCall & Bers, 1996). We think mode 2 openings are not a complication in our experiments because unlike BayK-8644 or FPL-64176, ISO increases I_Ca primarily by promoting channel availability, with mode 2 openings being quite rare (Hirano et al. 1999).

Increased SR Ca²⁺ content enhances RyR-mediated SR Ca²⁺ release by directly increasing driving force and through allosteric increase of P_o (Han et al. 1994; Sitsapesan & Williams, 1994; Györke & Györke, 1998; Bassani et al. 1995b; Shannon et al. 2000; Eisner et al. 2000). Thus controlling for SR Ca²⁺ load as shown in Fig. 7A is an absolute requirement for measuring the independent effects of PKA on RyR function in intact cells.

Even with load controlled, PLB phosphorylation by PKA could complicate our study by accelerating SR Ca²⁺ reuptake, which could curtail the peak [Ca²⁺]_i transient (Bassani et al. 1994). This complication was controlled for in the experiments with transgenic mice expressing only non-phosphorylatable PLB. As shown in Figs 3 and 12B, ISO did not affect Ca²⁺ release in the mouse model. Although a slight loss of fractional SR Ca²⁺ release with ISO was evident in rabbit versus mouse (Fig. 12B), no rabbit versus mouse differences were evident when the analyses in Figs 7B, C and 9 were repeated separately for rabbit and mouse (not shown).

Fractional SR Ca²⁺ release and ECC gain

Two complementary numerical indices of cardiac ECC efficacy are in common use: fractional SR Ca²⁺ release and ECC gain. Both are useful, but neither can completely describe ECC efficacy because they depend on both Ca²⁺ influx and SR load. In this study, for both SR Ca²⁺ release and ECC gain (in absolute and in dimensionless units), we have made explicit these functional dependencies. Both Ca²⁺ release and gain increase with increasing SR Ca²⁺ load but depend more complexly on I_Ca (see below).

The fact that our analyses (and choice of experimental conditions) effectively reproduce the known specific dependency of Ca²⁺ release and ECC gain on trigger and SR load shows that they are robust enough to support our conclusions.

Increasing ECC gain for small I_Ca

Most previous studies of ECC gain have used test E_m to vary I_Ca (e.g. López-López et al. 1994; Wier et al. 1994; Cannell et al. 1995; Santana et al. 1996). These studies demonstrated that ECC gain increased as I_Ca amplitude was reduced by increasingly negative test E_m. The higher gain at smaller I_Ca was attributed mainly to the higher single channel I_Ca expected at more negative E_m, due to higher electrochemical driving force. Our observation that ECC gain increased with smaller I_Ca at constant E_m (smaller probability of opening, but constant unitary I_Ca amplitude; Figs 6 and 9) indicates that this cannot be the entire explanation. Our working hypothesis is that the reduction in ECC gain at higher I_Ca amplitude is largely due to redundant Ca²⁺ channel opening at a single SR Ca²⁺ release site. That is, a single Ca²⁺ channel opening may be sufficient to activate a whole cluster of RyRs at a single junction, via CICR (Santana et al. 1996). Additional L-type Ca²⁺ channel openings at the same junction would increase I_Ca but not increase release. Thus the ECC gain denominator (I_Ca) would rise for the same numerator. A relatively high fidelity of triggered release (Inoue & Bridge, 2003) is consistent with data suggesting that there are ∼10–20 L-type Ca²⁺ channels at a single junction associated with ∼100 RyRs (Bers & Stiffel, 1993; Franzini-Armstrong et al. 1999). Thus increasing unitary I_Ca may be only a minor factor in ECC gain increase at negative E_m, and the likelihood of high Ca²⁺ channel opening probabilities producing redundant Ca²⁺ influx at more moderate E_m needs to be considered.

ECC gain continues to decline monotonically at more positive test E_m (> +20 mV) as I_Ca becomes smaller again. At these positive E_m virtually all available Ca²⁺ channels will be activated, so the redundancy effect to reduce ECC gain would already be maximal. The decrease in unitary I_Ca as E_m approaches the I_Ca reversal potential may then more critically limit ECC fidelity and gain in that E_m region. This is functionally important, because physiological SR Ca²⁺ release occurs during the early phases of the action potential where E_m is +20 to +50 mV.

Another factor which could affect E_m dependence of ECC gain is the I_Ca first latency, which would be most variable at small depolarizations (Rose et al. 1992), reducing fidelity and possibly gain by inducing more variability in kinetics and spatial uniformity of SR Ca²⁺ release.

Relationship to previous results

Single isolated cardiac RyRs in lipid bilayers have yielded mixed results with PKA phosphorylation. Valdivia et al. (1995) found that RyR P_o decreased with PKA activation at resting [Ca²⁺], while the measured RyR response to rapid jumps in [Ca²⁺] meant to simulate cellular I_Ca was an initially high P_o that relaxed back to a lower steady-state level, still exceeding that before [Ca²⁺] was elevated. This pattern is consistent with our cellular results.

Marx et al. (2000) studied only steady-state P_o of single RyRs and found that PKA increased open probability, but also revealed reduced unitary conductance substates. Similar subconductance states were observed after depleting FK-506 binding protein (FKBP) from the RyR (Kaftan et al. 1996) and further, PKA could cause FKBP to dissociate from RyR (Marx et al. 2000). Some of these observations were not confirmed by Jiang et al. (2002).

Marx et al. (2000) inferred that PKA phosphorylation would cause a net increase in Ca²⁺ release, consistent with our observed faster initial release. Increased RyR P_o may in time be counterbalanced by reduced conductance, leaving little or no net effect on release. Independently of RyR properties, enhanced I_Ca inactivation and/or SR Ca²⁺ uptake could also stabilize ECC gain with ISO in the intact cell (Fig. 12), but SR uptake (as relaxation rate) was unchanged in our mouse data.

Previously we showed that PKA-dependent phosphorylation of the RyR had no effect on any of frequency, kinetic or spatial properties of Ca²⁺ sparks in intact or permeabilized ventricular myocytes under diastolic conditions, provided that SR Ca²⁺ load and [Ca²⁺]_i were unaltered (Li et al. 2002). We confirmed that elevating cytosolic [Ca²⁺] or SR Ca²⁺ load potently increased Ca²⁺ spark frequency. This is consistent with our finding of no effect of PKA on amplitude-based measures of Ca²⁺ release here and the modest resting state depression of RyR P_o by PKA described by Valdivia et al. (1995).

In intact ventricular myocytes, ISO increased Ca²⁺ release during ECC (Hussain & Orchard, 1997), but this could be attributed to increased SR load and I_Ca. The bell-shaped trigger voltage dependence of Ca²⁺ release became flat-topped with ISO but reappeared if conditioning was adjusted to reduce SR Ca²⁺ load or if trigger strength was reduced with nifedipine. This emphasizes the importance of controlling I_Ca and SR Ca²⁺ load in assessing the independent effect of RyR phosphorylation on ECC.

Viatchenko-Karpinski & Györke (2001) found that ISO modestly increased SR Ca²⁺ release and ECC gain (as (ΔF/F_o)/peak (I_Ca), but they did not make gain comparisons where I_Ca was the same (nor did they measure Ca²⁺ release rates). They did find comparable SR Ca²⁺ loading ± ISO, but this was not measured in the same cells or conditions as ECC gain. PKA activation increased ECC gain only when Na⁺ was present in pipette and bath, not under Na⁺-free conditions. Possibly internal Na⁺ promoted Ca²⁺ influx via Na⁺–Ca²⁺ exchange, not accounted for in I_Ca, which could lower threshold, increase SR loading, and/or increase spatial spread of triggering and released Ca²⁺ among release units. Our use of Na⁺-free pipettes and keeping I_Na inactivated prevented Ca²⁺ influx via Na⁺–Ca²⁺ exchange.

In a preliminary report delPrincipe et al. (2001) found that PKA activation increased SR Ca²⁺ release in response to a flash-photolysis-evoked Ca²⁺ trigger. In this case the Ca²⁺ trigger may be more alike (± PKA), but it is unlike the spatially focused physiological I_Ca trigger.

Song et al. (2001) reported that PKA activation decreased ECC gain (based on Ca²⁺ release rates measured as Ca²⁺ spikes with millimolar cytosolic Ca²⁺ buffering). This outcome, under conditions which should emphasize changes in initial release rate, contradicts our finding of faster release. Their reduction in gain was only seen for E_m= 0 mV, not at positive E_m. In Song et al. (2001), I_Ca triggers were relatively large and not specifically matched ± PKA activation. Without specific matching, ISO data would fall along a more saturated part (larger I_Caversus control data) of a possibly unchanged ECC gain versus trigger function.

Earlier termination of Ca²⁺ release with ISO

RyR gating is sensitive to intra-SR free [Ca²⁺] (Sitsapesan & Williams, 1994; Györke & Györke, 1998; Bassani et al. 1995a; Shannon et al. 2000). Moreover, in direct measurements of intra-SR free [Ca²⁺], Shannon et al. (2003) showed that SR Ca²⁺ release appears to turn off robustly when SR [Ca²⁺] drops only partially (e.g. to ∼0.4 mm), regardless of initial SR Ca²⁺ load. With ISO, the faster initial release would then lead intra-SR free [Ca²⁺] to fall earlier to the threshold for termination, which could explain the lack of effect of ISO on the total amount released.

Contrasting PKA versus CaMKII effects on SR Ca²⁺ release and ECC gain

CaMKII can also modify RyR gating in lipid bilayers, but as with PKA phosphorylation the results are mixed, with increases and decreases in P_o reported (Witcher et al. 1991; Hain et al. 1995; Lokuta et al. 1995). We previously studied the effect of CaMKII activation on RyR function in intact ventricular myocytes, using a similar approach to that used here (Li et al. 1997). Activation of endogenous CaMKII during conditioning pulses dramatically increased fractional SR Ca²⁺ release and ECC gain (when both I_Ca and SR Ca²⁺ load were well matched before and after). In transgenic mice overexpressing the cytosolic form of cardiac CaMKII we found dramatic activation of Ca²⁺ spark frequency (despite lower SR Ca²⁺ load and diastolic [Ca²⁺]_i) which was acutely reversed by inhibition of CaMKII by KN-93 (Maier et al. 2003). Twitch fractional Ca²⁺ release was also increased in these mice, despite lower SR load (which normally depresses fractional release). These strong CaMKII effects on intact-cell RyR function contrast strikingly with our present study where PKA activation did not appreciably alter these parameters.

The strong CaMKII effect of increasing ECC efficacy shows that changes in RyR function are in principle detectable in intact cells using experimental designs like ours and that of Li et al. (1997). More importantly, our finding that Ca²⁺ release was faster but unchanged in strength with PKA may point to a general contrast between PKA and CaMKII phenomena (which may have a basis in the ability of CaMKII to phosphorylate sites on RyR not phosphorylated by PKA; Rodriguez et al. 2003). PKA and β-AR activation seem generally to hasten intact cardiac cellular responses (e.g. faster onset and relaxation of contraction, faster Ca²⁺ removal/uptake, faster pacemaker rate, action potential propagation and repolarization) while CaMKII activation may intensify them.

Conclusion – physiological implications

When I_Ca and SR Ca²⁺ load were controlled, we could detect no effect of ISO on amplitude-based measures of ECC efficacy (absolute or fractional SR Ca²⁺ release or ECC gain) over a broad range of I_Ca and load values. However, PKA activation increased the maximal rate of [Ca²⁺]_i rise (and ECC gain based on that) by nearly 50%. This outcome, considered along with the contrasting effect of CaMKII activation to increase Ca²⁺ release strength but not necessarily kinetics, may be part of a general pattern of PKA responses, where fight or flight transient behaviour is crucial (Marks, 2003).

‘Coordinated control’ of ECC has been proposed, where interventions expected to modulate RyR function affected ECC only transiently, due to feedback autoregulation of Ca²⁺ influx and SR loading (Díaz et al. 2000; Eisner & Trafford, 2000). While coordinated control could stabilize ECC with PKA activation in the intact setting, we have disabled this feedback path by specifically controlling Ca²⁺ influx and loading.