The elementary events of Ca²⁺ release elicited by membrane depolarization in mammalian muscle

Abstract

Cytosolic [Ca²⁺] transients elicited by voltage clamp depolarization were examined by confocal line scanning of rat skeletal muscle fibres. Ca²⁺ sparks were observed in the fibres' membrane-permeabilized ends, but not in responses to voltage in the membrane-intact area. Elementary events of the depolarization-evoked response could be separated either at low voltages (near −50 mV) or at −20mV in partially inactivated cells. These were of lower amplitude, narrower and of much longer duration than sparks, similar to ‘lone embers’ observed in the permeabilized segments. Their average amplitude was 0.19 and spatial half-width 1.3 μm. Other parameters depended on voltage. At −50 mV average duration was 111 ms and latency 185 ms. At −20 mV duration was 203 ms and latency 24 ms. Ca²⁺ release current, calculated on an average of events, was nearly steady at 0.5–0.6 pA. Accordingly, simulations of the fluorescence event elicited by a subresolution source of 0.5 pA open for 100 ms had morphology similar to the experimental average. Because 0.5 pA is approximately the current measured for single RyR channels in physiological conditions, the elementary fluorescence events in rat muscle probably reflect opening of a single RyR channel. A reconstruction of cell-averaged release flux at −20 mV based on the observed distribution of latencies and calculated elementary release had qualitatively correct but slower kinetics than the release flux in prior whole-cell measurements. The qualitative agreement indicates that global Ca²⁺ release flux results from summation of these discrete events. The quantitative discrepancies suggest that the partial inactivation strategy may lead to events of greater duration than those occurring physiologically in fully polarized cells.

As an intracellular messenger, Ca²⁺ participates in a wide range of processes. In muscle, action potentials in the plasma membrane and T tubules cause Ca²⁺ channels of the SR to open. The ensuing Ca²⁺ release initiates contraction (e.g. Cheung, 2002).

While the initial characterization of the voltage sensing and Ca²⁺ control functions was carried out largely in muscle of frogs and other amphibians, more recent work, especially at the molecular level, has been done with muscle from various mammalian species.

Additional interest in comparisons of frogs and mammalian muscle comes from the increasingly well-understood differences in molecular makeup of the junction. Initially, the binding assays for dihydropyridines and ryanodine showed a lower DHPR/RyR for frogs. A difference in the isoform complement later became known. This isoform difference has recently been shown to correspond to a major difference in the structural arrangement of channels (Felder & Franzini-Armstrong, 2002), whereby muscle of all species contains arrays of RyR channels in a junctional position, in direct or indirect mechanical contact with T tubular DHPRs. These arrays consist in the mammals exclusively of the RyR isoform 1 (Marks et al. 1989; Takeshima et al. 1989; Flucher et al. 1999) and in the non-mammals of a close homologue named α. Amphibians, and most muscle of fish and birds (rev. by Sutko & Airey, 1996; Murayama & Ogawa, 2002; Ogawa et al. 1999), additionally have arrays of channels in a parajunctional location, presumably containing exclusively the β isoform, homologous to the mammalian ‘brain’ or RyR3 isoform.

Based on these molecular differences we set out to compare systematically the function of Ca²⁺ release in mammals and amphibians, expecting to find a more complex picture in the amphibian, with features not present in the mammal. Reasonably, these features could then be ascribed to or explained by the parajunctional, β set of channels.

This plan appeared to produce results from the start. Shirokova et al. (1996) found that the waveform of Ca²⁺ release under voltage clamp, which in all muscles consists of an early peak that relaxes to a maintained lower level, was much ‘peakier’ in the frog. Moreover, the ratio of peak over steady components was highly voltage dependent in the frog, exhibiting a maximum at intermediate voltages, but flat and lower in the rat. The high peak and the voltage-dependent peak/steady ratio were attributed to the excess RyRs in the frog.

A study of release with confocal microscopy (Shirokova et al. 1998) then failed to find in the rat the early peak of fluorescence and the Ca²⁺ sparks (Cheng et al. 1993) that characterize the local response in the frog (Tsugorka et al. 1995; Klein et al. 1996). Again, this seemed to indicate that the sparks and local peak are features contributed largely by the extra release channels present in the frog.

Confocal studies in the mammal under voltage clamp (Shirokova et al. 1998, 1999) failed to reveal any local structure in the depolarization-induced Ca²⁺ transients. That and the later finding of Ca²⁺ sparks in rodent muscle (Conklin et al. 1999; Kirsch et al. 2001; Zhou et al. 2003a) made it pertinent to resolve and study the local release events. If not sparks, then what are the elementary Ca²⁺ events of mammalian muscle? The present work gives an answer to this question, and includes an analysis of the events that were resolved. It then addresses the ‘inverse problem’: can the global or cell-averaged signals be accounted for by superposition of local events?

Methods

Experiments were carried out in segments of skeletal muscle fibres from the extensor digitorum longus (EDL) or communis (EDC) of the rat (Rattus norvegicus, Sprague-Dawley) separated enzymatically by two variants of a method first described by Szentesi et al. (1997). Three-month-old male rats were killed by CO₂ inhalation, following procedural protocols approved by the Institutional Animal Care and Use Committee of Rush University. EDL or EDC muscles of both legs were separated to their branches and pinned to a Sylgard chamber, which was filled with a modified Krebs solution supplemented with 10% fetal bovine serum plus 2 mg ml⁻¹ collagenase type I, with no Ca²⁺ or Mg²⁺ added, and incubated in an orbital bath at 37°C. In the first variant of the technique muscles were incubated for 1 h, while in the second the incubation was prolonged, to the point where single fibres separated spontaneously. After the enzymatic treatment muscles were washed in Krebs solution plus fetal bovine serum (FBS) and kept for 30 min before further use. Muscles digested for 1 h were transferred to a dissecting solution (a high [K⁺] relaxing solution containing 0.1 mm Ca²⁺) where fibre segments of approximately 1.5 cm were removed by suction and transferred to a 2-Vaseline gap chamber. In the second variant, the fibres that separated spontaneously were directly transferred to the chamber.

Voltage clamp

The 2-Vaseline gap chamber is a 60% size version of chambers used in the past for work with frog or mammalian fibres, in which two partitions divide a small volume in three compartments (middle and sides), connected to voltage clamp electronics described by Francini & Stefani (1989). In the present version the thickness of the partitions was reduced to 150 μm and the width of the middle pool to 300 μm. Narrow grooves cut through the partitions reach all the way to the glass bottom of the chamber. The fibre segments were carefully lowered through these grooves and fixed slightly stretched (2.2–2.5 μm per sarcomere) to the glass bottom of the chamber. Seals of silicone grease were then made around the fibres within the partitions. The chamber was mounted on the stage of an inverted microscope (Axiovert 100 TV, Zeiss, Oberkochen, Germany), part of a confocal scanner of laser-excited fluorescence (MRC 1000, Bio-Rad, Hercules, CA, USA).

The fibre segments in the end pools were first permeabilized by immersion in a relaxing solution containing 0.002% saponin and 50 μm fluo-3. Saponization was carried out while monitoring fluorescence in the confocal system, so that penetration of dye could be assessed and exposure to saponin minimized. Usually after 1–2 min saponin was washed out and the working internal solution introduced in the chamber. An ‘external’ and an ‘internal’ solution were then placed in the middle and end pools, respectively.

Solutions

Experiments were carried out at 17°C. The internal solution, designed by Zhou et al. (2003a), contained (mm): K₂SO₄, 86.6; Na₂ATP, 5.15; Na₂PC, 10.29; EGTA, 1; glucose, 5; Hepes, 10; Dextran, 8%; and CaCl₂, 0.186 and MgCl₂, 10.73, for a nominal [Ca²⁺] of 100 nm and [Mg²⁺] of 2 mm. The external solution contained (mm): TEA, 150; CH₃SO₃, 154; Hepes, 10; Ca²⁺, 2; Mg²⁺, 2; 3,4-diaminopyridine, 1; and TTX, 0.001. For both solutions pH was set to 7.0 and osmolality to 320 mosmol kg⁻¹. The composition of Krebs and relaxing solutions used in the preparation stages was given by Shirokova et al. (1996).

Microscopy and image processing

The scanning microscope was in standard fluorescein configuration (Ríos et al. 1999) and used a 40×, 1.2 N.A. water immersion objective (Zeiss, Oberkochen, Germany). The excitation source was the 488 nm line of 100 mW Ar laser, attenuated to 3% power. Line scan images F(x,t) shown are of fluorescence of fluo-4, determined at 2 ms intervals at 768 points 0.1428 μm apart along a line parallel to the fibre axis, and digitally filtered in two dimensions at corner frequencies 83 Hz and 1.17 μm⁻¹ (or 4 ms and 0.4 μm rise time and distance). F(x,t) was normalized to the baseline intensity F₀(x), derived as an average of F(x,t) in the regions of the line scan image prior to the depolarization stimulus. Before the images were processed by the routine that detects individual events (described below), they were subjected to a digital high-pass filtering procedure, which removed a global increase in fluorescence. To do this, the normalized fluorescence was convolved in the spatial dimension with a 100-element kernel that performs a low pass filtering at 0.01 of the Nyquist frequency (3.5 μm⁻¹). The high-pass filtered image was obtained by subtracting this low-pass-filtered image from the original (after scaling by the value 0.88, found empirically to result in events that start from 0 in the subtracted image). An example of this procedure is shown in Fig. 2.

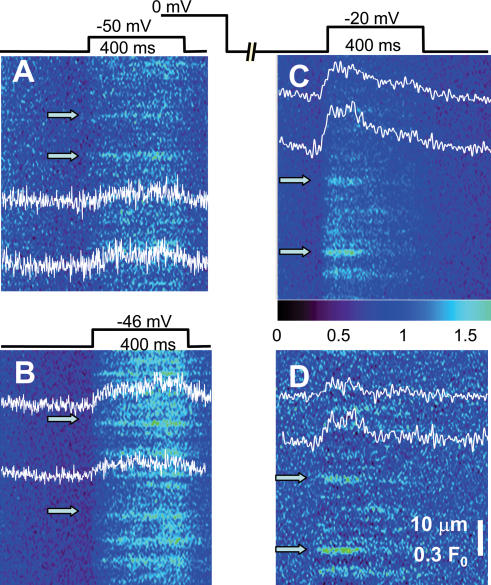
Figure 2. Events in middle pool ‘working’ regions, elicited by voltage clamp.

Fluorescence of fluo-4 in line scans parallel to the fibre axis. Scans were acquired while applying depolarization patterns shown schematically. Intensity normalized to resting fluorescence (averaged before the pulse). A and B, examples of responses to pulses to −50 and −46 mV (from a holding potential of −90 mV). Profiles were obtained averaging 7 central pixels at positions indicated by arrows. (Identifiers: 102102A13, 102102A2; fibre of Fig. 1B.) C, example of records obtained at a higher voltage after partial recovery from voltage-dependent inactivation (2.8 s at −90 mV). D, image in C after subtraction of global fluorescence (see Methods). (Identifier: 102802A28.)

To isolate small events it was necessary to optimize image quality. Several measures were taken to this end. The alignment of the confocal scanning system was optimized before the experiments. The point spread function (PSF), measured as described by Ríos et al. (1999), had parameters FWHMx = 0.42 μm and FWHM z = 1.25 μm. To reduce the influence of scattering, line scan images were taken at locations less than 10 μm away from the (bottom) surface of the fibre. It was found empirically that the images were best relatively early in the course of an experiment, 45 min to 1 h after exposure to the internal solution, suggesting that the increase in dye concentration beyond a certain level hampered the resolution of the local events. A related observation was that 300–500 pixel (45–75 μm)-wide areas of the working region close to the Vaseline seals often gave the best spatial resolution. Whenever the resolution of events in a portion of the 768 pixel-wide image was significantly better than in the rest of the image, that region was excised for analysis and the remnant of the image was discarded.

Detection and morphology of events

The quantitative characterization of event morphology was carried out on events identified by an objective detection program modified from one described by Cheng et al. (1999).

Five parameters were measured: total suprathreshold duration, amplitude (on a temporal average that started when the central intensity reached 90% of the first maximum and lasted until the end of the event), FWHM (2(2 ln2)^½ or 2.3548 ×σ, determined on a shifted Gaussian function of space fitted to the same temporal average), rise time (between initiation and 90% of amplitude) and latency (interval from the beginning of the depolarizing pulse to the first point above threshold).

Release flux, local events

Release flux was calculated as described by Ríos et al. (1999; reviewed by Ríos & Brum, 2002), on averages of the events located automatically. Events are assumed to be centred on the scanned line, and symmetrical. Using a specific model for dye reactivity and diffusion, the fluorescence of an event and its surrounding space–time region is first processed to derive free [Ca²⁺] as a function of space and time. Then release flux is computed as the sum of binding fluxes to the known ligands (calculated from diffusion–reaction equations). This calculation assumes values for a set of parameters, listed as Model 1 in Table 2 of Zhou et al. (2003a) with the following kinetic parameters for the reaction of Ca²⁺ and SO₄²⁻: ON rate = 5× 10⁸m⁻¹s⁻¹, OFF rate = 2.5 × 10⁷ s⁻¹, diffusion coefficient = 1.8 × 10⁻⁶ cm² s⁻¹. Volume integration of release flux density (with units of concentration over time) yields a flux rate (quantity per unit time) that is converted to Ca²⁺ current.

Table 2. Average values of parameters determined on all events identified by an automatic detector.

	Amplitude (μm)	FWHM (ms)	Duration (ms)	Rise time (ms)	Latency (ms)	N events (ms)
−50 mV	0.19 (0.01)	1.31 (0.05)	111 (6)	16.6 (0.81)	185 (11)	168
−20 mV	0.19 (0.01)	1.45 (0.07)	203 (13)	22.8 (1.54)	23.9 (1.6)	61

Data are means (s.e.m.). See Methods for definitions of parameters.

Release flux, global records

In some cases and for purposes of comparison with Ca²⁺ release reconstructed from local events, Ca²⁺ release flux was derived from line scans of fluorescence by the ‘removal’ method developed by Melzer et al. (1984, 1987) for the analysis of global (or cell-averaged) Ca²⁺ signals. The method was applied with modifications described by González & Ríos (1993) and Shirokova et al. (1996). First the line scan image was averaged over the spatial coordinate to generate a single function of time. This function was processed in the same way as the global fluorescence signal in the work of Shirokova et al. (1996) to first derive a time course of average cytosolic [Ca²⁺]. Then a model of Ca²⁺ removal was adjusted for best fit to the time course of fluorescence in the off portion of the record (after the depolarizing pulse). Ca²⁺ release flux was then computed as the sum of removal into all binding and transport compartments plus the time derivative of cytosolic [Ca²⁺]. All parameters had conventional values, except the kinetic constants of binding to EGTA, which were changed for best fit. Parameter values include the following.

Concentrations (mm): parvalbumin (Parv), 1; troponin sites (Trop), 0.24; EGTA, 1; Mg²⁺, 2; Ca²⁺ at rest, 0.00005; pump sites, 0.1.

ON rate constants (mm s⁻¹): Mg-Parv, 30; Ca-Parv, 10⁵; Ca-Trop, 1.25 × 10⁵; Ca Pump, 10⁶; Ca-Dye, 3.2 10⁴.

OFF rate constants (s⁻¹): Mg-Parv, 3; Ca-Parv, 1; Ca-Trop, 1200; Ca-Pump, 1000; Ca-Dye, 33 ([dye] was derived from the resting fluorescence).

Simulation of local events

Local fluorescence events were simulated as the result of release from a spheric source of subresolution diameter (0.2 μm) and known current, impinging on a homogeneous medium with the main Ca²⁺-binding and transport sites of the cytosol, as described by Ríos et al. (1999), with two modifications. Ternary reactions were assumed to take place among dye, Ca²⁺ and cell sites ‘P’ (Baylor et al. 2002). Additionally, the reaction between troponin and Ca²⁺ was described by a two-step cooperative scheme, whereby binding of one Ca²⁺ leads to an increase in affinity for a second ion (Baylor et al. 2002). Reaction–diffusion equations describing the movements of Ca²⁺, and Ca²⁺-bound and Ca²⁺-free ligands in an isotropic myoplasm were solved to calculate the concentration of Ca²⁺-bound dye, and hence the fluorescence. The parameter values used in the calculations are listed in Table 1. Reaction–diffusion equations were solved numerically by PDEASE (Macsyma Inc., Arlington, MA, USA) in a spherical volume of radius 4.3 μm. Changes in the computation volume did not lead to significant changes in results. The calculations generated a fluorescence ‘object’, a function of time and three spatial coordinates. The simulated object was then convolved with the experimentally determined PSF of the imaging system, idealized as a 3-D Gaussian function, with FWHM of 0.42 μm in the x–y plane, and 1.25 μm in the z direction. The convolution procedure, implemented in Fortran, could assume any spatial shift between scanning line and event source.

Table 1. Values of parameters used by the release flux algorithm and simulations.

Parameter	Value	Parameter	value
Fluo:Ca ON rate (107m−1 s−1)	26.7	Parv:Ca ON-rate (107m−1 s−1)	12.5
Fluo:Ca OFF rate (s−1)	136	Parv:Ca OFF-rate (s−1)	0.5
P-Fluo:Ca ON rate (107m−1 s−1)	1.72	Parv:Mg ON-rate (107m−1 s−1)	0.003
P-Fluo:Ca OFF rate (s−1)	33	Parv:Mg OFF-rate (s−1)	3
Fluo:P ON rate (107m−1 s−1)	1.15	SO4:Ca ON-rate (107m−1 s−1)	50
Fluo:P OFF rate (104 s−1)	0.42	SO4:Ca OFF-rate (107 s−1)	2.5
Ca-Fluo:P ON rate (107m−1 s−1)	1.15	Maximum pump rate (mm s−1)	9.8
Ca-Fluo:P OFF rate (104m−1 s−1)	1.59	DCa (10−7 cm2 s−1)	35
[P]+[P:Fluo] (mm)	3	Dfluo (10−7 cm2 s−1)	15
EGTA:Ca ON rate (107m−1 s−1)	0.2	DATP (10−7 cm2 s−1)	14
EGTA:Ca OFF rate (s−1)	2	DSO4 (10−7 cm2 s−1)	18
Trop:Ca ON-rate (107m−1 s−1)	20.3	Dparv (10−7 cm2 s−1)	0.16
Trop-Ca:Ca ON-rate (107m−1 s−1)	10.2	DEGTA (10−7 cm2 s−1)	0.36
Trop:Ca OFF-rate (104 s−1)	2.64	[Troponin sites] (mm)	0.36
Trop-Ca:Ca OFF-rate (s−1)	13.2	[Parvalbumin] (mm)	1
ATP:Ca ON-rate (107m−1 s−1)	15	[Pump sites] (mm)	0.24
ATP:Ca OFF-rate (104 s−1)	3	[EGTA] (mm)	1
ATP:Mg ON-rate (107m−1 s−1)	0.195	[ATP] (mm)	5
ATP:Mg OFF-rate (s−1)	195	[SO42−] (mm)	80

Model and parameters are as in Zhou et al. (2003a) with two modifications: ternary reactions take place among dye, Ca²⁺ and cell sites ‘P’ (Baylor et al. 2002). Additionally, the reaction between troponin and Ca²⁺ was described by a two-step cooperative scheme, whereby binding of one Ca²⁺ leads to an increase in affinity for a second ion (Baylor et al. 2002). Parv, parvalbumin. Trop, troponin. [Ca²⁺] was 0.05 μm[Mg²⁺] was 2 mm. In ternary reactions, the colon identifies the binding ligands. Thus, ‘P-Fluo:Ca’ designates rates of Ca²⁺ binding to site-bound dye, etc.

Simulations of global fluorescence

Global fluorescence (which could be gathered experimentally by spatially averaging line scan images) was simulated by convolution of the latencies of events detected in partially inactivated fibres, with the average fluorescence of an average event. Three averaging processes were therefore needed. (1) An average release flux event was constructed based on measured individual event parameters, and used as described in the previous paragraph to generate an elementary fluorescence object. (2) This object was then scanned assuming a range of locations of the source relative to the scanning line. A total of 169 locations were used, at 13 equidistant positions in the z axis, between −1.8 and 1.8 μm from the scanning line at z = 0, combined with 13 positions in the y axis, between y =−0.7 μm and 0.7 μm. No shifts in x were necessary as all values of x are sampled. The 169 contributions (which by symmetry reduce to 49) were added and multiplied by an arbitrary scaling factor. (3) The temporal profile of the average obtained in 2, ΔF/F₀ (t), simulates the global profile when all events start at t = 0. The simulation of a response to a pulse to voltage V_m must additionally contemplate the time of occurrence of individual events, given by the latency histogram L(t). The time course of the response ΔF/F₀ (V_m, t) was calculated as the convolution of ΔF/F₀ (t) and L(t).

Results

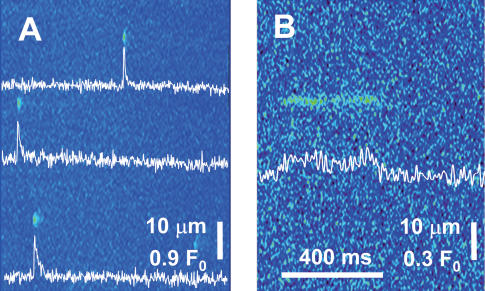
In mammalian muscle, Ca²⁺ sparks are difficult to demonstrate under any circumstance. Therefore, to understand their role, if any, in physiological release, the experimental strategy was to record local events under voltage clamp in fibres known to produce Ca²⁺ sparks spontaneously. As described earlier (Zhou et al. 2003a) two conditions result in the reliable observation of sparks in mammalian muscle. One is the treatment of fibres with saponin, which permeabilizes the plasmalemma and transverse tubules. This operation is done routinely in the segments located in the end pools of the 2-Vaseline gap chamber. The other condition is the exposure to an internal solution with SO₄²⁻ as main anion (Csernoch et al. 2003), which for reasons that are not yet understood renders the occurrence of sparks more predictable (see discussion in Zhou et al. 2003a). Therefore, the experiments were carried out using the SO₄²⁻ solution introduced in that paper. Routinely, the segments in the end pools were scanned for sparks, which were always found. Figure 1A presents an example line scan, with several sparks that have properties similar to those reported before. Figure 1B represents, at a different fluorescence scale, a ‘lone ember’, which was also a frequent observation in the side pools. These embers had morphological parameters not different from those reported by Zhou et al. (2003a). Their qualitative features include an abrupt beginning and end, with apparently constant amplitude and width, sustained for tens or hundreds of milliseconds, and occasional closings and reopenings.

Figure 1. Events in the side-pool regions of fibres under voltage clamp.

Fluo-4 fluorescence in line scans parallel to the fibre axis. Intensity normalized to resting fluorescence (see Methods). A, representative image showing multiple sparks. (Identifier: fibre 072602B record 1.) B, example of a ‘lone ember’. (102102A111.)

Discrete events elicited by pulse depolarization

Responses to voltage clamp pulses, in the working segment of the fibre that gave rise to the event in Fig. 1B, are shown in Fig. 2. By a combination of careful alignment of the confocal system and scanning very close to the fibre surface in the most favourable range of dye concentrations, it was possible to find images where the response at low suprathreshold voltages resolved into spatially separate events. Analogous results, not included in this study, were found in glutamate-based internal solutions. Figure 2A is a response to a −50 mV, 400 ms pulse, normalized to the fluorescence average over time in the interval before application of the pulse. Figure 2B is the response to a slightly higher voltage in the same fibre. The fluorescence response contains discrete events, which increase sharply in numbers at the higher voltage, and are similar to lone embers, lasting all or part of the interval of the applied pulse. The temporal profiles of these events (at arrows) show, additionally, evidence of a changing background, a global signal.

The global signal is obviously a consequence of global increase in [Ca²⁺], caused by opening of many channels near the scanning area. Two approaches were taken to minimize the interference and facilitate exploring the events produced at higher voltages. One was the partial ‘repriming’ (recovery from inactivation) protocol introduced by Klein et al. (1997). The other was a high-pass filtering that essentially subtracts the global fluorescence.

An example image elicited after partial repriming is shown in Fig. 2C. The fibre, held depolarized, was taken to −90 mV for 2.8 s, to allow for partial recovery from voltage-dependent inactivation, and a pulse to −20 mV was then applied. As observed for sparks by Klein et al. (1997), elementary events could then be resolved at −20 mV. Unlike the result with sparks, there was still interference by a global signal, clearly seen in the temporal profiles shown. Figure 2D shows the result of subtracting the global signal by spatial high-pass filtering.

After this procedure the events appeared flat, of constant amplitude. At −20 mV events tended to start early during the pulse, with few late openings. Their duration was variable.

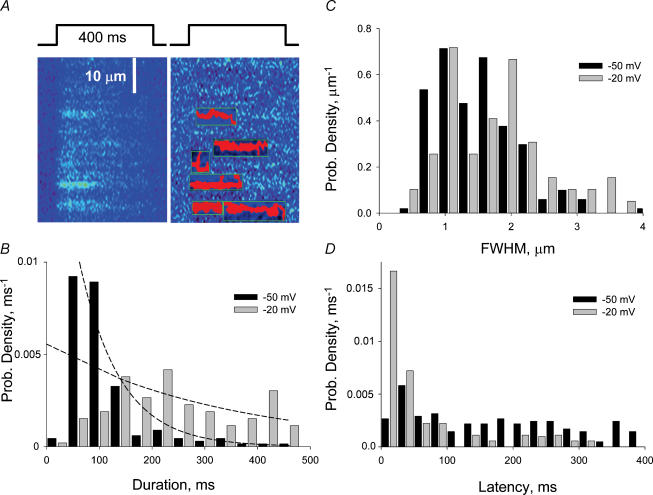
An objective event detector, evolved from programs described earlier (Cheng et al. 1999; Zhou et al. 2003a) was used on both the normalized and the normalized and high-pass filtered images. The detector identified events and measured their morphological parameters. Figure 3A illustrates the performance of the detector in the region of the image of Fig. 2C where events were located. In red is the suprathreshold footprint of each event, while green lines mark their x and t bounds.

Figure 3. Morphological properties of events at different voltages.

A, the operation of the automatic event detector, which identifies events and measures them. Marked in red is each event's suprathreshold footprint, and in green its x and t bounds. B, distributions of event durations. Curves represent best single exponentials fitted to the histograms (with two first bins omitted). Time constants of fits are 77.5 and 330 ms. C and D, histograms of FWHM and latency from start of the pulse. ‘−50 mV’ data pool all events (168) at −46, −48 and −50 mV. ‘−20 mV’ are events (66) from images at −20 mV after recovery times at −90 mV of 2.6, 2.8 or 3 s.

One hundred and sixty-eight events were identified in 29 images from 7 experiments at low voltages (−46 to −50 mV) and 66 were in 12 images at −20 mV from 2 partial repriming experiments. The average parameters are listed in Table 2. Three parameters were similar in these two groups, namely average amplitude (at about 0.2 units), spatial width (1.3–1.45 μm) and rise time (near 20 ms). These values are all characteristic of embers, rather than sparks (Kirsch et al. 2001; Zhou et al. 2003a).

Two parameters had very different values at these two voltages. The duration of the events (given by the time span within boundaries of each event in Fig. 3A) increased on average from about 100 ms at the low voltage to 200 ms at −20 mV. The distributions of these values at the two voltages are compared in the histograms of Fig. 3B. The distribution of durations was nearly flat at the high voltage, with all durations nearly equally represented, whereas it had a clear peak at short durations for the lower voltage. (Events with durations below 40 ms were scarce at either voltage, perhaps missed by the detector.) Additionally, the latency of events decreased sharply at the higher voltage, with most openings occurring early in the pulse, while the distribution at −50 mV was flat (Fig. 3D). The distributions of the other parameters were similar at both voltages and unremarkable. The histograms of spatial widths illustrate this point (Fig. 3C).

As can be seen directly comparing Fig. 2A and B, the frequency of events increased sharply with voltage (which in fact limited the range where events could be well separated in fully primed cells). This limitation, as well as intercell variation, severely restricted any study of voltage dependence. In one especially stable experiment, 15 line scan images were obtained, four at −46 mV and the rest at between −48 and −50 mV. The frequency of events detected, corrected for the useful scanned length, can be taken as a rough measure of frequency of events produced (even though the failures of detection increase with voltage, as superposition hinders detection). The average frequency of events at −46 mV and in the −48 to −50 mV group was 0.022 and 0.015 per sarcomere per second, corresponding to 4.3 and 2.9 events per image, respectively. Given standard errors of the order of the square root of the means (2.4 and 1.7 events per image, respectively), this difference is not statistically significant. However, it suggests a logarithmic slope of e-fold per 5.6 mV. This is not inconsistent with the value 6.7 mV derived from whole-cell measurements of Shirokova et al. (1996) for the range −60 to −50 mV. Within the substantial error of these estimates, it is therefore unnecessary to invoke other types of events to account for the voltage-dependent increase in whole-cell response. A similar conclusion is reached later in this section through a simulation of whole-cell fluorescence.

Ca²⁺ release underlying the elementary event

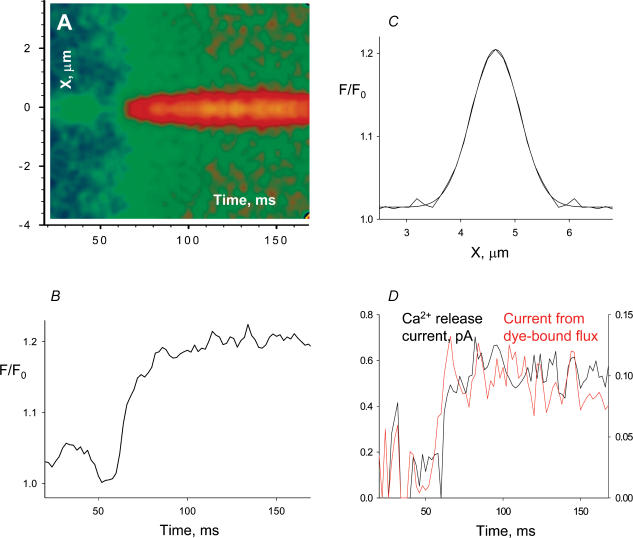
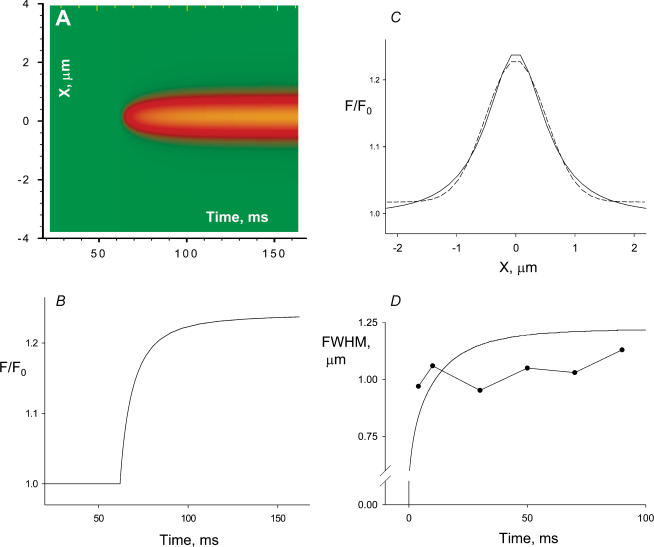
To further understand the release function underlying these events, we estimated the Ca²⁺ release current necessary to produce them. The estimation, as in previous work, was done in two ways. The ‘backward’ calculation described by Ríos et al. (1999) was applied to an average of all events detected automatically that satisfied two conditions: their average amplitude was 0.12 or greater and their duration 100 ms or greater. The first condition selects events scanned close to the scanning line (Ríos et al. 2001), the second insures that temporal features observed for the average event in the first 100 ms do not result from asynchronous channel closing. Sixty-six events satisfied both conditions. Sub-arrays containing the individual images were extracted centred at the position of the peak in the average over time, starting 60 ms before the time of first crossing of the detection threshold; their average is shown in Fig. 4A. The increase in global fluorescence visible in the average occurs because most events started after a brief latency from the beginning of the pulse. The small central ‘ridge’ that precedes the average event is due to other events originating in the same triad.

Figure 4. The average voltage-elicited event.

A, average of all normalized events that had (average) amplitude greater than 0.120 and duration greater than 100 ms. Events averaged (66) are from both fully and partially reprimed fibres. B, spatial profile of event, averaged between 50 and 100 ms after the first suprathreshold point. The smooth curve is a Gaussian best fit, of FWHM = 1.08 μm. C, temporal profile, obtained averaging 5 central pixels. D, black trace, Ca²⁺ release current, calculated from the average event; red trace (r.h.s. scale), dye-related component of the Ca²⁺ release current.

Figure 4C represents the spatial profile of the average event, averaged over time between 50 and 100 ms (from beginning of event), after correction for the global increase in fluorescence. The smooth line is a Gaussian fit with FWHM = 1.08 μm. That this value is less than the average of FWHM calculated in individual embers may simply be an indication that noise skews this measure toward greater values. In Fig. 4B is the temporal profile, calculated as the average of five central pixels. The profile reaches a relatively steady level after about 40 ms.

The Ca²⁺ release current, calculated by the method of Ríos et al. (1999; details in Methods) is shown in the black trace in Fig. 4D. It rises rapidly to a constant or slightly decaying level of between 0.5 and 0.6 pA. This level is consistent with estimates of single channel current derived from bilayer experiments (e.g. Kettlun et al. 2003). On this basis the analysis suggests that elementary embers are due to the opening of individual channels.

In red in the same panel is the portion of the release current that was bound to and removed by the Ca²⁺-monitoring dye (specifically it is the volume integral of the net binding flux, which is equal to the local rate of change of [Ca:dye] plus the exiting diffusional flux of Ca:dye). As argued by Ríos et al. (1999), this portion of the calculated current does not depend on assumptions about buffer or transport properties, as it only uses the measured fluorescence. This is therefore the most reliably known component of the release current. In turn the release current is expected to be roughly proportional to this component, and hence the time course in red may reflect release kinetics better than the full calculation. This time course rises more rapidly than the calculated total current, and has a slightly more marked tendency to decay after the early maximum.

Simulation of embers

An alternative estimation of release current was obtained through a simulation of the fluorescence event due to a source with known spatial and temporal characteristics, releasing Ca²⁺ into a model of the cytosol (detailed in Methods). The result of this approach for a spherical source of 0.1 μm radius, open for 100 ms with a current of 0.5 pA is presented in Fig. 5. The fluorescence is in Fig. 5A, the temporal profile in Fig. 5B, the spatial profile at the end of the 100 ms open time is in Fig. 5C (the Gaussian fit, smooth line, has a FWHM of 1.18 μm). In amplitude, time course and spatial profile, the result of the simulation is reasonably close to the experimental average represented in Fig. 3. Figure 5D compares the time course of spatial width in experimental average (symbols) and simulation (smooth line). This aspect of the simulation is also adequate, even though the increase in width at early times seen in the simulation was not clear in the average, perhaps because the small signal was too distorted by noise at these times. Simulations using a simpler model (Ríos et al. 1999), which did not contemplate binding of the fluorescent dye to cellular sites, led to a slower rise in spatial width, clearly inconsistent with the experimental record. The additional assumption of a two-step cooperative binding of Ca²⁺ to troponin, suggested by S. Baylor (University of Pennsylvania), contributed to a faster increase of spatial width to a much lesser degree than the inclusion of a ternary scheme of dye reactions with Ca²⁺ and cellular sites.

Figure 5. Simulation of the elementary event.

An event was generated using a source assumed to be in focus, of 0.1 μm radius and constant current of 0.5 pA, open for 100 ms. Details of the model are given in Methods. The result was blurred using the measured PSF. A, simulated line scan. B, central temporal profile. C, spatial profile of an average between times 50 and 100 ms. Smooth line is Gaussian best fit, of FWHM = 1.18 μm. D, FWHM, calculated on the fitted Gaussians, for spatial profiles of the simulation at different times (line) or the experimental average, in turn averaged over successive 20 ms intervals (symbols). (The FWHM value plotted at 5 ms was calculated on the spatial profile of the experimental average, averaged over the first 10 ms of the signal.)

The different estimations of release current are consistent with causation of the elementary event by opening of an individual channel.

Discussion

By the use of improved optics, confocal scanning close to the fibre surface (which reduces scattering of exciting and emitted light), optimized dye concentrations, low stimulus voltage or a partial repriming pulse strategy, combined with subtraction of a global signal, elementary events of Ca²⁺ release were resolved in fast-twitch skeletal muscle fibres of the adult rat. This result builds on, and is consistent with, the earlier conclusion that Ca²⁺ release under voltage clamp does not involve Ca²⁺ sparks (Shirokova et al. 1998).

Spatially resolved events are elementary

The events can be termed ‘elementary’ in the sense that they are discrete, isolated spatially and temporally. They seem to be irreducible to smaller ones, because their morphological parameter, amplitude and width are similar at two very different voltages. In contrast, event duration was found to be voltage-dependent, approximately double on average at −20 mV than at −50 mV. As proposed in the allosteric scheme of Ríos et al. (1993), the voltage sensors may be simply biasing Markovian channels towards the open state, lengthening open (and shortening closed) times as voltage is increased.

Elementary events are produced by individual open channels

The conditions used for the present experiments were those found in previous work to be optimum for the observation of spontaneously occurring Ca²⁺ sparks (Zhou et al. 2003a). These conditions included the use of SO₄²⁻ as the main anion. It must be noted, however, that the responses to voltage were qualitatively similar in experiments with glutamate as the main intracellular anion.

Sparks were found, as expected, in the regions of the fibre placed in the end pools of the 2-Vaseline gap chamber. In these regions lone embers were also found. These sparks and embers were of typical morphology. Sparks had rise times of about 5 ms, durations near 10 ms, amplitudes often surpassing 1 unit of resting fluorescence, and spatial widths near 2 μm. Embers by contrast had no peaks, amplitudes of 0.1–0.4, durations in the tens or hundreds of milliseconds, widths close to 1 μm and rise times of about 20 ms.

By analogy with the events observed in the cut ends, or with those described in previous work (González et al. 2000a; Zhou et al. 2003a), the events elicited by voltage in the working fibre segment may be called embers. Their average amplitude and spatial width are consistent with those of lone embers (Zhou et al. 2003a), and analogous events described by Szentesi et al. (2004) in mammalian fibres in the presence of thymol or by Hollingworth et al. 2003) in intact frog fibres. In amplitude and width they are also similar to ‘Ca²⁺ quarks’, small events observed after spatially limited photorelease of Ca²⁺ in cardiac myocytes (Lipp & Niggli, 1998). Unlike sparks (and quarks), their time course does not feature a peak followed by sharp decay.

Lone embers were attributed to opening of individual channels or small groups synchronized to open and close together (see arguments by Zhou et al. 2003a; Hollingworth et al. 2003; Szentesi et al. 2004). By the same arguments the present events reflect either a single open channel or a highly synchronized group. The first possibility is upheld by two estimates of current underlying the discrete event. The ‘backward’ calculation algorithm (Ríos et al. 1999) applied to an average of fluorescence events yielded a release current that rose rapidly and remained constant or decayed slightly during the first 100 ms, near a level of 0.5 pA (Fig. 4D). A simulation of the fluorescence arising from the opening of a source of subresolution size, to a sustained Ca²⁺ current of 0.5 pA, resulted in an event (Fig. 5) of morphology similar to that of the experimental average (Fig. 4). If the single channel current is 0.5 pA (as recorded by Kettlun et al. 2003; for the lumenal-to-cytosolic current through channels forcibly open by caffeine in the presence of 1 mm lumenal Ca²⁺ and physiological concentrations of K⁺ and Mg²⁺), then the ‘release unit’ will be a single channel. If the current was less than 0.5 pA, then the release unit would consist of two or more highly synchronized channels.

By comparison, the current underlying a Ca²⁺ spark has been estimated by similar methods at 8–27 pA (Ríos et al. 1999; Chandler et al. 2003) in cut amphibian muscle and 50–130 pA in saponized rat muscle (Zhou et al. 2003a). If lone embers represent a single channel, then sparks of mammalian muscle require a large number of simultaneously open channels, put at 35–260 by Zhou et al. (2003a).

Decay of Ca²⁺ release during a pulse

The Ca²⁺ release current during an elementary event appears to be either constant or slightly decaying. This feature and the observed occurrence of events of different durations indicate that the decay of release flux in whole-cell measurements is largely due to an attrition of events, rather than decreasing current within events. The constancy or slight decay in event current over time is at first sight inconsistent with the idea that release channels are closed by local depletion, proposed as the mechanism for termination of Ca²⁺ sparks (Sobie et al. 2002) and supported by recent experimental work in cardiac muscle (Terentyev et al. 2002, 2003). The elementary events, however, could be different when they occur during an action potential, or a high voltage pulse, in a fully polarized cell. In such conditions a much higher density of simultaneously open channels might lead to local depletion, which in turn could become a signal for event termination. This possibility informs the arguments in the following two sections.

From elementary event to cellular response

This section considers whether the cellular Ca²⁺ release waveform (first derived from whole cell photometric signals in amphibian muscle by Baylor et al. (1983) and Melzer et al. (1984), and in mammalian muscle by Delbono & Stefani, (1993) and García & Schneider (1993)) can be ‘explained’, that is, quantitatively accounted for, as the result of addition of the elementary events described here.

Again, two approaches were used. In the first, a cell-averaged release waveform was constructed by superposition of elementary release events and compared with the release waveform obtained from earlier whole-cell measurements. In the second, a cell-averaged fluorescence waveform was synthesized by superposition of elementary fluorescence events. Each procedure has different assumptions and drawbacks, but both provide tests of the same reductionist hypothesis.

The first approach follows a procedure introduced by Klein et al. (1997) and is illustrated in Fig. 6. Let the function of time E(t) represent the ‘elementary release event’ (assumed to be a pulse of current, with a distribution of durations). If this event is exclusive (i.e. there are no other types of release) and reproducible, and if the distribution L(t) of all latencies during a pulse is known (it is given by histograms in Fig. 3D), then the whole cell release time course R(t) will be the convolution:

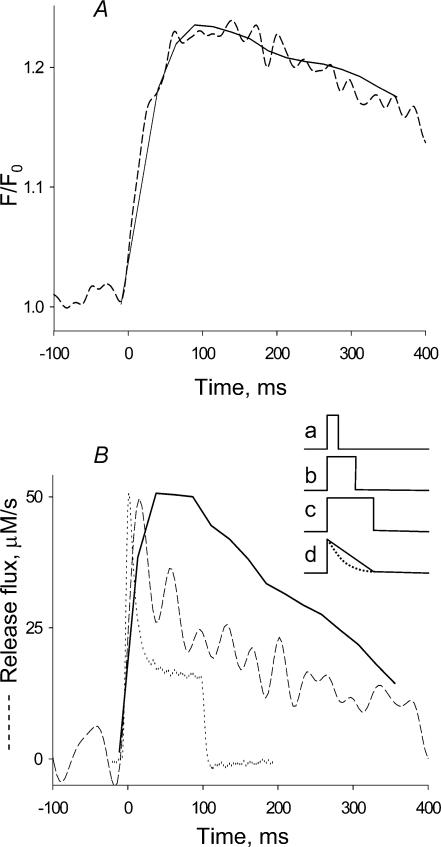
Figure 6. Fluorescence and release flux built as sum of elementary events.

A, dashed trace, global fluorescence, average over spatial coordinate of the image in Fig. 2B. Continuous trace, reconstruction of global fluorescence from elementary events as described in Methods. B, dashed trace, time course of release flux derived from the fluorescence record in A by the removal method of Melzer et al. (1984). Continuous trace, reconstruction of release flux by convolution (eqn (1) in Discussion) of the latency distribution L(t) and the elementary release E(t) (time dependence given by eqn (A2) in the Appendix). Dotted trace, time course of release flux at −20 mV, derived from photometric records in a ‘whole-cell’ experiment with a fully polarized fibre (record rescaled from Fig. 4B of Shirokova et al. 1996). Inset, the average time course of individual release current, E(t), results from averaging individual events of constant current and variable duration (represented by traces a–c). When a uniform distribution of durations is used, the result is the triangular record d (continuous line), obtained with eqn (A1). For a decaying exponential distribution of durations (with time constant 100 ms) the result is d (dotted line), obtained with eqn (A2).

Klein et al. (1997) assumed E(t) to be a pulse of constant current, lasting the average rise time of a spark, and obtained a qualitatively reasonable, but significantly blunted reproduction of the time course of release current in response to a depolarizing pulse in frog muscle.

A problem in the present application is that the events are not repetitions of an invariable time course, but have a broad distribution of durations, nearly flat from the lowest durations detected to 400 ms, the duration of the pulse. This variation was taken into account by using as an approximation to E in eqn (1) an average time course, calculated in the Appendix and illustrated in Fig. 6B, inset. When the distribution of durations is assumed to be uniform between 0 and the pulse span T, the average E(t) is the triangular function given by eqn (A1) and continuous trace d in the inset, decaying linearly with time. A slowly decaying exponential (the expected open time distribution of Markovian channels) is similar, but physically more plausible than a uniform distribution. The average E(t) for an exponential distribution is given as eqn (A2) in the Appendix, and represented by the dashed curve d in Fig. 6B, inset.

R(t) was calculated using eqn (A2) with τ= 330 ms as E(t) in eqn (1). The result is shown by the continuous trace in Fig. 6B. This estimation of release flux was compared with two others, obtained from global signals. The dashed curve in Fig. 6A is the time course of the fluorescence of the image shown in Fig. 2C (averaged over space). This record was processed following established procedures described in Methods for analysis of Ca²⁺ release from global records (e.g. Shirokova et al. 1996). The release flux record is shown in Fig. 6B (dashed line). Though qualitatively similar, this record appears to rise and decay faster than the record synthesized by convolution of elementary events.

One reason for the discrepancy is that the removal method used to derive the global release waveform may not be strictly applicable to the small signals obtained in largely inactivated cells. Particularly the assumption of spatial homogeneity of [Ca²⁺] and removal rate, which is at best an expedient approximation requiring linearity between flux, [Ca²⁺] and [Ca²⁺ dye] to be valid, could introduce kinetic errors. The analysis that follows upholds this explanation.

The robust agreement between the average fluorescence event, in Fig. 4, and the event simulated from a simple elementary release, in Fig. 5, suggested an alternative: to reconstruct a global fluorescence from simulated elementary events. If the simulation assumes constant release current, then a successful reconstruction of the experimental global fluorescence will constitute a positive test of this property. Since spatial homogeneity is not assumed, the approach avoids the problems of the whole-cell removal calculation stated in the last paragraph.

The hypothesis is that the whole-cell fluorescence signal (dashed line in Fig. 6A) results from superposition of elementary fluorescence events like the one simulated in Fig. 5. The procedure, described in Methods, simply sums events, spanning the possible ranges of three uncontrolled variables of known distribution: event starting time, duration and location relative to scanning line. The variable duration of elementary release events was taken into account by using the average of elementary release currents, eqn (A2). The simulation process described in the preceding section was then applied with this current to calculate the elementary fluorescence ‘object’. Global fluorescence was constructed as summation of scans of this object, placed at multiple equally spaced locations relative to the scanning line. Finally, the temporal profile of this fluorescence was convolved with the known distribution of latencies L(t).

The resulting time course is plotted as the continuous trace in Fig. 6A. The agreement is excellent. In sum, the cell-averaged fluorescence signal in partially reprimed fibres can be approximated by summation of embers, produced by release events of constant current. The results and analyses are consistent with a constant release current but do not rule out some decay of current during the source open time.

Ca²⁺ release of a fully polarized cell

An additional question is posed by the record represented in Fig. 6B by the dotted trace. This is the release flux at −20 mV, derived from global measurements in a fully polarized fibre and scaled to match the peaks (from Fig. 4B in Shirokova et al. 1996). Clearly the decay is faster than in the other records, and the difference is not the consequence of a trivial voltage shift, as global release obtained in similar experiments at −30 or −10 mV (op. cit.) was also much faster.

This discrepancy suggests that the partial inactivation imposed to isolate events alters the kinetics of the response. This much was demonstrated for globally determined Ca²⁺ release in frog muscle by Brum et al. (2003), who argued that the lower spatial and temporal density of elementary events, produced by design by the imposed inactivation, may alter interactions among channels. For instance, in fully primed cells Ca²⁺ from multiple open channels could act on the cytosolic side to increase channel inactivation. Or cause substantial depletion, which could have multiple effects from the luminal side. This could be true in mammalian muscle as well. Finally, it is still possible that Ca²⁺ sparks, never seen under low voltage stimulation or partial repriming, have a greater role in fully polarized cells.

In conclusion, while the whole-cell function of Ca²⁺ release can be qualitatively reproduced by superposition of the elementary events (embers) described here, the failure to account quantitatively for the fast kinetic features of Ca²⁺ release indicates that there must be modifications in the elementary events, presumably brought about by interactions among channels, when they activate at high density during the physiological response.

Comparison with Ca²⁺ release in amphibians

The present conclusions add to a body of evidence of functional differences in Ca²⁺ release control between mammals and amphibians. At the global level, the time course of cytosolic [Ca²⁺] elicited by pulse depolarization appears to have a marked peak in the frog, which is minor in the rat. Correspondingly the release flux waveform derived from the global records has in the frog a faster decay leading to a relatively lower steady level, and the ratio peak/steady flux is strongly voltage dependent. At the local level, the Ca²⁺ release unit, which in the frog consists of multiple channels (González et al. 2000b) perhaps in variable numbers (Schneider, 1999), is now shown to be different as well, apparently involving a single channel in the rat.

Our inability to demonstrate Ca²⁺ sparks under voltage stimulation might still reflect the experimental difficulty of working on these smaller and delicate cells (an explanation suggested by Hollingworth et al. 1996, to account for the differences in global Ca²⁺ transients under voltage clamp). It seems more likely, however, that the absence of sparks reflects the different molecular endowment and supramolecular assembly of Ca²⁺ release channels in the rat (Felder & Franzini-Armstrong, 2002). In view of the present results, Ca²⁺ sparks and the large, voltage-dependent peak of Ca²⁺ release in the frog can be largely attributed to the β isoform channels, arranged in parajunctional clusters. The mammal, with its single isoform and junctional-only channel clusters, may be incapable of generating Ca²⁺ sparks under pulse depolarization. If, following conventional wisdom, one took Ca²⁺ sparks to represent the operation of CICR, then the failure of sparks to appear under voltage clamp depolarization would confirm the evidence from global measurements of Ca²⁺ release (Shirokova et al. 1996) that CICR contributes little, or not at all. This is also consistent with the striking differences between activation of Ca²⁺ release by caffeine (understood to operate largely through CICR) and membrane depolarization (Lamb et al. 2001).

Ca²⁺ sparks of rat muscle

In spite of the present results, muscle fibres of rodents can produce sparks under certain conditions. That they occur spontaneously in cells with permeabilized plasmalemma and T tubules suggests that their production is normally inhibited by a molecule or structure related to T tubules, which is altered or removed in the permeabilized cells (Zhou et al. 2003b). A similar conclusion was reached in myotubes of primary murine cultures, where the production of Ca²⁺ sparks was segregated to regions of the cell that did not release Ca²⁺ in response to voltage, that is, not yet having the normal signalling interactions between T tubule and SR (Shirokova et al. 1999).

An additional insight comes from the fact that Ca²⁺ sparks in the rat are best recorded at cytosolic [Mg²⁺] of 2 mm (Kirsch et al. 2001; Zhou et al. 2003a), a concentration that should saturate the ‘Ca²⁺-activation site’ of release channels (e.g. Laver et al. 1997). This suggests that mammalian Ca²⁺ sparks may reflect an entirely different mechanism of channel coupling, perhaps unrelated to CICR, and is consistent with their major morphological differences with the Ca²⁺ sparks of frog muscle (Zhou et al. 2003a). Although the present results suggest that Ca²⁺ sparks do not participate in physiological release of rat muscle, it is still possible that they do so, given the kinetic discrepancies described above between release in fully and partially reprimed cells.

There are teleological reasons to expect a locally lower flux in mammalian muscle. Indeed in mammals the transverse tubules and triadic junctions are closer to the functional target of the released Ca²⁺– troponin C in the areas of filament overlap. As suggested by Dr Elizabeth Stephenson (cited by Shirokova et al. 1996) this diffusional advantage should make it possible to produce the contractile signal without the high local flux of the frog, and without the multiion coupling mechanisms needed to achieve it. A lower release flux would have many benefits, including faster rise and dissipation of [Ca²⁺] near the physiological target, improved stability of the release mechanism and a less demanding Ca²⁺ retrieval process.

Appendix

The goal of this appendix is to calculate an average time course of the elementary Ca²⁺ release current in two cases. Elementary event current is assumed to have constant amplitude I and variable duration u. In the first, simplest case, u has a flat distribution between 0 and the duration of the pulse, T = 400 ms.

Let U represent a uniform random variable on the interval [0, T]. Its probability density function (the probability p(u) that U∈[u,u+ du]) is:

With these definitions, the elementary current, a pulse of random duration U, is i(U,t).

It can be represented as i(U,t) =IH(U−t) H(t), where H is the Heaviside step function:

The average time course of the elementary current is the expected value of i:

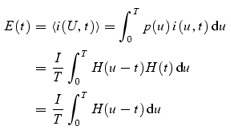The last integral can be calculated through the change of variable z = u – t, du = dz, as:

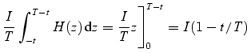This is a ‘triangular’ current that has value I at time 0 and 0 at time T, represented by trace d in the inset of Fig. 6B.

This average can be generalized for the case, physically more plausible, in which the distribution of event durations is not uniform, but a decaying exponential of time constant τ in [0,T]. In this case

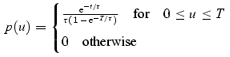Hence,

which with the change of variables z = u – t becomes:

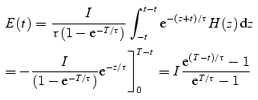Equation (A2) is used in the reconstructions of fluorescence and release flux illustrated in Fig. 6.