Activation of single heteromeric GABA_A receptor ion channels by full and partial agonists

Abstract

The linkage between agonist binding and the activation of a GABA_A receptor ion channel is yet to be resolved. This aspect was examined on human recombinant α1β2γ2S GABA_A receptors expressed in human embryonic kidney cells using the following series of receptor agonists: GABA, isoguvacine, 4,5,6,7-tetrahydroisoxazolo[5,4-c]pyridin-3-ol (THIP), isonipecotic acid, piperidine-4-sulphonic acid (P4S), imidazole-4-acetic acid (IAA), 5-(4-piperidyl)-3-isothiazolol (thio-4-PIOL) and 5-(4-piperidyl)-3-isoxazolol (4-PIOL). Whole-cell concentration–response curves enabled the agonists to be categorized into four classes based upon their maximum responses. Single channel analyses revealed that the channel conductance of 25–27 pS was unaffected by the agonists. However, two open states were resolved from the open period distributions with mean open times reduced 5-fold by the weakest partial agonists. Using saturating agonist concentrations, estimates of the channel shutting rate, α, ranged from 200 to 600 s⁻¹. The shut period distributions were described by three or four components and for the weakest partial agonists, the interburst shut periods increased whilst the mean burst durations and longest burst lengths were reduced relative to the full agonists. From the burst analyses, the opening rates for channel activation, β, and the total dissociation rates, k₋₁, for the agonists leaving the receptor were estimated. The agonist efficacies were larger for the full agonists (E ∼7−9) compared to the weak partial agonists (∼0.4–0.6). Overall, changes in agonist efficacy largely determined the different agonist profiles with contributions from the agonist affinities and the degree of receptor desensitization. From this we conclude that GABA_A receptor activation does not occur in a switch-like manner since the agonist recognition sites are flexible, accommodating diverse agonist structures which differentially influence the opening and shutting rates of the ion channel.

The γ-aminobutyric acid type A (GABA_A) receptor family is a major group of proteins in the central nervous system (CNS) whose main function is to enable neurones to swiftly and reproducibly control their excitability (Moss & Smart, 2001). This key role is reflected by the widespread distribution of these receptors throughout the brain and by their importance as targets for therapeutic agents (Sieghart, 1995; Sieghart & Sperk, 2002). Exogenous ligands can interact with GABA_A receptors at various loci, for example by binding at one of many different sites on the external domain of the receptor to allosterically modify receptor function, by directly binding to residues within the ion channel lumen, or by competing with the natural transmitter, GABA, for its recognition site (Sieghart, 1995; Rabow et al. 1996; Korpi et al. 2002).

Although the binding sites for many of the allosteric ligands that can affect GABA_A receptor function are mostly unresolved, the molecular determinants that form the boundaries and key interacting surfaces for the GABA binding site are increasingly being unravelled (Sigel et al. 1992; Amin & Weiss, 1993; Boileau et al. 1999; Wagner & Czajkowski, 2001; Boileau et al. 2002). Similarly, those external domains of the GABA_A receptor that are instrumental in linking the binding of GABA to the receptor with the activation of the ion channel are, at least in outline, becoming clearer (Horenstein et al. 2001; Scheller & Forman, 2002; Kash et al. 2003).

However, what is unclear is the impact the agonist molecule has on the activation, at the single channel level, of a largely homogeneous GABA_A receptor population. In particular, how does receptor activation correspond to variations in agonist affinity and efficacy? This question forms the basis of the present study, which examines the effects of GABA, and a range of GABA_A receptor agonists with variable affinities and efficacies, to deduce which kinetic parameters are changing at the single channel level to affect overall activation of the GABA_A receptor.

Methods

cDNA constructs

The human GABA_A receptor α1 and β2 subunit cDNAs were cloned into the pCDM8 vector, and the γ2 subunit cDNA was cloned into the pcDNAI/Amp vector as previously described (Hadingham et al. 1993a,b).

Cell culture and electroporation

Human embryonic kidney (HEK) cells were cultured as previously described (Wooltorton et al. 1997). HEK cells were plated onto poly l-lysine coated glass coverslips and transfected using a calcium phosphate protocol. DNA for the GABA_A receptor subunits and enhanced green fluorescent protein (pEGFP-C1) were present in equal amounts (0.5 μg each per culture dish). The DNA solutions were mixed with 340 mm CaCl₂ before the precipitate was formed by gently mixing the DNA–CaCl₂ solution with an equal volume of double-strength Hanks' balanced salt solution (280 mm NaCl, 2.8 mm Na₂HPO₄, 50 mm Hepes; pH 7.2) followed by a 20 min incubation at room temperature. The DNA–calcium phosphate suspension was added to the HEK cells with the transfection proceeding overnight. Cells were used for electrophysiological recording 18–72 h after transfection.

Patch clamp electrophysiology

GABA-activated membrane currents and single channel currents were recorded using whole-cell or outside-out patch clamp techniques from single HEK cells with a List EPC7 amplifier. Patch pipettes (resistance 3–5 MΩ for whole-cell and 10–15 MΩ for single channels) were filled with a solution containing (mm): 120 KCl, 1 MgCl₂, 11 EGTA, 30 KOH, 10 Hepes, 1 CaCl₂, and 2 adenosine triphosphate; pH 7.11. The cells were continuously perfused with Krebs solution containing (mm): 140 NaCl, 4.7 KCl, 1.2 MgCl₂, 2.52 CaCl₂, 11 glucose and 5 Hepes; pH 7.4. Membrane currents were filtered at 2 kHz (single channels) or 5 kHz (whole-cell currents; –3dB, 8 pole Bessel, 48 dB octave⁻¹) and recorded on a DTR-1201 digital tape-recorder prior to A/D conversion via a Digidata 1320A (Axon Instuments) and final off-line analysis with a PC Pentium III processor (Viglen/Dell). Individual single channel currents were analysed with Strathclyde electrophysiology software (John Dempster, WinEDR ver 2.3.8). Any change exceeding 10% in the membrane conductance and/or series resistance resulted in cessation of the recording. For the whole-cell recordings, series resistance compensation to approximately 50% was achieved.

Analysis of whole-cell current data: receptor model

The amplitudes of membrane currents activated by GABA and the analogues (I) were determined at −50 mV holding potential. The GABA/analogue concentration–response relationships were constructed by measuring the GABA/analogue currents, which were normalized to the response induced by a maximal, saturating concentration of GABA (3000 μm) in control Krebs solution (I_max) and subsequently fitted initially with the Hill equation:

where EC₅₀ represents the concentration of the agonist ([A]) inducing 50% of the maximal current evoked by a saturating concentration of the agonist and n is the Hill coefficient.

To provide a physically plausible mechanism to describe the whole-cell currents activated by GABA and the analogues, the following linear receptor model, based upon the scheme of Del Castillo & Katz (1957), was devised:

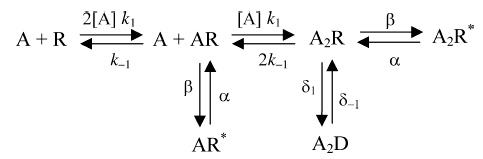where A represents the GABA_A receptor agonist and R the receptor, with forward and backward rate constants for binding and unbinding of k₁ and k₋₁, and β and α are rate constants for channel opening and shutting with active conducting forms of the receptor represented by AR* and A₂R*. The receptor can also access desensitized states depicted by D, with entry and exit rate constants of δ₁ and δ₋₁. Given the rarity of what might be considered as monoliganded receptor openings (see Results and Discussion), the AR* state was discounted from further analysis and consideration. Under such conditions (ignoring AR*), the function that describes this receptor model is:

where K represents the agonist dissociation constant (k₋₁/k₁) for dissociation from the receptor (both AR and A₂R forms), E represents efficacy (β/α) and D represents the desensitization conformation constant (δ₁/δ₋₁). Note for this form of the state function, in order to reduce the number of determined variables, the agonists are assumed to bind independently to equivalent binding sites on the receptor with equal rates of association and dissociation. Allowing cooperative agonist binding to the receptor does not alter the conclusions of this study (data not shown). The general case of eqn (2), describing ligand binding to multiple sites on the receptor, which includes a single desensitized state, was used to fit the GABA/analogue concentration–response relationships. This general form is given by:

where n signifies the number of ligand binding sites, and as [A]→∞, P_open→P_open,max, which is given by E/(1 + E + D). For the non-linear least squares data fitting procedure, E was accepted from the single channel measurements and deduced to be unaffected by desensitization (see Microscopic rate constants, below). These values were therefore fixed allowing the other parameter variables to free-run during fitting. The estimates of K and D that are derived in this manner will, however, depend on the accurate description of the whole-cell currents and these can be affected by fast desensitization. To obviate this, agonists can be rapidly applied to ensure near-accurate peak currents are obtained, but despite even the fastest application methods, one cannot completely discount the impact of even faster desensitization on the membrane current profiles. In our measurements, rapid desensitization could affect the estimates of K and D for the full agonists, but will be less important for the partial agonists where rates of desensitization are apparently much slower.

To assess the accuracy of the determined K and D values from the concentration–response curves, we attempted to reproduce the agonist-activated current profiles using two simulation methods. The first relied on numerically integrating the differential rate equations for the receptor model using a Runge-Kutta routine (ModelMaker ver. 3), and largely adopting the single channel estimates of β and α. The values of k₁, k₋₁, δ₁ and δ₋₁ were empirically adjusted until the theoretical currents were similar to their experimental counterparts. The robustness of this approach was assessed for the agonists, GABA, THIP, P4S and 4-PIOL, which are representatives of agonists in each of the groups I–IV (see Results). The second relied on a Q matrix simulation of the receptor model using the program ‘Scalcs’ (available from D. Colquhoun, http://www.ucl.ac.uk/pharmacology/dc.html). Both approaches allowed similar estimates of rate constants for agonist association and dissociation, as well as entry into and exit from desensitization. The derived constants of K and D corresponded well with those obtained using eqn (3).

Single-channel analysis

Single GABA channel currents were recorded in excised outside-out membrane patches, at −70 mV holding potential, on the condition that there appeared to be only one active channel, or the number of multiple channel openings never exceeded 2% of all detected openings. Stored prefiltered channel data were digitized at 20 kHz before analysis and a fixed time resolution based on the dead time of the system was set at 89 μs. The analysis of the single channel current amplitudes was performed by fitting Gaussian components to the amplitude distributions that defined the mean current, standard deviation and the total area of the component using a non-linear least-squares routine. The single-channel conductance was calculated from the mean unitary current, determined from the Gaussian curve fits, and the difference between the patch potential and GABA response reversal potential. Individual open and shut durations were measured using a 50% threshold cursor applied to the main single-channel current amplitude in each patch. The transition detection of open and shut events was then used to form an idealized record of the digitized data. The duration of events that were included in the analysis was not less than 200 μs (set at 1.3 times the filter rise time) before fitting the dwell time histograms. Frequency distributions were constructed from the measured individual open and shut durations and analysed by fitting a mixture of exponentials, defined in the function y(t) as:

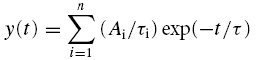where A_i is the area of the ith component to the distribution and τ_i represents the corresponding time constant. Using a Levenberg-Marquardt non-linear least-squares routine the area representing the individual exponential components, the relative time constants and standard errors of these parameters were determined. An F test was used to determine the optimal number of exponential components required to fit each individual dwell time histogram. The burst length analyses relied on determining a critical shut time (τ_crit); thus any series of open and shut periods where the shut periods do not exceed τ_crit were deemed to be contained in a single burst event (Colquhoun & Sakmann, 1985). For most of the agonists the critical shut time was determined between the shut time constants, τ_C2 and τ_C3 (see Results for rationale) from:

However, for the weakest agonists, thio-4-PIOL and 4-PIOL, bursts of activity usually consisted of single openings so τ_crit values for these compounds were calculated as three times the shortest intraburst closure (τ_C1). Inspection of the data (including burst lengths and number of openings per burst) suggested this to be a satisfactory margin to accurately reflect the activity of these weak partial agonists (see Discussion for further explanation). A correction for missed events was performed mostly according to the methods of Colquhoun & Sakmann (1985). Essentially, we considered that most open events were successfully detected and so concentrated on the likelihood that very short closures, particularly in the long bursts, were possibly undetected and the consequences this may have on the data analysis. The mean duration of closures within bursts was calculated from the total shut time within bursts (< t_crit)/total number of shut events with durations less than the defined t_crit for each patch. The true mean number of shut periods that occur during a burst (n_bs) was estimated as the total number of shut events (with durations < t_crit)/the total number of bursts (Colquhoun & Sakmann, 1985) and subsequently applied to eqn (7).

Number of active channels in a patch

One major problem when analysing single channels is the determination of the number of active channels in the patch (Colquhoun & Hawkes, 1990). When this is greater than 1, it will affect the accurate determination of long shut periods that arise between bursts of channel activity. To estimate the number of active channels per patch, we assessed the extent of simultaneous channel activation by agonists. Where multiple channel activation accounted for more than 2% of the total currents measured in one recording, the patch was rejected. Alternatively, we also determined the open probabilities (P_O) between patches that possessed, ostensibly, only one active channel and those that clearly had two or more channels. In these examples, the P_O values were not markedly dissimilar for the ‘one channel patches’ whereas those patches displaying multiple channel activation produced considerable variation in the P_O determinations.

Microscopic rate constants

The microscopic rate constants, α, β and k₋₁ in the linear receptor model, were calculated from the burst analyses. Estimates of the brief shut periods within a burst and the number of openings per burst were used to derive approximations for the channel opening rate constant, β (Colquhoun & Sakmann, 1985; Hatton et al. 2003). In essence, by adopting a scheme such as the receptor model, the brief shut periods of the channel during a burst are assumed to reflect a predominant residence in the A₂R state. The mean length of these shut periods (τ_BS, typified by τ_C1, see Results) will therefore be given by:

For this we have not unreasonably assumed that the two agonist binding sites are independent and equivalent and that dissociation from the fully diliganded state, A₂R, will be 2k₋₁, considered as a total dissociation rate. The mean number of brief shut periods (n_BS) per burst will then be given by:

As previously indicated (Colquhoun & Sakmann, 1985), by estimating the time constant from the brief shut periods and the number of shut periods per burst, we can now estimate β and k₋₁. Given that β was estimated from the length and number of brief gaps within bursts we would not intuitively expect desensitization to play any role as entry into this state would invariably be accompanied by long shut periods. To this end, determination of β by substitution using eqns (6) and (7) confirms that δ₁ has no role in determining β. Moreover, the desensitized periods of channel activity were essentially removed from the single channel analysis when considering only the kinetic properties of discrete burst events by disregarding the long shut periods to prevent any corruption. This procedure can be validated by modelling fits to single channel data including desensitized states, or by simply excising the individual bursts for kinetic analyses. The fitted rate constants are quite similar when compared for either analytical approach (see Colquhoun et al. 2003). The shutting rate of the ion channel, α, was estimated from the reciprocal of the longest open time constant (τ_O2) determined from the open period distributions compiled after receptor activation by the highest concentrations of the agonists. Similar results were also obtained for the determination of α by using the longest open time within bursts.

Drugs and solutions

Drugs and solutions were rapidly applied to the HEK cells using a modified Y-tube positioned approximately 300 μm from the recorded cell. The response rise times were within 20–30 ms (Wooltorton et al. 1997). All drugs were dissolved in external Krebs solution, and if required, readjusted to pH 7.4 with 1 m NaOH. All drugs were synthesised in our laboratory (BF and PK-L), except for isoguvacine and IAA (Sigma).

Results

Activation of GABA_A receptors by agonists: whole cell current properties

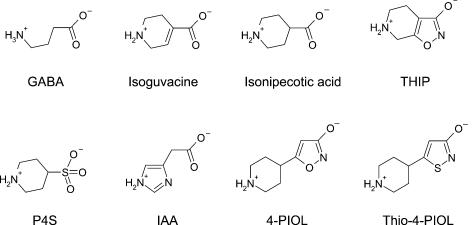
To assess the effects of activating GABA_A receptors by different agonists, α1β2γ2S subunit-containing receptors were expressed in HEK cells. Whole-cell currents were recorded following the rapid application of the agonists over the concentration range 0.1 μm to 3 mm. The Hill equation was used to fit agonist concentration–response curves providing estimates of the agonist EC₅₀ values (see Methods). Overall, eight ligands were selected for study, based upon variations in their potencies and maximal responses when activating GABA_A receptors (Kristiansen et al. 1991; Ebert et al. 1994, 2001). These included GABA, isoguvacine, 4,5,6,7-tetrahydroisoxazolo [5,4-c]pyridin-3-ol (THIP), isonipecotic acid, piperidine-4-sulphonic acid (P4S), imidazole-4-acetic acid (IAA), 5-(4-piperidyl)-3-isothiazolol (thio-4-PIOL) and 5-(4-piperidyl)-3-isoxazolol (4-PIOL) (Fig. 1).

Figure 1. Molecular structures of the full and partial GABA_A receptor agonists.

All the molecules have been aligned according to their structural similarities with the axis of the amino–carboxyl termini of the GABA molecule. The structures are shown with the locations of charge schematically indicated but it should be noted that in many structures, particularly those with unsaturated rings, these charges will be subject to delocalization.

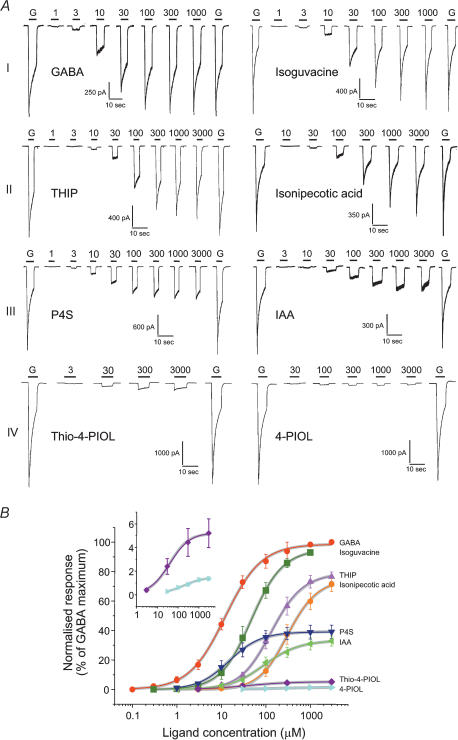
The agonist concentration–response curves were normalized within each HEK cell to control responses activated by a saturating concentration of GABA. This approach afforded a classification of the agonists into four distinct categories (arbitrarily assigned I–IV; Fig. 2A). The first class (I) included GABA and isoguvacine. Designating GABA as a full agonist, isoguvacine clearly behaved similarly, with a near identical maximum response but with less potency than GABA exhibiting a higher EC₅₀ value and a consequent parallel displacement in the concentration–response curve (Fig. 2B, Table 1). The second class (II) encompassed THIP and isonipecotic acid, which both displayed smaller relative maxima compared to GABA (70–80%) and also lower potencies with THIP being more potent than isonipecotic acid. Class III grouped P4S and IAA which exhibited much smaller relative maxima compared to GABA (30–40%); however, the potency for P4S was comparable to GABA, whilst the potency for IAA was lower compared to GABA (Table 1, Figs 2A, B). The fourth class (IV) brought together the two agonists, thio-4-PIOL and 4-PIOL. These agonists were difficult to study since the respective maxima of the concentration–response curves were markedly reduced to less than 10% compared to the GABA maximum response and both agonists displayed lower potencies compared to GABA (Table 1, Fig 2A, B). The low Hill slopes for thio-4-PIOL and 4-PIOL is notable but the Hill equation does not describe any physical scheme.

Figure 2. Characteristics of membrane currents activated by full and partial GABA_A receptor agonists and their associated concentration–response curves.

A, examples of whole-cell agonist-activated currents recorded from HEK cells transfected with α1β2γ2S GABA_A receptors. Different concentrations of agonists (numbers, μm) were applied for the durations indicated by the continuous lines. Prior to and after completing the concentration–response range for any agonist, responses to maximal concentrations of GABA (G, 3000 μm) were obtained for comparison. The agonists response profiles were grouped into four categories, I–IV (see text). B, GABA_A receptor agonist concentration–response curves were determined. The data are normalized with respect to the maximum GABA-activated currents (= 100%) measured in each expressing HEK cell and plotted against ligand concentration from n = 4–8 cells. In this and the proceeding figures, all data points represent the mean ± s.e.m. Theoretical curves were generated by the Hill equation and fitted to the weighted mean data points. The insert expands the concentration–response curves for thio-4-PIOL and 4-PIOL over 0–7% of the maximum response to GABA. The continuous grey lines are theoretical curves generated by eqn (3) using estimates of E, from the single channel measurements, that were fixed while values for D, K and n, were determined.

Table 1. Whole-cell current parameters for GABA_A receptor agonists obtained from fits with the Hill equation.

Agonist	Emax (%)	EC50 (μm)	nH	ECmin,mid,max (μm)
GABA	99 ± 0.9	12 ± 0.6	1.07 ± 0.04	1, 10, 1000
Isoguvacine	95 ± 0.7	48 ± 1.2	1.24 ± 0.03	3, 30, 1000
THIP	78 ± 0.7	134 ± 4	1.26 ± 0.04	10, 100, 3000
Isonipecotic acid	74 ± 1.7	311 ± 19	1.34 ± 0.08	30, 300, 3000
P4S	39 ± 0.3	15 ± 0.5	1.24 ± 0.04	3, 10, 3000
IAA	33 ± 0.7	93 ± 7	1.11 ± 0.08	10, 100, 3000
Thio-4-PIOL	5 ± 0.2	39 ± 7	0.88 ± 0.12	3, 30, 3000
4-PIOL	1.5 ± 0.1	173 ± 41	0.83 ± 0.13	30, 300, 3000

The data were obtained from 5 to 8 agonist concentration–response experiments on recombinant GABA_A α1β2γ2S receptors and mean values were subsequently fitted with curves generated by the Hill equation. E_max is the maximum agonist-induced response as a percentage of the maximum GABA response; the EC₅₀ represents the agonist potency, and n_H is the Hill slope. The agonist concentrations selected for the single channel experiments were approximated to the EC₁₀ (EC_min), EC₅₀ (EC_mid), and EC₁₀₀ (EC_max).

Although not an aim of this study, the profile of the agonist-induced whole-cell currents produced a further distinction in the apparent level of desensitization that was induced. At high concentrations, agonist currents induced by classes I and II, isoguvacine, THIP and isonipecotic acid, exhibited clear desensitization of the response in accord with GABA-activated responses (Fig. 2A). In contrast, the level of desensitization was apparently much smaller for P4S and IAA, although still discernible; however, for thio-4-PIOL and 4-PIOL, the activated currents showed virtually no desensitization, unless the receptor is driven rapidly into desensitized states by these agonists at rates that are faster than the application system (Fig. 2A).

The proposed receptor model (see Methods), based on the sequential binding of agonist to the receptor, could also account for the whole-cell agonist-activated currents on the α1β2γ2S receptor providing estimates of the dissociation constant, K, the gating constant, E, and the desensitization constant, D (data not shown). However, initial attempts to fit the whole-cell data with eqn (3) showed that with four variables many acceptable fits to the dose–response curve data could be achieved but with some variation in the values of D, E and K. This is not surprising since variations in agonist efficacy can produce not only changes in the maximum response but also lateral shifts in the whole-cell concentration–response curve without any change in the dissociation constant being required. The effect that a change in E has on the concentration–response curve will depend, to some extent, on the initial value of E (Colquhoun, 1998). For example, concentration–response curves for agonists evoking channel opening with high values of E (1000 or 10000) will only shift laterally (mimicking competitive-type inhibition) if E is reduced arbitrarily tenfold (to 100 or 1000). However, a similar tenfold reduction in E for a less efficacious agonist (say from E = 10 or 25 to 1 or 2.5) will produce a lateral shift with a clear reduction in the maximum response.

It is therefore probable that any alterations to the whole-cell currents, under conditions where receptor number is likely to stay constant, will reflect one or more changes to the channel open probability and the single channel current. To deduce how these parameters varied with the different agonist activation profiles, single channel studies were performed using outside-out patches. Furthermore, the single channel data were used to estimate the microscopic rate constants, α, β and k₋₁, for each agonist, which provided more accurate estimates of E for the receptor model fits to the agonist concentration–response curve data. The values of E were then constrained during the fitting procedure for the dose–response data to yield estimates of K and D (see Methods for limitations). This approach can then provide values of k₋₁, k₁, β and α that are consistent with both the single channel and dose–response curve data.

Single channel studies: consistency of the channel conductance

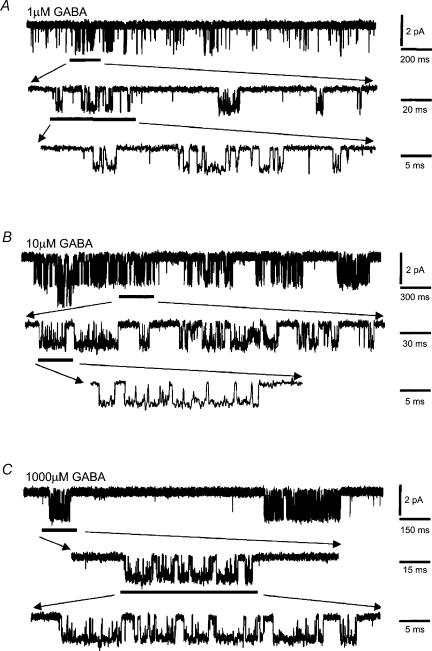
To analyse the properties of the single channels activated by the different agonists, three concentrations were selected from the respective concentration–response curves reflecting the different agonist potencies and maximal currents that were activated. The selected concentrations encompassed: an above threshold concentration designated as EC_min (near EC₁₀); a mid-range concentration defined as EC_mid (near the EC₅₀); and a saturating, ‘maximal’ concentration, EC_max (giving a response close to 100%; see Table 1 for the actual concentrations used for each agonist). For GABA, these concentrations were 1, 10 and 1000 μm. Using steady-state recording of single GABA channel currents from outside-out patches revealed openings to mostly one conductance level, referred to as the main state, at 26.7 ± 0.4 pS (n = 23; Fig. 3A). Although an occasional, less predominant lower conductance level may be observed at 13 ± 2 pS, the frequencies of the main and low conductance states were approximately >98% and <2% in all patches. The main conductance state was constant for channel currents activated by the range of agonists at all the concentrations used (Fig. 3B, mean for all agonists, at all concentrations, was 26.2 pS), and it was also independent of the patch holding potential over the range −80 mV to 40 mV (data shown for three examples in Fig. 3C).

Figure 3. Single channel conductances of GABA_A receptors activated by full and partial agonists.

A, examples of single channel openings activated by GABA (10 μm, upper trace), P4S (10 μm, middle trace) and 4-PIOL (300 μm, lower trace) in outside-out patches of HEK cells expressing α1β2γ2S GABA_A receptors at –70 mV. The dotted line indicates the main current level of open single channels for GABA, –1.9pA (27.1 pS); P4S, –1.85pA (26.4 pS); and 4-PIOL, –1.84pA (26.3 pS), respectively. B, 3D bar graph of the mean single channel conductances (γ) determined for each agonist at the different concentrations, EC_min (black bars), EC_mid (red bars) and EC_max (green bars). The conductances represent the means of 6–21 experiments. Standard errors of the mean are omitted for clarity and for all categories were less than ±1.2 pS. C, single channel current–voltage relationships for GABA (3 and 1000 μm), P4S (3 and 3000 μm) and 4-PIOL (30 and 3000 μm) determined over four patch potentials from n = 4 patches. The lines are individual linear regression fits to the data. D, examples of superimposed channel current amplitude histograms for the main open state activated by EC_mid concentrations of GABA, P4S, and 4-PIOL applied to the same patch. The data were fitted by single Gaussian distributions with similar peaks as indicated by the dotted line. The open probability of the channels (P_O) are 0.25, 0.12 and 0.09 for GABA, P4S and 4-PIOL, respectively. E, channel open probabilities following activation by GABA receptor agonists at three different concentrations (EC_min, EC_mid and EC_max) from 6 to 19 patches. Inset relates the maxima of the agonist-activated whole-cell currents (I_max) compared to the GABA response maximum (= 100%; data from Table 1) to the channel P_O values measured at the same concentrations. The symbols at 1.5%, 5%, 33%, 39%, 74%, 78%, 95% and 99% represent 4-PIOL, thio-4-PIOL, IAA, P4S, isonipecotic acid, THIP, isoguvacine and GABA, respectively.

In contrast to the single channel conductance, the probability that a channel is open (P_O) was dependent on the agonist type. The open probability was estimated from the area of the Gaussian curves used to fit the current amplitude histogram data (Fig. 3D). By varying the concentration of the agonist, the P_O was found to be higher for GABA and the full agonists than for the partial agonists (Fig. 3E). Moreover, the P_O values were also positively correlated with the maximum whole-cell current amplitudes (I_max) that were obtained using saturating concentrations of the agonists (Fig. 3E, insert). Taken together, these data suggest that the major difference between the activity profiles of the GABA_A receptor agonists does not rely on variations in channel conductance but probably depends upon the kinetics of channel gating. For the kinetic analyses of the single channel currents, only openings to and from the main state conductance were considered because openings to the low conductance state were quite infrequent, the relative proportions of main and low conductance states did not vary with the different GABA_A receptor agonists (data not shown), and there was no variation in the relative frequencies of the conductance states with the three agonist concentrations used.

Properties of the open states activated by the GABA_A receptor agonists

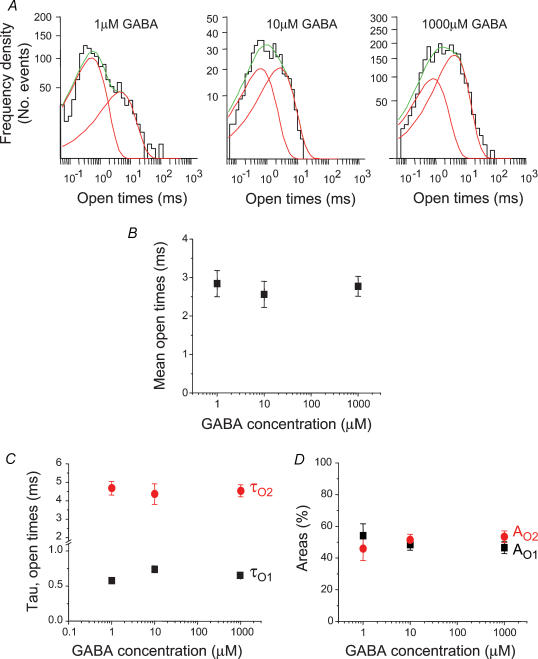
The open periods of the GABA ion channels were analysed at the three selected concentrations and the resulting distributions of all open periods were fitted mostly with two exponential probability density functions. Some of the open period frequency distributions were dominated by the short open period component at the lower GABA concentrations (EC_min), changing to an equal contribution from both components at the EC_mid concentration, before revealing an increasing contribution from the longer open period component at the higher GABA concentrations (EC_max, Fig. 4A). However, in many other patches, the frequencies of short and longer open periods were quite similar (Fig. 4D). Surprisingly, there was little change in the mean open times (τ_O,mean) with increasing GABA concentrations (Fig. 4B). This was reflected by the lack of change to the underlying time constants (τ_O1 and τ_O2, Fig. 4C). Although by comparing openings at different GABA concentrations it appeared that higher concentrations were associated with a greater frequency of the longer open periods, this was not a significant change when examined over all the patches (Fig. 4D). Thus raising the GABA concentration did not cause a fundamental change in the length of the openings and only in some patches were the relative frequencies of their occurrence affected such that at high GABA concentrations, the longer open periods appeared more frequent.

Figure 4. Open period analysis for GABA-activated ion channels.

A, examples of open period distributions for three different GABA concentrations (1 μm = EC_min; 10 μm = EC_mid; 1000 μm = EC_max). Two exponential probability density functions (grey lines) provided a best fit to each histogram and the sum of these are represented by the thick black lines. B, representation of the mean open periods for EC_min (n = 8), EC_mid (n = 9) and EC_max (n = 21) concentrations of GABA. C and D, relationships between the individual short (τ_O1) and long (τ_O2) open period time constants (C) and their respective areas (A_O1 and A_O2; D) with GABA concentration.

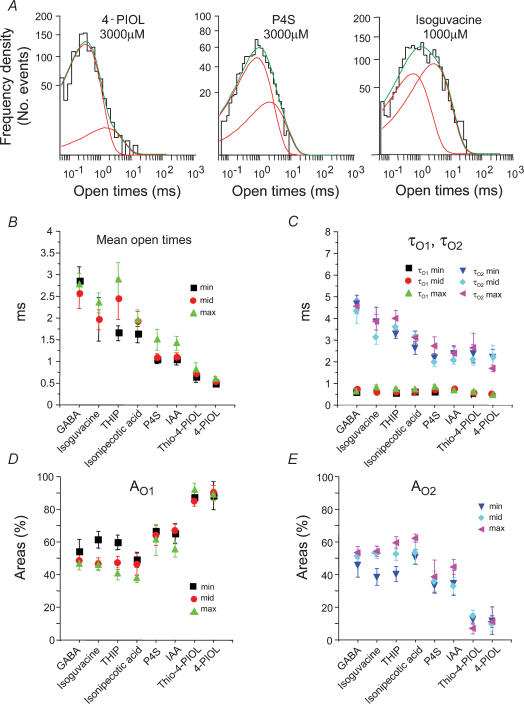
Largely similar results were obtained with the other seven GABA_A receptor agonists with all the open period distributions described by two exponential densities. However, inspection of the distributions indicated that the weaker agonists had a greater relative frequency of shorter openings compared to the full agonists (Fig. 5A). There are also several other differences between the agonists. Firstly, the mean open times were significantly dependent upon the identity of the agonist with the highest values obtained for those agonists producing the greatest maximal current responses at the whole-cell level, e.g. GABA and isoguvacine (Fig. 5B). In comparison, the smallest mean open times were observed for the weakest partial agonists, thio-4-PIOL and 4-PIOL (Fig. 5B). Although relatively independent of any changes in agonist concentration, the underlying open time constants and the associated areas for these components also varied between the different agonists. The short open time constant, τ_O1, was largely invariant between the different agonists; however, the long open time constant, τ_O2, was reduced by over 50% when comparing the full agonists, such as GABA and isoguvacine, with the weak partial agonists, thio-4-PIOL and 4-PIOL (Fig. 5C).

Figure 5. Open period analyses for GABA_A receptor agonists.

A, typical open period distributions for channels activated by 4-PIOL, P4S and isoguvacine. As in Fig. 4A, the sum (green line) of two exponentials (red lines) were required to fit the data. B, mean open times for single channels activated by the eight agonists at three different concentrations (EC_min: min; EC_mid: mid; and EC_max: max). C, D and E, individual open period time constants (τ_O1 and τ_O2; C) and their respective areas for short (A_O1; D) and long open periods (A_O2; E) for each of the three different agonist concentrations. Data were obtained from 6 to 19 patches.

Determination of the areas A_O1 and A_O2 (reflecting the frequencies of events) in the open period distributions for each agonist revealed that partial agonists caused a reduction in the frequency of long openings and a corresponding increase in the frequency of short openings when compared to the full agonists (Fig. 5D and E). This ranged for a potent agonist, such as GABA, where approximately equal proportions of short or long openings occurred (50%), to the weak agonists thio-4-PIOL and 4-PIOL, where approximately 90% of the openings were designated as short openings (Fig. 5D and E). Taken together, the data for thio-4-PIOL and 4-PIOL might suggest that these agonists were activating mostly brief, perhaps monoliganded openings; however, the lack of any dependence of the relative areas on the agonist concentration suggests these brief states are more likely to be fully diliganded.

Single channel shut times and the GABA_A receptor agonists

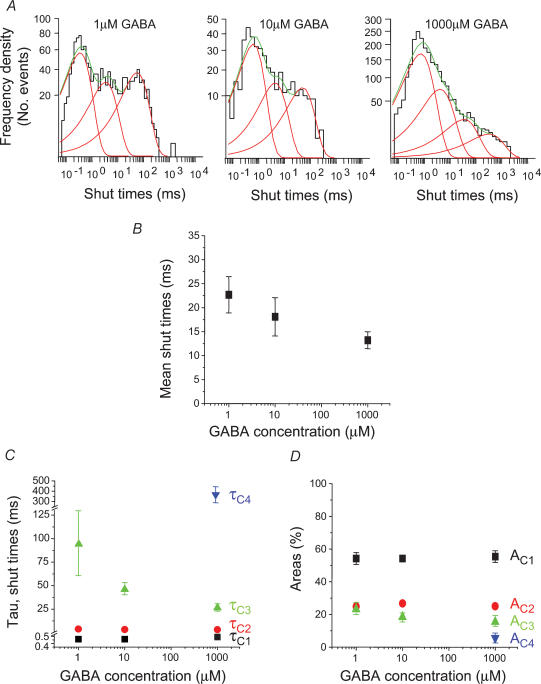
The shut periods provided information on the time the channel was dormant in shut and desensitized states and could also be used to define the bursting behaviour of the channels after activation by the different agonists. For GABA-activated channels, all patches required three exponential components to fit the distributions of all shut periods for the EC_min, EC_mid and EC_max concentrations (Fig. 6A). A fourth shut time was also resolved occasionally for EC_mid concentrations (2/8 patches) and more frequently for the EC_max concentration (14/21 patches), but it was never detected at the EC_min. As far as possible, patches were selected for shut time analyses where multiples of single channel currents were not observed; however, we cannot be absolutely sure that each patch contained only one active channel, and also at low concentrations of GABA, the number of shut events was usually quite small in contrast to the numbers evident with higher concentrations. As the GABA concentration increased, the mean shut time was slightly reduced (Fig. 6B). The underlying shut period frequency distributions for GABA possessed characteristic properties with no concentration dependence evident for the shorter shut periods defined by τ_C1 and τ_C2 (Fig. 6C), whilst for the longer shut periods, described by τ_C3 and τ_C4, both were concentration dependent with τ_C3 decreasing with higher GABA concentrations and τ_C4 only appearing at the higher agonist concentrations (Fig. 6C). The areas for the shortest shut period components (A_C1 and A_C2) were independent of GABA concentration whilst the area for the component described by τ_C3 (A_C3) was slightly reduced at high GABA concentrations probably due to the appearance of τ_C4 (Fig. 6D).

Figure 6. Shut period analysis for GABA-activated ion channels.

A, examples of single channel shut period distributions for GABA concentrations ranging from EC_min (1 μm) and EC_mid (10 μm), to EC_max (1000 μm). Three exponential probability density functions (grey lines) are required to fit the distributions for 1 μm and 10 μm GABA, whereas four exponentials are required for the shut period distributions obtained with the highest GABA concentration. The summated exponentials are represented by the thick black lines. B, representation of the mean shut times at EC_min (n = 8), EC_mid (n = 9) and EC_max (n = 21) GABA concentrations. C and D, individual shut period time constants (τ_C; C) and their respective areas (A_C; D). Note the appearance of τ_C4 and A_C4 only at the highest concentration of GABA.

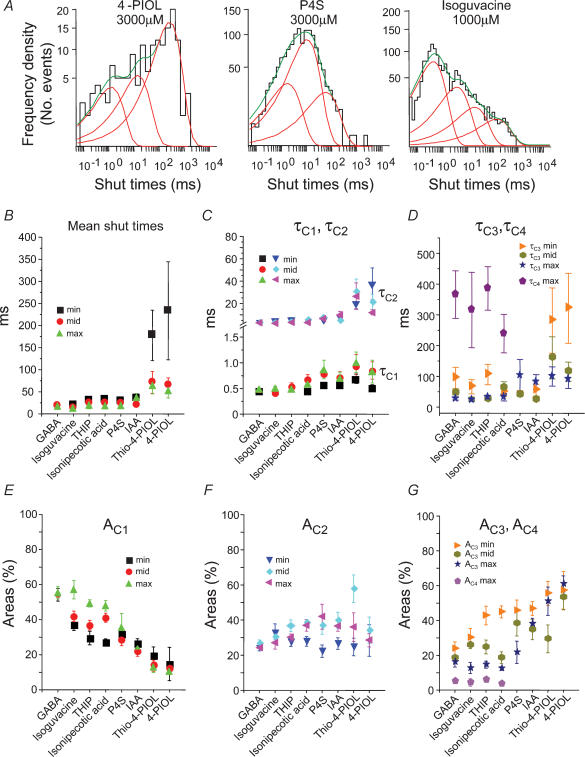
Similar to the open period analyses, the largest changes in the structure of the shut periods became evident when comparing the different agonists. As the activity profile of the agonists changed from full to partial, the distributions of all shut times revealed a marked increase in the frequencies of the long shut periods (Fig. 7A). The mean shut times were also increased for the partial agonists, particularly at low agonist concentrations (Fig. 7B). The underlying short shut period constants, τ_C1 and τ_C2, were mostly unchanged when compared to the values obtained for GABA, except for the weakest agonists thio-4-PIOL and 4-PIOL, where τ_C2 was increased (Fig. 7C). Similarly, τ_C3 was increased for the same two partial agonists whilst in contrast, τ_C4 appeared to decrease for the full agonists exhibiting lower potencies than GABA, eventually becoming unresolved for the weaker agonists (Fig. 7D). Overall, as the agonist profile changed from full to weak partial, only one longer shut period time constant, τ_C3, appeared to change, which increased for the weaker agonists. The lack of a resolvable τ_C4 for the partial agonists may explain part of the increase in τ_C3. It further suggests that the weaker agonists are spending more time in longer shut states, a feature reflected in the reduced whole-cell current amplitudes.

Figure 7. Shut period analyses for GABA_A receptor agonists.

A, shut period distributions for channels activated by 4-PIOL, P4S and isoguvacine. Shut periods were fitted with three exponential probability densities (red lines) for 4-PIOL and P4S, whereas the sum (green line) of four exponentials was required for the isoguvacine shut period distribution. B, mean shut times for the eight agonists at three different concentrations (EC_min; EC_mid; and EC_max). C and D, individual shut period time constants are shown for τ_C1 and τ_C2 (C); and τ_C3 and τ_C4 (D) at the different agonist concentrations. E, F and G, relative areas for the shut period time constants, A_C1 (E); A_C2 (F); and A_C3 and A_C4 (G). Data was taken from 6 to 19 patches.

The areas of the corresponding shut time components also varied between the agonists. Generally, A_C1 was reduced for the partial agonists compared to the full agonists (Fig. 7E) whereas A_C2 was largely unchanged (Fig. 7F). Similarly, A_C4 also remained mostly unaffected by the identity of the agonist, but A_C3 clearly increased as the agonist became less effective (Fig. 7G). Taken together, these data suggest that those agonists attaining smaller maximal whole-cell currents are residing for longer periods of time in shut states, typified not only by the increments in τ_C3 but also by increments in the areas describing the τ_C3 component with corresponding reductions in the area for the shortest shut times, A_C1. These changes would account for the greater mean shut times measured for the weaker agonists compared to the full agonists at each concentration (Fig. 7B).

Burst structures for the GABA_A receptor agonist-activated ion channels

To define bursts of channel activity a critical shut time (t_crit) was determined that signalled the cessation of individual bursts. We would expect the shut times between individual bursts of channel activity to be dependent upon agonist concentration but this may be complex. As agonist concentration increases, the interburst shut times should become smaller because channel opening becomes more frequent; however, at high agonist concentrations, when entry into desensitized states becomes more likely, these shut times may again lengthen. Thus if the two processes overlap, as seems likely, then the concentration dependence becomes obscure. In addition, long shut times will also depend upon the number of active channels in the isolated patch. The critical shut time was therefore determined between the shut time constants τ_C2 and τ_C3 since these were common to channels activated by all of the agonists and because τ_C1 and for the most part τ_C2 were independent of agonist concentration. This suggested that they described shut periods occurring during a single burst of channel activity, defined as the continued activation of a single receptor by retained agonist molecules until their dissociation. In contrast, τ_C3 was clearly concentration dependent in accord with a time constant describing shut periods that occur between individual bursts. The difference between τ_C3 and τ_C4 was not used to determine τ_crit since τ_C4 only appeared for high efficacy agonists in the highest concentrations and could not be reliably detected in all patches.

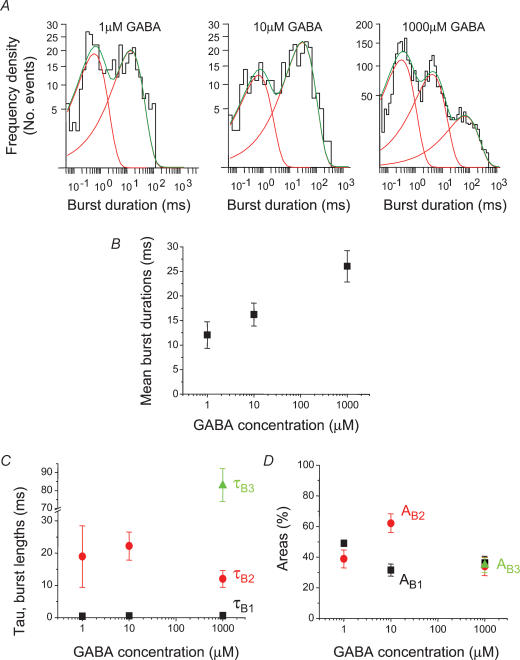
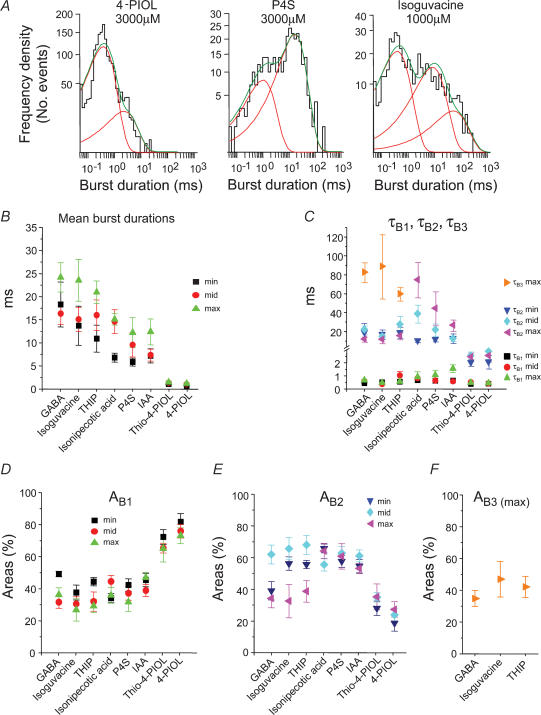
Examination of GABA channel activity revealed that the bursts had a complex structure. Even at low GABA concentrations (EC_min) rarely were bursts associated with single open events, instead presenting with multiple open and shut periods (Fig. 8A–C). The burst length distributions, at each GABA concentration, required multiexponential component fits. For 1 and 10 μm GABA, two exponentials were sufficient, but at 1 mm GABA, three exponential components were necessary in most patches (18/21, Fig. 9A). The third burst time constant (τ_B3) was never detected at lower concentrations of GABA. The mean burst length increased clearly with the GABA concentration (Fig. 9B) but the burst length distributions revealed that there was little change in the underlying burst length time constants, τ_B1 and τ_B2 (Fig. 9C). However, the relative areas of each of the burst components displayed some dependence on the GABA concentration. The area describing the shortest bursts (A_B1) was reduced, whereas the relative area for the long bursts (A_B2) was increased at 10 μm GABA. Eventually at the highest GABA concentration, a new longer burst component appeared for GABA (A_B3) which caused A_B2 to decrease (Fig. 9D).

Figure 8. Single channel burst activity for GABA-activated channels.

Examples of single channel burst activity of α1β2γ2S GABA_A receptors in outside-out patches from HEK cells activated by 1 μm (A); 10 μm (B) and 1000 μm (C) GABA at −70 mV. Burst activities are indicated at different time resolutions.

Figure 9. GABA-activated bursts at different concentrations.

A, examples of single channel burst length distributions for three GABA concentrations. Generally, two exponentials were required to fit the distributions for 1 μm and 10 μm GABA, whereas three exponentials have been fitted to the distribution for the highest concentration (1000 μm). B, mean burst lengths for GABA activated by EC_min (n = 8), EC_mid (n = 9) and EC_max (n = 21) concentrations. C and D, individual burst length time constants (τ_B; C) and their respective areas (A_B; D).

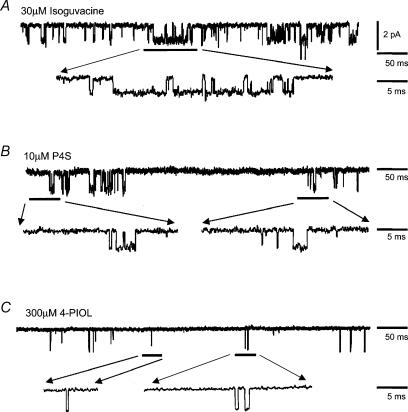
Burst activity of the ion channel was also observed with all of the other GABA_A receptor agonists. Individual bursts were again complex (Fig. 10A and B) with the exception of the weakest partial agonists (thio-4-PIOL and 4-PIOL), where burst structure was simplified, most often appearing as single openings (Fig. 10C). Analysing the frequency distributions of the burst lengths for each agonist revealed that usually two exponential components were required to describe the data (Fig. 11A). However, as for GABA-activated ion channels, those bursts activated by the maximum concentrations of the high efficacy agonists, isoguvacine and THIP, also required a third component to describe the longer bursts (Fig. 11A). These changes to the burst length distributions were also reflected in the mean burst lengths. For some of the agonists, the mean burst lengths were longer at the higher agonist concentrations and longer still for GABA, isoguvacine and THIP compared to the weak partial agonists, IAA, thio-4-PIOL and 4-PIOL (Fig. 11B).

Figure 10. Burst activity for the GABA_A receptor agonists.

Samples of single channel burst activity for α1β2γ2S GABA_A receptors activated by EC_mid concentrations of isoguvacine (30 μm; A); P4S (10 μm; B); and 4-PIOL (300 μm; C) at –70 mV. Bursts activities are shown at low and high time resolution.

Figure 11. Single channel burst kinetics for the GABA_A receptor agonists.

A, burst length distributions following receptor activation by 4-PIOL, P4S, and isoguvacine all at EC_max concentrations. Two exponentials have been fitted to the 4-PIOL and P4S burst distributions, whereas three exponentials are required for the isoguvacine burst distribution. B, mean burst lengths for the eight agonists at EC_min, EC_mid and EC_max concentrations. C–F, using three different agonist concentrations, individual burst length time constants (τ_B, C) are shown together with their relative areas A_B1 (D), A_B2 (E), and A_B3 (F). Data were obtained from 6 to 19 outside-out patches.

The underlying burst length time constants, τ_B1 and τ_B2, were unaffected by the agonist concentration for isoguvacine and THIP, and also for the weak partial agonists IAA, thio-4-PIOL and 4-PIOL (Fig. 11C). However, for those agonists of intermediate profile between the full and weaker partial agonists, e.g. isonipecotic acid and P4S, where τ_B3 was not detected, the values of τ_B2 were increased with the agonist concentration (Fig. 11C). Thus in changing the agonist activity profile from full to partial, the longest burst lengths, described variously by either τ_B3 or τ_B2, were progressively reduced (Fig. 11C), whilst τ_B1 remained unaltered.

A comparison of the relative areas for the burst components also revealed that for the partial agonists compared to the full agonists, the areas for τ_B1 were greater. For the full agonists, the relative areas for the τ_B2 components were generally larger compared to the partial agonists at EC_min and EC_mid, and at the high concentrations of the full agonists, τ_B3 appeared as a component at the expense of the area for τ_B2 (Fig. 11D–F). Taken together, with regard to the full agonists compared to the partial agonists, more bursts were occurring with longer burst lengths, and this change was accentuated by raising the agonist concentration.

The number of openings per burst

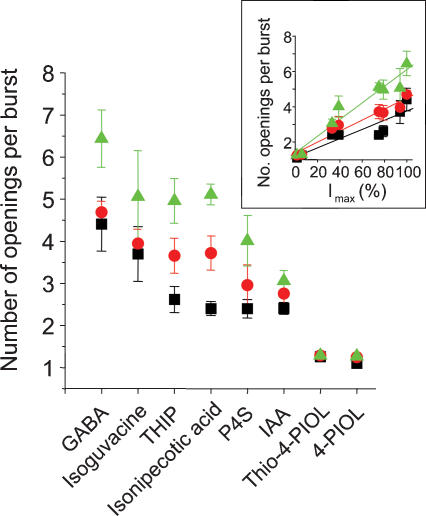
To gain further insight into the structure of the bursts induced by the GABA_A receptor agonists, the number of individual open periods that occurred in each burst was quantified for each agonist. The number of openings per burst was dependent on the agonist concentration with more openings evident at high agonist concentrations (Fig. 12). Moreover, more openings per burst occurred with the full agonists (6.4 ± 0.7 openings for 1000 μm GABA) compared to the partial agonists (1.3 ± 0.05 openings for 3000 μm thio-4-PIOL). The number of openings per burst was strongly correlated with the relative maximal whole-cell currents activated by the GABA_A receptor agonists (Fig. 12 inset).

Figure 12. Channel openings per burst.

The mean number of openings contained in single channel bursts following activation of α1β2γ2S GABA_A receptors by the agonists, GABA, isoguvacine, THIP, isonipecotic acid, P4S, IAA, thio-4-PIOL and 4-PIOL, at EC_min: black; EC_mid: red; and EC_max: green) concentrations. Data points are accrued from 6 to 21 experiments. Inset, relationship between I_max responses of GABA_A receptor agonists (data from Table 1) and the number of openings per burst. The symbols at 1.5%, 5%, 33%, 39%, 74%, 78%, 95% and 99% represent 4-PIOL, thio-4-PIOL, IAA, P4S, isonipecotic acid, THIP, isoguvacine and GABA, respectively.

Burst structure for agonist-activated channels: intraburst open periods

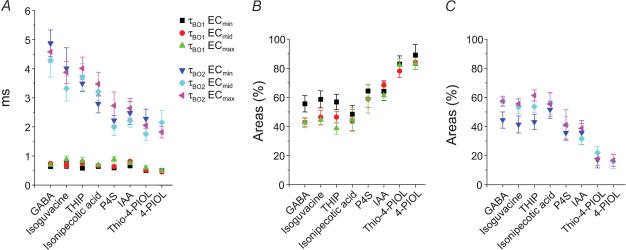
Given that the mean burst lengths and the number of openings per burst appeared to be dependent not only on the agonist concentration but on the type of agonist, the open periods that occur within individual bursts were analysed. In accord with the analyses for all of the open periods, those open periods within a burst were described by two exponential densities with time constants τ_BO1 and τ_BO2. The time constant for the short open period component was independent of concentration and the type of agonist used; however, the long open period time constant was reduced as the agonist profile changed from full to partial (Fig. 13A). The relative areas for short and long open periods within bursts varied depending upon the type of agonist activating the channels with the area for the short burst component, A_BO1, increasing for the partial agonists whilst A_BO2 was reduced (Fig. 13B). However, for the full agonists, the areas of the two components remained largely unaltered.

Figure 13. Open periods within bursts of channel activity.

Intraburst open period time constants (τ_BO, A) and their respective areas, A_BO1 (B) and A_BO2 (C) are shown for all the agonists at EC_min, EC_mid and EC_max concentrations. Data were obtained from 6 to 19 patches.

Discussion

The activation of the GABA_A receptor leads to rapid channel opening and the transmembrane flux of Cl⁻ ions. The efficacy of an agonist, following receptor activation, will depend essentially on the density of ion flux through the channel. In principle, larger responses will naturally follow if the channel resides in open states for a longer period of time, if the channel opens more frequently, and/or if the channel can adopt a larger single channel conductance when activated by particular agonists. The effectiveness of an agonist in causing channel activation will depend on multiple factors, including the agonist concentration around the receptors; the structure of the agonist, determining its geometric fit into the binding site pocket and engagement with key residues to initiate ion channel opening; and the ability of the agonist to induce entry of the channel into desensitized states. By examining how various agonists regulate GABA_A receptor activity at the single channel level, we were able to deduce the likely reasons why certain agonists are more effective at initiating responses compared to others.

Macroscopic current properties of full and partial agonists

On the basis of the concentration–response curves, the agonist profiles varied from the full agonists of GABA and isoguvacine, which differed in potency only, to the weakest partial agonists, thio-4-PIOL and 4-PIOL, which caused minimal activation of the receptor. The maximum responses evoked by all the agonists showed strong correlations with the individual channel open probabilities and the number of channel openings per burst. Overall, these results suggested that the interaction of the agonists with a single GABA_A receptor subtype induced the receptor to preferentially adopt different combinations of open, shut and desensitized states.

It is important to note that the shifts in the agonist concentration–response curves may be caused by changes in affinity, but this would not depress the dose–response maxima. By contrast, changes in agonist efficacy can induce curve shifts and alterations to the curve maxima and the latter would also be affected by the extent of desensitization. Thus, by obtaining estimates of E, K and D, the agonist concentration–response data may be described by theoretical curves, assuming the designated receptor model describing the data is reasonably accurate. However, even without further analysis we can conclude from a comparison of the dose–response curves that if a reduction in E alone explains the relative curve displacement and maximum response for a partial agonist, then the value of E must be low (<10). Otherwise, reductions in efficacy would simply cause a near parallel displacement of the curve and virtually no reduction in the maximum response. The second conclusion to be drawn is that a change in E alone will not account for the P4S curve since the maximum is depressed but the curve is also displaced leftwards in comparison to other more efficacious agonists, e.g. THIP and isonipecotic acid.

Agonist-induced differences at the single channel level: conductance

The single channel conductance will influence the size of the agonist responses. However, in our study the vast majority of single channel open events proceeded to a conductance level of 25–27 pS, in accord with previous determinations for recombinant αβγ subunit-containing and many neuronal GABA_A receptors (Jackson et al. 1982; Hamill et al. 1983; Mathers, 1985; Weiss et al. 1988; MacDonald et al. 1989; Smart, 1992; Angelotti & MacDonald, 1993). This conductance level was unaffected by the agonist or by variations in agonist concentrations, indicating that the channel conductance for the human α1β2γ2S isoform expressed in HEK cells is a constant parameter (cf. Eghbali et al. 1997, 2000). Earlier fluctuation analyses of GABA agonist-induced currents in spinal neurones also concluded that the channel conductance was unaltered by THIP, isoguvacine, IAA and P4S (Barker & Mathers, 1981), or by 4-PIOL (Kristiansen et al. 1995), when compared to GABA. However, in chick neurones, isoguvacine (and muscimol) preferentially activated subconductance states (Mistry & Hablitz, 1990), but this was not apparent in our experiments. Thus, the main changes to agonist affinity and efficacy must be derived from the kinetic properties of ion channel gating.

Open periods and the shutting rate of the channel

Analysis of the channel open times implied that two independent open states for the receptor could exist. These states may relate to the two agonist binding sites thought to reside at specific α–β subunit interfaces in the GABA_A receptor (Sigel et al. 1992; Amin & Weiss, 1993; Smith & Olsen, 1994; Tretter et al. 1997; Boileau et al. 1999; Hartvig et al. 2000; Baumann et al. 2001; Wagner & Czajkowski, 2001). Although the open time constants were independent of the agonist concentrations, the lower frequency and shortening of the ‘longest’ openings accounted for the reduced mean open times measured with the weaker agonists. This independence from the agonist concentration suggested that the two open states must be fully (di-) liganded and that monoliganded openings are relatively rare, supporting the receptor model proposed to explain the whole-cell current data. Such a model also predicted that at high agonist concentrations, the receptor would reside in a diliganded state, whereupon the longest openings (associated with τ_O2) would be observed. In this circumstance, the reciprocal of τ_O2 could provide an estimate of the ion channel shutting rate, α. For GABA and the other agonists, estimates of α ranged from 200 s⁻¹ to 600 s⁻¹ (Table 2), gradually increasing as the agonist profile changed from full to partial. These values proved similar to estimates used in other receptor models for GABA_A receptors (Twyman et al. 1990; Jones & Westbrook, 1995; Burkat et al. 2001). It is an interesting and possibly unexpected finding that the shutting rate is not a constant for the ion channel protein. The three-fold variation in α suggests that the channel is not simply closed in a switch-like manner, but is apparently sensitive to how it was activated by a particular agonist. This would suggest that even if a common sequence of conformational changes leads to channel activation (Kash et al. 2003; Miyazawa et al. 2003) this process is more flexible than realized hitherto.

Table 2. Rate constants and efficacies estimated for GABA_A receptor agonist-activated single channels.

Agonist	β (s−1)	α (s−1)	E	k−1 (s−1)	k1 (m−1 s−1)
GABA	1722	220	7.8	175	1.3 × 106
Isoguvacine	1951	223	8.7	271	0.71 × 106
THIP	1674	311	5.4	239	0.3 × 106
Isonipecotic acid	1363	321	4.3	189	0.15 × 106
P4S	862	368	2.4	147	1.9 × 106
IAA	968	417	2.3	238	0.3 × 106
Thio-4-PIOL	223	380	0.58	390	0.32 × 106
4-PIOL	256	592	0.43	483	0.03 × 106

The opening (β) and shutting (α) rate constants, together with efficacy (E) and the association (k₁) and dissociation (k₋₁) rates for agonist binding were determined as described in the Methods and Discussion.

Shut periods and burst structures

The shortest shut times were independent of agonist concentration whilst one of the longer shut times, τ_C3, was reduced with increasing concentration. This behaviour was expected, if the shortest shut times reflected closures within single bursts and the longer shut times represented shut periods between bursts. The longest shut time constant, τ_C4, was only resolved with the highest concentrations of relatively high efficacy agonists and may represent entry of the receptor into desensitized states. Although desensitization was seemingly absent for the weaker agonists at saturating concentrations and that τ_C4 was not resolved in their respective shut time distributions, we cannot exclude the possibility that weak agonists can drive the receptor into desensitized states which may be represented, in part, by τ_C3. The weaker agonists also reduced the number of short shut periods whilst increasing the number of longer shut periods between bursts thus causing the channel to open less frequently. The effect on the short shut times was surprising and suggested that within single bursts, the channel was not entering into as many short shut states. This may reflect the reduced burst length activated by these weak agonists and a reduction in the number of openings per burst leading to a reduction in the number of short shut periods. In addition, τ_C2 was increased for the weakest partial agonists (thio-4-PIOL and 4-PIOL) suggesting that this component was probably associated with shut periods between bursts. This was supported by estimating the number of openings per burst for thio-4-PIOL and 4-PIOL, which was close to one, indicating that the majority of bursts consisted of single openings with only 1 in 5–10 bursts containing shut periods. Taken together, the shut period analyses clearly indicated that the partial agonists induced a higher mean shut time for the GABA_A receptor compared to the full agonists.

The frequencies of the burst durations were largely independent of the agonist concentration; however, by changing the agonist profile from full to partial more short bursts occurred at the expense of the long bursts which most likely contributed to the reported small whole-cell currents activated by 4-PIOL in olfactory bulb neurones (Kristiansen et al. 1995). Whilst the open periods within bursts were independent of agonist concentration, for the weak partial agonists, not only were the longer open periods reduced, but their frequency was substantially reduced. Overall, for the partial agonists, bursts appeared less frequently with generally shorter durations, containing fewer numbers of channel openings and those openings tended to be briefer.

Channel opening rate and determining agonist efficacy

To determine the agonist efficacies, values for the opening and shutting rates of the ion channel were required. The opening rate constant, β, was determined from the (shortest) shut periods within a burst and the number of shut periods per burst (see Methods). Values for β ranged from 1700 s⁻¹ to 200 s⁻¹ and are unaffected by desensitization of the receptor. GABA, isoguvacine and THIP activated channels with the fastest opening rate, with isonipecotic acid, P4S and IAA being 40–50% slower, and thio-4-PIOL and 4-PIOL almost 90% slower (Table 2). This order of magnitude for β is similar to some previous estimates for GABA (Jones & Westbrook, 1995; Burkat et al. 2001) but lower values (approximately 10-fold) have also been reported (Twyman et al. 1990). Using the estimates of β and α, the efficacies for the full agonists, GABA and isoguvacine, were approximately 8 decreasing to 0.4 for the least efficacious agonists, overall a 20-fold change (Table 2). The dissociation rates for each agonist from the shut receptor (k₋₁) were also calculated from the burst analyses. These rates showed relatively slight variation, with GABA, P4S and isonipecotic acid exhibiting the slowest rates of 150−190 s⁻¹, and thio-4-PIOL and 4-PIOL the fastest, with k₋₁ of 390–480 s⁻¹. The other agonists exhibited quite similar dissociation rates of 240–270 s⁻¹ (Table 2). The increased prolonged occupancy of the receptor by agonists with fast association and slow dissociation rates may have promoted longer channel activations whilst the agonist was still bound to the receptor.

The estimates of E from the single channel data, together with consideration of the extent of receptor desensitization, were used with the receptor model to provide theoretical curves for the whole-cell current data. Essentially, the desensitization constant, D, determines the level of depression of the agonist concentration–response curves, with higher values increasing the depression of the maximum response. Thus for those agonists with the highest maxima (GABA, isoguvacine, THIP and isonipecotic acid), D ranged from 4 to 7, whilst for the weaker agonists (P4S, IAA, Thio-4-PIOL and 4-PIOL), D ranged from 7 to 50 (Table 3). The value of D is a ratio of δ₁/δ₋₁, and so no deduction regarding the rates of entry or exit from desensitization can be made from the value of D determined from the concentration–response curves. However, simulation of the agonist-activated currents using the receptor model allowed tentative estimations of the rate constants for desensitization, which are quite slow, with δ₁ approximately 1.6 s⁻¹ for GABA. From these simulations, it seems that entry into desensitization is at least 100-fold faster for GABA and the other full agonists compared to the weakest partial agonists typified by 4-PIOL. Moreover, exit from desensitization (δ₋₁) for the weakest partial agonists was estimated to be more than 1000-fold slower. These rates indicated that those agonists displaying the highest dose–response curve maxima also desensitized the receptor to a greater extent.

Table 3. Efficacies, dissociation and desensitization constants and slope factors obtained for full and partial GABA_A receptor agonists using the receptor model.

Agonist	E	D	K	n
GABA	7.8	5.3 ± 0.12	134 ± 20	1.09 ± 0.06
Isoguvacine	8.7	6.5 ± 0.09	381 ± 25	1.30 ± 0.03
THIP	5.4	5.7 ± 0.10	803 ± 86	1.33 ± 0.05
Isonipecotic acid	4.3	4.7 ± 0.16	1303 ± 215	1.47 ± 0.10
P4S	2.4	7.3 ± 0.05	78 ± 7	1.35 ± 0.05
IAA	2.3	9.1 ± 0.24	786 ± 194	1.15 ± 0.10
Thio-4-PIOL	0.58	18.1 ± 0.71	1221 ± 777	0.87 ± 0.13
4-PIOL	0.43	49.7 ± 3.3	20293 ± 17543	0.83 ± 0.13

The concentration-response data in Fig. 2B was fit using theoretical curves generated by the linear receptor activation mechanism. The estimates for E were fixed to provide estimates of K (μm), D and n in eqn (3) using a non-linear least squares analysis. Values are means ± s.e.m. for 5–8 experiments.

Agonist affinity for the receptor

The calculated dissociation rates (k₋₁) and the new values of the agonist dissociation constants provided from the dose–response curve analyses, enabled the estimation of the rates of association (k₁) for the agonists with the receptor. These association rates, apart from that for 4-PIOL (0.03 × 10⁶ m⁻¹ s⁻¹), which was comparatively slow, revealed no major trend with the type of agonist, with k₁ varying from 0.3 × 10⁶ to 1.9 × 10⁶ m⁻¹ s⁻¹ (Table 2). Slightly higher association rates were noted for GABA and P4S. The higher association rate for the ‘natural transmitter’ GABA might be expected and the high rate for P4S would explain the leftward shift in the dose–response curve when compared to all the other agonists (it is noteworthy that P4S has the lowest apparent dissociation constant, 78 μm). Given these association rates, the dissociation constants varied over several orders of magnitude from approximately 100 μm (for GABA and P4S) to 20 mm (for 4-PIOL), which would contribute to the relative positions of the dose–response curves along the abscissa. The estimates for K reveal that the agonist affinity is reduced almost 10-fold from GABA to isonipecotic acid, whilst affinity appears to double for P4S relative to GABA. For the remaining agonists, the affinities were reduced by approximately 6-fold, 9-fold and 151-fold for IAA, Thio-4-PIOL and 4-PIOL, respectively. Thus, to account for the positions of the concentration–response curves, E, D and K must vary between the agonists. Given that during the agonist application, the receptors will transition between many states, the accuracy of some of the estimates of D and K were assessed further by using the receptor model and the rate constant determinations to predict the profile of the agonist-activated currents. The rate constants in Tables 2 and 3 were used to initialize the model and then varied empirically to provide simulated currents matching the experimental responses. The resultant rate constants and current profiles demonstrate that the estimates of D and K, either from this method or obtained by curve fitting, are reasonably concordant (Table 4).

Table 4. Simulated membrane currents and rate constants for binding, desensitization and gating for selected GABA_A receptor agonists.

	GABA	THIP	P4S	4-PIOL

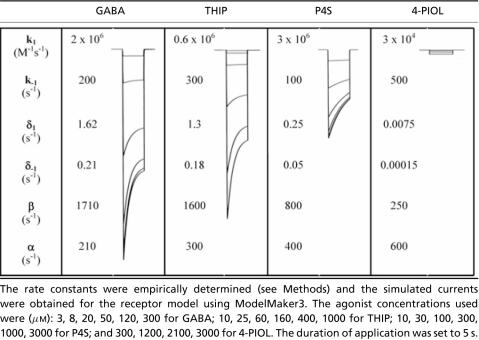
The rate constants were empirically determined (see Methods) and the simulated currents were obtained for the receptor model using ModelMaker3. The agonist concentrations used were (µM): 3, 8, 20, 50, 120, 300 for GABA; 10, 25, 60, 160, 400, 1000 for THIP; 10, 30, 100, 300, 1000, 3000 for P4S; and 300, 1200, 2100, 3000 for 4-PIOL. The duration of application was set to 5 s.

GABA_A receptor agonist structure: a determinant of function?

How do the agonist structures correlate with their ability to activate GABA_A receptor channels? The flexible GABA molecule can adopt multiple conformations, but to act as an agonist, the positive and negative charges must be separated by a maximal distance of approximately 5–6 Å (Kier & Truitt, 1970). This is achieved by adopting a trans conformation about the carbon backbone (Krogsgaard-Larsen, 1988; Pooler & Steward, 1988). Due to their ring structures, the other agonists used possess greater structural rigidity, with isoguvacine, THIP, isonipecotic acid, P4S and to some extent IAA possessing four atoms between the acidic moiety and the basic amino group. Interestingly, the high efficacy of THIP indicates that the distance between acidic and basic moieties may be comparable to that of GABA when residing in the binding site. In contrast, the weaker partial agonists, thio-4-PIOL and 4-PIOL, have six atoms separating the charge centres and this increased separation may be responsible for their poor efficacies. Molecular modelling of 4-PIOL and muscimol (Frølund et al. 2002) have indicated that the ‘acidic’ deprotonated 3-hydroxyisoxazole could interact with positively charged arginine side chains (e.g. R66 and R120) that may form part of the binding pocket in the α1 subunit (Westh-Hansen et al. 1999). However, if the amino groups for 4-PIOL and muscimol are aligned, the hydroxyisoxazole rings are not superimposed, indicating that the charge centres will occupy quite different spatial positions. Therefore for these agents to behave as agonists, the recognition site must be flexible and even quite cavenous. Such flexibility may cause the channel shutting rate, α, to become dependent upon the activating ligand, particularly if the binding site is differentially distorted during channel activation. The very similar structures of thio-4-PIOL and 4-PIOL suggest that they may adopt conformations which are energetically less favourable for binding when compared to the full agonists. This could slow their association with the receptor and certainly speed their dissociation, and even when bound, their interaction with residues in the binding site may be inefficient for the initiation of channel gating.

The different profiles of channel activation caused by the agonists could not be accurately assigned to differences in agonist affinity or efficacy from the dose–response curve data alone. The single channel analyses suggest that β is 7- to 9-fold higher and α is 2- to 3-fold lower for full compared to the partial agonists, providing clear differences in agonist efficacy. In addition, the agonist dissociation constants also varied, which revealed the following reciprocal order: P4S >GABA >Isoguvacine >IAA ≈ THIP >Thio-4-PIOL ≈ Isonepicotic acid >4-PIOL. This order does not concur with the ability of these ligands to act as full agonists. Thus prolonged residence at the agonist recognition site does not confer a full agonist profile. It therefore seems that the effectiveness of the full agonists largely resides in their high efficacies rather than the possession of high affinities. Overall, the variations in rate constants for channel opening and shutting indicates that the GABA receptor ion channel is not simply ‘tripping’ between two sets of rigidly fixed conformational states after agonist activation, but appears to be capable of adopting a spectrum of conformations that affect the channel kinetics but not the channel conductance.