Multiple mechanisms govern the dynamics of depression at neocortical synapses of young rats

Abstract

Synaptic transmission between pairs of excitatory neurones in layers V (N = 38) or IV (N = 6) of somatosensory cortex was examined in a parasagittal slice preparation obtained from young Wistar rats (14–18 days old). A combined experimental and theoretical approach reveals two characteristics of short-term synaptic depression. Firstly, as well as a release-dependent depression, there is a release-independent component that is evident in smaller postsynaptic responses even following failure to release transmitter. Secondly, recovery from depression is activity dependent and is faster at higher input frequencies. Frequency-dependent recovery is a Ca²⁺-dependent process and does not reflect an underlying augmentation. Frequency-dependent recovery and release-independent depression are correlated, such that at those connections with a large amount of release-independent depression, recovery from depression is faster. In addition, both are more pronounced in experiments performed at physiological temperatures. Simulations demonstrate that these homeostatic properties allow the transfer of rate information at all frequencies, essentially linearizing synaptic responses at high input frequencies.

Information transfer in neural networks is determined by the dynamics of synapses in response to sequences of presynaptic action potentials. Recordings from interconnected neurones reveal that synaptic transmission is indeed dynamic, i.e. synapses in the neocortex typically undergo activity-dependent changes in response to bursts of action potentials (Magleby, 1987; Thomson et al. 1993; Markram et al. 1997; O'Donovan & Rinzel, 1997; Reyes et al. 1998; Tarczy-Hornoch et al. 1998). Specifically, connections between neocortical pyramidal neurones often display a gradual decrease in postsynaptic response, a phenomenon known as synaptic depression.

However, the amplitudes of the postsynaptic response are determined not only by the input pattern, but also by the probabilistic nature of neurotransmitter release, which results in trial-to-trial fluctuations (Kuno, 1964; Jack et al. 1981; Korn et al. 1984). A quantal hypothesis for probabilistic synaptic transmission was developed for the frog neuromuscular junction (Del Castillo & Katz, 1954) and has later been extended to other preparations (reviewed in Redman, 1990). According to this hypothesis, the connection between two neurones is composed of several release sites that always contain at least one vesicle available for release. At the arrival of an action potential, each site releases at most one vesicle with a fixed probability, independent of the release of vesicles from other sites, and from preceding release at the same site (spatial and temporal independence). The postsynaptic response is proportional to the number of vesicles released.

At depressing synapses, it is thought that depletion of the releasable pool of vesicles (‘synaptic resource’) accounts for the reduced postsynaptic response during a burst, i.e. synaptic depression is release dependent. Particularly, in cases of failure to release transmitter during an individual trial, there is no vesicle depletion and therefore no reduction in availability of synaptic resources for subsequent release. This consideration indicates that synapses with low probability of release would be unable to reliably code presynaptic activity because based on vesicle depletion release would occur too infrequently to cause depression. Such a scenario would restrict information transfer related to presynaptic firing rate.

However, there is evidence that synaptic depression can also be release independent (Dobrunz et al. 1997; Thomson & Bannister, 1999; Brody & Yue, 2000; reviewed in Zucker & Regehr, 2002). Release-independent depression (RID) is observed if a decrease in the probability of release occurs even if the second synaptic response is preceded by a transmission failure. In contrast to the scenario above, such a mechanism would allow depression to occur even at synapses with low release probability and therefore would constitute a homeostatic mechanism potentially extending the range of information transfer considerably.

We therefore investigated these questions in a study where experimental observations were combined with the modelling of synaptic dynamics, since at this stage of investigation it is not possible to measure information transfer directly.

To gain a detailed understanding of the factors involved in governing depression and recovery from depression, we recorded from connected excitatory cell pairs in rat somatosensory cortex. This approach allows the delivery of precise presynaptic stimulus patterns and the measurement of the associated postsynaptic responses (EPSCs) under excellent signal-to-noise conditions. We investigated the synaptic dynamics by measuring both the depression caused by a burst of action potentials and the recovery gauged by an action potential delivered with a variable delay after the burst. By carefully quantifying depression, we found that at these connections, there is release-independent as well as release-dependent depression. In addition, at certain connections, recovery from depression is frequency dependent, the rate of which accelerates during periods of increased activity. We show that release-independent depression and frequency-dependent recovery are tightly correlated such that synapses, which significantly depress independently of vesicle depletion, also recover faster from depression under conditions of high frequency firing.

To match these experimental observations, we developed a model, which replicates both the average dynamics of neocortical synaptic transmission, as well as the fluctuations in synaptic release. The two properties of synaptic depression as well as frequency-dependent recovery from depression were incorporated into the model. Release-independent depression was implemented as a decrease in the probability of transmitter release to subsequent action potentials, which is independent of whether release actually occurred. Recovery from depression could be brought about by an activity-dependent decrease of the time constant of recovery from depression. Frequency-dependent recovery from depression has previously been observed at a number of invertebrate and vertebrate synapses (reviewed in Zucker & Regehr, 2002).

We show that these mechanisms enable a depressing synapse to transmit information about presynaptic firing rates, even at high input frequencies, and results in a synapse that can code rate information at all frequencies.

Methods

Slice preparation and whole-cell recording

Wistar rats, 14–18 days old, were killed by decapitation and parasagittal cortical slices were prepared as described in Simkus & Stricker (2002). The Department for Veterinary Affairs of the Canton of Zürich, Switzerland, approved the techniques used. Whole-cell recordings were made under visual control using infra-red differential interference contrast (IR-DIC) optics. The artificial cerebrospinal fluid (ACSF) contained (mm): NaCl, 125; KCl, 2.5; NaHCO₃, 25; NaH₂PO₄, 1.25; CaCl₂, 2.0; MgCl₂, 1.0; glucose, 25.0; gassed with 95% O₂ and 5% CO₂, pH 7.4. In most cases, 10 µm bicuculline methiodide was added to block GABA_A-mediated inhibitory transmission. All experiments, except where otherwise stated, were conducted at 36 ± 1°C. The intracellular solution contained (mm): potassium gluconate, 115; KCl, 20; HEPES, 10; phosphocreatine, 10; Mg-ATP, 4; Na-GTP, 0.3; pH 7.2; osmolarity, 305 mosmol l⁻¹. In a number of experiments, the Ca²⁺ dependence of the mechanisms governing synaptic depression was examined. In these cases the presynaptic neurone was re-patched after the control recording with a pipette, which then contained 0.5–5 mm ethylene glycol-bis (2-aminoethylether)-N,N,N′,N′-tetraacetic acid (EGTA). To examine whether Na⁺ current boosting of the postsynaptic response occurred at these connections, the intracellular solution contained 5 mm QX-314 (Alamone Laboratories, Jerusalem, Israel) and the appropriate reduction in potassium gluconate made to maintain iso-osmolarity.

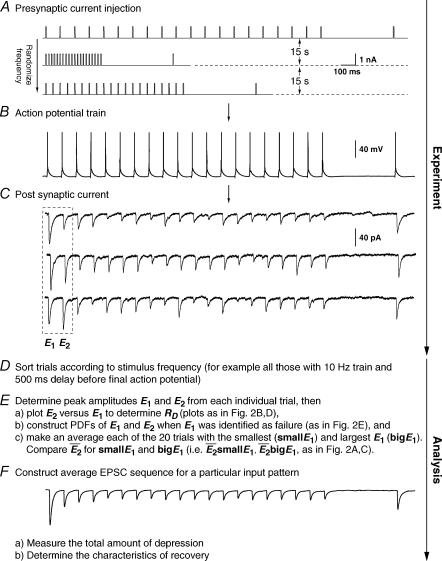
Recordings were obtained between connected pairs of layer V or IV cells. Access resistance was 10.1 ± 2.4 mΩ and was uncompensated. The presynaptic neurone was recorded in current-clamp mode (Axoclamp 2B, Axon Instruments), and action potentials were initiated (Fig. 1B) by injection of rectangular current pulses (5 ms, 0.5–1.5 nA, Fig. 1A). The postsynaptic neurone was held in voltage clamp at −70 mV and excitatory postsynaptic currents (EPSCs) recorded using an Axopatch 200B amplifier (Axon Instruments; Fig. 1C). The choice of postsynaptic voltage clamp was made for the following reason. Firing the cells at stimulus frequencies > 25 Hz would have contaminated the subsequent EPSP amplitudes by the decay phase of the previous responses. In voltage clamp, however, the current decays are markedly faster and allow the measurement of the peak amplitude even at these frequencies. Note that we do not claim to perfectly clamp postsynaptic currents, which is impossible in these distributed structures. The output was amplified (100–500 times) following a sample-and-hold step to ensure that the full resolution of the AD converter could be utilized (custom-built sample-and-hold amplifier integrated with a 8-pole Bessel filter, design JCSMR, ANU, Australia). The signal was filtered at 2 kHz and digitized at 5 kHz using an ITC-18 computer interface (Instrutech Corp, Port Washington, NY, USA). Data were acquired using software developed with IGOR Pro 4.0 (Wavemetrics, OR, USA). Each trial in an experiment involved generating a burst of action potentials (mostly 20) in the presynaptic neurone at a particular frequency (range 3–50 Hz). The frequency during each burst was randomly chosen from a set of a few predetermined frequencies (i.e. 3, 5, 10, 20, 25, 30, 40, 50) to avoid steady-state behaviour. Each burst of action potentials was then followed by a recovery interval (300–1200 ms; also randomized) before a single action potential was evoked to gauge recovery from depression. The trials were repeated every 10–15 s, and 50–900 trials were recorded for each of the frequencies studied (Fig. 1A and B).

Figure 1. Experimental protocol.

A, sample trials of 20 rectangular current pulse injections (5 ms, 1 nA at 10, 50 and 20 Hz, respectively) applied to the presynaptic neurone with a trial-to-trial interval of 10–15 s. The sequence of trials was randomized for frequency, and the repetitions for each input pattern were between 50 and 900. Recovery was gauged with a delayed current pulse (500 ms in this example). B, single burst of action potentials recorded in the presynaptic neurone in response to a current pulse sequence (A). C, the postsynaptic neurone was held in voltage clamp at −70 mV and excitatory postsynaptic currents (EPSCs) were recorded. For clarity, only sample EPSC trials in response to a burst of action potentials at 10 Hz are shown. In D–E, the analytical procedures are indicated. In D, the analysis starts with sorting trials according to stimulus frequency and delay of the action potential to gauge recovery. E, measuring E₁ and E₂ in each trial allows determination of the release dependence of depression (R_D), construction of the PDFs and comparison of 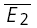for the 20 trials with the smallest E₁ (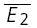small E₁) and those with the largest (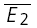bigE₁). F, the average of all trials for a particular input pattern are used to determine the total amount of depression, and the characteristics of recovery.

Data analysis

Averages are presented as mean ± 1 s.d., error bars in figures represent ± 1 s.e.m. For statistical comparison, a level of significance of < 0.05 was accepted and the following abbreviations are used: p_r for Pearson's r, p_KS for Kolmogorov-Smirnov, p_χ for χ² statistics, p_A for significance calculated based on analysis of covariance (ANCOVA), p_t for Student's t test and p_pt for Student's paired t test.

Extracting the amplitude of postsynaptic responses

In some cases, the amplitudes were measured manually according to the technique described in Stricker et al. (1996) and an estimate of the baseline noise was obtained (averaged over all experiments σ_n = 0.9 ± 0.2 pA). In other cases, the response amplitudes in single trials were determined automatically by a custom Matlab routine (MathWorks Inc., Natick, MA, USA). In this case the experimental recordings were low-pass filtered (Gaussian filter with σ= 0.2 ms) to remove high frequency fluctuations, and the baseline and peak of each synaptic response determined. The detection method was verified by comparing the amplitude of the average EPSC of all trials, with the average of the automatically determined amplitudes.

Since the experiments required a prolonged recording period (> 3 h), the stability of synaptic dynamics was assessed by comparing the mean response for the first and second half of all trials. Only experiments with stable dynamics were used (i.e. where p_t of the normalized averages > 0.05). In some cases, a drift (always run-down) in the average EPSC amplitude was sometimes observed (due to changes in access resistance). In these cases, stationary subsets of data were used for most analyses. However, for modelling, consistent drift in the data (< 50%) was corrected by normalizing the responses according to the slope of the linear regression of the amplitudes over time. To compare recordings under different conditions (e.g. different frequencies of stimulation), the magnitudes were normalized according to the average amplitude of the first EPSC.

Detecting and quantifying release-independent depression

RID is best demonstrated at connections with a low probability of release and a significant number of failures in response to the first action potential. Under conditions of release-dependent depression, the average, and amplitude distribution, of second EPSCs following a failure should equal those of all first EPSCs. To examine such differences in the amplitude distributions, amplitude probability density functions were calculated by kernelling each amplitude with a Gaussian as described in Stricker et al. (1994). Cumulative probability densities were determined, and significant differences tested using Kolmogorov-Smirnov statistics. However, when the initial release probability is high, there are at most few or no trials, where failures in response to the first action potential occur, and adequate statistics cannot be obtained. RID can still be demonstrated in the absence of transmission failures by examining the trials based on the amplitude of the first EPSC (smaller or larger than the mean response). If depression is release dependent, the average amplitude of the second EPSC in those 20 trials with the smallest first EPSC (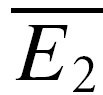smallE₁) should be larger than that of the 20 trials with the largest first EPSC (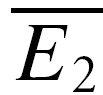bigE₁; Fig. 1F). This will not hold true for RID, and significant differences were tested using a Student t test. It should be noted that due to the small sample size, the two averages 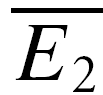smallE₁ and 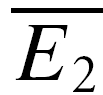bigE₁ typically constitute a biased sample and therefore deviations from the predictions of R_D (see below) are likely to be observed.

A further method based on the amplitudes of all first and second EPSCs was devised to quantify the relative contribution of release-dependent and -independent depression. This measure is subsequently called R_D and is proportional to the correlation coefficient between the first and second EPSCs, i.e.

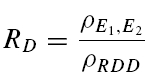where E₁ and E₂ are random variables representing the first and second EPSCs. ρ_E1,E2 is the correlation coefficient, and ρ_RDD is the correlation coefficient for pure release-dependent depression (RDD; see Appendix for details). The idea is that if transmitter release is purely release dependent, then E₂ is correlated with E₁ (Matveev & Wang, 2000), In contrast, at a connection with pure RID, no correlation is expected between E₁ and E₂, and therefore R_D equals 0. The measure quantifies the degree of RDD and (for a sufficiently large sample size) holds values between 0 ≤R_D≤ 1, where 0 indicates pure RID and 1 pure RDD.

An illustration of R_D is obtained in a plot of E₂versusE₁ (Waldeck et al. 2000; see Fig. 2B and D). For pure RDD, the slope of the regression line is ρ_RDD and the y-intercept 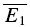(the average of second responses that follow a failure equals the simple average of all first responses). For pure RID, the slope is 0 by definition and the y-intercept is 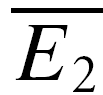(the average of all the second responses). R_D is the relative y-intercept normalized by 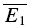(see eqn (20) in the Appendix).

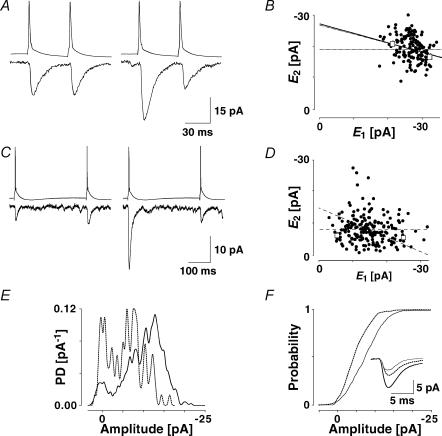
Figure 2. Release-dependent and -independent components of depression.

A, a layer V connection expressing prominent release-dependent depression (RDD). EPSCs were recorded in 148 successive trials, in which the presynaptic neurone was stimulated at a frequency of 20 Hz. Left: average (20 trials) depicting the first two EPSCs, in which the first EPSCs were the smallest (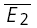smallE₁). Right: average EPSCs, in which the first EPSCs were the largest (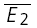bigE₁). Second EPSCs that follow small first EPSCs (left) are significantly larger than second EPSCs that follow large first EPSCs (right). B, plot of second versus first EPSCs for the same connection as in A. Filled circles: experimental data; continuous line: linear regression (r = −0.40, p_r < 0.05); dashed lines: theoretical line for pure release-independent depression (RID) (horizontal line) and RDD (oblique line). The y-intercept of the RDD line is the average of first EPSCs ( 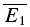= −27.3 pA) and that of the RID line, the average of the second EPSCs ( 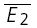= − 19.6 pA) The regression line overlaps the pure RDD line, and the y-intercept of the regression is clearly closer to 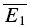than 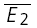. R_D = 1.03 ± 0.33, suggesting a strong component of RDD. The open squares indicate 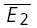smallE₁ and 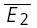bigE₁ as shown in A. C, a layer IV connection with dominant RID. The response was recorded in 191 successive trials, in which the presynaptic neurone was stimulated at a frequency of 3 Hz. Left, 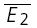smallE₁ and right, 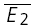bigE₁. The amplitudes of the second EPSCs are similar in both cases, largely independent of the first response. D, plot of second versus first EPSCs for the same connection as in C. Filled circles: experimental data; continuous line: linear regression (r = −0.12, p_r = 0.09); dashed lines: theoretical line for pure RID (horizontal line) and RDD (oblique line). The y-intercept of the RDD line is the average of first EPSCs (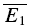= −14.7 pA) and that of the RID line, the average of the second EPSCs ( 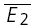= −8.0 pA). The y-intercept of the regression line clearly closer to 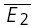than to 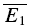(R_D = 0.21 ± 0.14), suggesting a strong component of RID. The open squares indicate 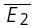smallE₁ and 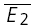bigE₁ as shown in C. E, additional evidence for release-independent depression in a layer IV connection. Probability density functions of the amplitudes of the first EPSC (continuous line, N = 554) and for the second EPSC when the first EPSC was a failure (dashed line, N = 75). The frequency of stimulation was 20 Hz. F, cumulative probability densities for the connection in E. The densities for E₁ (continuous line) and E₂ following a failure (dashed line) are significantly different (p_KS < 0.005). The inset shows the average time course for the first response (continuous black line), the second response, given the first was a transmission failure (dashed line), and all second responses (grey line).

Determining if a junction shows pure RID, RDD or intermediary forms is based on the following procedures. Using ANCOVA, we stringently test if R_D is significantly different from both hypotheses, namely pure RID (R_D = 0; no correlation) and RDD (R_D = 1; maximal correlation). Only if both hypotheses can be rejected do we conclude that R_D has taken an intermediate value and therefore consists of both RID and RDD. In addition, we also test whether the slope of the linear regression as well as the offset are different from that of RDD and/or RID.

Detecting and quantifying frequency-dependent recovery from depression

Frequency-dependent recovery (FDR) can be directly observed in the averaged data. It is present when the amplitude of the EPSC after a high frequency burst is greater than that of the EPSC evoked with the same delay following a burst at lower frequency. For the quantification of FDR, we calculated the normalized recovery amplitude (R_rec) for each stimulus frequency as

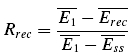where 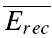is the mean amplitude of the EPSC induced with a delay (400–600 ms) after the burst (Fig. 1C). 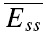is the mean EPSC amplitude in steady state (taken as the average of the last 4 EPSCs in the burst of 20 action potentials). The values will fall between 0 and 1, with a smaller number indicating faster recovery. To quantify the degree of FDR, we calculated the ratio between R_rec at 10 and 20 Hz (R_FDR). R_FDR > 1 indicates FDR, whereas R_FDR = 1 indicates no FDR. It would also be possible to define recovery as 1 −R_rec so that a bigger value indicates faster recovery. R_FDR would then be the ratio between R_rec at 20 and 10 Hz. However, in this case, connections with very little recovery (at an interval of 400–600 ms there was on occasion very little recovery) would have a very small denominator (close to zero) and therefore, R_FDR would be disproportionately large, i.e. in certain instances tend towards infinity. Equally, the measure described above is sensitive to the amount of recovery, and it would not be appropriate to use this measure for long recovery intervals where ().

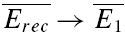Estimating the initial probability of transmitter release

We attempted to determine the initial release probability for each of the connections used in this study. This is usually done using quantal analysis. However, layer V pairs are not amenable to quantal analysis; the amplitude distributions of first responses are unimodal and overdispersed with more variance than would be expected from a binomial release process (A. Cowan & C. Stricker, unpublished observations). To overcome this problem, we attempted to use the extended moment analysis as described in Courtney (1978), where the probability (p_r, also U₀ in the model) is determined by

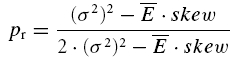where σ is the standard deviation of the sample and skew is calculated as follows

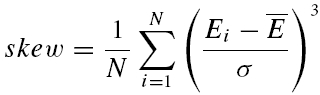where i is the trial number and N is the total number of trials. The quantal content (m) is

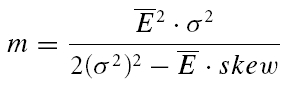In cases of overdispersion (too much variance when compared to a classical release process) (σ²)² becomes the dominant factor in both equations and renders this measure very insensitive. For these reasons, we are unable to provide a measure for release probability per se. However, we resorted to using the skew of the sample as an indication of p_r. For a purely binomial process of transmitter release, a negative skew indicates that p_r > 0.5. Such a distribution has an asymmetric tail extending towards EPSCs of smaller magnitude (remember, however, that since inward currents are measured, the tail extends towards less negative values). A skew of zero corresponds to p_r= 0.5, whereas a positive skew indicates p_r < 0.5 (such a distribution is characterized by an asymmetric tail extending towards large EPSCs). Correlations between the skew and various parameters of synaptic depression suggest a correlation of these parameters with initial release probability.

To examine whether synaptic depression in these connections was a result of a change in p_r, or could be accounted for by other factors (a change in the number of release sites (n) or the quantal size (q), we constructed plots of the inverse of the normalized coefficient of variation squared (CV⁻²) versus normalized mean amplitude (as reviewed in Korn & Faber, 1991).

Augmentation

To test if augmentation was present at the connections studied, we used a protocol similar to that described in Stevens & Wesseling (1999). Following a sequence of 100 action potentials at 10 Hz, action potentials were evoked in the presynaptic neurone at a rate of 0.5 Hz for the next 60 s. The amplitudes of the resultant EPSCs were measured and normalized to the final amplitude (i.e. the average value for the last 30 s, as in Stevens & Wesseling, 1999). The time course for the decay of augmentation was then determined by fitting a single exponential to the normalized EPSCs for the first 15 EPSCs following the high frequency burst.

Model

The model implementation is based on the classical quantal hypothesis, to which we add the dynamics of synaptic transmission. These are formalized in previously published deterministic (Tsodyks & Markram, 1997) and probabilistic (Fuhrmann et al. 2002) models, with extensions made to accommodate the experimental findings presented below.

The modelled connection is composed of n release sites each holding at most one vesicle. In response to an action potential, each available vesicle can be released with a constant probability, U_SE. After release, the site can be refilled within each time step dt with the probability dt/τ_rec, where τ_rec is the recovery time constant of the refilling process. In contrast to the classical quantal hypothesis, in this model the release sites may be depleted of vesicles, thus no vesicles would be available for transmission.

The processes of transmitter release and recovery from depression can be described by a single differential equation, determining the probability P_v, of vesicle availability at time t,

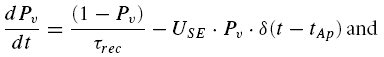and

where P_r(t_Ap) is the release probability at each release site at the time of an action potential, t_Ap. It is the product of P_V(t_Ap) and U_SE (see Zucker, 1973; Quastel, 1997). The postsynaptic response is proportional to the number of vesicles released.

Based on the experimental findings, we formalize the mechanism of depression as composed of two components. The first component is release dependent (RDD), which results from the depletion of synaptic resources, as formulated in eqn (5) above. The second component is RID, which is mediated by a decrease in the probability of release to subsequent action potentials, and which is independent of whether release actually occurred. It is formalized by U_SE being a dynamic variable, decreasing with subsequent action potentials in the sequence

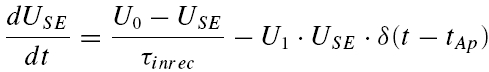where U₀ is the initial probability of release, U₁ a constant (0 < U₁ < 1) determining the decrease in U_SE per action potential, and τ_inrec is the recovery time constant of RID. The reason for this choice of implementation is discussed later (Results and Discussion). Thus, between bursts of action potentials (15 s), U_SE increases towards U₀, and when an action potential occurs (t_Ap), it decreases by U₁·U_SE(t_Ap).

To account for FDR, we suggest that τ_inrec itself is activity dependent. Its dynamics evolve according to

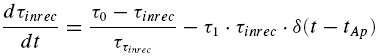where τ₀ is the initial value of the recovery time constant for RID, τ₁ is a constant determining the step-like decrease in τ_inrec per action potential (0 < τ₁ < 1), and τ_τinrec is the relaxation time constant of τ_inrec. Similar to the idea above, between bursts of action potentials, τ_inrec increases towards τ₀.

The mean synaptic response 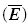can be calculated as

where A_SE =nq is the maximal response produced when all the sites release their vesicles. Note that even though a uni-vesicular hypothesis is implied here, the formalism does not preclude multivesicular release, because A_SE is simply a scaling factor and as such has no biological meaning. The variable R(t) is the fraction of vesicles available at time t and is calculated according to the following equation, which is analogous to eqn (5):

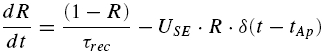In order to study the functional implications of RID and FDR (see Fig. 13), we explore the total postsynaptic current (I_syn) produced by the activity of a population of K = 1500 presynaptic neurones, connected to the target neurone by uniform synapses, since the discharge frequency of a neurone is proportional to the total postsynaptic current (Granit et al. 1966); i.e.

Figure 13. Functional implications of FDR.

Simulated net postsynaptic current (I_syn, calculated according to eqn (10)) generated by a population of 1500 presynaptic neurones, firing randomly (Poisson) and undergoing synchronous transitions (indicated by arrows) from a low firing rate to a higher firing rate. Left: transition from 5 to 50 Hz. Right: transition from 30 to 50 Hz. A, model with pure RDD and no FDR. At low firing rates (left), the connections can code both a transition (by a transient increase in response), and average firing rate (by the mean current). At high firing rates (right), the connections cannot code the firing rates, as the input current does not change. However, it can still code (with the transient response) a change in rate. Model parameters: U₀ = 0.4, U₁ = 0, τ_rec = 500 ms, τ₀ = 1000 ms, τ₁ = 0.2, τ_τinrec = 2000 ms and A_SE = −200 pA. B, model with pure RID and FDR. At low firing rates (left) the synapses can code both a transition (by a complex transient), and the firing rate. At high firing rates (right), the synapses retain their ability to code firing rates. Model parameters: U₀ = 0.4, U₁ = 0.2, τ_rec = 5 ms, τ₀ = 1000 ms, τ₁ = 0.2, τ_τinrec = 2000 ms and A_SE =−200 pA.

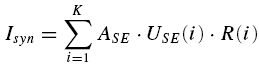Fitting the model to the data

There are seven parameters (A_SE, τ_rec, U₀, U₁, τ₀, τ₁, and τ_τinrec) in these equations, which determine the dynamics of transmission. While A_SE is a scaling parameter, and the ratio between U₀ and U₁ is determined by 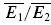, there are five free parameters remaining. The fitting of the model to the data is done in two steps. First, we choose the few parameter sets (approx. 50) which can best describe the dynamics of the EPSCs, and which are in the biologically plausible range. This is done by minimizing the sum of squared errors between the mean experimental and predicted responses to bursts of action potentials for each stimulus condition (eqn (9)). Second, the fit is chosen which also best describes the relation between experimental 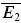bigE₁ and 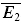smallE₁.

Results

The properties of synaptic depression were examined in 38 pairs of pyramidal neurones in layer V of the somatosensory cortex. In layer IV, four pairs between star pyramidal cells, one spiny stellate–star pyramid connection, and a star pyramid–spiny stellate connection were also examined. We included layer IV cells since these showed largely the same characteristics as in layer V and because in some of them, we were able to identify a significant number of transmission failures. All connections reported here failed to show any sign of facilitation at any frequency between 5 and 50 Hz, i.e. the average amplitudes of the first few EPSCs in the sequence were smaller than the preceding ones. The recordings were a subset of the connections recorded (∼80%; 20% of connections showed a facilitatory response). For neurones in layer V, the average resting membrane potential was −62.5 ± 4.0 mV, the action potential height 95.2 ± 8.7 mV, half-width 1.2 ± 0.3 ms and input resistance was 92.2 ± 30.1 mΩ. The EPSCs averaged −38.2 ± 30.1 pA, had a rise time (10–90%) of 1.2 ± 0.3 ms and a half-width of 6.4 ± 1.7 ms. The CV was 0.4 ± 0.2 and the skew of the amplitude distribution −0.3 ± 0.6. Paired-pulse depression (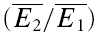) was 0.45 ± 0.15 (range: 0.35–0.77).

Release dependence of synaptic depression

Release-dependent depression (RDD) was identified at some of the connections. At these connections, as depicted for example in Fig. 2A, 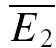smallE₁ (the average amplitude of E₂ for the 20 trials where E₁ was the smallest, see ‘Detecting and quantifying release-independent depression’ above) was significantly larger than 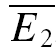bigE₁ (average E₂ for 20 traces where E₁ was the largest, Fig. 2A), indicating that there was some degree of release-dependent depression. In Fig. 2B, the second EPSC amplitude (E₂) is plotted as a function of the first (E₁). For guidance, the theoretical lines of pure RDD (oblique dashed line; for details see Appendix) and pure RID (horizontal dashed line) are depicted. It can be seen that the regression line for the data (continuous line) and the one for RDD (oblique dashed) are almost identical. The normalized factor indicating release dependence (R_D, eqn (20)) was 1.03 ± 0.33, suggesting that depression at this connection was dominated by RDD. ANCOVA verified that the regression line is not significantly different from pure RDD (p_A= 0.43 for RDD; p_A < 0.05 for RID).

In contrast, at some connections, synaptic depression was found to be highly release independent (Fig. 2C and D). This was deduced from the facts that, at these synapses, 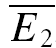bigE₁ and 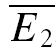smallE₁ were not significantly different from each other (Fig. 2C) and that R_D was close to zero. In Fig. 2D, the linear regression analysis confirms that depression in this example is largely release independent. It is evident that the y-intercept of the regression line is indeed closer to 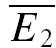than to 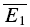. R_D was small (0.21 ± 0.14), and ANCOVA confirms that depression at this connection is significantly different from pure RDD (p_A < 0.0005), but not from pure RID (p_A= 0.45).

Additional evidence for the existence of RID is depicted in a layer IV connection in Fig. 2E and F, where the amplitude distribution of the first EPSCs, and that of the second EPSCs, given that the preceding EPSC was a failure, are shown (Fig. 2E). In Fig. 2F, the cumulative probabilities of the two distributions are significantly different (p_KS < 1e⁻⁹). The average synaptic response that follows a failure is also smaller than 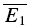, but slightly bigger than (inset).

Our results indicate that most of the recorded connections exhibit at least some degree of RID. This can be inferred from the results of ANCOVA, where six of the layer V connections and five of the layer IV connections showed pure RID. Sixteen layer V connections were significantly different from both RID and RDD, indicating that they express both forms of depression, whereas three of the layer V connections were not significantly different from either pure RID or RDD. One layer IV connection (star pyramid–star pyramid), and seven layer V connections were highly release dependent, i.e. not significantly different from RDD but significantly different from RID. The remaining six layer V pairs were used in other experimental protocols (augmentation, recovery times, see below). The mean value of R_D was 0.45 ± 0.35.

We investigated whether the existence of some degree of release-independent depression in most connections could be an artefact of our recording conditions. We do not believe this is the case for a number of reasons. Firstly, the degree of release dependence remained stable throughout long recording periods. For example, in Fig. 3, a plot of E₂versusE₁ for the first and last hour of a 4 h recording period is shown, during which the degree of release dependence remained unchanged (R_D = 0.45 ± 0.15 in Fig. 3A, 0.53 ± 0.22 in Fig. 3B, p_t= 0.7).

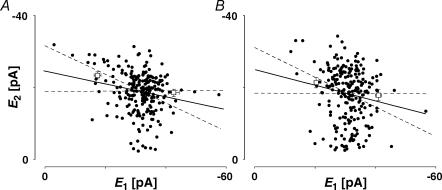
Figure 3. The properties of synaptic depression are stable.

A, plot of second versus first EPSCs for a layer V pair for the first hour of a prolonged recording period. R_D = 0.45 ± 0.15 (N = 228, r = −0.42, p_r < 0.05). B, plot of second versus first EPSCs for the same connection after 3 h of recording. The R_D of 0.53 ± 0.22 (N = 238, r =−0.38, p_r < 0.05) is not different (p_t= 0.7) from that in A and in both cases the linear regression line is significantly different from a horizontal line. The open squares indicate 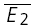smallE₁ and 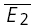bigE₁.

A potential artefact that could result in release-independent depression would be a change in the properties of synaptic depression as a result of wash-out during whole cell recording. In eight experiments, we evoked action potentials in the presynaptic neurone from cell-attached mode. R_D for these experiments (0.35 ± 0.27) was not significantly different from the average of all those recorded in whole-cell mode (0.45 ± 0.35, p_t= 0.4).

Since in most of our experiments we included bicuculline in the ACSF to block GABA_A-mediated transmission, and bicuculline has been shown to block Ca²⁺-dependent K⁺ channels (see for example Debarbieux et al. 1998), we investigated whether RID was still observed in the absence of bicuculline. In 15 experiments, R_D corresponded to 0.54 ± 0.35, which was not significantly different from when the ACSF contained bicuculline (p_t= 0.3).

A process that resulted in a positive correlation between E₁ and E₂ could potentially counterbalance the negative correlation of release-dependent depression, and result in an apparent lack of correlation. Such a process could include active postsynaptic boosting (Stuart & Sakmann, 1995) in imperfectly voltage-clamped neurones. Such a process would preferentially affect the largest E₁. However, subsets of data with only large or small E₁ resulted in the same R_D value as the complete data sets (p_pt > 0.5, data not shown). As a further test for this possibility we examined connections under control recording conditions and then after re-patching the postsynaptic neurone with an intracellular solution containing 5 mm QX-314. In four experiments, the presence of postsynaptic QX-314 did not change R_D(control: 0.48 ± 0.22; QX-314: 0.42 ± 0.10, p_pt= 0.6) or E₀/E₁(control: 0.71 ± 0.15; QX-314: 0.65 ± 0.11, p_pt= 0.5, data not shown).

We also examined whether RID was an artefact of the analysis technique, for example, whether quantal variance or the noise variance could mask a correlation between E₁ and E₂. However, we found that there was no correlation between the connections with a large CV and the expression of RID. In fact, there was the opposite correlation between large CV and the expression of RDD, as might be expected for connections with a higher initial release probability (see below, p_r= 0.002, data not shown). There was no correlation between the noise variance and R_D (p_r= 0.6).

The site of expression

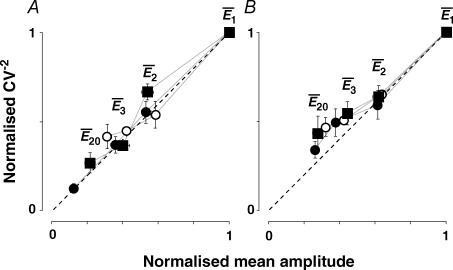
Depression could be a result of a change in release probability (P_r,eqn (5)), a change in the number of release sites (n), a change in quantal size (q), or a combination of these factors. To determine the mechanism of depression, a CV⁻² analysis was performed since depression resulting from changes in either n or q will be indicated by data points significantly above the 45 deg line (dashed lines in Fig. 4A and B), whereas changes in p_r alone are observed as data points on or below this line (for details see Korn & Faber, 1991). The plots of this analysis are illustrated in Fig. 4 for two types of connections, namely those which showed a high degree of RDD (R_D > 0.65; Fig. 4A) and those, where the depression was predominantly RID (R_D < 0.35; Fig. 4B). In both cases, the points followed the 45 deg line, thus suggesting that the most likely cause for depression in both cases is a change in the probability of release.

Figure 4. Synaptic depression results from a change in release probability.

A, plot of normalized CV⁻² versus normalized mean amplitude for those neurones with R_D > 0.65 (i.e. dominated by release-dependent depression). The points represent the average data for the first 3 and the last (20th) EPSCs. Open circles: 10 Hz burst; filled squares: 20 Hz burst; filled circles: 50 Hz burst. For guidance 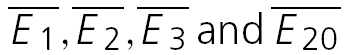, are labelled for the 20 Hz burst. B, plot of normalized CV⁻²versus normalized mean amplitude for those neurones with R_D < 0.35 (i.e. dominated by release-independent depression). Note that the dispersion of the data points is less than in A due to the fact that the EPSC during the sequence converges to a steady-state of similar amplitude for all frequencies of stimulation.

Based on these results we suggest that synaptic depression in the recorded connections is controlled by two mechanisms: one, which is release dependent (RDD) and the other, which is release independent (RID). In different synapses, the relative contribution of each of these components may vary, such that a synapse can express either pure RDD, or pure RID, or a mixture of the two forms. Experimentally, the whole range was observed (0 ≤R_D≤ 1). To replicate the observed features, the release-dependent component of depression is formulated in eqn (5), by the depletion of vesicles available for synaptic transmission. The release-independent component is formulated in eqn (6) by the activity-dependent decrease in the probability of release (U_SE). It is independent of whether vesicles were actually released in response to preceding action potentials. In terms of parameters, a synapse with very small τ_rec (relative to the scale of τ_inrec) will be dominated by RID, due to fast replenishment of synaptic resources. RDD could result from an opposite relation between these parameters, or from very small step changes in the probability of release (U₁ approaching zero).

Properties of RID and RDD

Dependence on initial release probability

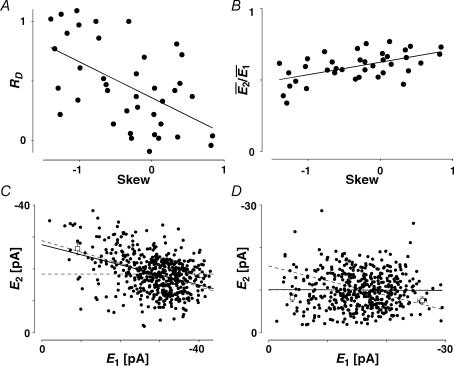
It appears that the type of synaptic depression (RID or RDD) is dependent on the initial release probability of the synapses. Firstly, there is a negative correlation between the values of R_D and the skew of the amplitude distribution (Fig. 5A, r =−0.54, p_r < 0.005 Courtney, 1978). Since a negative skew indicates a high initial release probability (U₀ > 0.5), this correlation is suggestive that RDD is more prominent for connections with a high initial probability. At the same time, we observed that the degree of paired-pulse depression (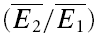) is inversely correlated with skew (Fig. 5B, r = 0.55, p_r < 0.005). Since a high initial release probability is expected to result in a large depression of the second pulse, this finding is consistent with the above observation and, thereby, serves as an internal check for consistency of using skew as an indirect measure of initial release probability. Secondly, for the same data set, R_D is correlated with the ratio 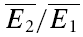(r =−0.41, p_r= 0.02, data not shown). Taken together, these correlations suggest that strongly depressing synapses (which have a relatively high initial probability of release, i.e. U₀ > 0.5) are more likely to express more RDD. Conversely, pure RID is most likely to be observed at synapses with low initial release probability and weak depression.

Figure 5. Features of RDD and RID.

A, the release dependence of depression (R_D) is correlated with release probability. Here the skew of the amplitude distribution is used as a coarse indicator of release probabilities. The continuous line indicates the linear regression (r = −0.54, p_r < 0.005). B, the amount of depression (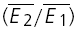) is also correlated with the skew of the amplitude distributions. The continuous line indicates the linear regression (r = 0.55, p_r < 0.005). C, temperature dependence. The response of a layer V connection maintained at 30°C to the first two action potentials in a sequence. Stimulation frequency was 10 Hz. E₂ is plotted as a function of E₁ for each trial. Continuous line: linear regression of the data. Dashed lines: theoretical line for pure RID (horizontal line) and pure RDD (oblique line). The connection displays a strong component of RDD (R_D = 0.88 ± 0.11). The open squares indicate 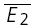smallE₁ and 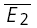bigE₁. D, same connection as in C, but at 36°C, showing a strong component of RID (R_D = 0.02 ± 0.11). The open squares indicate 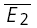smallE₁ and 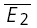bigE₁.

Temperature dependence of RID

We found that RID is more prominent at physiological temperature and that the mechanism of depression is highly temperature dependent. In seven experiments, connections were recorded at 30°C rather than 36°C. In the example shown in Fig. 5C and D, the same connection was recorded at both temperatures. At the higher temperature, the dominant mechanism of depression is release independent, as shown in Fig. 5D (R_D = 0.02 ± 0.11, significantly different from pure RDD, but not RID). At 30°C, the depression is largely release dependent (R_D = 0.88 ± 0.11, Fig. 5C), significantly different from pure RID, but not RDD. The effect of the change in temperature was reversible (data not shown). The mean R_D for all seven experiments at 30°C was 0.77 ± 0.22; this was significantly higher than R_D for experiments at 36°C (0.45 ± 0.35; p_t= 0.03). In parallel, the total amount of paired-pulse depression (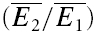) actually decreases at the lower temperature ( 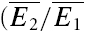= 0.45 ± 0.15 at 36°C; 0.64 ± 0.07 at 30°C, p_t= 0.05). The apparent Q_{10(30–36°C)} of R_D was 2.6 ± 0.2.

Ca²⁺ dependence of depression

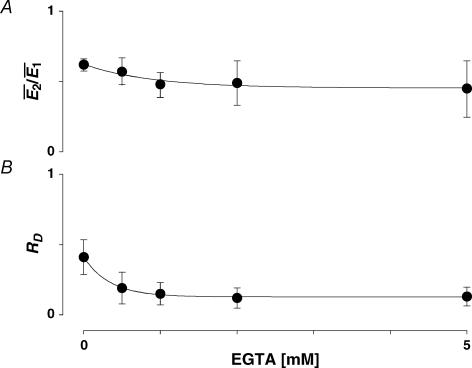
To investigate the Ca²⁺ dependence of synaptic depression, we re-patched the presynaptic neurone with electrodes containing the calcium buffer EGTA at increasing concentrations (0.5–5 mm, N = 5 for each concentration; Ohana & Sakmann, 1998; Rozov et al. 2001). In the presence of EGTA, the average EPSC amplitude decreased in comparison to the control recordings (77 ± 8% of control 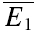after re-patching the presynaptic neurone with intracellular solution containing 5 mm EGTA). The amount of depression tended to increase, on average (Fig. 6A); however, the effect was variable with depression increasing at some and decreasing at other connections (thus the increase in the variance in Fig. 6A). R_D, however, consistently decreased at EGTA concentrations ≥ 1 mm (Fig. 6B). Using 1 mm EGTA, R_D was 0.15 ± 0.18 (p_pt= 0.02; the control R_D for the same 5 neurones was 0.41 ± 0.22). This finding is consistent with the correlation between R_D and skew (i.e. U₀), since EGTA is expected to decrease the initial release probability.

Figure 6. The effect of buffering presynaptic Ca²⁺on synaptic depression.

A, the amount of depression (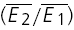) plotted as a function of EGTA concentration. With increasing concentration of EGTA, depression increases on average but this effect is variable; in some examples depression was reduced (note the increase in the error). B, plot of R_D as a function of EGTA concentration. With increasing concentration, the release dependence of depression decreases.

Frequency independence of R_D.

At connections stimulated at more than one frequency (5, 10 and 20 Hz; in some cases 25, 30, 40 and 50 Hz were also examined), there was no change in R_D with stimulus frequency (p_pt= 0.44 for 5 and 20 Hz, data not shown). However, we did not extensively examine the effects of higher input frequencies because of confounding effects produced by changes in action potential shape during the relative refractory period.

Frequency-dependent recovery from depression (FDR)

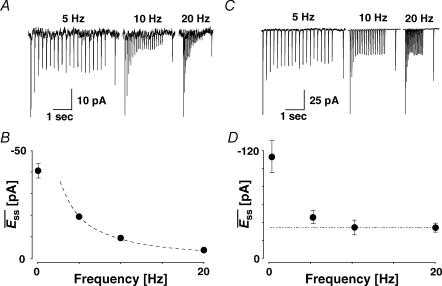
In this section, we present another phenomenon observed at the recorded connections. It relates to the mean EPSCs of a connection, evoked after a recovery interval and averaged over many repetitions of the same input pattern (Fig. 1C). In previous studies, the steady-state response at high frequencies (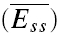) was shown to decrease in a manner inversely proportional to frequency (Abbott et al. 1997; Tsodyks & Markram, 1997). Indeed, some connections (Fig. 7A and B) exhibited such an inverse relationship. However, at other connections (Fig. 7C and D) the steady-state response at higher stimulus rates is frequency independent. This convergence to a similar steady state occurred for rates ≥ 10 Hz. For example in Fig. 7C, the magnitude of the steady-state response of a layer V connection is similar at 10 and 20 Hz. The convergence during steady-state to a constant value is shown in Fig. 7D.

Figure 7. Connections with and without apparent frequency-dependent recovery (FDR).

A, a layer V connection with no apparent FDR. The average response (N = 40) to action potentials triggered at three different frequencies (5, 10 and 20 Hz). In all cases, a further action potential was triggered 500 ms after the burst. The amplitudes of the steady-state response (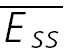) and the recovery EPSC (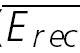) are smaller, with increasing input frequency. B, 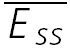of the connection in (A) is plotted as a function of frequency. There is no convergence to a steady-state of similar amplitude at different frequencies. The dashed line indicates the change proportional to 1/f. C, a layer V connection with FDR. The average response (N = 100) recorded at 5, 10 and 20 Hz. In all cases, a further action potential was triggered 600 ms after the burst. 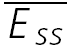is the same at 10 and 20 Hz, but 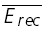is larger when the preceding burst was 20 Hz. D, 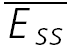of the connection in C. There is convergence to a similar 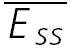at frequencies = 10 Hz. Dashed line indicates the analytically computed value of 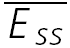for high input frequencies.

Additionally, we observed that at higher rates (≥ 10 Hz), the synaptic response to an additional action potential 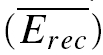, stimulated at a fixed recovery interval (600 ms), increases with the frequency of the preceding burst (Fig. 7C). Finally, there is a transient decrease in the magnitude of subsequent synaptic responses, which then recovers (see EPSCs 6–9 at 20 Hz in Fig. 7C). These three observations cannot be explained by the classical model of depressing synapses, where recovery is characterized by a single time constant (Abbott et al. 1997; Tsodyks & Markram, 1997). They could be explained, however, if there is an activity-dependent mechanism for recovery from depression, which is recruited at higher frequencies. We term this phenomenon frequency-dependent recovery (FDR; Dittman & Regehr, 1998; Stevens & Wesseling, 1998; Wang & Kaczmarek, 1998; Weis et al. 1999; Sakaba & Neher, 2003).

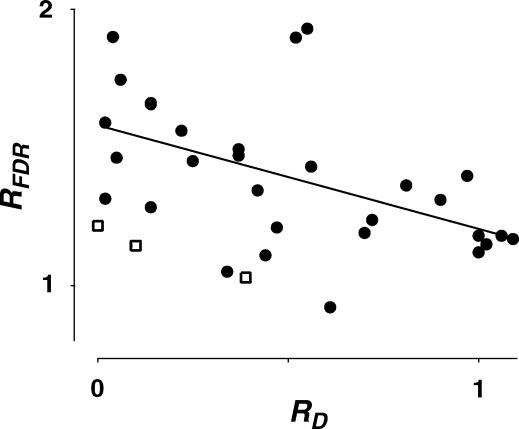
Analysis of the model indicates that the convergence of EPSCs to a steady-state value at high input frequencies requires that depression is strongly dominated by one of the two forms of depression (RDD or RID), which recovers in a frequency-dependent manner (see below). Since most connections exhibit some degree of RID, we investigated whether FDR was associated with release-dependent or -independent depression (Fig. 8). For this purpose, we used R_FDR (see Methods) to estimate the relative degree of FDR in all the recorded connections. We found that the expression of FDR was negatively correlated with R_D, indicating that connections with prominent RID also exhibited more FDR (r =−0.51, p_r= 0.005). Such a relationship can also be inferred from Fig. 4A and B, where the amplitude of the 20th EPSC following different frequencies of stimulation is distributed over a wider range along the diagonal for those neurones with R_D≥ 0.65 (Fig. 4A, see left-most symbols for each frequency) than for those with R_D≤ 0.35 (Fig. 4B).

Figure 8. Correlation between R_FDR and R_D.

The ratio of the normalized recovery amplitude following a burst at 10 and 20 Hz (R_FDR) is plotted against R_D(determined at 20 Hz) of layer V connections (filled circles) and 3 layer IV connections (open squares). There was a significant correlation between the two parameters as indicated by the linear regression for layer V connections (r =−0.51, p_r < 0.005).

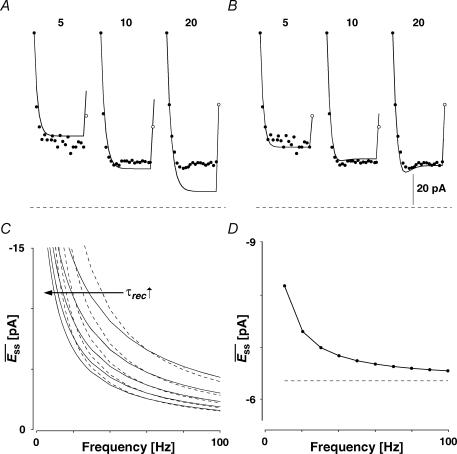
We therefore formulate FDR in eqn (7) by an activity-dependent recovery from the release-independent component of depression. The time constant associated with this recovery is called τ_inrec. In Fig. 9 the simple model with no FDR (A, i.e. with constant τ_inrec), and the extended model (B), in which the recovery time constant is frequency dependent are fitted to the synaptic response shown in Fig. 7C. The magnitudes of both experimental and predicted EPSCs to sequential action potentials are depicted. It is clear that the simple model cannot account for the similar steady state responses of a synapse stimulated at 10 and 20 Hz, nor for the increasing magnitude of the recovery response, and clearly not for the shape of the curves. In contrast, the extended model replicates both the steady-state responses of the connection, and the ratio between the recovery response and the steady-state response, at different frequencies. Moreover, the model exhibits the transient decrease in the amplitude of synaptic responses before reaching the steady state, as seen in the recordings (Fig. 9B and 20 Hz).

Figure 9. Modelling FDR.

The magnitudes of EPSCs of a layer V pyramidal–pyramidal connection expressing FDR (same as in Fig. 7C and D) at three frequencies of stimulation (5, 10 and 20 Hz) with the recovery EPSC (open circle) are shown with fits of two alternative models. A, simple model with no FDR (τ_τinrec constant; with pure RID). The experimental EPSC amplitudes (filled circles) and the modelled one (line) are plotted as a function of the number in the sequence. In all cases the last EPSC is the response to gauge recovery (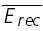). Model parameters: U₀ = 0.1, U₁ = 0.4, τ_rec = 1 ms, τ₀ = 700 ms, τ₁ = 0, τ_τinrec = 300 ms and A_SE =−1130 pA. B, full model with FDR (τ_inrec activity dependent; again with pure RID). Model parameters: U₀ = 0.4, U₁ = 0.4, τ_rec = 1 ms, τ₀ = 2000 ms, τ₁ = 0.4, τ_τinrec = 500 ms and A_SE = −282 pA. Dashed horizontal line indicates no response. C, steady-state response (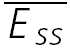) as a function of frequency for models with both RDD and RID for various values of τ_rec (continuous lines). Dashed lines represent the analytically calculated relation between 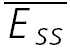and input frequency (f), expected at high input frequencies (1/f). Model parameters: U₀ = 0.3, U₁ = 0.1, τ₀ = 1800 ms, τ₁ = 0.5, τ_τinrec = 1800 ms and A_SE = −100 pA, τ_rec = 200, 300, 400, 500, 600 ms. D, 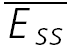of a connection with pure RID and FDR. (continuous line) of the connection converges to an analytically calculated constant value at high input frequencies (dashed line). Model parameters: U₀ = 0.4, U₁ = 0.4, τ_rec = 0 ms, τ₀= 2000 ms, τ₁ = 0.4, τ_τinrec = 500 ms and A_SE =−62 pA.

As mentioned above, the convergence of EPSCs to a steady-state of similar amplitude at high input frequencies depends on two conditions. First, the synapse must exhibit RID. Second, the recovery from the release-independent depression (τ_inrec) must be activity dependent. In Fig. 9D, the steady-state response of a synapse, which satisfies these conditions (continuous line), is depicted as a function of frequency. In contrast, for synapses with a mixture of RID and RDD, the steady-state response amplitudes decline in inverse proportion to the input frequency (Fig. 9C). If a synapse shows pure RDD, the steady-state amplitude should be inversely proportional to the input frequency (1/f, Tsodyks & Markram, 1997). Indeed, as the release-dependent component becomes more pronounced (longer τ_rec), the response converges to that predicted by 1/f at lower input frequencies (Fig. 9C).

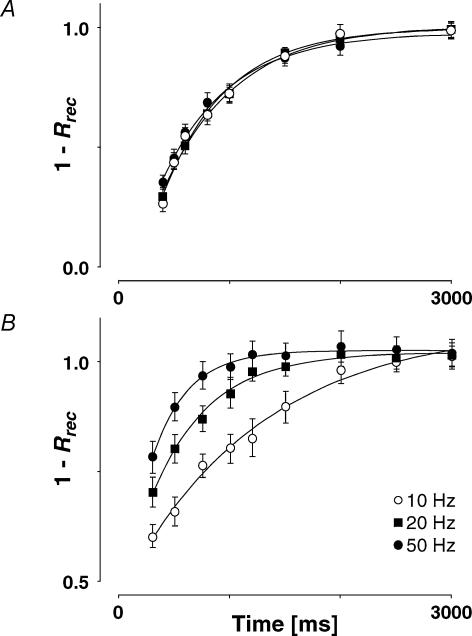
Further experimental evidence for FDR is provided in Fig. 10, where the normalized recovery amplitude is plotted against the delay before the final action potential for a connection where there was no increase in recovery rate with increasing frequency (Fig. 10A; note that 1 −R_rec is plotted so that recovery increases with time), and for an alternative example, where there was strong FDR (Fig. 10B). In every case, the data points were adequately fitted by a single exponential (p_χ < 0.05). The apparent recovery time constants (τ_a) for frequencies of 10, 20 and 50 Hz were not significantly different for the first example (580–660 ms). However, τ_a increased approximately 4-fold over this frequency range for the connection with FDR (Fig. 10B; from 1240 ± 184 ms at 10 Hz to 321 ± 112 ms at 50 Hz).

Figure 10. Time course of recovery from depression.

A, a connection showing no FDR. The time constant for recovery following a burst at 10 Hz (580 ± 78 ms, open circles) is not significantly different from that at 20 Hz (654 ± 81 ms, filled squares) or at 50 Hz (609 ± 73 ms, filled circles). B, a connection showing prominent FDR. The time constant for recovery following a burst at 10 Hz (1243 ± 184 ms, open circles) is significantly slower than that at 20 Hz (525 ± 76 ms, filled squares) and that at 50 Hz (321 ± 112 ms, filled circles). Note that 1 −R_rec (where R_rec is recovery amplitude) is plotted here so that recovery increases with time and the time constant of recovery is more easily demonstrated.

Averaged over all connections the normalized recovery amplitude (R_rec) following a burst at 10 Hz was 0.59 ± 0.12, with τ_a = 760 ± 150 ms. There was no significant difference in either of these parameters for those connections that demonstrated FDR and those that did not (p_t= 0.7 and 0.3, respectively). Following a burst at 20 Hz, the average normalized recovery amplitude was 0.43 ± 0.14 (p_t < 0.001 when compared with 10 Hz recovery amplitude). Thus, R_FDR (ratio between normalized recovery amplitude at 10 and 20 Hz, see Methods) was 1.37 ± 0.25. We examined whether there was a difference in τ_a between connections that demonstrated FDR and those that did not, and chose an arbitrary cut-off of R_FDR < 1.1 for no R_FDR(since this value was not significantly different from R_FDR = 1) and R_FDR > 1.2 for the sample that demonstrated R_FDR. The τ_a following a 20 Hz burst for those connections with R_FDR > 1.2 (528 ± 137 ms, N = 7) was significantly faster than those with R_FDR < 1.1 (691 ± 126 ms, N = 6, p_t= 0.05).

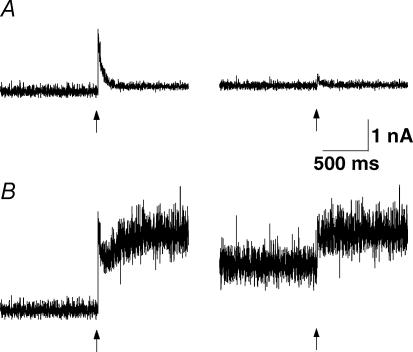
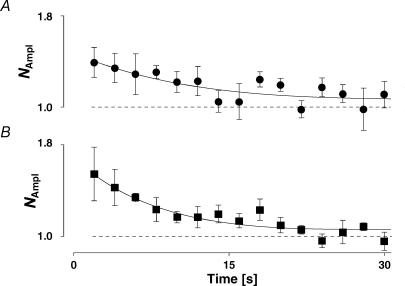
Since two processes seem to participate in the overall recovery from depression, we needed to find evidence that FDR was not caused by a process associated with eliciting a series of 20 action potentials at an intermediate frequency. Augmentation (Zengel et al. 1980; Stevens & Wesseling, 1999) is such a mechanism, which could superimpose on the depression and thereby mimic FDR. Despite the fact that we chose a subset of neurones that showed no signs of facilitation within the first few action potentials, we investigated whether augmentation was still present. When the presynaptic burst of action potentials was increased to 100 pulses at 10 Hz, we could discern a small amount of augmentation. This was maximally 40% greater than the initial EPSC amplitude (Fig. 11A) and decayed with a τ_Aug of 10.9 ± 5.3 s, which is much longer than τ_a at the same frequency (0.76 ± 0.15 s; p_t < 0.0002). In order to further corroborate that augmentation was not causing an apparent FDR, we checked the differential sensitivity to Ca²⁺ buffering by EGTA. Surprisingly, in our study presynaptic EGTA at a concentration of 5 mm did not affect augmentation (Fig. 11B). Under this condition, τ_Aug was 7.3 ± 2.4 s, which was not different from that with the control intracellular solution (N = 5, p_pt= 0.2). However, the inability of EGTA to block augmentation was significantly different from the effect on FDR, which was abolished at this concentration (see below).

Figure 11. Augmentation.

A, the recovery from augmentation is plotted as the normalized amplitude (N_Ampl) versus time following a sequence of 100 pulses at 10 Hz. Note that a normalized amplitude is used (see Methods and Stevens & Wesseling, 1999) not R_rec. The recovery time constant is 11 ± 5 s, the maximum increase in amplitude is 40% of control (N = 5). B, in the presence of 5 mm presynaptic EGTA, the recovery from augmentation is not significantly different from that in control for the same 5 connections. The recovery time constant from augmentation is 8 ± 2 s.

Properties of recovery

Temperature dependence of recovery

As was to be expected for a kinetic process, the recovery decreased when the temperature was 30°C rather than 36°C. The normalized recovery amplitude following a burst at 10 Hz was 0.84 ± 0.40 (N = 7) as compared to recordings at 36°C (0.59 ± 0.12, p_t= 0.05). Following a burst at 20 Hz it was 0.73 ± 0.31 (N = 7, 36°C: 0.43 ± 0.14, p_t= 0.005). Thus, R_FDR at 30°C was 1.15 ± 0.21, significantly different from the value at 36°C (1.37 ± 0.25; p_t= 0.02). The apparent Q_{10(30–36°C)} was 1.4 ± 0.1, significantly smaller than that for R_D(2.6 ± 0.2, p_t= 0.001).

Ca²⁺ dependence of recovery

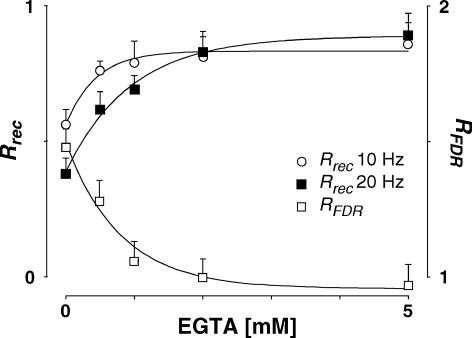
Previous studies have found that FDR-like phenomena are caused by an increase in intracellular Ca²⁺ (Dittman & Regehr, 1998; Wang & Kaczmarek, 1998; Sakaba & Neher, 2003). We tested this hypothesis directly by buffering Ca²⁺ concentration in the presynaptic neurone with 0.5–5 mm EGTA in the intracellular solution. Consistent with this hypothesis, recovery was prolonged. Even with 0.5 mm EGTA, the normalized recovery amplitudes at 10 and 20 Hz were significantly greater than for the same five connections in the absence of EGTA (10 Hz: 0.76 ± 0.08 versus 0.54 ± 0.13, p_pt= 0.005; 20 Hz: 0.62 ± 0.19 versus0.39 ± 0.13, p_pt= 0.02, Fig. 12). In addition to slowing the recovery, buffering intracellular Ca²⁺ abolished the difference in recovery following bursts of 10 and 20 Hz at concentrations ≥ 2 mm so that R_FDR under these conditions was not significantly different from unity (Fig. 12), suggesting that the expression of FDR requires intracellular Ca²⁺.

Figure 12. Effect of EGTA on the characteristics of recovery from depression.

The normalized recovery amplitude (R_rec,eqn (2)) following a burst at 10 Hz (open circles) and at 20 Hz (filled squares) is plotted against EGTA concentration in the presynaptic neurone. R_FDR, the ratio between R_rec at 10 and 20 Hz, is plotted (open squares). For EGTA concentration ≥ 2 mm, there is no significant difference in R_rec and therefore R_FDR is not different from unity. For clarity, only one-sided error bars are displayed.

Functional implications of FDR and RID

We simulated the implications of FDR and RID in order to gain insight into the capacity of the synapse to code rate as well as temporal information. The simulation describes the net postsynaptic current generated by the activity of a population of 1500 presynaptic neurones (as described by eqn (10)), each firing a sequence of action potentials according to Poisson statistics. The synapses all have the same characteristics, and all neurones have the same average firing frequency. After reaching steady-state, transitions from one frequency to another (indicated by arrow in Fig. 13) are induced. Consistent with earlier reports (Tsodyks & Markram, 1997), the analysis shows that at low firing rates, a synapse with pure RDD can transmit information about average firing rate and rate changes. However, at higher frequencies, it loses its ability to code information about firing rate, but can still signal transient changes (Fig. 13A).

In contrast, a synapse exhibiting pure RID and FDR operates in a very different manner (Fig. 13B): it can transmit information about the average firing rate and the rate transitions both at low and at high frequencies.

Discussion

Two characteristics of synaptic depression at connections in somatosensory cortex are described in this paper that may provide important functional properties to networks of connected neurones. The first, RID, is a depression, which occurs even after failure to release transmitter. The second, frequency-dependent recovery from depression (FDR), allows a faster recovery of transmission with increased input frequency. These characteristics are correlated and the functional significance of their expression was addressed.

Components of synaptic depression

Depression at excitatory neocortical connections is composed of release-dependent and -independent components. Forms of RID have been recognized in previous studies at invertebrate (Hatt & Smith, 1976; Gover et al. 2002) and vertebrate synapses (Dobrunz et al. 1997; Bellingham & Walmsley, 1999; Thomson & Bannister, 1999; Brody & Yue, 2000; Kraushaar & Jonas, 2000; Waldeck et al. 2000).

Reliability and range of R_D.

We base our finding of RID on three measures. Firstly, at connections with failures on the first response, the second EPSC is still depressed for the subset of EPSCs with preceding failures (Fig. 2E and F). This indicates that RID is presynaptic and is also activity dependent, i.e. caused by the preceding action potential and lasting for up to 300 ms. Secondly, even at connections without failures, when EPSCs are sorted into two categories depending on the size of the first EPSC, depression on the second EPSC is not bigger for large first responses (Fig. 2C). Thirdly, the measure R_D exploits the expected correlations between two successive EPSCs quantitatively and can be derived explicitly (see Appendix).

The reliability of R_D can be inferred from the following arguments. R_D is specific to a junction, is maintained during long recording sessions, does not ‘wash-out’, is the same for different recording modes (cell-attached and whole-cell), is restored to the same value when conditions are changed back to control (temperature) and is not affected by the presence of bicuculline and, thus, is not caused by a potential block of Ca²⁺-dependent K⁺ channels (SK-type; see for example Debarbieux et al. 1998). It is not dependent on artefacts induced by large quantal variance or recording noise.

Range of R_D

The relative contribution of the components of depression varies at different synapses (Fig. 2B and D), and the whole range of possibilities from purely release dependent to purely release independent was observed. The average value of R_D of 0.45 ± 0.35 suggests that, in our data set, at least 50% of the depression is release independent.

Potential causes of RID

One potential cause for an apparent RID could be an underlying facilitation, which obscured the release dependence of the dominant synaptic depression. We are certainly not disputing the fact that facilitation can occur at excitatory neocortical connections but believe that, by carefully choosing a subset of connections with evident depression only (∼80%), the influence of this form of plasticity on our results was small. The most convincing argument against an underlying facilitation is presented in Fig. 2E and F. If facilitation was an underlying mechanism, it should show up in the subset of EPSCs that follow a failure. However, even in this case we observed depression rather than facilitation. Furthermore, the facilitatory process would require a positive correlation between the amplitudes of the second and first EPSC; only in this way could it reduce the negative correlation in release-dependent depression. This is very unlikely since we have not seen such a correlation in any of our data sets and it would require that the amplitude of the second EPSC is larger even when the preceding EPSC was large, a scenario severely challenging vesicular depletion.

We can rule out a postsynaptic mechanism (i.e. Na⁺ current boosting of poorly clamped EPSCs) resulting in a counterbalancing positive correlation along similar lines. Firstly, Fig. 2E and F indicates that RID occurs when E₁ is a failure and is therefore clearly presynaptic. Secondly, a mechanism involving active dendritic properties would preferentially influence larger E₁, which was not observed. Finally, the experiments using QX-314 postsynaptically to block dendritic boosting showed that there was no significant involvement of postsynaptic Na⁺ currents in the observed EPSCs.

Site of expression

The rate of transmitter release is the product of release probability (P_r) and the number of quantal release units (n). Depression could theoretically result from a decrease in either or both of the parameters with, for a depletion model, the assumption that n represented the vesicular pool (Stevens & Wesseling, 1999; Kraushaar & Jonas, 2000). To investigate whether P_r changes during the sequence of action potentials, a CV⁻² analysis revealed that both RDD and RID appear to result from a change in P_r, given that the change in CV⁻² is largely identical to the change in normalized mean amplitude. If, in contrast, the change in the number of release sites and/or the quantal size occurred, one would expect such a plot to deviate horizontally and above the diagonal. An alternative explanation would be that changes in P_r, n and q are so finely balanced that the CV⁻² remains proportional to the change in amplitude despite such changes. We cannot rule this alternative out without further experiments, but such an explanation appears highly unlikely. The change in P_r does not identify whether the change is in the probability that a vesicle is available for release (P_v), which is a release-dependent process, or in the probability that an available vesicle can actually be released (U_SE), a release-independent process.

We provide evidence that R_D is correlated with the skewness of the amplitude distribution (Fig. 5A), a simple measure which might reflect the initial release probability of the connection. The correlation was such that there is more release-dependent depression in those connections with a higher release probability. Similarly, R_D is negatively correlated with the paired-pulse ratio. These correlations are to some extent intuitive: vesicle depletion is caused by release, and release is more likely to occur when there is a high release probability at the synapse. The fact that there is also more depression at these connections might suggest that RDD is an additional mechanism to RID, which only occurs or is apparent at synapses with a high release probability.

The temperature dependence of R_D (Fig. 5C and D) is such that release-independent depression is more pronounced when recording near physiological temperature. This could result from either an increase in RID or a decrease in RDD, indicating that both forms of depression might be temperature sensitive, but in opposite directions. An increased RID could result from an increase in, for example, channel inactivation, whereas a decreased RDD could be due to faster replenishment of the vesicular pool, as indicated in Results. At lower temperatures, it has been shown that release becomes less reliable (Hardingham & Larkman, 1998). This observation requires that at the lower temperature the correlation between R_D and skew is changed to allow RDD to dominate, while the probability of release decreases. At this stage, we are unable to comment on which mechanism(s) might be at work, since our major aim was to examine mechanisms of depression at physiological temperature. The Q_{10(30–36°C)} value for R_D is 2.6 ± 0.2 and indicates a higher activation energy requirement than for recovery from depression (see below). This value is in the range of voltage-gated channels and is about double the value for aqueous diffusion (Hille, 2001). It is consistent with the potential mechanism relying on a channel, for example a K⁺ (Huguenard et al. 1991), a Ca²⁺-activated K⁺, a Ca²⁺ channel (Coulter et al. 1989) or a ligand-gated ion channel (Dreyer et al. 1976).

Ca²⁺ sensitivity of RID.

In an attempt to investigate the mechanism(s) underlying RID, we examined its dependence on residual Ca²⁺ using EGTA as a chelator (Fig. 6). If RID is Ca²⁺ dependent, then a Ca²⁺-dependent reduction in release probability could be a likely cause. We could not, however, demonstrate a Ca²⁺ dependence of RID. This inability might result from several factors. Firstly, it might be that EGTA is too slow to cause an efficient Ca²⁺ concentration clamp at the synapse and/or that the concentration achieved in the terminals was not high enough or was saturated by Ca²⁺ influx. Secondly, since RDD is clearly Ca²⁺ dependent (most likely due to the effect that buffering residual Ca²⁺ has on the probability of release), and, at the same time, buffering slowed recovery from depression (see below), depression tended to increase and become more release independent. The decrease in the parameter R_D that was observed could indicate that only RDD was Ca²⁺ dependent, or that both types of depression are Ca²⁺ dependent, however, with a greater Ca²⁺ sensitivity of RDD.

Mechanisms generating RID

A number of potential mechanisms for the generation of RID have been suggested: inactivation of presynaptic Ca²⁺ channels (Thomson & Bannister, 1999), change in action potential shape (reviewed in Zucker & Regehr, 2002), extracellular Ca²⁺ depletion (Borst & Sakmann, 1999), desensitization of the release machinery to Ca²⁺ (Bellingham & Walmsley, 1999), voltage-dependent inactivation of release (Dobrunz et al. 1997; Kraushaar & Jonas, 2000) and axonal conduction failure (Hatt & Smith, 1976; Brody & Yue, 2000).

At mammalian central synapses, there is little evidence from in vivo recordings or slice preparations that conduction failure occurs under physiological conditions (Cox et al. 2000; Koester & Sakmann, 2000) even though studies of cultures have shown that axonal propagation might not always be reliable (Lüscher et al. 1994; Debanne et al. 1997). It is also unlikely that changes in action potential shape during the burst of presynaptic activity play a significant role in the RID observed in our experiments, since RID was seen at low firing rates (< 5 Hz), where the interspike intervals were much longer than the relative refractory period. We also think that desensitization is an unlikely candidate for the depression observed for the following reasons. Firstly, stimulus frequencies in the range of 10 Hz are sufficiently low for AMPA receptors to recover appreciably and, secondly, such a scenario would argue for a negative correlation between consecutive EPSCs (Matveev & Wang, 2000; Scheuss et al. 2002), a fact that is challenged by the observation that many connections do not show any sign of correlation at all. In addition, the same line of thought also rules out a major involvement of presynaptic autoreceptors, which could be activated by the release of glutamate. We therefore conclude that the mechanism(s) of depression occur(s) prior to the exocytotic step.

RID could be caused by three different scenarios. Firstly, if Ca²⁺ indeed causes this form of depression, activation of Ca²⁺-dependent K⁺ channels might hyperpolarize the terminals and thereby limit the Ca²⁺ influx on subsequent action potentials. A similar mechanism has been observed at terminals in the posterior pituitary (Bielefeldt & Jackson, 1993). Secondly, along a similar line, Ca²⁺-dependent inactivation of Ca²⁺ channels could provide a reduced Ca²⁺ influx on subsequent action potentials (Forsythe et al. 1998). We think that this mechanism is unlikely since recovery from inactivation is of the order of minutes rather than the ∼600 ms observed in our data. And, thirdly, if inactivation of the release machinery were the cause of this depression (Kraushaar & Jonas, 2000; Waldeck et al. 2000), it would require that those terminals with pronounced RID have an altered release machinery either by biochemical composition or, for example, by phosphorylation. Detailed investigation of the mechanism underlying the form of RID reported in our study remains for future investigation.

Recovery from depression

The second feature of depression we observed was that at certain synapses, a steady-state response is attained, which is largely independent of input frequency within a physiological range (≤ 50 Hz, Fig. 7C and D). This is in contrast to synapses in which the rate of recovery from depression is constant, and the steady-state response is inversely related to the presynaptic firing frequency (1/f, Abbott et al. 1997; Tsodyks & Markram, 1997). This feature of synaptic depression is explained by a frequency-dependent mechanism of recovery from depression (FDR).

FDR has been reported at invertebrate and mammalian synapses (reviewed in Zucker & Regehr, 2002). FDR at the giant synapse of mouse auditory brainstem (Wang & Kaczmarek, 1998; Sakaba & Neher, 2001, 2003) was shown to be regulated by Ca²⁺ influx via voltage-gated Ca²⁺ channels (although the data of Weis et al. 1999 does not support this hypothesis). This neuronal pathway needs to relay high frequency input in very precise temporal output and, thus, it is crucial that these synapses recover rapidly from depression. At this synapse, however, FDR occurs at frequencies > 100 Hz, a much higher rate than observed in our study. FDR at cerebellar climbing fibre–Purkinje cell synapses also depends on residual presynaptic calcium (Dittman & Regehr, 1998; Dittman et al. 2000).

In our study, FDR occurs in paired recordings at neocortical synapses performed at physiological temperature. Moreover, FDR occurs at frequencies as low as 10 Hz, definitely in the physiological firing range of excitatory cortical neurones in vivo (Brecht & Sakmann, 2002). The apparent FDR can be identified clearly in the different recovery rates following bursts at 10 and 20 Hz, and we quantified FDR by comparing the normalized recovery amplitudes (R_rec) at these frequencies. R_FDR ranges between 0.9 and 1.9 indicating that at some connections recovery is about twice as fast at the higher stimulus frequency whereas at others there is no significant FDR.

FDR and augmentation

An apparent FDR could theoretically be the result of augmentation, which is also frequency dependent (Magleby & Zengel, 1976; Swandulla et al. 1991). With 100 pulses at 10 Hz, we could demonstrate that augmentation is 40% and decays with a τ_Aug of 10.9 ± 5.3 s, which is consistent with other reports at neocortical synapses (Klein, 1994). Under our conditions and following 20 action potentials, augmentation (Magleby & Zengel, 1976) would only contribute about 8% to the increase in EPSC amplitude and therefore cannot explain the 200% increase in recovery amplitude observed. Furthermore, augmentation was not sensitive to 5 mm EGTA in the patch-pipette, whereas FDR was completely abolished at the same concentration. In addition, if augmentation were the underlying mechanism, it would have to precisely counterbalance the amount of depression since at different frequencies a steady-state of similar amplitude can still be observed. We therefore think that augmentation cannot explain our data and propose that FDR is a genuine mechanism operating at these synapses.

Ca²⁺ sensitivity

The inability to block augmentation at the chosen concentrations of EGTA could result from at least two factors. Firstly, the concentration reached in the terminal(s) is very likely smaller than that in the pipette solution and therefore might be saturated by the increase in background Ca²⁺. We think that this is unlikely since at the same time FDR was blocked. It suggests that the K_d value for the Ca²⁺ dependence of recovery is smaller than that for augmentation. Secondly, augmentation might be caused by smaller changes in background Ca²⁺ than could be effectively buffered by the EGTA concentrations used. It might be that very much higher concentrations, which we did not test, would be effective.

As a preliminary investigation into the mechanisms underlying FDR, we investigated its temperature and Ca²⁺ dependence. FDR was temperature dependent, but had a lower Q₁₀ than the one for R_D. A value of 1.4 ± 0.1 for Q₁₀ is suggestive of aqueous diffusion (Hille, 2001) and therefore consistent with the idea that background Ca²⁺ is the causative agent.

The sensitivity of FDR to presynaptic EGTA also provides evidence that there are no significant underlying postsynaptic mechanisms influencing the time course of recovery. Potentially, AMPA receptor desensitization could have the opposite effect to FDR in reducing recovery at higher frequencies. However, in the presence of EGTA, R_FDR was blocked but recovery was the same at 10 and 20 Hz, which would not have been the case if there were significant desensitization.

Correlation between RID and FDR

We noted that FDR is correlated with RID (Fig. 8), such that connections, which express pronounced RID, also show FDR. Such a correlation could occur in two ways. Firstly, FDR and RID could be causally related. This could be brought about if FDR consists of a frequency-dependent increase in the recovery rate from RID (τ_inrec; as implemented in the model). Secondly, FDR could be a frequency-dependent increase in the recovery rate of RDD (τ_rec). In this scheme, recovery from RDD would be sufficiently fast for it to only provide a negligible component of the depression. Then only RID would be observed and therefore it would appear to be correlated with FDR. The latter explanation appears more unlikely, since in this case the apparent recovery rate (combination of τ_rec and τ_inrec) following a burst at 10 Hz would be faster for those connections with dominant RID (as τ_rec would be sufficiently fast for negligible RDD to occur). This was not observed in our set of data.

Model of synaptic depression

Models replicating the dynamics of mean synaptic responses have previously been proposed (Abbott et al. 1997; Tsodyks & Markram, 1997) as well as models based on vesicle depletion (Quastel, 1997; Maass & Zador, 1999; Kraushaar & Jonas, 2000; Matveev & Wang, 2000; Fuhrmann et al. 2002). With the exception of Kraushaar & Jonas (2000), these models do not in general account for RID and FDR and therefore they cannot adequately describe most of our experimental data.

The model described here extends a previous version (Fuhrmann et al. 2002) and reproduces the responses of neocortical connections to sequences of action potentials, both in terms of the average response dynamics, and the response fluctuations. A synapse with short τ_rec (relative to τ_inrec) will exhibit prominent RID, because replenishment of the vesicular pool (i.e. recovery from RDD) will not be rate-limiting. RDD results from the opposite relation between the recovery time constants, or from negligible changes in release probability with subsequent action potentials (U₁→ 0, eqn (6)).

Since we noted that FDR and RID are correlated, FDR is formalized as a gradual acceleration of recovery from the release-independent component of depression, i.e. a mechanism counterbalancing the decrease in the probability of release. However, in theory, the independence of the steady-state response from input frequency and FDR could be expressed at connections with pure RDD (as discussed above). We cannot exclude the possibility, although we consider this less likely for the reasons given above.

Functional consequences of RID and FDR

The presence of RID has important consequences for information transfer (Fig. 13). If there were no RID, synapses with low probability of release would be unable to reliably code presynaptic activity because, based on vesicle depletion alone, release would occur too infrequently to cause depression. However, since RID is independent of release, it allows reliable coding at such synapses.

The functional significance of FDR is that at high frequencies of stimulation it enables information transmission by preventing the synapse from depressing too much, and therefore linearizing the dependence of the postsynaptic depolarization on the presynaptic frequency.

Our data suggest that there are different operating modes of synapses. At one extreme, dominated by RDD, the synapse cannot transmit rate information at high input rates due to the decrease in the amplitude of responses in proportion to the input frequency. This mode favours temporal information processing, as a transient response to a frequency change occurs at all frequencies. At the other extreme, if pure RID and FDR are expressed, rate information is transmitted even at high frequencies. Our data indicates that there is a continuum between the two extreme operating modes. Since different neuronal connections are dominated either by RDD or RID, it may be that different connections are optimized for relaying either rate or temporal information.

The underlying factors determining whether a synapse expresses RID and/or RDD are at present unknown. It could be that the type of depression is determined by the postsynaptic neurone (target specificity) or that there is presynaptic specificity. Presynaptic neurones whose response to depolarization consists of a brief burst of action potentials may only express RDD since continuous firing would quickly end up in no transmission. Similarly, tonically firing neurones may then have RID synapses. Functionally, the expression of both components of depression may be important in neural networks. The response times of many systems can be optimized by combining an appropriate mixture of signals of the first derivative (the rate change in the current context) and steady state (Wilts, 1960).

Appendix

Quantifying the release dependence of depression (R_D)

E₁ and E₂ are random variables representing the first and second EPSCs. The correlation coefficient is

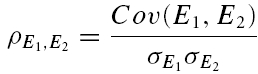where

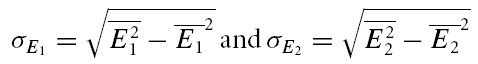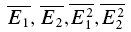,are the expectation values. The covariance is

Intuitively, if there is no correlation between E₁ and E₂(ρ_E1,E2= 0), the synaptic depression is purely release independent. As the correlation between E₁ and E₂ becomes more negative (Fig. 2B), there is more RDD. The maximal negative correlation between E₁ and E₂ occurs for pure RDD. ρ_E1,E2 can take values between 0 (pure RID) and ρ_RDD (pure RDD). We define R_D as the correlation coefficient between E₁ and E₂, normalized by ρ_RDD (eqn (1)), where 0 ≤R_D≤ 1. In practice, if the sample size is small, R_D might fall outside these boundaries.

To compute ρ_RDD, we assume that the frequency of stimulation approaches infinity; thus, there is no recovery from depletion between action potentials. We can then derive ρ_RDD using the formalism for a binomial process applied to a depressing synapse (eqn (5)). Based on this idea, at the arrival of the first action potential, there are n vesicles available for release. In the case of pure RDD, following the release of n₁ vesicles in response to the first action potential, there are only n − n₁=n₂ vesicles left. According to the binomial theorem in our notation

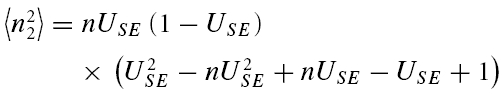The postsynaptic response to the release of n_i vesicles is proportional to n_i. Substitution of 〈n₁〉, 〈n₂〉, 〈n₁²〉, 〈n₁²〉 and 〈n₁n₂〉 into eqn (11), eqn (12) and eqn (13) gives

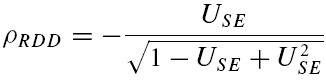which is equivalent to

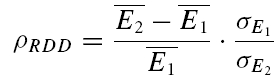when substituting the expectations given above. This expression can be evaluated from experimental recordings directly.

For a graphical illustration of R_D, we note that 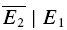(average E₂ for a given E₁) is linearly related to E₁ with E₁= A_SE.n₁/n, i.e.

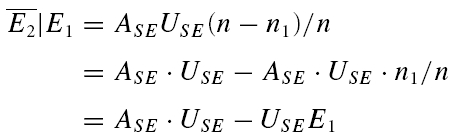We plot E₂ against E₁ and calculate the linear regression with the y-intercept

and slope

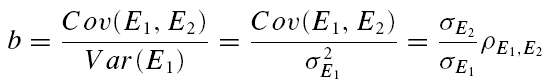Therefore, a can be rewritten as a function of the correlation coefficient

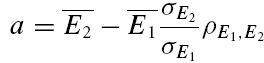For pure RID, there is no correlation between E₁ and E₂ and therefore a= 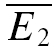. For pure RDD, the y-intercept is equal to 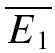(see and eqn (8) and eqn (16)). Therefore, R_D is the y-intercept of the regression line normalized within the range of 0–1, i.e.