Abstract
This paper quantifies recent experimental results through a general physical description of the mechanisms that might control two fundamental cellular parameters, resting potential (Em) and cell volume (Vc), thereby clarifying the complex relationships between them. Em was determined directly from a charge difference (CD) equation involving total intracellular ionic charge and membrane capacitance (Cm). This avoided the equilibrium condition dEm/dt = 0 required in determinations of Em by previous work based on the Goldman-Hodgkin-Katz equation and its derivatives and thus permitted precise calculation of Em even under non-equilibrium conditions. It could accurately model the influence upon Em of changes in Cm or Vc and of membrane transport processes such as the Na+–K+-ATPase and ion cotransport. Given a stable and adequate membrane Na+–K+-ATPase density (N), Vc and Em both converged to unique steady-state values even from sharply divergent initial intracellular ionic concentrations. For any constant set of transmembrane ion permeabilities, this set point of Vc was then determined by the intracellular membrane-impermeant solute content (X−i) and its mean charge valency (zX), while in contrast, the set point of Em was determined solely by zX. Independent changes in membrane Na+ (PNa) or K+ permeabilities (PK) or activation of cation–chloride cotransporters could perturb Vc and Em but subsequent reversal of such changes permitted full recovery of both Vc and Em to the original set points. Proportionate changes in PNa, PK and N, or changes in Cl− permeability (PCl) instead conserved steady-state Vc and Em but altered their rates of relaxation following any discrete perturbation. PCl additionally determined the relative effect of cotransporter activity on Vc and Em, in agreement with recent experimental results. In contrast, changes in Xi− produced by introduction of a finite permeability term to X− (PX) that did not alter zX caused sustained changes in Vc that were independent of Em and that persisted when PX returned to zero. Where such fluxes also altered the effective zX they additionally altered the steady state Em. This offers a basis for the suggested roles of amino acid fluxes in long-term volume regulatory processes in a variety of excitable tissues.
Cell volume (Vc) and resting potential (Em) constitute two fundamental and interdependent baseline parameters important for cellular function. Adrian (1956) showed that membrane potentials of skeletal muscle fibres varied with extracellular osmolarity in solutions where K+ constituted the only significant permeant ion. This Em shift followed predicted alterations in relative intracellular and extracellular K+ concentrations ([K+]i and [K+]e) as expected if Vc varied linearly with reciprocal extracellular osmolarity (Dydynska & Wilkie, 1963; Blinks, 1965). However, more recent findings suggested a more complex relationship between Vc and Em in more physiological extracellular solutions, and that this relationship diverged between different cell types. Ferenczi et al. (2004) suggested that osmotically induced shrinkage in skeletal muscle fibres activated inward Na+–K+–2Cl− cotransport (NKCC). This stabilized Em despite expected increases in [K+]i/[K+]e (Adrian, 1956), by holding [Cl−]i/[Cl−]e above its equilibrium value (cf. Aickin et al. 1989). There was an accompanying trivial volume recovery in agreement with earlier work (Blinks, 1965). This behaviour contrasted sharply with that of several other cell types in which shrinkage-induced cotransporter activity produces marked regulatory volume increases (RVIs) (reviews: Lang et al. 1998a; O'Neill, 1999), but does not influence Em (Lauf & Adragna, 2000). Similarly, while exhaustive exercise leads to increases in muscle fibre volume of up to 20% (Sjogaard et al. 1985), regulatory volume decrease (RVD) has never been demonstrated in mature skeletal muscle fibres (Sejersted & Sjogaard, 2000), although RVD is an almost ubiquitous response to swelling in non-excitable tissues (O'Neill, 1999; Okada et al. 2001). Yet long-term muscle fibre volumes in vivo remain remarkably stable (review: Proske & Morgan, 2001) despite this apparent regulation of Em in preference to Vc in the short term (Ferenczi et al. 2004).
The present study reconciled and clarified these findings through the introduction of a mathematical model that incorporated the principal factors known to influence Vc and Em. This interrelationship between Vc and Em is of potential importance particularly in excitable cells: Em depends on intracellular ion concentrations that are altered both by volume changes and by volume regulatory mechanisms. Skeletal muscle was used as a paradigm of excitable cells in view of recently recognized interactions between Vc and Em in this tissue (Geukes Foppen et al. 2002; Ferenczi et al. 2004; Geukes Foppen, 2004). This study examined how cellular volume and resting potential might be determined, maintained and regulated by the wide range of interdependent membrane transport systems in excitable cells.
The model was designed to permit direct and precise calculation of Em for any value of its rate of change, dEm/dt. Therefore Em was calculated directly from the membrane capacitance Cm and the intracellular charge difference, defined by the precise difference between the total charge carried by the positive and negative ions within the cell. This can be summarized in a charge difference (CD) equation:
where [X−]i denotes the internally sequestered osmolyte concentration and zX its mean charge valency. Using this formulation, it was possible to calculate Em precisely even under conditions where volume changes and/or volume regulatory mechanisms shifted transmembrane ion gradients away from electrochemical equilibrium, resulting in net transmembrane ion currents. Such currents would have violated the central assumption of earlier analyses that employed the Goldman-Hodgkin-Katz (GHK) equation (Goldman, 1943; Hodgkin & Katz, 1949), or derivatives such as the Mullins-Noda (MN) equation (Mullins & Noda, 1963) and the recent formulation of Armstrong (2003), which required dEm/dt = 0.
Successive iterations using the charge difference method could calculate the effect upon Em of any combination of quantitatively defined membrane transport processes after each suitably small time step of their activity. For example, the calculations incorporated a Na+–K+-ATPase model (Hernandez & Chifflet, 2000) and could simulate the electrogenic effect of this pump directly from the changing intracellular ion concentrations, without assuming the condition that dEm/dt = 0, which is required for inclusion of an electrogenic sodium pump term in GHK-derivative equations (e.g. Mullins & Noda, 1963; Armstrong, 2003). This study additionally incorporated passive Em-dependent ion fluxes (Goldman, 1943), membrane capacitance changes (Huang, 1981a, b), cation–chloride cotransport (Lauf & Adragna, 2000), non-monovalent organic anion fluxes (review: Strange et al. 1996), changes to zX such as may occur when organic anions buffer pH changes, and volume changes and the consequent concentration or dilution of intracellular ions. This formulation could also be used to model ion antiport, rectifying and other non-linear permeabilities, voltage-gated ion channels, and the influence of imposed voltage steps upon Vc. Many of these processes would be difficult or perhaps impossible to model accurately using a GHK-based formulation.
Finally, flexibility in the iteration time step would permit modelling over any rate of change in any of the parameters (e.g. even during action potentials), in direct contrast to the central requirement of models based on the GHK equation that dEm/dt = 0. Thus, comparison of the CD equation and the MN equation showed small but demonstrably significant discrepancies in calculated Em when dEm/dt ≠ 0. However, when dEm/dt = 0, substitution of the solute concentrations that were determined by the CD approach into the MN equation gave steady state Em values in perfect agreement with the CD modelling, providing important confirmation of the validity of the charge-difference approach.
This study first demonstrated that Vc and Em each converge to unique steady state values thereby offering fixed set points even in the absence of any specific cellular mechanisms sensing Vc or Em. Secondly, the set point of Vc at constant extracellular osmolarity was determined entirely by the internally sequestered solute content (Xi) and its charge (zX), given stable ion permeabilities and Na+–K+-ATPase density sufficient to maintain a stable volume. Thirdly, steady-state Em under such conditions was determined solely by zX, and relaxed to this value following any changes to intracellular inorganic ion concentrations or membrane capacitance. Fourthly, discrete changes in ion permeabilities, cotransport activity, Na+–K+-ATPase density, or extracellular osmolarity were shown to influence Vc and/or Em. However, whatever the magnitude of the resulting perturbations, they completely reversed with reversal of the underlying changes without any requirement for specific Vc- or Em-sensitive control mechanisms.
Finally, changes in Vc that in contrast were both sustained and independent of Em occurred only with changes in cellular X−i content. Where such changes were simulated by the introduction of a finite permeability term to X− (PX), the resulting transmembrane effluxes of organic anion then produced sustained Vc decreases that persisted when PX was returned to zero and did not influence the set-point of Em. This might offer a basis for the possible role of amino acid fluxes in volume regulatory processes in a variety of excitable tissues, including cardiac muscle (Rasmusson et al. 1993), barnacle muscle (Pena-Rasgado et al. 2001) and hippocampal neurones (Pasantes-Morales et al. 2000; Olson et al. 2003). In contrast, fluxes that resulted in a change in effective zX also altered the Em set point. This might occur, for example, if an efflux consisted only of uncharged X, thus altering the mean charge on the remaining Xi. The model thus confirmed that organic osmolyte fluxes are entirely feasible for long-term volume regulation without necessarily disrupting Em, and thus seem the most likely candidate for volume regulation in skeletal muscle, a cell type in which high PCl has been shown to prevent cation–chloride cotransport mechanisms for this purpose (Ferenczi et al. 2004). Furthermore, such changes to organic anion content appear to be both necessary and sufficient to produce volume changes of sufficient magnitude and permanence to underlie processes such as growth, atrophy and hypertrophy.
Mathematical model
The numerical model specifically avoided any dependence on the assumption of electrochemical equilibrium that was necessitated by earlier calculations of the membrane potential, Em, using the Goldman-Hodgkin-Katz (GHK) equation or its derivatives (Mullins & Noda, 1963; Armstrong, 2003). Thus Em was calculated at each iteration time point, t, from the difference between the sums of the intracellular positive and negative charges, i.e.
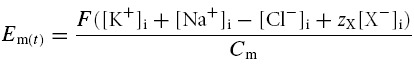 |
(1) |
F is Faraday's constant (C mol−1), Cm (C V−1 l−1) is the membrane capacitance referred to unit cell volume, [X−]i represents the total concentration (m) of a variety of osmotically active and normally membrane impermeant cellular constituents that include cytosolic proteins, amino acids, nucleotides and phosphorus-containing anions (Maughan & Recchia, 1985; Maughan & Godt, 2001) and zX (dimensionless) is the mean charge valency of X−. zX is negative; thus [X−]i balances the charge of the high intracellular cation concentrations. Note that this equation implicitly assigns the charge valencies of K+, Na+ and Cl− as +1, +1 and −1, respectively.
The passive ion fluxes were then modelled based on their electrochemical potentials, using the Goldman equations as modified by Hodgkin and Katz (Goldman, 1943; Hodgkin & Katz, 1949), such that for any solute S its flux (JS) per cm2 of cell membrane (mol cm−2 s−1) is given by:
| (2) |
where:
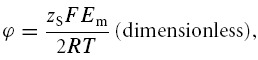 |
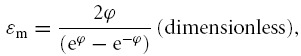 |
PS (cm s−1) is the permeability of the membrane to S, [S]e and [S]i the extracellular and intracellular concentrations of S (m), respectively, zS (dimensionless) the charge valency of S, and F, R and T have their usual meanings. Note that fluxes of X− could be simulated using this formulation, although unless otherwise stated, PX = 0.
Na+–K+-ATPase activity was described by the detailed kinetic model reported by Hernandez et al. (1989) using rate constants and other numerical parameters as presented in Hernandez & Chifflet (2000). This employs a six-stage sequential kinetic model of sodium pump activity and calculates the pump flux JP (mol cm−2 s−1) as:
| (3) |
where α is the product of six ‘forward’ rate constants, β the product of six ‘reverse’ rate constants, N the sodium pump density, and Σ is a function of all the rate constants and ligand concentrations, explicitly described in Hernandez et al. (1989). Therefore the outward sodium flux is 3JP and the inward potassium flux is 2JP. The rate constants α and β depend on the following concentrations: [ATP]i, [ADP]i, [inorganic phosphate] ([Pi]i), [K+]i2, [K+]e2, [Na+]i3, [Na+]e3 and Em, as described in detail in the original papers (Hernandez et al. 1989; Hernandez & Chifflet, 2000) and not reproduced in full here. Hernandez & Chifflet's model effectively indicates that JP depends on the free energy changes inherent in each pump cycle: thus JP increases if the free energy change of each pump cycle becomes more favourable, for example if the transmembrane Na+, K+ or Em gradients are reduced, or if the reaction ATP → ADP + Pi becomes more favourable (e.g. by an increase in [ATP]i). Such dependence of JP upon free energy changes has been explicitly demonstrated in cardiac muscle (Jansen et al. 2003). No further regulatory properties were added to this Na+–K+-ATPase activity.
The model also included contributions of the following cation–chloride cotransporters to transmembrane ion movements: the Na+–K+–2Cl− cotransporter (NKCC) and the K+–Cl− cotransporter (KCC). As the purpose of the study was to investigate the maximum possible contributions of these ion transport mechanisms, no regulatory processes were modelled over and above any dependence of the fluxes upon the intracellular and extracellular concentrations of their transported ions. These fluxes were modelled based on arbitrary permeability terms, PNKCC and PKCC (dimensionless) expressed relative to the membrane permeability of potassium. The ion fluxes through these cotransporters were then calculated from the product of the transported species' transmembrane concentration gradients. Note that ion fluxes through the cotransporters were therefore independent of Em, in agreement with experimental evidence (Lauf & Adragna, 2000). Thus:
| (4a) |
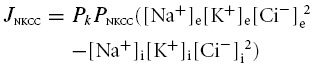 |
(4b) |
For example if PNKCC = 1, {([Na+]e[K+]e[Cl−]e2)/([Na+]i[K+]i[Cl−]i2)} = {[K+]e/[K+]i} and Em = 0, then for every 1 mol flux of K+ through background ‘leak’ channels, there would be a flux of 1 mol each of Na+ and K+, and 2 mol of Cl− through the NKCC. However, as the transmembrane K+ flux is dependent on Em while fluxes through the NKCC are not, the ‘permeability’ terms of the cotransporters are not straightforwardly comparable to the basic ionic permeabilities at other values of Em.
At this stage of calculation the net ionic fluxes were summed (expressed as JTOTAL (m s−1), positive inward), and water movement (volume change) calculated by assuming that all ion movements were accompanied by sufficient water to render the ion fluxes isosmotic to the extracellular medium. It is reasonable to assume water movement follows ion movement with no lag as cell permeability to water is at least 1000 times greater than to ions (Verkman, 1992; Frigeri et al. 2004). The relative volume after each time step was thus:
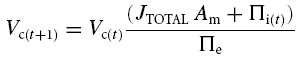 |
(5) |
where Am is the membrane area per unit volume (cm2 l−1) and Πi and Πe represent total intracellular and extracellular osmolarity, respectively (osmol l−1). Note that Am was maintained at a constant value that was independent of cell volume. Although it is likely that Am would indeed vary with volume in vivo, this was not modelled for two reasons. Firstly, ionic permeability per unit membrane area and sodium pump density would be unlikely to stay constant if absolute membrane area changed. Secondly, while Am does clearly influence the rate of transmembrane ion fluxes, it does not influence the relative rates of such fluxes. In other words, steady-state points of stability in the model are independent of the value of Am. For a similar reason, average membrane permeabilities were used with the assumption that each cell was a tube of 75 μm diameter, giving Am = 5 × 105 cm−2 l−1. No attempt was made to model the transverse tubular system separately, as this would influence the kinetics of the model, but not the final values of the modelled parameters.
During each iteration step the calculations were performed in the order of. Then the new membrane potential (Em(t +1)) was once again calculated from and the iteration cycles were repeated. The model was initiated with a step size of 10−8 s per iteration, and this step size was then dynamically adjusted with each iteration to maintain the rate of change of Em at < 10−6 V per iteration and the step size < 10−3 s per iteration. The validity of this method was checked by repeating several of the simulations with step sizes fixed at much smaller or much larger step sizes (between 10−9 and 10−2 s per iteration). These preliminary simulations confirmed that, although excessively large step sizes could result in oscillation of the calculated Em, if step size was small enough that such oscillations did not occur, step size had absolutely no effect on the overall rate of change of any parameter or on their final stable values. This step size above which oscillations would occur was dependant upon the rate of change of Em, and thus limiting the rate of change of Em in the variable step size model ensured such oscillations did not occur. Modelling based on the Mullins-Noda or Goldman-Hodgkin-Katz equation was performed with a fixed step size of 10−5 s per iteration. Each of these simulations was then repeated with a fixed step size of 10−4 s per iteration, and the results were identical in all cases.
Table 1 shows the standard parameters with which the modelling process was initiated, unless otherwise stated in the text. These parameters are representative of amphibian skeletal muscle, and are derived from a variety of sources. (Adrian, 1956; Eisenberg & Gage, 1969; Gage & Eisenberg, 1969; Maughan & Recchia, 1985; Hernandez et al. 1989; Huang & Peachey, 1989; Thompson & Fitts, 1992; Hernandez & Chifflet, 2000; Maughan & Godt, 2001; Clausen, 2003).
Table 1.
Symbols used in the text, and initial values of parameters used in the model
| Parameter | Symbol | Value | Refs. (see legend) |
|---|---|---|---|
| Extracellular Na+ concentration | [Na+]e | 112.5 mm | 1 (as frog Ringer) |
| Extracellular K+ concentration | [K+]e | 2.5 mm | 1 (as frog Ringer) |
| Extracellular Cl− concentration | [Cl−]e | 115 mm | 1 (as frog Ringer) |
| (Thus: Extracellular osmolarity) | Πe | 230 mosmol l−1 | 1 (as frog Ringer) |
| Intracellular ATP concentration | [ATP]i | 6 mm | 5, 7, 8 |
| Intracellular ADP concentration | [ADP]i | 6 × 10−3 mm | 5, 7, 8 |
| Intracellular inorganic phosphate | [Pi]i | 4.95 mm | 5, 7, 8 |
| Membrane Na+ permeability | PNa | 0.8 × 10−9 cm s−1 | 1, 2 |
| Membrane K+ permeability | PK | 4 × 10−8 cm s−1 | 1, 2 |
| Membrane Cl− permeability | PCl | 1.2 × 10−7 cm s−1 | 1, 2 |
| (Thus: Ratio of permeabilities) | PNa: PK: PCl | 0.02: 1: 3 | |
| Na+–K+-ATPase density | N | 5 × 10−12 mol cm−2 | 5, 8, 10 |
| Mean organic osmolyte valency | zX | − 1.6477 | 4, 9 |
| Membrane capacitance | Cm | 7 μF cm−2 | 3, 6 |
Key to references: (1) Adrian (1956). (2) Eisenberg & Gage (1969). (3) Gage & Eisenberg (1969). (4) Maughan & Recchia (1985). (5) Hernandez et al. (1989). (6) Huang & Peachey (1989). (7) Thompson & Fitts (1992) (8) Hernandez & Chifflet (2000). (9) Maughan & Godt (2001). (10) Clausen (2003).
Results
I. Volume determination in a cell with constant membrane ion permeabilities, sodium pump density and extracellular osmolarity
The intrinsic properties of Na+–K+-ATPase activity ensure both attainment and maintenance of stable physiological values of Em, Vc and intracellular solute concentrations
Animal cells normally maintain stable volumes (Vc), membrane potentials (Em) and intracellular ion concentrations: such homeostasis ultimately requires a functioning Na+–K+-ATPase resulting in effective sodium pump activity, without which cells inevitably swell and eventually lyse due to an unopposed net ion influx (Tosteson & Hoffman, 1960). A first test of charge-difference (CD) modelling accordingly examined whether a model cell with basic parameters derived from experimental data (Table 1) successfully reproduced such pump-dependant stability. The results were contrasted with approaches using the alternative Goldman-Hodgkin-Katz (GHK) equation and its variants.
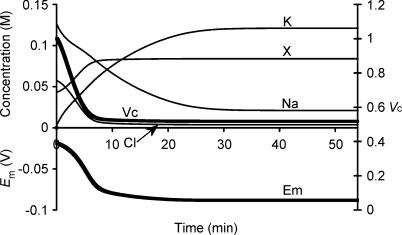
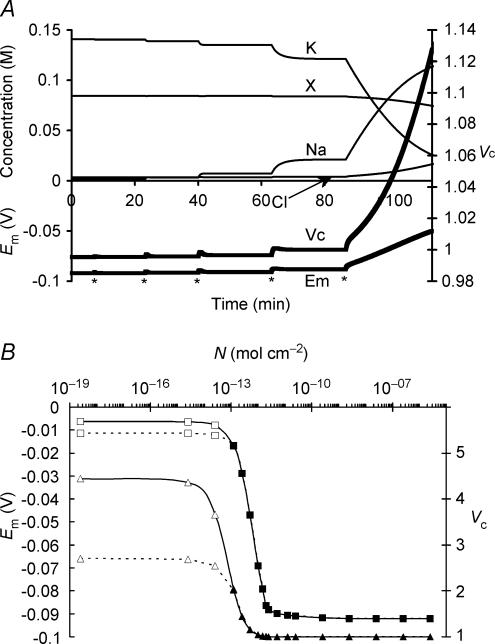
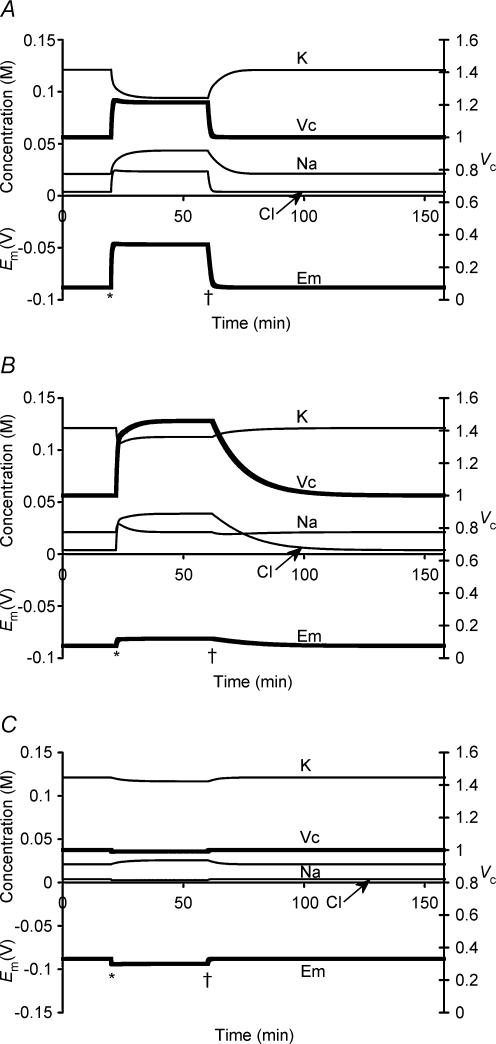
Figure 1 summarizes a simulation that used semiarbitrarily chosen, as opposed to physiological, initial solute concentrations in order to avoid presupposing points of stability in the model: (to one decimal place) [Na+]i = 126.7 mm, [K+]i = 2.5 mm, [Cl−]i = 57.5 mm and [X−]i = 43.5 mm. These initial values, with the exception of the replacement of approximately half the Cl− by organic anions (X−), approximated normal extracellular concentrations. Furthermore this particular choice of values gave a total initial intracellular charge difference of precisely zero, Em(t = 0) = 0 mV, by the CD method. Na+–K+-ATPase activity was left to be determined solely by its intrinsic dependences upon transported and energetic substrates, as described in the Mathematical model section, without any regulatory mechanisms involving any direct sensing of Em or Vc.
Figure 1. Activation of the sodium pump in a cell initially close to passive equilibrium.
The model was initiated with values of all intracellular ionic concentrations close to equilibrium with the extracellular fluid, although with approximately half the normal organic anion concentration and a consequently lower [Cl−]i to maintain a total intracellular charge difference of zero. Thus initially [Na+]i = 126.7 mm, [K+]i = 2.5 mm, [Cl−]i = 57.5 mm and [X−]i = 43.5 mm. Vc was initially defined as 1. Symbols are as follows: K: [K+]i; Na: [Na+]i; Cl: [Cl−]i; X: [X−]i; Em: Em, Vc: Vc. The basic parameters such as ion permeabilities and sodium pump density were derived from frog skeletal muscle (Table 1). Note that despite the arbitrary starting conditions, each intracellular ion concentration, Vc and Em all reach stable values that are strikingly similar to normal values for frog skeletal muscle.
Em, Vc and each of the intracellular solute concentrations gradually approached stable final steady state values that strikingly reproduced the intracellular ion concentrations and Em found in frog skeletal muscle (Hodgkin & Horowicz, 1959; Maughan & Recchia, 1985) despite such arbitrary starting parameters. The membrane potential Em(MN) was also calculated at each time point using the Mullins-Noda (MN) equation (Mullins & Noda, 1963) for comparison with the corresponding result Em(CD) from the charge difference equation. Em(CD) and the value of Em(MN) calculated from the values of the intracellular solute concentrations derived from CD modelling independently converged to identical final values (both precisely −88.235270 mV) despite the very different methods of calculation, particularly regarding the electrogenic sodium pump contribution. This strongly corroborates the validity of the CD modelling technique adopted here. However, Em(MN) was almost 1 mV less negative than Em(CD) in the initial transients. This may reflect the condition in the MN equation for calculation of resting membrane potential that requires perfectly balanced leak and electrogenic pump currents (Mullins & Noda, 1963). Similar requirements would apply to other analyses similarly based upon the Goldman-Hodgkin-Katz equation and its derivatives (see also Armstrong, 2003). The initial phase shown in Fig. 1 would generate significant net ionic fluxes that break this equilibrium assumption, result in dEm/ dt ≠ 0 and consequently additionally require treatment of the capacitive current term Cm(dEm/dt).
However, at physiological resting ion permeabilities and values of Na+–K+-ATPase density (N), dEm/dt appears relatively small even under disequilibrium conditions such as the starting conditions for Fig. 1. Accordingly, the significance of this early discrepancy between Em(CD) and Em(MN) was investigated. Alternative modelling, nevertheless using the same initial values as in Fig. 1, therefore calculated Em at each step in the simulation from the MN rather than the CD equation (eqn (1)) such that Em-dependant ion fluxes throughout the simulation ( eqns (2) and (3)) were dependant upon Em(MN) rather than Em(CD). This alternative model successfully reached stable final values of [Na+]i, [K+]i, [Cl−]i and [X−]i and Em, but these values significantly differed from those obtained using the CD model: [Na+]i = 17.6 mm; [K+]i = 105.6 mm; [Cl−]i = 4.3 mm [X−]i = 102.4 mm; and Em = −84.7 mV. These values appeared superficially reasonable; however, they produced a large charge discrepancy independent of the iteration time step employed such that;
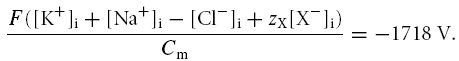 |
Thus, in contrast to the convergence of Em(MN) with Em(CD) as dEm/dt →0 in the CD equation model, these values instead diverged with each iteration that in the otherwise identical MN equation model to reach impossible values. This emphasized the importance of precise modelling of Em: transmembrane ion currents and Em are interdependent values. In Fig. 1, where dEm/dt is negative for each iteration until equilibrium is reached, Em(MN) is consistently slightly more positive than Em(CD). An example of the consequences of this is that outward K+ flux is slightly increased over this period, amplifying the small discrepancies in Em with each modelling step.
The recent formulation of Armstrong (2003) in which a sodium pump term was added to the GHK equation therefore shares its requirement that dEm/dt = 0, and can additionally become insoluble due to a negative logarithmic term when active fluxes are significantly greater than passive fluxes. It was not therefore possible to repeat the above comparison with the model based on Armstrong's equation.
CD modelling demonstrates a convergence of Vc and Em to unique steady-state values that are independent of the initial intracellular permeant ion concentrations and membrane capacitance
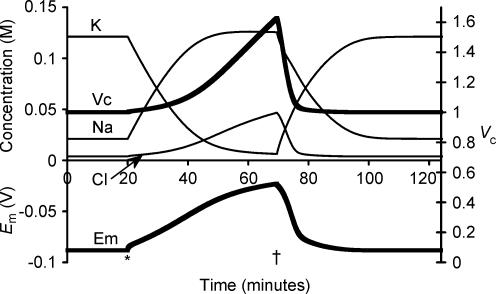
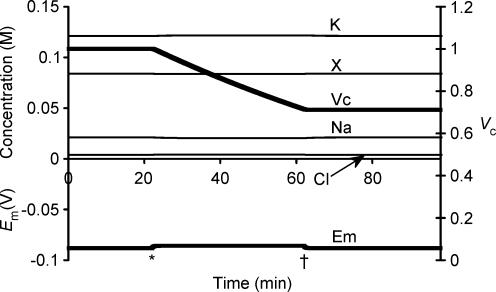
Figure 1 thus demonstrated that Na+–K+-ATPase activity alone, in the absence of any specific regulation towards predefined values of either Em or Vc, inherently causes their convergence to stable final values from an arbitrary starting point. The following simulations investigated the factors that determine these absolute values of Em, Vc and each intracellular solute concentration. First, Fig. 2 displays a simulation initiated from the final stable values from Fig. 1 apart from resetting Vc to 1. Complete inhibition of Na+–K+-ATPase activity after 20 min (marked with an asterisk) was followed as expected by the cell contents beginning gradually to equilibrate with the extracellular fluid. This was accompanied by a volume change that tracked the changing [Cl−]i as might be expected in the absence of any other extracellular anions. However, Cl− influx is not energetically favoured as Cl− is normally passively distributed and thus at electrochemical equilibrium (possible effects of cation–chloride cotransport mechanisms are considered in section IV). Nevertheless, it is apparent from Fig. 2 that the Cl− entry could follow the depolarization of Em, itself resulting primarily from the gradual reduction in [K+]i, as well as the loss of the small electrogenic contribution of the Na+–K+-ATPase. The time course of this cellular swelling was somewhat more rapid than has been observed in ouabain-treated skeletal muscle (e.g. Ferenczi et al. 2004), but closely agrees with previous attempts to model such phenomena (Hernandez & Cristina, 1998; Armstrong, 2003). Possible reasons for this apparent discrepancy are explored in section II below. Restoration of Na+–K+-ATPase activity 50 min later (marked with a dagger in Fig. 2) permitted recovery of each modelled variable to precisely its original value. Thus steady state Vc, Em and all intracellular solute concentrations were all unchanged by a period without Na+–K+-ATPase activity despite the considerable perturbations that resulted.
Figure 2. The effect of sodium pump inhibition.
The model was initiated with variables derived from the final results shown in Fig. 1, and therefore all variables were initially stable. For clarity, [X−]i is not shown, as it is membrane impermeant, and thus its concentration is straightforwardly related to Vc. At the point marked *, sodium pump density was reduced to zero, to simulate total sodium pump inhibition. Note the rapid small upward step in Em that resulted from the loss of the electrogenic pump activity. Following this there was a gradual slower depolarization as [K+]i and [Na+]i began to equilibrate with the extracellular fluid. This depolarization allowed [Cl−] influx and thus volume increase. At the point marked †, sodium pump density was returned to its original value. Note that Vc, Em and all intracellular ion concentrations returned to their starting values.
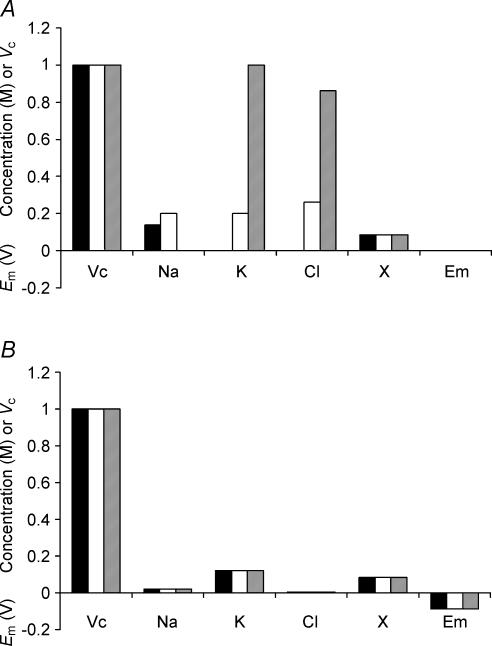
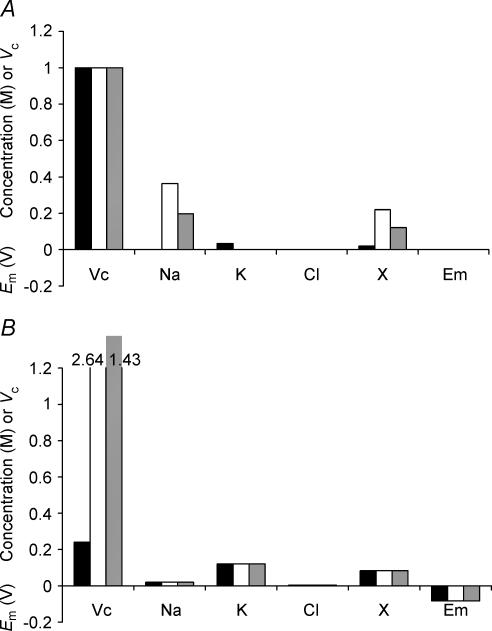
The second set of convergence tests used sharply contrasting initial intracellular concentrations of inorganic ions (Fig. 3A) but left [X−]i identical to the final value shown in Fig. 1 and all other cellular parameters identical to those in Table 1. Figure 3B shows that corresponding final values of Em, Vc, [Na+]i, [K+]i, [Cl−]i and [X−]i after a simulated 5 h period were entirely independent of these enormously divergent initial inorganic ion concentrations. Thus Cell 1 (filled column) began with [total intracellular osmolarity] < [extracellular osmolarity] and accordingly shrank in the initial stages of the simulation, concentrating all intracellular osmolytes. In sharp contrast, Cell 3 (grey column) began with a [total intracellular osmolarity] ≫ [extracellular osmolarity] and showed an initial swelling, which diluted all intracellular osmolytes. Nevertheless, both cells eventually equilibrated to exactly the same relative volumes and membrane potentials entirely independently of these initial intracellular ionic concentrations.
Figure 3. Initial intracellular inorganic ion concentrations do not influence eventual stable values of Vc or Em.
A, the starting conditions of three cells used as examples. The model was initiated with the intracellular organic anion concentration identical to that eventually reached in Fig. 1, but with three arbitrary and sharply different intracellular inorganic ion concentrations. Note that none of the cells were initially isotonic to the extracellular fluid. B, the final stable values reached after a 5-h modelling period. Variation in the initial intracellular inorganic ion concentrations has no influence on final stable values of Vc, Em, [Na+]i, [K+]i, [Cl−]i or [X−]i.
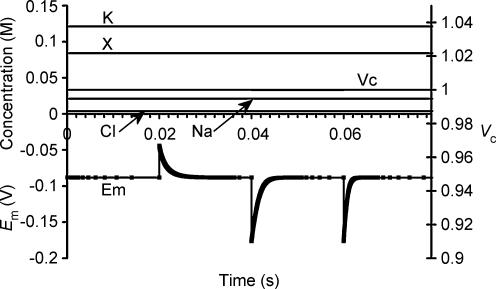
The possible influence of membrane capacitance (Cm) upon steady state value of Em and Vc was also investigated, as Cm is known to vary significantly in skeletal muscle with changes in Em even in the physiological range (Huang, 1981a,b). Figure 4 therefore shows the effects of large step changes in Cm in a simulation that was initiated with identical parameters to Fig. 2, although it should be noted that the results are plotted against a much faster time base. As shown, each step change in Cm resulted in a reciprocal change in Em, but Em then relaxed rapidly towards its original resting value. When Cm was doubled from its normal value of 7 μF cm−2 to 14 μF cm−2 or when it was halved from 14 μF cm−2 to 7 μF cm−2 the half-time of the Em recovery was 0.001 s. When Cm was halved from 7 μF cm−2 to 3.5 μF cm−2, the half-time of Em recovery was 0.0005 s. The half-time of relaxation of Em therefore follows the expected relationship with changing Cm that it should be directly proportional to the magnitude of that change and therefore to the total resultant transmembrane charge movement. It is therefore apparent that even large changes in Cm do not influence steady state values of Em. Furthermore, Em correction to its steady state value following a change in Cm occurs so quickly that any changes in Cm that are considerably slower than those considered here (i.e. that take place over more than a few milliseconds) would not be expected to cause a detectable change in Em. Vc and intracellular ion concentrations are grossly unaffected by changing Cm, although the Em corrections to steady state values do of course reflect submicromolar readjustments in the precise ion concentrations from which the charge difference equation calculates Em.
Figure 4. Membrane capacitance does not influence stable values of Vc or Em.
The model was initiated with variables derived from the final results shown in Fig. 1, and therefore all variables were initially stable. At 0.02 s, the membrane capacitance (Cm) was doubled from 7 μF cm−2 to 14 μF cm−2. This caused an immediate halving of Em, but Em then relaxed towards its original value extremely rapidly (half-time 0.001 s). Although this reflected a submicromolar change in the charge difference, the ion concentrations and Vc were grossly unchanged. At 0.04 s, Cm was returned to 7 μF cm−2, resulting in a reverse of the original step change in Em and a similar relaxation toward resting values (half time 0.001 s). Finally at 0.06 s Cm was halved to 3.5 μF cm−2, resulting in an immediate doubling of Em, followed by its rapid relaxation towards the original steady state value (half-time 0.0005 s). Note the rapid time scale: Em recovery to its steady state value following Cm changes occurs so rapidly that slow changes in Cm do not cause detectable Em changes.
Em, Vc and the concentrations of all intracellular solutes thus converge to fixed set points that are independent of other starting conditions given similar conditions of sodium pump density, ion permeabilities and intracellular impermeant organic anion content. This intrinsic regulatory property for baseline Vc and Em does not require any existence of control processes explicitly sensitive to either Vc or Em. Em and Vc similarly return to exactly these unique stable values after any discrete perturbation to intracellular inorganic ion concentrations such as may occur during discrete periods of transmembrane cation–chloride cotransport (explicitly demonstrated in section IV).
Modelling based on the GHK equation fails to demonstrate unique Vc and Em set points independent of initial intracellular inorganic ion concentrations
Table 2 demonstrates that simulations based upon the GHK equation and its derivatives yielded sharply divergent results. Although modelling using both the MN and the CD equations demonstrated that Em, Vc and intracellular solute concentrations all converge to final stable values, only the CD model predicted that these final values were independent of the initial intracellular inorganic ion concentrations. By contrast, in the MN model these final values markedly depended upon the initial intracellular inorganic ion concentrations. Furthermore, use of the MN model predicted enormous discrepancies between the total intracellular concentrations of positive and negative ions that would predict impossibly high transmembrane voltages (shown in bold type). The contrasting predictions of the two forms of model were further examined using an analytic relationship between steady state Vc and Em, for a cell with passive transmembrane distribution of Cl−, which is derived in the Appendix:
Table 2.
A comparison of charge-difference-based modelling with Mullins-Noda equation-based modelling
| Em equation | Cell | Vc | [Na+]i (m) | [K+]i (m) | [Cl−]i (m) | [X−]i (m) | Em(CD) (V) | Em(MN) (V) | Πi (m) |
|---|---|---|---|---|---|---|---|---|---|
| (Initial values) | 1, t = 0 | 1 | 0.138 | 0.000 | 0.000 | 0.084 | 0 | −0.09 | 0.222 |
| 2, t = 0 | 1 | 0.200 | 0.200 | 0.262 | 0.084 | 0 | +0.005 | 0.746 | |
| 3, t = 0 | 1 | 0.000 | 1.000 | 0.862 | 0.084 | 0 | +0.002 | 1.946 | |
| CD | 1, t = ∞ | 1 | 0.021 | 0.121 | 0.0038 | 0.084 | −0.088 | −0.088 | 0.230 |
| CD | 2, t = ∞ | 1 | 0.021 | 0.121 | 0.0038 | 0.084 | −0.088 | −0.088 | 0.230 |
| CD | 3, t = ∞ | 1 | 0.021 | 0.121 | 0.0038 | 0.084 | −0.088 | −0.088 | 0.230 |
| MN | 1, t = ∞ | 0.81 | 0.017 | 0.105 | 0.0044 | 0.103 | −1806 | −0.084 | 0.230 |
| MN | 2, t = ∞ | 1.12 | 0.023 | 0.129 | 0.0036 | 0.075 | +853 | −0.090 | 0.230 |
| MN | 3, t = ∞ | 2.4 | 0.034 | 0.158 | 0.0029 | 0.035 | +4509 | −0.095 | 0.230 |
The table shows [Na+]i, [K+]i, [Cl−]i, [X−]i (Vc) and (Em) for three cells with significantly different intracellular inorganic ion concentrations at t = 0, prior to modelling. The final stable values of each of these variables is shown for otherwise identical models based on either the charge-difference equation (CD) or the Mullins-Noda equation (MN) (t = ∞). Note that while the charge-difference model predicted that all three cells would stabilize with identical final values of each modelled variable, the Mullins-Noda model predicts final values that are dependant on the starting conditions. However, the Mullins-Noda model predicted final intracellular ion concentrations that were clearly impossible, as in each case there was a significant imbalance between the total concentrations of positive and negative ions within the cell (the magnitudes of the voltages suggested by these imbalances are shown in bold type). This resulted from the summation of many small errors in the calculation of Em produced at each iteration step of the Mullins-Noda model for which dEm/dt was not precisely zero, and hence Em-dependant fluxes were consistently inaccurately modelled. In contrast, the Mullins-Noda equation is in perfect agreement with the charge-difference equation if the former is applied at the final point of stability of the charge difference model, where the assumption that dEm/dt = 0 is entirely valid.
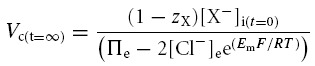 |
This formulation cannot be used to predict the steady state values of any of its variables but nevertheless usefully defines the physically permissible relationships between Vc, Em, zX, [X−]i, Πe and [Cl−] by delimiting the range of values under which intracellular and extracellular osmolarity are equal, and the charge difference is small. It thus provided an important assay of the validity of the results from CD and MN modelling. The results in Table 2 from the CD model followed this relationship accurately. In contrast, the results from the MN model did not, further suggesting that the small inaccuracy in the calculated value of Em under disequilibrium conditions was significant and that the precision of the CD model is an absolute requirement for accurate cellular modelling under such conditions. Furthermore, both the magnitudes and signs of these erroneous voltages themselves varied with the initial conditions. Using the basic GHK equation worsens these discrepancies (results not shown). These findings contrast sharply with charge difference-based modelling, which provides steady state values of Em that are in precise agreement with the MN calculation based on the final concentrations derived from the CD model.
II. The effects of ion permeabilities and sodium pump density on cellular volume determination
Although the sodium pump is required to maintain Vc and Em, variations in its activity within defined limits have little influence on their values in a stable cell
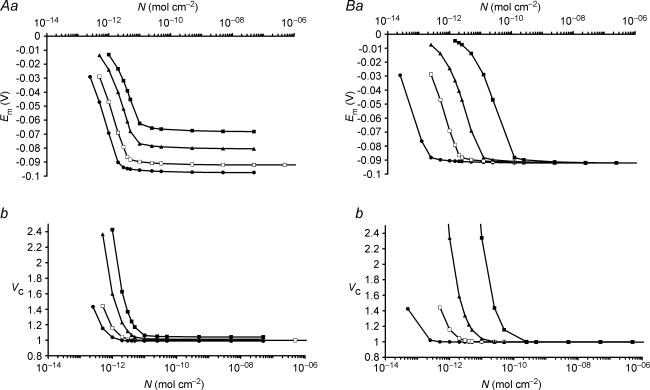
The demonstration that Vc and Em converge to stable values that are independent of the initial intracellular inorganic ion concentrations prompted investigation of alternative factors that might determine these apparent set points. This began with an investigation of the relative importance of the sodium pump density (N) and transmembrane ion permeabilities in the determination of Vc and Em. The simulation in Fig. 5A began from after a period in which the model was run from the final solute concentrations of Fig. 2 to its point of stability with an extremely high sodium pump density (N = 10−7 mol cm−2) (Else et al. 1996; Clausen, 2003). Thereafter, at each point marked with an asterisk, the sodium pump density was reduced 10-fold, and the model allowed to re-equilibrate. This process was repeated until the resultant pump rate could no longer maintain a stable cell volume as reflected in the relative magnitudes of the leakage currents and the maximum pump rate: the latter is achieved when [Na+]i is at a maximum and Em and [K+]i are at a minimum. Figure 5B summarizes such effects of sodium pump density upon Em and cell volume. Where N < approximately 2 × 10−13 mol cm−2, Vc and Em did not reach stable values, and therefore Vc and Em are plotted for t = 50 min (dashed line) and 150 min (continuous line) following a reduction in N to the lower value after a period of equilibration with N = 5 × 10−12 mol cm−2.
Figure 5. Sodium pump activity is required for volume stability, but within limits, variations in its activity leave Vc and Em conserved.
A, the effect of successive 10-fold reductions (each marked *) in sodium pump density (N) from an initial value of 5 × 10−8 mol cm−2. Notice that at values of N sufficient to allow stable cell volume, large changes in N had relatively little effect on Vc or Em, such that a 10 000-fold reduction to N = 5 × 10−12 mol cm−2 resulted in <1% increase in Vc and < 5% depolarization of Em. However, a further 10-fold reduction in N destabilized cell volume. B, a summary of the relationship between N, Vc (triangles) and Em (squares). Filled symbols denote final stable values, while for values of N insufficient to stabilize cell volume, the open symbols denote values of Em or Vc obtained either 50 min (dashed line) or 150 min (continuous line) after N was reduced from 5 × 10−12 mol cm−2 to the value indicated. Note that, for this particular set of ion permeabilities, a pump density of at least 2.5 × 10−13 mol cm−2 was necessary for stability of Vc or Em. Note that for all values of N sufficient to result in Em of at least −80 mV (N > 3 × 10−12 mol cm−2), variation in N has little influence on Vc or Em. Thus for an excitable cell at least, variation of sodium pump density could not be expected to regulate or determine Vc or Em.
Figure 5 thus demonstrates that even extremely large variations in N can leave Em and Vc unchanged. In part this is a consequence of the fixed stoichiometry of the sodium pump, as this would imply that there is a point where the free energy output of hydrolysis of 1 molecule of ATP is insufficient to balance the free energy requirements of pumping 3 Na+ and 2 K+ against their respective electrochemical gradients. At this point, the sodium pump density becomes irrelevant. In excitable cells the electrochemical gradients are indeed extremely close to the point where activity of the Na+–K+-ATPase becomes energetically unfavourable (Jansen et al. 2003).
These findings suggest that if an excitable cell is to remain highly polarized, then while a sufficient level of sodium pump activity is clearly required to attain and maintain a stable volume, changes in its activity or density within such limits can have very little effect on Vc as sodium pump activity cannot influence Vc and Em independently. Indeed, if N is the minimum sufficient to maintain Em at less than −80 mV, then increasing it more than 1000-fold would decrease the cell volume by less than 2%. Conversely, although a small reduction in N from this point might result in significant swelling, this swelling would occur secondarily to a proportionately larger depolarization. Furthermore, such depolarization may result in a destabilization of cell volume due to Cl− entry. In other words, such very low pump densities may be insufficient to maintain a stable cell volume, as maximum total pump activity may therefore be less than the resultant net leakage current. Finally, these properties arise simply from the intrinsic dependences of its sodium pump activity upon transported and energetic substrate in the absence of mechanisms that involve any direct sensing of Vc and Em.
Transmembrane ion permeabilities influence Em but cannot independently determine Vc
Figure 6A summarizes an investigation of how interactions between sodium pump density and transmembrane ion permeabilities influence Vc and Em. Figure 6Aa explores the influence of the PNa: PK ratio at constant PK showing only values of N that result in stable values of Em and Vc for clarity. Increasing the PNa: PK ratio in isolation depolarizes Em for all values of N and produces an upward shift of the Em against N plot. It also increased the minimum value of N required to maintain a stable cell reflected in the additional rightward shift of the Em against N plot. Figure 6Ab, shows that the change in Em and the resultant change in [Cl−]i shown in Fig. 6Aa secondarily influenced Vc.
Figure 6. The influence of sodium and potassium permeabilities on Vc and Em.
In each figure, open symbols mark the line showing the relationship between N and Vc or Em for the case of PNa: PK = 0.02: 1, the permeability ratio explored in detail in Fig. 5. For clarity, only N-values that result in stable values of Em and Vc are plotted in this figure. A, at constant PK, the relationship between N and (a) Em or (b) Vc for four different PK: PNa ratios. PNa: PK ratios: • 0.01: 1; □ 0.02: 1; ▴ 0.05: 1; ▪ 0.1: 1. B, at constant PK/PNa, the relationship between N and (a) Em or (b) Vc for four different values of PK. PNa: PK ratios: • 0.002: 0.1; □ 0.02: 1; ▴ 0.1: 5; ▪; 1: 50. Note that increases in PK without alteration of the PNa: PK ratio resulted in a rightward shift of the Em or Vc against N plots of equal magnitude, such that variation in PK with a constant PNa: PK: N ratio did not change Em or Vc set point. In contrast, an increase of the PNa: PK ratio at constant PK resulted primarily in an upward shift of the Em or Vc against N curves. PCl did not influence the steady state values of any of the modelled variables (not shown).
In contrast Fig. 6B shows that increases in both PNa and PK in proportion simply produced a proportional rightward shift of the Em or Vc against N curves, and therefore the original steady state set points of both Vc and Em would be conserved provided the proportions PNa: PK: N remained constant. Instead, any change in the magnitude of these values altered the kinetics with which Em and Vc returned to their set values following any discrete perturbation. It may be noted that the rate of cell swelling following sodium pump inhibition shown in Fig. 2 would fit better with experimental observations (Ferenczi et al. 2004) were PK rather lower than published values (Adrian, 1956) while maintaining the ratio PNa: PK: N.
Finally, all changes in PCl where PCl > 0 had no effect on the Em or Vc set points where the transmembrane distribution of Cl− was entirely passive, as its intracellular concentration, and hence Vc would then be determined entirely by the set point of Em, which would be defined by the other factors discussed. However, PCl can influence the rate at which Em and Vc return to their set points following, for example, cotransporter activation (see section IV).
III. The role of intracellular impermeant solute in cellular volume determination
Cellular volume is primarily determined by impermeant ion content and charge
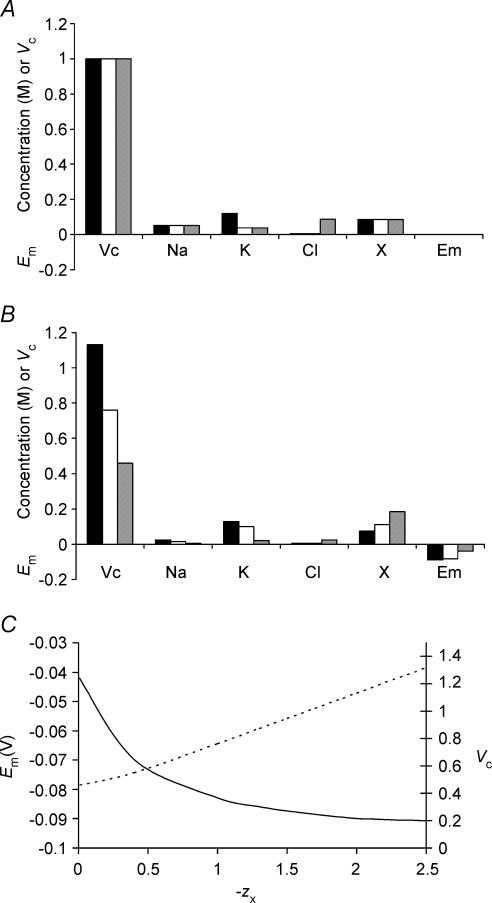
The previous simulations clearly showed that sodium pump activity provides both a necessary and sufficient condition for attainment and maintenance of a stable Vc (Figs 1 and 2), that Vc is then determined independently of initial intracellular ion concentrations (Fig. 3) and membrane capacitance (Fig. 4), and that changes to sodium pump density (Fig. 5) or inorganic ion permeabilities (Fig. 6) within stable limits could have relatively little influence on Vc without a far greater effect on Em. The simulations in Fig. 7 provide a contrasting demonstration that it is the intracellular impermeant anion content (modelled as a change in the ratio [X−]i: Πe) that influences the set point of Vc, but that this has no influence on the set point of Em. Note that initial charge neutrality, despite these variations in the initial value of [X−]i, was achieved by adjusting the initial concentrations of inorganic ions (Fig. 7A). Nevertheless Fig. 3 showed that the initial concentration of inorganic ions does not influence set points of either Vc or Em. Figure 7B shows that, whereas alterations in the initial concentration of inorganic ions leaves Vc and Em constant, changes in [X−]i(t = 0) altered the set point of Vc while leaving the corresponding set points of all other parameters, including Em, unaffected. The simulation could be extended to the limit to demonstrate that intracellular impermeant anion is necessary to prevent the action of the sodium pump resulting in Vc → 0.
Figure 7. Intracellular organic ion concentration determines the eventual stable value of Vc but does not influence Em.
A, the starting conditions of three cells. These cells were modelled with initially different intracellular organic anion concentrations. Note that although initial intracellular inorganic ion concentrations also varied between the three cells, this would have no influence on the final stable values of Vc or Em (see Fig. 3). B, the final stable values reached after a 5-h modelling period. Each cell reached identical stable values of Em, [Na+]i, [K+]i, [Cl−]i or [X−]i, demonstrating that variation of intracellular organic anion content has no influence on these variables. In contrast, the final stable volumes were sharply different.
As the impermeant anion, X−i, could potentially influence Vc and Em through both its osmotic effect and its electrical charge, the model was next extended to clarify the effect of the mean charge valency of X− (zX). Once again initial concentrations of inorganic ions were appropriately corrected to maintain an initial charge difference of zero, but such changes do not influence the set points of Vc or Em. Figure 8 summarizes the effect upon Vc of varying zX at a fixed initial [X]i (Fig. 8A) using three values of zX = 2 (filled column), 1 (open column) and 0 (grey column), respectively. Figure 8B shows that the value of zX influenced the set points of all modelled variables, including those of both Vc and Em. Figure 8C summarizes the precise relationship between zX, Vc and Em and this shows that, for a given initial concentration of impermeant intracellular anion ([X−]i(t = 0)), the set point of Vc is almost linearly related to zX; the relationship is linear for higher magnitudes of zX, while at lower magnitudes of zX, the effect of the osmolarity of X−i has a proportionately greater influence. For zX ≫ 0, at physiological initial values of [X−]i (approximately 85 mm), Vc is proportional to the magnitude of the valency with the approximate relationship Vc = 0.37zX + 0.39 (a more general relationship is derived in the Appendix). This should be compared with the results of Fig. 3, in which it was shown that cells with identical [X−]i(t = 0) reach identical final values of Vc, Em and all intracellular solute concentrations. Figure 8C thus shows that this conclusion is dependent upon zX. Furthermore, it is probable that the value of zX may change in vivo, for example in response to pH changes, and this could result in changes to steady state Vc, Em and all intracellular solute concentrations.
Figure 8. The mean valency of intracellular organic osmolyte influences the eventual stable values of both Vc and Em.
A, the starting conditions of three cells. These cells were modelled with initially identical intracellular organic osmolyte concentrations, but in each cell the mean charge valency of this osmolyte (zX) was different. Note that although initial intracellular inorganic ion concentrations also varied between the three cells, this would have no influence on the final stable values of Vc or Em (see Fig. 3). Filled columns: zX = 2; open columns, zX = 1; grey columns, zX = 0. B, the final stable values reached after a 5- h modelling period. Each cell reached stable values of Vc, Em, [Na+]i, [K+]i, [Cl−]i or [X−]i, but there were no similarities between the three cells. Increasing the negative charge on intracellular organic osmolyte produced larger, more highly polarized cells. C, a summary of the influence of zX upon Em (continuous line) and Vc (dashed line).
One further finding was that lower magnitudes of zX required fewer Na+–K+-ATPase cycles to maintain stable Vc and Em, in a sense because reducing zX reduces the tendency of the cell to swell. Although the maximum obtainable Em is also reduced by this manipulation, it may be that non-excitable cells have lower zX than excitable cells in order to conserve energy.
IV. Short-term versus long-term volume regulation
Cation–chloride cotransport permits short-term changes in Vc and/or Em and such changes depend upon cellular Cl− content and permeability
The simulations above show that cell volume is ultimately maintained by Na+–K+-ATPase activity, and when membrane ion permeabilities are constant, is determined primarily by the intracellular impermeant anion content and its charge. However, many cell-types exhibit RVI and RVD driven by transmembrane ion fluxes (reviews: Lang et al. 1998a, b). Furthermore, skeletal muscle is known to express at least the K+–Cl− cotransporter (KCC) (Lauf & Adragna, 2000) and the Na+–K+–2Cl− cotransporter (NKCC) (Wong et al. 1999; Lindinger et al. 2002). Together with the findings above (see, for example, Fig. 3) that Vc and Em set points appear independent of intracellular ion concentrations, this prompted direct examination of the potential roles of the cation–chloride cotransporters in volume regulation.
Figure 9A shows the effect of a 40-min period of Na+–K+–2Cl− cotransporter (NKCC) activation in skeletal muscle. The value of PNKCC was initially zero, was then increased to 10 000 at 20 min, and was finally returned to zero at 60 min. This transient activity had three main effects. First, NKCC activity resulted in an increase in Vc (∼20%) that was small in comparison to the significant depolarization of Em (> 50%). This was because NKCC activity held [Cl−]i/[Cl−]e above its normal electrochemical equilibrium, and due to the high PCl of skeletal muscle, this resulted in significant depolarization of Em. Secondly, sustained NKCC activation did not result in continued swelling or depolarization. Rather, it shifted Vc and Em to new stable values. This new steady state reflected a gradual reduction in the rate of NKCC activity and a parallel increase in Na+–K+-ATPase activity. The decreased NKCC activity resulted from a gradual reduction in the initially favourable gradient for coupled Na+, K+ and 2 Cl− entry as NKCC activity increased the [Na+]i[K+]i[Cl−]i2 product. The increased Na+–K+-ATPase activity was primarily due to increased [Na+], and to a lesser degree to the depolarization of Em and the reduction in [K+]i, this latter change occurring despite K+ influx, due to the diluting effect of water influx. Thirdly, it must be noted that cessation of NKCC activity allowed complete and rapid recovery of Em and Vc to their original set points.
Figure 9. The effects of cation–chloride cotransport activity.
NKCC activity in a tissue with PCl/PK = 3 (similar to that of skeletal muscle) (A) and PCl/PK = 0.05 (similar to that of an erythrocyte) (B). All other parameters were identical, and both cells were subjected to the same levels of NKCC activity. Thus in each case PNKCC was initially 0, was stepped to 10 000 after 20 min (marked *), and was then returned to 0 at 60 min (marked †). Note that in each case, the NKCC caused a rapid increase in [Na+]i and [Cl−]i, and a paradoxical reduction in [K+]i despite an increase in cellular K+ content, due to the concomitant water influx. In addition, both cells reached new stable values of Vc, Em and all intracellular solute concentrations despite the continued ion influx through the NKCC. This was due to a reduction in NKCC activity as the [Na+]i[K+]i[Cl−]i2 product increased, and an increase in Na+–K+-ATPase activity as the [Na+]i increased, [K+]i decreased and Em depolarized. However, in the cell depicted in panel A, Em depolarized very significantly (>50% reduction) while Vc increased by approximately 20%. In contrast, the cell depicted in panel B showed very significant swelling (>40%) and very little depolarization of Em (<10%). The rate of recovery to normal values of Em and Vc following cessation of NKCC activity is also significantly different between the two cells. C, corresponding effects of KCC activity in a high PCl cell. Although efflux of K+ and Cl− was initially favourable, the efflux was severely limited by the low [Cl−]i in such a highly polarized cell. Vc therefore decreased by <1%, while Em hyperpolarized by 5 mV. Note the small increase in [Na+]i and decrease in [K+]i due to the effect of this hyperpolarization upon the Na+–K+-ATPase.
Figure 9B shows the effect of NKCC activity in a cell with the PCl: PK ratio reduced from the approximately 3: 1 ratio of skeletal muscle (Hodgkin & Horowicz, 1959) to a 0.05: 1 ratio similar to that of, for example, erythrocytes (Freedman & Novak, 1997). All other parameters, including starting conditions and PNKCC were identical to those in Fig. 9A to allow direct comparison of the interaction between NKCC and PCl. It is clear that PCl profoundly influences the possible consequences of NKCC activity. Firstly, the increase in Vc (> 40%) was very much greater in a cell with low PCl. Secondly, this significant swelling was accompanied by only a small depolarization of Em (< 10% change). Thirdly, the rate of volume recovery following cessation of NKCC activity was very much slower, reflecting the much slower return of the accumulated Cl−i to a passive transmembrane distribution.
In addition, final stable intracellular ion concentrations were also changed considerably less than in the cell with high PCl during NKCC activity. This is because the cell with high PCl showed a high rate of ion influx through the NKCC even at the point of Vc and Em stability due to the much greater Cl− efflux through the background leak channels, and despite the resultant increase in Na+–K+-ATPase activity, intracellular ion concentrations were significantly perturbed. In contrast, in the low PCl cell, the rate of ion influx through the NKCC was eventually severely limited by the sustained high [Cl−]i, and this allowed relatively normal levels of Na+–K+-ATPase activity to restore other ion concentrations to close to their usual values. An important consequence of this finding is that maintenance of volume stability during similar levels of NKCC activity would require much greater energy expenditure in a cell with high PCl than in one with low PCl.
The simulations of high PCl tissue thus fully reconstruct the experimental findings of Ferenczi et al. (2004) which showed that NKCC activity in skeletal muscle increased the volume of cells shrunken in hypertonic solutions only marginally, and instead depolarized cells sufficiently to compensate for the hyperpolarization otherwise seen in similarly treated muscle fibres in Cl−-free solutions (as Adrian, 1956), or in which the NKCC had been inhibited. It was therefore concluded that NKCC served to stabilize Em in skeletal muscle in hypertonic solutions, and the current findings correspond well with this conclusion. The relative magnitudes of the influence upon Vc and Em of cation–chloride cotransport in the high PCl simulation are close to those reported experimentally by Ferenczi et al. (2004). In each case, the magnitude of the influence upon Em is 2–3 times the magnitude of the influence upon Vc. Similarly, in the low PCl simulation, the magnitude of the influence of NKCC activity upon Em is < 20% of the magnitude of the change in Vc, compatible with the role of this transporter as a primarily volume regulatory mechanism in the majority of non-excitable tissues (Russell, 2000).
Finally, the effects of K+–Cl− cotransporter (KCC) activity (PKCC = 100) were also investigated (Fig. 9C). Its activity resulted in a slight reduction in [Cl−]i, although its activity was clearly limited by the initially low [Cl−]i. However, although this precluded significant volume decrease by this mechanism, there was a small (∼5 mV) hyperpolarization of Em. Higher or lower values of PKCC (1000 or 10) produced very similar changes to Vc and Em, reflecting the fact that activation of this transporter quickly equalizes the [K+]i[Cl−]i and [K+]e[Cl−]e products. Finally, Vc and Em returned to their original values on cessation of KCC activity.
Organic anion fluxes result in significant and sustained changes to cell volume without causing sustained changes to Em
Cation–chloride cotransport thus appeared unable to significantly change Vc in skeletal muscle due to the high PCl, and was unable to produce Vc changes that were sustained following cessation of cotransport activity, with the rate of recovery to resting Vc influenced by PCl. Instead, they caused significant, although similarly unsustained, changes to Em, resulting primarily from the effect of changes to [Cl−]i.
In contrast, volume-sensitive organic anion fluxes have been implicated in the volume regulatory process in a variety of excitable tissues, including cardiac muscle (Rasmusson et al. 1993), barnacle muscle (Pena-Rasgado et al. 2001) and hippocampal neurones (Pasantes-Morales et al. 2000; Olson et al. 2003). Their contributions to volume and Em regulation were accordingly investigated by introducing a term to the model reflecting a small permeability to X−i (PX). Figure 10 demonstrates that introduction of PX = 0.0001 resulted in gradual volume reduction accompanied by a small depolarization of Em. However, in contrast to the effect of cation–chloride cotransport activity, this volume reduction could continue indefinitely, while Em stabilized at this slightly depolarized value. Most significantly, reduction of PX back to zero resulted in a return of Em and all intracellular ionic concentrations to normal, but at a significantly reduced Vc. Furthermore, linkage of organic anion fluxes to cation fluxes (Schultz & Curran, 1970; Hudson & Schultz, 1984, 1988), using electroneutral cotransport models analogous to that used for the cation–chloride cotransporters, allowed volume decrease or increase without the transient Em shift that resulted from organic anion flux alone (data not shown). However, at cessation of the activity of such transporters, the steady state values of Vc and Em were determined solely by the magnitude of the change in X−i and zX, and were not influenced by the accompanying cation flux. Finally, organic ion influx similarly resulted in sustained volume increase without Em change (data not shown).
Figure 10. Organic osmolyte efflux.
Organic osmolyte efflux was simulated by introducing a small membrane permeability to organic anions, PX = 0.0001, at the point marked *, allowing gradual outward diffusion of X−. Such efflux drove steady water efflux and volume reduction. It also caused a small depolarization from −89 mV to −86 mV, as would be expected from the introduction of a permeability term for an otherwise internally sequestered anion. In contrast to the effect of a similar period of cation–chloride cotransport (Fig. 9), the volume change was able to continue almost indefinitely without any further alteration to the membrane potential. Most strikingly, the cessation of organic osmolyte efflux (at the point marked †) showed that the volume reduction was not reversed by continued activity of the sodium pump, in sharp contrast to volume changes resulting from inorganic ion fluxes.
Organic anion fluxes therefore emerge as the sole mechanism by which muscle cells may change both Vc and the Vc set point without simultaneously changing Em. This is in marked contrast to every other mechanism by which Vc could be changed that was investigated in the current study, including cation–chloride cotransport activity, inorganic ion permeability or content changes, sodium pump density and changes to the mean valency of intracellular impermeant anions. Thus it seems likely that such fluxes could underlie volume change in short-term volume regulation as well as longer-term changes such as muscle growth, hypertrophy and atrophy. In contrast, cells with low PCl could employ cation–chloride cotransporters to cause volume changes, with little influence on Em, although long-term changes to Vc or Em set points may still require changes to the cellular content or mean valency of intracellular organic anions.
Discussion
This paper clarifies the quantitative relationships between two fundamental and related functional parameters, cell volume, Vc, and resting potential, Em, and investigates the possible mechanisms for their determination, maintenance and regulation, particularly in excitable cells. It used a novel approach to calculate Em directly from the intracellular charge difference, rather than using the Goldman-Hodgkin-Katz (GHK) equation or one of its more recent derivatives. It therefore represents the first quantitative analysis of the interdependence of Vc and Em to calculate Em using a method that does not require any assumption of steady state, permitting precise calculation of Em even under non-equilibrium conditions. This approach was necessary because the steady state assumption (dEm/dt = 0) that is central to the GHK equation and its derivatives precludes entirely accurate calculation of Em and Vc in the same formalism, as this assumption is violated when Vc and hence Em is changing. Earlier papers therefore separately considered Em regulation in excitable cells such as skeletal muscle (Adrian, 1956; Hodgkin & Horowicz, 1959), and nerve (Hodgkin et al. 1952; reviews: Noble, 1966; Thomas, 1972) using the GHK approach, while Vc regulation was considered, again separately, in terms of electrolyte and organic solute fluxes in non-excitable cells (Tosteson & Hoffman, 1960; Schultz & Curran, 1970; Hudson & Schultz, 1984, 1988).
This analysis was made possible by the quantitative characterization now available about individual processes that might influence Em and Vc. The present model thus incorporated all the known major steady state membrane permeabilities and transport processes, including electrogenic ion transport (Hernandez et al. 1989; Hernandez & Chifflet, 2000). It also incorporated identified membrane transport processes that are known to influence and/or respond to cell volume (review: Lang et al. 1998b) including cation–Cl− cotransport (Lauf & Adragna, 2000; Russell, 2000) and changes in cation or anion permeability (Zhang et al. 1993; Nilius et al. 1996; Strange et al. 1996) or membrane capacitance (Huang, 1981a,b). Finally, the effects of organic anion fluxes (Rasmusson et al. 1993; Pasantes-Morales et al. 2000; Olson et al. 2003) were simulated explicitly through modelling of otherwise membrane-impermeant anions with non-unity valency.
This study was therefore able to show quantitatively, for the first time to our knowledge (O'Neill, 1999), that even in the absence of specific cellular mechanisms for volume detection, Vc converges to a fixed set point and that this is largely determined by the intracellular membrane-impermeant solute content (X−i) and its mean charge valency (zX). Furthermore, for given sodium pump densities and sets of membrane ion permeabilities, Em was shown to be determined solely by zX. This approach thus provided straightforward demonstrations, for the first time to our knowledge, of a number of strategic properties of the determination of Em and Vc in the reconstituted system. It was further shown that the charge-difference model introduced here was necessary to demonstrate these apparent set points, as they were not predicted by otherwise identical GHK- or Mullins-Noda-based models.
The principles of volume regulation were also investigated. The specific modelling examples were prompted by a number of both early and more recent experimental observations of manoeuvres designed to modify both Em and Vc. First, early experiments demonstrated that under conditions where K+ was the only significant membrane-permeant ion skeletal muscle Vc followed a simple inverse dependence upon extracellular osmolarity, while Em followed the resultant K+ Nernst potential (Adrian, 1956; Dydynska & Wilkie, 1963; Blinks, 1965). Subsequent studies demonstrated swelling-induced regulatory volume decreases (RVDs) (O'Neill, 1999; Okada et al. 2001) and shrinkage-induced regulatory volume increases (RVIs) brought about by cotransporter activity in many other, often non-excitable, cell types (reviews: Lang et al. 1998a; O'Neill, 1999). However, such regulatory volume adjustments have not been observed in mature skeletal muscle fibres (Sejersted & Sjogaard, 2000). Instead, recent findings have suggested a complex relationship between Em and Vc that may vary between cell types. For example, a recent study reported that skeletal muscle fibres in Cl−-containing extracellular solutions did not hyperpolarize following osmotically induced shrinkage despite increased [K+]i/[K+]e (Adrian, 1956). Ferenczi et al. (2004) demonstrated that in this situation Na+–K+–2Cl− cotransport (NKCC) held [Cl−]i/[Cl−]e above equilibrium values but did not cause significant regulatory volume increases (RVIs) in agreement with earlier work (Blinks, 1965). Thus in skeletal muscle the volume-sensitive cation–chloride transport processes that underlie volume regulation in other cell types appeared instead to influence Em (Baumgarten & Clemo, 2003; Geukes Foppen, 2004) apparently in place of significant influences upon Vc (Ferenczi et al. 2004). However, while exercise increases muscle fibre volume by up to 20% (Sjogaard et al. 1985), long-term muscle fibre volumes in vivo remain remarkably stable (review: Proske & Morgan, 2001) despite the apparent short-term regulation of Em in preference to Vc (Ferenczi et al. 2004). These discrepancies were explored in the present study, and mechanisms by which Em and Vc may be regulated independently were identified.
The present study was therefore able to formulate several principles underlying volume determination and regulation. These principles are summarized in Table 3.
Table 3.
Summary of main findings for a cell with constant Na+–K+-ATPase density and ion permeabilities
| In a cell with constant Na+–K+-ATPase density and ion permeabilities: | |
| • The steady state volume (Vc) is determined by the total impermeant anion content (X−i) and its mean valency (zX). | |
| • The steady state membrane potential (Em) and intracellular solute concentrations are determined by zX alone. | |
| • zX must be significantly negative if a cell is to be highly polarized. | |
| • The Na+–K+-ATPase is able to attain and maintain these steady-state values of Vc and Em without extrinsic regulation of its activity. | |
| • Cation-chloride cotransport activity may change Vc and Em by altering the transmembrane Cl− distribution. | |
| • Vc and Em recover to their set points following cessation of cation-chloride cotransport activity at a rate determined primarily by the Cl− permeability (PCl). | |
| • Sustained changes to the Vc set point that do not change Em can only result from mechanisms that change Xi. | |
| • When chloride is passively distributed, Vc and Em are related as follows: | |
First, the CD model inherently converged to stable final values that closely reproduced in vivo intracellular ion concentrations and Em. The latter additionally agreed precisely with the corresponding value calculated from these final ionic concentrations using the Mullins-Noda (MN) equation (Mullins & Noda, 1963). This convergence did not require any extrinsic modulation of Na+–K+-ATPase activity through either Em or Vc. These steady state values were independent of initial intracellular inorganic ion concentrations, membrane capacitance, and any interposed perturbations given similar conditions of sodium pump density, ion permeabilities and intracellular impermeant osmolyte content. In contrast, simulations whose individual steps calculated Em from the MN rather than the CD equation converged to significantly different [Na+]i, [K+]i, [Cl−]i and [X−]i and Em values that were influenced by initial intracellular inorganic ion concentrations. However, the final ion concentrations contained large charge discrepancies reflecting accumulating errors from the inherent assumption that dEm/dt = 0, and failed an analytic criterion constraining the relationship between steady state Vc and Em for cells with passive transmembrane distributions of Cl− (see Appendix).
Secondly, investigation of the relative importance of the sodium pump density (N) and transmembrane ion permeabilities in the determination of Vc and Em demonstrated that even large variations in Na+–K+-ATPase activity above a critical value had little influence on Vc and Em values. This is explicable in terms of a fixed pump stoichiometry that would define a point where the free energy output of hydrolysis of 1 molecule of ATP is insufficient to balance the free energy requirements of pumping 3 Na+ and 2 K+ against their respective electrochemical gradients (Jansen et al. 2003). Stepwise reductions in N from a high value had little influence on Vc or Em until a critical value of N, below which Vc and Em became unstable. Only when N was very close to this critical value could its value significantly influence Vc and Em. Furthermore, changes in N could not independently influence Vc and Em.
Thirdly, the critical value of N necessary to maintain stable values of Vc and Em was determined primarily by the overall cation permeability. Proportional increases in both PNa and PK altered this critical value. Conversely, altering the magnitude of PNa, PK or N at a constant PNa: PK: N proportion left the final stable values of Vc and Em unchanged but produced a directly proportional change in the rate at which these stable values of Vc and Em recovered from any given perturbation. In contrast, alterations in the PNa: PK ratio influenced Em (Hodgkin & Katz, 1949; Hodgkin & Horowicz, 1959), with an increase in this ratio resulting in depolarization at any given sodium pump density. Finally, PCl did not influence either the stable values of Vc or Em, or the critical value of N for any non-zero value of PCl.
Fourthly, in contrast to the independence of Vc and Em from initial intracellular inorganic ion concentrations, the simulations demonstrated that the intracellular membrane-impermeant solute content (X−i) and its mean charge valency (zX) are the primary determinants of the steady state value of Vc. Thus given stable ion permeabilities and a fixed sodium pump density sufficient to attain a stable cell volume, cells with identical initial [X−]i and zX reached identical final stable values of Em, Vc, [Na+]i, [K+]i, [Cl−]i and [X−]i that were entirely independent of other starting conditions, including the initial values of Em, [Na+]i, [K+]i and [Cl−]i and initial total intracellular osmolarity. Furthermore, use of accepted values of N (Clausen, 2003), PNa, PK and PCl (Adrian, 1956) gave final values of Em, [Na+]i, [K+]i, [Cl−]i and [X−]i that were similar to those found in the literature (Maughan & Recchia, 1985) and independent of the initial values of any of the dependent variables and of membrane capacitance. However, while initial [X−]i did not influence the final values of Em, [Na+]i, [K+]i, [Cl−]i and [X−]i, it profoundly influenced final cell volume.
In contrast, zX influences the final stable values of Em, [Na+]i, [K+]i, [Cl−]i, [X−]i and Vc. It is thus the primary determinant of Em, assuming constant ion permeabilities and sodium pump density. Thus more negative charge valencies resulted in larger, more polarized cells. Strikingly, the negative charge on X−i was shown to be an absolute requirement for significantly polarized values of Em at any value of N. For example, at the PNa: PK ratio of skeletal muscle the stable values of Em were at least −85 mV for all values of zX > 1, but if zX < 0.1, the maximum polarization of Em at any value of N was approximately −50 mV. If zX is very low or zero, it is not possible to obtain the high intracellular [K+]i necessary to produce polarized values of Em, as clearly a similarly high concentration of some negatively charged ion is then required. The negative charge carried by X−i normally balances this charge on K+i, and Cl− cannot perform a similar role, as it is excluded from a polarized cell.
Fifthly, the final simulations in the model suggested that separate mechanisms mediate transient and steady-state changes in Vc, particularly in skeletal muscle. Short-term volume regulatory mechanisms particularly involving volume-sensitive cation–chloride cotransport systems (Lauf & Adragna, 2000; Russell, 2000) or anion channels (Zhang et al. 1993; Nilius et al. 1996; Strange et al. 1996) have been reported in a wide range of cell types. Yet mature skeletal muscle does not perform RVI or RVD in response to applied osmotic stress (Sejersted & Sjogaard, 2000). Furthermore there is considerable evidence for the presence of the NKCC cotransporter in skeletal muscle and for its activation by cellular volume changes (Dorup & Clausen, 1996; Wong et al. 1999; Russell, 2000; Lindinger et al. 2002). Recent experimental evidence suggests that it may stabilize Em following cell shrinkage rather than perform RVI (Ferenczi et al. 2004). The current study corroborates this suggestion by showing that the high membrane PCl of skeletal muscle precludes NKCC activity increasing Vc without also resulting in depolarization of Em. Furthermore, ion fluxes through the NKCC decreased as they increased intracellular [Cl−]i, and such fluxes were opposed by increases in Na+–K+-ATPase activity secondary to increased [Na+]i and depolarization of Em. Therefore a new steady-state Vc and Em could be reached despite continued NKCC activation. In cells with low PCl, such as erythrocytes (Tosteson & Hoffman, 1960), the simulations showed that an identical NKCC activation could increase Vc without greatly depolarizing Em. Furthermore, the Vc at the new steady-state was considerably greater, and the increase in Na+–K+-ATPase activity considerably lower, than in the high PCl cell. Due to reduced passive re-equilibration of Cl− in low PCl tissues, [Cl−]i was greater at the new steady state, and this resulted in a greater opposition to ion influx through the NKCC. This in turn caused a lesser increase in Na+ influx at steady state, when compared to that in high PCl tissues, and so provoked a lesser increase in Na+–K+-ATPase activity, and therefore less opposition to the NKCC-driven Vc increase.
The mechanism of RVD using the KCC, a method common to a number of cell types (Lang et al. 1998a; O'Neill, 1999), was also studied. One might expect its activity to be severely limited in excitable cells, simply because [Cl−]i is extremely low in such highly polarized cells. However, the KCC is expressed in skeletal muscle (Lauf & Adragna, 2000), and the present simulations showed that KCC activity is energetically favoured in resting muscle, and that its activity, whilst unable to significantly alter cell volume, may be able to reduce [Cl−]i/[Cl−]e below the ratio determined by passive distribution according to the membrane potential. Thus it was shown that KCC activity could potentially cause significant hyperpolarization in skeletal muscle, as due to the high PCl in this tissue a change in the equilibrium potential of Cl− will be reflected by a changed Em. Thus this cotransporter could potentially have a role in stabilizing muscle Em, for example during exhaustive exercise.
It was shown that the Vc and Em changes resulting from cation–chloride cotransport were entirely reversed on cessation of their activity, due to the action of the sodium pump. Again, this was principally true for muscle tissue: although Na+–K+-ATPase activity was shown eventually to restore cell Vc and Em following any discrete perturbation of intracellular ionic content in a cell with any non-zero PCl, the rate at which it was able to do so was dependent on the PCl and therefore recovery was slow if PCl was low. In other words, high PCl was shown to assist the activity of the sodium pump in restoring normal intracellular ionic concentrations, Vc and Em following a perturbation of any of their values, and likewise a low PCl significantly hampered it. It is interesting to speculate whether this constitutes a part of the physiological significance for the high PCl in skeletal muscle (Adrian, 1956), reflecting the high and unpredictable levels of activity in this tissue.
This influence of PCl is also of wider interest in view of the broad range of tissues in which volume-sensitive Cl− channels have been identified (review: Nilius et al. 1996). It is clear that PCl can have no influence on Vc or Em if its transmembrane distribution is entirely passive. This study has shown, however, that PCl influences the rate at which a cell attains its set volume. Therefore any change in the set volume, such as would follow organic ion fluxes, would result in a more rapid cellular volume change if PCl was simultaneously increased, thereby facilitating re-equilibration of Cl−i.
Finally, a mechanism by which excitable cells, and skeletal muscle in particular, may be able to regulate volume without simultaneously changing Em was identified. The efflux of organic anions was shown to result in volume decrease limited only by the initial cellular content of this class of osmolyte, and without the large changes in membrane potential resulting from cation–chloride fluxes. Indeed, volume-related organic ion fluxes have been identified in a number of excitable tissues including cardiac muscle (Rasmusson et al. 1993), barnacle muscle (Pena-Rasgado et al. 2001) and hippocampal neurones (Pasantes-Morales et al. 2000; Olson et al. 2003). In contrast, NKCC and KCC activity may, in certain tissues, regulate Em and not cellular volume.
Acknowledgments
The authors thank the Medical Research Council for project (G9900365 and G0100188) and Co-operative Group Grants (G9900182 and G01001986, respectively), and the Wellcome Trust Joint Research Equipment Initiative (JREI: 055203/Z/98/Z/ST/RC) for equipment funding support. CLHH also thanks the Leverhulme Trust and the British Heart Foundation for support. J.A.F. holds a George Henry Lewes Studentship.
Appendix
The relationship between Vc, Em, Πe, Xi and zX at steady state is constrained as follows:
(1) Intracellular and extracellular osmolarity must be equal:
(2) Total intracellular charge is almost exactly zero:
(3) Substituting for [Na+]i + [K+]i = [Cl−]i - zX[X−]i
(4) X− is membrane impermeant, and thus any change to X−i (i.e. a transient change in [X−]i) drives transmembrane water fluxes until [X−]i is restored to its original value (see Fig. 7). If Vc = 1 at t = 0, then at steady state:
(5) Therefore the relationship between Vc, X− and zX is:
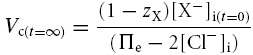 |
(6) If Cl− is passively distributed, then:
(7) Therefore at steady state and under conditions of passive chloride distribution, the relationship between Vc and Em is:
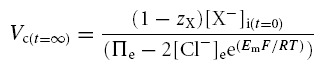 |
This can also be expressed as:
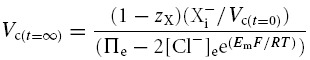 |
References
- Adrian RH. The effect of internal and external potassium concentration on the membrane potential of frog muscle. J Physiol. 1956;133:631–658. doi: 10.1113/jphysiol.1956.sp005615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aickin CC, Betz WJ, Harris GL. Intracellular chloride and the mechanism for its accumulation in rat lumbrical muscle. J Physiol. 1989;411:437–455. doi: 10.1113/jphysiol.1989.sp017582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong CM. The Na/K pump, Cl ion, and osmotic stabilization of cells. Proc Natl Acad Sci U S A. 2003;100:6257–6262. doi: 10.1073/pnas.0931278100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumgarten CM, Clemo HF. Swelling-activated chloride channels in cardiac physiology and pathophysiology. Prog Biophys Mol Biol. 2003;82:25–42. doi: 10.1016/s0079-6107(03)00003-8. [DOI] [PubMed] [Google Scholar]
- Blinks JR. Influence of osmotic strength on cross-section and volume of isolated single muscle fibres. J Physiol. 1965;177:42–57. doi: 10.1113/jphysiol.1965.sp007574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clausen T. Na+-K+ pump regulation and skeletal muscle contractility. Physiol Rev. 2003;83:1269–1324. doi: 10.1152/physrev.00011.2003. [DOI] [PubMed] [Google Scholar]
- Dorup I, Clausen T. Characterization of bumetanide-sensitive Na+ and K+ transport in rat skeletal muscle. Acta Physiol Scand. 1996;158:119–127. doi: 10.1046/j.1365-201X.1996.542296000.x. [DOI] [PubMed] [Google Scholar]
- Dydynska M, Wilkie DR. The osmotic properties of striated muscle fibres in hypertonic solution. J Physiol. 1963;169:312–329. doi: 10.1113/jphysiol.1963.sp007258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg RS, Gage PW. Ionic conductances of the surface and transverse tubular membranes of frog sartorius fibers. J General Physiol. 1969;53:279–297. doi: 10.1085/jgp.53.3.279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Else PL, Windmill DJ, Markus V. Molecular activity of sodium pumps in endotherms and ectotherms. Am J Physiol Regul Integr Comp Physiol. 1996;271:R1287–R1294. doi: 10.1152/ajpregu.1996.271.5.R1287. [DOI] [PubMed] [Google Scholar]
- Ferenczi EA, Fraser JA, Chawla S, Skepper JN, Schwiening CJ, Huang CL-H. Membrane potential stabilization in amphibian skeletal muscle fibres in hypertonic solutions. J Physiol. 2004;555:423–438. doi: 10.1113/jphysiol.2003.058545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman JC, Novak TS. Electrodiffusion, barrier, and gating analysis of DIDS-insensitive chloride conductance in human red blood cells treated with valinomycin or gramicidin. J General Physiol. 1997;109:201–216. doi: 10.1085/jgp.109.2.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frigeri A, Nicchia GP, Balena R, Nico B, Svelto M. Aquaporins in skeletal muscle: reassessment of the functional role of aquaporin-4. FASEB J. 2004;18:905–907. doi: 10.1096/fj.03-0987fje. [DOI] [PubMed] [Google Scholar]
- Gage PW, Eisenberg RS. Capacitance of the surface and transverse tubular membrane of frog sartorius muscle fibers. J General Physiol. 1969;53:265–278. doi: 10.1085/jgp.53.3.265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geukes Foppen RJ. In skeletal muscle the relaxation of the resting membrane potential induced by K+ permeability changes depends on Cl− transport. Pflugers Arch. 2004;447:416–425. doi: 10.1007/s00424-003-1165-1. [DOI] [PubMed] [Google Scholar]
- Geukes Foppen RJ, Van Mil HGJ, Van Heukelom JS. Effects of chloride transport on bistable behaviour of the membrane potential in mouse skeletal muscle. J Physiol. 2002;542:181–191. doi: 10.1113/jphysiol.2001.013298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman DE. Potential, impedance and rectification in membranes. J General Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hernandez JA, Chifflet S. Electrogenic properties of the sodium pump in a dynamic model of membrane transport. J Membr Biol. 2000;176:41–52. doi: 10.1007/s00232001074. [DOI] [PubMed] [Google Scholar]
- Hernandez JA, Cristina E. Modeling cell volume regulation in nonexcitable cells: the roles of the Na+ pump and of cotransport systems. Am J Physiol. 1998;275:C1067–C1080. doi: 10.1152/ajpcell.1998.275.4.C1067. [DOI] [PubMed] [Google Scholar]
- Hernandez J, Fischbarg J, Liebovitch LS. Kinetic model of the effects of electrogenic enzymes on the membrane potential. J Theor Biol. 1989;137:113–125. doi: 10.1016/s0022-5193(89)80153-5. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Horowicz P. The influence of potassium and chloride ions on the membrane potential of single muscle fibres. J Physiol. 1959;148:127–160. doi: 10.1113/jphysiol.1959.sp006278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF, Katz B. Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J Physiol. 1952;116:424–448. doi: 10.1113/jphysiol.1952.sp004716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Katz B. The effect of sodium ions on the electrical activity of the giant squid axon. J Physiol. 1949;108:37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang CL-H. Dielectric components of charge movements in skeletal muscle. J Physiol. 1981a;313:187–205. doi: 10.1113/jphysiol.1981.sp013658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang CL-H. Membrane capacitance in hyperpolarized muscle fibres. J Physiol. 1981b;313:207–222. doi: 10.1113/jphysiol.1981.sp013659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang CL-H, Peachey LD. Anatomical distribution of voltage-dependent membrane capacitance in frog skeletal muscle fibers. J General Physiol. 1989;93:565–584. doi: 10.1085/jgp.93.3.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RL, Schultz SG. Sodium-coupled sugar transport: effects on intracellular sodium activities and sodium-pump activity. Science. 1984;224:1237–1239. doi: 10.1126/science.6328650. [DOI] [PubMed] [Google Scholar]
- Hudson RL, Schultz SG. Sodium-coupled glycine uptake by Ehrlich ascites tumor cells results in an increase in cell volume and plasma membrane channel activities. Proc Natl Acad Sci U S A. 1988;85:279–283. doi: 10.1073/pnas.85.1.279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen MA, Shen H, Zhang L, Wolkowicz PE, Balschi JA. Energy requirements for the Na+ gradient in the oxygenated isolated heart: effect of changing the free energy of ATP hydrolysis. Am J Physiol Heart Circ Physiol. 2003;285:H2437–H2445. doi: 10.1152/ajpheart.00534.2003. [DOI] [PubMed] [Google Scholar]
- Lang F, Busch GL, Ritter M, Volkl H, Waldegger S, Gulbins E, Haussinger D. Functional significance of cell volume regulatory mechanisms. Physiol Rev. 1998a;78:247–306. doi: 10.1152/physrev.1998.78.1.247. [DOI] [PubMed] [Google Scholar]
- Lang F, Busch GL, Volkl H. The diversity of volume regulatory mechanisms. Cell Physiol Biochem. 1998b;8:1–45. doi: 10.1159/000016269. [DOI] [PubMed] [Google Scholar]
- Lauf PK, Adragna NC. K-Cl cotransport: properties and molecular mechanism. Cell Physiol Biochem. 2000;10:341–354. doi: 10.1159/000016357. [DOI] [PubMed] [Google Scholar]
- Lindinger MI, Hawke TJ, Lipskie SL, Schaefer HD, Vickery L. K+ transport and volume regulatory response by NKCC in resting rat hindlimb skeletal muscle. Cell Physiol Biochem. 2002;12:279–292. doi: 10.1159/000067898. [DOI] [PubMed] [Google Scholar]
- Maughan DW, Godt RE. Protein osmotic pressure and the state of water in frog myoplasm. Biophys J. 2001;80:435–442. doi: 10.1016/S0006-3495(01)76026-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maughan D, Recchia C. Diffusible sodium, potassium, magnesium, calcium and phosphorus in frog skeletal muscle. J Physiol. 1985;368:545–563. doi: 10.1113/jphysiol.1985.sp015875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullins LJ, Noda K. The influence of sodium-free solutions on the membrane potential of frog muscle fibers. J General Physiol. 1963;47:117–132. doi: 10.1085/jgp.47.1.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilius B, Eggermont J, Voets T, Droogmans G. Volume-activated Cl− channels. General Pharmacol. 1996;27:1131–1140. doi: 10.1016/s0306-3623(96)00061-4. [DOI] [PubMed] [Google Scholar]
- Noble D. Applications of Hodgkin-Huxley equations to excitable tissues. Physiol Rev. 1966;46:1–50. doi: 10.1152/physrev.1966.46.1.1. [DOI] [PubMed] [Google Scholar]
- Okada Y, Maeno E, Shimizu T, Dezaki K, Wang J, Morishima S. Receptor-mediated control of regulatory volume decrease (RVD) and apoptotic volume decrease (AVD) J Physiol. 2001;532:3–16. doi: 10.1111/j.1469-7793.2001.0003g.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson JE, Kreisman NR, Lim J, Hoffman-Kuczynski B, Schelble D, Leasure J. Taurine and cellular volume regulation in the hippocampus. Adv Exp Med Biol. 2003;526:107–114. doi: 10.1007/978-1-4615-0077-3_14. [DOI] [PubMed] [Google Scholar]
- O'Neill WC. Physiological significance of volume-regulatory transporters. Am J Physiol. 1999;276:C995–C1011. doi: 10.1152/ajpcell.1999.276.5.C995. [DOI] [PubMed] [Google Scholar]
- Pasantes-Morales H, Franco R, Torres-Marquez ME, Hernandez-Fonseca K, Ortega A. Amino acid osmolytes in regulatory volume decrease and isovolumetric regulation in brain cells: contribution and mechanisms. Cell Physiol Biochem. 2000;10:361–370. doi: 10.1159/000016369. [DOI] [PubMed] [Google Scholar]
- Pena-Rasgado C, Pierce SK, Rasgado-Flores H. Osmolytes responsible for volume reduction under isosmotic or hypoosmotic conditions in barnacle muscle cells. Cell Mol Biol. 2001;47:841–853. [PubMed] [Google Scholar]
- Proske U, Morgan DL. Muscle damage from eccentric exercise: mechanism, mechanical signs, adaptation and clinical applications. J Physiol. 2001;537:333–345. doi: 10.1111/j.1469-7793.2001.00333.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmusson RL, Davis DG, Lieberman M. Amino acid loss during volume regulatory decrease in cultured chick heart cells. Am J Physiol. 1993;264:C136–C145. doi: 10.1152/ajpcell.1993.264.1.C136. [DOI] [PubMed] [Google Scholar]
- Russell JM. Sodium-potassium-chloride cotransport. Physiol Rev. 2000;80:211–276. doi: 10.1152/physrev.2000.80.1.211. [DOI] [PubMed] [Google Scholar]
- Schultz SG, Curran PF. Coupled transport of sodium and organic solutes. Physiol Rev. 1970;50:637–718. doi: 10.1152/physrev.1970.50.4.637. [DOI] [PubMed] [Google Scholar]
- Sejersted OM, Sjogaard G. Dynamics and consequences of potassium shifts in skeletal muscle and heart during exercise. Physiol Rev. 2000;80:1411–1481. doi: 10.1152/physrev.2000.80.4.1411. [DOI] [PubMed] [Google Scholar]
- Sjogaard G, Adams RP, Saltin B. Water and ion shifts in skeletal muscle of humans with intense dynamic knee extension. Am J Physiol. 1985;248:R190–R196. doi: 10.1152/ajpregu.1985.248.2.R190. [DOI] [PubMed] [Google Scholar]
- Strange K, Emma F, Jackson PS. Cellular and molecular physiology of volume-sensitive anion channels. Am J Physiol. 1996;270:C711–C730. doi: 10.1152/ajpcell.1996.270.3.C711. [DOI] [PubMed] [Google Scholar]
- Thomas RC. Electrogenic sodium pump in nerve and muscle cells. Physiol Rev. 1972;52:563–594. doi: 10.1152/physrev.1972.52.3.563. [DOI] [PubMed] [Google Scholar]
- Thompson LV, Fitts RH. Muscle fatigue in the frog semitendinosus: role of the high-energy phosphates and Pi. Am J Physiol. 1992;263:C803–C809. doi: 10.1152/ajpcell.1992.263.4.C803. [DOI] [PubMed] [Google Scholar]
- Tosteson DC, Hoffman JF. Regulation of cell volume by active cation transport in high and low potassium sheep red cells. J General Physiol. 1960;44:169–194. doi: 10.1085/jgp.44.1.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verkman AS. Water channels in cell membranes. Annu Rev Physiol. 1992;54:97–108. doi: 10.1146/annurev.ph.54.030192.000525. [DOI] [PubMed] [Google Scholar]
- Wong JA, Fu L, Schneider EG, Thomason DB. Molecular and functional evidence for Na+-K+-2Cl− cotransporter expression in rat skeletal muscle. Am J Physiol. 1999;277:R154–R161. doi: 10.1152/ajpregu.1999.277.1.R154. [DOI] [PubMed] [Google Scholar]
- Zhang J, Rasmusson RL, Hall SK, Lieberman M. A chloride current associated with swelling of cultured chick heart cells. J Physiol. 1993;472:801–820. doi: 10.1113/jphysiol.1993.sp019974. [DOI] [PMC free article] [PubMed] [Google Scholar]