Revision of the Starling principle: new views of tissue fluid balance

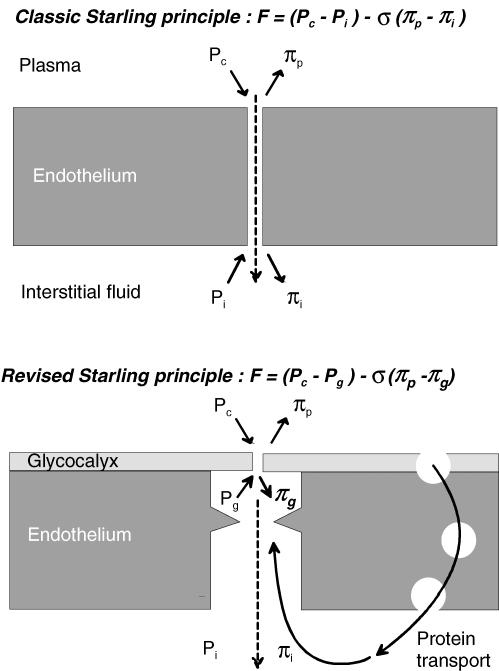
Tissue fluid balance, plasma volume regulation and clinical oedema formation are governed by the Starling principle of microvascular fluid exchange. This states that transendothelial filtration is driven by capillary pressure (P_c) and interstitial protein osmotic pressure (π_i), while a counteracting absorptive force is exerted by plasma protein osmotic pressure (π_p) and interstitial pressure (P_i). Since P_c falls along a capillary, the plausible concept of filtration from arterial capillaries and sustained reabsorption into venous capillaries has become embedded in the literature. Most of us learned this as first year undergraduates and took it to be a well proven, somewhat fossilized truth. In recent years, however, this ‘accepted’ view has undergone substantial experimental and theoretical re-evaluation; see the Classical Perspective by Michel (2004) in this issue of The Journal of Physiology. In particular, a landmark study of the P_c–filtration relation by Michel & Phillips (1987) demonstrated that although absorption occurs transiently at P_c < π_p, absorption cannot be sustained, probably because π_i increases with time. A further problem was the ‘low lymph flow paradox’, namely that net capillary filtration rate calculated from tissue-averaged Starling forces (including π_i) is much greater than the tissue lymph production. These observations, along with new structure–function findings, led to the proposal of novel endothelial filtration models by Michel and by Weinbaum (Michel, 2004 and below). Now Adamson et al. (2004), also in this issue of The Journal of Physiology, report a direct investigation of the little-studied effect of π_i on fluid exchange, with results that conflict dramatically with classical Starling predictions but support the Michel–Weinbaum model.

In an elegant, rigorous study, Adamson et al. (2004) measured trans-endothelial fluid flux in cannulated postcapillary venules (a non-fenestrated ‘model’ for capillaries) in the rat mesentery and changed π_i by albumin superfusion. The key finding was that raising π_i increased the filtration rate by only a small fraction of that predicted by the Starling principle. The fraction was 25% under their specific experimental conditions but depends on the filtration rate (see below). Continuous endothelium thus displays osmotic asymmetry, unlike the symmetrical Starling principle. Indeed, in an analogous study in frogs Professor Roy Curry's group found that altering π_i had virtually no effect at all on filtration rate (Hu et al. 2000).

Adamson et al. (2004) combined their experiments in vivo with confocal imaging of interstitial albumin distribution, reconstruction of the endothelial intercellular pathway geometry by serial electron micrography and a sophisticated mathematical model of the exchange pathway, to explain their results quantitatively. The semipermeable membrane (selective pores) across which protein osmotic pressure is exerted is the luminal glycocalyx of endothelium (Fig. 1). The outside of this membrane is not in direct contact with interstitial fluid (π_i) but is connected to it by a long, narrow but open paracellular cleft. The subglycocalyx fluid is of lower protein concentration than the interstitial fluid because it is dominated by a continuously formed ultrafiltrate (osmotic pressure π_g). Protein concentration is higher in the bulk interstitial fluid (30–60% of plasma concentration) because plasma proteins cross the endothelial barrier by a separate pathway, the large pore system. To have any effect on the glycocalyx, interstitial protein has to diffuse against the current of fluid sweeping out through the intercellular cleft.

Figure 1. Changing nature of Starling principle for fluid exchange across non-fenestrated endothelium.

F, sum of ‘forces’ acting across semipermeable membrane. σ, reflection coefficient. Other symbols as in text. Continuous short arrows denote force directions; dashed arrows denote flow.

Can the concept of osmotic asymmetry be generalized to other tissues? In the structurally different fenestrated capillary, the exit from the ultrafilter (glycocalyx overlying fenestral membrane apertures) is much less enclosed. Here an analogous but less extreme osmotic asymmetry has been observed; changes in π_i have 50% of the effect of changes in π_p. This is again due to an abluminal protein gradient, in this case around the filtering fenestrations (Levick, 1994). However, in the only other study of continuous (non-fenestrated) endothelium and π_i (Smaje et al. 1970) the results seem at first to conflict with the asymmetry model. Smaje et al. varied π_i around rat cremaster and rabbit omental capillaries perfused with blood at normal pressures and found that filtration rate increased linearly with π_i, in approximately the amount expected from the capillary filtration coefficient. Adamson et al. (2004) argue that this may be because native P_c and filtration velocity are low, allowing interstitial protein to diffuse up the cleft into the subglycocalyx space. (Control filtration rate was deliberately set high in the Adamson et al. study to test the concept of a ‘protected’ subglycocalyx space.) The authors estimate that 70–90% of the bulk π_i may be effective in the subglycocalyx space (π_g) under conditions of low P_c at heart level.

The new paradigm has important implications for fluid balance and oedema formation. First, it renders untenable the popular argument that sustained venular absorption accounts largely for tissue fluid balance. During fluid absorption the subglycocalyx π_g will increase quickly, due to reverse ultrafiltration, and thus prevent sustained absorption – as Michel & Phillips (1987) proved experimentally. To explain tissue fluid balance we must now focus increasingly on lymphatic function.

Second, the findings may help to resolve the low lymph flow paradox (see earlier). Use of bulk π_i overestimates the net filtration force and hence the lymph production, because the effective abluminal osmotic pressure π_g is smaller than π_i. The size of the difference is itself a function of filtration rate.

Third, reduction of bulk π_i is traditionally considered a major part of the ‘safety margin’ against oedema formation. This is evidently untrue at high filtration rates. Physiological filtration rates in many tissues, however, are probably slower than in the Adamson et al. experiment, so it remains possible that increases in filtration from low initial rates are buffered by reduced π_g. Indeed the authors argue that the effectiveness of this buffering process is enhanced. This could be tested by repeating their study over a range of π_i and P_c values.

The paper by Adamson et al. (2004) is an important step forward but it also raises a new, medically important puzzle; how is the life-supporting reabsorption of interstitial fluid sustained in clinical shock? In human hypovolaemic shock ∼500 ml of interstitial fluid can be absorbed over ∼30 min, topping up the depleted circulation, as Starling himself noted. Hyperglycaemic hyperosmolarity may influence the fluid shift in the whole animal. However, even in an isolated perfused cat or dog hind-limb, the absorption process can continue for 15 min. The steady-state model of Adamson et al. (2004) does not address the time course of reabsorption; but since the intercellular cleft volume is extremely small, a very short time constant might be implied, possibly seconds. The time course of absorption remains inadequately understood and constitutes a medically important challenge for the future.