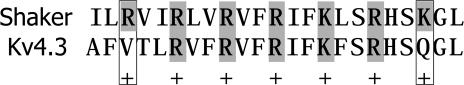Activation properties of Kv4.3 channels:time, voltage and [K⁺]_o dependence

Abstract

Rapidly inactivating, voltage-dependent K⁺ currents play important roles in both neurones and cardiac myocytes. Kv4 channels form the basis of these currents in many neurones and cardiac myocytes and their mechanism of inactivation appears to differ significantly from that reported for Shaker and Kv1.4 channels. In most channel gating models, inactivation is coupled to the kinetics of activation. Hence, there is a need for a rigorous model based on comprehensive experimental data on Kv4.3 channel activation. To develop a gating model of Kv4.3 channel activation, we studied the properties of Kv4.3 channels in Xenopus oocytes, without endogenous KChIP2 ancillary subunits, using the perforated cut-open oocyte voltage clamp and two-electrode voltage clamp techniques. We obtained high-frequency resolution measurements of the activation and deactivation properties of Kv4.3 channels. Activation was sigmoid and well described by a fourth power exponential function. The voltage dependence of the activation time constants was best described by a biexponential function corresponding to at least two different equivalent charges for activation. Deactivation kinetics are voltage dependent and monoexponential. In contrast to other voltage-sensitive K⁺ channels such as HERG and Shaker, we found that elevated extracellular [K⁺] modulated the activation process by slowing deactivation and stabilizing the open state. Using these data we developed a model with five closed states and voltage-dependent transitions between the first four closed states coupled to a voltage-insensitive transition between the final closed (partially activated) state and the open state. Our model closely simulates steady-state and kinetic activation and deactivation data.

Rapidly inactivating, voltage-dependent K⁺ channels play important roles in both neurones and cardiac myocytes. In pre-and postsynaptic neurones, rapid (A-type) inactivating K⁺ currents can strongly modulate excitability, thereby influencing events such as interspike interval (Hille, 2001). In the heart, the rapidly inactivating voltage-dependent K⁺ current, I_to, contributes to the action potential plateau and, as a result, to the magnitude of Ca²⁺ influx during the plateau. In addition, these K⁺ currents also determine the duration of repolarization and the propensity to cardiac arrhythmias (Campbell et al. 1995; Brahmajothi et al. 1999; Nerbonne, 2000; Strauss et al. 2001; Antzelevitch & Shimizu, 2002). It is currently accepted that Kv4 channels form the basis of these currents in many neurones and cardiac myocytes (Jerng & Covarrubias, 1997; Brahmajothi et al. 1999; Nerbonne et al. 2001).

The cardiac I_to is formed by the association of Kv4.2 and Kv4.3 α subunits with KChIP2 ancillary subunits (An et al. 2000; Patel et al. 2002a, b; Rosati et al. 2003). Recent studies have demonstrated that the Kv4.2 and Kv4.3 channel α subunits associate with KChIP ancillary subunits, and that both are colocalized in the ventricular myocardium (Patel et al. 2002a, b; Rosati et al. 2003). Although this family of ancillary subunits has been demonstrated to increase the expression of K⁺ channels, they also have been shown to modify the gating of the Kv4 channels. However, the underlying mechanism(s) is unresolved.

Kv4 channels have recently attracted great interest because their mechanism of inactivation appears to differ significantly from that reported for Shaker and Kv1.4 channels. In Shaker and Kv1.4 channels, inactivation is governed by N- and C-type inactivation attributed to a ball and chain mechanism occluding the inner vestibule (N-type) and pore closure (C-type) (Hoshi et al. 1991; Liu et al. 1996; Rasmusson et al. 1998; Jiang et al. 2003a; Gebauer et al. 2004). In contrast, Jerng & Covarrubias (1997) and Jerng et al. (1999) showed that inactivation in Kv4.1 channels occurs from both a partially activated closed and an open state. In most ion channels, inactivation is coupled to activation (Bezanilla & Armstrong, 1977; Papazian et al. 1991; Hille, 2001). As a result, models of inactivation are critically dependent on the kinetics and steady-state activation and deactivation properties. Currently, activation data on the Kv4.3 α subunit expressed in the absence of an ancillary subunit is incomplete, either because the appropriate kinetic data were not obtained or because the Kv4.3 α subunit was expressed in cells containing an endogenous KChIP2 ancillary subunit (Jerng et al. 1999; Bähring et al. 2001; Beck et al. 2002; Patel et al. 2002a). In all cases, models of Kv4.x activation have not been developed from a rigorous comparison of the experimental steady-state and kinetic activation and deactivation data.

While significant progress has been made in our understanding of the biophysical basis of gating of Kv4 channels, especially Kv4.1 channel inactivation gating, further study of Kv4.3 channel activation gating kinetics was warranted for four important reasons. First, Kv4.3 channels form the basis of the cardiac I_to in several animal species and the human heart (Näbauer et al. 1993; Brahmajothi et al. 1999; Nerbonne et al. 2001). Second, Kv4.1 and Kv4.3 channels display significant functional differences (Jerng & Covarrubias, 1997; Jerng et al. 1999; Beck & Covarrubias, 2001). Third, the model developed by Bähring et al. (2001) was based on a study of heterologously expressed Kv4.2 channels in HEK293 cells, which contain an endogenous KChIP protein (Patel et al. 2002a). Finally and most importantly, the development of a model of activation that is based on accurate measurements is a foundation for any model of inactivation.

Therefore, in this paper, we set out to systematically study the properties of Kv4.3 channels in a heterologous expression system that did not express endogenous KChIP2 ancillary subunits (Patel et al. 2002a). A comprehensive analysis of activation of Kv4.3 currents expressed in Xenopus oocytes was implemented using the cut-open oocyte voltage clamp technique. We obtained high-frequency resolution measurements of the activation properties of Kv4.3 channels and developed a discrete state Markov model that closely describes the experimental data. The voltage dependence of the activation time constants was best described by a biexponential function corresponding to at least two different equivalent charges for activation. Our analysis suggests that the equivalent charge movement during activation can vary as a function of voltage. Finally, in contrast to other voltage-sensitive K⁺ channels (HERG, Shaker), we found that markedly elevated extracellular K⁺ concentrations modulated the activation process by slowing deactivation and stabilizing the open state.

Methods

cRNA preparation and channel expressions

Wild type (WT) cDNA of Kv4.3 channels (short form), a gift of Dr David McKinnon (Stony Brook, SUNY) was utilized in these studies. The construct has been previously described (Wang et al. 2002).

Mature female Xenopus laevis (Xenopus One, Ann Arbor, MI, USA) were anaesthetized by immersion in tricaine solution (1.5 g l⁻¹). Ovarian lobes were removed through a small incision in the abdominal wall. The follicular layer was removed enzymatically by placing the lobes in a collagenase-containing, Ca²⁺-free OR2 solution (mm):82.5 NaCl, 2 KCl, 1 MgCl₂, 5 Hepes, pH 7.4; 1–2 mg ml⁻¹ collegenase (Type I, Sigma, St Louis, MO, USA). After removal of the ovarian lobe, the incisions were sutured closed and the frogs were then allowed to recover in a small water-filled container as previously described (Comer et al. 1994). Typically, lobes were obtained three times from a single frog. When individual frogs no longer yielded acceptable oocytes, they were anaesthetized and killed by an overdose of tricaine (20 g l⁻¹).

The oocytes were gently shaken for about 2 h and collagenase activity was then halted by bovine albumin as previously described (Comer et al. 1994). Defolliculated oocytes (stage V–VI) were then injected with transcribed cRNA (up to 50 nl) using a ‘Nanoject’ microinjection system (Drummond Scientific Co., Broomall, PA, USA) and incubated at 18°C for 24–72 h in an antibiotic-containing Barth's solution (mm):88 NaCl, 1 KCl, 2.4 NaHCO₃, 0.82 MgSO₄, 0.33 Ca(NO₃)₂, 0.41 CaCl₂, 10 Hepes (pH:7.4), 2% (v/v of 100 × stock) antibiotic–antimycotic (Invitrogen).

Electrophysiological techniques

Experiments were performed using a cut-open oocyte clamp amplifier (CA-1b, Dagan Corp., Minneapolis, MN, USA) (Taglialatela et al. 1992) as previously described (Comer et al. 1994). Microelectrodes were fabricated from 1.5 mm o.d. borosillicate glass tubing (TW150F-4, WPI) using a two-stage puller (L/M-3 P-A, Adams & List Associates, Ltd, Great Neck, NY, USA) filled with 3 m KCl with resistances of 0.6–1.5 MΩ. During recording, oocytes were continuously superfused externally (upper pool) with control ND 96 solution (mm):96 NaCl, 2 KCl, 1 MgCl₂, 1.8 CaCl₂, 10 Hepes, pH 7.4, adjusted with NaOH or ND 98 solution (mm):98 KCl, 1 MgCl₂, 1.8 CaCl₂, 10 Hepes, pH 7.4 adjusted with NaOH. The composition of the upper and middle (guard) pool solutions were identical. Intracellular (lower pool) solution contained (mm):98 KCl, 1.8 MgCl₂, 1 EGTA and 5 Hepes-NaOH, pH 7.4. Currents were recorded at room temperature (21–23°C) and were sampled at 250 kHz. The time resolution of decay was determined by the time constants of capacitance transients that were in the range of 50–125 μs. Currents from the cut-open oocyte clamp technique were leakage and capacitance subtracted using a P/4 pulse protocol, unless otherwise noted. Cut-open oocyte clamp data were filtered at 10 kHz.

Experiments were also performed on oocytes using a two-microelectrode bath clamp amplifier (OC-750A, Warner Instruments Corp., Hamden, CT, USA) as has been described in detail elsewhere (Comer et al. 1994). Microelectrodes were fabricated from 1.5 mm o.d. borosilicate glass tubing (TW150F-4, WPI) using a two-stage puller (L/M-3 P-A, Adams & List Associates) to produce electrodes with resistances of 0.6–1.5 MΩ when filled with 3 m KCl. During recording, oocytes were continuously perfused with control solution (mm:96 NaCl, 2 KCl, 1 MgCl₂, 1.8 CaCl₂ and 10 Hepes, adjusted to pH 7.4 with NaOH) or 98K solution (mm:98 KCl, 1 MgCl₂, 1.8 CaCl₂ and 10 Hepes, adjusted to pH 7.4 with NaOH). Solutions with 5, 10 and 50 mm KCl contained 93, 88 and 48 mm NaCl, respectively. Currents were recorded at room temperature (21–23°C) and were sampled at 20 kHz. The two-electrode voltage clamp data were filtered at 10 kHz.

Data analysis

Data were recorded on a computer and were digitized and analysed directly using pCLAMP 9 and Clampfit 9 software (Axon Instruments, Inc.). The pulse protocols and the equations that best fit the data are presented in the corresponding figure legends. Data are shown as means ± s.e.m. Confidence levels were calculated using Student's paired t test. A fourth power Boltzmann function (f(V) = 1/{1 + exp[−(V − V_½)/k]}⁴) was used to fit the data to calculate the steady-state activation relationship.

Gating model and simulation

For model development we used Fortran 90 and ran the program on DEC Alpha workstation. The Markov model was implemented as a set of evolution differential equations for five closed states, C₀–C₄, and one open state, O. One inactivated state, I, was added to simulate effect of inactivation on determination of the activation time constant τ_act. Numerical solution of differential equations was performed by fourth-order Runge-Kutta method. We assumed that initially, at a resting potential of −90 mV, all channels were in the state C₀, C₀ = 1.0, and all other states were empty.

Results

Activation

Prior studies that evaluated the kinetics of activation of Kv4.3 channels have been limited by the use of the two-electrode voltage clamp technique in the study of transfected oocytes or by the inadvertent use of a heterologous expression system containing endogenous KChIP2 subunits. With the standard two-electrode voltage clamp technique, the duration of the capacitive transient (∼2 ms) could obscure the initial part of the relatively fast activation process of channels such as Kv4.3 (Taglialatela et al. 1992). Therefore, we set out to measure the kinetics of activation of Kv4.3 in transfected oocytes obtained from Xenopus laevis using the cut-open oocyte voltage clamp technique. As [K⁺]_o has been shown to modify the gating properties of this and other K⁺ channels (Rasmusson et al. 1995, 1998; Wang et al. 1997; Eghbali et al. 2002), both the kinetics and steady-state activation relationships were measured at several [K⁺]_o.

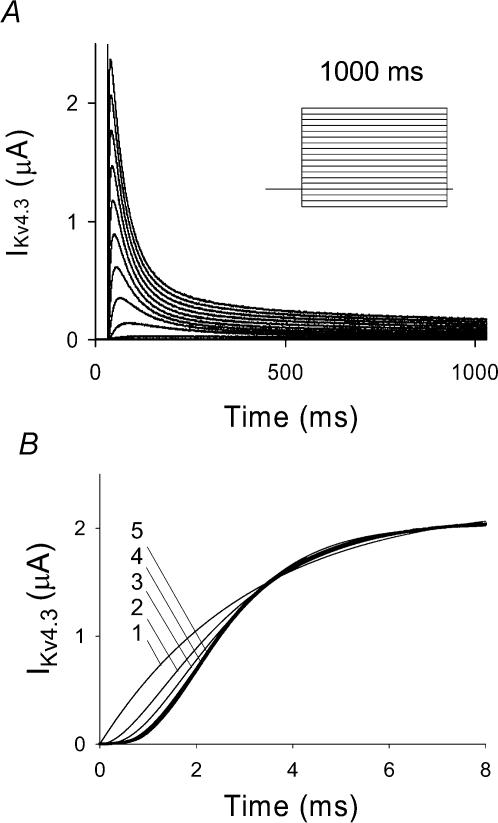
Typical responses of Kv4.3 channels to a series of test depolarizations illustrate the rapid activation and inactivation of the channel measured at 2 mm [K⁺]_o (Fig. 1A). As the study of the voltage dependence of activation can be compromised by fast inactivation, we set out to measure the activation properties using two series of depolarizing pulses, 10 and 1000 ms (Figs 1 and 2A, B). Ten-millisecond pulses were used to minimize inactivation. Activation data shown in Fig. 2A and B were obtained following capacitance subtraction and demonstrated a sigmoid delay and voltage dependence. The voltage dependence was manifest by an increase in both the rate of activation and the magnitude of the current. The sigmoidal activation time course was fitted with a Hodgkin–Huxley-like activation equation of the general form C[1 − exp(−t/τ_act)]ⁿ, where C is a constant and n was allowed to vary between 1 and 5. Optimal fits were obtained at n = 4 and 5, but the difference was not significant and as a result a value of n = 4 was selected for subsequent analysis (Fig. 1B).

Figure 1. Experimental Kv4.3 current.

A, experimental traces of Kv4.3 current recorded using a holding potential of −90 mV and a series of 1000 ms depolarizing pulses from −120 to +50 mV in 10 mV steps at an extracellular K⁺ concentration of 2 mm using the cut-open oocyte voltage clamp technique. Inset, voltage clamp protocol, used for generation of I_Kv4.3 traces. B, comparison of the time course of experimental I_Kv4.3 at depolarization to +50 mV (10 ms pulse) and fitting by function f_a(t) =C(1 − exp[−t/τ_act])ⁿ, where n is varied from 1 to 5. In the cases of n = 4 and n = 5, the function f_a(t) gave the best fit to the experimental data.

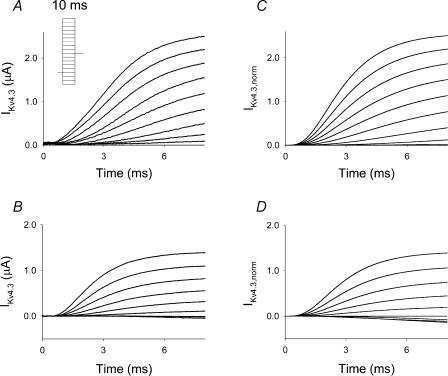
Figure 2. Series of experimental traces of activation of I_Kv4.3 obtained at different [K⁺]_o, 2 mm (A) and 98 mm (B), and simulated traces of activation of I_Kv4.3 for different [K⁺]_o, 2 mm (C) and 98 mm (D).

A series of 10 ms voltage steps were applied from a holding potential of −90 mV ranging between −120 and +50 mV in 10 mV steps using the cut-open voltage clamp technique. Capacitance transients were subtracted by fitting with exponential functions. Simulated traces were generated using the same experimental protocol as described above in A and B and are based on a discrete state Markov model. Depolarization pulses during simulations were applied at the end of a 20 ms holding potential at which time test depolarizations were initiated and designated as occurring at t = 0 ms. A 20 ms holding potential was used to allow the channel to reach equilibrium. Traces were normalized to the experimental value of I_Kv4.3 at the end of the depolarization pulse to +50 mV and at 2 and 98 mm[K⁺]_o. Inset in A, voltage clamp protocol, used for generation of I_Kv4.3 traces.

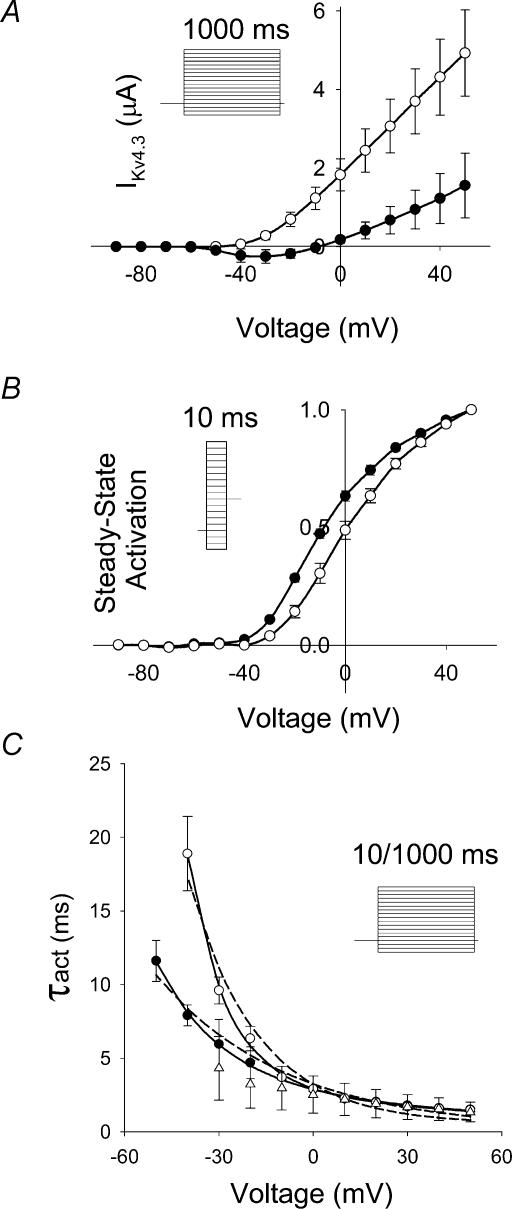
To examine the effects of elevated [K⁺]_o on activation, we initially compared activation data at 2 mm[K⁺]_o with those at 98 mm[K⁺]_o and demonstrated that the currents at 98 mm[K⁺]_o were smaller at all potentials than at 2 mm[K⁺]_o (Fig. 2A and B). These differences could be attributed to a reduced electrochemical gradient. Peak I–V relationship at 2 mm[K⁺]_o was linear at voltages positive to −10 mV and demonstrated a threshold for activation of −40 mV (Fig. 3A, unfilled circles). At 98 mm[K⁺]_o (Fig. 3A, filled circles), activation threshold was shifted to more negative potentials when compared to 2 mm[K⁺]_o. The best fit of steady-state activation data at 2 mm[K⁺]_o (Fig. 3B, unfilled circles) using a fourth-power Boltzmann function, f(V) = 1/{1 + exp[−(V − V_½)/k]}⁴, yielded a V_½ of − 29.4 mV and a k of 19.4 mV. This k-value corresponds to an equivalent charge of 1.31e₀ per subunit. At 98 mm[K⁺]_o (Fig. 3B, filled circles), the same fitting function yielded a V_½ of −37.7 mV and a k of 18.2 mV, which corresponds to an equivalent charge of 1.40e₀ per subunit. As the slope factor of macroscopic current will only provide a lower limit of the charge movement per subunit, the estimates of equivalent charge represent a minimal value (Schoppa et al. 1992; Aggarwal & MacKinnon, 1996; Seoh et al. 1996).

Figure 3. Effects of two different extracellular [K⁺] on peak I–V relationship and activation properties.

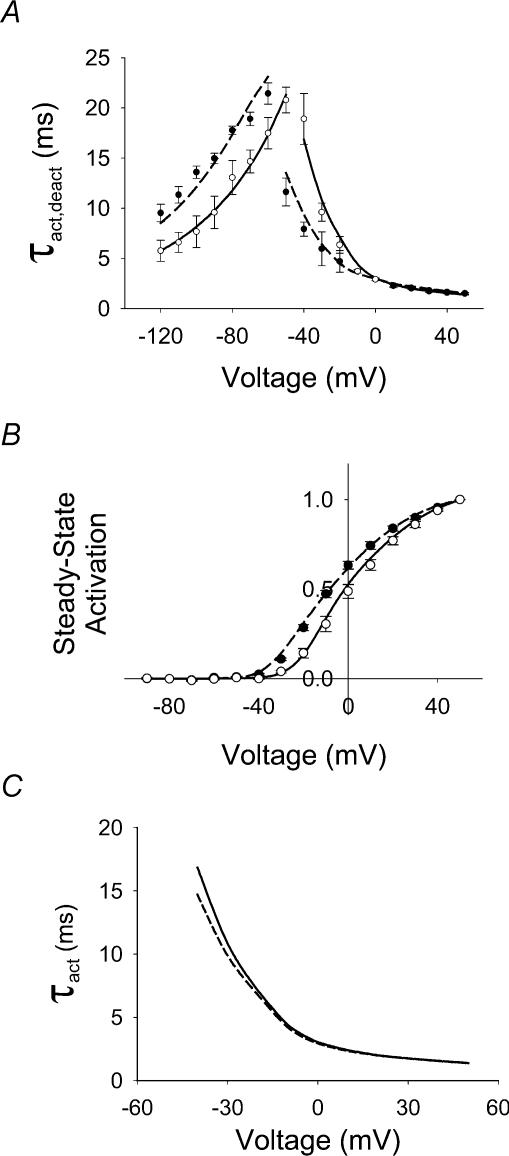
A, experimental I–V relationship for I_Kv4.3, 2 mm (○, n = 5) and 98 mm (•, n = 4). Data were obtained using 1000 ms voltage steps from a holding potential of −90 mV to variable voltages ranging between −120 and +50 mV in 10 mV steps (see inset in A). B, experimental steady-state activation functions were obtained for I_Kv4.3 using a two-pulse protocol. Ten-millisecond voltage pulses, P1, applied from a holding potential −90 mV ranged between −120 and +50 mV (10 mV increment), with P2 set at −40 mV and 500 ms duration (inset in B). Data recorded at [K⁺]_o 2 (n = 3) and 98 mm (n = 5), are represented by ○ and •, respectively. C, the time constants of activation (τ_act) were determined by fitting the rising phase of I_Kv4.3 obtained during both 10 and 1000 ms depolarizing pulses (inset in C). Current traces were then fitted with the function f_a(t) = C(1 − exp(−t/τ_act))⁴. The data obtained with a 1000 ms pulse are shown by ○ (2 mm[K⁺]_o, n = 5) and • (98 mm[K⁺]_o, n = 4). Experimental data obtained at 2 mm[K⁺]_o using a 10 ms pulse (n = 4) are shown as □. Dashed and continuous lines show fits of τ_act(V) with single- and double-exponential functions, respectively. All data shown in this figure were obtained using the cut-open oocyte voltage clamp technique.

The voltage dependence of activation time constants was measured using both 10 and 1000 ms pulses at 2 mm[K⁺]_o and is shown in Fig. 3C. Substantial differences in the voltage dependence of activation were observed. The relationship obtained from fitting the rising phase of current traces recorded with 1000 ms pulses was much steeper than with 10 ms pulses. Closer analysis revealed that activation kinetics (τ_act) determined with 10 and 1000 ms (unfilled triangles and circles, respectively) closely approximated each other between 0 and +50 mV. However, the steep voltage dependence seen with 1000 ms pulses between −40 and 0 mV was not observed with 10 ms pulses, reflecting truncation of slower activation processes. For example, 1000 and 10 ms pulses at −30 mV yield substantial differences in the value of τ_act (τ_act = 9.6 ms and 4.3 ms, respectively). These substantial differences in the values of τ_act indicate that use of short duration pulses results in an underestimation of τ_act and precludes the use of a 10 ms pulse to characterize activation kinetics at these potentials. On the other hand the rising phase of the current during longer pulses, used to estimate τ_act, can be influenced by inactivation.

The next analysis of activation kinetics was performed using data obtained with 1000 ms pulses. At voltages positive to 0 mV the voltage dependence of τ_act was much more shallow than at more negative potentials. As a result, voltage dependence of activation could not be fitted adequately by a single exponential function (dashed line in Fig. 3C); however, the experimental values were well fitted by a biexponential function. At 98 mm[K⁺]_o, the voltage dependence of activation kinetics between −40 and −10 mV was less steep than at 2 mm[K⁺]_o (Fig. 3C) and at voltages positive to 0 mV, the voltage dependence was even less apparent. Activation kinetics converged at positive potentials at the two different [K⁺]_o. Using the values derived from fitting with the biexponential function, the equivalent charges were found to be 0.27e₀ and 2.11e₀ per subunit for 2 mm[K⁺]_o and 0.23e₀ and 1.24e₀ per subunit for 98 mm[K⁺]_o. These data indicate that less charge movement was needed to activate the Kv4.3 channel at high [K⁺]_o, particularly at smaller depolarizing pulses near the threshold for activation.

Deactivation

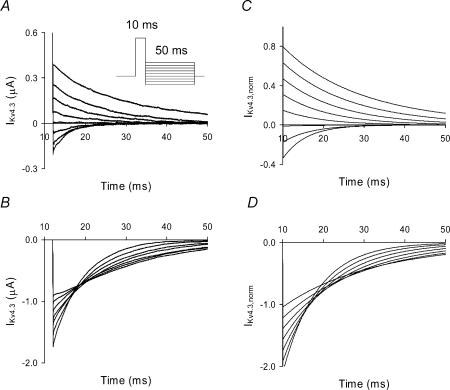
Deactivating tail current kinetics (τ_deact) were measured and shown to be monoexponential and voltage dependent (Fig. 4A and B for 2 and 98 mm[K⁺]_o, respectively). Current traces shown in Fig. 4 are capacitance subtracted. At 2 mm[K⁺]_o deactivation currents were both inward and outward in the potential range between −120 to −50 mV (Fig. 4A), but at 98 mm[K⁺]_o only inward deactivation tail currents were observed (Fig. 4B). Deactivation kinetics were voltage dependent at both 2 and 98 mm[K⁺]_o and slower at 98 mm[K⁺]_o throughout the voltage range evaluated (Fig. 5A). The equivalent charges were 0.48e₀ per subunit for 2 mm[K⁺]_o and a smaller value of 0.33e₀ per subunit was obtained at 98 mm[K⁺]_o.

Figure 4. Effects of two different extracellular [K⁺] on deactivation of I_Kv4.3.

Experimental records of deactivation at [K⁺]_o concentrations of 2 mm (A) and 98 mm (B) are shown. A two-pulse protocol was used. Holding potential was −90 mV and the P1 pulse was set to +50 mV for 10 ms and followed by a second pulse that ranged between −120 to −40 mV for 50 ms in steps of 10 mV (inset in A). Capacitance transients were subtracted. Simulated traces of deactivation of I_Kv4.3 for different [K⁺]_o, 2 mm (C) and 98 mm (D), were obtained using the same voltage clamp protocol described in A and B, respectively. Depolarization pulses during simulations were applied at the end of a 20 ms holding potential at which time test depolarizations were initiated and designated as occurring at t = 0 ms. A 20 ms holding potential was used to allow the channel to reach equilibrium. Data shown in A and B in this figure were obtained using the cut-open oocyte voltage clamp technique.

Figure 5. Comparison between simulated and experimental data.

A, experimental and simulated voltage dependence of the kinetics of activation (τ_act) and deactivation (τ_deact) of the I_Kv4.3. The time constants of activation are the same as shown in Fig. 3C. The time constants of deactivation were obtained from the experimental traces of I_Kv4.3 using single exponential fitting function for 2 (○, n = 3) and 98 mm (•, n = 3) [K⁺]_o. Unfilled and filled symbols with error bars represent plotted experimental data for 2 and 98 mm[K⁺]_o, respectively. Continuous and dashed lines show calculated values for 2 and 98 mm[K⁺]_o, respectively. The deactivation two-pulse protocol was the same as in Fig. 4. B, experimental (circles) and simulated (continuous and dashed lines) steady-state activation functions. Symbols are the same as in A. C, voltage dependence of τ_act obtained from simulations using the discrete state Markov model of Kv4.3 channel activation, without (continuous line) and with (dashed line) an incorporated inactivated state. Simulated data almost coincide in the voltage range from 0 to +50 mV. Small differences in the estimation of (τ_act) in the voltage range from −40 to 0 mV were observed. Voltage clamp protocol used for simulation is the same as in Fig. 1. Data shown in A and B in this figure were obtained using the cut-open oocyte voltage clamp technique.

To examine the [K⁺]_o dependence of activation over a physiological and pathophysiological range, we measured steady-state activation and deactivation at different [K⁺]_o ranging between 2 and 50 mm, using the two-electrode voltage clamp technique. Peak tail current values following a 10 ms P1 pulse from −90 to +50 mV (10 mV steps) were used to determine the steady-state activation relationships. Deactivation time constants were measured from tail currents held at −45 mV (250 ms) following a 10 ms P1 pulse to +50 mV. Data shown in Table 1 indicate that there were no significant effects of [K⁺]_o on V_½, k and τ_deact in the concentration range between 2 and 10 mm[K⁺]_o. When comparisons were made for these three variables between 10 and 50 mm[K⁺]_o significant differences were observed for all three parameters (Table 1). The slope factor decreased, the V_½ shifted to more negative values, and τ_deact increased at 50 mm[K⁺]_o.

Table 1.

Effects of [K⁺]_o on steady-state activation properties and deactivation kinetics measured with the two-electrode voltage clamp techinque

[K+]o (mm)	k (mV)	V½ (mV)	τdeact(ms)
2.0 (n = 5)	19.7 ± 0.7	− 31.7 ± 2.1	21.7 ± 0.8
5.0 (n = 5)	20.7 ± 0.7	− 32.1 ± 2.2	22.1 ± 0.7
10.0 (n = 5)	21.7 ± 1.2	− 30.2 ± 2.4	20.5 ± 0.6
50.0 (n = 5)	18.2 ± 0.7*	− 34.7 ± 1.5**	30.1 ± 2.4***

Data are expressed as means ±s.e.m. P statistics are based on comparison of data at 10 and 50 mm [K⁺]_o.

^*P < 0.03

^**P < 0.02

^***P < 0.01. τ_deact was measured at −45 mV.

Discrete state Markov model and simulations of Kv4.3 channel activation

Experimental data were used to create a model for activation that contained five closed states and one open state. The rate constants of transitions between the closed states are voltage dependent, whereas the rate constant of transitions between the last closed state and the open state is voltage independent (Zagotta et al. 1994b). The model is shown in Scheme 1.

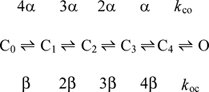
The forward and backward rate constants of activation for 2 mm[K⁺]_o are given by the following equations:

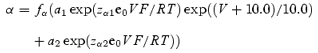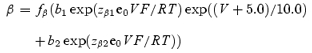where factors

Voltage-independent rate constants k_co and k_oc are equal to 6000 and 1500 s⁻¹, respectively. Equations for α and β were chosen so that they approach the exponential functions:

when V→+50 mV and

when V→−120 mV. In the case of high [K⁺]_o (98 mm), forward and backward rate constants of activation are described by equations

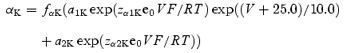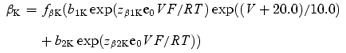where

The net current through the channel is given by

where G_max is the maximum potassium conductance for that particular K⁺ concentration, P_o is the open probability and E_K is given by the Nernst relationship below:

The voltage-independent rate constant k_co is not changed at 98 mm[K⁺]_o, but k_oc is decreased from 1500 to 1200 s⁻¹. The constants used in the equations are given in Table 2.

Table 2.

Model parameters

Parameter	Normal [K+]o (2 mm)	Parameter	High [K+]o (98 mm)
a1	425 s−1	a1K	425 s−1
zα1	0.27	zα1K	0.27
a2	83.6 s−1	a2K	83.6 s−1
zα2	0.83	zα2K	0.83
b1	224.4 s−1	b1K	179.52 s−1
zβ1	−0.54	zβ1K	−0.54
b2	25.2 s−1	b2K	20.16 s−1
zβ2	−0.48	zβ2K	−0.48
kco	6000 s−1	kco	6000 s−1
koc	1500 s−1	koc	1200 s−1

The decrease in k_oc at the higher [K⁺]_o reflects the slowed deactivation kinetics measured in our experiments. The slowed deactivation kinetics also led to a reduced value of β at high [K⁺]_o (β_K), which is smaller than the value of β at low [K⁺]_o (β). This decrease in β was also responsible for the shift in steady-state activation relationship shown in Fig. 3B.

Figure 2C and D shows simulated traces of Kv4.3 current obtained using a holding potential of −90 mV and a series of depolarizing steps from −80 to +50 mV (10 mV increments). The time course of the currents are similar to that observed in the experiment (compare to Fig. 2A and B). G_max was estimated from the measured current at the end of a 10 ms depolarizing pulse to +50 mV in 2 and 98 mm[K⁺]_o. Simulated and experimental currents at 98 mm[K⁺]_o are correspondingly smaller at all voltages due to changes in driving force. The simulated time courses of Kv4.3 current deactivation for 2 and 98 mm[K⁺]_o are shown in Fig. 4C and D, respectively. In relatively low [K⁺]_o, simulations and experiments produce both inward and outward tail currents, depending on the membrane potential. In high external [K⁺], only inward tail currents were observed.

Comparison of experimental and simulated values of time constants for activation and deactivation are plotted in Fig. 5A and demonstrated the close fit between the experimental and simulated values. Simulated voltage dependence for the activation time constants fitted with biexponential functions yielded equivalent charges of 0.24e₀ and 1.39e₀ per subunit for 2 mm[K⁺]_o and 0.16e₀ and 1.21e₀ per subunit for 98 mm[K⁺]_o, respectively. Simulated voltage dependence of the deactivation time constants were well fitted by a single exponential function, with equivalent charges 0.48e₀ per subunit for 2 mm[K⁺]_o and 0.42e₀ per subunit for 98 mm[K⁺]_o, respectively. Figure 5B shows a comparison of experimental and simulated steady-state activation relationships. Simulated data reproduced the negative shift of V_½ for steady-state activation as [K⁺]_o was increased from 2 to 98 mm.

A classical Hodgkin–Huxley model of activation should show a smooth bell-shaped voltage-dependent transition between τ_act and τ_deact. As shown in Fig. 5A, there is a steep transition between the τ_act and the τ_deact over a narrow voltage range between −60 and −40 mV at 2 mm[K⁺]_o, which was more marked at high [K⁺]_o. The steep transition within this voltage range can be explained by the presence of a voltage-insensitive transition between the final closed state, C₄, and the open state, O, which has different forward and reverse rate constants. The difference between these two rate constants determines the value of effective charge in the transition region and as a result the slope of the voltage dependence of τ_act in this region. The enhancement of the gap in values of τ_act and τ_deact at high [K⁺]_o reflects the slowing of deactivation.

To evaluate the possibility that our model of activation could be biased by the failure to include inactivation, we added a fast open to inactivated state transition to our model. Experimental values of fast component of inactivation at +50 mV was τ_inact,fast = 49 ± 4 ms (n = 5). The value of 50 ms used for the fast time constant of inactivation in our model closely approximates the experimental value. An inactivation time constant of 50 ms closely approximates the value for the time constant of open-state inactivation reported for Kv4.3 channels (Beck et al. 2002; Patel et al. 2002a). We then fitted activation kinetics obtained from simulated data that did and did not contain a fast open-inactivated state using a Hodgkin–Huxley-like activation equation C[1 − exp(−t/τ_act)]⁴ (dashed and continuous lines in Fig. 5C, respectively). There are no differences in τ_act for both models at potentials positive to 0 mV, but at negative potentials a small effect on τ_act was observed. In the latter case, the deviation is within the error of measurements (compare with data in Fig. 5A). Hence, analysis of our experimental activation data should not be biased by the fast inactivation process.

Discussion

This paper is the first to describe a detailed quantitative analysis of the activation properties of Kv4.3 channels. We studied Kv4.3 activation with the cut-open voltage clamp technique in Xenopus laevis oocytes, a heterologous expression system that does not contain an endogenous KChIP ancillary subunit (Patel et al. 2002a). We demonstrated that:(1) activation is sigmoid and well described by a fourth power exponential function; (2) activation kinetics are voltage dependent, but the voltage dependence of activation is bi-exponential; (3) deactivation kinetics are voltage dependent and this voltage dependence is monoexponential; (4) both activation and deactivation kinetics are substantially dependent on extracellular [K⁺] outside of the physiological range; (5) the model closely simulated our experimental data; and (6) inclusion of fast open-state inactivation in our model has little effect on the simulations of activation.

In prior studies, limited data from different voltage clamp experiments were used to generate complex models for Kv4 family channels. The use of the standard two-electrode voltage clamp technique in oocytes typically results in capacitive transients that could obscure the initial part of the relatively fast activation process of Kv4.3 channels (Taglialatela et al. 1992) and as a result limits development of accurate models of activation. The studies on the gating of the Kv4.x subfamily have focused on inactivation kinetics, and as a result, studies on activation kinetics received much less attention in these investigations (Jerng & Covarrubias, 1997; Jerng et al. 1999; Bähring et al. 2001; Beck et al. 2002). For example, experiments on activation often used the time-to-peak current as a measure of activation kinetics (Beck et al. 2002). Furthermore, in the study carried out on Kv4.2 channels expressed in HEK cells, with a broader frequency band (Bähring et al. 2001), experiments were implemented in a cell line, which subsequently has been shown to express an endogenous KChIP protein (Patel et al. 2002a). Since, the ancillary subunit, KChIP, has been shown to modify inactivation and the recovery from inactivation, it would be highly desirable to measure Kv4.3 activation in a system that is free of the KChIP ancillary subunit. In this paper, we set out to analyse in detail the activation and deactivation processes in a Kv4.3 channel. For this purpose, we used the cut-open oocyte technique that has a wider frequency range and faster capacitance transients. This allowed us to perform quantitative measurements of both activation and deactivation.

Accurate measurement of activation kinetics can be obscured by rapid inactivation (Almers, 1978; Hille, 2001). To address this issue we used both 10 and 1000 ms test pulses. Comparison of the currents demonstrated close approximation for test pulses between 0 and +50 mV. However, a significant difference was observed for pulses between −40 and 0 mV. The value of τ_act at −30 mV was too long (9.6 ms) to be accurately measured by a 10 ms pulse. Hence, only the data obtained using 1000 ms test pulses, digitized at a high rate were used for development of the model for Kv4.3 channel activation. The measurement of activation in the presence of inactivation has been shown to be problematic in cases where inactivation is much faster than activation (Almers, 1978; Wang et al. 1997; Hille, 2001). However, in Kv4.3 channels the rate of activation exceeds the rate of inactivation by an order of magnitude, which minimizes this complication.

Activation kinetics have been studied in detail in Shaker (Kv1 subfamily) channels (Schoppa et al. 1992; Hoshi et al. 1994; Zagotta et al. 1994a, b; Aggarwal & MacKinnon, 1996; Seoh et al. 1996; Schoppa & Sigworth, 1998a, b, c; Smith-Maxwell et al. 1998a; Ledwell & Aldrich, 1999). Zagotta et al. (1994a) focused on the sigmoidicity of activation. Using discrete state Markov models, they found that activation models of the Shaker K⁺ channel needed at least five or six closed states and an open state to account for their activation data. In addition, the estimations of voltage dependence of Shaker K⁺ channel open probability give an optimal fit with a fourth power of Boltzmann distribution function (Zagotta et al. 1994a). They also reported that the time constants of activation and deactivation are voltage dependent and this dependence can be described by monoexponential functions with equivalent charges 0.42e₀ and 1.1e₀ per subunit, respectively. The complex Markov model developed to account for Shaker K⁺ channel activation contained eight independent conformational changes (Zagotta et al. 1994b). In a subsequent study, Schoppa & Sigworth (1998c) proposed an even more complex model for activation of Shaker K⁺ channel, containing more closed states.

Our model for activation of the Kv4.3 channel contains only five closed states, with four voltage-dependent and one voltage-independent transitions. We investigated the time course of activation development and found that the best fit is achieved with the exponential function C[1 − exp(−t/τ_act)]ⁿ, where n = 4 or n = 5, but the differences between the fits were minor. Therefore, we used a model with four voltage-dependent steps to analyse Kv4.3 channel activation. In addition, we found a biexponential voltage dependence for activation time constants (Fig. 3C), which would appear to be at variance with prior studies on Shaker K⁺ channels. Despite the numerous studies describing a monoexponential dependence of τ_act on voltage in many Shaker K⁺ channel modelling studies, further experimentation indicated a more complex voltage dependence of τ_act, with larger effective charge at voltages near the activation threshold (Zagotta et al. 1994a; Schoppa & Sigworth, 1998a, c). Experimental data on Kv2.1 channel activation also indicates a more complex voltage dependence of τ_act (Islas & Sigworth, 1999). Deactivation kinetics of the Kv4.3 channel used in our study were monoexponential and similar to the experimental data for Shaker K⁺ channels (Zagotta et al. 1994b) and Kv2.1 channels (Islas & Sigworth, 1999). However, other experiments with Kv4.x channels report both monoexponential (Bähring et al. 2001) and biexponential (Beck et al. 2002) time course of deactivation.

A single voltage-dependent activation step is usually characterized by an exponential dependence of the rate, or time constant. The measured time constants of activation of Kv4.3 channels in this study are complex. At very positive and very negative potentials, there is evidence of saturation of rate, indicating that a voltage-insensitive step becomes rate limiting. Our model accounts for this behaviour by a voltage insensitive final opening transition similar to that reported for other channels (Zagotta et al. 1994b; Bähring et al. 2001). However, taking this behaviour into account, the measured and modelled behaviour of activation and deactivation in the transition range of potentials can still not be accounted for by αs and βs with a simple exponential dependence on voltage. We chose to reconcile the fourth order sigmoid onset of the current with this complex voltage dependence with an analysis that assumes that four independent gates modulate channel activation, but that each gate has at least two populations of charge movement that operate the gate. Such an analysis yields the bi-exponential voltage dependence of τ_act, and we can calculate that the two charge movements yield an effective charge of 0.27e₀ and 2.11e₀ per subunit in 2 mm[K⁺]_o. At extremes of potential, the larger charge movement transition is essentially instantaneous and the smaller charge movement governs activation and deactivation voltage dependence. However, at intermediate potentials (i.e. near threshold of activation) the larger charge component dominates, giving rise to the steep voltage dependence of the time constants of activation and deactivation in this range.

The slope of the steady-state activation relationship, which has been used to estimate the effective gating charge, was 19.4 mV at 2 mm[K⁺]_o, which corresponds to values reported by Smith-Maxwell et al. (1998a), Bähring et al. (2001) and Beck et al. (2002). The voltage dependence of steady-state open probability was obtained from experiments in which the limiting slope approach was used to minimize the error introduced by inactivation (Almers, 1978). The steepness of the voltage dependence of gating current measurements provided estimates of gating charge movement that were approximately double the values obtained from the data showing the voltage dependence of the relative conductance of the channel (Hille, 2001). The steady-state activation relation in Kv4.3 channels is ∼2–3 times less steep than it is for Shaker K⁺ channels (Smith-Maxwell et al. 1998a; Hille, 2001; Beck et al. 2002). A comparison of the amino acid sequence between the S4 of Kv4.3 and Shaker K⁺ channels reveals significant differences (Fig. 6). First, the S4 region of Kv4.3 channels contains two fewer positive charges than in Shaker K⁺ channels. Although the outer four charges make the largest contribution to gating charge, the neutralization of the first charged residue in Kv4.3 channels cannot fully account for the difference in slope factor between Kv4.3 and Shaker K⁺ channels (Aggarwal & MacKinnon, 1996). Comparison of these S4 regions also shows seven differences among the uncharged residues, six of which are in the outer portion of S4 (Fig. 6). These uncharged residues may be important because Lopez et al. (1991), McCormack et al. (1991) and Smith-Maxwell et al. (1998b) have shown that they can also affect the kinetic, steady-state and voltage-dependent properties of K⁺ channels. Finally, the impact of the recent structural studies on S4 suggests a more complex model of S4 position and movement during activation than previously suspected (Gonzalez et al. 2000; Jiang et al. 2003b; Cohen et al. 2003). Perhaps the relatively shallow, complex voltage dependence of τ_act, reflects a more complex movement of S4 charge than that described by the sliding helix model (Catterall, 1986).

Figure 6. Comparison of the S4 sequences in Shaker and Kv4.3.

The S4 in Kv4.3 has two fewer charges than in Shaker. In addition, there are seven other differences in the uncharged residues.

Effects of extracellular K⁺ concentration

Our experimental data show no substantial dependence of activation and deactivation on the extracellular [K⁺] in the range from 2 to 10 mm. However, we found that an increase in [K⁺]_o from 10 to 98 mm had significant effects on channel gating. With the cut-open oocyte data, we found that the increase in [K⁺]_o from 2 to 98 mm slows deactivation and speeds activation by shifting its voltage dependence to negative values. Similar effects of elevated [K⁺]_o on deactivation were observed in the delayed rectifier K⁺ currents in squid axon and on activation in Kv4.3 channels (Swenson & Armstrong, 1981; Eghbali et al. 2002; Shahidullah & Covarrubias, 2003). These findings are in contrast to those for Shaker K⁺ (Zagotta et al. 1994b) and HERG channels (Wang et al. 1997), where [K⁺]_o had no effect on activation and deactivation. In addition to the effects of high extracellular [K⁺] on the delayed rectifier K⁺ currents, Swenson & Armstrong (1981) reported that in the squid giant axon, Rb⁺ slowed deactivation of this K⁺ current. Rb⁺ had similar effects on Kv4.2 deactivation (Bähring et al. 2001; Shahidullah & Covarrubias, 2003). Thus, our data along with the data of others mentioned above support the view that increased occupancy of an outer cation binding site, whether due to increased concentration or increased affinity for the channel binding site, inhibits the channel from making its transition from the open state to a non-conducting closed state. The appearance of an effect on deactivation kinetics only at high [K⁺]_o suggests that the dissocation kinetics of K⁺ from its binding site are too rapid for an effect to be seen at physiological [K⁺]_o.

In our experiments, the effect of increased [K⁺]_o on the rate of deactivation is likely to be associated with increased occupancy of the outer binding site in the channel pore. Hence, we suggest that the presence of K⁺ in the outer pore region of the Kv4.3 channel stabilizes the open state and slows deactivation. These data suggest that the gate responsible for deactivation is different in Kv4.x from that in Shaker and HERG. In Shaker K⁺ channels, an activation gate has been localized to the intracellular face of the pore, particularly on S6 (Jan & Jan, 1994; del Camino & Yellen, 2001; Perozo, 2002), although additional ‘gates’ have been suggested. One interpretation of our K⁺ dependence data is that occupancy of the pore modulates activation through an allosteric linkage between pore occupancy and an intracellular gate as has been proposed based on the crystal structure of KcsA (Doyle et al. 1998). A simpler interpretation is that Kv4.3 activation is controlled by an extracellular gate. This hypothesis is supported by the drug binding evidence in native and cloned Kv4.x channels that the intracellular pore mouth remains open at rest (Campbell et al. 1993; Tseng et al. 1996; Yeola & Snyders, 1997). While our data do not allow us to distinguish between allosteric modulation of an intracellular gate and direct gating at the extracellular pore, there is clear evidence from this study and the work of others, for the involvement of permeant ions in stabilizing the open conformation of the channel (Eghbali et al. 2002).