Abstract
We set out to fully examine the frequency domain relationship between arterial pressure and cerebral blood flow. Oscillatory lower body negative pressure (OLBNP) was used to create consistent blood pressure oscillations of varying frequency and amplitude to rigorously test for a frequency- and/or amplitude-dependent relationship between arterial pressure and cerebral flow. We also examined the predictions from OLBNP data for the cerebral flow response to the stepwise drop in pressure subsequent to deflation of ischaemic thigh cuffs. We measured spectral powers, cross-spectral coherence, and transfer function gains and phases in arterial pressure and cerebral flow during three amplitudes (0, 20, and 40 mmHg) and three frequencies (0.10, 0.05, and 0.03 Hz) of OLBNP in nine healthy young volunteers. Pressure fluctuations were directly related to OLBNP amplitude and inversely to OLBNP frequency. Although cerebral flow oscillations were increased, they did not demonstrate the same frequency dependence seen in pressure oscillations. The overall pattern of the pressure–flow relation was of decreasing coherence and gain and increasing phase with decreasing frequency, characteristic of a high-pass filter. Coherence between pressure and flow was increased at all frequencies by OLBNP, but was still significantly lower at frequencies below 0.07 Hz despite the augmented pressure input. In addition, predictions of thigh cuff data from spectral estimates were extremely inconsistent and highly variable, suggesting that cerebral autoregulation is a frequency-dependent mechanism that may not be fully characterized by linear methods.
Maintenance of cerebral perfusion over a wide range of systemic pressures is thought to be carried out through a mechanism dubbed cerebral autoregulation (Strandgaard et al. 1984; Paulson et al. 1990). This function counter-regulates systemic pressure changes through cerebrovascular resistance adjustments. Originally, cerebral autoregulation was conceived as encompassing the time scale from minutes to hours, such that changes in cerebral blood flow that fully counteract sustained arterial pressure changes indicate effective autoregulation (Strandgaard et al. 1984; Paulson et al. 1990). As the time resolution of measurement techniques has increased, however, results have suggested that autoregulation works on a much more ‘dynamic’, beat-by-beat basis (Aaslid et al. 1989; Newell et al. 1989). Specifically, the beat-by-beat relationship between pressure and flow has been modelled as a simple high-pass filter (Newell et al. 1989; Blaber et al. 1997; Diehl et al. 1998; Panerai et al. 1998; Zhang et al. 1998). This assumes that slower oscillations in pressure (below ∼0.07 Hz) are effectively blunted (low transfer function gain) while faster oscillations pass through unaffected (a gain of one) (Zhang et al. 1998). These observations have led researchers to hypothesize that cerebral autoregulation is a frequency-dependent phenomenon that operates most effectively in the frequency range below 0.07 Hz.
For several reasons, we were skeptical that spectral analyses of cerebral blood flow can support this hypothesis. Spontaneous pressure fluctuations are extremely inconsistent and small in amplitude in the purported autoregulatory region (Taylor et al. 1998). The relationship between pressure and flow in this low frequency region is similarly inconsistent, with periods of high correlation interspersed with sections of extremely low correlation and oscillations in blood flow appearing with no apparent blood pressure drive (Giller & Mueller, 2003). Consequently, cross-spectral coherence, a statistic gauging confidence in cross-spectral measures, tends to be very low between beat-by-beat cerebral flow and arterial pressure in the region of interest (Zhang et al. 1998). Feasibly, this low coherence might indicate that pressure changes are being regulated against (Zhang et al. 1998; Narayanan et al. 2001) but could also simply result from either small amplitude random fluctuations (i.e. noise) or a non-linear relationship between the two signals in this frequency range. Low coherence merely means that one cannot confidently assign a linear input–output relationship to the two variables in question (Giller & Mueller, 2003). To truly examine the cross-spectral relationship between two signals, one needs sufficient amplitude oscillations and significant cross-spectral coherence, conditions often absent in resting steady-state data.
We examined the frequency domain relationship between arterial pressure and cerebral blood flow through a technique known as oscillatory lower body negative pressure (OLBNP) (Hamner et al. 2001). Through this technique we created consistent blood pressure oscillations of varying frequency and amplitude, and could assess the cerebral blood flow response. Thus, we could rigorously test for the frequency- and/or amplitude-dependent relationship between arterial pressure and cerebral blood flow velocity. As a method of cross-validation, we examined the predictions from OLBNP data for the cerebral flow response to the stepwise arterial pressure drop subsequent to ischaemic thigh cuff deflation. The cerebral blood flow response to this manoeuvre has also been proposed as a method of assessing dynamic cerebral autoregulation. Our findings suggest that a frequency-dependent regulatory mechanism is indeed at work, but a linear model may not be sufficient to characterize it.
Methods
Subjects
Nine healthy volunteers aged 23–40 years (3 females) gave informed consent for this study. Volunteers were free from cardiovascular and neurological disorders and cardioactive medications. The participants were normotensive and refrained from alcohol, caffeine and nicotine at least 24 h prior to study. This protocol was approved by the Institutional Review Board of the Hebrew Rehabilitation Center for Aged and conformed with The Declaration of Helsinki.
Protocol and measurements
Electrocardiogram lead II, beat-by-beat photoplethysmographic arterial pressure (Finapres, Ohmeda) and lower body negative pressure level were recorded in the supine position. A transcranial Doppler ultrasonograph (2 MHz probe; Companion, Nicolet) measured cerebral blood flow velocity at the M1 segment of the middle cerebral artery at a depth of 50–65 mm. A Mueller-Moll probe fixation device held the probe. Expired respiratory volume, end-tidal CO2, and mixed expired CO2 were monitored via a facemask. All signals were digitized and stored at 500 Hz (Windaq, Dataq Instruments, Inc.).
Generally, studies of cerebrovascular blood flow control do not employ paced breathing due to possible hyperventilation and the concordant arterial CO2 drop. However, breathing patterns vary from moment to moment and from subject to subject, resulting in the problem of respiratory oscillations interfering with slower oscillations. Therefore, prior to data acquisition, we derived each subject's target expired volume for a fixed breathing frequency of 10 breaths min−1 (0.167 Hz) from 5 min of resting, normal breathing. Resting alveolar ventilation (v̇A) was measured via the Boer equation, as the difference between minute ventilation and physiological dead space ventilation (V̇D), calculated from end-tidal CO2, mixed expired CO2, average expiratory volume, and breathing frequency. Thus, target volume was the sum of dead space (l breath−1) and calculated alveolar ventilation (l min−1) at 10 breaths min−1. Target volume was displayed on an oscilloscope and a tone provided the target rate to control respiration. This approach has been used previously to successfully pace subjects' respiration at frequencies from 0.25 Hz down to 0.05 Hz without significant change in end tidal CO2 (Taylor et al. 2001).
For thigh cuff testing, inflatable cuffs were placed around the upper thigh of both legs. Data were acquired during 2 min of baseline, 3 min of thigh cuff inflation to 190 mmHg, and 3 min of recovery after rapid cuff deflation. This was repeated twice. Controlled breathing was not used during thigh cuff manoeuvres.
To create blood pressure oscillations of varying frequency and amplitude, OLBNP was used in a manner similar to a method previously described. (Hamner et al. 2001) The subject's lower body was sealed in a tank and a vacuum pump with timing mechanism controlled suction intervals (0.03, 0.05 and 0.10 Hz) and tank pressure (0, −20, and −40 mmHg). The protocol consisted of seven 10-min measurement periods, one of which consisted of controlled breathing without OLBNP (i.e. 0 mmHg) and six of which consisted of controlled breathing with OLBNP.
Data analysis
Beat-by-beat arterial pressure and cerebral blood flow waveforms were averaged between successive R-waves of the electrocardiogram to provide beat-by-beat means. These values were subsequently averaged for each condition to provide overall means.
For spectral analysis, 500 Hz waveforms were decimated to 5 Hz (Matlab, 6.1 Mathworks, Natick, MA, USA); this accurately preserves the energy in the signal below 2.5 Hz. Data were filtered with a cut-off of 0.4 Hz to prevent aliasing. Power spectral estimates for each signal were calculated via Welch's averaged, modified periodogram method. (Welch, 1967) The filtered time series were divided into 29 equally overlapping segments of 200 points each. Although this creates low frequency resolution (0.0125 Hz), it provides a high level of confidence in spectral estimates at each frequency of interest; this is crucial to accurately assess the spectral relations between pressure and cerebral flow. While the inconsistency of naturally occurring fluctuations typically requires high frequency resolution, OLBNP forced oscillations are explicitly and narrowly focused (Hamner et al. 2001), allowing us to pursue accuracy without concern for frequency resolution. The signals in each segment were linearly detrended, smoothed via a Hanning window, and fast-Fourier transformed. Spectral powers were averaged across all windows. The product of the pressure signal with the complex conjugate of the cerebral flow signal provided the cross-spectrum, from which coherence and the transfer function were derived. It should be noted that the cross-spectral gain of these two signals represents the complex impedance of the system, or in other words, an index of cerebrovascular resistance in the frequency domain.
We examined coherence between arterial pressure and cerebral flow at the frequencies of OLBNP and at the frequency of respiration. Although many researchers consider a coherence of 0.5 to be significant, this can produce unacceptably large phase errors in the transfer function. For example, based on the number of data points and window parameters (Taylor et al. 1998) significant coherence in our data results in a value of only 0.21 being statistically acceptable, corresponding to a 100 deg phase range. In addition, stationary random process theory (Koopmans, 1995) yields an estimate for the precision of transfer function gain and phase based on coherence. Gain and phase were weighted by their precision to obtain the most accurate estimate of means for statistical analysis. In this way, unreliable estimates of gain and phase receive appropriately small weights when group averages or statistics are computed (Searle, 1987).
Spectral powers and cross-spectral estimates were derived at the frequency of OLBNP. For comparison to the 0 mmHg condition, mean spectral powers and cross-spectral values were calculated at the three frequencies of OLBNP. Respiratory oscillations were similarly defined as oscillations in pressure and flow at 0.167 Hz.
Thigh cuff prediction
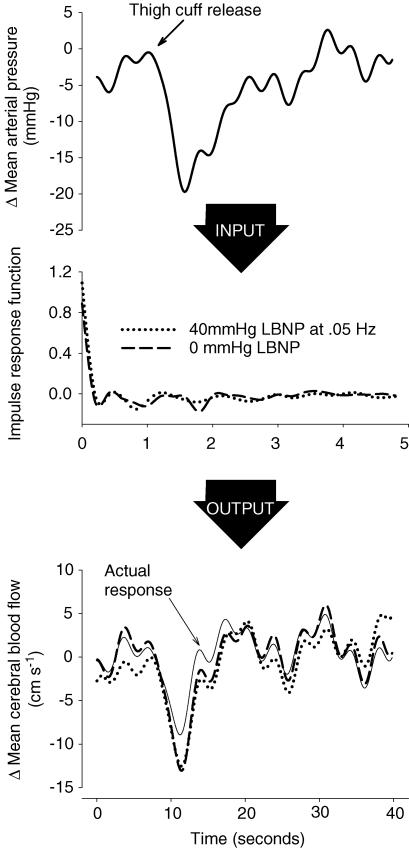
To examine the possibility that transfer functions derived from OBNP fluctuations recapitulate an alternative assessment of dynamic cerebral blood flow control, we computed the prediction of cerebral flow from the pressure change induced by thigh cuff deflation. Pressure and flow time series derived from the downsampling and filtering described above were further low-pass filtered with a cutoff frequency of 0.3 Hz. This restricted the frequency content of the signals to a range considered to encompass autoregulation. Estimated transfer functions from all frequencies and amplitudes of OLBNP (7 transfer function estimates per subject) were inverse Fourier transformed to provide impulse response functions. To predict the blood flow response, each impulse response was convolved with the pressure change from the thigh cuff trials. To avoid boundary effects, the entire thigh cuff series was predicted. However, only the 10 s prior to thigh cuff release and 30 s after release were used to determine the accuracy of the prediction. The correlation coefficient between the resultant time series and the actual cerebral flow response was used as an index of the predictive ability of the estimated transfer function (Mahony et al. 2000).
Statistics
Log transformations were applied to spectral powers, arcsine to phase, and the inverse hyperbolic tangent to coherence to provide estimates with asymptotically standard distributions (Koopmans, 1995). However, for ease of interpretation, values and confidence intervals presented herein are standard units. For averages and analyses of variance, gain and phase were weighted, as described above. Effects of frequency and amplitude of OLBNP on spectral powers and on gain and phase were evaluated by two-way ANOVA with a Tukey post hoc correction for significant differences at P < 0.05. Values are mean ± standard deviation.
Results
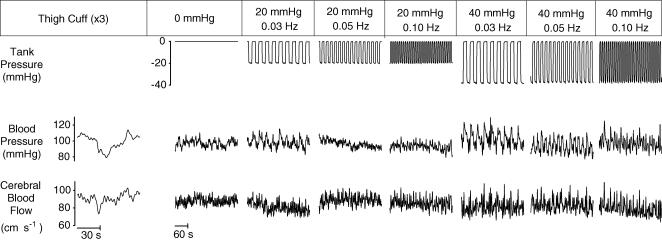
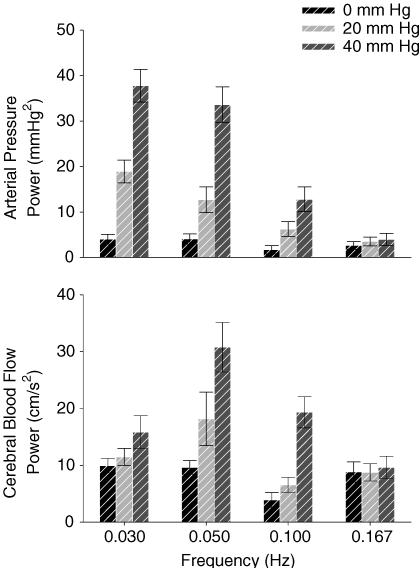
Table 1 shows the effect of OLBNP on mean values. Figure 1 shows the arterial pressure and cerebral blood flow responses to OLBNP. Figure 2 demonstrates the large magnitude and narrow bandwidth of OLBNP-induced arterial pressure oscillations, as well as the concordant cerebral blood flow response. Figure 3 shows the frequency and amplitude dependence of spectral powers across all subjects. Arterial pressure oscillations were related directly to OLBNP amplitude (P < 0.05) and inversely to OLBNP frequency, except that they were not significantly different with 0.03 and 0.05 Hz OLBNP (P < 0.05). Generally, the greater pressure fluctuations were associated with greater cerebral flow oscillations. These tended to be greatest with 40 mmHg OLBNP, but significantly greater only at the two lower frequencies (P < 0.05). Cerebral flow oscillations did not demonstrate the same frequency dependence seen in pressure oscillations. Both cerebral flow and arterial pressure power were greater with 0.05 Hz than with 0.10 Hz OLBNP (P < 0.05). However, despite comparable pressure fluctuations, cerebral flow oscillations were fewer with 0.03 than 0.05 Hz OLBNP. This suggests a dampening effect of pressure to flow below 0.05 Hz.
Table 1.
Response to OLBNP
| OLBNP amplitude: | 0 mmHg | 20 mmHg | 40 mmHg | ||||
|---|---|---|---|---|---|---|---|
| Frequency: | N | 0.03 Hz | 0.05 Hz | 0.10 Hz | 0.03 Hz | 0.05 Hz | 0.10 Hz |
| Mean blood pressure (mmHg) | 95.2 ± 3.7 | 100.7 ± 3.6 | 100.1 ± 3.5 | 101.3 ± 3.6 | 98.4 ± 3.6 | 99.2 ± 2.6 | 104.0 ± 4.0 |
| Mean cerebral blood flow (cm s−1) | 67.5 ± 4.5† | 64.1 ± 5.4 | 64.9 ± 5.2 | 61.9 ± 5.3 | 61.6 ± 5.1 | 60.3 ± 5.0 | 61.3 ± 4.7 |
| R-R interval (ms) | 928 ± 46 | 913 ± 44 | 916 ± 45 | 911 ± 45 | 908 ± 44 | 903 ± 45 | 898 ± 48 |
| End-tidal CO2 (%CO2) | 4.88 ± 0.34 | 4.83 ± 0.32 | 4.80 ± 0.32 | 4.54 ± 0.33 | 4.70 ± 0.33 | 4.75 ± 0.31 | 4.81 ± 0.31 |
P < 0.05 versus 40 mmHg OLBNP. Mean values across subjects for each experimental condition.
Figure 1. Schematic of protocol, showing the decimated and filtered waveforms of a representative subjectv.
OLBNP was not always administered in the sequence shown. Only 5 of the 10 min recorded during each period are shown.
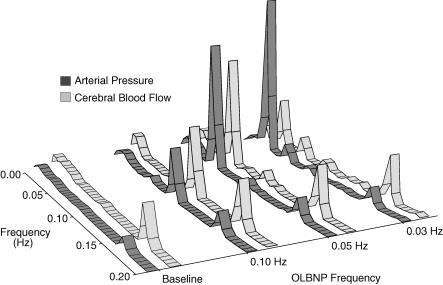
Figure 2. Average spectral powers across subjects for baseline and 40 mmHg OLBNP.
Figure 3. Arterial pressure and cerebral flow spectral powers with OLBNP.
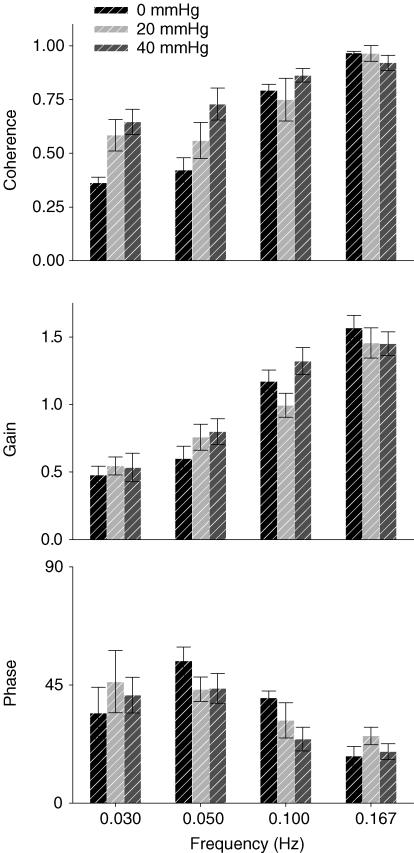
OLBNP increased coherence between pressure and flow (Fig. 4), except, of course, at the respiratory frequency (0.167 Hz), where it was greater than 0.95 under all conditions. OLBNP generated the greatest coherence at the 40 mmHg amplitude and the 0.10 Hz frequency (P < 0.05), but coherence tended to decrease with decreasing frequency. Thirty per cent (11 out of 36) of low frequency (0.03 and 0.05 Hz) trials had coherence below 0.3 while only 11% (3 out of 27) of the high frequency (0.10 Hz and respiration) had non-significant coherence. Comparing transfer function gains and phases, there was no difference between LBNP amplitudes, but there was a frequency effect. Gain was similarly low at 0.03 and 0.05 Hz and significantly higher at 0.10 and 0.167 Hz (P < 0.05). As gain increased, phase decreased; there was a smaller phase delay at 0.167 Hz than at 0.05 and 0.10 Hz (P < 0.05). However, phase at 0.03 Hz had such large variability that no statistically significant differences were found. This might also evidence a dampening effect as well as non-linearities between pressure and flow at frequencies below 0.05 Hz. Moreover, the overall pattern of increasing gain and smaller phase is characteristic of a high-pass filter.
Figure 4. Coherence between arterial pressure and cerebral flow oscillations and their gain and phase relations during OLBNP.
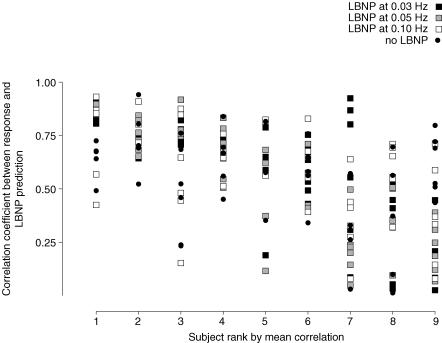
Figure 5 displays a schematic diagram of the prediction for one subject's thigh cuff test. Mean arterial pressure and cerebral flow responses to cuff deflation are shown at the top and bottom, and a section of the impulse responses derived from 0 and 40 mmHg OLBNP in the centre. The predictions from the impulse responses had a reasonable average correlation (r = 0.56) and there appeared to be no significant difference in predictive ability across trials (P = 0.545). However, the correlations were actually extremely variable (Fig. 6). For example, the subject with the best average correlation had only three correlations below average whereas the subject with the worst correlations had only five above average.
Figure 5. Schematic diagram of the prediction of thigh cuff responses from OLBNP cross-spectra.
Figure 6. Scatter-plot of thigh cuff predictions for all subjects all trials.
Subjects are ordered by average correlation.
Discussion
We successfully augmented blood pressure oscillations across three different frequencies at two distinct amplitudes, allowing accurate quantification of the frequency characteristics of the arterial pressure–cerebral blood flow relationship. Originally, we were skeptical of the conclusions drawn from resting data. Extremely small spectral power in pressure below 0.07 Hz makes any estimated relationship to another signal in this range suspect. Therefore, we drove pressure at low frequencies, creating oscillations in both pressure and cerebral flow that were 3- to 10-fold greater, resulting in increased coherence between the two signals. Coupled with a rigorous approach to the spectral analysis, this provides considerable confidence in the conclusions that can be derived from these data. These results are broadly compatible with conventional views of cerebral flow regulation derived from resting data, and confirm a frequency dependence in the transfer function relating pressure and flow oscillations. This frequency dependence in transfer function gain, coherence and phase has the characteristics of a high-pass filter. That is, gain and coherence decrease with decreasing frequency, while phase increases. Furthermore, this was unaffected by the amplitude of the pressure input; gain and phase were similar at both 20 and 40 mmHg OLBNP, even though pressure oscillations were graded.
The high-pass filter model of cerebral flow regulation postulates that fast changes in arterial pressure are passively transmitted into cerebral flow, but that slow changes are effectively counter-regulated by downstream resistance adaptations. This model was proposed based upon observations made from resting data that suggested decreased transfer function gain between pressure and flow at frequencies slower than 0.1 Hz. Numerous mechanisms have been suggested over the years for the general concept of cerebral autoregulation (i.e. maintenance of cerebral perfusion across a range of input pressures) (Paulson et al. 1990). However nearly any reflex which incorporates a time delay could explain the frequency dependence observed. For example, the cerebrovascular bed is well innervated by both sympathetic and parasympathetic nerve fibres (Edvinsson, 1975), but their role in autoregulation is poorly understood in humans. Zhang and colleagues showed a dramatic increase in transfer function gain with ganglionic blockade (Zhang et al. 2002). Though suggestive of a parasympathetic and/or sympathetic role, they also observed a marked decrease in arterial pressure variability and a concordant drop in low frequency cross-spectral coherence, below even the unreliable values typically present in resting data (i.e. coherence < 0.5). They attempted to address this issue by administering mild (10 mmHg) OLBNP at a frequency of 0.05 Hz during blockade, but the error of coherence remained high. Thus, it remains unknown if autonomic mechanisms underlie cerebral flow regulation. Another possible mechanism for cerebral autoregulation derives from the myogenic response to changes in wall tension that vascular smooth muscle can demonstrate. For example, renal blood flow in the denervated rat kidney shows frequency characteristics of a high-pass filter with a cut-off frequency around 0.1 Hz (Pires et al. 2001; DiBona & Sawin, 2004). This is similar to the proposed characteristics of cerebral blood flow regulation. Moreover, myogenic responses have been observed in isolated cerebral arteries from both animals and humans (Harder, 1984; Osol & Halpern, 1985; Wallis et al. 1996). However, how these myogenic properties relate to frequency response characteristics in the cerebral vasculature is still unknown. In addition, the simple characteristics of a compliance vessel may produce the high-pass filter characteristics. At the cardiac cycle frequency, flow through a compliant vessel is proportional to pressure, but becomes progressively damped as the frequency of pressure changes slows. Thus the general frequency response characteristics of arterial vessels may play some role in autoregulation, independent of either reflex or myogenic effects.
Our results provide empirical evidence of the high-pass nature of the relationship between arterial pressure changes and cerebral blood flow, but cannot discern what mechanisms underlie this relationship. Nonetheless, the relationship our data discloses has import for regulation of brain blood flow in response to regularly encountered conditions that can rapidly alter cerebral perfusion pressure, such as abrupt changes in posture or head position. Although average cerebral flow in healthy individuals is unchanged by 5 min of head-down rotation (Cooke et al. 2004) or 5 min of head-up tilt (Bondar et al. 1997), changes in cerebral perfusion pressure faster than approximately 14 s should result in almost proportional changes in cerebral blood flow. Notably, individuals with autonomic failure demonstrate marked arterial baroreflex impairment (Furlan et al. 1995) and significant and sustained decreases in both arterial pressure and cerebral flow with head-up tilt (Bondar et al. 1997). This would suggest that maintenance of systemic pressure is paramount for maintenance of cerebral flow. However, when pressure changes are accounted for, autonomic failure patients continue to demonstrate decreases in flow almost 70% greater than healthy individuals, also suggesting an important role for autonomic mechanisms in cerebral flow regulation beyond blood pressure control.
Our data highlight important caveats for spectral approaches. We were able to generate high coherence at frequencies below 0.07 Hz, due to the large arterial pressure and resultant cerebral blood flow oscillations induced by OLBNP. However, despite improving our transfer function estimates and providing better approximations of the cerebral blood flow responses to arterial pressure, average coherence was significantly lower in the frequency region below 0.1 Hz. In fact, one-third (11 out of 36) of all low frequency OLBNP trials had a squared coherence value of 0.3 or less. In these cases, this means that the linear assumptions of transfer function analysis account for only 30% of the variance. Moreover, despite the large pressure fluctuations, a number of cases had coherence that was not significantly different from zero. Thus, regardless of the amplitude in pressure fluctuations, non-linearities in the regulation of cerebral blood flow create profound limitations for spectral characterization. In other words, greater counter-regulation to pressure creates greater uncertainty in any spectral estimate of it. For example during 0.03 Hz OLBNP at 20 mmHg, the mean coherence was 0.58 (60% higher than that observed during rest); however, this equates to errors in gain of 0.2 and in phase of 30 deg. Thus, a frequency-dependent damping effect seems clearly evident, but a transfer function analysis falls short in illuminating the physiology.
Recent studies have used the low coherence observed in frequencies below 0.07 Hz as a rationale for evaluating various non-linear models of the pressure–flow relationship (Panerai et al. 1999; Giller & Mueller, 2003). As noted by Giller & Mueller, low coherence, in and of itself, does not indicate that a non-linear relationship exists, especially in the presence of such minimal and non-stationary low frequency power present in resting data. Nonetheless, our data do suggest that cerebral blood flow oscillations cannot be adequately explained by a linear model alone. The large forced oscillations in pressure and flow with OLBNP exhibited little more than adequate coherence, indicative of a possible non-linear mechanism. However, pursuing non-linear models would require long data sets with broad band input power. Blood pressure would have to be manipulated to produce oscillations of sufficient amplitude across the entire range of the non-linearities. The physiology may not allow this; blood pressure counter-regulatory mechanisms (e.g. baroreflexes) would effectively limit the ability to probe the slowest frequencies.
We also determined the predictive capacity of our transfer function estimates for the cerebral flow response to a manoeuvre that has also been proposed as an estimate of cerebral flow regulation – release of bilateral ischaemic thigh cuffs. The caudal shift in blood volume resultant from thigh cuff release causes a near stepwise drop in arterial blood pressure; ideal for validating the linear system modelled through transfer function analysis. If the model is valid and thigh cuff response is mediated through the same autoregulatory mechanism, the more robust oscillations and higher coherence during OLBNP should improve the predictive ability of the transfer function. However, none of the conditions proved better at predicting the flow response to stepwise arterial pressure drops with thigh cuff release. This agrees with prior work showing that the transfer function from 0.05 to 0.20 Hz data did not predict the cerebral flow response to a sit-to-stand manoeuvre (Narayanan et al. 2001) which also generates stepwise pressure drops. In contrast, Zhang et al. (1998) found that the group average transfer function up to 0.30 Hz produced a cerebral flow pattern that was not different from the averaged thigh cuff response. However, this may not be surprising; considering our mean correlation appeared reasonable, averaged data could predict quite well. Instead, the findings on a subject-by-subject and trial-by-trial basis clearly show considerably different powers, gains, and phases that make simple averaging inappropriate. Indeed, even application of more complex models, such as neural networks, which are marginally better than transfer function, demonstrates that the variability in the prediction error is greater between subjects than between different methods (Panerai et al. 2004).
It should be noted that coherence during OLBNP showed no relationship to the prediction for the thigh cuff response. We also applied time domain approaches in an attempt to improve the predictability; however, no significant improvements in predictive power could be made. This raises the possibility that cerebral blood flow response engendered by thigh cuff deflation does not consistently engage the same mechanism responsible for the buffering steady-state pressure oscillations. Baroreflex engagement, concomitant with the caudal blood volume shift, could play some role in this discrepancy. In fact, the large heart rate response that accompanies the pressure drop has spurred several researchers to utilize the thigh cuff response for baroreflex assessment (Fadel et al. 2001; Zhang et al. 2001). Although our data set does not allow examination of a possible reflex interplay, this possibility should not be ignored in the interpretation of data from the ischaemic thigh cuff technique. Another possibility is a failure of the linear assumptions of transfer function analysis. If a non-linear mechanism mediates cerebral autoregulation, the observed variability in predictability may not be surprising.
Despite skepticism of conclusions derived from resting data, the high-pass filter model of autoregulation that has been proposed broadly describes the relationship between cerebral flow and arterial pressure. However, even with large increases in pressure and flow oscillations in frequencies below 0.07 Hz, cross-spectral coherence remains problematic. Coupled with the inability of transfer function analysis to consistently predict response to thigh cuff; this may suggest that traditional linear approaches are inadequate to fully examine the physiology underlying cerebral autoregulation.
Acknowledgments
We wish to thank the subjects for their generous participation. This research was supported by Grants AG04390 (L.A.L) and AG014376 (J.A.T) from the National Institute on Aging. Dr Lipsitz holds the Irving and Edyth S. Usen and Family Chair in Geriatric Medicine at HRCA. There are no conflicts of interest.
References
- Aaslid R, Lindegaard KF, Sorteberg W, Nornes H. Cerebral autoregulation dynamics in humans. Stroke. 1989;20:45–52. doi: 10.1161/01.str.20.1.45. [DOI] [PubMed] [Google Scholar]
- Blaber AP, Bondar RL, Stein F, Dunphy PT, Moradshahi P, Kassam MS, Freeman R. Transfer function analysis of cerebral autoregulation dynamics in autonomic failure patients. Stroke. 1997;28:1686–1692. doi: 10.1161/01.str.28.9.1686. [DOI] [PubMed] [Google Scholar]
- Bondar RL, Dunphy PT, Moradshahi P, Kassam MS, Blaber AP, Stein F, Freeman R. Cerebrovascular and cardiovascular responses to graded tilt in patients with autonomic failure. Stroke. 1997;28:1677–1685. doi: 10.1161/01.str.28.9.1677. [DOI] [PubMed] [Google Scholar]
- Cooke WH, Carter JR, Kuusela TA. Human cerebrovascular and autonomic rhythms during vestibular activation. Am J Physiol Regul Integr Comp Physiol. 2004;286:R838–R843. doi: 10.1152/ajpregu.00562.2003. [DOI] [PubMed] [Google Scholar]
- DiBona GF, Sawin LL. Effect of renal denervation on dynamic autoregulation of renal blood flow. Am J Physiol Renal Physiol. 2004;286:F1209–1218. doi: 10.1152/ajprenal.00010.2004. [DOI] [PubMed] [Google Scholar]
- Diehl RR, Linden D, Lucke D, Berlit P. Spontaneous blood pressure oscillations and cerebral autoregulation. Clin Auton Res. 1998;8:7–12. doi: 10.1007/BF02267598. [DOI] [PubMed] [Google Scholar]
- Edvinsson L. Neurogenic mechanisms in the cerebrovascular bed. Autonomic nerves, amine receptors and their effects on cerebral blood flow. Acta Physiol Scandsupplement. 1975;427:1–35. [PubMed] [Google Scholar]
- Fadel PJ, Stromstad M, Hansen J, Sander M, Horn K, Ogoh S, Smith ML, Secher NH, Raven PB. Arterial baroreflex control of sympathetic nerve activity during acute hypotension: effect of fitness. Am J Physiol Heart Circ Physiol. 2001;280:H2524–H2532. doi: 10.1152/ajpheart.2001.280.6.H2524. [DOI] [PubMed] [Google Scholar]
- Furlan R, Piazza S, Bevilacqua M, Turiel M, Norbiato G, Lombardi F, Malliani A. Pure autonomic failure: complex abnormalities in the neural mechanisms regulating the cardiovascular system. J Auton Nerv Syst. 1995;51:223–235. doi: 10.1016/0165-1838(94)00135-7. [DOI] [PubMed] [Google Scholar]
- Giller CA, Mueller M. Linearity and non-linearity in cerebral hemodynamics. Med Eng Phys. 2003;25:633–646. doi: 10.1016/s1350-4533(03)00028-6. [DOI] [PubMed] [Google Scholar]
- Hamner JW, Morin RJ, Rudolph JL, Taylor JA. Inconsistent link between low-frequency oscillations: R-R interval responses to augmented Mayer waves. J Appl Physiol. 2001;90:1559–1564. doi: 10.1152/jappl.2001.90.4.1559. [DOI] [PubMed] [Google Scholar]
- Harder DR. Pressure-dependent membrane depolarization in cat middle cerebral artery. Circ Res. 1984;55:197–202. doi: 10.1161/01.res.55.2.197. [DOI] [PubMed] [Google Scholar]
- Koopmans LH. The Spectral Analysis of Time Series. vol. 22. New York: Academic Press; 1995. [Google Scholar]
- Mahony PJ, Panerai RB, Deverson ST, Hayes PD, Evans DH. Assessment of the thigh cuff technique for measurement of dynamic cerebral autoregulation. Stroke. 2000;31:476–480. doi: 10.1161/01.str.31.2.476. [DOI] [PubMed] [Google Scholar]
- Narayanan K, Collins JJ, Hamner J, Mukai S, Lipsitz LA. Predicting cerebral blood flow response to orthostatic stress from resting dynamics: effects of healthy aging. Am J Physiol Regul Integr Comp Physiol. 2001;281:R716–R722. doi: 10.1152/ajpregu.2001.281.3.R716. [DOI] [PubMed] [Google Scholar]
- Newell DW, Grady MS, Sirotta P, Winn HR. Evaluation of brain death using transcranial Doppler. Neurosurgery. 1989;24:509–513. doi: 10.1227/00006123-198904000-00004. [DOI] [PubMed] [Google Scholar]
- Osol G, Halpern W. Myogenic properties of cerebral blood vessels from normotensive and hypertensive rats. Am J Physiol. 1985;249:H914–H921. doi: 10.1152/ajpheart.1985.249.5.H914. [DOI] [PubMed] [Google Scholar]
- Panerai RB, Chacon M, Pereira R, Evans DH. Neural network modelling of dynamic cerebral autoregulation: assessment and comparison with established methods. Med Eng Phys. 2004;26:43–52. doi: 10.1016/j.medengphy.2003.08.001. [DOI] [PubMed] [Google Scholar]
- Panerai RB, Dawson SL, Potter JF. Linear and nonlinear analysis of human dynamic cerebral autoregulation. Am J Physiol. 1999;277:H1089–H1099. doi: 10.1152/ajpheart.1999.277.3.H1089. [DOI] [PubMed] [Google Scholar]
- Panerai RB, Rennie JM, Kelsall AW, Evans DH. Frequency-domain analysis of cerebral autoregulation from spontaneous fluctuations in arterial blood pressure. Med Biol Eng Comput. 1998;36:315–322. doi: 10.1007/BF02522477. [DOI] [PubMed] [Google Scholar]
- Paulson OB, Strandgaard S, Edvinsson L. Cerebral autoregulation. Cerebrovasc Brain Metab Rev. 1990;2:161–192. [PubMed] [Google Scholar]
- Pires SL, Barres C, Sassard J, Julien C. Renal blood flow dynamics and arterial pressure lability in the conscious rat. Hypertension. 2001;38:147–152. doi: 10.1161/01.hyp.38.1.147. [DOI] [PubMed] [Google Scholar]
- Searle SR. Linear Models for Unbalanced Data. New York: Wiley; 1987. [Google Scholar]
- Strandgaard S, Barry DI, Paulson OB. Converting enzyme inhibition and autoregulation of cerebral blood flow in spontaneously hypertensive and normotensive rats. Scand J Urol Nephrol Suppl. 1984;79:35–38. [PubMed] [Google Scholar]
- Taylor JA, Carr DL, Myers CW, Eckberg DL. Mechanisms underlying very-low-frequency RR-interval oscillations in humans. Circulation. 1998;98:547–555. doi: 10.1161/01.cir.98.6.547. [DOI] [PubMed] [Google Scholar]
- Taylor JA, Myers CW, Halliwill JR, Seidel H, Eckberg DL. Sympathetic restraint of respiratory sinus arrhythmia: implications for vagal-cardiac tone assessment in humans. Am J Physiol Heart Circ Physiol. 2001;280:H2804–H2814. doi: 10.1152/ajpheart.2001.280.6.H2804. [DOI] [PubMed] [Google Scholar]
- Wallis SJ, Firth J, Dunn WR. Pressure-induced myogenic responses in human isolated cerebral resistance arteries. Stroke. 1996;27:2287–2290. doi: 10.1161/01.str.27.12.2287. discussion 2291. [DOI] [PubMed] [Google Scholar]
- Welch PD. The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroaccoust. 1967;15:70–73. [Google Scholar]
- Zhang R, Behbehani K, Crandall CG, Zuckerman JH, Levine BD. Dynamic regulation of heart rate during acute hypotension: new insight into baroreflex function. Am J Physiol Heart Circ Physiol. 2001;280:H407–H419. doi: 10.1152/ajpheart.2001.280.1.H407. [DOI] [PubMed] [Google Scholar]
- Zhang R, Zuckerman JH, Giller CA, Levine BD. Transfer function analysis of dynamic cerebral autoregulation in humans. Am J Physiol. 1998;274:H233–H241. doi: 10.1152/ajpheart.1998.274.1.h233. [DOI] [PubMed] [Google Scholar]
- Zhang R, Zuckerman JH, Iwasaki K, Wilson TE, Crandall CG, Levine BD. Autonomic neural control of dynamic cerebral autoregulation in humans. Circulation. 2002;106:1814–1820. doi: 10.1161/01.cir.0000031798.07790.fe. [DOI] [PubMed] [Google Scholar]