Using models of the myocyte for functional interpretation of cardiac proteomic data

Abstract

There has been significant progress towards the development of highly integrative computational models of the cardiac myocyte over the past decade. Models now incorporate descriptions of voltage-gated ionic currents and membrane transporters, mechanisms of calcium-induced calcium release and intracellular calcium cycling, mitochondrial ATP production and its coupling to energy-requiring membrane transport processes and mechanisms of force generation. There is an extensive literature documenting both the reconstructive and predictive abilities of these models and there is no question that an interplay between quantitative modelling and experimental investigation has become a central component of modern cardiovascular research. As data regarding the cardiovascular proteome in both health and disease emerge, integrative models of the myocyte are becoming useful tools for interpreting the functional significance of changes in protein expression and post-translational modifications (PTMs). Data of particular importance include information on: (a) changes of expressed protein level, (b) changes of protein PTMs, (c) protein localization, and (d) protein–protein interactions, as it is often possible to incorporate and interpret the functional significance of such findings using computational models. We provide two examples of how models may be used in this fashion. In the first example, we show how information on altered expression of the sarcoplasmic reticulum Ca²⁺-ATPase, when interpreted through the use of a computational model, has provided key insights into fundamental mechanisms regulating cardiac action potential duration. In the second example, we show how information on the effects of phosphorylation of L-type Ca²⁺ channels, when interpreted through the use of a model, provides insights on how this post-translational modification alters the properties of excitation–contraction coupling and risk for arrhythmia.

The science of proteomics has three broad goals: (a) to measure the complement of proteins expressed in a subcellular compartment, cell or tissue at a given instant of time; (b) to understand how these proteins are organized as networks; and (c) to understand how the dynamic behaviours of these protein networks give rise to physiological and pathophysiological function at the level of cell and tissue. Other articles in this special issue address the first two topics. In this article, we consider the third issue of how the dynamic behaviours of protein networks influence integrative function of the cell in health and disease. Our fundamental premise is that due to the complexity of biological systems, quantitative mathematical and computational models are necessary for understanding how protein network function determines integrative behaviour at the cellular level.

We will illustrate this approach using models of the cardiac ventricular myocyte. There is now a 40 year history of integrative modelling of the myocyte and the level of biochemical and biophysical detail incorporated in these models has reached the point where many key proteins and protein networks determining electro-mechanical function have a direct, quantitative and experimentally validated representation in the models. This in turn suggests that these models may be used as a tool for investigating how altered expression and post-translational modifications of these key proteins affect physiological function. We will review two examples of how models may be used to obtain insights into the functional importance of altered protein expression and regulation in heart disease.

Integrative models of the cardiac myocyte

The first model of the cardiac action potential (AP) was developed shortly after the Hodgkin-Huxley model of the squid AP, and was formulated to explain the experimental observation that unlike neuronal APs, cardiac APs exhibit a long duration plateau phase (Noble, 1960). Refinement of this model by incorporation of emerging experimental data on the properties of voltage-gated membrane currents, transport and exchange processes regulating intracellular ion concentrations and mechanisms of calcium (Ca²⁺)-induced Ca²⁺ release (CICR) led to the first integrative model of the cardiac AP (DiFrancesco & Noble, 1985). This landmark model of the Purkinje fibre AP provided a mathematical framework upon which to build, thus stimulating development of a broad range of integrative cardiac myocyte models. These now include models of canine, guinea pig, human and rabbit ventricular myocytes (Luo & Rudy, 1994; Winslow et al. 1999; Puglisi & Bers, 2001; Iyer et al. 2004) as well as sino-atrial node and atrial myocytes.

Recent research efforts have been directed at extending the range of biophysical and biochemical mechanisms included in these models to enhance their explanatory and predictive capabilities. Figure 1 provides an example of the extent to which such integration has been achieved. This figure illustrates a computational model of the guinea pig ventricular myocyte developed recently in our laboratory. Single-channel and whole-cell current data in combination with knowledge of channel protein structure has been used to develop continuous time Markov chain models of the activity of voltage-gated channels and membrane transporters. Voltage-gated membrane currents represented in the model of Fig. 1 include potassium (K⁺) currents (the fast- and slow-activating delayed rectifier K⁺ currents I_Kr and I_Ks, the depolarizing-activated plateau K⁺ current I_Kp, the inward-rectifier K⁺ current I_K1) (Luo & Rudy, 1994; Jafri et al. 1998; Mazhari et al. 2001), the L-type Ca²⁺ current I_CaL (Jafri et al. 1998), the fast inward sodium (Na⁺) current I_Na (Irvine et al. 1999), and background Na⁺ and Ca²⁺ currents (I_Na,b and I_Ca,b, respectively). Membrane transporter currents represented in the model include the Na⁺–Ca²⁺ exchanger current I_NaCa, the sarcolemmal Ca²⁺-ATPase current I_pCa and the Na⁺,K⁺-ATPase current I_NaK (Jafri et al. 1998). The model also describes mechanisms of CICR and intracellular Ca²⁺ cycling processes, including the gating of ryanodine receptor (RyR) channels located in the junctional sarcoplasmic reticulum (JSR) membrane and JSR Ca²⁺-ATPase activity (Jafri et al. 1998). JSR Ca²⁺ release drives isometric force generation through the incorporation of a model describing Ca²⁺ binding to troponin, followed by conformational change of tropomyosin and crossbridge formation (Rice et al. 2000). Finally, mitochondrial ATP production including the tricarboxylic acid cycle and oxidative phosphorylation, its regulation by cytosolic Ca²⁺, and its coupling to ATP-dependent transport processes, is incorporated (Cortassa et al. 2003).

Figure 1. Schematic illustration of a computational model of the guinea pig ventricular myocyte.

Membrane ion channel and transporter currents are based on recently developed models (see text for details). Details of CICR are modeled as in Jafri et al. (1998). Force generation is based on the model of Rice et al. (2000). Mitochondrial ATP production is incorporated using the detailed model of Cortassa et al. (2003).

While the number of proteins and/or protein complexes represented in the model is small relative to the number of proteins that may be assayed using modern high-throughput techniques, experimental data on the direct or indirect regulation of these proteins can be incorporated in the model and functional consequences on myocyte electrophysiological responses may be assessed. The following sections provide two examples of such analyses. The first illustrates how information on altered level of protein expression may be incorporated into a myocyte model to assess the functional effects of such changes on properties of the AP and the Ca²⁺ transient. The second illustrates how the functional consequences of a post-translational modification (e.g. phosphorylation) may be analysed.

Modelling functional consequences of altered protein expression

Heart failure (HF), now the most common cardiovascular disorder, is characterized by ventricular dilatation, decreased myocardial contractility and cardiac output. Prevalence in the general population is over 4.5 million, and increases with age to levels as high as 10%. New cases number approximately 400 000 per year. Patient prognosis is poor, with mortality roughly 15% at 1 year, increasing to 80% at 6 years subsequent to diagnosis.

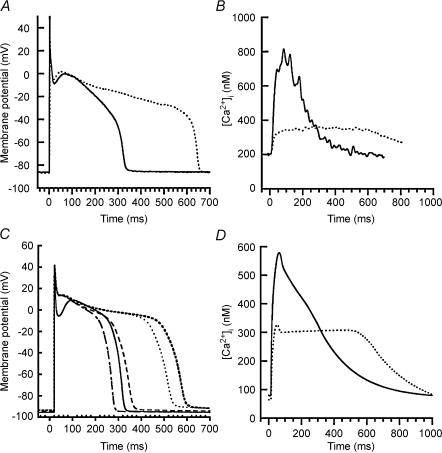
Experimental studies have identified two critical aspects of the cellular phenotype of heart failure. First, ventricular myocytes isolated from failing human and canine hearts exhibit significant AP prolongation (Beuckelmann & Erdmann, 1992; O'Rourke et al. 1999). An example is shown in Fig. 2. APs shown by continuous and dotted lines in Fig. 2A were recorded from normal and failing canine midmyocardial ventricular myocytes, respectively. Duration of the failing AP (∼660 ms) is roughly twice that of the normal (∼330 ms). Second, failing ventricular myocytes exhibit altered Ca²⁺ transients. An example of normal and failing Ca²⁺ transients obtained simultaneously with the AP recordings of Fig. 2A is shown in Fig. 2B. Differences between normal (continuous line) and failing (dotted line) Ca²⁺ transients include reduced amplitude and reduced rate of decline of the Ca²⁺ transient subsequent to repolarization of the AP.

Figure 2. Model versus experimental action potentials and Ca²⁺ transients.

Each action potential (AP) and Ca²⁺ transient is in response to a 1 Hz pulse train, with responses measured in the steady state. A, experimentally measured membrane potential (millivolts, ordinate) as a function of time (milliseconds, abscissa) in normal (continuous line) and failing (dotted line) canine myocytes. B, experimentally measured cytosolic Ca²⁺ concentration (nanomolar, ordinate) as a function of time (milliseconds, abscissa) for normal (continuous line) and failing (dotted line) canine ventricular myocytes. C, membrane potential (ordinate) as a function of time (abscissa) simulated using the normal canine myocyte model (continuous line), and with the successive down-regulation of I_to1 (dot–dashed line, 66% down-regulation), I_K1 (long-dashed line, down-regulation by 32%), junctional sarcoplasmic reticulum Ca²⁺-ATPase (rightmost short-dashed line, down-regulation by 62%) and Na⁺–Ca²⁺ exchanger (dotted line, up-regulation by 75%). D, cytosolic Ca²⁺ concentration (ordinate) as a function of time (abscissa) simulated using the normal (continuous line) and heart failure (dotted line) model. Reproduced from Winslow et al. (2001) with permission from The Royal Society.

Down-regulation of voltage-gated K⁺ currents is known to occur in HF. Measurements of whole-cell inward rectifier current I_K1 show that current density at hyperpolarized membrane potentials is reduced in HF by ∼50% in the human (Beuckelmann et al. 1993), and by ∼40% in the canine (Kääb et al. 1996). Measurements of the Ca²⁺-independent transient outward K⁺ current I_{to 1} show that in end-stage HF human current density is reduced by up to 70% (Näbauer et al. 1996). Measurement of the expression level of proteins involved in intracellular Ca²⁺ cycling indicate that there is an approximately 50% reduction of expressed SR Ca²⁺-ATPase protein level and direct SR Ca²⁺-ATPase uptake rate during HF (O'Rourke et al. 1999). There is also an approximate factor of two increase in Na⁺–Ca²⁺ exchanger protein (O'Rourke et al. 1999).

Each of the four proteins described above has a function described in a computational model of the canine ventricular myocyte developed within our laboratory (Winslow et al. 1999). The functional consequences of altered protein expression were therefore assessed by varying the model density of these four membrane transporters within the experimentally determined limits. Figure 2C shows a normal model AP (continuous line), and model APs corresponding to the additive effects of sequential down-regulation of I_to1 (dot–dashed line), I_K1 (long-dashed line) and the SR Ca²⁺-ATPase (rightmost short-dashed bold line), followed by up-regulation of the Na⁺–Ca²⁺ exchanger (dotted line). Model simulations indicate that down-regulation of I_to1 produces a modest shortening, not lengthening, of AP duration. The mechanism of this AP duration (APD) shortening has been investigated in detail using computational models (Greenstein et al. 2000) and results show that reduction of the Phase 1 notch depth through down-regulation of I_to1 reduces the electrical driving force on inward Ca²⁺ current and hence shortens AP duration. The additional down-regulation of I_K1 (long-dashed line) produces modest AP prolongation, consistent with the fact that outward current through I_K1 is activated primarily at potentials which are hyperpolarized relative to the plateau potential. The most striking result is shown by the short-dashed bold line in Fig. 2C– significant AP prolongation occurs following down-regulation of the SR Ca²⁺-ATPase. This down-regulation leads to a near doubling of AP duration that is similar to that observed experimentally (Fig. 2A). Finally, the model predicts that up-regulation of the Na⁺–Ca²⁺ exchanger, when superimposed on these other changes, contributes to modest APD shortening due to reverse mode Na⁺–Ca²⁺ exchange and generation of a net outward current during the plateau phase of the AP.

Subsequent studies have led to the following interpretation of these results (Winslow et al. 1999, 2001; Greenstein & Winslow, 2002). In HF, decreases in JSR Ca²⁺ load produced by down-regulation of the SR Ca²⁺-ATPase and up-regulation of the Na⁺–Ca²⁺ exchanger lead to reduced Ca²⁺ release. This reduced Ca²⁺ release in turn produces a reduction of Ca²⁺-dependent inactivation of I_CaL (Peterson et al. 1999, 2000) thereby increasing the late component of the L-type Ca²⁺ current (Fig. 2D) and prolonging AP duration. Thus, a fundamental hypothesis to emerge from these modelling studies is that coupling between JSR Ca²⁺ load, JSR Ca²⁺ release and I_CaL mediated by Ca²⁺-dependent inactivation of I_CaL is a critically important modulator of APD. This hypothesis is supported by more recent data showing that selective ablation of Ca²⁺-dependent inactivation through site-directed mutagenesis of Ca²⁺-binding sites on calmodulin dramatically prolongs APD (Alseikhan et al. 2002). Thus, despite its simplicity, the approach of interpreting the functional significance of altered expression of proteins through the use of experimentally validated computational models can provide important insights regarding the functional consequences of altered protein expression.

Modelling functional consequences of protein post-translational modifications

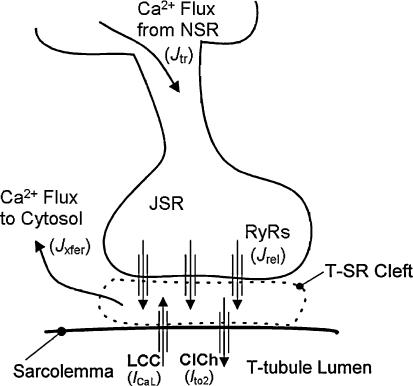
Contraction of cardiac muscle cells occurs when individual L-type Ca²⁺ channels (LCCs) located in the transverse (T)-tubular membrane open in response to membrane depolarization. The resulting influx of Ca²⁺ through LCCs increases Ca²⁺ concentration in a small microdomain known as the diad (Shacklock et al. 1995) (see Fig. 3). This in turn leads to the opening of Ca²⁺-sensitive Ca²⁺-release channels (ryanodine receptors, or RyRs) located in the closely apposed JSR membrane and further flux of Ca²⁺ into the microdomain (Cheng et al. 1993; Sham et al. 1995; Wang et al. 2001). These two sources of Ca²⁺ flux underlie the global intracellular Ca²⁺ transient producing cardiac muscle contraction. The local control theory of excitation–contraction (EC) coupling (Stern, 1992) asserts that tight regulation of CICR is made possible by the fact that LCCs and RyRs within the diad are sensitive to local (microdomain) rather than global Ca²⁺ levels and that graded control of Ca²⁺ release is achieved by statistical recruitment of elementary JSR Ca²⁺ release events in response to trigger Ca²⁺ entering via individual LCCs (Stern, 1992).

Figure 3. Schematic representation of the Ca²⁺ release unit model.

Trigger Ca²⁺ influx through L-type Ca²⁺ channels (LCCs) enters into the T-tubule–sarcoplasmic reticulum (T-SR) cleft (diadic space). The rise in local Ca²⁺ level promotes the opening of ryanodine receptor channels (RyRs) and Ca²⁺-dependent chloride channels (ClChs). The excess local Ca²⁺ passively diffuses out of the cleft into the cytosol, and junctional sarcoplasmic reticulum (JSR) Ca²⁺ is refilled via passive diffusion from the network sarcoplasmic reticulum (NSR).

Activation of the β₁- and β₂-adrenergic (β_1,2-AR) signalling pathway enhances cardiac function during stress or exercise through protein kinase A (PKA)-mediated phosphorylation of target proteins that are directly involved in the process of EC coupling (Xiao et al. 1999). Both PKA and phosphatase molecules of the β₂-AR pathway have been demonstrated to be co-localized to the microdomain via anchoring proteins (Davare et al. 2001), allowing for phosphorylation of local LCCs. Signalling through the β₁-AR pathway produces more global effects, including phosphorylation of LCCs, phospholamban (and thus disinhibition of the JSR Ca²⁺-ATPase) and I_Kr and I_Ks channel proteins.

We have recently developed a model of the canine ventricular myocyte which incorporates local control of CICR via a description of the stochastic gating of individual LCCs and RyRs and their interactions within the diadic space (Greenstein & Winslow, 2002) and have further modified this model to incorporate the regulatory role of EC coupling protein phosphorylation in response to β_1,2-AR stimulation (Greenstein et al. 2004). The fundamental unit of CICR in this model is called a Ca²⁺ release unit (CaRU) and is shown schematically in Fig. 3. The CaRU model is intended to mimic the properties of Ca²⁺ sparks in the T-tubule–SR (T-SR) junction (Cheng et al. 1993). The stochastic local control model simulates the random openings and closings of channels of LCCs and RyRs within each of a large ensemble of CaRUs. One of the bases for local control of SR Ca²⁺ release is the structural separation of T-SR clefts at the ends of sarcomeres (Franzini-Armstrong et al. 1999). Each CaRU is therefore simulated independently in agreement with this observation.

β_1,2-AR-induced phosphorylation is modelled based on experimental data describing the actions of the β-AR agonist isoproterenol (isoprenaline; Iso) applied at a concentration of 1 μm. Phosphorylation of LCCs is modelled by increasing the fraction of active (phosphorylated) LCCs from 25% in control to 60% during stimulation with Iso (Herzig et al. 1993). Of the population of active LCCs, 15% are assumed to occupy a high activity gating mode, known as mode 2, with enhanced channel open time (Yue et al. 1990). The SR Ca²⁺-ATPase and membrane K⁺ currents I_Kr and I_Ks are also enhanced by β-AR stimulation in this model, as described by experimental data.

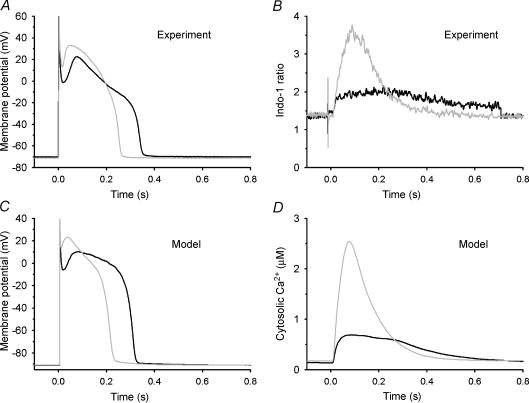
Figure 4 shows the ability of the control and the β-AR-stimulated models to reproduce experimental data on cell responses to 1 μm Iso. Simultaneous measurements of APs and Ca²⁺ transients are shown in Fig. 4A and B, respectively, for control (black lines) and following application of Iso (grey lines). AP duration (APD) in response to Iso (Fig. 4A) is shortened by ∼30%, the plateau potential becomes ∼10–15 mV more depolarized, and phase 1 notch depth and duration are reduced. In addition, Iso produces a ∼3-fold increase in Ca²⁺ transient amplitude and speeds the relaxation rate of the Ca²⁺ transient ∼3-fold (Fig. 4B). The model AP during β-AR stimulation (Fig. 4C) exhibits shortening of duration, depolarization of the AP plateau, and reduction in phase 1 notch depth and duration similar to that seen experimentally. Peak amplitude of the model Ca²⁺ transient (Fig. 4D) is increased ∼3-fold, and the rate of decay of the transient is increased (shortening its overall duration), as seen in experiments. The membrane currents underlying the model APs demonstrate that the rise in AP plateau is in response to increased I_CaL, whereas the shortening of the AP is attributed to the increased functional magnitude of I_Kr (data not shown). Increases in Ca²⁺ transient amplitude and rate of cytosolic Ca²⁺ removal are due to enhanced function of the SR Ca²⁺-ATPase.

Figure 4. Model and experimental APs and Ca²⁺ transients for control and β-AR stimulation.

A, representative APs measured in isolated canine myocytes in control bath (black line) and isoproterenol (grey line). B, indo-1 fluorescence ratio measured simultaneously with the APs in A (Greenstein et al. 2004). C, control (black line) and β-AR-stimulated (grey line) model APs. D, model cytosolic Ca²⁺ concentration (μm) corresponding to the APs in C Reproduced from Greenstein et al. (2004) with permission from the New York Academy of Sciences.

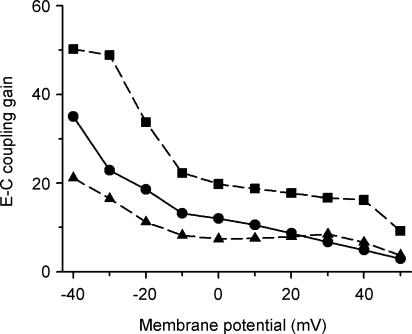
A fundamental measure of CICR function is EC coupling gain, defined as the ratio of peak SR Ca²⁺ release flux to peak LCC Ca²⁺ influx in response to membrane depolarization. EC coupling gain, measured in response to 200 ms voltage clamp steps, is shown in Fig. 5. Under control conditions (•), the gain function is monotonically decreasing with increasing clamp voltage, with a gain of ∼10 measured at 0 mV, in close agreement with experiments (Wier et al. 1994). Upon β-AR stimulation, gain is increased at all potentials (▪). This increase in gain is primarily due to the increase in SR Ca²⁺ load associated with enhanced function of the SR Ca²⁺-ATPase, and is absent when SR Ca²⁺ is normalized to control levels (data not shown) in agreement with experiments (Ginsburg & Bers, 2004). One functional consequence of LCC phosphorylation, not included in the β-AR model thus far, that has been observed in some (but not all) experiments in rat ventricular myocytes is an increase in LCC open probability associated with a ∼3- to 4-fold increase in open frequency (i.e. a reduction in channel closed times) (Chen-Izu et al. 2000). Figure 5 shows that a 4-fold increase in LCC open frequency produces a reduction in gain of up to 50% at potentials more negative than 10 mV (▴). A similar reduction in gain has been observed in response to noradrenaline (norepinephrine) in rat ventricular myocytes (Song et al. 2001). The underlying behaviour of the model demonstrates that the loss of gain is due to local saturation of the trigger Ca²⁺ signal (data not shown).

Figure 5. EC coupling gain.

EC gain as a function of voltage measured in response to 200 ms voltage clamp steps for the control model (•), the β-AR-stimulated model (▪), and the β-AR-stimulated model following a 4-fold increase in LCC open frequency and normalization of SR Ca²⁺ concentration to control level (▴).

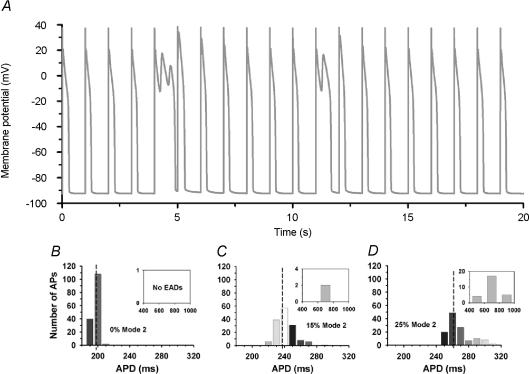
As noted previously, phosphorylation of LCCs can induce these channels to gate in a mode (mode 2) characterized by longer channel open time (Yue et al. 1990; Chen-Izu et al. 2000). By incorporating these findings into the local control myocyte model, we have recently demonstrated that the occurrence and frequency of early after-depolarizations (EADs) during β-AR stimulation are influenced by the modal gating properties of LCCs (Tanskanen et al. 2004). Figure 6A shows a representative train of 20 APs paced at 1 Hz with 25% of LCCs gating in mode 2. Two of the APs display at least one EAD, and the timing of EADs appears random. The occurrence of EADs in this model is in fact stochastic in nature due to the gating noise inherent in I_CaL. Figure 6B–D summarizes the results of long-term simulations, showing APD distributions measured from a series of 150 APs simulated with 0%, 15% and 25% of LCCs gating in mode 2, respectively. These simulation results demonstrate that: (a) the rate of EAD occurrence is a monotonic increasing function of the fraction of LCCs gating in mode 2, such that no EADs occur when the fraction is zero; and (b) the average APD and variability in APD increase with increased ratio of LCCs gating in mode 2. As the ratio of LCCs gating in mode 2 is increased, conditions for EAD occurrence become more favourable via a mechanism whereby the likelihood of such events is raised by stochastic prolongation of APD and subsequent reactivation of LCCs (Tanskanen et al. 2004). This finding offers an explanation of the increased rate of occurrence of EADs which is observed experimentally in response to both β-AR stimulation and overexpression of calcium–calmodulin-dependent protein kinase II (Tanskanen et al. 2004).

Figure 6. Early after-depolarizations (EADs) during β-AR stimulation.

A, membrane potential (millivolts) as a function of time (seconds) for the β-AR-stimulated model in response to 1 Hz pacing; action potential duration (APD) distribution in simulations of 150 APs with 0% (B), 15% (C), or 25% (D) of LCCs gating in mode 2 (10 ms bins) Reproduced from Tanskanen et al. (2005) with permission from the Biophysical Society.

Summary

We have provided two examples which illustrate the value of using computational models of the cardiac myocyte as a tool for interpreting the functional consequences of altered protein expression level and post-translational modifications. We feel this approach is useful and will only continue to develop in scope and application for the following reason. Cardiac electrophysiological research has proceeded in a very ‘top down’ fashion. That is, experimental research over the past several decades has focused on the identification and physiological characterization of properties of membrane proteins (ion channels and transporters) playing a fundamental role in shaping the properties of the cardiac AP and Ca²⁺ transient and which thus influence risk for arrhythmia. While, of course, more work remains to be done, we now have highly reproductive and predictive computational models of these processes. The direction of both experimental and modelling research is to now understand and model those subcellular processes which, either directly or indirectly, exert an influence on the cardiac AP through the modulation of these ion channels and transporters. This focus is seen clearly in the recent development of experimentally based models of subcellular processes such as β-AR signalling (Saucerman et al. 2003) and mitochondrial ATP production and its control (Cortassa et al. 2003). As computational models of the cardiac myocyte become more integrative, their value in the functional interpretation of proteomic data will only increase.