The ATP hydrolysis and phosphate release steps control the time course of force development in rabbit skeletal muscle

Abstract

The time course of isometric force development following photolytic release of ATP in the presence of Ca²⁺ was characterized in single skinned fibres from rabbit psoas muscle. Pre-photolysis force was minimized using apyrase to remove contaminating ATP and ADP. After the initial force rise induced by ATP release, a rapid shortening ramp terminated by a step stretch to the original length was imposed, and the time course of the subsequent force redevelopment was again characterized. Force development after ATP release was accurately described by a lag phase followed by one or two exponential components. At 20°C, the lag was 5.6 ± 0.4 ms (s.e.m., n = 11), and the force rise was well fitted by a single exponential with rate constant 71 ± 4 s⁻¹. Force redevelopment after shortening–restretch began from about half the plateau force level, and its single-exponential rate constant was 68 ± 3 s⁻¹, very similar to that following ATP release. When fibres were activated by the addition of Ca²⁺ in ATP-containing solution, force developed more slowly, and the rate constant for force redevelopment following shortening–restretch reached a maximum value of 38 ± 4 s⁻¹ (n = 6) after about 6 s of activation. This lower value may be associated with progressive sarcomere disorder at elevated temperature. Force development following ATP release was much slower at 5°C than at 20°C. The rate constant of a single-exponential fit to the force rise was 4.3 ± 0.4 s⁻¹ (n = 22), and this was again similar to that after shortening–restretch in the same activation at this temperature, 3.8 ± 0.2 s⁻¹. We conclude that force development after ATP release and shortening–restretch are controlled by the same steps in the actin–myosin ATPase cycle. The present results and much previous work on mechanical–chemical coupling in muscle can be explained by a kinetic scheme in which force is generated by a rapid conformational change bracketed by two biochemical steps with similar rate constants – ATP hydrolysis and the release of inorganic phosphate – both of which combine to control the rate of force development.

Force generation in muscle is driven by ATP hydrolysis in a cyclical interaction of myosin head domains or cross-bridges with actin filaments. The mechanism of ATP hydrolysis by isolated myosin heads and actin filaments has been extensively studied in solution (Rosenfeld & Taylor, 1984; White et al. 1997) and may be summarized as the series of reactions in Scheme 1. Here M refers to the myosin head, A to actin, and P_i to inorganic phosphate. The prime superscript in AM′·ADP·P_i and AM′·ADP identifies them as possible

scheme 1

force-generating states in a muscle fibre (Lund et al. 1987; White et al. 1988; Millar & Homsher, 1990; Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992). The mechanism of mechanical–chemical coupling in muscle could be described in terms of the series of reactions in Scheme 1 by assigning mechanical characteristics to each biochemical state, and rate constants to each transition. In general the rate constants in muscle will be different from those in solution. Moreover, the dependence of the rate of ATP utilization on mechanical conditions – the Fenn effect (Fenn, 1923; Kushmerick & Davies, 1969) – shows that some of the rate constants depend on whether the muscle is contracting at fixed length (isometric), shortening, or being stretched.

In the present study we characterized the kinetics of force generation by isolated permeabilized fibres from rabbit psoas muscle in isometric conditions, and used the results to assign isometric rate constants and mechanical properties to the reactions in Scheme 1. This general approach has been adopted in many previous studies of mechanical–chemical coupling in muscle, using length perturbations, e.g. (Brenner & Eisenberg, 1986; Zhao & Kawai, 1994; Ranatunga et al. 2002), pressure jumps (Fortune et al. 1994), temperature jumps (Bershitsky & Tsaturyan, 1992; Davis & Rodgers, 1995), rapid changes in inorganic phosphate (Dantzig et al. 1992; Tesi et al. 2002) and rapid release of ATP in an ATP-depleted (rigor) fibre (Goldman et al. 1984).

These studies established two main temporal components of isometric force generation. The force response to most of the experimental perturbations listed above can be described in terms of a sum of exponential components, the major one occurring at about 20 s⁻¹ in rabbit psoas muscle fibres at 10°C. This process has a high temperature sensitivity (Q₁₀≃ 4–5), and is accelerated by millimolar concentrations of inorganic phosphate. It is generally considered to be closely associated with release of P_i from the actin–myosin complex. A much faster force-generating process, with a rate constant of about 1000 s⁻¹ in psoas fibres at 10°C, is observed in response to rapid length steps (Huxley & Simmons, 1971; Lombardi et al. 1995; Ranatunga et al. 2002).

Mechanical (Huxley & Simmons, 1971) and structural (Irving et al. 1992; Lombardi et al. 1995) studies have identified the 1000 s⁻¹ process with a force-generating working stroke in the actin-attached myosin head. In Huxley & Simmons' (1973) terminology, this process is called ‘phase 2’. The slower process that dominates the response in the other perturbation studies listed above may be identified with the slowest component of the force response to a length step, called ‘phase 4’. Phase 2 is less sensitive to temperature and P_i than phase 4 (Ranatunga et al. 2002; Piazzesi et al. 2003).

The experiments described below focus on the slower process, and combine two of the experimental interventions used in previous studies. Muscle fibres were put into rigor by washing out the MgATP and activated by release of ATP from caged ATP in the presence of Mg²⁺ and Ca²⁺. The caged ATP approach (Goldman et al. 1984) has the advantage that the force perturbation starts from a defined biochemical state: the rigor or AM state in scheme 1. The protocols used in previous caged ATP experiments (Goldman et al. 1984) were modified in three respects: force development started from a very low level, measurements were made at 5 and 20°C to determine the temperature dependence of the force response, and filament sliding during force generation was minimized by feedback control of sarcomere length. After force had reached a steady level the fibre was allowed to shorten by about 10% of its initial length under low load. It was then restretched to the original length in less than 1 ms (Brenner, 1983), and force redeveloped under isometric or sarcomere-isometric conditions.

The rates of force development at 20°C determined previously using the shortening–restretch protocol (Brenner & Eisenberg, 1986) were lower than those reported using the caged ATP protocol (Goldman et al. 1984). Here we characterized both types of force response in the same preparation and in the same activation. We interpreted the results in terms of the biochemical reaction sequence in scheme 1. We propose a set of rate constants for these reactions as they occur during isometric contraction, and an identification of the reactions that control the rates of the slower force generation associated with phase 4 and the faster force generation associated with phase 2.

Methods

Materials

All mechanics experiments used single fibres obtained from the psoas major muscle of small adult male Dutch or New Zealand White rabbits. Rabbits (2–2.5 kg) were killed by overdose of sodium pentobarbitol (150 mg kg⁻¹), administered intravenously in one ear, followed by exsanguination, in accordance with the UK Animals (Scientific Procedures) Act 1986. Small bundles of muscle fibres were tied to sticks at their in situ length and gently agitated in skinning solution (Table 1 of accompanying paper, Burton et al. 2005) containing 0.5% Brij 35 detergent for 1–2 h on ice, rinsed, and either used within 3–4 days or glycerinated in 1: 1 (v/v) glycerol–skinning solution and stored at −20°C for up to 1 month. Protease inhibitors (phenylmethylsulphonyl fluoride (PMSF, 0.1 mm), leupeptin (8 μg ml⁻¹), and trypsin inhibitor (0.1 mg ml⁻¹)) were added to the skinning and storage solutions. Single fibres were isolated from bundles in skinning solution, which for glycerinated fibres contained 25% glycerol. Single fibres were usually separated from small bundles by gripping the ends and gently pulling the fibre axially (Julian et al. 1981; Yu & Brenner, 1989). Less force was required for fibres that had not been glycerinated, apparently due to changes in connective tissue during storage in glycerol-containing solutions. Single fibres were chosen based on homogeneity of light scattering, absence of visible damage, and straightness. Fibres were transferred from the dissecting dish to the experimental apparatus in a small capillary tube which had been filled with relaxing solution (Table 1). Fibre cross-section was estimated through a dissecting microscope at × 50 magnification by rotating the fibre in the dissecting dish (2–4 μm precision); in addition, measurements of the major axis were made on the experimental apparatus at × 200 magnification.

Table 1.

Composition of experimental solutions

	Relaxing	Pre-activating	Activating	cATP	cATP + regen	EDTA rigor	0 Mg2+ rigor
MgAc	7	7	7	7	7	—	—
ATP	5	5	5	—	—	—	—
Caged ATP	—	—	—	5	5	—	—
KAc	44	74	44	74	44	115	145
Imidazole-Ac	50	50	50	50	50	50	50
EGTA	10	0.1	—	—	—	—	—
CaEGTA	—	—	10	10	10	—	—
Glutathione	10	10	10	10	10	—	—
EDTA	—	—	—	—	—	10	—
Phosphocreatine	10	10	10	—	10	—	—
CK (mg ml−1)	2	2	2	—	2	—	—
Apyrase (μg ml−1)	—	—	—	—	7	—	—

Abbreviations: cATP, caged ATP; regen, phosphocreatine/creatine kinase regenerating system; Ac, acetate; CR-kin, creatine kinase. Concentrations are millimolar, except for CR-kin (mg ml⁻¹) and apyrase (μg ml⁻¹).

The experimental solutions had an ionic strength of 170 mm, acetate being the variable anion. Free [Mg²⁺] was 2 mm in all except rigor solutions. Glutathione (10 mm) was added to the caged ATP solution to avoid degradation of the fibre by reaction with the acetophenone product of photolysis (Goldman et al. 1984). Caged ATP was a gift from David Trentham (NIMR, Mill Hill, UK). The compositions of the routine solutions are given in Table 1. The concentration of released ATP was monitored using a luciferin–luciferase assay. A 5 μl sample of the flash trough was taken with a Hamilton syringe and frozen. An aliquot was added to 50 μl of ATP Monitoring Reagent (LKB 1243-200) in a 0.5 ml Eppendorf tube. The emitted light was monitored using a photomultiplier.

Apparatus

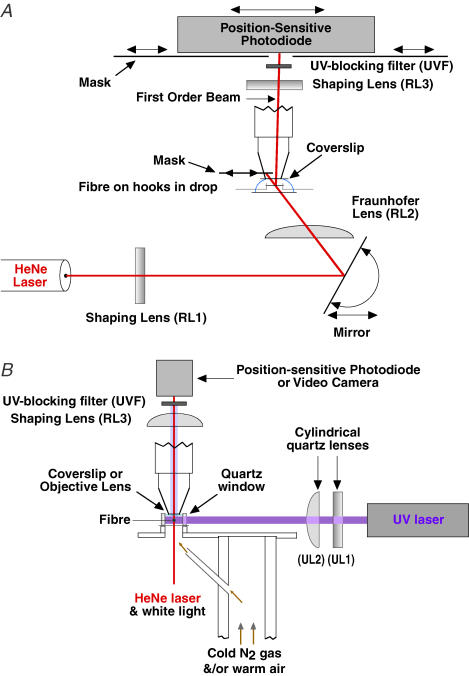
The experimental apparatus was built on an upright microscope (Fig. 1). Sarcomere length in relaxed fibres on the experimental apparatus was initially measured with a × 20 water-immersion objective, either from the striation spacing, or more commonly, from the spacing of the two first-order diffraction lines visible at the back focal plane of the objective lens using monochromatic illumination through a narrow aperture. Each fibre was attached at one end to a hook from a servomotor (Ford et al. 1977) for controlling fibre length, and at the other to a hook from a semiconductor strain gauge (Akers AE801; AME) for force measurements. Aluminium foil T-clips crimped onto the fibre ends were glued to the hooks with water-polymerizing cyanoacrylate (Histoacryl, Braun, Melsungen, FRG; Brenner & Eisenberg, 1986) to minimize movement on the hooks during transfer between solutions and during large, rapid length steps. In many experiments the end of the fibre itself was also glued to the T-clips as this was found to reduce end compliance; a drop of glue flowed around the fibre and into the space between folds of the clip. The control signal to the servo-motor controlling fibre length was from a voltage proportional either to fibre length or to the position of the first-order beam produced by laser diffraction, which was used to calculate sarcomere length. To produce the diffraction pattern, the fibre was illuminated by a 5 mW HeNe laser beam focused by two cylindrical lenses (Fig. 1A). The first (RL1) focused the beam onto the fibre perpendicular to its axis to increase diffraction intensity. The second (RL2) was a Fraunhofer lens focused at the photodetector (Brenner, 1985), thus minimizing movements of the fine structure in the diffraction order arising from fibre translation. The top of the solution was flattened by a coverslip attached to an objective tube from which the lenses had been removed. Nitrogen was blown down the inside of the tube onto the coverslip to prevent condensation. A third cylindrical lens (RL3) focused the first-order diffracted beam onto a position-sensitive photodiode (UDT LSC 30D, United Detector Technology, CA, USA) (Fig. 1A). The fibre was illuminated at a position (1) giving a relatively bright and narrow first-order diffracted beam, indicating a high degree of striation order (usually less than 20 nm dispersion), (2) with adjacent areas having the same sarcomere length so as to reduce translation artifact, and (3) usually less than 1 mm from the fixed end of the fibre to minimize translation of the fibre through the beam during length changes. The difference/sum of the two outputs from the position-sensitive photodiode was used to signal the position of the diffracted beam. The photodiode was calibrated with respect to position either by translation of the photodiode or by comparing movement of the diffraction order projected onto a grid with the change in divider output for a given change in active fibre length. Additional details of mechanical and sarcomere length measurements will be published (K. Burton et al. in preparation).

Figure 1. Diagram of experimental apparatus.

A, laser diffractometer. The beam from a 5 mW HeNe laser was passed through shaping (RL1) and Fraunhofer (RL2) lenses (see text) via a mirror that adjusted the angle of incidence onto the fibre. The fibre was mounted horizontally in a small drop of solution (8 or 40 μl) between a glass pedestal and a glass coverslip by hooks attached to a servomotor and force transducer (not shown). The zeroth-order beam was blocked by a movable mask, whilst the first-order beam was focused onto a position-sensitive photodiode by a third cylindrical lens (RL3). Additional masks at the photodiode blocked scattered and unwanted diffracted light. The fibre was positioned ∼110 mm from the photodiode. Drawing not to scale. B, uncaging beam and temperature control. The pulse from the ultraviolet (UV) laser passed horizontally through the fibre and was shaped by an orthogonal pair of cylindrical quartz lenses (UL1 and UL2) to match the front face of the uncaging chamber (∼4 mm × 2 mm). The front face of the uncaging chamber was made of quartz; the rear face was a no. 3 glass coverslip mirrored on its rear face to increase the UV illumination of the caged ATP. The uncaging chamber was mounted on a rotating platform that contained four additional pedestals in a pentagonal array holding 40 μl drops of pre-activating or non-caged-ATP-activating solutions (see text). Lenses represented as rectangles indicate cylindrical lenses with their axes in the plane of the page. A UV-blocking filter (UVF) prevented scattered UV light from reaching the position-sensitive photodiode.

The arrangement for changing solutions and for temperature control has been described briefly elsewhere (Sleep, 1989). Drops of solution (40 ml) were placed on four pieces of oval coverslip. A fifth position was designed to receive the laser flash and had a pedestal 4 mm × 1 mm, with a quartz window at the front and a mirror at the back to increase the intensity of the light in the solution. A volume of 7 μl was adequate to bathe the fibre. The nearside of the fibre was generally set to be about 100 μm from the front window. Temperature was monitored using a small (100 μm diameter) thermistor (Thermometrics, New Haven, CT, USA) and was controlled using a feedback system, in which a heating coil in a Dewar of liquid nitrogen controlled the rate at which cold N₂ gas was blown at the underside of the oval coverslips. For experiments at 20°C a constant supply of warm dry air was mixed with the controlled supply of cold N₂ to facilitate relatively rapid rises of temperature. The dry N₂ also solves the problem of condensation on the optical surfaces.

The methods used for release of ATP were broadly similar to those of Goldman et al. (1984). The 8 mm diameter beam from a frequency-doubled ruby laser (347 nm: Lumonics QSR2/6) was focused down with a cylindrical lens (UL2: focal length 200 mm) in the vertical direction to a height of about 1 mm at the fibre and masked off in the horizontal direction so that the fibre plus about 200 μm of the aluminium T-clip holding each end of the fibre was illuminated. A removable mirror at 45 deg to the UV laser beam was used to introduce the beam from a 1 mW HeNe laser (not shown) which had been expanded to match that of the UV laser. This tracking laser allowed the UV laser to be focused on the fibre and the masks to be adjusted precisely. A beam splitter and photodiode were used to record the relative energy of laser flashes.

Experimental protocol

To make the comparison between the initial tension development and the tension redevelopment after a shortening ramp and restretch as direct as possible, it was necessary to avoid the fall in tension that occurs when the initial rigor state carries tension (Goldman et al. 1984). The following protocol was developed to minimize this tension rise. The fibre was transferred from a relaxing solution to a 10 mm EDTA rigor solution for 3 min. After one or two further 1 min washes in this solution the fibre was transferred to a rigor solution containing neither EDTA nor Mg²⁺ for 3 min. The fibre was then transferred to a flash solution at least 5 min before the flash. This procedure worked reliably at 5°C but not at 20°C and for this reason fibres were put into rigor at 5°C whatever the temperature of the experiment at the time of ATP release. Raising the temperature once the fibre was in rigor did not result in a significant rise in tension. However, if the experiment involves activation of the fibre for more than 1 s at 20°C it is essential to use an ATP-regenerating system to avoid ATP depletion in the centre of the fibre. A typical sample of our 5 mm caged ATP contained about 2 μm ATP and 8 μm ADP, which in the presence of an ATP-regenerating system would give 10 μm ATP (cf. K_m for fibre ATPase, ∼15 μm; Glyn & Sleep, 1985). This situation can be avoided by reducing contaminant ATP and ADP and for this purpose we used apyrase, which hydrolyses both ATP and ADP to AMP (Sleep & Burton, 1989). The concentration of (ATP + ADP) was reduced to < 50 nm by a 1 h treatment with 7 μg ml⁻¹ apyrase. The concentration of apyrase chosen was sufficiently low that for a typical release of 1 mm ATP the half-time of the decrease in [ATP] due to the apyrase was about 10 min. The fibre was incubated in EDTA rigor solution with apyrase before transferring it to the treated caged ATP solution with regenerating system.

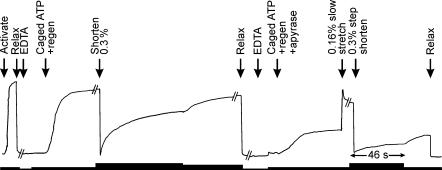
The effect of apyrase is shown in Fig. 2. In the absence of apyrase, when a fibre with a low rigor tension (about 5% of the isometric value P_o) was put into a caged ATP solution with an ATP-regenerating system, the tension rose to about P_o with a half-time of about 2 min at 20°C. When the fibre was released by 0.3% to reduce the tension to zero, tension recovered with a somewhat faster half-time. After 15 min apyrase treatment, tension rose to about 35%P_o. Apyrase did not have much effect on the instantaneous stiffness of the fibre, measured with a rapid shortening step, but it dramatically reduced the size of the tension recovery after the step. With this procedure, rigor tensions prior to the photolytic release of ATP at 20°C were typically less than 15%P_o. In some experiments a low Mg²⁺ relaxing solution was used to further increase the rate of depletion of MgATP, but in general this was not necessary. No sarcomere length change or movement of the fine structure of the diffraction pattern was observed when fibres went into rigor at low tension, whereas without apyrase, there was a significant loss of order.

Figure 2. Suppression of rigor force by apyrase in the presence of an ATP-regenerating system at 20°C.

Chart records showing active and ‘rigor’ forces in the absence of apyrase (4.5 μm ATP in free solution) and in the presence of 7 μg ml⁻¹ apyrase (no ATP detected). Solution changes and length changes were applied at the times indicated (see Table 1). ‘EDTA’ refers to a triple rinse in EDTA rigor solution, ‘regen’ to the cATP + regen solution (see Table 1). Trace digitized from a larger chart record for this fibre. Rigor force in the presence of apyrase was raised to that in its absence by a 0.16% slow stretch. The thickness of the line below the force records varies with the chart recorder speed, being greatest immediately after step releases (46 s for the period indicated between arrows), and slowing to 0.1, 0.05 and 0.02 times that speed for periods indicated by progressively thinner line segments. Sarcomere length = 2.34 μm.

Data acquisition and analysis

Tension, fibre length, and intensity and position of the first-order diffracted beam were recorded using a 100 kHz Tecmar board. For 20°C records data were acquired at a rate of 12.5 kHz at the time of the flash and restretch and 1.25 kHz at other times. The data file included the temperature and the energy of the UV laser flash. Tension and temperature were also recorded on a slow time base using a strip chart recorder with a high frequency response.

Force records were fitted with functions consisting of one or more exponential terms using the method of Provencher (1976). This software generates its own initial estimates, accepts variable sampling frequencies in a single record, and in each run fitted up to four functions with 1–4 exponential terms. It ranks the fits based on a comparison of the residuals using a modified F test.

Double-exponential fits to the force rise at 5°C were usually superior to single-exponential fits on the basis of the residuals of the fit and of the standard errors. The simplest approach was to start the fit at the point of inflexion between the initial lag and the dominant exponential components of negative amplitude (rising components). Typically 10–15% of the tension rise had taken place at the time of the start of the fit. The second approach was to allow exponential components of positive amplitude (falling components which describe the initial lag). When a single rising component (−ve amplitude) was fitted, the second method generally gave a slightly faster rate but the difference was generally less than 10%. Inclusion of components of +ve amplitude did not allow a satisfactory fit of the complete record from the time of the flash but did allow fits to characterize 99% of the tension rise and were helpful for isolating the important −ve amplitude components. Typically the first method was used for characterization in terms of a single rising component and the second for two rising components. The effect of the two approaches is shown in the residual plot at the bottom of Fig. 3. The single-component fit deviates at early times because of a lack of a fast +ve amplitude component, and at later times for lack of a slow −ve amplitude component. At 20°C, records of recovery after ramp shortening and restretch were also well described by the sum of two exponentials (9 of 12 records, Table 2). In two cases that were not well fitted the exponential term with the low rate constant (slow rising component) appeared to be obscured by a slow fall, the effects of which are discussed in detail elsewhere (K. Burton et al. in preparation). This behaviour can also be partly explained by the observation that the proportion of force recovery in the fast component after a restretch increases with temperature between 0 and 20°C (Table 2 and Burton et al. 2004), making detection of the slow component more difficult. In contrast, two exponential rising components were detected in only a few records of force development after ATP release at 20°C (Table 2). The presence of a lag in these kind of data may contribute to the difficulty in distinguishing two rising components, since if it is not extracted it reduces the apparent amplitude and rate of the fast rising component, making it less distinguishable from the slow rising component. It is not obvious why the lag should cause greater difficulty at high temperature, but we note from Table 2 that the ratio of the lag time to the time constant of the subsequent force rise is nearly twice as great at 20°C as at 5°C. The rates of force development and redevelopment are therefore described by double-exponential functions where possible, and also by single exponentials because the latter (1) could be obtained under conditions where double exponentials could not, (2) provide a single parameter for the rate of ‘overall’ recovery, and (3) allow comparison with previous analyses. In the text, the exponential fits are described by rate constants k_t*, k_t*s, k_t*f which refer, respectively, to the single, slow rising, and fast rising components (where *=‘d’ for initial tension development after release of ATP from caged ATP and ‘r’ for tension redevelopment after a shortening–restretch). A′_f is the amplitude of the fast component relative to the magnitude of recovery.

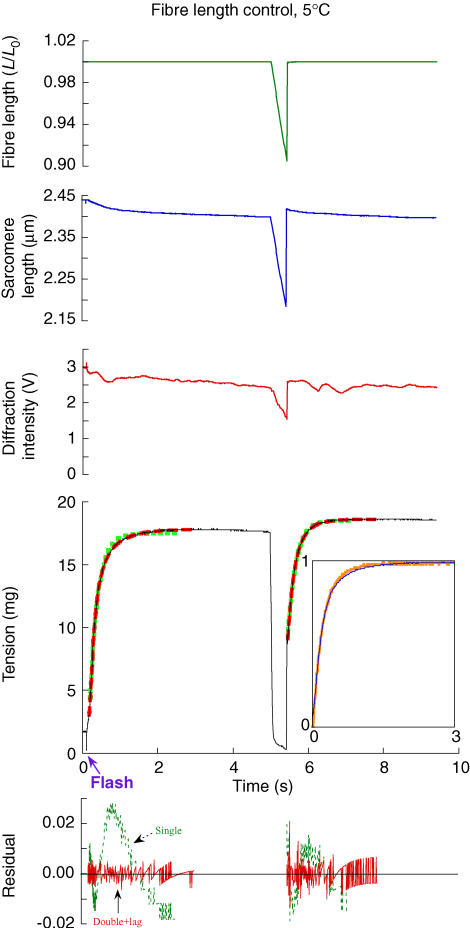
Figure 3. Force development at 5°C.

The experimental records, from top to bottom, are fibre length, sarcomere length, intensity of the first-order diffraction beam, force and residuals of exponential fits. The activation was initiated by a UV laser flash at 0.1 s. The sampling was too slow to capture a spike of force during and immediately after the restretch when force was greater than isometric for ∼1 ms and reached a transient minimum within ∼10 ms before recovery began. Exponential functions fitted to force development are shown overlaid onto the records (single-exponential rise, squares; double-exponential rise, green squares, red dashes). Force development after the flash could be fitted by one or two rising exponentials: k_td= 4.6 s⁻¹, k_tds= 2 s⁻¹, k_tdf= 7.9 s⁻¹, and A′_{f =} 0.62. For tension recovery after the restretch, k_tr= 4.6 s⁻¹, k_trs= 3.3 s⁻¹, k_trf= 8.51 s⁻¹, and A′_f= 0.41 (for definitions of fitted parameters, see 'Data acquisition and analysis' in Methods). The fibre cross-section (CS) was 2.1 × 10³μm², and fibre length (FL), 2.5 mm. The plots showing the residual error between the fits and the data have been normalized by the observed magnitude of force recovery. Inset to force record: force development after the flash (narrow line) has been overlaid onto that after the restretch (wide line) by scaling both records between 0 and ∼1 and offsetting on the time axis. The lag in force development after the flash occurs at negative values on the offset time axis and is not shown.

Table 2.

Time course of isometric force development at 5°C and 20°C

	Single-exponential fit		Two-exponential fit
	Rate constant (s−1) ktd (cATP) ktr (RR)	Lag time (ms)	Rate constant; fast component (s−1) ktdf, ktrf	Rate constant; slow component (s−1) ktds, ktrs	Fractional amplitude of fast component (s−1) A′f
5°C cATP	4.3 ± 0.4 (22)	58 ± 3 (22)	6.1 ± 0.3 (22)	1.9 ± 0.2 (22)	0.64 ± 0.04 (22)
5°C RR	3.8 ± 0.2 (22)		6.5 ± 0.4 (22)	2.2 ± 0.2 (22)	0.49 ± 0.07 (22)
20°C cATP	71 ± 4 (12)	5.6 ± 0.4 (11)	121 ± 5 (3)	34 ± 3 (3)	0.60 ± 0.07 (3)
20°C RR	68 ± 3 (12)		88 ± 3 (9)	27 ± 3 (9)	0.80 ± 0.02 (9)

cATP denotes force development following release of ATP from caged ATP; RR denotes force development following shortening ramp–restretch. Nomenclature for rate constants defined in Methods. Mean ± s.e.m. for the number of observations given in parentheses. At 20°C each fibre was subject to a single activation and cATP and RR rates are all paired. At 5°C we observed no difference between the rate constant measured in the first caged ATP activation in each fibre (4.3 ± 0.2 s⁻¹) and that observed for subsequent activations (4.3 ± 0.7 s⁻¹, n = 12). These data were derived from 10 fibres. The lag was determined by extrapolating the force fit to the pre-photolysis force. For the three fibres for which two-exponential fit parameters are reported for activation by caged ATP at 20°C the mean single-exponential rate constant was 64 s⁻¹ for both cATP and RR. All 5°C data were obtained at constant fibre length; in 9 of the 12 fibres studied at 20°C force development took place at constant sarcomere length (see text).

In some experiments a video camera was used to record the image of a fibre or the diffraction order. The video camera was mounted in place of the photodiode, and a water-immersion objective replaced the coverslip contacting the top of the bathing solution (Fig. 1B). Images were acquired at 40 ms intervals and recorded onto videotape; some records were digitized using a frame-grabber and image processing software. Digital image processing techniques were used to clarify the original brightfield video images.

Results

Photolysis of caged ATP at 5°C

Single fibres from rabbit psoas muscle were activated by photolysis of caged ATP in the presence of Ca²⁺ (Fig. 3). The experimental protocol (see Methods) was designed to minimize the rigor force before photolysis (arrow below time axis), and to maintain sarcomere order. Pre-photolysis force was 13 ± 12% (mean ±s.d., n = 37) of the active isometric force at this temperature. The sarcomeres were well aligned across the fibre and sarcomere length was uniform. Sarcomere order, monitored by the intensity of the first-order diffracted beam, was maintained following activation (Fig. 3).

The time course of force development following release of ATP was approximately exponential, and the rate constant obtained from single-exponential fits (green squares superimposed on force trace) was 4.3 ± 0.4 s⁻¹ (mean ± s.e.m., n = 22; Table 2). The time course was more accurately described by two exponential terms (red dashes), as shown by a comparison of the residuals in the lower panel. In two-exponential fits, the rate constants of the fast and slow components were 6.1 ± 0.3 s⁻¹ and 1.9 ± 0.2 s⁻¹, and the fractional amplitude of the fast component was 0.64 ± 0.04. Due to an initial lag after ATP release, the fits did not reproduce the first ∼100 ms of the force response. The lag was estimated by extrapolation of the two-exponential fit to the pre-photolysis force level, and its mean value was 58 ± 3 ms (Table 2).

Shortening ramp and restretch at 5°C

About 5 s after the release of ATP from caged ATP, when force was steady, a shortening ramp of about 10% fibre length was imposed (Fig. 3). Force fell to almost zero during the ramp. At the end of the ramp the fibre was restretched to its original length in less than 1 ms. This produced a large, brief force spike (not visible at the sampling rate used for Fig. 3), followed by an approximately exponential force recovery. When this recovery was scaled (inset panel, thicker orange line) to the same amplitude as force development after ATP release from caged ATP (inset panel, thinner blue line) and shifted in time to account for the lag after ATP release, the two time courses nearly superimposed. A single-exponential fit to the force recovery after restretch (green squares) had rate constant 3.8 ± 0.2 s⁻¹ (mean ± s.e.m.; n = 22; Table 2), similar to that of the initial force rise after release of ATP from caged ATP. A two-exponential fit again described the time course of force recovery more accurately (red dashes), with fast and slow components 6.5 ± 0.4 s⁻¹ and 2.2 ± 0.2 s⁻¹ (Table 2), very close to the values observed following ATP release. The fractional amplitude of the fast component was 0.49 ± 0.07.

In paired comparisons the ratio of the rate constant of force development after release of ATP from caged ATP to that following the restretch was 1.17 ± 0.10 (mean ± s.e.m.) for a single-exponential fit (n = 22), and 1.00 ± 0.06 and 0.95 ± 0.10 for the fast and slow components of double-exponential fits (n = 22). None of these ratios is significantly different from 1 (t > 0.05).

These results show that force development after ATP release and shortening–restretch at 5°C have prominent components with the same time course, best described as the sum of two exponential terms of roughly equal amplitudes, and rate constants about 6 and 2 s⁻¹. This common component is preceded by distinct initial phases: a 58 ms lag after ATP release from caged ATP, compared with an initial force jump to about half the plateau force during the restretch.

Photolysis of caged ATP at 20°C

Force development following ATP release was almost 20 times faster at 20°C (Fig. 4A) than at 5°C (Fig. 3). The protocol used for the caged ATP experiments was designed to minimize the pre-photolysis force (see Methods), which was only 4 ± 4% (mean ±s.d., n = 10) of the plateau force at this temperature. The time course of force development was again described reasonably well by a lag followed by an exponential rise. At 20°C the lag was 5.6 ± 0.4 ms (n = 11), and the rate constant of the rising phase was 71 ± 4 s⁻¹ (mean ± s.e.m.; n = 12; Table 2). In most fibres a two-exponential fit did not describe the experimental time course at 20°C better than a single-exponential fit. In three fibres, however, a two-exponential fit was significantly better, and the rate constants of the fast and slow components were 121 ± 5 and 34 ± 3 s⁻¹. The fractional recovery in the fast component was 0.60 ± 0.07.

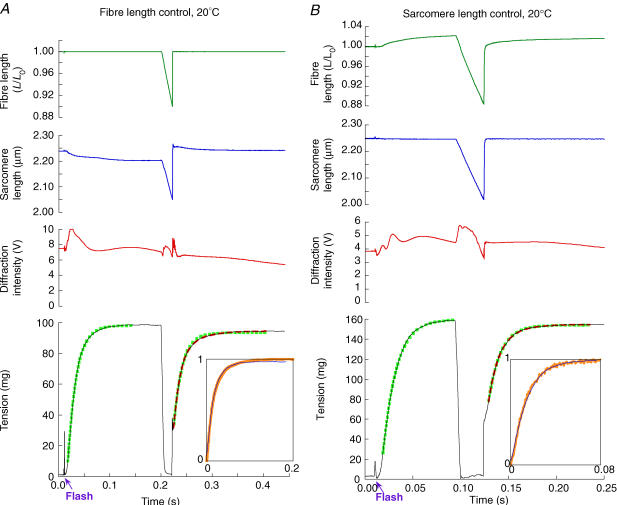
Figure 4. Force development in sarcomere length or fibre length control at 20°C.

A, fibre length control. The experimental records are as in the top four panels of Fig. 3, but at a temperature of 20°C. Exponential functions fitted to force development are shown overlaid onto the records (single-exponential rise, green squares; double-exponential rise with +ve amplitude component, red dashes). Force development after the flash could be satisfactorily fitted by a single exponential (k_td = 60 s⁻¹). Two rising components could not be reliably fitted to the initial force development. For tension recovery after the restretch, k_tr = 64 s⁻¹, k_trs = 28 s⁻¹, k_trf= 90 s⁻¹, and A′_f = 0.66. CS = 8.4 × 10³μm², FL = 2.7 mm.B, sarcomere length control. As in A, but this fibre was put into sarcomere length control in rigor. It was not possible to fit two rising components to the initial tension development. For tension recovery after the restretch (single-exponential rise, green squares; double-exponential rise, red dashes), k_tr = 80 s⁻¹, k_trs = 43 s⁻¹, k_trf = 92 s⁻¹, and A′_{f =} 0.83. CS = 7.3 × 10³μm², FL = 2.6 mm. Insets as in tension panel of Fig. 3.

Shortening ramp and restretch at 20°C

A shortening ramp was imposed 0.2 s after ATP release, when force was steady (Fig. 4A). The shortening velocity was chosen so that force fell to a very low level during shortening. Restretch to the original length produced a fast force jump, as at 5°C, followed by an approximately exponential force rise. The scaled and time-shifted force recovery after restretch (inset panel, thicker orange line) superimposed that after release of ATP from caged ATP (inset panel, thinner blue line). The rate constant of a single-exponential fit to force recovery following restretch was 68 ± 3 s⁻¹ (n = 12; Table 2), very close to that of the force rise following ATP release in the same group of fibres. In nine fibres two-exponential functions gave a better fit than one, and the rates of the fast and slow components were 88 ± 3 and 27 ± 3 s⁻¹. The fractional recovery in the fast component was 0.80 ± 0.02, significantly larger than at 5°C. The ratio of the rate constants of force development after ATP release to those after shortening and restretch averaged 1.06 ± 0.05 for a single-exponential fit (n = 11), which is not significantly different from 1. Thus, as at 5°C, the time course of the main component of force development is the same after ATP release and after shortening–restretch. This component is preceded by a small (ca 5 ms) lag in the former case, and a transient minimum following a force jump in the latter.

Control of sarcomere length during force development

During force generation at constant fibre length (Figs 3 and 4A), the sarcomere length measured in the centre of the fibre segment decreased slightly, typically by less than 2% in the preparations used here, as the end regions of the fibre were stretched. The length redistribution observed in the same fibre preparation following shortening–restretch at 5°C reduces the rate of force development by about 10% (K. Burton et al. in preparation). We therefore investigated the effect of sarcomere shortening on the rate of force development following ATP release from caged ATP and shortening–restretch at 20°C using feedback to the motor controlling fibre length (Fig. 4B). The procedure used here to induce low-force rigor (see Methods) largely eliminated sarcomere movements that otherwise occur during the development of rigor force, so that sarcomere length uniformity was maintained in rigor and the sarcomere length in the central segment of the fibre could be controlled in rigor and throughout the time course of force development following release of ATP from caged ATP. The rate of force development following ATP release from caged ATP at constant sarcomere length was 73 ± 3 s⁻¹ (n = 9 fibres), compared with 64 ± 3 s⁻¹ (n = 3 fibres) at constant fibre length. The corresponding values for the shortening–restretch were 71 ± 4 and 64 ± 1 s⁻¹, respectively. Thus, as at 5°C (K. Burton et al. in preparation), the rate of force development at 20°C was only about 10% greater at constant sarcomere length than at constant fibre length under the conditions of our experiments, for both the caged ATP and shortening–restretch protocol. Results from both conditions were combined in Table 2.

Rate of force development during activation from the relaxed state

The rate constant for the force development that we observed with the shortening–restretch protocol at 20°C, about 70 s⁻¹ (Table 2), is much larger than that reported previously using this protocol. For example Brenner & Eisenberg (1986) measured 15 s⁻¹ at 15°C and 26 s⁻¹ at 25°C. One significant difference between the present and previous measurements with the shortening–restretch protocol is that we activated the fibres by photolysis of caged ATP in the presence of Ca²⁺, whereas in previous studies fibres were activated by transfer from a low-Ca²⁺ relaxing solution to a high-Ca²⁺ activating solution. We therefore investigated the effect of the method of activation on the rate of force development measured with the shortening–restretch protocol. The length changes were imposed many times in each activation, so that progressive changes in the rate of force development after restretch could be monitored.

The rate of force development following the restretch declined rapidly during activations initiated by photolysis of caged ATP in the presence of Ca²⁺ at 20°C (Fig. 5A, circles). In this fibre, the rate measured 0.2 s after ATP release was 69 s⁻¹, similar to the average value in Table 2, but by 3 s after ATP release it had decreased to 41 s⁻¹. This decrease was accompanied by a decline in the amplitude of the force recovery (data not shown) and by disorder of the sarcomeres (Fig. 5B). Sarcomere disorder was apparent in fibre images after a few hundred milliseconds of activation at 20°C and always appeared with a similar time course to the fall in the intensity of the first-order diffracted beam from the sarcomeres, which allows a useful measure of the loss. For the two fibres in Fig. 4 the intensity fell to about 40% of its initial value in 3 s and changed relatively little thereafter. The sarcomere disorder and the decline in the amplitude and rate of force development were irreversible, and only data from the first activation by photolysis of caged ATP at 20°C in each fibre are presented in Fig. 4 and Table 2.

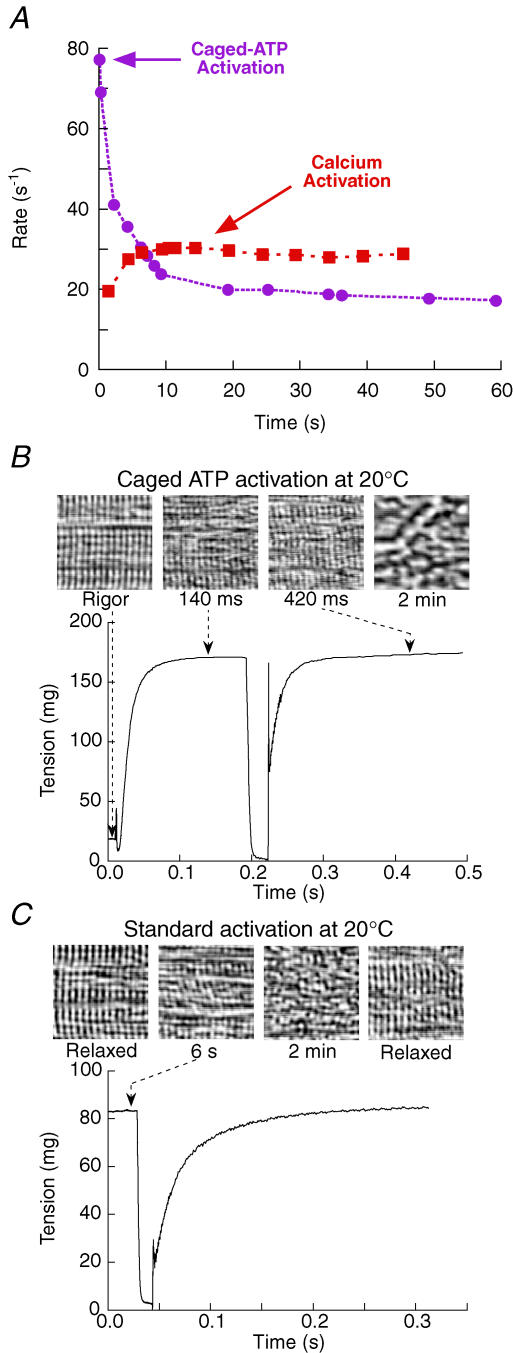
Figure 5. Fibre deterioration during activations at 20°C.

A, rate constant of force recovery (single-exponential fits). Changes during activation by ATP release (circles; same activation as in B) or calcium (squares; same activation as in C). In the normal Ca²⁺ activation, force and rate of force recovery rose nearly in proportion, with force at 70%P_o after 1.4 s, and increasing by a further 30% over the following 10 s. B and C, striation patterns imaged using brightfield microscopy with an objective positioned in place of the coverslip above the fibre (Fig. 1B). B, activation by release of 0.6 mm ATP at 20°C. Images were acquired at 40 ms intervals and representative regions are shown (left to right) in rigor just before activation, and at 140 ms, 420 ms and 2 min after activation. The images at 140 ms and 420 ms correspond to tension development and tension recovery, respectively. Striation patterns were not recovered upon relaxation after this kind of activation. CS = 5.9 × 10³μm², FL = 2.6 mm. C, activation by calcium at 4 mm ATP, 20°C. Images of the fibre before activation, at 6 s and 2 min after activation, and when relaxed, showing recovery of the striation pattern after several minutes of activation. Sarcomere length = 2.34 μm in rigor in B, and 2.39 μm before activation in C. CS = 5.1 × 10³μm², FL = 2.9 mm.

When fibres are activated by the addition of Ca²⁺ (Fig. 5A, squares), the rate of force development is limited by Ca²⁺ diffusion into the fibre. A pre-activating solution with a low EGTA concentration (see Table 1) was used to maximize the rate of force rise, which had a reproducible component with half-time 0.40 ± 0.03 s⁻¹ (mean ±s.d., n = 6). In some fibres, including that in Fig. 5A, this was followed by a slower force increase, of up to 30% of the steady force, over the next few seconds. Repeated shortening–restretch cycles were imposed during the force rise, and the rate of force redevelopment following the restretch increased in parallel with the isometric force (Fig. 5A), presumably because it also depends on the Ca²⁺ concentration (Brenner, 1988). In the example in Fig. 5A, the first restretch was imposed 1.4 s after transferring the fibre to activating solution, and the rate constant of force redevelopment after the restretch was 20 s⁻¹. The rate constant increased slightly in subsequent shortening–restretch cycles, and was 29 s⁻¹ after 6 s, when the isometric force was steady. In six fibres, the rate constant was 38 ± 4 s⁻¹ after 6.2 ± 1.6 s of activation. It then slowly declined to 84 ± 5% of this peak value after 50 ± 3 s of activation. Sarcomere disorder developed more slowly following Ca²⁺ activation (Fig. 5C) than after activation by photolysis of caged ATP (Fig. 5B), and the sarcomere disorder induced by Ca²⁺ activation was reversible, in contrast to that following activation with caged ATP.

The rate of force development after a restretch in fibres activated by the addition of Ca²⁺ was always lower than that following a shortening–restretch imposed 0.1–0.3 s after activation by release of ATP from caged ATP (Fig. 4; Fig. 5A, circles). These results suggest that the true rate of force development under conditions of maximal Ca²⁺ activation at 20°C cannot be observed by transferring fibres from relaxing to activating solution. By the time Ca²⁺ has diffused into the fibres under these conditions, the disordering of fibre structure may have already progressed to such an extent that the rate of force development has been substantially reduced. In contrast, when fibres were activated by ATP release in the presence of Ca²⁺, the time course of force development following ATP release at 20°C was the same as that following a shortening–restretch imposed 0.1–0.3 s after ATP release (Fig. 4, Table 2). Thus the time course of isometric force development at 20°C can be measured by either protocol, provided that the shortening–restretch is imposed sufficiently early in the activation, before the development of sarcomere disorder (Fig. 5).

The decline in fibre performance and sarcomere order were not observed at 5°C during activations lasting more than 1 min. Moreover, the rate of force development following a restretch was the same with Ca²⁺ and caged ATP activation at this temperature. The rate reported above for fibres activated by release of ATP from caged ATP at 5°C, i.e. 4 s⁻¹ for a single-exponential fit (Table 2), is similar to previously published values for force development following a restretch (Brenner & Eisenberg, 1986).

Discussion

The time course of isometric force development

We characterized the time course of isometric force development from an initial force close to zero in two experimental protocols. In the caged ATP protocol, fibres were initially in rigor, and force development was initiated by release of ATP in the presence of Ca²⁺. In the ramp shortening–restretch protocol, force developed after a period of rapid shortening at low force followed by a quick restretch to the original length. The first few milliseconds of the force response was markedly different in the two protocols; there was a lag in the caged ATP case and a rapid force jump followed by a transient minimum during the restretch in the shortening–restretch case. After this initial response, however, the time courses of isometric force development were essentially identical. Moreover, this identity was maintained when the rates were increased by a factor of almost 20 by raising the experimental temperature from 5 to 20°C (Table 2).

Force development at 5°C was best fitted by two exponential components, and the rate constants and relative amplitudes of these components were the same in the caged ATP and shortening–restretch protocols (Fig. 3, Table 2). The faster component is more sensitive to changes in temperature, inorganic phosphate (P_i) concentration, and the load during shortening (Burton et al. 2005; K. Burton et al. in preparation). Its rate is similar to those of force responses to perturbations of temperature, pressure or [P_i], and it seems to be closely related to a fundamental step in mechanical–chemical coupling. The presence of multiple exponential components may arise from the strain dependence of the rates of myosin attachment to and detachment from actin or a redistribution of myosin heads between different actin binding sites (K. Burton et al. in preparation). At 20°C, the slower component is less prominent. The time course of force development after release of ATP could be satisfactorily described as a single exponential (Fig. 4), but two exponential components gave a more accurate fit to force development after shortening and restretch.

In the original studies of force development following release of ATP from caged ATP (Goldman et al. 1984), the pre-photolysis force was a large fraction of the final steady force, and ATP release produced a transient force decrease followed by a slower force increase. The present experiments differ in several respects from those original studies. First, the fibres were put into rigor at low temperature in the presence of EDTA, almost abolishing the development of force in rigor and the transient force decrease following ATP release. Second, we used apyrase to minimize contaminant ATP and ADP, and to reduce the force developed in rigor solutions that contain an ATP-regenerating system (Fig. 2). Third, the sarcomere length in the central region of the fibre was held constant by feedback to the motor controlling the fibre length (Fig. 4B), eliminating the shortening of this region associated with force development at constant fibre length (Fig. 4A). Despite these differences, the rate of force development following release of ATP from caged ATP at 20°C in the present experiments, 71 ± 4 s⁻¹ (Table 2), is similar to the 83 s⁻¹ deducedfrom the original studies by fitting biphasic force transients observed at 20°C with a kinetic scheme (Goldman et al. 1984).

In contrast, the time course of isometric force development in the shortening–restretch protocol at 20°C was much faster than reported in the original studies using that approach (Brenner & Eisenberg, 1986). In the present work a single-exponential fit to the force rise after the restretch at 20°C had a rate constant of 68 ± 3 s⁻¹ (Table 2), much larger than the values reported in the original study, 15 s⁻¹ at 15°C and 26 s⁻¹ at 25°C (Brenner & Eisenberg, 1986). Part of the discrepancy is related to the activation protocol. In previous studies of the rate of force development using the shortening–restretch protocol, fibres were activated by the addition of Ca²⁺ in the presence of MgATP. In these conditions the rate constant varies during the course of the activation, with a maximum value of 38 ± 4 s⁻¹ at 20°C (Fig. 5A, squares). Prolonged activation at 20°C leads to a loss of sarcomere order accompanied by a decrease in the rate of force redevelopment following shortening–restretch (Fig. 5). Activation by photolysis of caged ATP allows the time course of force recovery to be characterized using the shortening–restretch protocol at maximally activating [Ca²⁺], before significant sarcomere disorder has taken place. The measured time course of force development following such a restretch was essentially identical to that of the original force development following ATP release (Fig. 4).

The similarity of the time courses of force development in the caged ATP and shortening–restretch protocols suggest that the rate of force development is determined by the same process or biochemical transition. This interpretation is strengthened by the observation that the two responses have the same temperature dependence (Figs 3 and 4), and are modulated in the same way by the addition of inorganic phosphate (Burton et al. 2005). The next section considers the identity of the underlying process in the case of the caged ATP protocol, where the biochemical transitions are well characterized. We then discuss the implications for the interpretation of the shortening–restretch results.

Biochemical transitions limiting the rate of force development: kinetic scheme

The release of ATP from caged ATP initiates the series of biochemical transitions shown in Scheme 2. This is based on scheme 1 of the Introduction, with the addition of the ATP release step (step 0), and numerical values for the rate constants. The values of the rate constants in Scheme 2 were estimated for the conditions of the present experiments on rabbit psoas fibres at 20°C and 170 mm ionic strength. k₀, k₂, k₋₂ and k₄ were assumed to be the same in a muscle fibre and in solution. The states M·ATP and M·ADP·P_i are in rapid equilibrium with actin-bound states and each pair of states is treated as a single component. Measurements of k₂ and k₋₂ in active myofibrils are very similar to solution measurements for myosin subfragment-1 (S-1), indicating that the M·ATP→M·ADP·P_i pathway is dominant (Ma & Taylor, 1994; Herrmann et al. 1994). The second-order binding constant of ATP to AM (k₁) was reduced from its solution value to account for the inhibitory effect of caged ATP (Sleep et al. 1994). The value used here is consistent with mechanical and fluorescent probe measurements of the rate of detachment of myosin from actin following ATP release in fibres under the conditions of the present experiments (Goldman et al. 1984; Allen et al. 1996). Step 3,

scheme 2

the force-generating transition in this scheme, is assumed to be fast compared with the other steps, and is represented as a reversible equilibrium with equilibrium constant K₃. The requirement for this step to be fast is discussed further below. The rate of phosphate release from AM·ADP·P_i (k₄) was measured in solution by adding actin to an equilibrium mixture of M·ATP and M·ADP·P_i (White et al. 1997). This approach cannot be used with muscle fibres, but measurement of the rate of P_i release following ATP release with a fluorescent phosphate-binding protein showed that k₄ in rabbit psoas fibres at 20°C must be at least ∼40 s⁻¹ (He et al. 1997). During isometric contraction of a muscle fibre, overall rate limitation is generally assigned to step 5, the ADP release step, and k₅ was chosen to match the observed rate of ATP utilization during isometric contraction of rabbit psoas fibres at 20°C (6 s⁻¹; Hilber et al. 2001).

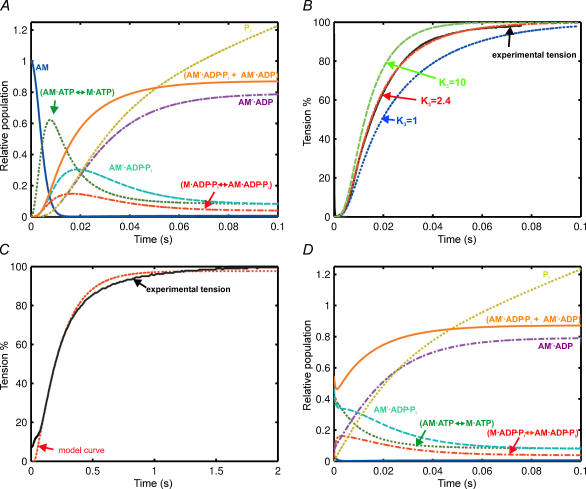
According to Scheme 2, the photolysis of caged ATP to produce 0.8 mm ATP in a fibre would cause the concentration of the rigor complex (AM, Fig. 6A, dark blue) to decrease rapidly during the first few milliseconds. AM·ATP↔M·ATP, M·ADP·P_i↔AM·ADP·P_i, and AM′·ADP·P_i are formed in the first 10−20 ms, and their concentrations subsequently decline. The predominant steady-state intermediate during isometric contraction is AM′·ADP. The force-generating states AM′·ADP·P_i and AM′·ADP are in this model, and the sum of their concentrations (orange, Fig. 6A and B) accurately reproduces the observed time course of force development (black, Fig. 6B). A single-exponential fit to the time courseof force development calculated from the model had a rate constant of 67 s⁻¹, in good agreement with the experimental value of 71 ± 4 s⁻¹ (Table 2). The only free parameter in the kinetic simulation was K₃, which was set to 2.4. Increasing K₃ accelerates the calculated rate of force rise with little effect on the lag (Fig. 6B).

Figure 6. Relative populations of the myosin intermediates.

A, after release of ATP at 20°C. (AM′·ADP·P_i+ AM′·ADP) = predicted tension. Rate constants used: k₀= 90 s⁻¹, k₁= 10⁶m⁻¹ s⁻¹, k₂= 100 s⁻¹, k_–2= 50 s⁻¹, k₃= 1200 s⁻¹, k₋₃= 500 s⁻¹, k₄= 80 s⁻¹, k₅= 7.3 s⁻¹. The predicted steady-state ATPase rate was 6 s⁻¹. B, effect of K₃ on the rate of tension rise showing experimental data, and predicted tension rise with K₃= 10, 2.4 and 1. Model curves scaled so that tension plateaus at the same level as the single-exponential fit to the experimental data. C, release of ATP at 5°C. Continuous line is experimental record; dotted line is the model curve. Rate constants used: k₀= 35 s⁻¹, k₁= 5 × 10⁵m⁻¹ s⁻¹, k₂= 7.7 s⁻¹, k₋₂= 4.6 s⁻¹, k₃= 150 s⁻¹, k₋₃= 300 s⁻¹, k₄= 23 s⁻¹, k₅= 1.2 s⁻¹. This model curve has been shifted laterally by +25 ms to account for the unexplained additional lag at 5°C. D, ramp restretch at 20°C. Colour as for Fig. 6A.

The model in Scheme 2 was also able to reproduce the main features of the slower force development observed at 5°C, using solution rate constants appropriate for that temperature (Fig. 6C). The hydrolysis step (step 2) is the most temperature sensitive, and for this temperature we used the measurements of k₂ and k₋₂ reported in Burton et al. (2005) (7.7 s⁻¹ and 4.6 s⁻¹, respectively). The rate constant of ADP release (k₅) was chosen to fit the steady-state rate of ATP utilization in rabbit psoas fibres at 5°C (1 s⁻¹; Hilber et al. 2001). The equilibrium constant of the force-generating transition (K₃) was a free parameter, and a reasonable fit was obtained with K₃= 0.5. The other rate constants are given in the legend of Fig. 6 (referring to panel C). A single-exponential fit to the calculated force rise had a rate constant of 5.0 s⁻¹, similar to the rate of the experimental record, 4.6 s⁻¹ (Fig. 6C) and to the average value, 4.3 s⁻¹ (Table 2). The model reproduces the main time course of force development at this temperature reasonably well, but not the initial lag; the model curve in Fig. 6C has been shifted to the right by 25 ms. The observed lag is more temperature sensitive than expected from the relatively weak temperature dependence of the photolysis and ATP binding steps. This discrepancy suggests that strain dependence or co-operativity of detachment from the rigor state (Dantzig et al. 1991) may contribute to the initial component of the force transient following ATP release at 5°C.

The time course of force development in the shortening–restretch protocol

The observation that the time course of force development in the shortening–restretch protocol is similar to that in the caged ATP protocol, and that both time courses are modulated in the same way by temperature and addition of inorganic phosphate (Burton et al. 2003b), suggests that both are limited by the same biochemical transitions. According to Scheme 2, these rate-limiting transitions are expected to be ATP hydrolysis (step 2) and P_i release (step 4). It follows that the predominant biochemical intermediates at the start of force development in the shortening–restretch protocol should be M·ATP and AM′·ADP·P_i. Since the restretch does not affect the time course of force development after the first few milliseconds (Burton et al. in preparation), it is likely that these states accumulate during rapid shortening. Chemical analysis of extracts from frog muscles frozen during rapid shortening has provided independent evidence for the accumulation of ATP-bound states (Homsher et al. 1981).

We made a quantitative test of these ideas using a specific proposal for how the rate constants in Scheme 2 are modified during rapid shortening. We have already postulated that the rate constants of the hydrolysis and P_i release steps (k₂, k₋₂ and k₄) have the same values in a muscle fibre as in the isolated proteins in solution, so these rate constants were not modified. The increased rate of ATP utilization during rapid shortening (Kushmerick & Davies, 1969; Sun et al. 2001) shows that the rate of ADP release (k₅) must be substantially larger than its isometric value (6 s⁻¹ at 20°C). k₅ is generally considered to limit the rate of detachment of myosin heads from actin during shortening, and thereby to control the unloaded shortening velocity. At 20°C this velocity is > 4000 nm s⁻¹ (Fig. 4), so if heads can remain attached to actin during filament sliding of about 10 nm (Huxley & Simmons, 1971; Piazzesi et al. 2002, 2003), k₅ must be at least 400 s⁻¹. We rounded this value up to 500 s⁻¹: larger values for k₅ during unloaded shortening did not significantly alter the results. Finally, general theoretical considerations suggest that K₃, the equilibrium constant of the force-generating step, must be larger during unloaded shortening than during isometric contraction, and we set K₃ to 20 during unloaded shortening. This parameter also had little effect on the time course of isometric force development after shortening.

The increase in k₅ and K₃ during rapid shortening leads to a build-up of (AM·ATP↔M·ATP) and AM′·ADP·P_i in roughly equal amounts. Myosin heads in the AM′·ADP·P_i state were proposed to bear force during isometric contraction, but during unloaded shortening they would repeatedly detach from and reattach to actin, because the detachment rate (> 400 s⁻¹ as estimated above) is much faster than the rate of P_i release (80 s⁻¹), and the net force is zero. Repeated transient detachments resulting from rapid filament sliding have been postulated to explain the biphasic dependence of the rate of enthalpy production on velocity (Huxley, 1973). The AM′·ADP·P_i heads would also slip between actin monomers during the rapid restretch at the end of the shortening, but at the end of the restretch they have a mean strain similar to that during isometric contraction (Burton, 1992). About half of the heads are in the AM′·ADP·P_i state at this time, compared with nearly all the heads being in force-bearing states during isometric contraction according to this kinetic scheme (Fig. 6A). Thus the model provides an explanation for force development starting from a force level of about half the isometric force at the end of the restretch (Figs 3 and 4; Burton et al. 2003a).

The time course of isometric force development following rapid shortening–restretch at 20°C was quantitatively reproduced by the model in Scheme 2 (Fig. 6D). The rate constants were assumed to revert to their isometric values at time zero, the end of the restretch. This results in a very fast re-equilibration of the force-generating step (step 3), associated with a decrease in (AM′·ADP·P_i) and an increase in (M·ADP·P_i↔AM·ADP·P_i). The main time course of force development is, however, associated with a decrease in (AM·ATP↔M·ATP) and AM′·ADP·P_i and an increase in AM′·ADP, and in this respect is similar to the main time course of force development after release of ATP from caged ATP (Fig. 6A). A single-exponential fit to the calculated force time course (AM′·ADP·P_i+ AM′·ADP) had a rate constant of 65 s⁻¹, in good agreement with the experimental value, 68 ± 3 s⁻¹ (Table 2).

The time course of force recovery following shortening–restretch at 5°C was calculated in a similar way using the rate constants given with reference to panel C in the legend to Fig. 6. The calculated force rise had a rate constant of 5.2 s⁻¹, similar to 5 s⁻¹ calculated for force development after ATP release (Fig. 6C) and 4.6 s⁻¹ observed experimentally (Fig. 3). The general conclusion of this section is that Scheme 2 can reproduce the main features of the observed force development after shortening–restretch as well as after ATP release from caged ATP.

Mechanical–chemical coupling in muscle

The key postulates of the model (Scheme 2) that we proposed to describe the experimental time courses of force development are:

1. Both AM′ADP.P_i and AM′.ADP contribute to the isometric force, i.e. force generation (step 3) precedes phosphate release (step 4).

2. The force-generating transition (step 3) is much faster than either ATP hydrolysis (step 2) or phosphate release (step 4).

3. Both ATP hydrolysis and P_i release are independent of the strain in the myosin head, and the rate constants of these steps are the same in muscle fibres and in solution.

Postulate 1 has been made in many previous studies of mechanical–chemical coupling in muscle fibres (Lund et al. 1987, 1988; Kawai & Halvorson, 1991; Fortune et al. 1991; Dantzig et al. 1992). The alternative hypothesis, that P_i must be released before force is generated, is not consistent with the time course of force development after ATP release from caged ATP observed here (Fig. 4), because the time course of force development would then follow that of [AM′·ADP] in Scheme 2. Since both ATP hydrolysis and phosphate release are slow in this model, the calculated time course of the rise in [AM′.ADP] is slower than the observed force rise (Fig. 6A).

The proposal that force is generated by the transition from AM·ADP·P_i to AM′·ADP·P_i fits well with recent structural studies. The zero-force state AM·ADP·P_i corresponds to the transition-state complex observed in crystals of myosin head fragments with bound ADP·vanadate or ADP·AlF₄ in which the nucleotide-binding pocket of myosin is closed and the light chain domain or lever arm of the myosin head is in the pre-power stroke conformation (Smith & Rayment, 1995; Dominguez et al. 1998; Geeves & Holmes, 1999). The force-generating state AM′·ADP·P_i would have an open nucleotide-binding pocket (mimicked by ADP·BeF_x in some crystal forms and also seen in the absence of nucleotide), with the lever arm in the post-power stroke conformation (Rayment et al. 1993).

As far as we are aware, postulate 2 has not been considered explicitly in previous work, but is implied by the hypothesis that the elementary force-generating process is a fast transition with a rate constant of the order of 1000 s⁻¹ (Huxley & Simmons, 1971; Irving et al. 1992). This process is sufficiently fast that it may be considered to be in equilibrium on the time scale of the force development observed here. If the rate constant of the ATP hydrolysis step in muscle fibres is the same as observed in solution (100 s⁻¹ at 20°C), the rate of the force-generating step must be much faster than this to be consistent with the time course of force development following ATP release (Fig. 4). If the force-generating step were slower, the lag preceding the force rise would be larger than that observed.

In most previously published kinetic schemes in which force generation precedes P_i release, it was assumed that force generation was the slower of the two transitions (Millar & Homsher, 1990; Kawai & Halvorson, 1991; Dantzig et al. 1992; Zhao & Kawai, 1994; Ranatunga et al. 2002). These studies were primarily concerned with the effects of inorganic phosphate (P_i) on fibre mechanics. The present model (Scheme 2) provides an alternative explanation for these effects. Addition of P_i drives step 4 backwards, and force is reduced by re-equilibration of the force-generating transition (step 3). A small rapid increase in [P_i], such as that produced by photolysis of caged P_i, produces a force decrease with rate constant about 80 s⁻¹ at 20°C (Dantzig et al. 1992). When larger concentrations of P_i are released, the force decrease is faster, as expected from a greater contribution of the reverse rate k₋₄. Scheme 2 would not reproduce the observed non-linear dependence of the rate of the force transient on [P_i], but this feature can be reproduced if, in common with the dissociation of many small ligands, P_i release occurs in two steps: an 80 s⁻¹ isomerization followed by rapid dissociation. Introducing such an additional step would not alter the other predictions of Scheme 2. The simpler scheme also reproduces the observed effects of P_i on the rate of force development after shortening–restretch, and on the rate of force development following release of ATP from caged ATP (Burton et al. 2005). Takagi et al. (2004) recently reported experiments in which they controlled the duration of actomyosin interactions using an optical trap assay. The rate of detachment was independent of [P_i] for interactions of < 10 ms, whereas it became dependent on [P_i] only for longer interactions. Such results imply that a slow step of ∼100 s⁻¹ associated with P_i release follows a rapid force-generating transition, as in the above scheme. This sequence contrasts with the model of Dantzig et al. (1992) in which the force development step itself is slow.

According to the model in Scheme 2, the parameters that are the primary determinants of the observed rate of force development in the present experiments, the rate constants of the ATP hydrolysis and P_i release steps, do not depend on the strain in the myosin heads, and are the same in muscle fibres as in isolated proteins (postulate 3). The strain dependence of the rates of the biochemical transitions remains a fundamental feature of mechanical–chemical coupling in this scheme, but is confined to the force-generating transition and ADP release. Strain dependence of the force-generating transition is expected to have a large effect on the rate of the ∼1000 s⁻¹ transients following a rapid length or force step (Huxley & Simmons, 1971; Piazzesi et al. 2003), but a relatively small effect on the slower force development observed in the protocols used here. On this slower time scale, strain affects the rate by altering the equilibrium constant K₃. Large changes in the rate of step 3 have much smaller effects on the time course of force development in the protocols used here (Fig. 6B). The effect could, however, be large enough to account for the multiple exponential components in force development that we observe, with rate constants differing by a factor of 3–4, as discussed elsewhere (K. Burton et al. in preparation).

In summary, we have presented a relatively simple model of force development, in which a rapid and strain-dependent force-generating process is bracketed by two strain-independent biochemical transitions that limit the rate of isometric force development in physiological conditions. This model provides a quantitative explanation of the present results, and of the results of many previous studies of mechanical–chemical coupling in muscle.