Stomatal Constraints May Affect Emission of Oxygenated Monoterpenoids from the Foliage of Pinus pinea^,

Abstract

Dependence of monoterpenoid emission and fractional composition on stomatal conductance (G_V) was studied in Mediterranean conifer Pinus pinea, which primarily emits limonene and trans-β-ocimene but also large fractions of oxygenated monoterpenoids linalool and 1,8-cineole. Strong decreases in G_V attributable to diurnal water stress were accompanied by a significant reduction in total monoterpenoid emission rate in midday. However, various monoterpenoids responded differently to the reduction in G_V, with the emission rates of limonene and trans-β-ocimene being unaffected but those of linalool and 1,8-cineole closely following diurnal variability in G_V. A dynamic emission model indicated that stomatal sensitivity of emissions was associated with monoterpenoid Henry's law constant (H, gas/liquid phase partition coefficient). Monoterpenoids with a large H such as trans-β-ocimene sustain higher intercellular partial pressure for a certain liquid phase concentration, and stomatal closure is balanced by a nearly immediate increase in monoterpene diffusion gradient from intercellular air-space to ambient air. The partial pressure rises also in compounds with a low H, but more than 1,000-fold higher liquid phase concentrations of linalool and 1,8-cineole are necessary to increase intercellular partial pressure high enough to balance stomatal closure. The system response is accordingly slower, and the emission rates may be transiently suppressed by low G_V. Simulations further suggested that linalool and 1,8-cineole synthesis rates also decreased with decreasing G_V, possibly as the result of selective inhibition of various monoterpene synthases by stomata. We conclude that physicochemical characteristics of volatiles not only affect total emission but also alter the fractional composition of emitted monoterpenoids.

Monoterpenoids emitted by plants constitute a major source of volatile organic compounds (VOC) in the atmosphere (Guenther et al., 1994). Because they play an important part in atmospheric chemistry, in particular in ozone-forming reactions (Guenther et al., 1994; Simpson, 1995), considerable effort has been put toward measuring and prediction of monoterpenoid emission rates from the foliage of emitting species (Guenther et al., 1994).

All plant monoterpenoids are synthesized in plastids (Chappell, 1995; Lichtenthaler, 1999; Davis and Croteau, 2000). In many species, the rates of monoterpenoid synthesis are dependent on both light and temperature similarly to carbon assimilation rates (Schuh et al., 1997; Shao et al., 2001), and there is conclusive evidence that a part of the emitted compounds originates from a small pool of immediately assimilated carbon. However, the current monoterpenoid emission models mostly use a simple two-parameter empirical temperature equation to describe the monoterpene efflux from the foliage (Tingey et al., 1980, 1991; Guenther et al., 1993) assuming that monoterpenoids are emitted primarily from the storage pools such that their emission rates are uncoupled from the synthesis rates. In species without specific storage pools like the Mediterranean sclerophyll holm oak (Quercus ilex), it has been demonstrated that light may also control monoterpenoid emission (Staudt and Seufert, 1995; Ciccioli et al., 1997; Staudt and Bertin, 1998), and light effects on emission are generally described by a hyperbolic equation derived from foliar isoprene emission measurements (Guenther et al., 1993). Evidence has also accumulated to indicate that monoterpenoid efflux rates may even be light sensitive in species with storage pools such as conifers from the genera Pinus (Janson, 1993; Staudt et al., 1997; Kesselmeier and Staudt, 1999; Shao et al., 2001) and Picea (Schürmann, 1993; Schürmann et al., 1993; Steinbrecher and Ziegler, 1997). Light-dependent emissions in these species may be explained by a slower emission from the storage pools in resin ducts compared with the emission from chloroplastic monoterpenoid pools in the mesophyll cells (Schürmann et al., 1993). Such differences in the turnover rates of various pools may result from large diffusion resistances between the outside air and the resin ducts, which are lined by a layer of epithelial cells and an additional layer of thick-walled sclerenchyma cells (Steinbrecher and Ziegler, 1997). Despite of the appealing simplicity of the emission algorithms employing either only temperature or temperature and light as drivers, these models frequently provide relatively poor fits to the experimental observations (e.g. Juuti et al., 1990; Staudt et al., 1997; Llusiá and Peñuelas, 2000; Sabillón and Cremades, 2001) with explained variances generally not exceeding 50% to 70%. A relatively low percentage of explained variance suggests that monoterpenoid emission is not purely a physical phenomenon driven by temperature and also that important foliar characteristics and monoterpenoid physicochemical parameters may affect the emission rates.

Although the experimental work has demonstrated that both isoprene (Fall and Monson, 1992) and monoterpenoids (Schürmann, 1993; Loreto et al., 1996b) are emitted through the stomata (for review, see Kesselmeier and Staudt, 1999), a key assumption of all current empirical emission models is that stomata do not control the isoprenoid efflux. This apparently contrasts with previous observations that there is a strong correlation between foliar monoterpene emission and transpiration rates (Steinbrecher, 1989; Kesselmeier et al., 1996, 1997). Moreover, positive relations between leaf conductance to water vapor (G_V) and monoterpenoid emission rates have frequently been observed (Steinbrecher, 1989; Schuh et al., 1997). The correlation between monoterpenoid emission and transpiration rates (E) may, of course, result from simultaneous positive effects of temperature on monoterpene efflux rates and on water vapor pressure deficit between leaf and atmosphere (ΔP; E = ΔPG_V). Positive effects of light on both G_V and monoterpenoid synthesis rate (e.g. Schuh et al., 1997) may similarly provide an explanation for the scaling of emission rates with G_V.

So far, the lack of significant stomatal control over the emission rates has been shown only for isoprene (Monson and Fall, 1989; Fall and Monson, 1992) and for α-pinene (Loreto et al., 1996b) and has been generalized to all volatile compounds (Sharkey, 1991; Kesselmeier and Staudt, 1999). Missing stomatal control has been explained by low- and non-saturated foliar gas phase concentrations of isoprenoids, which readily increase in response to a stomatal closure and thereby balance the decrease in conductance by an enhanced diffusion gradient from the intercellular air space to outside air (Sharkey, 1991; Fall and Monson, 1992; Kesselmeier and Staudt, 1999). In fact, if the monoterpene synthesis rate remains constant after a decrease in G_V, no sustained stomatal limitation of the emission rates is possible. An alternative explanation would be the emission of isoprenoids through the cuticle. However, calculations demonstrate that cuticle may account for only up to 10% to 20% of total monoterpenoids emitted (Schürmann, 1993). Thus, cuticular emission alone could not sustain the observed monoterpenoid emission rates in the absence of the emission through stomata.

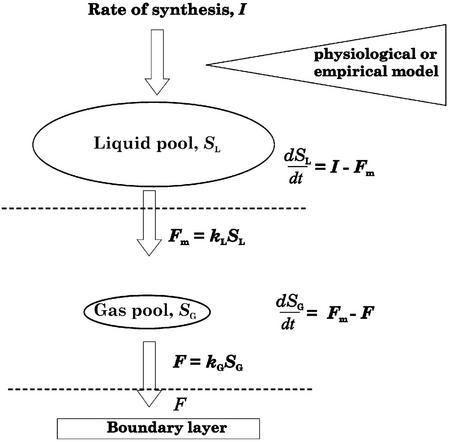
To gain mechanistic insight into varying stomatal controls over the emission of specific compounds, we developed a dynamic model describing the dependence of the VOC emission rate on G_V and the compound physicochemical characteristics. Mass-balance approach is employed to simulate the dynamics of leaf gas and liquid pools (Fig. 1). The model explains the compound-specific emission responses to G_V by different half-times of the monoterpene internal gas and liquid pools. The compounds that partition primarily to liquid phase such as short-chain alcohols, aldehydes, and carboxylic acids require larger increases in the liquid pool size for a certain rise in partial pressure than the compounds that partition primarily to the gas phase. Thus, provided that the compound intercellular partial pressure (P_i) changes more slowly than stomatal aperture, G_V may affect VOC emission in non-steady-state conditions.

Figure 1.

Outline of the dynamic model of foliar monoterpene emission. The leaf internal monoterpene content is divided between liquid and gas pools, and a mass balance approach is used to determine the dynamics of the pools. The rate of monoterpenoid synthesis, I, may be computed by either a process-based model or an empirical model (Eqs. 15–17). The diffusion flux density from the site of synthesis to outer surface of cell walls, F_m, is given by Equation 6, and the diffusion flux density through the stomata, F, by Equation 5.

Apart from the potential stomatal limitations attributable to the slow rise in P_i, increases in the liquid phase VOC concentrations may also directly affect the compound synthesis rates, thereby leading to curbed rates of emission in the steady-state conditions. It is know that accumulation of certain end products and intermediates may lead to differences in the activity profiles of various plant monoterpene synthases (Davis and Croteau, 2000). We use the model developed to discriminate between stomatal and biochemical controls on plant VOC emission in the Mediterranean evergreen conifer Pinus pinea. This species has a distinct emission pattern emitting large amounts of oxygenated monoterpenoids linalool and 1,8-cineole that may potentially be strongly controlled by stomata in a non-steady-state situation. The light-dependent emissions in this species are an order of magnitude larger than the emissions in the dark (Staudt et al., 1997), suggesting that de novo synthesis rather than the storage in resin ducts is the primary source of emitted monoterpenes. Empirical models based on leaf temperature and incident irradiance alone have provided especially poor fits to the diurnal dynamics of oxygenated compounds in P. pinea (Staudt et al., 1997; Sabillón and Cremades, 2001). We further demonstrate that the fractional composition of emitted monoterpenoids changes during the day as the result of selective constraints on the synthesis and emission of oxygenated monoterpenoids. Because various monoterpenoids differ largely with respect to the gas phase rate coefficients for reaction with ozone and hydroxyl radicals (Fehsenfeld et al., 1992; Guenther et al., 1994), a mechanistic prediction of changes in monoterpenoid composition provides an important basis to determine diurnal changes in atmospheric reactivity.

RESULTS

Simulated Responses of Plant Volatile Emission to Changes in Stomatal Conductance (G_V). Gas Phase Dynamics

Provided that the volatile synthesis rate is unaffected by changes in G_V, stomatal closure leads to an increase in internal leaf volatile concentration. In a steady-state situation, the rise in the internal concentration exactly balances the decrease in G_V, and the same flux as before the changes in G_V is maintained at a lower stomatal aperture. This means that when the volatile build-up does not affect its synthesis rate, stomata may affect the VOC emission only in a non-steady-state situation, and the turnover rate of leaf gas and liquid phases apparently determines the time required to reach the steady state.

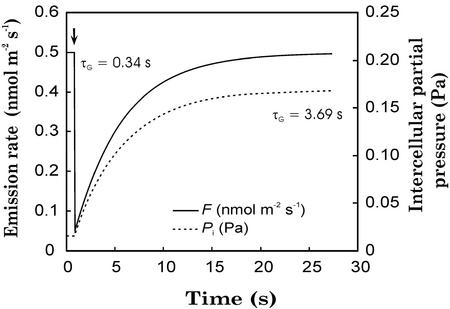
We first use the model version with a gas pool only (Fig. 1; dS_G/dt = F_m − F, where F_m is the VOC flux from the site of synthesis to the outer surface of cell walls and F is the flux through stomata) to demonstrate that the size of the gas phase pool is far too small to explain stomatal limitations on VOC emission. Taking G_V to water vapor equal to 30 mmol m⁻² s⁻¹—a low value that corresponds to highest daily G_V values in water-stressed foliage of P. pinea—the rate constant (Eq. 10) of the gas pool of trans-β-ocimene, k_G, is 2.05 s⁻¹, and the half-time of the gas pool, τ_G (Eq. 11), will be 0.34 s (Fig. 2). When G_V is low, e.g. 1.5 mmol m⁻² s⁻¹, a value corresponding to a closed-stomata situation at night, k_G = 0.19 s⁻¹, and τ_G increases to 3.69 s. Figure 2 illustrates changes in trans-β-ocimene emission rate (Fig. 1; Eq. 10) in response to a hypothetical instant decrease in G_V from 30 to 1.5 mmol m⁻² s⁻¹, with a trans-β-ocimene input rate from chloroplasts to substomatal cavities of 0.5 nmol m⁻² s⁻¹. A new steady state is reached in approximately 15 s. After that, the flux is maintained, because the higher monoterpene P_i compensates for the stomatal closure. Given that the binary diffusion coefficients of monoterpenoids in air vary less than 10% among monoterpenoids (Table I), the system behaves very similarly for other monoterpenoids. Additional simulations demonstrated that the half-times of the gas phase pool, τ_G, are less than 5 s for all monoterpenoids emitted by P. pinea, even for very low finite gas phase conductances. These values are much lower compared with the time constants of stomatal closure and opening that measure in minutes (e.g. Tinoco-Ojanguren and Pearcy, 1993). Thus, we conclude that the gas phase pool is fast and that changes in gas phase dynamics cannot lead to stomatal limitations of monoterpene emission.

Figure 2.

Gas phase dynamics in P. pinea. Modeled (Fig. 1; Eqs. 8–10) effects of an instant stomatal closure on trans-β-ocimene emission rate (F) and intercellular partial pressure (P_i) at 25°C. Stomatal conductance to water vapor was changed from 30 to 1.5 mmol m⁻² s⁻¹ at time 1 s (denoted by arrow). A value of 0.5 nmol m⁻² s⁻¹ was used for the initial emission rate. τ_G is the half-time of the gas pool (Eq. 11). Physicochemical characteristics of trans-β-ocimene are given in Table I, and leaf structural data used for model parameterization are given in an electronic supplement (which can be viewed at www.plantphysiol.org).

Table I.

Physicochemical properties of selected monoterpenoids at 25°C

Property	Linalool	1,8-Cineole	Trans-β-Ocimene	d-Limonene
Diffusion coefficient in air (DA, m2 s−1)	5.17  × 10−6	5.46  × 10−6	5.46  × 10−6	5.64  × 10−6
Diffusion coefficient in water (DW, m2 s−1)	6.26  × 10−10	6.64  × 10−10	6.52  × 10−10	6.82  × 10−10
Saturated vapor pressure (PV, Pa)	21.3	253	197	253
Water solubility (δ, mol m−3)	10.2	19.1	0.0797	0.0886
Henry's law constant (H; Pa m3 mol−1)	2.078	13.27	3330	2850
Log[octanol-water partition coefficient (Ko/w, mol mol−1)]	2.97	2.61	4.45	4.485
Gas-phase internal conductance (Gias, m s−1)	1.59  × 10−3	1.67  × 10−3	1.68  × 10−3	1.73  × 10−3
Liquid-phase internal conductance (GL, m s−1)	5.88  × 10−4	3.46  × 10−4	1.54  × 10−3	1.61  × 10−3

Supplemental data of derivation of and references to the physicochemical monoterpene characteristics and internal diffusion conductances are provided at www.plantphysiol.org. Averages were calculated whenever multiple estimates were available.

Simulated Liquid Phase Dynamics

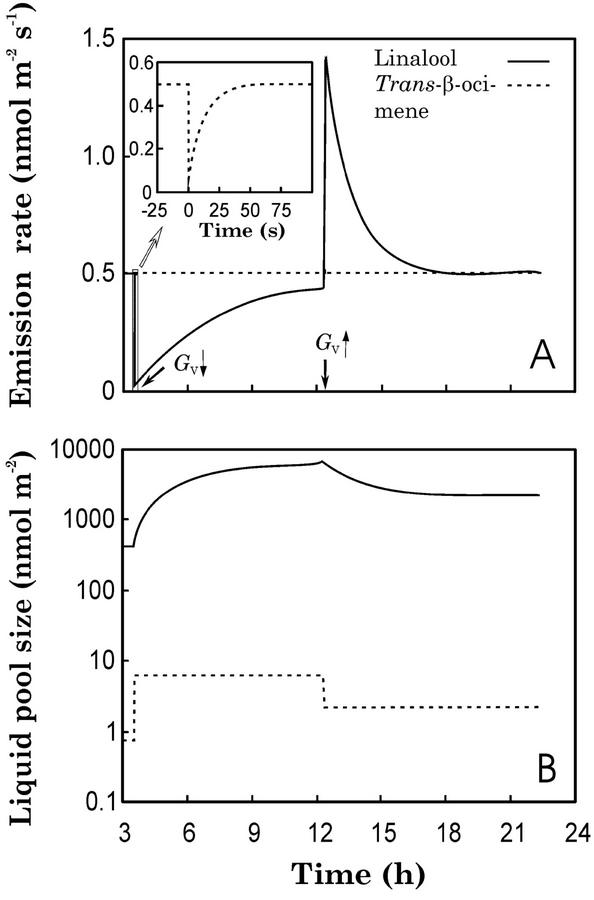
Provided that the gas phase is in the steady state, we now investigate the possibility that compound-to-compound differences in liquid phase dynamics lead to different stomatal sensitivities of VOC emissions. Figure 3 demonstrates the response of the system (Eqs. 12–14) to an instant decrease in G_V from 30 to 1.5 mmol m⁻² s⁻¹ and a subsequent rise to 5 mmol m⁻² s⁻¹ in two monoterpenoids of contrasting Henry's law constant (H, the equilibrium air-water partition coefficient; Eq. 7). Trans-β-ocimene, an olefin, has a H value of 3,330 Pa m³ mol⁻¹, and linalool, a terpene alcohol, has a H of 2.078 Pa m³ mol⁻¹ (see Table I for the physicochemical characteristics of monoterpenoids). For trans-β-ocimene, the half-time of the liquid pool (τ_L) is 1.03 s before the decrease in G_V, and the corresponding value is 551 s for linalool. After simulated stomatal closure, τ_L increases to 8.5 s in trans-β-ocimene and to 10,120 s in linalool. Thus, the P_i increases rapidly in response to the simulated stomatal closure for trans-β-ocimene, and the rise in the partial pressure balances the stomatal closure in approximately 30 s (Fig. 3A). In contrast, more than 10 h are needed to reach a steady-state situation for linalool (Fig. 3A). This striking difference in compound behavior results from the circumstance that a certain liquid phase concentration supports more than 1,000-fold higher P_i of trans-β-ocimene relative to linalool (Fig. 3B). As a consequence, slow increases in the liquid phase linalool concentration slow down the system response to changes in stomatal aperture.

Figure 3.

Performance of the dynamic model of monoterpene emission for P. pinea (Fig. 1; Eqs. 12–14) with linalool that has a Henry's law constant (H; Eq. 7) of 2.078 Pa m³ mol⁻¹ and with trans-β-ocimene (H = 3,330 Pa m³ mol⁻¹; Table I) at 25°C. The liquid-phase pools were allowed to reach a steady state at a G_V of 30 mmol m⁻² s⁻¹, and G_V was decreased to 1.5 mmol m⁻² s⁻¹ at time 3.5 h (denoted by an arrow). The conductance was kept at this value until 12.5 h, and then G_V was risen to 5 mmol m⁻² s⁻¹. Inset in A shows the initial changes after the decrease in G_V in trans-β-ocimene in a higher resolution.

The emission rate dynamics also behaves differently after a moderate increase in stomatal openness. Again, a new steady state is reached in seconds for trans-β-ocimene. However, linalool exhibits a large overshoot of the emission, because the liquid phase pool exceeds severalfold the steady-state linalool pool corresponding to new conditions (Fig. 3A). Such bursts of emission after a change in stomatal openness have been experimentally observed for methanol (Nemecek-Marshall et al., 1995) and acetaldehyde (Holzinger et al., 2000), and they demonstrate the decay of the extensive VOC pool accumulated during periods of low G_V.

These simulations demonstrate that the emission rate is essentially always in a steady state in compounds with a high H, but potentially large effects of G_V on the emission dynamics are expected for compounds with low values of H. Thus, we predict strong stomatal effects on emission of monoterpenes that preferably partition to aqueous phase (linalool and 1,8-cineole) and no stomatal effects for compounds primarily partitioning to gas phase (pinenes, ocimenes, and limonene; Table I).

Experimental Observations. Seasonal Changes in Monoterpenoid Emission

Emission of all monoterpenoids was strongly light dependent and was lower more than an order of magnitude at night than during the day at a common leaf temperature (Fig. 4). The highest total emission rates with daily maxima (F_max) of 4 to 9 nmol m⁻² s⁻¹ were observed during the July 31 to August 6, 1994 campaign and were followed by the emission rates during June 1 to 14, 1993 (F_max = 3–8 nmol m⁻² s⁻¹), May 5 to 28, 1994 (F_max = 1–3 nmol m⁻² s⁻¹), and October 23 to 27, 1994 (F_max = 0.5–0.6 nmol m⁻² s⁻¹). Periods of low monoterpenoid emission rates in May and October 1994 were accompanied by lower temperatures and reduced emission factors (F_s). F_s is the emission rate at defined standard temperature and light conditions (Eq. 15) and represents the overall foliar capacity to produce monoterpenoids. Periods of high monoterpenoid emission rates in June 1993 and August 1994 were accompanied by high emission factors, high temperatures (Fig. 4A), and foliar water stress. Maximum daily G_V values of approximately 45 (June 1993) and 25 mmol m⁻² s⁻¹ (August 1994) were observed in early morning, and G_V decreased thereafter gradually during the day with moderate recovery in afternoon (Fig. 4B). In contrast, maximum values of G_V of up to 120 mmol m⁻² s⁻¹ were observed in midday in non-stressed leaves (May and October 1994; data not shown; for further details on seasonal variability in G_V in P. pinea, see Manes et al., 1997).

Figure 4.

Examples of diurnal variability (August 3) in incident quantum flux density (Q, dots) and leaf temperature (T_L, lines; A), foliar net assimilation rates and G_V to water vapor (B), measured (dots) and predicted (lines) emission rates of trans-β-ocimene (C), limonene (D), 1,8-cineole (E), and linalool (F) in P. pinea. Monoterpenoid emission rates were simulated by Guenther et al. (1993) algorithm (Eqs. 15–17), assuming no stomatal effects on the diffusion flux density through the stomata and monoterpene synthesis rate and computing the emission factor, F_S (Eq. 15), from the measurements between 9 am and 12 pm.

The most important monoterpenoids emitted were cyclic monoterpene limonene and acyclic monoterpenoids linalool, trans-β-ocimene, and myrcene (Table II). In addition, ether 1,8-cineole and cyclic monoterpenes α- and β-pinene were emitted in large quantities during certain periods. The fraction of monoterpenoids emitted as trans-β-ocimene was large in water-stressed leaves in June 1993 and August 1994 but was low in May and October 1994 when there was no significant foliar water stress.

Table II.

Daily average (±se) fractions of total emission of major^a monoterpenoids emitted in P. pinea

Monoterpenoid	Campaign
	May 5–28, 1994	June 1–14, 1993	July 3–August 6, 1994	October 23–27, 1994
Limonene	0.413  ± 0.027	0.486  ± 0.035	0.067  ± 0.014	0.400  ± 0.067
Linalool	0.124  ± 0.013	0.180  ± 0.024	0.225  ± 0.029	0.248  ± 0.053
Trans-β-ocimene	0.051  ± 0.006	0.208  ± 0.023	0.397  ± 0.049	0.0114  ± 0.0021
1,8-Cineole	0.0325  ± 0.0029	0.0315  ± 0.0042	0.0397  ± 0.0037	0.167  ± 0.027
Myrcene	0.174  ± 0.023	0.0355  ± 0.0018	0.0149  ± 0.0017	0.0559  ± 0.0055
α-Pinene	0.161  ± 0.012	0.0377  ± 0.0030	0.0200  ± 0.0038	0.0524  ± 0.0048
β-Pinene	0.0259  ± 0.0033	0.0286  ± 0.0042	0.0052  ± 0.0043	0.0100  ± 0.0025

^aAltogether, 19 monoterpenoids have been detected in the foliar emission patterns of P. pinea (Kesselmeier et al., 1997). 

Diurnal Variability in Emission Rates of Various Monoterpenoids

In non-water limited leaves in May and October 1994, the empirical Guenther et al. (1993) model (Eqs. 15–17) that does not include stomatal effects on emission provided good fits to the emission rates of all monoterpenoids (data not shown). In water-stressed leaves in June 1993 (data not shown) and in August 1994, the model gave an excellent description of the emission of monoterpenoids with a low aqueous solubility and a large value of H (Table I) such as trans-β-ocimene (Fig. 4C) and limonene (Fig. 4D). However, the model strongly overestimated the emission of compounds with higher water solubility and a low H such as 1,8-cineole (Fig. 4E) and linalool (Fig. 4F). Diurnal variability in linalool and 1,8-cineole emission rates was similar to G_V (compare Fig. 4B with E and F) with the emission rates being highest in early morning and decreasing during the day with a modest rise of the emissions in the afternoon. Because of the strong decrease of more than an order of magnitude of linalool and 1,8-cineole efflux rates, the total emission rate of all monoterpenoids (F_sum) also decreased in midday (Fig. 5). Nevertheless, because the decline in linalool and 1,8-cineole emission rates was somewhat compensated for by increases in the emission of other monoterpenoids, F_sum decreased during the day only by 10% to 25% (Fig. 5).

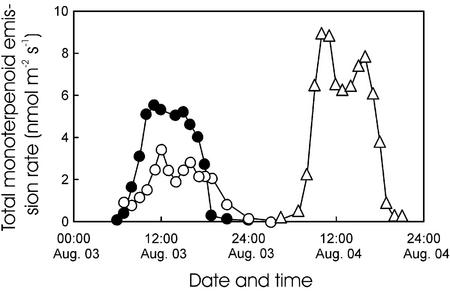
Figure 5.

Sample plot of the diurnal variability in total monoterpenoid emission rates on August 3 in two trees of P. pinea (●, tree 1; ○, tree 2), and on August 4 (▵, tree 1). The samples were analyzed gas-chromatographically by three different laboratories (●, JCT; ○, GRECA; and ▵, ENSCT; for details, see “Materials and Methods”).

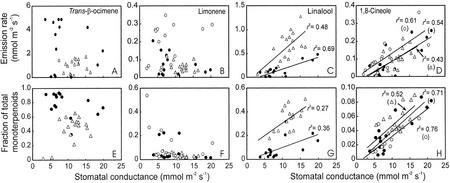
Emission rates of monoterpenoids with a low H value—linalool and 1,8-cineole—were closely related to G_V (Fig. 6, C and D). No correlations between the emission rates and G_V was observed for monoterpenoids with a high H value such as trans-β-ocimene and limonene (Fig. 6, A and B).

Figure 6.

Correlations of the G_V with the emission rates (A–D) and the fractions of total emitted monoterpenoids (E–H) of trans-β-ocimene (A and E), limonene (B and F), linalool (C and G), and 1,8-cineole (D and H) in P. pinea. The G_V to specific monoterpenoid is given as G_VD_A/D_V (Eq. 1), where D_V is the binary diffusion coefficient for water vapor in air and D_A is the diffusion coefficient of specific monoterpenoid in air (Table I). The emission rates were measured on August 3 and 4 in two trees, and all data sampled during these days are given (for an example of daily time-courses, see Fig. 4; for the explanation of symbols, see Fig. 5). Because of problems in resolution of linalool and trans-β-ocimene for tree 2 on August 3 (○) only data for tree 1 are provided for these monoterpenoids. All linear regressions drawn are significant at least at P < 0.05.

Modification of the Composition of Emitted Volatiles

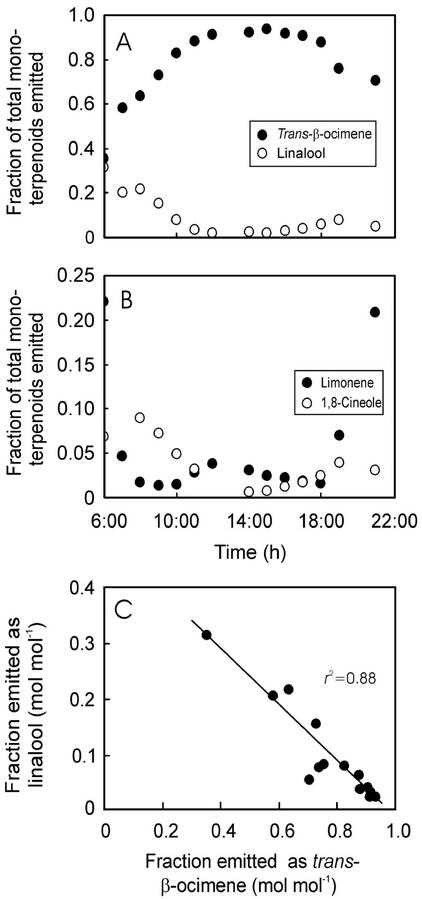
Similarly to the emission rates, the fractions of total monoterpenoids emitted as linalool and 1,8-cineole were strongly related to G_V (Fig. 6, G and H) but not the fractions of other monoterpenoids (Fig. 6, E and F). These correlations resulted from parallel diurnal changes in the composition of emitted monoterpenoids (Fig. 7, A and B) and G_V (Fig. 4B). In general, the fractions of linalool and 1,8-cineole emitted were the lowest in midday corresponding to lowest emission rates (compare Fig. 4, E and F, with Fig. 7, A and B), whereas the emission rates of trans-β-ocimene and limonene did not exhibit midday minima (Fig. 7, A and B). Because of large increases in trans-β-ocimene emission, the fraction of acyclic monoterpenoids (sum of the fractions of linalool, trans-β-ocimene, and myrcene) were largest in midday (data not shown). Very similar diurnal changes in emission dynamics and fractional composition were observed during all other days. These contrasting variation patterns resulted in a strong negative relationship between the fraction of trans-β-ocimene and the fraction of monoterpenoids emitted as linalool (Fig. 7C). There were no other correlations between the fractional emissions of compounds with large and small H values.

Figure 7.

Sample plots of diurnal variability in the fractions of total monoterpenoids emitted as trans-β-ocimene and linalool (A) and limonene and 1,8-cineole (B), and the correlation between the fractions emitted as linalool and trans-β-ocimene (C) in P. pinea. The data were fitted by a linear regression (P < 0.001). The same data set as in Figure 4.

Stomatal or Biochemical Constraints on Monoterpene Emission?

According to the dynamic monoterpene emission model (Fig. 1; Eqs. 12–14), the midday decline in linalool and 1,8-cineole emission rates may potentially result from changes in G_V, because both of these compounds have a low H, and the P_i values of these volatiles respond slowly to modifications in G_V. Alternatively, increases in monoterpenoid partial pressures after stomatal closure may suppress the synthesis rates and thereby reduce the emission. To discriminate between these two possible mechanisms, we constructed three contrasting scenarios to simulate the diurnal emission dynamics on the example of linalool (Fig. 8) and trans-β-ocimene (Fig. 9).

Figure 8.

Comparison of measured (Fig. 4F, dots) and modeled (Eqs. 12–14, lines) daily time courses of linalool emission from the needles of P. pinea. In scenario 1 (A–C), G_V was assumed to be invariable during the light period and to increase in the morning and decrease symmetrically in the evening with the rate constant determined from the data (solid line in A), whereas the synthesis rate (I) was modeled according to Equations 15 to 17 (dashed line in A). In scenario 2 (D–F), G_V was varied in accordance with the measurements in the field (solid line in D), whereas I was as in scenario 1. In scenario 3 (G–I), G_V followed the data, and the linalool synthesis rate was assumed to be proportional to actual G_V, i.e. the rate of synthesis is equal to G_V/G_V,maxI, where I is the rate of synthesis predicted in A and D and G_V,max is the maximal G_V observed during the day. Solid lines in simulated linalool emission rate (B, E, and H) and liquid pool size (C, F, and I) plots are predicted for a temperature-dependent H (inset in F). The punctuated lines in E, H, F, and I demonstrate the hypothetical system dynamics for a constant H of 2.078 Pa m³ mol⁻¹. In simulations, the initial liquid phase pool size at 0 h was taken equal to that at 24 h. The emission factor (F_S) was determined from the measurements between 9 and 12 h.

Figure 9.

Measured (Fig. 4C, dots) and simulated (Eqs. 12–14, lines) diurnal variability in trans-β-ocimene emission rates (A) and liquid pool sizes (B) in P. pinea. The synthesis of trans-β-ocimene was predicted as in Figure 8A, and the G_V was either as in Figure 8A (dotted line in B) or changed according to data (solid line in A and B). The estimates of trans-β-ocimene emission rate did not differ for these scenarios, and thus, only a single line is provided in A.

In the first scenario (Figs. 8, A–C, and 9), we assumed no diurnal decline in G_V (Fig. 8A) while keeping the synthesis at a maximal potential rate determined by actual leaf temperature and incident irradiance (Fig. 4, C and F; Eqs. 15–17). In the second scenario (Figs. 8, D–F, and 9), G_V tracked the actual measurements while the synthesis rates were not modified by stomata. In the third scenario (Fig. 8, G–I), the diurnal variation in G_V followed the data, and the synthesis rate was set proportional to G_V.

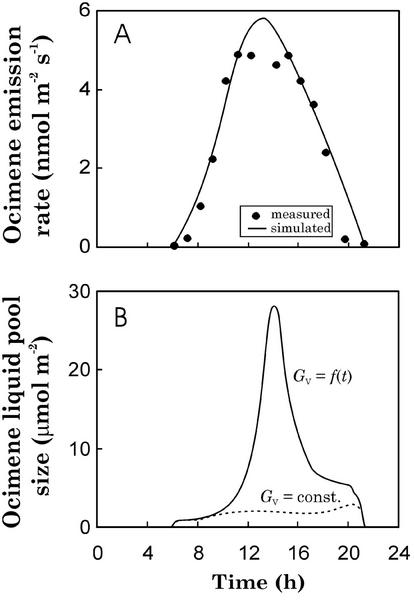
Scenario 1 (Figs. 8, A–C, and 9) demonstrates that without G_V limitations, both linalool and trans-β-ocimene emission rates closely follow the rates of their synthesis. The second scenario (Figs. 8, D–F, and 9) suggests that stomata may significantly modify the emission rates of linalool. As the stomata close in midday, the half-time of the liquid pool (τ_L) increases from 502 to 3,040 s, indicating that the liquid phase linalool pool (Fig. 8F) rises more slowly than the changes in G_V occur, leading to a midday depression in the emission rates. Yet after a moderate increase in stomatal openness, the suppression is followed by a burst of linalool emission that temporarily exceeds the synthesis rate (Fig. 3). No effect of G_V is observed for trans-β-ocimene because the increase in gas phase pool of this monoterpene immediately balances changes in G_V (Fig. 9).

However, scenario 2 overestimated the emission rates at low values of G_V, hinting at simultaneous changes in linalool synthesis rates with G_V. The hypothesis of declining synthesis rates was further strengthened by excellent fits to the data when the linalool synthesis rate was set proportional to G_V (Fig. 8, G–I). Thus, these simulations suggested that both stomatal and biochemical constraints modified the linalool emission from the leaves.

The latter model is supported by good fits to diurnal time courses of monoterpenoid P_i (Fig. 10), which determines the gradient for monoterpenoid diffusion from intercellular air space to the outside air. There was a moderate midday overestimation of P_i for trans-β-ocimene (Fig. 10B) that resulted from the higher predicted emission rates during this period (Fig. 9A). This may indicate that the trans-β-ocimene synthesis rate was also somewhat down-regulated compared with the potential rate predicted by the empirical model (Eqs. 15–17). However, given that the needle inclination angles were vertical but the light sensor was arranged horizontally, this may also be associated with a midday overestimation of incident quantum flux densities on needle surface (Staudt et al., 1997).

Figure 10.

Linalool (A) and trans-β-ocimene (B) P_i values during August 3 (emission data in Fig. 4, C and F). The partial pressure was determined according to Equation 2 (measured) or from Equation 8 using the simulations in Figures 8, G to I, and 9 (G_V changed to track the measurements). P_i is the intercellular partial pressure in equilibrium with cell wall monoterpene concentrations. The total emission data are depicted in Figure 4, C and F.

The evidence that the P_i values of linalool (Fig. 10A) and 1,8-cineole were constant in midday and did not balance the decreases in G_V that would have been expected for a constant synthesis rate (Fig. 8, D–F) further suggests that stomatal closure, accompanied by monoterpene build-up in the liquid phase, may potentially shift the chemical equilibrium between the production and interconversion of specific monoterpenoids or lead to changes in gene expression and/or changes in activity profiles of multiple terpene synthases.

In these simulations, the H of linalool was expected to vary from 1.46 to 5.32 Pa m³ mol⁻¹ for a diurnal variability in temperature from 20.3°C to 38.4°C (compare Fig. 4A with Fig. 8F, inset). For trans-β-ocimene, H was predicted to change from 2,520 to 6,620 Pa m³ mol⁻¹ for the same temperature range. Given that the exact temperature relationships of H are not available for these compounds, we also considered the hypothetical situation with an invariable H in scenarios 2 and 3 (Fig. 8F, inset) to determine the potential temperature effect on emission dynamics attributable to varying H (supplemental data can be viewed at www.plantphysiol.org). These simulations indicate that a smaller increase in H is compatible with a more efficient stomatal control of linalool emission in midday but also with a greater linalool burst in response to an increase in stomatal openness (Fig. 8E). A similar modification of the emission dynamics is also observed for the scenario 3 (Fig. 8H), but the effect is damped because of a lower liquid pool of linalool than that in the scenario 2 (Fig. 8, D–F).

Implicit in these calculations was the assumption that the production of oxygenated and nonoxygenated compounds can be described by the same light and temperature algorithms (Eqs. 15–17), allowing the estimation of the basal emission factor, F_S (Eq. 15) from emission measurements between 9 and 12 am for all compounds. Given that there may be a burst of emission of monoterpenoids with a low H after increases in stomatal opening (Fig. 3A), the high morning rates of linalool and 1,8-cineole emission (Fig. 4, E and F) may also partly rely on the decay of the liquid phase monoterpenoid pool retained over or accumulated during the night. However, such an mechanism would imply that there is a moderate linalool and 1,8-cineole emission rate in the darkness, which either decreases during the night as the liquid phase pool present after stomatal closure is depleted or increases as the monoterpenoids accumulate in the leaf (Fig. 4A). Given that the emission rates of oxygenated monoterpenoids were essentially zero during the night (Fig. 4), we consider this mechanism unlikely.

DISCUSSION

Diurnal Variability in Monoterpenoid Emission Rates

The current study demonstrated a strong midday decline in the emission rates of oxygenated monoterpenoids linalool and 1,8-cineole in water-stressed needles (Fig. 4, E and F) but no apparent decrease in the efflux rates of other compounds (Fig. 4, C and D). A strong decrease in the emission of linalool, 1,8-cineole, and total monoterpenoids (Fig. 5) clearly indicates that the emission algorithm driven by light and temperature only (Eqs. 15–17) is an oversimplification and does not allow reproduction of the diurnal emission courses of monoterpenoids in P. pinea.

The decline in the emission rates of oxygenated monoterpenoids was accompanied by decreases in G_V and decreases in net carbon assimilation rate (Fig. 4B). Because a certain fraction of emitted plant monoterpenoids is always synthesized in chloroplasts (Chappell, 1995) and the synthesis of isoprenoids may rely on a small pool of photosynthetic intermediates (Loreto et al., 1996a; Zimmer et al., 2000), monoterpenoid emission rates often scale positively with carbon assimilation rates (Kesselmeier et al., 1996; Loreto et al., 1996b). Thus, the diurnal decline in monoterpenoid emission rate may have resulted from daily decreases in foliar net carbon assimilation rates. However, this suggestion does not explain away the insensitivity of limonene and trans-β-ocimene to net photosynthesis rates and to G_V. Furthermore, recent evidence indicates that the rates of monoterpenoid synthesis may be more closely controlled by the rate of photosynthetic electron transport, i.e. the availability of NADPH and ATP in chloroplasts (Niinemets et al., 1999, 2002a, 2002b). Photosynthetic electron transport is relatively insensitive to G_V because photorespiration may effectively substitute for carbon assimilation as an electron sink in water-stressed leaves with closed stomata, thereby avoiding down-regulation of photosynthetic electron transport rates (Kozaki and Takeba, 1996). The control of potential monoterpenoid synthesis rates by photosynthetic electron transport and the close to immediate rise in monoterpene partial pressure after a decrease in stomatal openness is likely the mechanistic explanation of the lack of midday decline in the efflux of the compounds with a high value of H such as limonene and trans-β-ocimene as demonstrated by our simulations (Figs. 2, 3, and 9). Thus, the results of these simulations, quantitatively describe the hypothesis of Sharkey (1991) and Fall and Monson (1992). However, this mechanism cannot account for the stomatal sensitivity of VOC emission observed for linalool and 1,8-cineole in our study.

Explanation of the Stomatal Sensitivity of Oxygenated Compounds

The circumstance that stomata cannot limit the emission over the long term does not mean that they cannot control the emission at all. In fact, slow turnover of leaf liquid phase in compounds that preferably partition to aqueous phase may result in a limited rise of gas phase volatile concentrations and strong temporal stomatal limitations as simulated in Figure 3.

In the current study, there were strong positive correlations between G_V and linalool and 1,8-cineole emission rates (Fig. 6, C and D). According to simulations (Figs. 8–10), the slow rise in the monoterpenoid P_i (Fig. 8, D–F) partly explained the midday decline in linalool and 1,8-cineole emission rates. However, for a constant rate of synthesis, the P_i values would have risen to a value supporting high flux rates in the afternoon, indicating that the sustained stomatal limitation is not possible over the entire day for these compounds (Fig. 8E). Thus, our model analyses provide indirect evidence that the synthesis rates of these two monoterpenoid also declined (Fig. 8, G–I) with decreasing G_V. More than 1,000-fold higher linalool and 1,8-cineole liquid phase concentrations than limonene and trans-β-ocimene concentrations would have been necessary to overcome the stomatal limitations (compare Fig. 8F with 9B). Although the reductive equivalents and carbon were apparently available to maintain the synthesis at a constant level, high chloroplastic concentrations of linalool and 1,8-cineole apparently inhibited further enzymatic conversion of monoterpenoid precursors to these compounds.

Apart from our study, there is currently conclusive experimental evidence of a strong stomatal sensitivity of methanol emission (Nemecek-Marshall et al., 1995). Given the H values of 0.0132 Pa m³ mol⁻¹ for acetic acid, 5.23 Pa m³ mol⁻¹ for acetaldehyde, and 0.461 Pa m³ mol⁻¹ for methanol (Staudinger and Roberts, 1996), effective stomatal control over the rates of emission of these compounds is expected (Fig. 3). Kesselmeier et al. (1997) observed a large midday depression paralleling changes in G_V in the efflux rates of acetic and formic acids and of the respective aldehydes from the foliage of P. pinea. Possibly because of larger stomatal sensitivity, the isoprene emission algorithm of Guenther et al. (1993), which does not consider stomatal effects on emission, predicted emission rates with much greater uncertainty for organic acids (average error 40%) and aldehydes (65%) than the emissions of total monoterpenoids (28%; Kesselmeier et al., 1997), where the contribution of oxygenated compounds was relatively low.

Overall, the stomatal effects are apparently more important than has been acknowledged so far. For example, in deserts, the emission rates are low during drought periods (Winer and Karlik, 2001), but there is often a burst of smell just before a rain. Such a phenomenon can be explained within our modeling framework by stomatal opening attributable to increasing humidity as the rain is approaching. Because in a closed-stomata situation, there is an extensive gas and liquid phase pool within the leaves, a burst of emission is expected for fragrant compounds such as linalool, 1,8-cineole, camphor, thymol, and other oxygenated monoterpene derivatives that may be emitted in trace quantities in steady-state situations (Fig. 3). Such burst of emission have been observed previously for alcohols (Nemecek-Marshall et al., 1995) and aldehydes (Holzinger et al., 2000) but could not be explained by current steady-state emission models.

Diurnal Changes in Monoterpenoid Composition

Composition of monoterpenoids emitted may change during the day (Staudt et al., 1997, 2000) and during the season (Llusiá and Peñuelas, 2000; Staudt et al., 2000). Both seasonal (Table II) and diurnal changes (Fig. 7) in monoterpenoid composition were observed in our study. In particular, the fraction of oxygenated monoterpenoids linalool and 1,8-cineole had a pronounced midday minimum, whereas the fractions of trans-β-ocimene and limonene were generally highest in midday. Because the gas phase rate coefficients (Meylan and Howard, 1993) for reactions with ozone (K_O3) and hydroxyl radicals (K_OH) differ for various monoterpenoids, the changes observed in monoterpenoid fractional composition have a direct bearing on atmospheric chemistry.

The fraction of acyclic monoterpenoids (sum of the fractions of linalool, myrcene, and trans-β-ocimene) emitted increased during the day, but a reverse correlation was observed between the fractions of linalool and trans-β-ocimene (Fig. 7C). The decrease in emission of linalool during the day was accordingly compensated by increases in the emission of more volatile trans-β-ocimene and myrcene. This may indicate that the reactions leading to linalool and trans-β-ocimene are tightly linked and that their synthesis is regulated in a coordinated manner.

Overall, single monoterpenoid synthases catalyze the multistep reactions leading from the common monoterpene precursor geranyl-pyrophosphate (GPP) to monoterpenoids (Croteau, 1987; Gershenzon and Croteau, 1993; Steinbrecher and Ziegler, 1997). Given that the first step, isomerization of GPP to linalylpyrophosphate, is common for both the synthesis of trans-β-ocimene and linalool, binding of the GPP to a respective terpene synthase may control the product formation. Thus, selective inhibition of linalool synthase activity, e.g. as the result of accumulation of linalool because of stomatal closure, may favor trans-β-ocimene synthesis. So far, the empirical data to support such a substrate level inhibition are scarce, and discrimination between various hypotheses of regulation of stoichiometry of emitted compounds warrants further detailed experimental study. Nevertheless, our study suggests that synthesis of certain monoterpenoids may be selectively inhibited by stomatal closure, leading to a compensatory synthesis of other compounds. In conditions of low volatilization rates of linalool, the whole-reaction pathway may shift toward synthesis of trans-β-ocimene, thereby explaining the observed negative relationship between these compounds (Fig. 7C).

CONCLUSIONS

Analyses of daily time courses of VOC emissions by dynamic models allow gaining fundamental insight into diurnal variabilities in synthesis and emission rates of various volatiles. According to our simulations, the gas pool is very fast for all compounds, and the assumption of a steady state in the gas phase is justified for analyses of the emission responses to stomatal openness. However, the turnover rates of leaf liquid pools differ dramatically among various compounds (Fig. 3). Because stomatal resistance is always finite, stomata may exert a control over VOC efflux from the foliage for minutes to days depending on the H values of specific compounds. Our study provides experimental evidence and a theoretical explanation of strong stomatal sensitivity of emission of oxygenated volatiles from the leaves of plants. Because many important emitting plant species grow in habitats where water stress regularly occurs and because there are also characteristic diurnal variation patterns in G_V in non-stressed conditions, our results have major implications for the application and modification of current emission models. Although the simple emission algorithms may provide reasonable fits for the daily average emission rates, accurate simulation of diurnal courses of emission and monoterpenoid composition is extremely relevant for the prediction of atmospheric reactivity. We conclude that stomatal effects on emission of compounds with a low H such as alcohols, aldehydes, carboxylic acids, and oxygenated monoterpenoids are significant under realistic values of G_V and must be accounted for in the further models of plant VOC fluxes. As our study demonstrates, a model including the liquid to gas phase monoterpenoid partitioning may provide a valuable tool to differentiate between stomatal and biochemical controls on monoterpenoid emission.

MATERIALS AND METHODS

Dynamic Model of Monoterpene Emission

Steady-State Monoterpene Emission Rates

Because monoterpenes are mainly emitted through the stomata, we relate terpene flux (F, nmol m⁻² s⁻¹) from the leaves to stomatal conductance (Tingey et al., 1991) by an equation analogous to that previously employed for CO₂ diffusion into the leaf (Farquhar and Sharkey, 1982; Field et al., 1989):

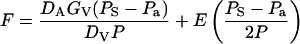1

where D_A (m² s⁻¹) is the air phase diffusion coefficient for specific monoterpene (Table I) and D_V that for water vapor (m² s⁻¹), G_V is stomatal conductance for water vapor (mmol m⁻² s⁻¹), P_S is the monoterpene partial pressure in substomatal cavities, P_a is the monoterpene partial pressure in the ambient air (Pa), P is the total air pressure, and E is the leaf transpiration rate (mmol m⁻² s⁻¹). The first part of the equation describes the control of F by stomata, and the second part of the flux results from mass flow attributable to net water efflux through the stomata. From Equation 2, the steady-state P_S is given by:

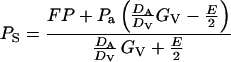2

The transpiration correction to the entire flux is generally small. For example, for a typical non-stressed actively transpiring leaf with a G_V of 200 mmol m⁻² s⁻¹, and moderate water vapor pressure deficit of 1.7 kPa, E equals to 3.4 mmol m⁻² s⁻¹, and the flux attributable to mass flow is 120 times less than the flux attributable to diffusion through the stomata. In a situation with closed stomata, the mass flow correction may be larger because of the rise of water vapor pressure deficit and E as the result of an increase in leaf temperature. However, even for a high vapor pressure deficit of 5 kPa and low G_V of 5 mmol m⁻² s⁻¹, the mass flow correction is less than 2.5%. Thus, for simplicity, we neglect the contribution of mass flow. Further considering that no terpene build-up generally occurs in the boundary layer as well as in the ambient air, P_a is practically zero under natural conditions. Thus, Equation 2 simplifies to:

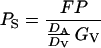3

In addition to stomatal conductance, the gas phase monoterpene flux is also limited by the compound diffusion from the outer surface of cell walls to substomatal cavities. This part of the diffusion pathway is determined by the intercellular gas phase conductance, G_ias. For the two conductances in series, the total gas phase diffusion conductance is given as:

4

The internal conductance, G_ias, essentially measures the average path-length from outer surface of cell walls to substomatal cavities (supplemental data can be viewed at www.plantphysiol.org) and differs between various monoterpenoids because of differing binary diffusion coefficients in air (Table I). The flux from the outer surface of the cell walls to the ambient air is further given as:

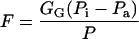5

where P_i is the steady-state intercellular partial pressure of the volatile.

Analogously to CO₂ diffusion (Laisk and Oja, 1998), we express the monoterpene efflux from the site of synthesis in chloroplasts to substomatal cavities, F_m, as:

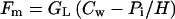6

where G_L is the liquid phase diffusion conductance (meters per second) for specific volatile from the site of synthesis to the outer surface of cell walls, C_w is the liquid phase monoterpene concentration in the site of synthesis (mol m⁻³). H, the Henry's law constant (Pa m³ mol⁻¹; Table I), is the equilibrium air-water partition coefficient, which for dilute aqueous solutions is defined as (Staudinger and Roberts, 1996):

7

where C_a (mol m⁻³) is the liquid phase monoterpene concentration at a monoterpene partial pressure of P_i. For environmental applications, aqueous solutions with less than 0.001 to 0.01 mol fraction of solute are considered dilute (Staudinger and Roberts, 1996). Use of H values is justified for all of the 19 monoterpenoid species emitted by Pinus pinea (Staudt et al., 1997), because the aqueous solubility of these compounds is typically in the range of 10⁻⁶ to 10⁻⁷ mol fraction at 25°C, and for the most soluble monoterpenoid emitted—1,8-cineole—the solubility is 3.44 × 10⁻⁴ mol fraction at 25°C (Table I; for the solubility data, see Staudinger and Roberts, 1996).

The internal liquid phase diffusion conductance, G_L, is a composite conductance consisting of several conductances in series. This conductance is determined by the monoterpenoid liquid phase diffusion coefficient (Table I), permeabilities of plant membranes, and leaf anatomical characteristics. Supplemental data of calculation of the internal conductances of the diffusion pathway can be viewed at www.plantphysiol.org, and the diffusion conductances used in current simulations are provided in Table I. The values of G_L vary because of varying liquid phase diffusion coefficients, but also because of differing membrane permeabilities of monoterpenoids. As the sensitivity analyses demonstrate (Ü. Niinemets and M. Reichstein, unpublished data), the dynamics of the VOC emission rates are not very sensitive to large changes in internal leaf conductance.

Dynamic Model of Monoterpene Diffusion through the Stomata

Given that the rate of monoterpene synthesis, I, is unaffected by modifications in gas phase conductance (G_G, Eq. 4), I is equal to the diffusion flux density through the stomata and mesophyll in a steady-state situation, i.e. F = F_m = I (Eqs. 5 and 6). This means that any change in G_G is balanced by an appropriate change in P_i such that F is equal before and after stomatal closure and that there could be no stomatal control on F in the steady state. Stomata may accordingly curtail F only in a non-steady-state situation, and the vital question to solve is how fast the leaf reaches a new steady state after a change in G_G.

To simplify the analysis, we consider gas (S_G, nmol m⁻²) and liquid (S_L, nmol m⁻²) pools for each monoterpenoid, and use the mass balance approach to describe the dynamics of the pools (Fig. 1). The size of the gas pool is determined as:

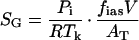8

where R is the gas constant (8.314 J mol⁻¹ K⁻¹), T_k is leaf temperature (K), V (m³) is leaf volume, A_T total leaf surface area, and f_ias the fraction of gas volume in total leaf volume. Thus, f_iasV/A_T gives the intercellular leaf volume per leaf surface area. The liquid pool size is given as:

9

where f_w is the liquid fraction of total leaf volume. All leaf structural data needed for model parameterization for P. pinea are provided in the electronic supplement, which can be viewed at www.plantphysiol.org.

Dynamics of the Gas and Liquid Phase Pools

Combining Equations 5 and 8, assuming that P_a is negligible, and revealing F leads to a first order kinetics of the gas pool:

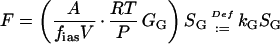10

where k_G (s⁻¹) is the rate constant of the gas phase, and the half-time of the gas pool, τ_G, is:

11

The following analysis may be significantly simplified if we could consider S_G as essentially in a steady state, i.e. if the values of τ_G are very small relative to the time constants of stomatal closure and opening. According to the “Results” (Fig. 2), the gas phase pool half-time is on the order of seconds. Given that the half-time of stomatal movements is on the order of minutes (Tinoco-Ojanguren and Pearcy, 1993), the gas phase is effectively in a steady state. Thus, F_m = F, allowing the substitution of P_i from Equation 5 into Equation 6, giving:

12

Replacing C_w = S_LA/(f_wV) from Equation 9 in Equation 12, the governing differential equation becomes:

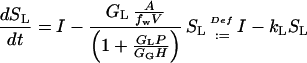13

The product k_LS_L is the flux into the gas pool and, because the gas pool is in a steady state, also the emission flux. Thus, the efflux from the liquid pool obeys a first order kinetics, where the rate constant k_L depends on the G_L and G_G and on the H. The analytical solution of this differential equation is:

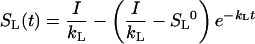14

with S_L⁰ being the pool size at t = 0. The analytical solution is applicable for simulations with a constant k_L and I. In all other cases, numerical solutions were employed.

Field Measurements

Study Site, Foliar Monoterpenoid Emission, and CO₂ and H₂O Exchange Measurements

The research was conducted at Castelporziano (Rome, 41°45′N, 12°26′E) mixed evergreen forest in frames of the Biogenic Emissions in the Mediterranean Area (BEMA) project (see Seufert et al., 1997). Enders et al. (1997) provide a detailed description of the stand, which is dominated by P. pinea (50%–60% coverage) and Quercus ilex (10%–20% coverage). Some of the results of the Castelporziano field campaigns have been published previously (Staudt et al., 1997). The current study analyses data from intensive field campaigns conducted by the Environment Institute, Joint Research Centre of the European Commission, Italy (JRC) (Bertin et al., 1997; Staudt et al., 1997) during June 1 to 14, 1993; May 5 to 28, 1994; July 31 to August 6, 1994; and October 23 to 27, 1994.

The techniques for foliar photosynthesis and transpiration and terpenoid emission measurements have been reported in full detail in Bertin et al. (1997) and in Staudt et al. (1997). The cylindrical gas exchange chambers (volume of either 0.02 or 0.05 m³) consisted of a Plexiglas frame supporting a 50-μm-thick, transparent Teflon foil (Nowofol Kunststoffprodukte, Siegsdorf, Germany). The chambers were installed on proximal branch positions in the upper crown at a height of 9 m in the forest of 8 to 12 m total height. The cuvettes enclosed 0.1 to 0.4 m² of total needle surface area, and multiple trees were sampled simultaneously. Depending on chamber size, the flow rate of charcoal-filtered ambient air (CO₂ concentrations around 350 μmol mol⁻¹) was maintained at 0.03 to 0.06 m³ min⁻¹ with a thermal mass flow controller (MKS Instruments, Andover, MA) to yield a mean air residence time of 0.5 to 2 min. Chamber inlet and outlet CO₂ concentrations were determined with an infrared CO₂ analyzer (BINOS 100, Fisher-Rosemount, Hasselroth, Germany) operated in an absolute mode, and water vapor concentrations were measured with a set of dew point mirrors (MTS-2, H. Walz, Effeltrich, Germany). Foliar gas exchange parameters were computed according to von Caemmerer and Farquhar (1981). Needles enclosed in the cuvette were harvested at the end of the measurement campaign, and the projected surface area was measured with an optical planimeter (Delta-T, Cambridge, UK). An experimentally determined total to projected needle area ratio of 2.25 was used to convert the projected areas to total needle area (Staudt et al., 1997), and foliage photosynthesis rates, G_V values, and monoterpenoid emission rates were expressed on the total area basis.

Several labs participated in monoterpenoid sampling from the chamber air and latter monoterpenoid determination. In the current study, the data provided by the JRC, by the Universite Joseph Fourier, Groupe de Recherche sur l'Environnement et la Chimie Appliquée, Grenoble, France (GRECA), and by the Institut National Polytechnique, Ecole Nationale Supérieure de Chimie de Toulouse, France (ENSCT), were used. A comparison with blind monoterpene mixtures between these three and seven other laboratories participating in the BEMA project revealed that the analytical monoterpene sampling and analysis methods allowed efficient detection of most monoterpenes emitted by plants in all laboratories (Larsen et al., 1997). Despite qualitatively similar results, there were occasionally relatively large differences in absolute amounts of various monoterpenoids determined (Larsen et al., 1997). Therefore, we used only complete daily time courses sampled and analyzed by the same group.

Bertin et al. (1997; see also Larsen et al., 1997) gives an overview of the monoterpenoid determination methods employed by JRC, GRECA, and ENSCT. We provide here the outline of the analytical methods for all of these groups, and we provide details of the JRC group protocols, because our conclusions primarily rely on these data. In all cases, monoterpenoids were trapped with Tenax TA adsorbent resin (20–35 mesh, surface area of 35 m² g⁻¹; Alltech Associates, Deerfield, IL). Tenax TA was selected because it has been demonstrated to completely adsorb all plant monoterpenoids and to release them by thermal desorption without decomposition (Ciccioli et al., 1992). Either glass (JRC) or stainless steel tubes (GRECA) were used for trapping, and the gas-chromatographic analysis with flame ionization detector was independent of trapping and was conducted later in the laboratory (JRC and GRECA). On-line gas-chromatographic analysis including an automated adsorption-desorption device was alternatively employed (ENSCT). To avoid adsorbent trap breakthrough, the air flow rate through the sampling tube was controlled at 0.15 to 0.2 dm³ min⁻¹, and 3 to 6 L of air was sampled. Thus, each sample was a weighted average of a 15- to 40-min time period. Given also the 5- to 10-min bypass periods before and after sampling, one or two samples per hour were obtained. Gas chromatographic analysis (gas-chromatograph CP9001, Chrompack, Varian Medical Systems, Palo Alto, CA) of samples by the JRC group included precooling at −100°C for 3 min, desorption at 200°C (TCT/PTI CP4001, Chrompack) for 10 min, and injection at 200°C for 1 min. After injection, the 25-m column (0.32-mm capillary column coated with 1.2-μm Chrompack CP-Sil 8 CB) was maintained at 65°C for 4 min, followed by 2.5°C min⁻¹ to 80°C, 2.0°C min⁻¹ to 100°C, and 20°C min⁻¹ to 240°C. Purified monoterpene standards (Aldrich Chemie, Steinheim, Germany) were used for monoterpenoid identification and calibration (Bertin et al., 1997). Overall, the detection limit was less than 1 pmol m⁻² s⁻¹ for all monoterpenoids.

Empirical Fitting of Diurnal Courses of Monoterpenoid Emission

Because the monoterpene emission rates depend both on incident quantum flux density and temperature in P. pinea (Staudt et al., 1997; Sabillón and Cremades, 2001), we employed an empirical emission algorithm of Guenther et al. (1993), which has been demonstrated to successfully simulate isoprene emission in a broad variety of species (Guenther et al., 1993) as well as monoterpenoid emission rates in Q. ilex (Bertin et al., 1997; Ciccioli et al., 1997). In P. pinea, the application of the isoprene emission algorithm is supported by close to zero monoterpene emission rates at night, indicating that the efflux from the storage pools contributes negligibly to the total emission rate.

According to the model, the emission rate of a specific monoterpenoid, F (nmol m⁻² s⁻¹), is given as:

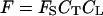15

where C_T is the temperature correction factor, C_L is the light correction factor, and F_S is the basal emission rate measured in standard conditions (emission factor). As a rule, F_S is estimated at a leaf temperature (T_L) of 30°C and incident quantum flux density (Q) of 1,000 μmol m⁻² s⁻¹. Implicit in Equation 15 is that stomata exert no control over monoterpenoid emission. We use the equation of Tingey et al. (1980) for C_T:

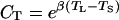16

where T_S is the leaf temperature in standard conditions (30°C), and β an empirical parameter determining the shape of the F versus T_L response curve. Although the values of β may vary depending on the physicochemical properties of specific monoterpenoids as well as temperature characteristics of various monoterpenoid synthases, an estimate of β = 0.09°C⁻¹ appears applicable for a wide range of species and monoterpenoids (Guenther et al., 1993) and was used in the current study. The original model (Guenther et al., 1993) includes a more complex five-parameter temperature function to describe the decrease of emission rates in supra-optimal temperatures. However, we favor Equation 16 in our model exercise, because no appreciable decrease in emission rates was observed even under the highest temperatures of 35°C to 40°C during the measurements in conditions of high soil water availability. The light correction factor is calculated as:

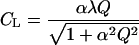17

where α and λ are empirical parameters describing the shape of the F versus Q response curve. We used values of α = 0.0027 and λ = 1.066, which were originally determined for isoprene-emitting species (Guenther et al., 1993) and later demonstrated to provide good fits to monoterpenoids emitted by Q. ilex (Ciccioli et al., 1997). Having determined C_T and C_L, the emission factor (F_S, Eq. 15), was computed as an average for the entire measurement campaign using the morning measurements (9 am–12 pm).