Abstract
We describe a novel method for jointly estimating crossing-over and gene-conversion rates from population genetic data using summary statistics. The performance of our method was tested on simulated data sets and compared with the composite-likelihood method of R. R. Hudson. For several realistic parameter values, the new method performed similarly to the composite-likelihood approach for estimating crossing-over rates and better when estimating gene-conversion rates. We used our method to analyze a human data set recently genotyped by Perlegen Sciences.
MEIOTIC recombination is a fundamental biological mechanism that leads to the exchange of genetic material between homologous chromosomes. This process is believed to be associated with some important cellular functions such as the formation of synaptonemal complex and proper chromosomal segregation at the time of meiosis. In evolutionary biology, recombination is important because it generates novel allelic combinations and increases the genetic diversity within a population. The knowledge of how recombination levels vary across a genome is crucial for the design of association-mapping studies as well as evolutionary inference studies and is also of interest from the point of view of basic molecular biology. Therefore, characterizing this variation in the human genome has been the focus of several current research efforts (e.g., Crawford et al. 2004; McVean et al. 2004; Fearnhead and Smith 2005; Jeffreys et al. 2005; Myers et al. 2005). In particular, such studies have been extremely useful for detecting recombination hotspots across the genome as well as in identifying sequence features that are associated with them.
Recombination rates can be estimated using a variety of techniques, such as sperm typing (e.g., Jeffreys et al. 2001), pedigree studies (e.g., Kong et al. 2002), and population genetic methods. Although sperm typing can provide estimates at the finest possible resolution, it is currently not practical for whole-genome studies. Existing pedigree studies, on the other hand, can offer whole-genome coverage but cannot provide the required resolution (i.e., at the kilobase scale). Therefore, population genetic approaches have proved to be valuable. These are faster and easier to implement than sperm-typing techniques and can offer much higher resolution than is possible from current pedigree studies.
Population genetic methods use polymorphism data from DNA sequences sampled from a population. They infer the population-scaled recombination rate ρ (= 4Nr) (where N denotes the effective population size and r denotes recombination fraction) on the basis of simplified models of population evolution. ρ estimation is a well-studied problem in the field of population genetics and many different estimators are currently available. The simplest methods are based on ad hoc moment estimators. These are quick and easy to compute but are inaccurate since they do not use the available information efficiently (e.g., Hudson 1987; Hey and Wakeley 1997; Wakeley 1997). In contrast, full-likelihood methods are elegant (Griffiths and Marjoram 1996; Kuhner et al. 2000; Nielsen 2000; Fearnhead and Donnelly 2001) and make full use of the available haplotype information, but prove to be computationally infeasible for larger data sets (e.g., >15-kb regions in humans). To overcome both these limitations, several practically useful compromise approaches have been proposed. These approaches try to avoid the computational expense of calculating exact likelihoods for the observed data while maintaining some likelihood-based framework (e.g., Wall 2000; Hudson 2001; Fearnhead and Donnelly 2002; Li and Stephens 2003; Wall 2004).
The method used in Wall (2000) involves describing data sets with one or more summary statistics and then performing maximum-likelihood inference using the reduced data. The success of this approach depends on finding summaries that efficiently collect information from the data. The combination of the number of distinct haplotypes and the minimum number of inferred recombination events (Hudson and Kaplan 1985) has been found to work reasonably well (Wall 2000; Hudson 2001).
The methods described by Hudson (2001), Fearnhead and Donnelly (2002), and Wall (2004) utilize composite likelihoods. In this approach, we break a data set into smaller subsets, calculate full likelihoods for these subsets, and then multiply these likelihoods together to get “composite” likelihoods. For example, Hudson's method calculates the likelihoods of the haplotype configurations for all possible SNP pairs and multiplies these likelihoods together. Theoretical results show that a simple modification to this method, where SNP pairs are given weights that decay with the distance between them, can give a consistent estimator of the recombination rate (Fearnhead 2003). The composite-likelihood curve can provide a good point estimate of ρ. Because there is dependency between the subsets, standard asymptotic maximum-likelihood assumptions do not apply and therefore the uncertainty in estimates has to be calculated from simulations. The method of Wall (2004) is similar to the method of Hudson (2001) but considers all triplets of sites instead of pairs. The Fearnhead and Donnelly (2002) method is slightly different from the other two methods and calculates full likelihoods for small nonoverlapping windows along the sequence.
An alternate approach, proposed by Li and Stephens (2003), consider the likelihood of ρ for a given data set as a product of the conditional distributions of observing a haplotype, given a subset of the other haplotypes. If H1, H2, …, Hn denotes a sample of n haplotypes, then
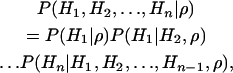 |
where P denotes likelihood. Li and Stephens then describe computationally tractable approximations for the conditional distributions on the right-hand side and estimate ρ by maximizing their product. Since this method is sensitive to the order in which the haplotypes are considered, the authors estimated their likelihoods by averaging over several possible orders. There are no theoretical results available for this method.
Many of the estimation methods mentioned previously assume that recombination happens only in the form of crossing-over events. However, this model is not biologically realistic. Current meiotic recombination models allow for two different kinds of events (e.g., Szostak et al. 1983). We call these two forms of recombination “crossing over” and “gene conversion,” respectively. Crossing over refers to the reciprocal exchange of large chromosomal fragments whereas gene conversion refers to short exchanges between chromosomes that are not accompanied by crossing over. Theoretical results that incorporate both these mechanisms have been developed before (e.g., Andolfatto and Nordborg 1998; Wiuf and Hein 2000). Using these models, it is possible to generalize the composite-likelihood approach of Hudson (2001) for estimating both crossing-over and gene-conversion rates (e.g., Frisse et al. 2001; Ptak et al. 2004). To do so, it is only necessary to specify the effective recombination rate between a pair of sites (from both crossing over and conversion) as a function of distance (e.g., Andolfatto and Nordborg 1998 or Langley et al. 2000). The method of Wall (2004) can also be used for jointly estimating both crossing-over and gene-conversion rates and has been shown to give more accurate estimates than the method of Hudson (2001).
In this article, we introduce a novel method for jointly estimating both crossing-over and gene-conversion rates from single-nucleotide polymorphisms (SNPs) using summary statistics. We first tested the performance of this method on simulated data sets and compared it with that of the composite-likelihood approach (Hudson 2001). For this comparison, we simulated both phased and unphased data with uniform and nonuniform recombination rates along the sequence. We then applied our method to a human data set recently genotyped by Perlegen Sciences (Hinds et al. 2005).
MATERIALS AND METHODS
Summary statistics method:
Our approach to estimating recombination rates from SNPs is similar to that of Wall (2000) and we describe a data set with multiple summary statistics and then perform maximum-likelihood inference using the reduced data. The summaries used here are similar to the ones described in Padhukasahasram et al. (2004) for estimating gene-conversion rates alone. These were based on multilocus linkage patterns that are indicative of conversion events in short-range data. Here, we extend this approach for jointly estimating both gene-conversion and crossing-over rates from haplotype and genotype data.
In the summary statistics method, we first define patterns for SNPs on the basis of the absolute value of pairwise D′ (D′ denotes the normalized measure of linkage disequilibrium, LD). For example, for a pair of SNPs A and B, D′(AB) < 1.0, D′(AB) < 0.5, D′(AB) < 0.1, etc., denote patterns. Similarly, for three SNPs A, B, and C, D′(AB) < 1.0 and D′(BC) < 1.0, D′(AB) < 0.5 and D′(BC) < 0.5, etc., denote patterns. Informally, we try to summarize the distribution of LD levels for all triplets or pairs of SNPs within a data set by calculating the fraction that show any particular pattern. Since our summary statistics are based on all triplets or pairs, our method uses approximately full sequence information. Note that the expectation of pairwise D′ and its distribution depends on the underlying recombination rate. So, the probability of observing a given pattern increases monotonically with the recombination rate.
Coestimating crossing-over and gene-conversion rates:
Although both mechanisms of recombination lead to the decay of LD, the effects of crossing over and gene conversion are qualitatively different. While the rate of decay of LD by crossing over increases as the distance between the markers increases, with gene conversion it is independent of distance for markers that are sufficiently far apart (Wiehe et al. 2000). Therefore, the effects of gene conversion are significant only for short-range markers whereas the effects of crossing over dominate for long-range markers (Andolfatto and Nordborg 1998; Wiehe et al. 2000). To jointly estimate both these parameters, we collect summary statistics from both long-range and short-range data. This allows us to distinguish models with gene conversion from those with crossing over alone.
For all the data sets considered here, we estimated rates using the following patterns:
For three SNPs A, B, and C, ordered from left to right,
SNPs are defined to be in pattern I if D′(AB) < D′(AC) or D′(BC) < D′(AC),
SNPs are defined to be in pattern II if D′(AB) < D′(AC) and D′(BC) < D′(AC),
SNPs are defined to be in pattern III if D′(AB) < 0.5 and D′(BC) < 0.5.
For two SNPs A and B, SNPs are defined to be in pattern IV if D′(AB) < 1.0.
Let P5(I) and P5(II) denote the fraction of all triplets with the outer SNPs within 5 kb of each other that show patterns I and II, respectively. Let P10(II) denote the fraction of all triplets with outer SNP pairs within 10 kb of each other that show pattern II. These denote our short-range summary statistics. Patterns I and II are indicative of gene-conversion events in short-range data and can potentially arise from a single gene-conversion event including the middle SNP in a triplet (Wiehe et al. 2000; Padhukasahasram et al. 2004). Let P50(III) denote the fraction of all triplets with outer SNPs within 50 kb of each other that show pattern III and P50(IV) denote the fraction of all SNP pairs within 50 kb of each other with D′ < 1.0. These denote our long-range summary statistics.
Choice of patterns:
The choice of summary statistics that capture key features of full sequence information is important for our method to work efficiently. To find such informative summaries, we first tested the performance of many different patterns (listed in appendix a) for simulated data sets. We found that patterns that are too rare are not suitable estimators for low recombination values because they are almost never observed. Similarly, patterns that are too common are not suitable estimators for high recombination values because summaries based on them become almost insensitive to recombination in that range. Using multiple patterns in both long-range and short-range data worked better than any individual summaries. In general, it appears that a few (two or three) different patterns are sufficient to describe the distribution of recombination levels in a data set accurately and can roughly approximate full sequence information for a wide range of recombination rates (e.g., as in Table 1). We selected a combination of patterns that performed well for the values considered in Table 1. Adding more summary statistics to this combination did not bring any significant improvements in performance. Therefore, we decided to use this set of patterns for comparing our method with the composite-likelihood approach.
TABLE 1.
Performance for models with uniform recombination rates with phased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(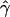 )d )d
|
E(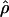 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite likelihood method | |||||||||
| 5 | 5 | 0.246 | 0.696 | 0.555 | 0.611 | 8.917 | 5.097 | 2.842 | 0.994 |
| 10 | 10 | 0.324 | 0.828 | 0.609 | 0.580 | 12.590 | 11.140 | 1.769 | 0.829 |
| 20 | 20 | 0.368 | 0.792 | 0.671 | 0.590 | 19.250 | 21.650 | 1.274 | 0.770 |
| 40 | 40 | 0.468 | 0.874 | 0.638 | 0.512 | 34.880 | 43.490 | 0.936 | 0.591 |
| 80 | 80 | 0.460 | 0.840 | 0.691 | 0.490 | 59.820 | 92.520 | 0.766 | 0.624 |
| 100 | 100 | 0.518 | 0.820 | 0.665 | 0.462 | 77.190 | 115.04 | 0.727 | 0.604 |
| Summary statistics method | |||||||||
| 5 | 5 | 0.242 | 0.746 | 0.574 | 0.394 | 7.768 | 5.735 | 2.402 | 0.914 |
| 10 | 10 | 0.358 | 0.842 | 0.533 | 0.588 | 14.230 | 10.543 | 1.752 | 0.694 |
| 20 | 20 | 0.522 | 0.842 | 0.580 | 0.601 | 22.717 | 20.810 | 1.215 | 0.662 |
| 40 | 40 | 0.638 | 0.888 | 0.543 | 0.498 | 43.060 | 43.540 | 0.937 | 0.567 |
| 80 | 80 | 0.604 | 0.860 | 0.514 | 0.534 | 89.060 | 86.640 | 0.839 | 0.562 |
| 100 | 100 | 0.652 | 0.846 | 0.484 | 0.491 | 109.58 | 109.32 | 0.743 | 0.554 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 500 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (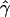 ) and crossing over (
) and crossing over (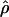 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(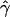 ) and E(
) and E(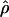 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
Rejection method:
To jointly estimate crossing over (ρ) and gene conversion (γ) from a test data set, we calculate both short-range and long-range summaries and use all of them in a simple rejection-sampling scheme. In this scheme, we first simulate a large number of data sets for a finite grid of parameter values and compute summary statistics for each. Then, we accept a simulated data set if each one of its summaries lies within 30% of the corresponding values observed in the test data set (we chose a high acceptance rate so that we accept a reasonably large number of the simulated data sets given the summary combination chosen and the total number of data sets simulated; see appendix b for performance for a few other choices) and reject it otherwise. Likelihood for a parameter value is approximated as the fraction of data sets (simulated at that value) that are accepted (for more details about rejection methods see Weiss and von Haeseler 1998 and Marjoram et al. 2003).
Extension to genotype data:
To extend our summaries to genotype data, we simply omit double heterozygotes (phase unknown) when determining D′ between any pair of SNPs.
Simulations:
DNA sequences were simulated under the coalescent, assuming no population structure, a large constant population size (N), no selection, and the infinite-sites model for mutations The population mutation rate θ (=4Nu) was assumed to be uniform along the sequence. Here, u denotes the per-generation, per-sequence probability of a mutation event.
For modeling gene conversion, we used the coalescent with both crossing over and gene conversion, as described by Wiuf and Hein (2000). Gene-conversion tract lengths are assumed to be geometrically distributed with a mean length L. The population crossing-over rate ρ (=4Nr) and population gene-conversion rate γ (=4Nc) are assumed to be uniform along the sequence. Here, r denotes the per-generation, per-sequence probability of a crossing-over event, and c denotes the per-generation, per-sequence probability of a gene-conversion event. Note that this model is equivalent to the assumption that events occur at a total rate of ρ + γ and that each recombination event results in crossing over with probability ρ/(ρ + γ) and in gene conversion otherwise. The ratio of gene conversion to crossing over is denoted by f (=γ /ρ).
In addition to the standard model of gene conversion, we also simulated data under some alternate models where either crossing over alone or both conversion and crossing over were nonuniform along the sequence. For modeling nonuniform recombination, we assumed that recombination rates are elevated for some 1-kb regions (called hotspots) that occur at certain fixed locations along the sequence. A significant fraction of events occur within these hotspots, whereas the rest of the events occur in the intervening regions. Recombination within hotspots as well as within non-hotspot regions was assumed to be uniform. All hotspots have identical (higher) levels of recombination. Similarly, all non-hotspot regions also have identical (lower) levels of recombination.
To compare estimation methods, we tested them on 50-kb DNA sequences simulated with θ set to 0.8/kb (estimates for human data from Innan et al. 2003) and sample size of n = 18 for haplotype data and 2n = 36 for genotype data. It is usually difficult to estimate both gene-conversion rates and tract lengths from SNPs (Padhukasahasram et al. 2004). Therefore, conversion rates were always estimated with the tract length (L) fixed at 500 bp and this also facilitates comparisons with previous studies (such as Frisse et al. 2001; Padhukasahasram et al. 2004; Ptak et al. 2004). For smaller tract lengths, the estimated conversion rates are expected to be much higher. To summarize the performance of methods, we used the following criteria:
The accuracy (g), which is defined as the proportion of estimates that lie within a factor of 2 of the true value (Wall 2000).
The nature of bias (B), which is defined as the proportion of estimates lower than the true value, given that it is not equal to the true value. This statistic shows whether any method overestimates or underestimates a recombination parameter more often. A value close to 0.5 would indicate that the estimator is roughly unbiased.
Error (V), which is defined as the root mean square relative error for the estimates.
Average (E), the arithmetic mean of the estimated values.
Unphased data sets were generated by first simulating haplotypes and then grouping random pairs of chromosomes together into individuals. We then assumed that within any individual, phase is unknown for double heterozygotes. For estimating rates from the human genotype data set, we simulated 50 kb DNA sequences with θ set to 0.8/kb and sample size 2n =142.
The Perlegen data set:
Perlegen genotyped ∼1.6 million SNPs across the human genome that are likely to be common in individuals of diverse ancestry (Hinds et al. 2005). These SNPs were identified by performing array-based resequencing of 24 diverse human DNA samples. Seventy-one unrelated individuals from three populations were genotyped: 24 European Americans, 23 African Americans, and 24 Han Chinese from the Los Angeles area. These 71 individuals were not related to the individuals previously used for SNP discovery.
Ascertainment and missing data:
We omit haplotypes with missing data while calculating our summaries for real data. The proportion of missing data in the Perlegen genotypes is extremely small (<2%) and thus our estimates are not significantly affected by ignoring these. In addition, when estimating rates for human data, SNPs with low minor allele frequency (<9%) were removed from both real and simulated data sets. To simulate the effects of ascertainment, we retained only those SNPs that were polymorphic in a randomly chosen sample of 24 chromosomes of the simulated data (the same 24 chromosomes for all SNPs).
Maxhap and Maxdip:
Maxhap and Maxdip are programs for estimating recombination rates from haplotype and genotype data, respectively, on the basis of the composite-likelihood approach of Hudson (2001). We used them for estimating recombination rates from simulated data sets and compared their performance with our summary statistics method.
RESULTS
Performance with haplotypes for the standard model of gene conversion:
First, we tested the performance of our method on data simulated under a simple model where both crossing-over and gene-conversion rates are uniform along the sequence. We simulated 500 phased data sets of 50-kb DNA sequences with θ set to 0.8/kb, n = 18, and L fixed at 500 bp.
For each simulated data set, we estimated gene-conversion and crossing-over rates using our rejection method (described in materials and methods) as well as using Maxhap. Estimates for both the methods were obtained by calculating likelihoods for a finite grid of ρ-and γ-values (identical grids were used for both methods). The grids of ρ and γ used for the first three rows and next three rows in Table 1 were (0.1, 0.50, 1.00, 2.50, 5.00, 7.50, 10.0, 15.0, 20.0, 30.0, 40.0, 60.0, 80.0, 100.0, 120.0, 140.0) and (0.0001, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 220, 240), respectively. Likelihoods for the summary statistics method were approximated using 40,000 simulated data sets (for each ρ, γ combination) for the first grid and using 10,000 data sets for the second. We did not smooth likelihood surfaces for obtaining the maximum-likelihood estimates.
Likelihoods for the two-locus configurations in Maxhap were based on 2 × 106 replicates. Estimating rates for 500 data sets using our method took ∼868 sec once the data for approximating the likelihoods have been simulated (which took ∼111 hr for the first and 245 hr for the second grid) on a 2-Ghz Xeon processor machine. Estimating rates using Maxhap took ∼2.25 and 5.2 sec/50-kb data set for the first grid (with 256 values) and the second grid (with 529 values).
Table 1 summarizes accuracy (g), nature of bias (B), and error (V) for both these methods. We found that for estimating gene-conversion rates, the summary statistics method has higher accuracy than Maxhap, which tends to underestimate the conversion rate more often. For estimating crossing-over rates, both the methods have similar accuracy and nature of bias. The root mean square relative error was also roughly similar for both the methods.
Confidence intervals and their coverage properties:
We constructed ∼90% confidence intervals for the gene-conversion and crossing-over rate estimates obtained using our method and examined their coverage properties. For doing this, we first simulated 5000 data sets each for five different parameter combinations and estimated gene-conversion and crossing-over rates on the basis of the first grid used for Table 1. Because this grid is coarse and we did not use smoothing, it is difficult to obtain precise confidence intervals for our method. We increased the interval width around the estimated conversion or crossing-over rate until it included at least 90% of the total sum of the likelihoods. Then, we chose a subset (∼1000) of these simulated data sets for which the confidence intervals contained 90–91% of the total and calculated the fraction of such data sets for which these intervals included the true value (Table 2). This crude coverage study suggests that the actual coverage probabilities obtained from the rejection method used here may differ slightly from the nominal probabilities. Note that we assume a uniform prior distribution for the parameters along the grid values used and confidence intervals were calculated jointly for both the recombination parameters.
TABLE 2.
Coverage probabilities of confidence intervals obtained using the summary statistics method
| γa | ρa | P(γ)b | P(ρ)b |
|---|---|---|---|
| 5 | 5 | 0.941 | 0.927 |
| 10 | 10 | 0.966 | 0.899 |
| 15 | 15 | 0.913 | 0.919 |
| 20 | 20 | 0.871 | 0.925 |
| 30 | 30 | 0.887 | 0.940 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which data sets were simulated.
P(γ) and P(ρ) denote the fraction of the data sets for which the true values of conversion or crossing over lie within the confidence intervals with 90–91% of the total posterior probability.
Performance with genotype data for the standard gene-conversion model:
To test the performance of our method with genotypes, we simulated 500 unphased data sets of 36 chromosomes for the same model as in Table 1. For each simulated data set, we estimated gene-conversion and crossing-over rates using our rejection method as well as using Maxdip. Estimates were obtained by calculating likelihoods for a finite grid of ρ (0, 10, 20, 30, 40, … , 90) and γ (0, 10, 20, 30, 40, 60, … , 200) values and likelihoods in our method were approximated using 10,000 simulated data sets (for each combination of ρ and γ in this grid). Likelihoods for the two-locus configurations for Maxdip were based on 2 × 106 replicates.
Table 3 summarizes the accuracy (g), nature of bias (B), and error (V) for unphased data. We find that for estimating conversion rates our method has similar accuracy and higher error compared to Maxdip, which tends to underestimate more often, whereas for estimating crossing over it has lower accuracy, higher error, and similar nature of bias.
TABLE 3.
Comparison between haplotype and genotype data: performance for models with uniform recombination rates with unphased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(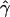 )d )d
|
E(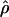 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite-likelihood method | |||||||||
| 20 | 20 | 0.452 | 0.968 | 0.600 | 0.573 | 22.060 | 20.170 | 1.273 | 0.495 |
| 60 | 20 | 0.692 | 0.954 | 0.545 | 0.491 | 55.259 | 21.594 | 0.650 | 0.573 |
| 80 | 20 | 0.794 | 0.962 | 0.626 | 0.543 | 74.119 | 20.908 | 0.534 | 0.564 |
| 20 | 40 | 0.420 | 0.968 | 0.662 | 0.484 | 19.919 | 42.000 | 1.345 | 0.426 |
| 40 | 40 | 0.572 | 0.960 | 0.619 | 0.534 | 36.620 | 40.880 | 0.863 | 0.417 |
| Summary statistics method | |||||||||
| 20 | 20 | 0.580 | 0.910 | 0.445 | 0.498 | 27.600 | 22.700 | 1.387 | 0.715 |
| 60 | 20 | 0.732 | 0.850 | 0.454 | 0.453 | 70.278 | 24.090 | 0.763 | 0.822 |
| 80 | 20 | 0.748 | 0.838 | 0.468 | 0.514 | 89.940 | 23.226 | 0.654 | 0.872 |
| 20 | 40 | 0.488 | 0.904 | 0.516 | 0.521 | 28.076 | 42.582 | 1.673 | 0.512 |
| 40 | 40 | 0.600 | 0.828 | 0.501 | 0.541 | 51.814 | 43.050 | 1.169 | 0.590 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 500 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (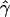 ) and crossing over (
) and crossing over (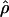 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(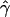 ) and E(
) and E(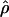 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
Note that both Maxhap and Maxdip tend to underestimate the gene-conversion rate more often whereas our method is roughly unbiased. Therefore, when estimating conversion rates our method tends to have relatively higher error for many parameters. However, because of the lower bias, the accuracy tends to be higher compared to Hudson's method.
Comparison between haplotype and genotype data:
We also simulated 500 phased data sets (Table 4) for a sample size of 18 chromosomes for comparison with Table 3 and estimated rates using our method and Maxhap. From this comparison, we find that the accuracy of estimates using Maxdip and 18 genotypes was higher than the accuracy obtained with Maxhap and 18 haplotypes. For the summary statistics method, the accuracy with 18 genotypes was slightly lower than the accuracy obtained from 18 haplotypes. The nature of bias was roughly similar for both unphased and phased data sets for both the methods (Tables 3 and 4).
TABLE 4.
Comparison between haplotype and genotype data: performance for models with uniform recombination rates with phased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(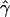 )d )d
|
E(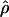 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite-likelihood method | |||||||||
| 20 | 20 | 0.382 | 0.916 | 0.669 | 0.550 | 20.06 | 20.86 | 1.396 | 0.624 |
| 60 | 20 | 0.626 | 0.890 | 0.589 | 0.481 | 51.56 | 23.44 | 0.672 | 0.765 |
| 80 | 20 | 0.672 | 0.856 | 0.717 | 0.431 | 62.19 | 25.36 | 0.600 | 0.869 |
| 20 | 40 | 0.326 | 0.890 | 0.696 | 0.496 | 18.94 | 42.49 | 1.557 | 0.519 |
| 40 | 40 | 0.440 | 0.862 | 0.686 | 0.495 | 33.48 | 43.00 | 0.994 | 0.550 |
| Summary statistics method | |||||||||
| 20 | 20 | 0.610 | 0.944 | 0.482 | 0.523 | 26.48 | 21.76 | 1.427 | 0.635 |
| 60 | 20 | 0.740 | 0.922 | 0.478 | 0.530 | 67.46 | 21.74 | 0.714 | 0.661 |
| 80 | 20 | 0.804 | 0.894 | 0.509 | 0.492 | 83.16 | 22.80 | 0.566 | 0.717 |
| 20 | 40 | 0.440 | 0.914 | 0.489 | 0.560 | 30.06 | 40.06 | 1.742 | 0.471 |
| 40 | 40 | 0.642 | 0.892 | 0.534 | 0.498 | 43.56 | 42.76 | 0.929 | 0.510 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 500 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (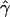 ) and crossing over (
) and crossing over (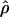 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(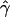 ) and E(
) and E(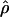 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
Models with nonuniform crossing over and uniform gene conversion:
The simulations for Tables 1, 3, and 4 assumed that recombination rates are uniform along the sequence. However, this assumption is not realistic. For example, there is considerable evidence that crossing-over rates vary across the human genome at all scales (e.g., Fullerton et al. 1994; Dunham et al. 1999; Jeffreys et al. 2001; Innan et al. 2003). To examine the effects of nonuniform crossing over, we simulated data under a model where crossing over is nonuniform and gene conversion is uniform along the sequence. This model assumes that 50% of all crossing-over events happen in 1-kb hotspots that occur once every 25 kb along the sequence. We simulated 500 phased and unphased data sets for this alternate model of recombination for the same parameters as in Tables 3 and 4 and estimated rates similarly. Tables 5 and 6 show the summaries of accuracy (g), nature of bias (B), and error (V) for these data sets.
TABLE 5.
Performance for models with nonuniform crossing over and uniform gene conversion with unphased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(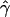 )d )d
|
E(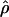 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite-likelihood method | |||||||||
| 20 | 20 | 0.420 | 0.972 | 0.780 | 0.509 | 12.499 | 20.320 | 0.986 | 0.448 |
| 60 | 20 | 0.592 | 0.958 | 0.763 | 0.413 | 39.479 | 22.390 | 0.668 | 0.533 |
| 80 | 20 | 0.636 | 0.948 | 0.776 | 0.418 | 59.159 | 22.102 | 0.611 | 0.535 |
| 20 | 40 | 0.288 | 0.964 | 0.841 | 0.654 | 9.440 | 37.000 | 1.047 | 0.360 |
| 40 | 40 | 0.384 | 0.984 | 0.853 | 0.578 | 18.940 | 39.720 | 0.856 | 0.356 |
| Summary statistics method | |||||||||
| 20 | 20 | 0.578 | 0.938 | 0.501 | 0.528 | 24.482 | 21.220 | 1.208 | 0.598 |
| 60 | 20 | 0.732 | 0.866 | 0.529 | 0.498 | 66.330 | 22.578 | 0.745 | 0.773 |
| 80 | 20 | 0.772 | 0.832 | 0.518 | 0.486 | 84.518 | 24.412 | 0.600 | 0.911 |
| 20 | 40 | 0.458 | 0.894 | 0.549 | 0.695 | 25.312 | 36.030 | 1.462 | 0.457 |
| 40 | 40 | 0.608 | 0.88 | 0.561 | 0.623 | 42.800 | 38.464 | 0.974 | 0.503 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 500 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (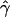 ) and crossing over (
) and crossing over (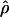 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(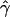 ) and E(
) and E(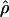 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
TABLE 6.
Performance for models with nonuniform crossing over and uniform gene conversion with phased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(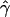 )d )d
|
E(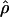 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite-likelihood method | |||||||||
| 20 | 20 | 0.360 | 0.930 | 0.800 | 0.522 | 12.59 | 21.35 | 1.164 | 0.603 |
| 60 | 20 | 0.548 | 0.902 | 0.683 | 0.538 | 42.21 | 21.74 | 0.713 | 0.684 |
| 80 | 20 | 0.612 | 0.860 | 0.776 | 0.476 | 54.12 | 23.72 | 0.608 | 0.797 |
| 20 | 40 | 0.226 | 0.894 | 0.839 | 0.593 | 10.99 | 39.24 | 1.187 | 0.489 |
| 40 | 40 | 0.380 | 0.898 | 0.787 | 0.555 | 22.22 | 39.98 | 0.907 | 0.476 |
| Summary statistics method | |||||||||
| 20 | 20 | 0.566 | 0.936 | 0.524 | 0.486 | 25.66 | 22.08 | 1.410 | 0.628 |
| 60 | 20 | 0.748 | 0.912 | 0.562 | 0.504 | 61.88 | 22.48 | 0.688 | 0.714 |
| 80 | 20 | 0.780 | 0.894 | 0.502 | 0.473 | 84.60 | 23.08 | 0.602 | 0.733 |
| 20 | 40 | 0.482 | 0.898 | 0.555 | 0.625 | 23.82 | 36.64 | 1.380 | 0.465 |
| 40 | 40 | 0.668 | 0.902 | 0.588 | 0.602 | 39.54 | 37.98 | 0.837 | 0.465 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 500 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (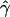 ) and crossing over (
) and crossing over (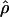 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(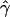 ) and E(
) and E(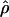 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
When estimating gene-conversion rates, the performance of the composite-likelihood method appears to be slightly sensitive to the presence of crossing-over hotspots. In particular, the tendency to underestimate the gene-conversion rate increases and the accuracy is a little lowered compared to data simulated with uniform crossing-over rates. In contrast, our method's performance seems to be relatively unaffected in these regards (compare Tables 3 and 5 and Tables 4 and 6). For estimating crossing-over rates, both methods seem to be reasonably robust to the nonuniform crossing-over model considered here and the accuracy of estimation did not change significantly (compare Tables 3 and 5 and Tables 4 and 6). However, the tendency to underestimate the crossing-over rate appears to be higher for some parameter combinations.
Models with nonuniform crossing over and nonuniform conversion:
Sperm-typing experiments of Jeffreys and May (2004) have revealed the presence of highly localized gene-conversion activity in some crossing-over hotspots in humans. Thus, both conversion and crossing over may be elevated for some regions in the human genome. We also tested the performance of our method and Maxhap for phased data simulated under models where both crossing over and gene conversion are nonuniform along the sequence. This model assumes that 50% of both conversion and crossing-over events happen in 1-kb hotspots that occur once every 25 kb along the sequence. We simulated 500 data sets for this nonstandard model of recombination for the same parameters as in Tables 3 and 4 and estimated rates similarly. Table 7 shows results for these data sets.
TABLE 7.
Performance for models with nonuniform crossing over and nonuniform gene conversion with phased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(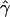 )d )d
|
E(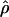 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite-likelihood method | |||||||||
| 20 | 20 | 0.294 | 0.914 | 0.844 | 0.524 | 9.419 | 21.40 | 1.020 | 0.627 |
| 60 | 20 | 0.332 | 0.868 | 0.835 | 0.465 | 24.279 | 23.49 | 0.803 | 0.746 |
| 80 | 20 | 0.340 | 0.902 | 0.892 | 0.427 | 32.260 | 23.98 | 0.746 | 0.732 |
| 20 | 40 | 0.210 | 0.900 | 0.874 | 0.535 | 8.120 | 39.48 | 1.136 | 0.464 |
| 40 | 40 | 0.260 | 0.878 | 0.881 | 0.545 | 13.820 | 40.50 | 0.906 | 0.493 |
| Summary statistics method | |||||||||
| 20 | 20 | 0.486 | 0.946 | 0.704 | 0.553 | 17.78 | 20.80 | 1.397 | 0.596 |
| 60 | 20 | 0.528 | 0.920 | 0.842 | 0.489 | 34.52 | 22.66 | 0.664 | 0.683 |
| 80 | 20 | 0.494 | 0.910 | 0.879 | 0.484 | 42.10 | 22.80 | 0.635 | 0.696 |
| 20 | 40 | 0.418 | 0.882 | 0.724 | 0.729 | 16.08 | 32.94 | 1.331 | 0.438 |
| 40 | 40 | 0.454 | 0.912 | 0.835 | 0.698 | 22.18 | 34.56 | 0.828 | 0.426 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 500 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (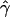 ) and crossing over (
) and crossing over (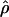 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(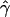 ) and E(
) and E(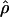 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
The presence of nonuniform gene conversion reduces the accuracy of both the methods considerably and biases them toward underestimating the gene-conversion rate (compare Tables 4 and 7). The accuracy of estimating crossing-over rates did not change much for either method whereas the tendency to underestimate the crossing-over rate seems to increase for some parameter combinations in the summary statistics method.
Recombination in human data:
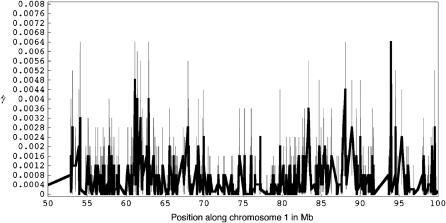
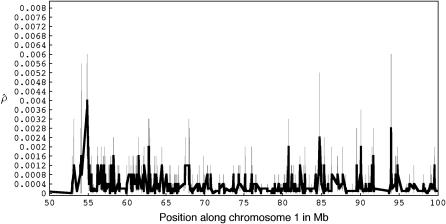
To illustrate our method in real data, we applied it to the Perlegen genotype data set and estimated gene conversion and crossing over along human chromosome 1 (Figure 1). Likelihoods were calculated by simulating 10,000 data sets each for a grid of ρ (0, 5, 10, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300, 320) and γ (0, 5, 10, 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300, 320) values. Gene-conversion and crossing-over rate estimates averaged over all 50-kb windows (with ≥ 30 SNPs) in chromosome 1 are 0.00066 and 0.00038/bp, respectively (f = 1.736), assuming that L = 500 bp. These are similar to estimates for chromosome 21 haplotypes in Padhukasahasram et al. (2004). Note that conversion estimates are highly sensitive to the assumed conversion tract length and estimates are expected to be much higher for smaller tract lengths (e.g., compare estimates for different tract lengths in Padhukasahasram et al. 2004).
Figure 1.—
Recombination rate estimates for 50-kb overlapping windows across a 50-Mb region in chromosome 1. (Top) The population gene-conversion rates and (bottom) the population crossing-over rates, estimated under a model with uniform recombination for a mean conversion tract length (L) of 500 bp. The shaded bars represent confidence intervals with at least 90% of the total mass and are constructed around the estimated values at positions corresponding to the centers of the windows.
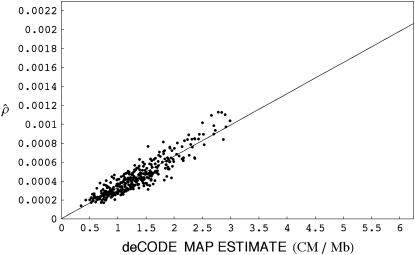
Myers et al. (2005) recently applied the method of McVean et al. (2004) to this Perlegen data set and estimated recombination rates across the human genome. They also used the pedigree data from Kong et al. (2002) to estimate rates in humans. To compare our results with this study, we estimated recombination rates for 50-kb regions along chromosomes 1–22 under a model with uniform crossing over alone using only the long-range summary statistics. Rates were first estimated for all 50-kb windows with at least 10 SNPs and then averaged over 5-Mb intervals. At these scales, estimates obtained using our method are highly correlated (Pearson's coefficient R = 0.9181, P ≪ 10−2) with those obtained from the pedigree data used in Myers et al. (2005) (Figure 2). Myers et al. found that pedigree-based estimates and those obtained using the McVean et al. (2004) method are almost equivalent when averaged over such large intervals in humans.
Figure 2.—
Comparison of recombination rates estimated from population genetic data using the summary statistics method with those obtained from human genetic maps (data from Kong et al. 2002 used in Myers et al. 2005). A scatter plot is shown of the estimates of population-scaled crossing-over rate with the deCODE pedigree-based estimates (centimorgans per megabase) for 5-Mb regions across the human genome. The correlation coefficient between these estimates is 0.9181.
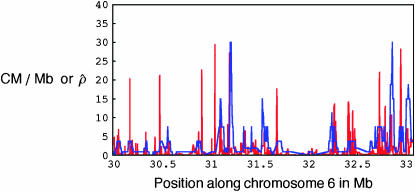
In addition to this, we compared the patterns of crossing-over estimates obtained using the summary statistics method (using only long-range summary statistics) for overlapping 50-kb regions in the human chromosome 6 MHC region (where sperm typing shows evidence of hotspots) with estimates obtained for the same region in Myers et al. (2005), using the McVean et al. (2004) method (Figure 3). Because we estimated average rates for 50-kb windows, it is not possible to directly compare recombination intensities. Nonetheless, there is broad agreement between the recombination patterns obtained using these two different methods and there is considerable overlap between the positions of the peaks in Figure 3.
Figure 3.—
Crossing-over estimates in a 3.3-Mb MHC region in human chromosome 6. The red curve shows estimates (centimorgans per megabase) obtained in Myers et al. (2005) using the McVean et al. (2004) method. The blue curve shows sliding-window population crossing-over estimates (multiplied by some constant) for overlapping 50-kb regions along chromosome 6 obtained using the summary statistics method.
Are gene-conversion and crossing-over rates correlated?
We investigated the relationship between gene-conversion and crossing-over rates in our data. This issue has been addressed previously in Drosophila by Langley et al. (2000) and by Andolfatto and Wall (2003). Our data set is much larger than the data sets used in these previous studies. To examine the relationship between the two different mechanisms of recombination, we first chose 232 nonoverlapping 50-kb windows with high SNP density (≥70 SNPs) from chromosome 1–22 and estimated recombination rates for a tract length of L = 500 bp. Then, we calculated the correlation coefficient between the estimated rates of gene conversion and crossing over. We found that these estimates were not strongly correlated (Pearson's coefficient R = 0.102, P = 0.12).
Because the level of uncertainty associated with our estimates is high, it is not clear how high a correlation should be expected even if these two parameters happen to be perfectly correlated across the genome. To get an idea of this, we first simulated 100 data sets of 232 independent 50-kb windows each, with crossing-over rates set to corresponding estimates in real data and f set to the ratio of the average conversion rate to average crossing-over rate estimated from the 232 windows in humans. Recombination rates were assumed to be uniform within windows in these simulations. For each simulated data set, we estimated rates as we did for the human data set and computed the correlation coefficient between conversion and crossing over. The lowest value of R observed in these simulations was 0.50.
Fine-scale recombination rate variation within windows can greatly increase the levels of uncertainty associated with our estimated rates. To see if R is expected to be much lower for some plausible models with nonuniform recombination, we simulated another set of 100 data sets where the overall recombination rates were set to the same values as before. In these simulations, we allowed both crossing-over and gene-conversion rates to vary within windows, assuming that a significant fraction (x) of events happen in hotspots that occur at certain fixed locations along the sequence. x was given values of 0.25 or 0.5 or 0.75 with equal frequency among the 232 windows. Note that in this model conversion and crossing over covary in an identical pattern, so that f remains uniform along the sequence. We then looked at the distribution of the correlation coefficient between the estimated conversion and crossing-over rates for these data sets. The lowest value of R observed in these simulations was 0.245 and values <0.3 were observed in only 3 of the 100 simulated data sets. These results seem to suggest that our data set deviates significantly from models where crossing-over and gene-conversion rates are pefectly correlated with one another and therefore that either the parameter f or the conversion tract length (L) may vary along the human genome.
Relationship between GC content and recombination rates:
We also calculated GC percentage for 50-kb windows with high SNP density (≥70 SNPs) and looked at the correlation with the estimated crossing-over and gene-conversion rates. At this scale, crossing-over rates are positively correlated with the GC content (Pearson's coefficient R = 0.3138, P = 9.224 × 10−7) whereas gene-conversion rates for L = 500 bp are less strongly associated (Pearson's coefficient R = 0.1269, P = 0.05195). However, note that gene-conversion estimates may be highly unreliable because they are sensitive to assumptions about tract lengths.
DISCUSSION
We have described a novel method for jointly estimating crossing-over and conversion rates from population genetic data. In this method, we collect summary statistics that use approximately full sequence information from both short-range and long-range data and use all of them simultaneously in a simple rejection scheme. For estimating uniform rates from phased data sets, a comparison with the pairwise composite-likelihood approach proposed by Hudson (2001) suggests that the methods are roughly comparable (Tables 1 and 3; also see appendix b). The summary statistics approach generally worked better for estimating the gene-conversion rate (at least for some subset of parameters considered here; also see Padhukasahasram et al. 2004). It seems that the pairwise composite-likelihood estimator tends to underestimate the gene-conversion rate more often whereas our method is less biased. However, similar to results obtained in Wall (2004), we found that both methods are not efficient on an absolute scale for estimating gene-conversion rates. For estimating crossing-over rates, the summary statistics method performed similarly to the composite-likelihood method for the parameters considered in this study. Overall, our approach represents a computationally feasible alternative to existing methodologies for co-estimating crossing-over and gene-conversion rates from SNPs.
In contrast to other approximate-likelihood methods that also utilize full sequence information (such as Hudson 2001; Fearnhead and Donnelly 2002; Li and Stephens 2003), the uncertainty in estimates in the summary statistics method can be evaluated directly. Another important advantage of our approach could be its flexibility. It is relatively easy to extend our method to any complex demographic scenario provided that data can be simulated under that scenario within the coalescent framework. Demography can affect the performance of some of the other currently available methods (e.g., see Smith and Fearnhead 2005). Our method can be made more robust to such effects if we first estimate demographic parameters from the data and then infer recombination rates under a suitable model (or alternately estimate both recombination rates and demography jointly).
We have used a simple rejection-sampling scheme for estimating the recombination parameters in this study. The main limitation of rejection-sampling methods is that only a small number of summary statistics can usually be handled. Otherwise, acceptance rates become prohibitively low or tolerance levels must be increased, which can distort the approximation of likelihoods. The efficiency of rejection methods such as ours can be improved by using techniques like smooth weighting and regression adjustment (e.g., by using local linear regression) described in Beaumont et al. (2002). The key benefit of these techniques is that they use approximations that are insensitive to tolerance and this can permit us to increase the number of summary statistics used and also widen the tolerance levels.
The population mutation parameter was assumed to be uniform along the sequence for our simulations. A better way to use our method might be by simulating data sets conditional on the observed number of segregating sites (S) in the same positions as in real data. This approach was first proposed in Hudson (1993) and can be useful for surveys of regions with intervening gaps. Although using a fixed S scheme will result in a null model that is slightly different from the standard coalescent model, simulation studies (Wall 2000) suggest that the performances of estimation methods do not change much.
When estimating rates from unphased data sets (Table 4), we expected that the relative performance of our method would drop because we simply ignored double heterozygotes in such data sets. Maxdip, on the other hand, considers all genotypes exactly for estimating rates. In agreement with this expectation, we found that the accuracy of gene-conversion estimates using our method was similar to that of Maxdip, whereas estimates of crossing over were less accurate. However, note that reconstructing the phase first by using some phase-estimating program (such as PHASE) and then using our method or Maxhap on the resulting data set may yield more accurate estimates than Maxdip for unphased data sets (see Smith and Fearnhead 2005).
S. Ptak, M. Przeworski and R. R. Hudson (unpublished results cited in Ptak et al. 2004) have reported that using k genotypes should work better than k haplotypes for estimating recombination rates using Hudson's composite-likelihood method. Our simulation results support this conclusion. We found that the accuracy of estimates for Maxdip using 18 genotypes was higher than the accuracy obtained from Maxhap using 18 haplotypes. In contrast, since the summary statistics method is inexact for genotype data, we found that the accuracy with 18 genotypes was slightly lower than the accuracy obtained from 18 haplotypes.
Given that recombination rates vary substantially along the genome on a fine scale, we also tested the performance of methods for data simulated with recombination hotspots. For models with nonuniform crossing-over and uniform gene-conversion rates, the performances of Maxhap and Maxdip seem to be slightly sensitive to variation in the crossing-over rates. In particular, the accuracy of estimating conversion rates and the tendency to underestimate gene conversion became a little worse compared to data simulated with uniform recombination. In contrast, the performance of our method appears to be relatively unaffected in these regards. We note that in the summary statistics approach, we estimate conversion rates on the basis of the difference between long-range and short-range summary statistics. The robustness of our method to nonuniform crossing over suggests that this difference (between long-range and short-range data) depends mainly on the gene-conversion rate and may be insensitive to moderate deviations from the uniform crossing-over model. For models with nonuniform gene conversion and nonuniform crossing over, the accuracy of estimating gene-conversion rates decreased substantially for both methods and there is considerable bias toward underestimating the gene-conversion rate. This may be because gene-conversion hotspots may sometimes not contain any SNP and in these cases a majority of conversion events do not leave a trace in the sample. On the other hand, both methods generally appear to be more robust to nonuniform crossing over and the accuracy of estimating crossing-over rates did not change much for the nonstandard models considered here.
Although both gene conversion and crossing over are thought to arise from common intermediates (i.e., Holliday junctions), the relationship between these two processes has not been clear so far. Some recent results have challenged the original Holliday model that was proposed for the mechanisms underlying conversion and crossing over (Allers and Litchen 2001). While meiotic crossing over is believed to be essential for the precise disjunction of homologous chromosomes (because it maintains physical connections between homologous DNA) and creates genetic diversity, the significance of meiotic gene conversion is not well understood. Because gene-conversion estimates are highly sensitive to the assumed tract length and human data on the distribution of tract lengths are limited, it is difficult to draw any strong conclusions about the relationship between these two different recombination mechanisms from our data set. If conversion and crossing-over rates are indeed not strongly correlated across the human genome, this could be because the biological pathways leading to these mechanisms might be different (e.g., see results in yeast in Allers and Litchen 2001).
Acknowledgments
We thank Perlegen Sciences for the data set used in this study and M. Przeworski for comments on the manuscript. Two anonymous reviewers gave helpful comments that significantly improved the submitted manuscript. This work was supported by a National Institutes of Health Center for Excellence in Genomic Sciences grant (1P50 HG002790-01A1) to P.M. and M.N.
APPENDIX A
For long range, we tested summaries based on the following patterns for the 50-kb range:
For two SNPs A and B: D′(AB) < 1.00, D′(AB) < 0.75, D′(AB) < 0.50, D′(AB) < 0.25, D′(AB) < 0.10.
For three SNPs A, B, and C, ordered from left to right:
D′(AB) < 1.00 and D′(BC) < 1.00, D′(AB) < 0.75 and D′(BC) < 0.75,
D′(AB) < 0.50 and D′(BC) < 0.50, D′(AB) < 0.25 and D′(BC) < 0.25,
D′(AB) < 0.10 and D′(BC) < 0.10, D′(AB) < 1.00 and D′(AC) < 1.00,
D′(AB) < 0.75 and D′(AC) < 0.75, D′(AB) < 0.50 and D′(AC) < 0.50,
D′(AB) < 0.25 and D′(AC) < 0.25, D′(AB) < 0.10 and D′(AC) < 0.10.
For short range, we tested the following patterns for both the 5-kb and the 10-kb range for outer SNPs in triplets:
For three SNPs A, B, and C, ordered from left to right:
D′(AB) < D′(AC) or D′(BC) < D′(AC), D′(AB) < D′(AC) and D′(BC) < D′(AC),
D′(AB) < 1.00 or D′(BC) < 1.00, D′(AB) < 0.75 or D′(BC) < 0.75,
D′(AB) < 0.50 or D′(BC) < 0.50, D′(AB) < 0.25 or D′(BC) < 0.25,
D′(AB) < 0.10 or D′(BC) < 0.10, D′(AB) < 1.00 and D′(BC) < 1.00,
D′(AB) < 0.75 and D′(BC) < 0.75, D′(AB) < 0.50 and D′(BC) < 0.50,
D′(AB) < 0.25 and D′(BC) < 0.25, D′(AB) < 0.10 and D′(BC) < 0.10.
APPENDIX B: PERFORMANCE FOR DIFFERENT ACCEPTANCE RATES
TABLE B1.
Performance for models with uniform recombination rates with phased data
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(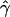 )d )d
|
E(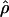 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite likelihood method | |||||||||
| 5 | 5 | 0.246 | 0.696 | 0.555 | 0.611 | 8.917 | 5.097 | 2.842 | 0.994 |
| 10 | 10 | 0.324 | 0.828 | 0.609 | 0.580 | 12.590 | 11.140 | 1.769 | 0.829 |
| 20 | 20 | 0.368 | 0.792 | 0.671 | 0.590 | 19.250 | 21.650 | 1.274 | 0.770 |
| 40 | 40 | 0.468 | 0.874 | 0.638 | 0.512 | 34.880 | 43.490 | 0.936 | 0.591 |
| 80 | 80 | 0.460 | 0.840 | 0.691 | 0.490 | 59.820 | 92.520 | 0.766 | 0.624 |
| 100 | 100 | 0.518 | 0.820 | 0.665 | 0.462 | 77.190 | 115.04 | 0.727 | 0.604 |
| Summary statistics method: acceptance rate = 15% | |||||||||
| 5 | 5 | 0.265 | 0.647 | 0.547 | 0.408 | 12.1873 | 9.7706 | 4.619 | 4.024 |
| 10 | 10 | 0.398 | 0.766 | 0.589 | 0.520 | 14.7102 | 13.4611 | 2.075 | 1.590 |
| 20 | 20 | 0.483 | 0.816 | 0.594 | 0.572 | 23.1785 | 21.957 | 1.282 | 0.771 |
| 40 | 40 | 0.588 | 0.868 | 0.476 | 0.462 | 48.44 | 44.90 | 1.046 | 0.639 |
| 80 | 80 | 0.576 | 0.850 | 0.488 | 0.479 | 91.54 | 90.08 | 0.843 | 0.581 |
| 100 | 100 | 0.648 | 0.852 | 0.480 | 0.472 | 109.68 | 112.82 | 0.742 | 0.563 |
| Summary statistics method: acceptance rate = 30% | |||||||||
| 5 | 5 | 0.242 | 0.746 | 0.574 | 0.394 | 7.768 | 5.735 | 2.402 | 0.914 |
| 10 | 10 | 0.358 | 0.842 | 0.533 | 0.588 | 14.230 | 10.543 | 1.752 | 0.694 |
| 20 | 20 | 0.522 | 0.842 | 0.580 | 0.601 | 22.717 | 20.810 | 1.215 | 0.662 |
| 40 | 40 | 0.638 | 0.888 | 0.543 | 0.498 | 43.060 | 43.540 | 0.937 | 0.567 |
| 80 | 80 | 0.604 | 0.860 | 0.514 | 0.534 | 89.060 | 86.640 | 0.839 | 0.562 |
| 100 | 100 | 0.652 | 0.846 | 0.484 | 0.491 | 109.58 | 109.32 | 0.743 | 0.554 |
| Summary statistics method: acceptance rate = 60% | |||||||||
| 5 | 5 | 0.233 | 0.783 | 0.565 | 0.463 | 6.913 | 4.856 | 2.020 | 0.754 |
| 10 | 10 | 0.407 | 0.832 | 0.568 | 0.656 | 12.446 | 9.655 | 1.514 | 0.631 |
| 20 | 20 | 0.555 | 0.823 | 0.571 | 0.673 | 23.043 | 18.874 | 1.197 | 0.558 |
| 40 | 40 | 0.654 | 0.908 | 0.567 | 0.593 | 39.66 | 39.10 | 0.858 | 0.496 |
| 80 | 80 | 0.634 | 0.872 | 0562 | 0.623 | 80.14 | 79.12 | 0.739 | 0.520 |
| 100 | 100 | 0.68 | 0.822 | 0.570 | 0.556 | 98.66 | 101.74 | 0.690 | 0.539 |
TABLE B2.
Performance for models with uniform recombination rates with phased data for some additional parameters [n = 50, L = 125 bp, 50-kb sequences with θ = 40.0, grid (0, 2, 4, 6, 8, … , 50)]
| γa | ρa | g(γ)b | g(ρ)b | B(γ)c | B(ρ)c |
E(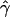 )d )d
|
E(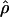 )d )d
|
V(γ)e | V(ρ)e |
|---|---|---|---|---|---|---|---|---|---|
| Hudson's composite-likelihood method | |||||||||
| 12 | 12 | 0.172 | 0.915 | 0.618 | 0.535 | 14.66 | 12.28 | 1.616 | 0.459 |
| 16 | 8 | 0.206 | 0.884 | 0.592 | 0.553 | 17.35 | 8.24 | 1.261 | 0.570 |
| Summary statistics method | |||||||||
| 12 | 12 | 0.328 | 0.895 | 0.484 | 0.511 | 18.05 | 12.62 | 1.499 | 0.505 |
| 16 | 8 | 0.404 | 0.857 | 0.478 | 0.528 | 20.28 | 8.50 | 1.083 | 0.595 |
γ and ρ denote the true values of the gene-conversion and crossing-over rates under which 1000 data sets were simulated.
g(γ) and g(ρ) denote the fraction of the data sets for which the estimates of gene conversion (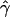 ) and crossing over (
) and crossing over (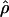 ) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
) lie within a factor of 2 of the true values (i.e., γ and ρ), respectively.
B(γ) and B(ρ) denote the fraction of times the estimates of gene conversion and crossing over are lower than the true values, given that they are not equal to the true values.
E(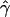 ) and E(
) and E(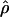 ) denote the mean of the estimates of gene-conversion and crossing-over rates.
) denote the mean of the estimates of gene-conversion and crossing-over rates.
V(γ) and V(ρ) denote the root mean square relative error for the estimates.
References
- Allers, T., and M. Litchen, 2001. Differential timing and control of noncrossover and crossover recombination during meiosis. Cell 106: 47–57. [DOI] [PubMed] [Google Scholar]
- Andolfatto, P., and M. Nordborg, 1998. The effect of gene-conversion on intralocus associations. Genetics 148: 1397–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andolfatto, P., and J. D. Wall, 2003. Linkage disequilibrium patterns across a recombination gradient in African Drosophila melanogaster. Genetics 165: 1289–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaumont, M. A., W. Zhang and D. J. Balding, 2002. Approximate Bayesian computation in population genetics. Genetics 162: 2025–2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford, D. C., T. Bhangale, N. Li, G. Hellenthal, M. J. Rieder et al., 2004. Evidence for substantial fine-scale variation in recombination rates across the human genome. Nat. Genet. 36: 700–706. [DOI] [PubMed] [Google Scholar]
- Dunham, I., N. Shimizu, B. A. Roe, S. Chissoe, A. R. Hunt et al., 1999. The DNA sequence of human chromosome 22. Nature 402: 489–495. [DOI] [PubMed] [Google Scholar]
- Fearnhead, P., 2003. Consistency of estimators of the population-scaled recombination rate. Theor. Popul. Biol. 64: 67–79. [DOI] [PubMed] [Google Scholar]
- Fearnhead, P., and P. Donnelly, 2001. Estimating recombination rates from population genetic data. Genetics 159: 1299–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fearnhead, P., and P. Donnelly, 2002. Approximate likelihood methods for estimating local recombination rates (with discussion). J. R. Soc. Sci. Ser. B 64: 657–680. [Google Scholar]
- Fearnhead, P., and N. G. Smith, 2005. A novel method with improved power to detect recombination hotspots from polymorphism data reveals multiple hotspots in human genes. Am. J. Hum. Genet. 77: 781–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisse, L., R. R. Hudson, A. Bartoszewicz, J. D. Wall, J. Donfack et al., 2001. Gene-conversion and different population histories may explain the contrast between polymorphism and linkage disequilibrium levels. Am. J. Hum. Genet. 69: 831–843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fullerton, S. M., R. M. Harding, A. J. Boyce and J. B. Clegg, 1994. Molecular and population genetic analysis of allelic sequence diversity at the human-globin locus. Proc. Natl. Acad. Sci. USA 91: 1805–1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths, R. C., and P. Marjoram, 1996. Ancestral inference from samples of DNA sequences with recombination. J. Comput. Biol. 3: 479–502. [DOI] [PubMed] [Google Scholar]
- Hey, J., and J. Wakeley, 1997. A coalescent estimator of the population recombination rate. Genetics 145: 833–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinds, D. A., L. L. Stuve, G. B. Nilsen, E. Halperin, E. Eskin et al., 2005. Whole genome patterns of common DNA variation in three human populations. Science 307: 1072–1079. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., 1987. Estimating the recombination parameter of a finite population model without selection. Genet. Res. 50: 245–250. [DOI] [PubMed] [Google Scholar]
- Hudson, R. R., 1993. The how and why of generating gene genealogies, pp. 23–36 in Mechanisms of Molecular Evolution, edited by N. Takahata and A. G. Clark. Sinauer Associates, Sunderland, MA.
- Hudson, R. R., 2001. Two-locus sampling distributions and their application. Genetics 159: 1805–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson, R. R., and N. L. Kaplan, 1985. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111: 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innan, H., B. Padhukasahasram and M. Nordborg, 2003. The pattern of polymorphism on human chromosome 21. Genome Res. 13: 1158–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys, A. J., and C. A. May, 2004. Intense and highly localized gene-conversion activity in human meiotic crossover hotspots. Nat. Genet. 36: 151–156. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., L. Kauppi and R. Neumann, 2001. Intensely punctuate meiotic recombination in the class II region of the major histocompatibilty complex. Nat. Genet. 29: 217–222. [DOI] [PubMed] [Google Scholar]
- Jeffreys, A. J., R. Neumann, M. Panayi, S. Myers and P. Donnelly, 2005. Human recombination hotspots hidden in regions of strong marker associations. Nat. Genet. 37: 601–606. [DOI] [PubMed] [Google Scholar]
- Kong, A., D. F. Gudbjartsson, J. Sainz, G. M. Jonsdottir, S. A. Gudjonsson et al., 2002. A high-resolution recombination map of the human genome. Nat. Genet. 31: 241–247. [DOI] [PubMed] [Google Scholar]
- Kuhner, M. K., J. Yamato and J. Felsenstein, 2000. Maximum likelihood estimation of recombination rates from population data. Genetics 156: 1393–1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langley, C. H., B. P. Lazzaro, W. Phillips, E. Heikkinen and J. M. Braverman, 2000. Linkage disequilibrium and the site frequency spectra in the su(s) and su(wa) regions of the Drosophila melanogaster X chromosome. Genetics 156: 1837–1852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, N., and M. Stephens, 2003. Modeling linkage disequilibrium, and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 165: 2213–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marjoram, P., J. Molitor, V. Plagnol and S. Tavare, 2003. Markov chain Monte Carlo without likelihoods. Proc. Natl. Acad. Sci. USA 100: 15324–15328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean, G. A. T., S. R. Myers, S. Hunt, P. Deloukas, D. R. Bentley et al., 2004. The fine-scale structure of recombination rate variation in the human genome. Science 304: 581–584. [DOI] [PubMed] [Google Scholar]
- Myers, S., L. Bottolo, C. Freeman, G. A. T. McVean and P. Donnelly, 2005. A fine-scale map of recombination rates and hotspots across the human genome. Science 310: 321–324. [DOI] [PubMed] [Google Scholar]
- Nielsen, R., 2000. Estimation of population parameters and recombination rates from single nucleotide polymorphisms. Genetics 154: 931–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padhukasahasram, B., P. Marjoram and M. Nordborg, 2004. Estimating the rate of gene-conversion on human chromosome 21. Am. J. Hum. Genet. 75: 386–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptak, S. E., K. Voelpel and M. Przeworski, 2004. Insights into recombination from patterns of linkage disequilibrium in humans. Genetics 167: 387–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, N. G. C., and P. Fearnhead, 2005. A comparison of three estimators of the population-scaled recombination rate: accuracy and robustness. Genetics 171: 2051–2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szostak, J. W., T. L. Orr-Weaver, R. J. Rothstein and F. W. Stahl, 1983. The double-strand-break repair model for recombination. Cell 33: 25–35. [DOI] [PubMed] [Google Scholar]
- Wakeley, J., 1997. Using the variance of pairwise differences to estimate the recombination rate. Genet. Res. 69: 45–48. [DOI] [PubMed] [Google Scholar]
- Wall, J. D., 2000. A comparison of estimators of the population recombination rate. Mol. Biol. Evol. 17: 156–163. [DOI] [PubMed] [Google Scholar]
- Wall, J. D., 2004. Estimating recombination rates using three site likelihoods. Genetics 167: 1461–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss, G., and A. Von Haeseler, 1998. Inference of population history using a likelihood approach. Genetics 149: 1539–1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiehe, T., J. Mountain, P. Parham and M. Slatkin, 2000. Distinguishing recombination and intragenic gene-conversion by linkage disequilibrium patterns. Genet. Res. 75: 61–73. [DOI] [PubMed] [Google Scholar]
- Wiuf, C., and J. Hein, 2000. The coalescent with gene-conversion. Genetics 155: 451–462. [DOI] [PMC free article] [PubMed] [Google Scholar]