Networks of interneurons with fast and slow γ-aminobutyric acid type A (GABA_A) kinetics provide substrate for mixed gamma-theta rhythm

Abstract

During active exploration, hippocampal neurons exhibit nested rhythmic activity at theta (≈8 Hz) and gamma (≈40 Hz) frequencies. Gamma rhythms may be generated locally by interactions within a class of interneurons mediating fast GABA_A (GABA_A,fast) inhibitory postsynaptic currents (IPSCs), whereas theta rhythms traditionally are thought to be imposed extrinsically. However, the hippocampus contains slow biophysical mechanisms that may contribute to the theta rhythm, either as a resonance activated by extrinsic input or as a purely local phenomenon. For example, region CA1 of the hippocampus contains a slower class of GABA_A (GABA_A,slow) synapses, believed to be generated by a distinct group of interneurons. Recent evidence indicates that these GABA_A,slow interneurons project to the GABA_A,fast interneurons that contribute to hippocampal gamma rhythms. Here, we use biophysically based simulations to explore the possible ramifications of interneuronal circuits containing separate classes of GABA_A,fast and GABA_A,slow interneurons. Simulated interneuronal networks with fast and slow synaptic kinetics can generate mixed theta-gamma rhythmicity under restricted conditions, including strong connections among each population, weaker connections between the two populations, and homogeneity of cellular properties and drive. Under a broader range of conditions, including heterogeneity, the networks can amplify and resynchronize phasic responses to weak phase-dispersed external drive at theta frequencies to either GABA_A,slow or GABA_A,fast cells. GABA_A,slow synapses are necessary for this process of amplification and resynchronization.

A prevalent feature of activity in the brain is the presence of distinct patterns of synchronous oscillatory activity that are linked tightly to the behavioral state of the animal. A particularly prominent rhythmic pattern is that of synchronous firing in the gamma (≈40 Hz) and theta (≈8 Hz) bands, seen under conditions of active exploration in the rat hippocampal formation, a set of structures necessary for declarative memory. A recent flurry of experimental, computational, and theoretical work (1–6) has made the convincing argument that the gamma rhythm is generated intrinsically by networks of inhibitory interneurons in the hippocampus. The theta rhythm, on the other hand, is commonly believed to be imposed on the hippocampus by phasic input from the medial septum/diagonal band of Broca and entorhinal cortex (7–12).

Two lines of evidence, however, imply that the traditional picture of nested theta and gamma rhythms in the hippocampal formation may be incomplete. First, recordings from the medial septum/diagonal band of Broca indicate that the theta-locked cells of the region do not fire with a common phase (13). This result seems inconsistent with the pacemaker hypothesis, unless, as has been suggested (14), a functionally significant subset of septal cells with common phase are the true pacemakers of the region. Second, under the appropriate pharmacological conditions, hippocampal brain slices can generate synchronous firing at both gamma and theta frequencies in the absence of phasic stimulation (11, 15). Several biophysical properties of the hippocampal formation, including slow inhibitory synaptic dynamics (16–18) and cellular spiking dynamics (19–21), may contribute to this phenomenon, which may in turn contribute to synchrony at theta frequencies in the hippocampal formation of living animals.

Previous studies have demonstrated that two kinetically distinct GABA_A receptor-mediated synaptic currents are observed in CA1 pyramidal cells and some interneurons. The fast GABA_A component (GABA_A,fast) is a rapidly decaying (τ_decay = 9 ms at 35°C), somatic current mediated by basket cells and other interneurons projecting to perisomatic regions. It is believed to underlie gamma frequency rhythms in interneuronal networks (1–6). The slow GABA_A component (GABA_A,slow) is a dendritic current that is activated by stimuli applied to stratum lacunosum-moleculare (SL-M) and is much slower to decay (τ_decay = 50 ms). GABA_A,fast and GABA_A,slow synaptic responses appear to arise from distinct populations of interneurons (18). In much the same way that GABA_A,fast cells seem to control the gamma rhythm, GABA_A,slow cells represent a prime candidate mechanism, wholly within the hippocampal formation, that may contribute to the theta rhythm. Here, we use computational models to argue that interconnected populations of GABA_A,slow and GABA_A,fast interneurons are useful for generating, amplifying, and resynchronizing coherent theta and gamma rhythms in region CA1 of the hippocampus.¶

Materials and Methods

Experimental Methods.

Techniques are described in detail elsewhere (18, 23). Briefly, experimental data were obtained by using hippocampal brain slices obtained from young rats (13–39 days). Whole-cell recordings were made at room temperature (24°C) in a recording chamber perfused with artificial cerebrospinal fluid buffer (127 mM NaCl/1.21 mM KH₂PO₄/1.87 mM KCl/26 mM NaHCO₃/2.17 mM CaCl₂/1.44 mM MgSO₄/10 mM glucose/saturated with 95% 0₂/5%CO₂). Interneurons in stratum radiatum (SR) of CA1 were visualized by using infrared differential interference contrast video microscopy. Data were filtered at 2–5 kHz, and then sampled at 5–10 kHz. Borosilicate patch pipettes were fire polished and coated with Sylgard (World Precision Instruments, Sarasota, FL) to reduce capacitance. Patch pipettes had open-tip resistances of 2–4 MΩ when filled with the recording solution [140 mM CsCl/10 mM NaCl/10 mM Hepes/5 mM EGTA/0.5 mM CaCl₂/2 mM MgATP/5 mM QX-314 (pH 7.3)]. Access resistances were typically 10–20 MΩ and were then compensated 60–80%. Cells were held at −60 mV. Evoked and spontaneous GABA_A inhibitory postsynaptic currents (IPSCs) were isolated by bath application of 20 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) and 40 μM d,l-2-amino-5-phosphonovaleric acid (APV) to block α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and N-methyl-d-aspartate (NMDA)-mediated currents, and by the inclusion of CsCl and QX-314 in the patch pipette to block γ-aminobutyric acid type B-mediated currents. Stimuli (5–80 μA) were applied to SL-M to evoke GABA_A,slow. 6-cyano-7-nitroquinoxaline-2,3-dione, 2-amino-5-phosphonovaleric acid, and QX-314 were obtained from Research Biochemicals. Biocytin was obtained from Molecular Probes. All other drugs and reagents were obtained from Sigma.

Computational Methods.

Individual interneurons were modeled by using a single-compartment, Hodgkin–Huxley-type model (5) that replicates the major electrophysiological properties of hippocampal interneurons (e.g., width of spikes, range of firing rates; see www.cbd.bu.edu/research/ndrp1.html#ndr1a for equations). Interneurons were connected in an all-to-all fashion by using simulated, nonsaturating chemical synapses that triggered biexponential conductance changes in the postsynaptic neuron. Kinetics of inhibitory synapses reflected values measured at 35°C. For GABA_A,fast synapses, we used rising time constants of 1 ms and falling time constants of 9 ms. For GABA_A,slow synapses, we used rising time constants of 5 ms and falling time constants of 50 ms. For simulations related to Fig. 3, both rising and falling time constants were scaled by the same amount. Connections were all-to-all. Simulations were written in C and run on a UNIX workstation (INDY R5000, Silicon Graphics, Mountain View, CA).

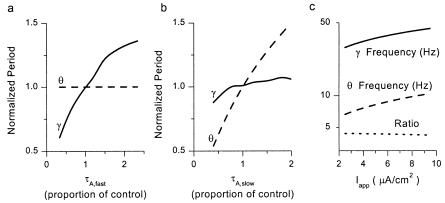
Figure 3.

Dependence on theta and gamma frequencies on synaptic kinetics and applied current. (a) Normalized periods of theta and gamma rhythms from autonomously oscillating, noiseless networks, plotted vs. τ_A,fast, the time constant of decay of GABA_A,fast synapses. Parameter values other than τ_A,fast and noise level were the same as in Fig. 2. Control values of τ_A,fast, theta period, and gamma period are 9, 143, and 26 ms, respectively. (b) Normalized periods of theta and gamma rhythms vs. τ_A,slow, the time constant of decay of GABA_A,slow synapses. Parameter values other than τ_A,slow and noise level were the same as in Fig. 2. Control values of τ_A,slow, theta period, and gamma period are 50, 143, and 26 ms, respectively. (c) Frequencies of theta and gamma rhythms plotted vs. I_app, the amount of current delivered to each cell in the simulated network. Also plotted is the ratio (γ/θ) of the gamma frequency to theta frequency. All parameters other than I_app and noise level were the same as in Fig. 2.

Analysis of Computational Data.

Spike times of individual cells were determined by using a simple thresholding algorithm (threshold = 0 mV). Population firing histograms were determined by using a bin width of 0.5 ms. Histogram values were divided by the number of cells in a given population (50 cells) to convert them to firing probabilities. Magnitude spectra were determined by applying a fast Fourier transform to population histograms.

Vector strengths were calculated from GABA_A,slow population histograms in response to periodic stimuli. In these calculations, each spike in each cell was converted to a vector of unit magnitude and phase relative to the input sinusoid. Vector strength equals the normalized magnitude of the vector sum of these components, varying between 0 (for random phases) and 1 (for perfect phase-locking). Vector strength among the GABA_A,slow cells was chosen as the metric because we found it to be the most reliable in determining the ability of the network to respond with coherent theta-gamma responses to periodic drive. A host of other metrics were tried and found to be lacking in some important regard. For example, vector strength at 8 Hz among the GABA_A,fast cells is not appropriate because this measure penalizes the network for generating a robust theta-gamma pattern, with multiple spikes in GABA_A,fast cells per theta cycle; methods based on spectral content from fast Fourier transforms were inaccurate because they could not easily account for different envelopes of firing, which imply different relative sizes of the fundamental frequency and its harmonics.

Results

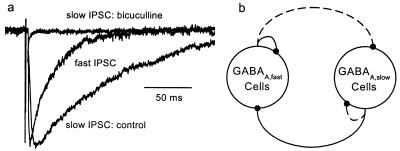
Previous experiments (23) have established the existence of projections from GABA_A,slow to GABA_A,fast cells of sufficient strength to induce extended pauses in the spontaneous activity of the latter population in brain slices. This projection can be demonstrated directly by recording from interneurons of SR with perisomatic projections to CA1 pyramidal cells. In SR interneurons, electrical stimuli applied to SL-M evoke GABA_A,slow IPSCs (Fig. 1a). The interneuronal circuit suggested by existing data are shown in Fig. 1b, in which demonstrated connections between and among cell classes are shown as solid lines and hypothesized connections are shown as dashed lines.

Figure 1.

Interconnections between two classes of inhibitory interneurons. (a) Slow IPSC evoked in a SR interneuron by SL-M stimulation. The slow IPSC was completely blocked by 40 μM bicuculline. Also shown is the averaged fast spontaneous IPSC from the same cell for comparison. Magnitudes are normalized for comparative purposes. (b) Suggested interneuronal circuitry in region CA1. Solid lines show established connections. Dashed lines show hypothetical connections. GABA_A,fast and GABA_A,slow cells are so-named because of the kinetics of their postsynaptic effects.

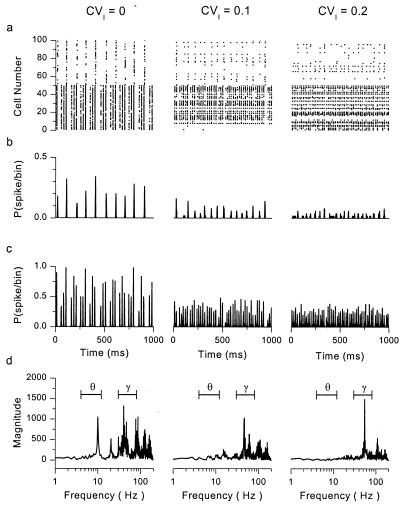
We used computer simulations to determine whether or not two such populations are capable of generating theta-gamma rhythmic patterns analogous to those seen experimentally, under conditions of constant or periodic drive. The simulated network, reduced to include only the essential details necessary to study interneuronal interactions, did not include descriptions of excitatory pyramidal cells, thought to be important for long-range but not local synchrony (24), multicompartmental representations of interneurons, or γ-aminobutyric acid type B (GABA_B)-mediated effects. Fig. 2a shows spike trains, in raster form, from such a network of 50 GABA_A,slow and 50 GABA_A,fast cells. In addition to known connections (solid lines in Fig. 1b), this network includes hypothesized connections among GABA_A,slow cells. From left to right, the raster plots represent networks with identical parameters but increasing levels of heterogeneity, imposed by randomly distributing the level of current bias in the cells with a given coefficient of variation (CV_I, the ratio of standard deviation to mean). In the homogeneous case (CV_I = 0), GABA_A,slow cells fire periodically at theta frequencies, under the control of the strong‖ slow synapses among them. GABA_A,fast cells respond in a pattern resembling that seen in vivo, firing bursts at gamma frequencies with periodic interruptions every theta cycle. This pattern of activity is evident in raw spike trains (Fig. 2a Left), population histograms (Fig. 2 b and c Left), and in frequency spectra of spike trains from GABA_A,fast cells (Fig. 2d Left). Synchronous gamma-frequency firing within bursts is controlled by GABA_A,fast synapses among the cells; synchronous activity among GABA_A,slow cells at theta frequencies drives the periodic pauses in firing of GABA_A,fast cells.

Figure 2.

Autonomous theta-gamma oscillations in networks with mixed GABA_A kinetics. (a) Raster plots for a network containing 50 GABA_A,fast (Bottom) and 50 GABA_A,slow (Top) neurons. CV_I = the coefficient of variation (ratio of standard deviation to mean) of the level of dc current drive given to the population of cells. Increasing CV_I implies increasing heterogeneity in drive. (b and c) Population histograms for (b) GABA_A,slow and (c) GABA_A,fast cells, generated from the spike trains in a. (d) Magnitude spectra of the histograms of the GABA_A,fast cells. The theta (4–12 Hz) and gamma (30–80 Hz) frequency bands are marked. Model specifications: mean values of applied current = 5 μA/cm² for GABA_A,fast cells and 3 μA/cm² for GABA_A,slow cells. In addition to randomly distributed mean currents, time-dependent current noise (normally distributed, σ = 5 μA/cm²) was added to each cell independently. Cells were all-to-all coupled with coupling conductances (in mS/cm²): G_fast,fast = 0.04, G_fast,slow = 0, G_slow,slow = 0.08, G_slow,fast = 0.04.

In neuronal models with uniform synaptic kinetics, the frequencies of robust synchronous rhythms are controlled by the decay time constant of inhibition (1, 4, 5). In tuned networks with fast and slow synaptic kinetics, the frequencies of autonomous gamma and theta rhythms in GABA_A,fast and GABA_A,slow cells are controlled somewhat independently by the decay time constants of fast and slow inhibition, respectively. Fig. 3 (a and b) shows plots of the two rhythms in autonomously oscillating networks with varying speeds of decay of the fast or slow synapses. Increasing the decay time constant of GABA_A,fast responses (τ_A,fast; Fig. 3a) leads to monotonic increases in the period of the gamma rhythm; the theta frequency, set by the network of GABA_A,slow cells, is unaffected by changes in τ_A,fast, because this network has no connections from the GABA_A,fast to GABA_A,slow cells. In cases with a nonzero connection from fast to slow cells, the effect of τ_A,fast on the theta rhythm is measurable but small (data not shown). Increasing the decay time constant of GABA_A,slow responses (τ_A,slow; Fig. 3b) creates complementary changes. Proportional changes in the gamma frequency are much smaller than those for the theta frequency. At a given value of τ_A,fast and τ_A,slow, the frequencies of autonomous theta and gamma oscillations depend similarly on the value of driving current I_app, which is uniform to all cells in this case (Fig. 3c). The ratio of gamma and theta frequencies stays nearly constant over a large range of applied currents (dotted line). This result is reminiscent of those seen in vivo (25).

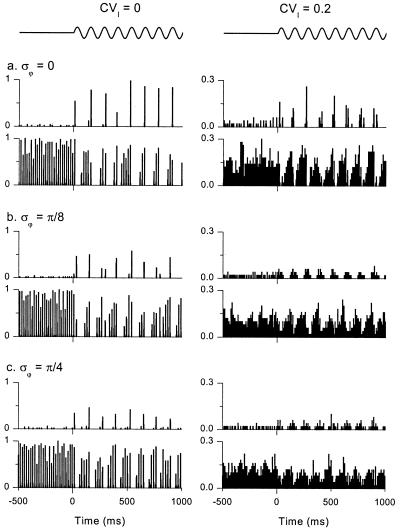
The distinct theta-gamma firing pattern is fragile, requiring parameters that are both carefully tuned and homogeneous. In models with no connections from GABA_A,fast to GABA_A,slow cells (e.g., Fig. 2), parameters must be tuned to give strong interconnections among cells of the same kinetic class; appropriate levels of drive to each population to give firing rates (under conditions of inhibition) that are compatible with the speed of decay of GABA_A,fast or GABA_A,slow inhibition, and tuning of the connections from GABA_A,slow to GABA_A,fast cells to create a pause of the appropriate duration in activity of GABA_A,fast cells. In models including connections from GABA_A,fast to GABA_A,slow cells, as is likely the case in the biological network (21, 26), parameters must be tuned even more carefully, with strong connections between cells of a given class, weaker connections between classes, and precise values of drive. Slight mistuning leads to a population rhythm that is dominated by one population or the other (e.g., Fig. 4 Left, for t < 0).

Figure 4.

Networks with weak 8-Hz, oscillatory drive show robust theta-gamma activity. Each group of two plots shows population histograms for GABA_A,slow (upper plots) and GABA_A,fast (lower plots) cells. The average stimulus for each cell is shown schematically above the top two panels. For t < 0, all cells in the network are driven with constant current. For t > 0 (note the tick mark on the x axis), a small 8-Hz component (magnitude 2 μA/cm²) is added to the drive of the GABA_A,slow cells. CV_I = coefficient of variation (ratio of standard deviation to mean) in dc current drive. σ_ϕ = the standard deviation of the phase of the small 8-Hz input. Both current levels and phases were normally distributed. Model specifications: mean values of applied current = 7 μA/cm² for GABA_A,fast cells, 4.5 μA/cm² for GABA_A,slow cells. Mean values were perturbed with coefficient of variation CV_I as before. Time-dependent current noise (normally-distributed, σ = 7 μA/cm²) was added to each cell independently. Cells were all-to-all coupled with coupling conductances (in mS/cm²): G_fast,fast = 0.04, G_fast,slow = 0.03, G_slow,slow = 0.06, G_slow,fast = 0.06.

Even for appropriately tuned circuits, responses quickly lose their theta-band energy with increasing levels of heterogeneity (Fig. 2 a–d Center and Right). With small levels of heterogeneity (CV_I = 0.1), activity in some GABA_A,slow cells is suppressed, leaving the surviving cells to fire more frequently but less coherently. The unsuppressed GABA_A,fast cells fire mostly at gamma frequencies, with less interruption. This trend continues with increasing heterogeneity (Right).

Responses to phasic input are more robust to poorly tuned parameters than responses to DC input (Fig. 4). At the beginning of Fig. 4a Left, the GABA_A,fast cells dominate the network in response to DC stimulation of both populations (t < 0), because parameters are mistuned. However, when weak 8-Hz sinusoidal stimulation is presented to the GABA_A,slow cells (t > 0; onset indicated by the tick mark on the x axis), roughly equivalent in magnitude to the effect of a single synaptic connection between two cells of the same kinetic class, the network amplifies this weak input and thus regenerates coherent theta-gamma activity. Corresponding magnitude spectra, derived from the GABA_A,fast cells for t > 0, quantify this result in the frequency domain (Fig. 5).

Figure 5.

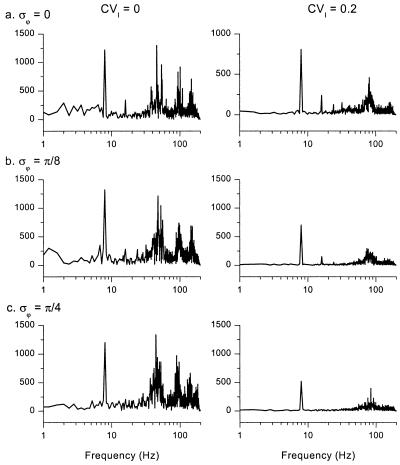
Frequency spectra of networks with oscillatory drive. Magnitude spectra of histograms of the GABA_A,fast cells, arranged in the same order as in Fig. 4. Spectra were derived from fast Fourier transforms (see Materials and Methods) of data traces in Fig. 4 for t > 0.

Theta-gamma oscillations driven by weak periodic drive are more robust to heterogeneity than autonomous oscillations. Fig. 4a Right shows population histograms with heterogeneity in average drive to the modeled neurons. The corresponding magnitude spectrum for the GABA_A,fast cells is plotted in Fig. 5a Right. Even at this relatively high level of heterogeneity (CV_I = 0.2), theta-gamma activity is preserved; gamma coherence is reduced but still present. This result holds for networks with no GABA_A,fast to GABA_A,slow connections as well (data not shown).

The ability of the network to generate coherent theta-gamma oscillations also persists when individual GABA_A,slow cells receive input with random perturbations of phase, as might be expected when the cells are driven by remote pacemakers with differing mean phases, conduction velocities, or axon path lengths (Figs. 4 b and c and 5 b and c; σ_ϕ is the standard deviation of the randomly distributed phases, in radians). Thus, a network of interneurons with mixed GABA_A,fast and GABA_A,slow kinetics can serve to “resynchronize” periodic input with dispersed phase relationships.

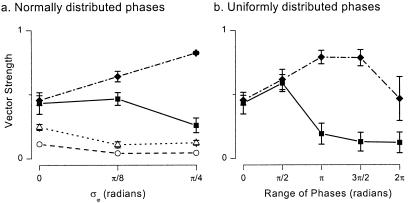
GABA_A,slow synapses are crucial for the amplification and resynchronization of weak phase dispersed inputs. Fig. 6a shows plots of vector strength, a measure of the ability of the GABA_A,slow cells to phase lock to a weak 8-Hz sinusoidal input (see Materials and Methods), plotted versus phase dispersion σ_ϕ (the standard deviation of the normally distributed phases of sinusoidal input). The solid symbols show vector strengths for weak periodic input applied to either the GABA_A,slow (squares) or GABA_A,fast (diamonds) population. With periodic stimulation of GABA_A,slow cells, these cells are able to select a common phase and thus keep vector strength high even with relatively large phase dispersion. With periodic stimulation of the GABA_A,fast cells, theta coherence actually rises with increased phase dispersion. The interconnected subnetwork of GABA_A,slow cells is necessary for this result, which disappears if (i) slow synaptic kinetics are converted to fast kinetics (Fig. 6a, open symbols); (ii) connections from GABA_A,fast to GABA_A,slow cells are removed (data not shown); or (iii) interconnections among GABA_A,slow cells are disrupted (data not shown).

Figure 6.

GABA_A,slow synapses are necessary for theta-gamma responses to weak periodic drive. Model parameters as in Figs. 4 and 5 for control simulations (filled symbols). Vector strengths measure the degree to which the GABA_A,slow cells synchronize at the stimulus frequency. (a) Vector strengths (means ± σ; n = 5) in response to normally distributed phases of sinusoidal input (σ_ϕ = standard deviation). Solid squares and diamonds indicate delivery of the 8-Hz input to the GABA_A,slow and GABA_A,fast cells of the control network, respectively. Open symbols indicate responses of a network in which the postsynaptic responses driven by GABA_A,slow cells have been transformed into GABA_A,fast responses. Vector strengths are measured in the population of formerly GABA_A,slow cells. For open circles (error bars too small to resolve), the new network had maximal conductances as in the control case. Open triangles indicate a network with uniform GABA_A,fast kinetics in which values of synaptic conductance have been scaled up to preserve the area of the postsynaptic response, and thus leave the average amount of inhibition at a given firing rate unchanged from the control case. (b) Vector strengths in GABA_A,slow cells, measured in response to uniformly distributed phases of 8-Hz input to GABA_A,slow (squares) or GABA_A,fast cells (diamonds).

Noting that performance actually improves with phase dispersion in the case where phasic input is delivered to the GABA_A,fast cells, we reexamined phase dispersion results over a larger range of uniformly distributed phases of sinusoidal input (Fig. 6b).** For periodic input to GABA_A,slow cells, vector strength remains elevated as long as the range of input phases is less than π/2. For periodic input to GABA_A,fast cells, vector strength remains very high until the range of phases approaches the fully phase-dispersed (2π) case. Even in this case, vector strength is reasonably large.

Discussion

Rhythms within a neuronal network can be generated by local mechanisms, imposed by inputs from remote locations, or created by a combination of extrinsic and intrinsic properties. The hippocampus receives rhythmic input at theta frequencies from the medial septum and diagonal band of Broca, as well as the entorhinal cortex; either or both of these input sources may serve as a pacemaking source for this common rhythm. Nevertheless, the existence of prominent slow cellular and synaptic properties within the hippocampal formation suggests that the hippocampus does not in general react passively to an imposed rhythm. In this paper, we use new evidence for connections from GABA_A,slow cells to the more well-known GABA_A,fast interneurons to create a network based on two populations of inhibitory neurons. The network is able under restricted circumstances to autonomously create the observed nested theta-gamma rhythm. These restrictions include strong connections among kinetically homogeneous populations, weaker connections between populations (it is particularly important to keep the connections from GABA_A,fast to GABA_A,slow cells small), and carefully tuned input drives. It is possible that the fragility we see could be mitigated by the presence of excitatory cells in the network, to provide a method for periodic escape for cells that have been shut out by a more dominant population, but we suspect that this excitation would also have to be tuned extremely carefully to support the autonomous theta-gamma rhythm.

A more surprising property of the simulated GABA_A,fast/GABA_A,slow network is its ability to amplify and resynchronize phase-dispersed periodic input signals. This property of resynchronization is more robust to heterogeneity and mistuned parameters than are the autonomous theta-gamma oscillations. Resynchronization may be particularly functionally important, given that the periodic drive from the septum to hippocampus is likely to be highly phase dispersed (13). Like synchronization, resynchronization depends crucially on the presence of strongly interconnected GABA_A,slow cells. We speculate that theta frequency input drives GABA_A,slow cells to fire at the appropriate frequencies, allowing the GABA_A,slow interconnections to pull cells to a common phase. We have further shown that theta frequency input to the GABA_A,fast cells accomplishes the task of resynchronization more effectively than input to the GABA_A,slow cells, perhaps because the summed phasic input that each GABA_A,slow cell receives from the pool of GABA_A,fast cells is similar. Some phase dispersion of input to GABA_A,fast cells can actually boost theta power in GABA_A,slow cells, possibly by providing a more sinusoidal (as opposed to pulsatile) theta frequency drive to the GABA_A,slow cells.

The topography of the model used here is based on the assumption that there are two populations of interneurons in region CA1, with distinct kinetics of postsynaptic effects. Evidence for distinct populations of interneurons, with corresponding GABA_A,slow or GABA_A,fast postsynaptic effects, comes from a number of sources. First, minimal stimulation in the neuropil of region CA1 evokes either GABA_A,slow (for stimulation in SL-M or distal SR) or GABA_A,fast responses (for stimulation in stratum pyramidale) in pyramidal cells (18). Evoked GABA_A,slow IPSCs are roughly five times slower and five times smaller than GABA_A,fast IPSCs. Second, recordings from CA1 pyramidal cells reveal similarly sized but kinetically distinct GABA_A,slow and GABA_A,fast spontaneous IPSCs (18). Both slow and fast spontaneous IPSCs are a mixture of IPSCs evoked by spontaneous action potentials and miniature IPSCs seen in the presence of tetrodotoxin (18). Like evoked IPSCs, spontaneous GABA_A,slow IPSCs are roughly five times slower to rise and fall than their GABA_A,fast counterparts. Third, selective stimulation of SL-M interneurons via a cell-attached patch electrode gives rise to IPSCs that are slower than those evoked by simulation of interneurons from the stratum pyramidale, stratum oriens, or stratum radiatum (17). The difference in kinetics recorded by Ouardouz and Lacaille (17) is not as dramatic as that reported by Pearce (16) or Banks et al. (18), but this discrepancy may be caused by differences in recording conditions such as holding potential and pipette solution.

A second crucial feature of the model is that GABA_A,slow and GABA_A,fast populations connect with each other to some degree. Connections from GABA_A,fast to GABA_A,slow cells play conflicting roles, depending on the stimulus conditions. For dc stimulation, these connections disrupt theta-gamma synchrony. On the other hand, their presence allows robust resynchronization of phase-dispersed periodic input to GABA_A,fast cells (from, e.g., the medial septum). Experimental evidence in support of this connection awaits unambiguous identification of the GABA_A,slow population (see below). Circumstantially, fast spontaneous IPSCs are seen in interneurons throughout the hippocampus (26), but only at low rates in SL-M interneurons (27), which may correspond to the GABA_A,slow cells. In our model, connections from GABA_A,slow to GABA_A,fast cells are crucial for supporting either the generation or resynchronization of the theta-gamma rhythm. Indirect evidence supporting the existence of this connection comes from the observation that stimulation of SL-M induces a pause in spontaneous, fast GABA_A IPSCs recorded in pyramidal cells (23). More direct evidence comes from recordings of slow GABA_A IPSCs in SR interneurons (Fig. 1 and ref. 23), which terminate near the somata of pyramidal cells and presumably contribute to GABA_A,fast IPSCs. However, not all evidence supports the notion that these two populations are interconnected. For example, the small existing body of paired current-clamp recordings between presynaptic interneurons on the SR/SL-M border and postsynaptic interneurons elsewhere does not show signs of slow synaptic connections (28, 29). This discrepancy may be caused by the difficulty in distinguishing between fast and slow inputs under current clamp, or by the possibility that the presynaptic cells from the dual-cell recordings may not be the same ones activated by an extracellular stimulus in SL-M. It should also be noted that GABA_A,slow spontaneous IPSCs have not been reported in recordings from interneurons (26). Their absence in published data may reflect a rarity of spontaneous activity in GABA_A,slow interneurons, as implied by the rarity (but documented presence) of spontaneous GABA_A,slow IPSCs in recordings from pyramidal cells (18).

Although we use a conductance change with slow kinetics to represent GABA_A,slow synapses in our single-compartment models, we do not believe that it is critical to assume that the rise and fall times of the conductance change at the postsynaptic site be slow. Rather, our conclusions are likely to depend only on the presence of any mechanism (e.g., slow postsynaptic receptors, sluggish reuptake of GABA, active and passive properties of dendrites) that gives rise to slow inhibition near the site of action potential generation. A slow decay time constant is particularly important to control the theta component of the rhythm. A slow rising time constant is probably not necessary for the rhythm, but it does allow a longer time window for additional spikes in the GABA_A,fast cells after the GABA_A,slow cells have fired.

The precise identity of the GABA_A,slow interneurons is not known, but they may correspond to the SL-M interneurons reported by Lacaille and colleagues (17, 21, 27, 30, 31). These interneurons are conditional oscillators, with slow voltage-gated membrane currents that constrain them to fire at theta frequencies under some experimental conditions. It may be asked if such oscillators can account for the phasing results reported above, without invoking the kinetics of GABA_A,slow. Although this is beyond the scope of the current paper, we note that the coherence of a rhythm cannot be taken for granted from the fact that cells themselves can oscillate with appropriate frequency when depolarized. This is particularly true when the network interactions are dominated by mutual inhibition, which is known to be effective at synchronization (3, 5, 32, 33), but only if specific constraints on the rise and fall time scales of the inhibition relative to the intrinsic time scales of the oscillators are met (34, 35). Furthermore, the properties of the currents, and not just the intrinsic time scales, can play a large role in whether neural oscillators synchronize with certain synaptic interactions (36). Using an existing cellular model (37), the component currents of which are very similar to those reported by Ouardouz and Lacaille (17), and which oscillates at theta frequencies, we found that mutually inhibitory interactions with either GABA_A,fast or GABA_A,slow kinetics create antiphase, not synchrony (data not shown). Thus, if these cells indeed correspond to GABA_A,slow cells, we are left with the counterintuitive suggestion that the theta rhythm may be best supported by eliminating the theta frequency oscillations via neuromodulation or some other means.

Two consistent properties of our model make it possible to test its validity experimentally. First, both autonomous and periodically driven theta-gamma activity require the presence of connections among the GABA_A,slow cells. Second, autonomous and periodically driven theta-gamma activity in our model network is rather stereotypical in form. In particular, GABA_A,slow cells invariably fire synchronously at theta frequencies. Thus, the crucial results in support of our model would be the verification in paired recordings that GABA_A,fast and GABA_A,slow interneurons exist as two distinct populations, that GABA_A,slow cells are interconnected relatively strongly, and that they fire synchronously at theta frequencies in either conditions of autonomous theta-gamma (e.g., hippocampal brain slices in the presence of carbachol) or periodically driven theta-gamma (e.g., in the living animal under conditions of voluntary locomotion).

Abbreviations

GABA_A

γ-aminobutyric acid type A

GABA_B

γ-aminobutyric acid type B

IPSC

inhibitory postsynaptic current

SL-M

stratum lacunosum-moleculare

SR

stratum radiatum

GABA_A,fast

fast GABA_A component

GABA_A,slow

slow GABA_A component

τ_A,fast

decay time constant of GABA_A,fast responses

τ_A,slow

decay time constant of GABA_A,slow responses

CV_I

coefficient of variation