Abstract
Ecophysiological models predict quantitative traits of one genotype in any environment, whereas quantitative trait locus (QTL) models predict the contribution of alleles to quantitative traits under a limited number of environments. We have combined both approaches by dissecting into effects of QTLs the parameters of a model of maize (Zea mays) leaf elongation rate (LER; H. Ben Haj Salah, F. Tardieu [1997] Plant Physiol 114: 893–900). Response curves of LER to meristem temperature, water vapor pressure difference, and soil water status were established in 100 recombinant inbred lines (RILs) of maize in six experiments carried out in the field or in the greenhouse. All responses were linear and common to different experiments, consistent with the model. A QTL analysis was carried out on the slopes of these responses by composite interval mapping confirmed by bootstrap analysis. Most QTLs were specific of one response only. QTLs of abscisic acid concentration in the xylem sap colocalized with QTLs of response to soil water deficit and conferred a low response. Each parameter of the ecophysiological model was computed as the sum of QTL effects, allowing calculation of parameters for 11 new RILs and two parental lines. LERs were simulated and compared with measurements in a growth chamber experiment. The combined model accounted for 74% of the variability of LER, suggesting that it has a general value for any RIL under any environment.
In an agricultural context, a plant that tolerates water deficit can produce a maximum harvested biomass under moderate water deficits. Involved mechanisms are not necessarily common with those underlying the ability of cells to survive tissue dehydration (e.g. Cushman and Bohnert, 2000; Seki et al., 2001). In maize (Zea mays), moderate water deficits usually cause no appreciable decrease in leaf water status because of an efficient stomatal control combining hydraulic and chemical messages (Tardieu and Davies, 1993; Wilkinson et al., 1998). A similar combination of messages allows maize plants to dramatically reduce leaf elongation rate (LER) under moderate water deficits sensed either in the soil or in the air, before that leaf water status is appreciably altered (Sharp et al., 2000; Tardieu et al., 2000). Reductions in stomatal conductance and in leaf expansion decrease transpiration rate, thereby saving soil water and maintaining leaf water potential at high values. They also reduce photosynthesis, growth, and yield, so optimum tolerance strategies cannot be common to different climatic scenarios. Plants with steepest responses might be most adapted to scenarios with most severe water deficits, whereas maintenance of growth and photosynthesis under deficit might be appropriate for scenarios with milder deficits. Therefore, identification of sources of variability in the responses to water deficit is necessary for designing plants adapted to a given climatic scenario.
We aimed to identify and analyze the genetic variability of responses of leaf elongation to water deficits caused either by partial soil water depletion or by high evaporative demand. We did not adopt the method consisting of comparing quantitative trait loci (QTLs) of a trait in control and stressed treatments (e.g. Sanguineti et al., 1999; Theulat et al., 1998; Hirel et al., 2001). Because water deficit and climatic conditions fluctuate in natural conditions, it is impossible to reproduce experiments with exactly similar environmental scenario in terms of temperature, soil water status, and water vapor pressure deficit (VPD) in the air. This may result in non-stable QTLs caused by the difference in climatic scenarios between experiments (e.g. Ribaut et al., 1997; Simko et al., 1999).
An alternative consists in using an ecophysiological model that relates quantitative traits to environmental conditions. Ben Haj Salah and Tardieu (1995, 1997) proposed such a model, which combines response curves of maize LER to environmental conditions. Response curves are based on experimental relationships common to several experiments in the field, greenhouse, and growth chamber, and valid over a large range of environmental conditions for a given genotype. Therefore, they can be considered as a stable characteristic of a genotype. The model combines response curves, and dissects LER observed at a given time into: (a) an intrinsic elongation rate that is a characteristic of the genotype at a given temperature, and (b) two additive negative effects, one of evaporative demand (characterized by meristem to air water VPD) and one of soil water deficit characterized by soil water potential (Ψ). These two effects were linear over the studied ranges.
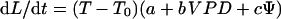 |
1 |
where dL/dt is LER, T is meristem temperature, a and T0 are the slope and the x intercept of the relationship between meristem temperature and LER, b is the slope of the relationships between LER (corrected for temperature) and VPD, and c is the slope of the relationship between LER (corrected for temperature) and soil water potential. The combined model also applied locally to the spatial distribution of elongation rate in the leaf (Tardieu et al., 2000).
The study presented here is a genetic analysis of the parameters of the model presented in Equation 1. It was carried out on a population of recombinant inbred lines (RILs) presented earlier (Causse et al., 1996). Each parameter of the model presented in Equation 1 was dissected into a sum of QTLs, so a genetic model could predict the value of each of these parameters for all RILs of the studied population. If both the genetic and the ecophysiological models are correct, their combination should be able to predict elongation rate of any RIL of the mapping population, even not taken into account in the QTL study, under any climatic scenario. This possibility was tested successfully, suggesting that the resulting model is valid.
RESULTS
Intrinsic LER and Response of LER to Evaporative Demand in Well-Watered Plants
LER was first analyzed during night periods, in the absence of evaporative demand, and then during day periods with evaporative demands that varied between consecutive days. An example of this analysis is presented in Figure 1, A through D, for two RILs.
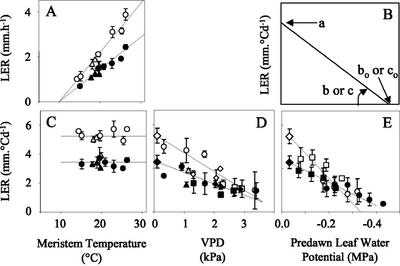
Figure 1.
Dissection of the responses of LER to temperature, evaporative demand, and soil water status in two typical RILs (white and black symbols). A, LER per unit clock time, plotted against meristem temperature. C, LER per unit thermal time, plotted against meristem temperature. The mean LER is an estimate of parameter a of Equation 1. D, LER per unit thermal time, plotted against meristem to air water vapor pressure difference (VPD) in well-watered plants. E, LER per unit thermal time during night periods, plotted against predawn leaf water potential. B, Graphical representations of parameters a, b, b0, c and c0 of Equation 1. A through D, experiments GC1 (▵), GC2 (○), FC1 (□), and FC2(▿). E, Experiments GS1 (□), GS2 (○), and mean values of LER in experiments GC1 and GC2 in the absence of evaporative demand and water deficit (◊).
The response to temperature was analyzed in a series of nights with mean meristem temperatures ranging from 14°C to 28°C (Fig. 1A; Table I). Common linear relationships applied, in this range, to experiments GC1 and GC2 in each RIL (r2 = 0.86 and 0.93) with an x intercept close to 10°C in both cases (nonsignificant difference). Slopes significantly differed, indicating that one RIL grew more rapidly than the other at any temperature. If LER of an RIL (dL/dt) is proportional to meristem temperature minus 10°C (T − 10), the ratio (a) of both values is a temperature-independent expression of the ability of the RIL to elongate (Fig. 1C). This ratio was named the intrinsic elongation rate (parameter a).
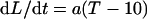 |
2 |
This is equivalent to expressing elongation rates per unit thermal time where, a is expressed in mm °C d−1 (see “Materials and Methods”).
Table I.
Experiments performed in this study
| Experiment | Sowing Date | Treatmenta | Night Temperatureb | Day VPDeqc | Leaf Ψwd |
|---|---|---|---|---|---|
| °C | kPa | MPa | |||
| FC1 (field) | May 20, 1999 | T, VPD | 15.8–20.8 | 1.5–2.8 | −0.03 to −0.05 |
| FC2 (field) | July 5, 1999 | T, VPD | 16.3–22.8 | 1.0–2.5 | −0.03 to −0.05 |
| GC1 (greenhouse) | March 10, 2000 | T, VPD | 17.4–19.8 | 0.6–1.5 | −0.03 to −0.05 |
| GC2 (greenhouse) | June 10, 2000 | T, VPD | 14.7–27.8 | 0.2–3.2 | −0.03 to −0.05 |
| GS1 (greenhouse) | March 10, 2000 | Ψ | 17.4–19.8 | 0.6–1.5 | −0.03 to −0.25 |
| GS2 (greenhouse) | October 5, 2000 | Ψ | 16.7–19.7 | 0.2–1.3 | −0.10 to −0.50 |
| GcC (growth chamber) | April 25, 2001 and July 1, 2002 | T, VPD | 16.0–28.0 | 1.0–2.2 | −0.03 to −0.05 |
Environmental conditions that varied in the considered experiment. T, Temperature; VPD, evaporative demand; Ψ, soil water status.
Range of mean night temperatures.
Range of mean day VPDeq.
Range of predawn leaf water potential.
The sensitivity to evaporative demand was estimated via the response curve of LER (expressed per unit thermal time) to evaporative demand estimated by leaf to air water vapor pressure difference corrected for the effect of light (VPDeq; see “Materials and Methods”). Night values were taken into account in regressions, with the corresponding VPDeq. In the examples presented in Figure 1D, common linear relationships applied to the four experiments in the field and in the greenhouse without water deficit (r2 = 0.79 and 0.68 for the two RILs). For each RIL, sensitivity to evaporative demand, therefore, was common to four experiments in the studied range of VPDeq. It was estimated either by the slope of the relationship between LER and VPDeq (b, Fig. 1B), or by the VPD at which elongation would cease (b0, Fig. 1B). Because VPDs as high as 4 to 7 kPa (Fig. 2) cannot usually be observed together with temperatures lower than 35°C, compatible with maize leaf growth, b0 should be considered in a statistical way. It represents the x intercept of a linear relationship, rather than the actual value of VPD at which leaf elongation ceases. Although the response to evaporative demand was calculated in all experiments, the response to temperature was calculated in the greenhouse experiments only. The putative “night” periods in field experiments comprised evening hours with unexpectedly high evaporative demand. The analysis of the response of LER to meristem temperature, therefore, was restricted to the greenhouse experiments GC1 and GC2. However, the fact that values were common to all experiments at a given VPD during day periods (Fig. 1D) suggests that intrinsic elongation rates per unit thermal time were common to field and greenhouse experiments.
Figure 2.
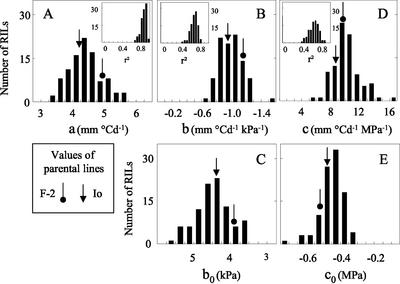
Frequency distributions of parameters of the response curves in the 100 studied RILs. A, Intrinsic LER (parameter a). B, Slope of the relationship between LER and meristem to air vapor pressure difference (parameter b). C, x Intercept of the same relationships (parameter b0). D, Slope of the relationship between LER and predawn leaf water potential (parameter c). C, x Intercept of the same relationships (parameter c0). The values corresponding to parental lines (PLs) are also shown. Insets in A, B, and D, Frequency distributions of r2 corresponding to each RIL.
QTLs of Intrinsic LER
The responses to meristem temperature were estimated in the 100 RILs with data originating from the two experiments as in Figure 1, A and C. All relationships were linear in the studied range, with individual r2 ranging from 0.69 to 0.99 (Fig. 2A, inset). None of the x intercepts significantly differed from 10°C. Therefore, responses of LER to meristem temperature differed between RILs by one parameter only, the slope of response curves (parameter a). The genetic variability of this character was appreciable, ranging from 3.3 to 5.7 mm °C d−1 (Fig. 2A). Its heritability was 0.81 over the whole set of data.
The QTL detection yielded a genetic model that explained 55% of the total phenotypic variability of parameter a, analyzed jointly in experiments GC1 and GC2 (Table II). This model comprised nine significant QTLs with high LOD scores, among which three were detected as main effect QTLs and six were detected as epistatic interactions. Several QTLs detected in epistatic interactions had high bootstrap values (e.g. that on chromosome 7 with a value of 57%, meaning that a QTL was detected at that position in 57% of the 1,000 studied cases), although bootstrap analysis was carried out, taking into account the main effect of QTLs. Three QTLs corresponded to high bootstrap values and two others had lower values because two QTLs coexisted on one chromosome (Table II).
Table II.
QTLs detected by composite interval mapping for each of the parameters of the ecophysiological model and for concentration of ABA in the xylem sap
| Trait | rpa | Type | Chrb | Markerc | Distanced | Effecte | Log of the Odds (LOD) Score | rindivf | Bootstrapg |
|---|---|---|---|---|---|---|---|---|---|
| % | |||||||||
| a | 0.55 | Main | 2 | sc348c | 30.0 | −0.046 | 4.65 | 0.108 | 30∼ |
| Main | 2 | sc348c | 45.0 | +0.057 | 6.18 | 0.149 | 54∼ | ||
| Main | 4 | sc431pd | 58.7 | +0.028 | 3.19 | 0.072 | 52∼ | ||
| Epistatic | 8 | sc179_cs | 49.5 | −0.060 | 6.88 | 0.169 | 36 | ||
| 9 | sc143_c | 119.3 | – | – | – | 13∼ | |||
| Epistatic | 6 | sc236_ag | 229.5 | +0.032 | 3.33 | 0.075 | 26 | ||
| 7 | sc155_cs | 9.7 | – | – | – | 57 | |||
| Epistatic | 4 | umc66 | 148.9 | +0.059 | 4.87 | 0.114 | 14∼ | ||
| 9 | bnl1428 | 159.4 | – | – | – | 39∼ | |||
| b | 0.47 | Main | 1 | sc19_kn1 | 192.7 | −0.008 | 2.21* | 0.058 | 92 |
| Main | 8 | umc36a | 171.7 | +0.009 | 2.90 | 0.077 | 72 | ||
| Epistatic | 4 | sc431pd | 58.7 | −0.019 | 6.35 | 0.183 | 60 | ||
| 5 | umc43 | 84.8 | – | – | – | 19 | |||
| Epistatic | 2 | umc44a | 13.6 | −0.013 | 3.96 | 0.107 | 41 | ||
| 7 | sc345_o2 | 0.0 | – | – | – | 37 | |||
| c | 0.43 | Main | 2 | umc6 | 5.5 | −0.013 | 3.75 | 0.094 | 76 |
| Epistatic | 1 | adh1_iso | 198.5 | −0.018 | 4.34 | 0.271 | 41 | ||
| 6 | umc85c | 58.4 | – | – | – | 9 | |||
| Epistatic | 5 | umc104a | 235.6 | +0.015 | 3.26 | 0.133 | 55∼ | ||
| 9 | sc66_sh1 | 16.9 | – | – | – | 71 | |||
| Epistatic | 4 | sc431_pd | 58.7 | −0.017 | 3.34 | 0.121 | 47 | ||
| 5 | sc343b_1 | 119.9 | – | – | – | 2∼ | |||
| b0 | 0.35 | Epistatic | 7 | umc110 | 55.5 | +0.49 | 4.32 | 0.158 | 20 |
| 9 | sc330td | 160.2 | – | – | – | 54 | |||
| Epistatic | 8 | umc36a | 171.7 | +0.56 | 3.96 | 0.141 | 14 | ||
| 10 | bnl304 | 10.0 | – | – | – | 9 | |||
| Epistatic | 1 | sc19_kn1 | 192.7 | −0.59 | 2.69* | 0.084 | 64 | ||
| 5 | sc343b_1 | 104.9 | – | – | – | 56 | |||
| c0 | 0.39 | Main | 10 | sc329_pp | 58.7 | −0.066 | 4.93 | 0.154 | 94 |
| Epistatic | 7 | umc116 | 26.4 | −0.108 | 6.47 | 0.210 | 90 | ||
| 8 | sc224b_s | 150.6 | – | – | – | 54 | |||
| Epistatic | 4 | sc419_at | 129.9 | −0.073 | 4.84 | 0.151 | 40∼ | ||
| 5 | umc104a | 235.6 | – | – | – | 78 | |||
| Epistatic | 4 | sc59c_bt | 113.9 | +0.076 | 3.65 | 0.111 | 23∼ | ||
| 8 | umc32a | 182.2 | – | – | – | 38∼ | |||
| Concentration of ABA in the xylem sap | 0.38 | Main | 5 | sc403_pa | 132.4 | −46.2 | 4.02 | 0.134 | 50 |
| Main | 9 | sc143a_c | 109.3 | −39.7 | 4.43 | 0.150 | 80∼ | ||
| Epistatic | 7 | sc155_cs | 14.7 | +52.1 | 3.90 | 0.131 | 60 | ||
| 9 | sc183_cs | 65.0 | – | – | – | 8∼ | |||
| Epistatic | 4 | sc315_su | 100.5 | −36.7 | 3.00 | 0.098 | 40 | ||
| 6 | umc65 | 88.9 | – | – | – | 49 |
a, Intrinsic elongation rate; b, slope of the response of elongation rate to meristem to air VPD; c , slope of the response of elongation rate to predawn leaf water potential; b0 and c0, x intercept of the LER to VPD and LER to predawn water potential relationships, respectively (see Fig. 1B).
Percentage of the phenotypic variance explained by the genetic model.
Chromosome no.
Closest left marker.
Genetic distance of the QTL from the top of the chromosome.
Additive effect of parent F2 allele.
Individual r of the QTL.
Proportion of cases in which a QTL was detected in 1,000 random samplings. ∼, More than one QTL was detected in the considered chromosome, thereby reducing the boostrap value; *, QTL was detected in simple interval mapping with an LOD score higher than 3, although the LOD of the composite interval mapping was lower.
QTLs of Response of LER to VPD
The responses to evaporative demand, estimated in the 100 RILs, were linear in the studied range and applied to the four experiments (r2 from 0.6–0.8 except in five RILs, Fig. 2D, inset). The heritability of the slope of relationships was 0.47, with a 3-fold phenotypic variation (b from −1.50 to −0.56 mm °C d−1 kPa−1, Fig. 2D). For instance, elongation rates measured at 2.5 kPa ranged from 1.05 to 4.55 mm °C d−1. RILs with greatest slopes had highest intrinsic elongation rates (r2 = 0.53, Table III). The use of parameter b0 (x intercept of the relationships presented in Fig. 2D) avoided possible confusion of effects because it was independent of intrinsic elongation rate (r2 = 0.0), but was well related to the slope b (r2 = 0.46, Table III).
Table III.
Determination coefficients (r) between parameters of the ecophysiological model
| Parameter | r of Correlation between Parameters
|
|||
|---|---|---|---|---|
| a | b | c | b0 | |
| b | 0.53 | – | – | – |
| c | 0.43 | 0.26 | – | – |
| b0 | 0.00 | 0.46 | 0.00 | – |
| c0 | 0.00 | 0.00 | 0.56 | 0.00 |
a, Intrinsic elongation rate; b, slope of the response of elongation rate to meristem to air VPD; c, slope of the response of elongation rate to predawn leaf water potential; b0 and c0, x intercept of the LER to VPD and LER to predawn water potential relationships, respectively (see Fig. 1B).
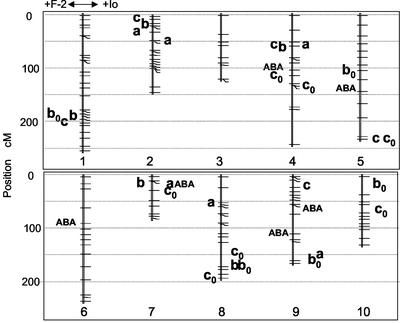
A genetic model of response to evaporative demand (parameter b) applied to the four presented experiments, in the field as well as in the greenhouse, and accounted for 47% of the total phenotypic variability (Table II). This model comprised six significant QTLs, two detected as the main effect and four detected as epistatic interaction. LOD values were high except in one QTL (chromosome 1), which had an LOD larger than 3 in simple interval mapping and had the highest bootstrap value, and, therefore, was conserved in the analysis. Bootstrap values were very high in the main effect QTLs (72% and 92%). Three other QTLs detected as epistatic interaction had still high bootstrap values, from 37% to 60%. Two QTLs were common to characters a and b, consistent with the correlation between them (Table III). One was located on chromosome 4 at 59 cM, and the second was on chromosome 7 between 0 and 7 cM (Fig. 3). In contrast, the genetic model of the character b0 (Fig. 1B) was completely independent of intrinsic elongation rate (Table III). This model accounted for 35% of the phenotypic variability. It had two QTLs in common with those of b on chromosome 1 at 192.7 cM and chromosome 8 at 171.7 cM (Table II).
Figure 3.
Positions of the most relevant QTLs detected. a, Intrinsic elongation rate; b, slope of the response of elongation rate to meristem to air VPD; c, slope of the response of elongation rate to soil water potential; b0 and c0, x intercept of the same relationships (see Fig. 1B). QTLs of concentration of abscisic acid (ABA) in the xylem sap in plants grown at a predawn leaf water potential of −0.20 MPa. Only QTLs with highest F and high bootstrap values are presented, for better legibility (see Table II for other QTLs). QTLs that decrease the value of the trait in the PL F-2 are on the left side of the chromosomes and those that increase it are on the right.
The QTLs of a, b, and b0 presented in Table II and Figure 3 were detected on measurements carried out on leaf 6, over the set of data originating from all experiments considered together. However, the models detected in this way also applied to leaf 7 (r2 = 0.45, 0.19, and 0.15 for parameters a, b, and b0, respectively). They also applied to individual experiments. The genetic model of parameter a applied to Exp GC2 alone (r2 = 0.53), and the model of parameter b explained 28% to 35% of the phenotypic variability of individual experiments.
QTLs of Response of LER to Soil Water Deficit
The response of LER to soil water status was studied in the absence of evaporative demand during nights of two greenhouse experiments (Table I). Soil water status, estimated by the predawn leaf water potential, ranged from −0.5 (severe deficit) to −0.03 MPa (well-watered plants). Two experiments with well-watered plants in the greenhouse were also considered in the analysis, with corresponding predawn leaf water potentials. Responses are presented in Figure 1E, for the same two RILs shown in Figure 1, A through D. For each RIL, a common linear relationship applied to the four experiments, with high regression coefficients (r2 = 0.65 and 0.66). As in the case of evaporative demand, two estimates of the response to soil water potential were considered (Fig. 1B): the slope of the relationship between LER and soil water potential (parameter c), and the x intercept of this relationship (parameter c0), an estimate of the soil water potential at which leaf elongation ceases.
Linear relationships were observed in the 100 studied RILs, with r2 ranging from 0.50 to 0.87 in 91% of cases and a peak r2 of 0.64 (Fig. 2D, inset). The slope of this relationship (parameter c) had a 3-fold variability, from 5.6 to 18 mm °C d−1 MPa−1 (Fig. 2D). Its heritability was 0.42. Parameter c0 ranged from −0.575 to −0.350 MPa (Fig. 2E). As in the case of evaporative demand, a high correlation was observed between parameters c and a (r2 = 0.43, Table III). The parameter c0 was independent of a (r2 = 0.0), but was well related to c (r2 = 0.56).
The QTL detection yielded a genetic model explaining 43% of the phenotypic variation of the slope of the response to soil water potential (parameter c), with seven QTLs, among which one was detected in the main effect and six were detected as epistatic interaction (Table II). These QTLs had high LOD scores and QTLs found in epistatic interactions had high bootstrap values as main effect QTLs. Seven QTLs were found for parameter c0, which explained 39% of its phenotypic variability. One QTL colocalized for c and c0 (Fig. 3).
Concentration of ABA in the Xylem Sap
The concentration of ABA in the xylem sap was measured while all RILs had a predawn leaf water potential of −0.20 ± 0.02 MPa. It ranged from 3 to 231 μmol m−3 in the studied set of RILs (Fig. 4). The QTL detection carried out on ABA concentrations yielded a genetic model that explained 38% of the phenotypic variability of ABA concentration, with six QTLs, among which two were detected as the main effect and four were detected as epistatic interaction (Table II). All QTLs showed high bootstrap values (40%–80%) except for one (chromosome 9, 65 cM), which had low value because of the high value of another QTL on the same chromosome (chromosome 9, 109 cM). Two of these QTLs were located near QTLs of parameters c or c0 (Fig. 3, chromosome 4 between 100–114 cM and chromosome 7 between 15–26 cM). In both cases, the allele causing higher ABA concentration in the xylem was associated with a lower sensitivity to soil water deficit.
Figure 4.
Frequency distributions of the concentration of ABA in the xylem sap of the 100 RILs at a predawn leaf water potential of −0.20 MPa.
Combination of Ecophysiological and Genetic Models to Predict LER of Any RIL under Fluctuating Temperature and Evaporative Demand
Because genetic analyses were carried out on the parameters of the ecophysiological model (Eq. 1), both QTL and ecophysiological models theoretically can be combined to predict the elongation rate of any RIL of the studied cross under any climatic scenario. This possibility was first tested on the 100 studied RILs to test the overall performance of the model presented in Eq. 1 (Fig. 5, A and B). LERs measured in our experiments were compared with elongation rates calculated from Equation 1 and measured meristem temperature, evaporative demand, and soil water potential. Parameters a, b, and c of Equation 1 were estimated in two ways, either by individual regression for each RIL, as in Figure 1, or by using the QTL models of Table II. To do so, we estimated for each RIL the allelic probability at QTL positions, given the information at flanking markers, and then used them in the QTL model. LER was accurately predicted in both ways, with r2 of 0.83 and 0.80, respectively, for the first and second method of parameter estimation (Fig. 5, A and B). Although the QTL models of a, b, and c accounted for only part of the genetic variance of each parameter, their use, therefore, generated a very small decrease in the r2 of the regression in comparison with the use of individual estimates of a, b, and c for each RIL.
Figure 5.
Test of the combined QTL and ecophysiological model of LER, either on the same RILs as in the QTL analysis (A and B) or on 13 lines that were not taken into account in the QTL analysis (C). A and B, Measured values plotted against predicted values using Equation 1. Parameters of Equation 1 were determined either by individual regression for each RIL as in Figure 1A or by using the QTL models of Table II (B). C, Measured values originating from growth chamber experiments (11 RILs and two PLs) or a greenhouse experiment with water deficit (two PLs). C, Each symbol represents an RIL or a PL.
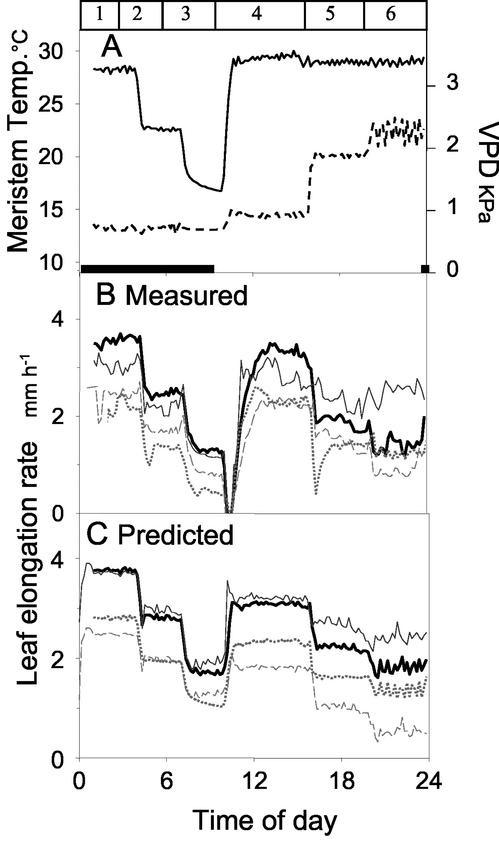
The combination of ecophysiological and genetic models was then tested on 13 lines not involved in the construction of the QTL models. These were the two PLs and 11 additional RILs of the population, chosen to maximize the expected differences in responses to temperature and evaporative demand. These responses were predicted using the QTL models of Table II and the allelic probabilities at QTL positions. LERs measured in a growth chamber experiment were compared with those predicted by the model, using measured temperature, VPD, and soil water potential as inputs. Plants were subjected to a near-zero evaporative demand during the night, and to varying evaporative demands at a constant meristem temperature during the day (Fig. 6A). Examples of predicted and measured time courses of LERs of five RILs are presented in Figure 6, B and C (two RILs with similar predicted and measured LERs are presented via average values). LER had similar time courses in modeled and observed data. It decreased in three steps during the night, simultaneously with temperature (periods 1–3). It decreased steeply when lights were turned on and temperature was returned to 28°C. It partly recovered and stabilized under the low VPD (period 4). It decreased afterward in two steps simultaneously with VPD (periods 5 and 6). The model predicted differences in elongation rates observed between RILs during the night at all temperatures. It also predicted the difference in response to evaporative demand during the day: One RIL (thin line) had a low response compared with the others, consistent with predicted values. The effect of evaporative demand tended to be slightly overestimated by the model in all RILs. In addition, the transient decrease in elongation rate just after illumination was not predicted by the model.
Figure 6.
Time courses of measured and modeled LERs during a climatic scenario in the growth chamber. Five RILs are presented, which were not taken into account in the detection of QTLs. Values corresponding to two RILs with similar predicted and measured values were averaged for better legibility. The modeled values were obtained from the ecophysiological model (Eq. 1) whose parameters were calculated as a sum of QTL effects with the genetic models (Table II). A, Change with time of meristem temperature (plain line) and VPD (dotted line). Numbers on the top of the panel represent periods, identified for better legibility in the text. Black bars on the bottom indicate the night periods. B, LER measured with linear variable displacement transducers (LVDTs), averaged on two or more plants of each RIL. Each line style represents a RIL. C, Modeled LER for the same RILs.
A regression analysis was carried out on the whole set of data, for the 13 studied lines over the five experiments in growth chamber, together with the results of one experiment with water deficit in the greenhouse (Fig. 5C). Data taken into account corresponded to periods with stable environmental conditions and elongation rates, i.e. the transient changes in elongation rate associated with changes in light were not taken into account. Predicted elongation rates were closely related to observed elongation rates (r2 = 0.74). In 10 RILs of 13, the model was accurate with a ranking between RILs conserved in measured and modeled data. The most sensitive RILs according to the genetic model were also the most sensitive in measured data. Three RILs had systematic bias toward either higher (two cases) or lower (one case) elongation rates in the model compared with observed values, probably because of extra QTLs that were not detected in this study.
DISCUSSION
A Genetic Analysis of the Response of a Trait to Environmental Conditions Allows Modeling the Genotype x Environment Interaction
A major difficulty in the use of QTLs of traits depending on environmental conditions is their instability in different experiments. For instance, Ribaut et al. (1996, 1997), found 13 QTLs in a study of flowering dates of maize, but only three were common to three experiments with different levels of water deficit. Keller et al. (1999) found 16 QTLs of lodging in wheat (Triticum aestivum) but only five were common to three experiments. Tuberosa et al. (1998) found 16 QTLs involved in leaf ABA concentration but only four were common to four experiments. Such an instability is not surprising because these traits strongly depend on environmental conditions. To take this dependence into account, a genotype x environment interaction term can be used in the genetic analysis (Epinat-Le Signor et al., 2001) but QTLs of interaction are not easy to interpret. Here, we used a different approach because the trait analyzed was itself a response to an environmental condition, which can be interpreted per se. This approach implies that the response is stable among experiments and does not depend on additional terms. This was the case here in several experiments in the field and in the greenhouse. The test of the method with independent RILs and new climatic scenarios in the growth chamber suggests that modeling the genotype x environment interaction is feasible.
Dissection and Integration of Elementary Processes
Dissecting a phenotype into elementary responses is associated with several risks. First, this dissection may be inadequate, thereby resulting in non-stable elemental traits. Following a reasoning similar to that presented here, Yin et al. (1999a , 1999b) dissected plant growth following the models SUCROS (Goudriaan and Van Laar, 1994) and ORYZAI (Kropff et al., 1994). Leaf expansion rate was considered to depend on the carbon import by the leaf and on the specific leaf area (ratio of leaf area to leaf mass). In contrast with QTLs of flowering date that were found to be relatively stable (Yin et al., 1999b), QTLs for a specific leaf area were particularly non-stable. This result could be because of the fact that leaf expansion rate is not related to the plant carbon status on short timescales, so specific leaf area is highly variable with environmental conditions and cannot be considered as a characteristic of a genotype (Tardieu et al., 1999). This is in contrast with the stability of the dissection proposed here for each RIL over several experiments, resulting in common QTLs.
Second, the dissection into elementary processes may generate noise that results in low heritability, impeding the detection of QTLs. For instance, an inadequate separation of night and day periods in our field experiments generated “night” periods with appreciable evaporative demand, thereby lowering mean elongation rate. Therefore, these data had to be discarded to recover an acceptable heritability. Obtaining a large number of data with high heritability was helped by the fact that maize LER is stable for 4 to 7 d (Muller et al., 2001), so measurements during successive days can be considered as replicates.
Finally, the combination of ecophysiological and genetic models is not necessarily robust enough to allow reconstruction of the time course of the analyzed trait. The combined model accounted for observed data on the same RILs (Fig. 5B), but the real test involved a genetic material independent of the QTL detection and climatic scenarios in the growth chamber that differed from those in the experiments used to establish response curves. Therefore, this test cumulated three sources of error: (a) the experimental error linked to LVDT measurements, (b) the error linked to the model applied to one RIL, and (c) the error of the genetic models, which accounted for about one-half of the phenotypic variability of the responses to temperature and evaporative demand. Despite that, the overall precision of the combined model was still high (r2 = 0.74, Fig. 5C). A first explanation is that the three sources of error were not statistically independent, because errors in the determination of slopes contribute to the global error of the genetic model. Second, the correlation between expected and observed values was carried out on actual values of LER and not on parameters of response curves as in the QTL model. Because the range of environmental conditions was wide, this has generated high values of r2.
Interpretation of QTLs of Responses to Environmental Conditions
One of the interests of the method presented here is that each series of QTLs corresponds to relatively well-defined functions. Most QTLs of intrinsic elongation rate, response to evaporative demand, and response to soil water deficit did not coincide on the genome (Fig. 3), suggesting that these traits are not regulated by the same genes.
QTLs of intrinsic elongation rate are linked to the ability of leaves of a given RIL to elongate with a near-zero water flux in the absence of water or nutrient deficits. It is expected that they could be associated to a genetic variability of the rheological characteristics of cell walls, depending, for instance, on genes that code for expansins (Cosgrove, 2000), endoglucanases (Yuan et al., 2001), or xyloglucan endotransglycosylase (Reidy et al., 2001).
QTLs of the response to evaporative demand are linked to the ability of a RIL to elongate in the presence of a water flux, but in the absence of soil water deficit. We have shown previously that the concentration of ABA in the xylem sap was very low and root water potential was close to zero in this case (Ben Haj Salah and Tardieu, 1997). These QTLs might be linked to differences in osmotic adjustment in elongating cells, associated with differences in turgor at low leaf water potential because of high water flux. Alternatively, they might be linked to any plant characteristic affecting the resistance to water flux in the plant, such as stomatal aperture, aquaporins, xylem, or apoplast characteristics. It is noteworthy that two QTLs associated with stomatal conductance, found by Lebreton et al. (1995) on chromosome 7 and 8, are close to QTLs of response to evaporative demand found in the present study.
QTLs of response to soil water deficit, determined in the absence of water flux, can be expected to be linked to differences in any step in the signaling cascade of water deficit such as synthesis of ABA or ethylene (Milborrow, 2001) or sensitivity to these hormones (Leung and Giraudat, 1998). The QTL of response of leaf elongation to soil water potential located on chromosome 10 is close to the gene ASR, a protein expressed in drought conditions and responsive to ABA (de Vienne et al., 1999). Two QTLs of the same character coincided with QTLs of concentration of ABA in the xylem sap (chromosomes 4 and 7, Fig. 3). One QTL, located on chromosome 1, was close to the gene coding for the 9-cis-epoxycarotenoid dioxygenase (Schwartz et al., 1997), which was proposed to be a water responsive limiting step in ABA biosynthesis (Qin and Zeevaart, 1999; Iuchi et al., 2001). The QTL located on chromosome 2 was close to a robust QTL of leaf ABA found by Tuberosa et al. (1998). Although no QTLs of ABA were found on these last two positions, these results might argue in favor of an involvement of ABA in the response of LER to soil water deficit. The alleles conferring higher xylem ABA concentration were associated with lower response to soil water deficit, consistent with an hypothesis recently raised that a high ABA concentration could prevent rather than favor the reduction of elongation under water deficit (Sharp and LeNoble, 2002).
MATERIALS AND METHODS
Genetic Material
The mapping population used in this study consisted of RILs with six generations of self pollination, derived from a cross between two PLs, maize (Zea mays) F-2 (an early French flint) and Io (a late North American semident). A total of 145 RILs was produced from this cross and 152 RFLP probes were used for mapping these RILs (Causse et al., 1996). A first subset of 100 RILs of this cross (the same in all experiments) was used for QTL identification and a second subset of 11 others RILs plus the two PLs was used for testing the combination of the ecophysiological and QTL models.
Field Experiments
Two field experiments were carried out near Montpellier, southern France (FC1 and FC2, Table I). Sowing dates were May 20, 1999, and July 5, 1999. Soil was watered twice a week, with water amounts larger than Penman evapotranspiration during the same periods so plants experienced no water deficit. In experiment FC1, 20 seeds per RIL were sown in pair. Plants were thinned to one when leaf 3 emerged. Analysis of leaf elongation was carried out on four plants per RIL, chosen for homogeneity among the 10 plants. The same procedure was used in experiment FC2, but 30 seeds were sown and five plants were used for analysis of leaf growth. In experiment FC2, plants were sown under a mobile shelter allowing us to manipulate temperature and VPD.
Air temperature and relative humidity were measured every 20 s (HMP35A, Vaisala Oy, Helsinki). Temperature of the meristematic zone of 10 plants was measured with a fine copper-constantan thermocouple (0.4-mm diameter) located inside the stem in the meristematic zone. Light was measured continuously using a photosynthetic photon flux density (PPFD) sensor (LI-190SB, LI-COR, Lincoln, NE). All temperatures referred to hereafter are meristem temperatures. All data of temperature, PPFD, and relative humidity were averaged and stored every 600 s in a data logger (Campbell Scientific, LTD-CR10 Wiring Panel, Shepshed, Leicestershire, UK). Water vapor pressure difference between meristem and air (VPD in kPa) was calculated as the difference between saturation vapor pressures at meristem temperature and at air dew point temperature. The water flux cumulated over the day period (J, kg m−2 d−1) was approximated as:
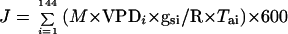 |
3 |
where M is the molar weight of water (kg mol−1) and R is the gas constant (Pa m3 mol−1 K−1). VPDi (Pa) is the mean leaf to air VPD during the considered time step of 600 s, and gsi and Tai are the mean stomatal conductance (m s−1) and air temperature (K) during the same time step (144 time steps in a day). Consistent with this calculation, we calculated an equivalent VPD for a 1-d period by averaging measured VPDs corrected for changes in stomatal conductance because of diurnal variations of PPFD. For that, we multiplied mean VPDs at each time step of 600 s by a coefficient (ki) that was 0 and 1, respectively, at PPFDs of 0 and 500 mmol m−2 s−1 and proportional to PPFD between these two values.
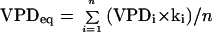 |
4 |
where VPDeq is the equivalent VPD corresponding to the considered period and n is the number of 600-s time steps during this period. During the night, VPDeq was close to 0 kPa (PPFD close to 0 μmol m−2 s−1).
Thermal time (tth; °C d) elapsed during a period was calculated by cumulating and integrating, at each time step, the differences between the mean meristem temperature (Ti) and the x intercept of the relationship between meristem temperature and LER (T0, Eq. 1 and Fig. 1).
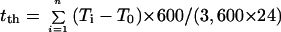 |
5 |
where n is the number of 600-s time steps during the considered period.
Meristem temperatures averaged during night periods ranged from 15.8°C to 21°C in experiment FC1. They reached 23°C in experiment FC2 during nights when the mobile shelter was placed above plants. Daytime temperatures ranged form 19°C to 35°C in experiment FC1 and from 17°C to 34°C in experiment FC2. VPDeq, estimated as in Equation 4, ranged between 1.5 and 2.8 kPa. During experiment FC2, the use of the mobile shelter combined with spraying water on the soil allowed us to get lower VPDs during some days (1 kPa).
The vertical position of the tip of the sixth and seventh leaves was measured twice a day, in the morning (6 ± 1 am solar time) and in the evening (5 ± 1 pm) during the period from appearance of the leaf tip above the whorl until the end of the period with linear elongation, checked a posteriori (Muller et al., 2001). The position of the leaf tip was measured using a ruler attached to a 2.5-m horizontal bar fixed on vertical metal sticks permanently left in the soil (fixed reference). Leaf elongation was calculated as the rate of displacement of the leaf tip either during the night (5 pm–6 am) or during the day (6 am–5 pm).
Greenhouse Experiments and Well-Watered Plants
Two experiments were carried out in the greenhouse in well-watered conditions (experiments GC1 and GC2, Table I). On March 10 and June 10, 2000, seeds were placed at 0.025-m depth in columns (0.15-m diameter and 0.4-m height) containing a 40:60 (v/v) mixture of a loamy soil and an organic compost. RILs were sown in pairs and thinned to one when leaf 3 emerged. Each column contained three different RILs and each RIL was sown in three columns. Soil was maintained at retention capacity by daily watering with a modified one-tenth-strength Hoagland solution corrected with minor nutrients. Columns were individually weighted every 3rd d to check that the soil water content was between 35% and 40% of dry soil. Leaf water potential of 10 plants was measured before dawn every week to check that plants experienced no water deficit.
Meristem temperature was measured and VPDeq (Eq. 4) was estimated as in the field experiment. To get a large range of climatic conditions, plants were covered on two nights of experiment GC2 with a 4.0- × 4.7-m plastic shelter and air temperature was lowered by two air conditioners, allowing meristem temperature to reach 18.7°C. The same shelter was used on other two nights but air was heated so meristem temperature reached 26.1°C and 27.4°C. Finally, all plants were moved into a growth chamber at 15.1°C and 14.4°C on two nonconsecutive nights to measure LER at low meristem temperature. Daytime VPD was varied either by turning off the water of air cooling (2–3.5 kPa), or leaving the water circulation in the air cooling system (0.6–1.5 kPa). Low VPDs were obtained by spraying continually water on the soil (0.2–1 kPa).
Measurement of LER was carried out as in the field. The positions of the tips of leaves 6 and 7 were measured twice a day (6 ± 1 am and 5 ± 1 pm solar time) on three plants per RIL during the period with steady LER. A ruler fixed on the top of the columns was used for that, providing night and day elongation rates.
Greenhouse Experiments and Water-Deficient Plants
Two experiments with the 100 RILs were carried out with soil water deficit (experiments GS1 and GS2). Plants were sown with the same procedure as in other experiments on March 10 and October 6, 2000. While filling columns, a soil sample was taken every second column to determine the initial soil water content. It was checked that soil water content was similar in all columns and homogenous within each column (not shown). Soil water content was determined afterward by weighing columns every day. Differences in weight were attributed to changes in soil water content. In a preliminary experiment, predawn leaf water potential was measured in leaves 4 and 5 at contrasting water contents. At any water content, predawn leaf water potential did not differ significantly between RILs (not shown). A water release curve relating soil water content to predawn leaf water potential, therefore, was built irrespective of the RIL.
Irrigation was stopped when leaf 5 appeared. A predawn leaf water potential of −0.3 MPa was reached in 3 to 6 d, depending on the leaf area of the considered RIL. Soil water status was then controlled by daily irrigation, in such a way that each plant experienced a range of predawn leaf water potential from −0.03 to −0.5 MPa (Table I). Light, meristem, or air temperatures and meristem to air VPD were measured as in well-watered experiments. The concentration of ABA in the xylem sap, extracted by pressurization, was measured on 95 RILs in experiment GS1. Soil water potential was first set to −0.20 MPa, corresponding to a soil water content of 0.23 g g−1. On the following morning, 100 mm3 of sap was collected in each RIL before dawn with a pressure of 0.5 MPa above the balancing pressure. The sap of three plants of the same RIL was pooled and stored at −80°C for subsequent ABA analysis. The same sequence of measurements was carried out on three successive nights. The concentration of ABA in crude sap was analyzed by radio-immunoassay (Quarrie et al., 1988).
Test Experiments
Experiments were carried out in the growth chamber and in the greenhouse to test the combination of ecophysiological and QTL models (Figs. 5 and 6C). Eleven RILs that were not used in the former experiments were sown in the greenhouse on April 25, 2001 (six RILs) and July 1, 2002 (five RILs and the two PLs). Upon the emergence of leaf 6, plants were moved into the growth chamber and watered twice a day during the experiment. Air temperature and VPD were varied as shown in Figure 6. This experiment was repeated for consecutive days, with four RILs (eight plants) in the growth chamber on each day. LER was measured continuously with a linear variable differential transducer (LVDT-L100, Chauvin Arnoux, Paris). The LVDT was attached to the tip of each sixth leaf and connected to the data logger. At least two leaves were measured on each date for each RIL. A LVDT was fixed on a metal bar to measure changes in string length with temperature or VPD treatments. In addition, the two PLs were sown in the greenhouse and managed as in the experiments with water deficit. LER was measured using LVDTs.
Genetic Analysis
Genetic analysis were performed on Statistical Analysis System software (SAS Institute Inc., Cary, NC). QTLs were detected by composite interval mapping (Jansen, 1993; Zeng, 1994) using the linear regression (Haley and Knott, 1992), with research of epistatic interactions (Holland et al., 1997). We tested the presence of a QTL taking into account the effect of cofactors, which are putative QTLs located at the marker locations. The choice of cofactors was first carried out using a step-wise regression between the studied trait and the allele value at each marker. At each step, we retained the marker that best explained the phenotypic variability of the quantitative character, with cofactors already accepted in previous steps. The percentage of phenotypic variability explained by all cofactors was not allowed to be higher than the heritability of the studied character. To refine this first selection, a backward regression was carried out in each chromosome between the studied trait and the allele value at each marker, including all the markers of the considered chromosome and the cofactors retained by the step-wise regression on the others chromosomes. At each step, we removed the marker that less explained the phenotypic variability of the trait. This allowed determination of the best model involving the same number of cofactors as that determined in the step-wise analysis.
Presence of main effect QTLs was tested every 5 cM between the 152 markers (445 positions on the genome) using a multiple regression with the cofactors. For that, the allele value was determined every 5 cM as the probability of occurrence of allele F2 at this position according the genotype at flanking markers (Martinez and Curnow, 1994). When the tested position on the genome was close to a cofactor (±10 cM), the effect of this cofactor was removed. Because the theoretical distribution of the test statistics (the F of the linear regression) was unknown for multiple regression with cofactors, the threshold value was determined by 1,000 permutations (Churchill and Doerge, 1994). The empirical distribution of the statistical test allowed definition of a threshold value corresponding to a type I error of 5%. The corresponding F value was close to 14, resulting in threshold LOD scores ranging from 2.98 to 3.04 depending on QTL number (Haley and Knott, 1992). In the last step, a regression was carried out between the studied trait and all combinations of two positions on the genome, taking into account the main effect QTLs previously determined. This allowed determination of epistatic QTLs.
The final formalism of the genetic model was:
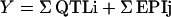 |
6 |
where Y is the studied trait, QTLi are the effects of each main effect QTL, and EPI is the effect of each epistatic interaction. The total phenotypic variability explained by the model (r2p) was also estimated. The partial r2 of each QTL (main or interaction) was also estimated after accounting for the effects of all other QTLs found for the same trait.
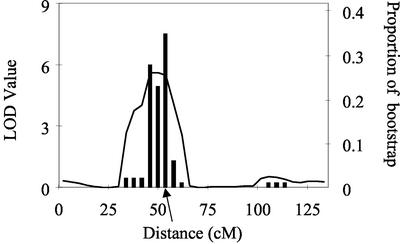
Because some QTLs can be linked to a few number of RILs generating significant but non-stable QTLs, we detected QTLs on subpopulations of the studied RIL population (bootstrap). Thousand random sampling of 100 RILs with replacements were carried out among the 100 studied RILs. A QTL detection was carried out for each sample, using the same cofactors as in the original population. The most significant QTL was detected in each chromosome (Visscher et al., 1996). The proportion of cases in which a QTL was detected in a given position was recorded for the 445 positions on the genome (Fig. 7). Bootstrap proportions were also estimated at both loci of epistatic interactions.
Figure 7.
Example of output of the bootstrap analysis for a QTL located on chromosome 10. Each vertical bar indicates the proportion of cases in which a QTL was detected at the considered position in a series of 1,000 random samplings. Positions were 5 cM apart. In the case considered here, a QTL was found in 94% of cases in an interval of 20 cM encompassing the QTL. The trace of LOD values in the composite interval mapping on the 100 RILs is also shown.
Heritability was estimated according to Gallais (1990):
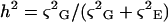 |
7 |
Where ς2G is the genetic variance and ς2E is the environmental variance, estimated using mean square expectations of a classical ANOVA model. Observations in this ANOVA correspond to parameter estimates for each individual plant and genotype effect to that of the RIL.
ACKNOWLEDGMENTS
Philippe Hamard (Laboratoire d'Ecophysiologie des Plantes sous Stress Environmentaux) helped us during the field experiments. The active participation of several students (Myriam Serghini, Hugues Lefevre, Armand Fonda, Elmire Santoni, and Stéphane Theulier Saint Germain, University of Montpellier II, France) in some of the experiments is gratefully acknowledged.
Footnotes
This work was supported by Génoplante (ZmS2P1 program: tolerance to water deficit in maize).
Article, publication date, and citation information can be found at www.plantphysiol.org/cgi/doi/10.1104/pp.013839.
LITERATURE CITED
- Ben Haj Salah H, Tardieu F. Temperature affects expansion rate of maize leaves without spatial distribution of cell length. Plant Physiol. 1995;109:861–870. doi: 10.1104/pp.109.3.861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben Haj Salah H, Tardieu F. Control of leaf expansion rate of droughted maize plants under fluctuating evaporative demand. Plant Physiol. 1997;114:893–900. doi: 10.1104/pp.114.3.893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Causse M, Santoni S, Damerval C, Maurice A, Charcosset A, Deatrick J, de Vienne D. A composite map of expressed sequences in maize. Genome. 1996;39:418–432. doi: 10.1139/g96-053. [DOI] [PubMed] [Google Scholar]
- Churchill GA, Doerge RW. Empirical threshold values for quantitative trait mapping. Genetics. 1994;138:963–971. doi: 10.1093/genetics/138.3.963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cosgrove DJ. Expansive growth of plant cell walls. Plant Physiol Biochem. 2000;38:109–124. doi: 10.1016/s0981-9428(00)00164-9. [DOI] [PubMed] [Google Scholar]
- Cushman JC, Bohnert HJ. Genomic approaches to plant stress tolerance. Curr Opin Plant Biol. 2000;3:117–124. doi: 10.1016/s1369-5266(99)00052-7. [DOI] [PubMed] [Google Scholar]
- de Vienne D, Leonardi A, Damerval C, Zivy M. Genetics of proteome variation for QTL characterization: application to drought-stress responses in maize. J Exp Bot. 1999;50:303–309. [Google Scholar]
- Epinat-Le Signor C, Dousse S, Lorgeou J, Denis JB, Bonhomme R, Carolo P, Charcosset A. Interpretation of genotype x environment interactions for early maize hybrids over 12 years. Crop Sci. 2001;41:663–669. [Google Scholar]
- Gallais A. Théorie de la Sélection en Amélioration des Plantes. Paris: Masson Ed; 1990. [Google Scholar]
- Goudriaan J, Van Laar HH. Modelling Potential Crop Growth Processes. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1994. [Google Scholar]
- Haley CS, Knott SA. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity. 1992;69:315–324. doi: 10.1038/hdy.1992.131. [DOI] [PubMed] [Google Scholar]
- Hirel B, Bertin P, Quilleré I, Bourdoncle W, Attagnant C, Dellay C, Gouy A, Cadiou S, Retaillau C, Falque M et al. Towards a better understanding of the genetic and physiological basis for nitrogen use efficiency in maize. Plant Physiol. 2001;125:1258–1270. doi: 10.1104/pp.125.3.1258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland JB, Moser HS, O'Donoughue LS, Lee M. QTLs and epistasis associated with vernalization responses in oat. Crop Sci. 1997;37:1306–1316. [Google Scholar]
- Iuchi S, Kobayashi M, Taji T, Naramoto M, Seki M, Kato T, Tabata S, Kakubari Y, Yamaguchi-Shinozaki K, Shinozaki K. Regulation of drought tolerance by gene manipulation of 9-cis-epoxycarotenoid dioxygenase, a key enzyme in abscisic acid biosynthesis in Arabidopsis. Plant J. 2001;27:325–333. doi: 10.1046/j.1365-313x.2001.01096.x. [DOI] [PubMed] [Google Scholar]
- Jansen RC. Interval mapping of multiple quantitative trait loci. Genetics. 1993;135:205–211. doi: 10.1093/genetics/135.1.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller M, Karutz C, Schmid JE, Stamp P, Winzeler M, Keller B, Messmer MM. Quantitative trait loci for lodging resistance in a segregating wheat × spelt population. Theor Appl Genet. 1999;98:1171–1182. [Google Scholar]
- Kropff MJ, Van Laar HH, Matthews RB. ORYZA1: An Ecophysiological Model for Irrigated Rice Production. Los Banos, Philippines: International Rice Research Institute; 1994. [Google Scholar]
- Lebreton C, Lazic-Jancic V, Steed A, Pekic S, Quarrie SA. Identification of QTL for drought responses in maize and their use in testing causal relationships between traits. J Exp Bot. 1995;46:853–865. [Google Scholar]
- Leung J, Giraudat J. Abscisic acid signal transduction. Annu Rev Plant Physiol Plant Mol Biol. 1998;49:199–222. doi: 10.1146/annurev.arplant.49.1.199. [DOI] [PubMed] [Google Scholar]
- Martinez O, Curnow RN. Three marker scanning of chromosomes for QTL in neighbouring intervals. In: van Ooijen JW, Jansen J, editors. Biometrics in Plant Breeding Applications of Molecular Markers. Proceedings of the Ninth Meeting of the EUCARPIA Section Biometrics in Plant Breeding. 6–8 July 1994, The Netherlands: Wageningen; 1994. pp. 153–162. [Google Scholar]
- Milborrow BV. The pathway of biosynthesis of abscisic acid in vascular plants: a review of the present state of knowledge of ABA synthesis. J Exp Bot. 2001;52:1145–1164. [PubMed] [Google Scholar]
- Muller B, Reymond M, Tardieu F. the elongation rate at the base of a maize leaf shows an invariant pattern during both the steady-stage elongation and the establishment of the elongation zone. J Exp Bot. 2001;52:1259–1268. [PubMed] [Google Scholar]
- Qin X, Zeevaart JA. The 9-cis-epoxycarotenoid cleavage reaction is the key regulatory step of abscisic acid biosynthesis in water-stressed bean. Proc Natl Acad Sci USA. 1999;96:15354–15361. doi: 10.1073/pnas.96.26.15354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quarrie SA, Whitford PN, Appleford MEJ, Wang TL, Cook SK, Henson IE, Loveys BR. A monoclonal antibody to (S)-abscisic acid: its characterization and use in radioimmunoassay for measuring abscisic acid in crude extracts of cereals and lupin leaves. Planta. 1988;173:330–339. doi: 10.1007/BF00401020. [DOI] [PubMed] [Google Scholar]
- Reidy B, Nosberger J, Fleming A. Differential expression of XET-related genes in the leaf elongation zone of F. pratensis. J Exp Bot. 2001;52:1847–1856. doi: 10.1093/jexbot/52.362.1847. [DOI] [PubMed] [Google Scholar]
- Ribaut JM, Hoisington DA, Deutsch JA, Jiang C, Gonzalez-de-Leon D. Identification of quantitative trait loci under drought conditions in tropical maize: I. Flowering parameters and the anthesis-silking interval. Theor Appl Genet. 1996;92:905–914. doi: 10.1007/BF00221905. [DOI] [PubMed] [Google Scholar]
- Ribaut JM, Jiang C, Gonzalez –de-Leon D, Edmeades GO, Hoisington DA. Identification of quantitative trait loci under drought conditions in tropical maize: II. Yield components and marker-assisted selection strategies. Theor Appl Genet. 1997;94:887–896. [Google Scholar]
- Sanguineti MC, Tuberosa R, Landi P, Salvi S, Maccaferri M, Casarini E, Conti S. QTL analysis of drought-related traits and grain yield in relation to genetic variation for leaf abscisic acid concentration in field-grown maize. J Exp Bot. 1999;50:1289–1297. [Google Scholar]
- Schwartz SH, Tan BC, Gage DA, Zeevaart JA, McCarty DR. Specific oxidative cleavage of carotenoids by VP14 of maize. Science. 1997;276:1872–1874. doi: 10.1126/science.276.5320.1872. [DOI] [PubMed] [Google Scholar]
- Seki M, Narusaka M, Abe H, Kasuga M, Yamaguchi-Shinozaki K, Carninci P, Hayashizaki Y. Monitoring the expression pattern of 1300 Arabidopsis genes under drought and cold stresses by using a full-length cDNA microarray. Plant Cell. 2001;13:61–72. doi: 10.1105/tpc.13.1.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp RE, LeNoble ME. ABA, ethylene and the control of shoot and root growth under water stress. J Exp Bot. 2002;53:33–37. [PubMed] [Google Scholar]
- Sharp RE, LeNoble ME, Else MA, Thorne ET, Gherardi F. Endogenous ABA maintains shoot growth in tomato independently of effects on plant water balance: evidence for an interaction with ethylene. J Exp Bot. 2000;51:1575–1584. doi: 10.1093/jexbot/51.350.1575. [DOI] [PubMed] [Google Scholar]
- Simko I, Vreugdenhil D, Jung CS, May GD. Similarity of QTLs detected for in vitro and greenhouse development of potato plants. Mol Breed. 1999;5:417–428. [Google Scholar]
- Tardieu F, Davies WJ. Integration of hydraulic and chemical signalling in the control of stomatal conductance and water status of droughted plants. Plant Cell Environ. 1993;16:341. :349. [Google Scholar]
- Tardieu F, Granier C, Muller B. Modelling leaf expansion in a fluctuating environment: Are changes in specific leaf area a consequence of changes in expansion rate? New Phytol. 1999;143:33–43. [Google Scholar]
- Tardieu F, Reymond M, Hamard P, Granier C, Muller B. Spatial distributions of expansion rate, cell division rate and cell size in maize leaves. A synthesis of effect of soil water status, evaporative demand and temperature. J Exp Bot. 2000;51:1505–1514. doi: 10.1093/jexbot/51.350.1505. [DOI] [PubMed] [Google Scholar]
- Theulat B, This D, Khairallah M, Borries C, Ragot C, Sourdille P, Leroy P, Monneveux P, Charrier A. Several QTLs involved in osmotic-adjustment trait variation in barley (Hordeum vulgare L.) Theor Appl Genet. 1998;96:688–698. [Google Scholar]
- Tuberosa R, Sanguineti MC, Landi P, Salvi S, Casarini E, Conti S. RFLP mapping of quantitative trait loci controlling abscisic acid concentration in leaves of drought-stressed maize. Theor Appl Genet. 1998;97:744–755. [Google Scholar]
- Visscher PM, Thompson R, Haley C. Confidence intervals in QTL mapping by bootstrapping. Genetics. 1996;143:1013–1020. doi: 10.1093/genetics/143.2.1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson S, Corlett JE, Oger L, Davies WJ. Effects of xylem pH on transpiration from wild-type and flacca tomato leaves. A vital role for abscisic acid in preventing excessive water loss even from well-watered plants. Plant Physiol. 1998;118:703–709. doi: 10.1104/pp.117.2.703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin X, Kropff MJ, Stam P. The role of ecophysiological models in QTL analysis: the example of specific leaf area in barley. Heredity. 1999a;82:415–421. doi: 10.1038/sj.hdy.6885030. [DOI] [PubMed] [Google Scholar]
- Yin X, Stam P, Johan Dourleijn C, Kropff MJ. AFLP mapping of quantitative trait loci for yield-determining physiological characters in spring barley. Theor Appl Genet. 1999b;99:244–253. [Google Scholar]
- Yuan S, Wu Y, Cosgrove DJ. A fungal endoglucanase with plant cell wall extension activity. Plant Physiol. 2001;127:324–333. doi: 10.1104/pp.127.1.324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng ZB. Precision mapping of quantitative trait loci. Genetics. 1994;136:1457–1468. doi: 10.1093/genetics/136.4.1457. [DOI] [PMC free article] [PubMed] [Google Scholar]