Criteria for the control of drug-resistant tuberculosis

Abstract

Antibiotic resistance is a growing impediment to the control of infectious diseases worldwide, tuberculosis (TB) being among them. TB kills two million people each year and foci of multidrug-resistant TB (MDR-TB) have been identified in Eastern Europe, Africa, Asia, and Latin America. A critical question for health policy is whether standardized short-course chemotherapy for TB, based on cheap first-line drugs, can prevent and reverse the spread of drug resistance. Here we use mathematical modeling, in conjunction with treatment results from six countries, to show that best-practice short-course chemotherapy is highly likely to bring strains resistant to either of the two key drugs isoniazid and rifampicin under control and to prevent the emergence of MDR-TB. However, it is not certain to contain MDR-TB once it has emerged, partly because cure rates are too low. We estimate that approximately 70% of prevalent, infectious MDR-TB cases should be detected and treated each year, and at least 80% of these cases should be cured, in order to prevent outbreaks of MDR-TB. Poor control programs should aim to increase case detection and cure rates together for three reasons: (i) these variables act synergistically; (ii) when either is low, the other cannot succeed alone; and (iii) the second-line drugs needed to raise MDR-TB cure rates are few and extremely costly. We discuss the implications of these results for World Health Organization policy on the management of antibiotic resistance.

Multidrug-resistant tuberculosis (MDR-TB) is among the most worrisome elements of the pandemic of antibiotic resistance (1) because TB patients that fail treatment have a high risk of death. TB is the second largest cause of death from an infectious agent after HIV/AIDS, and in developing countries, Mycobacterium tuberculosis is one of the most important opportunistic infections associated with HIV (2). MDR-TB now has been found on all continents, with especially high rates in countries of the former Soviet Union (3).

The World Health Organization currently recommends, for all new cases of TB, standardized short-course chemotherapy (SCC) based on a regimen of four first-line drugs taken for 6–8 months (4). MDR-TB is produced by the selection of MDR strains (resistant to at least isoniazid and rifampicin) in patients who fail to complete chemotherapy with the correct combination of drugs. MDR-TB cases will continue to arise this way as long as drug-susceptible (DS) and other drug-resistant (DR) strains persist anywhere, and as long as some patients fail treatment. Even if some countries manage to eliminate TB, the risk of disease, and drug-resistant disease, will persist through immigration.

Cases of MDR-TB generated by inadequate treatment can transmit infection to others. Interrupting the transmission cycle is the limiting factor in MDR-TB control, because the cure rates of MDR strains are significantly lower than those of DS or DR strains (5). In other words, it is easier in any setting to prevent MDR-TB from arising in the first place than to stop transmission by curing it.

Although treatment failure can have grave consequences for individual patients, it will not necessarily generate epidemics of MDR-TB through the transmission cycle. Epidemiological theory states that an outbreak of MDR-TB requires a cure rate below some threshold, which will be <100%. Our goal in this paper is to try to identify that threshold by using mathematical modeling in conjunction with the latest treatment results from MDR-TB patients in six countries (5). Our approach is to establish a set of epidemiological criteria for MDR-TB elimination and to determine whether these criteria can be met by the best possible application of SCC. The alternative will be to resort to a limited number of second-line drugs, which are expensive and comparatively toxic. Data describing the global spread of antibiotic resistance are relatively good for TB (3); therefore, both the methods and results of the present analysis may hold lessons that can be applied to the control of other infectious diseases.

Methods

Mathematical Model of Tuberculosis.

To establish criteria for MDR-TB control, we have developed a compartmental model of the dynamics of pulmonary MDR-TB in adults over 15 years of age which account for more than 95% of infectious cases (Fig. 1). The model works with persons infected, rather than with pathogen gene frequencies; it is thus epidemiological rather than genetic. It joins a growing family of compartmental models for TB (6–11), but has been tailored (from ref. 11) to investigate the above questions about antibiotic resistance (see Appendix). New pulmonary cases are of two types, infectious and noninfectious. Prior infection with M. tuberculosis, whether of DS or DR strains, provides partial protection against reinfection and is therefore an obstacle to the spread of disease. Case detection removes infectious cases from the prevalent pool. If cases are not detected and treated, they will either die or self-cure. Of those cases treated with drugs, a proportion is cured, with a very low chance of relapse, which is assumed to be zero. Treatment failures are all cases that are not permanently cured, including cases that remain sputum smear-positive after 5 months of treatment and cases that become temporarily smear-negative and relapse some months later. Failures are presumed to be less infectious on average than are new smear-positive cases. The basic case reproduction number, R₀, is the number of secondary cases arising from one primary case introduced into a fully susceptible population (12). Here, R₀ = bcτ, the product of parameters determining susceptibility (b), contact rate (c), and the duration of infectiousness (τ) (Table 1). We define R_θ as the case reproduction number modified to allow for chemotherapy, so that R_θ ≤ 1 must be satisfied to prevent an outbreak of, or to eliminate, the disease. R_0m (without treatment) and R_θm (with treatment) are the equivalent case reproduction numbers for MDR-TB, and R_θm ≤ 1 is required to interrupt the MDR-TB transmission cycle. We measure the rate of decline of MDR-TB under chemotherapy by the time taken to achieve a 10-fold reduction in incidence from the point of intervention, determined by simulation (see Appendix).

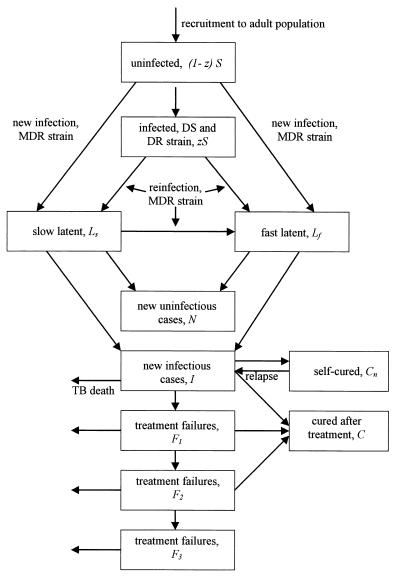
Figure 1.

Flow chart of the mathematical model for MDR-TB. Each box represents a state variable of the model (see Methods). The population is followed from the point at which infected and uninfected individuals join the adult population. DS and DR refer to drug-susceptible and drug-resistant (but not MDR) strains of M. tuberculosis, respectively. Individuals in all states may die of causes unrelated to TB (data not shown). Infections leading to MDR-TB are transmitted from new cases, I, and treatment failures, F_i.

Table 1.

Definitions and values of model parameters and control variables

Parameter or control variable	Definition	Lower	Mode	Upper
c	Per capita contact rate, adjusted for age structure; subscript m denotes MDR	7.0	9.8	12.6
z	Fraction of population infected with DS or DR strains	0.3	0.3	0.3
x	Fraction of reinfected persons that develops MDR-TB at rate vf	0.1	0.35	0.6
p	Fraction of newly infected persons that develops primary progressive MDR-TB	0.08	0.14	0.25
f	Fraction of MDR-TB cases that is infectious	0.5	0.65	0.65
n	Per capita rate at which infectious cases self-cure	0.15	0.2	0.25
rn	Per capita rate of relapse to infectious MDR-TB after self-cure	0.02	0.03	0.04
μ	Per capita death rate from causes other than MDR-TB	0.015	0.015	0.015
μi	Per capita death rate from untreated, MDR-TB; μif, for treatment failures, was assumed to be 0.5 (range 0–1) of μi	0.2	0.3	0.4
φ	Fractional infectiousness of treatment failures	0	0.25	0.5
vf	Per capita rate of breakdown to progressive primary MDR-TB	0.76	0.88	0.99
vs	Per capita rate of breakdown to MDR-TB by endogenous reactivation	0.0001	0.00011	0.0003
d	Per capita detection and treatment rate of new cases	Variable
r	Per capita detection and retreatment rate of failures; subscripts specify the number of times treatment has failed	Variable
k	Proportion of cases cured; subscripts as for r	Variable

Rates are year(s)⁻¹. 

Sources and Analysis of Data.

To calculate case reproduction numbers, we have relied on epidemiological studies of DS-TB in large populations (13). There have been significant outbreaks of MDR-TB in institutions such as hospitals (14, 15) and prisons (16) where the contact rate or susceptibility to disease, especially in HIV-infected persons, could be greater. This analysis therefore is intended to apply to the general population, and our criteria for containment may be insufficient to prevent outbreaks in these special cases. Model parameter values are for adult (>15 years old) TB (ref. 11 and Table 1). The per capita contact rate, c, was estimated to be 14 ± 4 per year (ref. 13 and C. J. L. Murray, unpublished data), and then adjusted for the fraction of persons over 15 years of age in a typical highly endemic country (i.e., India, 0.7). MDR strains probably generate fewer secondary infectious cases than do DS strains, because MDR-TB has not become common without drug pressure whereas DS strains have. There is direct evidence both from animal experiments (17) and from epidemiological studies (18) that certain isoniazid-resistant strains have lower relative fitness than do DS strains. No such data exist for MDR strains, and any cost of resistance could be small (19, 20) and temporary (21, 22). Based on refs. 18 and 20, we cautiously set modal c_m = c, but giving relative fitness c_m/c range 0.7–1 in uncertainty and sensitivity analyses (see Uncertainty and Sensitivity Analysis). Treatment success rates reported from six countries are the fractions of cohorts of patients whose sputum smears became negative for acid-fast bacilli after 6–8 months of treatment, plus a small fraction who completed treatment without a final smear examination (5).

Uncertainty and Sensitivity Analysis.

We used Monte Carlo simulation to calculate the probability that R_θm < 1, using 5,000 iterations for each of 24 × 21 combinations of case detection and cure. R_θm was calculated as described in the Appendix. Parameter values were assumed to follow independent, triangular distributions with modes and lower and upper limits given in Table 1. The same distributions were used to put bounds (5th and 95th centiles) on estimates of R_θm and in multivariate sensitivity analysis.

Results

Best estimates of model parameters give R_0m = 1.60 (5th and 95th centiles, 1.02 and 2.67, respectively) in the absence of chemotherapy and when MDR-TB is invading a population where 30% of the population already is infected with M. tuberculosis. With a reproduction number of this magnitude, MDR-TB incidence doubles every 5.3 years while the epidemic is growing exponentially. A 10-fold increase takes 18.6 years. R_0m would rise to 1.98 (1.29–3.62) if MDR-TB were spreading through a fully susceptible population, i.e. no one infected with DS or other DR strains except the index case. As a rough check on the value of R_0m, we used the approximation R_0m ≈ 1/(s* + x(1 − s*)), in which s* is the fraction of people uninfected with M. tuberculosis at equilibrium and x is defined in Table 1. For the approximately stable, endemic disease seen in many developing countries (2), s* ranges from 30% to 50% and R_0m is <2.

Point estimates of R_θm over a wide range of case detection and cure rates are shown in Fig. 2a, where case detection is expressed more intuitively as its reciprocal, the duration of infectiousness. This value is the approximate number of months to treatment, or to retreatment for those that fail the first course. The right-hand axis indicates the cure rate of new, infectious MDR-TB cases; the cure rates of retreatment cases were assumed to be 38% (range 15–62%) lower (5). The contours on this map join points of equal R_θm, and the contours become flatter as R_θm increases. At very low rates of cure, more active case finding can even increase R_θm. This pattern arises because there is formally an interaction between case detection and cure such that case finding is less effective, pro rata, when the cure rate is low (see Appendix, Eq. A15). If patients take drugs intermittently, if they default from treatment, or if they are given the wrong drugs, a high proportion will remain persistently infectious, no matter how promptly they are treated (23). R_θm = 1 is the most important contour in Fig. 2a: Any combination of infectious duration and cure rate lying above that line will interrupt the transmission cycle of MDR-TB. If DS, DR, and MDR strains have equal average fitness, then R_θm ≤ 1 interrupts the transmission cycles of all strains, and all will eventually be eliminated, including MDR-TB.

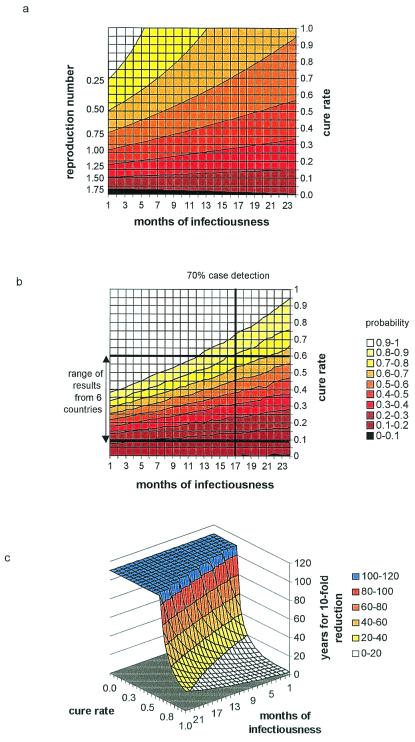
Figure 2.

Criteria for the control of MDR-TB. (a) Case reproduction numbers of MDR-TB, R_θm, for combinations of cure rate and duration infectiousness (months until first treatment, or between the start of first and subsequent treatments). Contours join lines of equal R_θm. The contour for R_θm = 1 separates MDR-TB persistence from decline. (b) Probability that R_θm ≤ 1 for various combinations of treatment interval and cure rate. Contours join lines of equal probability. Horizontal lines mark the best (Hong Kong) and worst (Ivanovo Oblast, Russian Federation) outcomes of treatment for MDR-TB cases using standard SCC (5). Countries with intermediate results were the Dominican Republic, the Republic of Korea, Italy, and Peru. The vertical line marks the interval between treatment corresponding to an annual detection rate of 70% of prevalent cases. (c) Three-dimensional surface showing the number of years required for a 10-fold reduction in the incidence of MDR-TB, with different combinations of cure rate and months of infectiousness. Some solutions >120 years are generated by combinations of case detection and cure that cause incidence to rise instead of fall.

To make a more careful assessment of the impact of control, we calculated the probability that R_θm ≤ 1 (rather than making point estimates of R_θm) by using Monte Carlo methods to carry out multivariate uncertainty analysis (Table 1 and Fig. 2b). Interruption of the transmission cycle of MDR-TB is most likely in the upper left-hand corner of the graph. The vertical line on this map marks the duration of infectiousness (17 months) corresponding to an annual detection rate of 70% of prevalent infectious cases. The horizontal lines mark the range of cure rates for MDR-TB patients observed under SCC in six countries, from Ivanovo Oblast in Russia (treatment success rate 11%), through the Dominican Republic, Italy, Korea, and Peru, to Hong Kong (treatment success rate 60%). The wide gap between these lines indicates that the quality of case management varies enormously among countries. In the best cases, Hong Kong and Peru, the probability that R_θm ≤ 1 would be 80%, assuming an annual case detection rate of 70%. The probability will be lower if some MDR-TB patients deemed to be “cured” after 5 months of uninterrupted treatment later relapse. Multivariate sensitivity analysis shows that these results are most responsive to parameters p and c but are insensitive to incidence rate at the time of intervention.

The cure rates of patients carrying fully susceptible bacilli, or bacilli resistant to either rifampicin or isoniazid, are much higher than 60%—approximately 80% in Hong Kong and Peru (5). Reconstructing Fig. 2b for non-MDR strains (with higher relative fitness given by c instead of c_m) indicates that the probability of preventing an outbreak of, or eliminating, disease caused by these strains (R_θ ≤ 1) is better than 90% (data not shown). This result is correct even when allowing for the fact that approximately 10% of rifampicin-resistant cases may later relapse (24). Ultimately, these high cure rates should eliminate all forms of TB (see Appendix).

If the incidence of MDR-TB is likely to decline, we need to know how long it will take to achieve a significant reduction. Fig. 2c shows the number of years needed to reduce MDR-TB incidence by a factor of 10. Even for Hong Kong this period would be over 40 years with 70% case detection. Moreover, the gradient of the surface is very steep in this region of the graph, indicating that small changes in the treatment interval and cure rate would dramatically affect the rate of decline of MDR-TB. Thus, the transmission cycle would never be interrupted if the cure rate fell just 10% from 60% to 50%. Fig. 2c suggests that the cure rate should be at least 80% to be confident of a 10-fold reduction in the incidence of MDR-TB within 20 years. The cure rate would need to be higher than 80% where less than 30% of people are already infected with DS or DR strains.

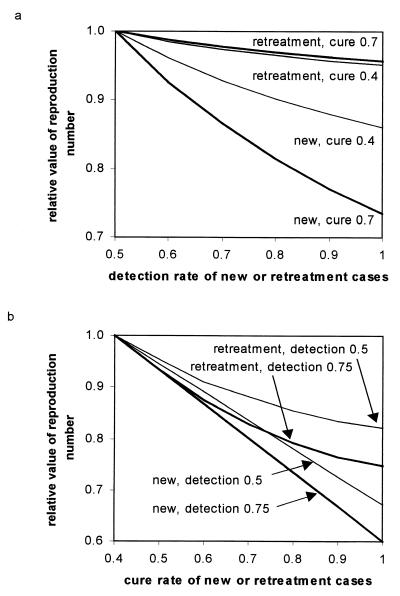
The interaction between case detection and cure is revealed more fully in Fig. 3. It is better to increase the detection rate of new cases rather than of treatment failures, especially when the cure rate is high (Fig. 3a). Likewise, it is better to improve the cure rate of new cases rather than of treatment failures, though the differential advantage of curing new cases over treatment failures almost is independent of the rate of case finding (Fig. 3b). Thus, where control programs are poor, efforts should be made to improve both case detection and cure rates, especially of new cases, because these two variables act synergistically.

Figure 3.

Interactions between case detection and cure rates in the control of MDR-TB. Initial values of the reproduction number, R_θm, have been scaled to 1 on the vertical axis to aid comparison of different strategies. Horizontal axes explore the impact of improving case detection (a) and cure rates (b). In a, R_θm is more effectively reduced by improving the case detection rate of new cases rather than of retreatment cases (previous failures). The impact of detecting and treating new cases is greater when the cure rate is higher (thick lines), and so is the relative advantage of treating new cases over retreatment cases (bigger gap between thick lines than between thin lines). In b, R_θm is more effectively reduced by improving the cure rate of new cases rather than of retreatment cases. The impact is greater when the detection rate is higher (0.75 instead of 0.5), and this applies to both new and retreatment cases (same gap between thick lines as between thin lines).

Conclusions

Three conclusions about the control of antibiotic resistance emerge from these comparisons of model and data. First, to be sure of preventing MDR-TB epidemics under present assumptions, second-line drugs will be needed to raise MDR-TB cure rates above the maximum that can be achieved by SCC. To be cautious about the management of MDR-TB, we have chosen values of the relative fitness of MDR strains that probably err on the high side. If MDR strains are in the future found to be less transmissible (lower c) or less virulent (lower b or τ), then lower rates of case detection and cure will be needed to prevent an epidemic. The analytical framework set out in this paper could be used to interpret any new data on the relative fitness of MDR-TB. The essence of the problem is to calculate the basic case reproduction number for MDR-TB; in this context, our estimates of R_0m are lower than suggested by an earlier analysis (6, 7) mainly because we have set the average duration of infectiousness for untreated patients realistically to 2 years (13) instead of to more than 4 years. In this instance, accurate parameter estimates are more important than are some structural details of the model.

Second, we already know that it is easier to prevent MDR-TB from arising through inadequate treatment than to bring an established epidemic under control. The present analysis suggests that best-practice SCC, by achieving cure rates over 80%, can control epidemics of isoniazid- or rifampicin-resistant disease and can prevent the emergence of MDR-TB, provided the interval from becoming infectious to treatment is not excessive. It is vital that control programs achieve the best possible results with first-line drugs, thereby preventing the selection of MDR strains, before attempting to interrupt the transmission cycle with second-line drugs (4).

Third, a new strategy to treat MDR-TB cases more promptly is highly desirable, making case detection more active than passive. We estimate that approximately 70% of prevalent, infectious MDR-TB cases should be detected and treated each year, and at least 80% of these cases cured, to interrupt the transmission cycle. Poor control programs should aim to increase case detection and cure rates together because these variables act synergistically and because, when either is low, the other cannot succeed alone. One way of improving case detection is to target those individuals known to be at high risk of carrying drug-resistant TB, such as the homeless or those in hospitals and prisons (14, 16, 18, 24, 25).

A further step in devising a rational approach to the containment of drug resistance will be to quantify the costs of unit increases in case detection and cure rates, for resistant strains of various types. A course of second-line drugs for MDRTB treatment costs at least 100 times as much as SCC ($2,000–5,000 U.S. for drugs alone), so there is a high premium on balancing drug choice with rapid case finding and improved case management.

Abbreviations

TB

tuberculosis

MDR-TB

multidrug-resistant TB

SCC

standardized short-course chemotherapy

DS

drug-susceptible

DR

drug-resistant

Appendix

Mathematical Model of TB.

The following system of differential equations (with S^⋅ = dS/dt, etc.) describes the dynamics of infection and pulmonary disease in adults.

Uninfected:

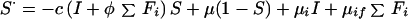A1

Latent (slow breakdown to disease):

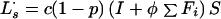A2

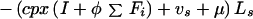Latent (fast breakdown to disease):

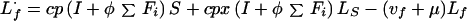A3

Infectious:

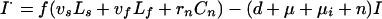A4

Noninfectious:

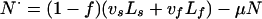A5

Treatment failure (F_i, i = 1 to 3):

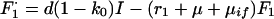A6

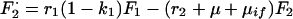A7

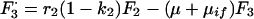A8

Self-cure:

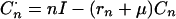A9

Cure (by treatment):

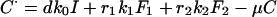A10

Definitions and values of parameters and control variables come mostly from previous work (11) and are given in Table 1. The basic case reproduction number, assuming no chemotherapy, is R₀ = bcτ, in which c is the rate of contact per unit time between an infectious case and others in the population, and b is the proportion of infections that leads to infectious cases,

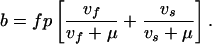A11

Without treatment, the average time a case remains infectious, τ, is

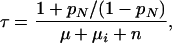A12

where p_N is the proportion of cases that self-cures and later relapses to infectious disease,

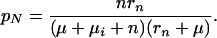A13

Impact of Chemotherapy.

SCC reduces the average duration of infectiousness. Here we use R_θ to denote R₀ modified to allow for chemotherapy. Then R_θ = bcτ_θ, and R_θ ≤ 1 guarantees, in a deterministic model, the elimination of disease or the prevention of outbreaks. With the introduction of case-finding and treatment comes the possibility of treatment failure, so τ in Eq. A12 must be replaced by τ_θ, the sum of the components τ₁–τ₄.

New cases:

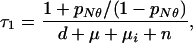A14

Treatment failures:

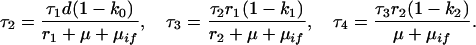A15

Case-finding also intercepts some patients who would otherwise have self-cured, so p_N in Eqs. A12 and A13 becomes

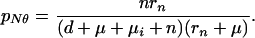A16

We confirmed by numerical simulation of equations A1–A10 (Euler method; time step, 0.1 year) that TB incidence increases when R_θ > 1 and decreases when R_θ ≤ 1.

MDR-TB.

Among drug-resistant strains of M. tuberculosis, MDR is outstandingly important because treatment success is markedly lower under SCC. Based on the arguments above, we can derive two criteria for MDR-TB elimination, one for MDR-TB arising from DR strains by mutation and selection and the other to interrupt the MDR transmission cycle. It is clear that MDR-TB will arise by mutation and selection as long as DS or other DR strains continue to exist, and as long as some patients fail treatment. R_θ ≤ 1 is therefore required to prevent MDR-TB emerging in previously treated patients, as well as to break the transmission cycle of non-MDR strains.

The most stringent criterion for interrupting the transmission cycle arises when one infectious case is introduced into a population uninfected with any strain of M. tuberculosis. MDR-TB strains are likely to have different relative fitness, because one or more of b, c, and τ_θ are different (typically lower, via parameters p, v_f, v_s, etc.). Here we allow for the potentially lower fitness of MDR strains by replacing contact rate c with c_m, so that R_0m = bc_mτ (no treatment), R_θm = bc_mτ_θ (under treatment), and R_θm ≤ 1 is required to prevent an outbreak of MDR-TB. If R_θm ≤ 1 but R_θ > 1, we expect to see MDR-TB in previously treated patients, but only rarely in new TB cases. If R_θm > 1 but R_θ ≤ 1, MDR strains ultimately will replace all others.

In practice, we are more likely to see an infectious case of MDR-TB arise in a population where the fraction of individuals already infected, z, is large (typically 1/4 to 1/3) and fairly steady (2). Assuming constant z, Eqs. A1–A10 can be used to model the short-term dynamics of MDR-TB if c in Eqs. A1–A3 is replaced with c_m(1 − z + zx) (Fig. 1). With z > 0, MDR-TB will spread more slowly, because those infected are partially immune to reinfection. Then, to calculate R_θm, a more general expression for b_m (replacing Eq. A11) is needed,

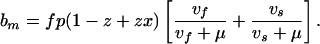A17

The long-term rate of decrease is determined by the principal eigenvalue of Eqs. A1–A10 and its corresponding eigenvector. Here we are more interested in the time taken to achieve a 10-fold reduction in incidence from the point of intervention, which was determined by simulation using Eqs. A1–A10 and transmission term c_m(1 − z + zx). More accurate calculations of the rate of decline can be carried out by extending Eqs. A1–A10 to model simultaneously the dynamics of both drug-susceptible and drug-resistant TB.