The emergence of visual objects in space–time

Abstract

It is natural to think that in perceiving dynamic scenes, vision takes a series of snapshots. Motion perception can ensue when the snapshots are different. The snapshot metaphor suggests two questions: (i) How does the visual system put together elements within each snapshot to form objects? This is the spatial grouping problem. (ii) When the snapshots are different, how does the visual system know which element in one snapshot corresponds to which element in the next? This is the temporal grouping problem. The snapshot metaphor is a caricature of the dominant model in the field—the sequential model—according to which spatial and temporal grouping are independent. The model we propose here is an interactive model, according to which the two grouping mechanisms are not separable. Currently, the experiments that support the interactive model are not conclusive because they use stimuli that are excessively specialized. To overcome this weakness, we created a new type of stimulus—spatiotemporal dot lattices—which allow us to independently manipulate the strength of spatial and temporal groupings. For these stimuli, sequential models make one fundamental assumption: if the spatial configuration of the stimulus remains constant, the perception of spatial grouping cannot be affected by manipulations of the temporal configuration of the stimulus. Our data are inconsistent with this assumption.

Vision uses small receptors to sample optical information. Spatial grouping is the process by which samples are linked across space to form more complex visual entities, such as objects and surfaces. Temporal grouping is the process by which visual entities are linked over time. Spatial grouping and temporal grouping either are sequential or they interact. If the perception of dynamic scenes is the result of the successive application of these two kinds of grouping, we have a sequential model of motion perception. If the perception of dynamic scenes is the result of spatial and temporal grouping operating in parallel, we have an interactive model.

The Sequential Model.

Let us consider two versions of the sequential model: one in which spatial grouping comes first, the other in which temporal grouping comes first. The perception of most dynamic stimuli can be explained by describing them as a succession of snapshots (1). For example, according to Ullman (2), vision first does grouping within each snapshot and then finds a mapping between these groupings across the snapshots. These groupings are often called matching units. In this view, spatial grouping alone determines the matching units that will undergo temporal grouping.

Some stimuli, however, are designed to prevent us from applying spatial grouping first. These are, for example, random-dot cinematograms (3). These are dynamic displays in which each frame contains a different random texture. If the frames are not correlated, one sees random dynamic “snow.” If dots in a patch of the display are correlated across frames, the patch will segregate, and its shape will be visible. A sequential model can account for the perception of such displays by assuming that temporal grouping extracts coherently moving elements [a process known as grouping by common fate (4)], which then undergo spatial organization.

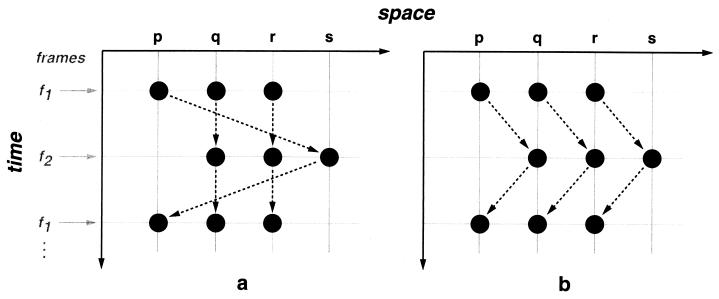
Some data that appear to imply an interactive model can actually be explained by a sequential model. Consider, for example, the Ternus display (5), which consists of two rapidly alternating frames—f₁ and f₂—in which dots can occupy four equally spaced collinear positions pqrs (Fig. 1). The dots in f₁ are at pqr; the dots in f₂ are at qrs. This display can give rise to two percepts: (i) Element motion (e-motion) is seen when the two dots in positions q and r appear immobile, while one dot appears to move between the positions p and s. (ii) Group motion (g-motion) is seen when three dots appear to move, as a group, back and forth between pqr and qrs. The longer the interstimulus interval (ISI; interframe interval in this context), the higher the likelihood of g-motion (6). This is called the ISI effect. It is tempting to view this phenomenon as evidence for an interactive model (7). To see why, assume that the shorter the ISI, the stronger the temporal grouping. When the ISI is sufficiently short, temporal grouping could be stronger than spatial grouping. Thus, rather than grouping with the dot at r in f₁, the dot at q in f₁ would group with the dot at q in f₂. The result is e-motion. As ISI grows, the strength of temporal grouping drops, and concurrent dots group within frames, resulting in g-motion. However, a sequential model can also account for the ISI effect. Suppose that longer ISIs have two effects: (i) they weaken temporal grouping, and (ii) they give spatial grouping more time to consolidate the organization of concurrent dots. According to (ii), the ISI effect is caused by spatial rather than temporal grouping and is consistent with a sequential model (8).

Figure 1.

Ternus display. The dotted arrows show the directions of perceived motion. (a) Element motion. (b) Group motion.

The Interactive Model.

Only an interactive model can account for the perception of motion when neither spatial grouping alone nor successive spatial and temporal grouping operations could derive matching units. Unfortunately, the only persuasive evidence in favor of the interactive model comes from displays in which objects and surfaces (transparent or opaque) overlap, and their spatial relation changes dynamically. For example, in certain kinetic occlusion (9–11) displays, we see a hitherto visible part of the scene become occluded by an opaque surface. In such displays, there is no simple correspondence between successive frames, because one frame contains a different number of elements than the next.†

We are concerned that the evidence from such displays is not general enough to refute sequential models as a class, because such displays may trigger a specialized mechanism that processes kinetic occlusion in which spatial and temporal grouping interact. For example, kinetic occlusion offers two characteristic clues: (i) the accretion or deletion of texture, as a textured object emerges from or disappears behind an occluder (9), and (ii) the presence of “T-junctions” between the contours of an occluder and the contours of an object it occludes (14, 15). To address these concerns, we designed displays that are not likely to trigger specialized motion-perception mechanisms.

Motion Lattices.

To refute the sequential models, we will show that spatial and temporal grouping mechanisms interact even when simple matching between the successive frames is possible. We created spatiotemporal dot lattices (motion lattices) in which we could independently vary the strength of spatial and temporal grouping by manipulating the spatial proximity of concurrent and successive dots [a generalization of the stimuli used by Burt and Sperling (16)]. We varied the strength of temporal grouping by manipulating the spatial proximity between successive dots. To avoid ambiguities of data interpretation that beset the Ternus display (i.e., the ISI effect), we held ISI constant. In our displays, as in the Ternus display, observers see either e-motion or g-motion. The advantage of motion lattices over the Ternus display is that in lattices the directions of e-motion and g-motion differ. The direction of e-motion is determined by matching individual dots in successive frames of the display. The direction of g-motion is determined by the matching of dot groupings in successive frames.

If we show an observer a single frame of a motion lattice, its spatial grouping is determined by the relative distance between concurrent dots (17). Although we hold the ISI constant, temporal grouping can be determined only by spatial distances between successive dots. According to the sequential model, the propensity of dots to group within frames—and thus yield g-motion—is independent of the determinants of temporal grouping. To test this prediction, we ask whether the frequency of g-motion changes when we hold constant the relative distance between concurrent dots and vary the spatial distance between successive dots. We find that it does, and on this basis we will claim that we have refuted the sequential model in favor of the interactive model.

General Methods

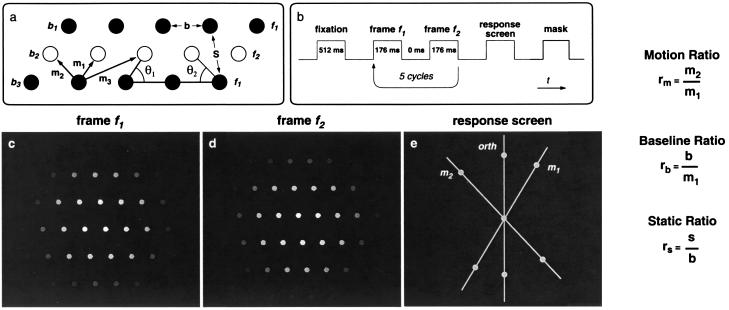
A motion lattice is a lattice of locations, whose rows we call baselines (b₁, b₂, b₃, … ; Fig. 2a), displayed in two frames, f₁ and f₂. In f₁, dots occupy the locations of the odd-numbered baselines; in f₂, dots occupy the locations of the even-numbered baselines. When these frames rapidly alternate (f₁, f₂, f₁, …) under appropriate spatial and temporal conditions, motion lattices are perceived as a continuous flow of apparent motion. Motion lattices are specified by two temporal and three spatial parameters. The two temporal parameters were kept constant: ISI (= 0) and frame duration (= 176 ms). The three spatial parameters are: |b|, the distance between adjacent dots in a baseline; |m₁|, the shortest distance between a dot in an f₁-frame and a dot in an f₂-frame; θ₁, the angle between the orientations of b and m₁.

Figure 2.

(a) Three rows (baselines) of a motion lattice. The solid and open circles stand for dots that appear in frames f₁ and f₂, respectively. The three spatial parameters of motion lattices are: |b|, the distance between adjacent dots in a baseline; |m₁|, the shortest distance between successive dots; and θ₁, the acute angle between the orientations b and m₁. The acute angle between b and m₂ is θ₂. S is the second (after b) shortest distance within a frame. To minimize edge effects, we modulated the luminance of lattice dots [radius = 0.3 degrees of visual angle (dva)] according to a Gaussian distribution (σ = 1.5 dva). We held m₁ (= 0.9 dva) constant. (b) Time line of each trial. We kept the total duration of each presentation at 1.76 s to prevent the percept of oscillatory motion, which sometimes is seen with longer presentations. (c and d) Two successive frames of a motion lattice captured from the computer screen (not to scale). (e) A response screen with three response options. (Labels were not presented in the display.)

Two kinds of apparent motion can be seen in motion lattices:

• e-motion is based on element-to-element matching. In e-motion, each dot in a baseline is matched with a dot in an adjacent baseline. The three shortest distances between successive dots are |m₁|≤|m₂|≤|m₃| (Fig. 2a). The shorter the distance between dots, the more often the dots are linked in apparent motion (18, 19). Motion along m₁ is seen more often than along m₂ and never along m₃. The strength of grouping between successive elements is called affinity (2), which is inversely related to interdot distance.

• g-motion is based on grouping-to-grouping matching. That is to say, in g-motion matching occurs between dot groupings (called virtual objects) as wholes. For example, in Figs. 2 c–d, suppose that the observer sees the lattice organized into virtual objects that coincide with the baselines, i.e., into horizontal strips of dots. If the observer sees vertical motion, it must be g-motion, because neither m₁ nor m₂ is vertical. In other cases, the virtual objects may not coincide with the baselines, but g-motion is always orthogonal to the virtual objects.‡

The sequential model predicts (for our stimuli) that the direction of motion will be determined solely by spatial grouping. To test this prediction, we measure the relative frequency of e-motion and g-motion, where we hold the determinants of spatial grouping constant and vary the spatial determinants of temporal grouping.

Spatial Grouping.

The determinants of spatial grouping in static lattices are known: the dots group by proximity alone independent of lattice configuration. The strength of this grouping is called attraction. Attraction decreases exponentially, as the relative distance between dots increases (17). Analogously, within each frame of a motion lattice, the likelihood of different spatial groupings is controlled by the ratio of the two shortest interdot distances, r_s = (|s|/|b|) (Fig. 2a). (|S| is equal to the shortest of the two distances: 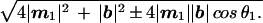) We call r_s the static ratio. If we hold this ratio constant, the likelihood of different virtual objects within a frame will remain constant.

Temporal Grouping.

In motion lattices temporal grouping is the outcome of two competitions:

• e-motion vs. g-motion: Because we are holding the temporal parameters constant, the outcome of this competition is controlled by the baseline ratio, r_b = (|b|/|m₁|). For example, if r_b is low, then attraction within the baselines is high; therefore, observers are likely to see g-motion orthogonal to the baseline. If r_b is higher, then attraction within the baselines is lower; therefore, observers are less likely to see g-motion orthogonal to the baseline and—depending on the parameters of the motion lattice—they will see either e-motion or g-motion orthogonal to other virtual objects.

• between alternative e-motions: The outcome of this competition is controlled by the motion ratio, r_m = (|m₂|/|m₁|). If r_m is high, then temporal grouping favors m₁ motion over m₂ motion.

The time line of a trial is shown in Fig. 2b. After fixating a central dot, observers viewed the motion sequence. In the trials with three response options, the response screen displayed three radial lines (Fig. 2e): two were parallel to the most probable orientations of e-motion (m₁ and m₂), and one was orthogonal to the baselines, orth. In the trials with two response options, the response screen displayed two radial lines, parallel to the orientations of m₁ and m₂. Observers reported the orientation of the motion by clicking on one of the circles attached to the lines on the response screen. The mask was an array of randomly moving dots. We randomized the orientation of the lattice between trials to minimize carryover from trial to trial.

Experiment 1

In Experiment 1, which is a control experiment, we show that changes in the frequency of g-motion are not attributable to observers' confusion between the response options. This possibility arises because as the orientations of m₁ and m₂ vectors approach the orthogonal to the baseline, confusion between orth and affinity responses (m₁, m₂) might increase. Response confusion might mimic an effect of interaction between the two types of grouping.

Methods.

We held θ₁ (= 60°) constant and chose six motion lattices, each of which is defined by a (r_m, r_b) pair: (1.00, 1.00), (1.07, 1.13), (1.15, 1.24), (1.23, 1.35), (1.30, 1.44), (1.38, 1.54). Because of the geometry of motion lattices, when one holds θ₁ constant, r_m and r_b covary: r_m = r_b (/|b|).

Our six observers had normal or corrected-to-normal vision and were naive as to the purpose of the experiment. Each observer went through 100 trials per motion lattice (i.e., 600 trials) for each of two 1-hour sessions—one with two (m₁ and m₂) and the other with three (m₁, m₂, and orth) response options in the response screen.

Results and Discussion.

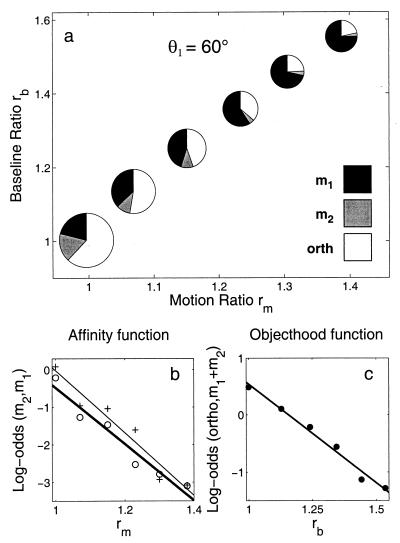
The pie charts in Fig. 3a represent the relative proportion of m₁, m₂, and orth responses as a function of r_m, r_b. Because θ₂ varied, we represent this variation by changing the diameters of the pie charts in proportion to e^r_θ, where r_θ = [(tan θ₂)/(tan θ₁)]. We split this three-way variation into two independent parts:

• Affinity function: In Fig. 3b, we plot the logarithm of odds (log-odds) with which observers chose e-motion along m₂ over m₁ for the two sessions. First, we note that because log-odds(m₂, m₁)§ decrease linearly as a function of r_m = (|m₂|/|m₁|), the odds [p(m₂)]/[p(m₁)] decrease exponentially as a function of r_m. Further, we note that the confusion between the orth responses and the affinity responses (m₁, m₂) had little effect on response frequencies in the three-response sessions. The affinity function with three response options (thick line, “○” symbols) differed little from the affinity function with two response options (thin line, “+” symbols), compared to the effect of r_m.

• Objecthood function: In Fig. 3c, we plot the log-odds with which observers chose g-motion over e-motion for the three-response session. This function reflects the tradeoff between group-to-group and element-to-element matching. Because log-odds (orth, m₁ ∨ m₂)¶ decrease linearly as a function of r_b = (|b|/|m₁|), the odds p(orth)/[p(m₁) + p(m₂)] decrease exponentially as a function of r_b.

Figure 3.

Results of Experiment 1. (a) The pie charts (averaged over observers) show how the distribution of the responses (m₁, m₂, and orth) varied as a function of the motion ratio, r_m, and the baseline ratio, r_b, in the three-response sessions. These data are decomposed in (b and c). (b) Affinity function: the tradeoff between the probabilities of two alternative e-motions. Two affinity functions were obtained in different sessions: with three response options (the thick line through “○” symbols) and with two response options (the thin line through “+” symbols). (c) Objecthood function: the tradeoff between the probability of e-motion (m₁ or m₂) and the probability of g-motion (orth).

As in previous studies of perceptual grouping in space–time, these data cannot adjudicate between the sequential model and the interactive model. The sequential model implies that the frequency of g-motion will decrease as a function of r_b because when baseline ratios are high, the tendency of concurrent dots to form virtual objects is low. The interactive model implies that the frequency of g-motion will decrease as a function of r_m because larger motion ratios strengthen temporal grouping and thus favor element-to-element matching at the expense of group-to-group matching.

Experiment 2

Methods.

In Experiment 2, we crossed five values of r_m (1.0, 1.1, 1.2, 1.3, and 1.4) with four values of r_b (1.11, 1.43, 1.25, and 1.67) to create 20 types of motion lattices. This was possible because we allowed θ₁ to vary. Our seven observers had normal or corrected-to-normal vision and were naive as to the purpose of the experiment. On each trial, they were offered three response options—m₁, m₂, and orth. Every observer went through 40 trials per motion lattice, i.e., 800 trials in one session. In all other respects, the experiment was identical to Experiment 1.

Results and Discussion.

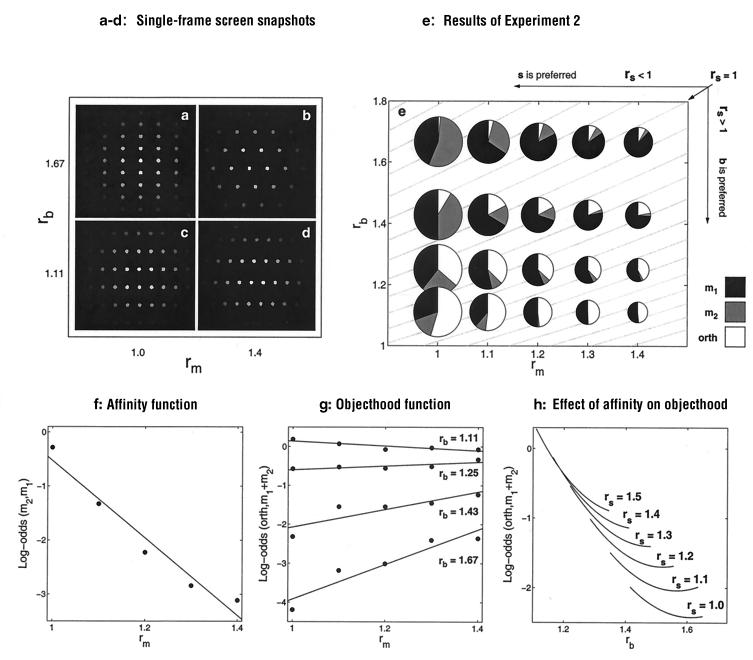
The distribution of the three responses varied systematically as a function of r_m, r_b, and r_θ (Fig. 4e). In Fig. 4g, we plot four linear objecthood functions to show the tradeoff between g-motion and e-motion as a function of both r_m and r_b. The statistical model used to fit these functions accounts for 98% of variance in the data. (We used this model to interpolate the response frequencies for Fig. 4h). The frames in Fig. 4 a–d illustrate different outcomes of spatial grouping within the frames. When spatial grouping favors the formation of salient virtual objects orthogonal to the baselines (Fig. 4a: low r_m and high r_b), g-motion orthogonal to the baselines is never seen, and e-motion dominates (Fig. 4g). As r_b decreases within the same r_m (Fig. 4, a and c), spatial grouping progressively favors the formation of objects within the baselines, and the frequency of g-motion grows relative to the frequency of e-motion. As r_m increases within the high r_bs (Fig. 4, a and b), the virtual objects not parallel to the baselines become less orthogonal to the baselines and less salient and thus allow a higher frequency of g-motion. Within the small r_bs, the growing r_m does not cause appreciable change in the high salience of virtual objects (Fig. 4, c and d), and the frequency of g-motion does not change.

Figure 4.

(a–d) Single frames captured from the computer screen with the extreme values of r_m = (|m₂|/|m₁|) and r_b = (|b|)/|m₁|). The snapshots are arranged in the (r_m, r_b) space, parallel to the plot in e. (e) The pie charts show the distribution of the three responses in the 20 motion lattices. The gray lines on the background are the iso-r_s lines, where r_s = (|s|/|b|), which are the contours for which within-frame spatial grouping should remain constant. For the isoline r_s = 1.0, the organizations along s and b are equiprobable. It is marked with an oblique arrow (Upper Right). Conditions that favor dot grouping within the baselines (r_s > 1.0; e.g., c and d) lie to the right of the isoline of r_s = 1.0; in the rest of the conditions (r_s < 1.0), dots tend to form groupings not along the baselines (as in a). (f) Affinity function collapsed across the r_b conditions. (g) Four objecthood functions summarize the effects of the baseline and motion ratios, r_b and r_m. The frequency of g-motion grows rapidly as r_b drops and groupings along the baselines become more prominent. This effect is evident both when r_b is low (high ambiguity of e-motion) and when r_b is high (m₁ wins the competition with m₂). The plot in h explicates the effect of r_s. Dot organizations within the baselines dissolve as r_s grows, which reduces the frequency of g-motion. In contrast to the prediction of the sequential model, e-motion and g-motion tradeoff within the iso-r_s sets.

The gray curves in the background of Fig. 4e are iso-r_s lines. Each of these curves represents the set of lattice configurations for which spatial grouping favors the formation of identical virtual objects. As Fig. 4e shows, the frequency of g-motion changes along iso-r_s lines. To make this observation explicit, we interpolated the empirical frequencies of g-motion and plotted them within the iso-r_s sets in Fig. 4h: as r_b increases, the frequency of g-motion within the iso-r_s sets drops rapidly. As temporal grouping progressively becomes stronger than spatial grouping, observers tend to see g-motion less frequently and e-motion more frequently. (Note that as one moves within each iso-r_s set from high to low g-motion frequencies, r_m grows, and therefore one of the e-motions, m₁ motion, becomes increasingly salient.) The interactive model can explain this result, for example by pitting against each other the two scales of spatial grouping (elements vs. element aggregates) after the temporal grouping operation (24): g-motion wins the competition with e-motion when the latter becomes ambiguous at low r_m, so that the dot aggregates (virtual objects), and not the individual dots, become the moving entities. (We thank one of the anonymous reviewers for suggesting we emphasize this point.)

We conclude that the sequential model does not hold: Invariant conditions for spatial grouping contribute to the perception of apparent motion differently, depending on the conditions for temporal grouping.

General Discussion

Using spatiotemporal dot lattices, we varied the spatial distances between concurrent dots and spatiotemporal distances between successive dots. Each dot could be grouped either (i) with a successive dot to generate e-motion or (ii) with concurrent dots to form (virtual) objects that are matched to generate g-motion. According to the sequential model, the only factor that can determine which of these is seen is the attraction between concurrent dots. We held attraction between concurrent dots constant and found that affinity between successive dots determines whether e-motion or g-motion will be seen. Thus we have refuted the sequential model in favor of the interactive model. Our findings imply that matching units can arise at any level in the cascade of visual processes, as late as the level of complex objects (25), in contrast to the view that matching units were derived early in visual perception (2).

Current theories of motion perception distinguish between three systems that compute motion. The systems differ by the complexity of the spatial representations on which they are based (26–29). The first-order system can detect the temporal modulation of raw luminances but is insensitive to spatial configuration. In our stimuli, this system can detect e-motion, because the displacement of each dot is a temporal modulation of luminance, but it cannot detect g-motion, because the direction of g-motion does not correspond to the direction of motion of any dot. The perception of g-motion requires a system that can take advantage of the spatial organization of the stimulus. Thus, g-motion is detected either by a second-order system that matches spatial features or by a third-order system that derives motion of more complex visual constructs.

How does vision decide which of the spatial representations will determine what is moving? According to the sequential model, the alternative spatial representations compete before motion matching, whereas according to the interactive model these representations compete after motion matching, i.e., among the outputs of the alternative motion systems: first-, second-, or third-order (30).

Most theories of motion perception are versions of the sequential model (30). A notable theory that agrees with the interactive model has been proposed by Wilson, Ferrera, and Yo (24). According to this theory, matching is applied in parallel to the raw visual input (the first-order system) and to the output of a preprocessor (the second-order system). When the outputs of the two motion systems support different motion directions, they compete, and the winner takes all. Wilson et al.'s model is interactive because the competition between different spatial representations occurs after motion computation. As it happens, the evidence that inspired their model is actually consistent with a sequential model.‖ Our data, on the other hand, do support the model of Wilson et al. (24).

To summarize, the interactive model holds that spatial organization and motion matching are tightly integrated. The identity of moving visual entities is determined both by spatial proximities between elements at each moment and by spatial proximities between elements that occur at successive moments. Thus visual objects emerge when motion matching between element aggregates (Gestalts) is stronger than motion matching between elements.

Abbreviations

ISI

interstimulus interval

element motion

e-motion

group motion

g-motion

log-odds

logarithm of odds