Abstract
Alternative splicing plays an important role in regulating gene expression. Currently, most efficient methods use expressed sequence tags or microarray analysis for large-scale detection of alternative splicing. However, it is difficult to detect all alternative splice events with them because of their inherent limitations. Previous computational methods for alternative splicing prediction could only predict particular kinds of alternative splice events. Thus, it would be highly desirable to predict alternative 5′/3′ splice sites with various splicing levels using genomic sequences alone. Here, we introduce the competition mechanism of splice sites selection into alternative splice site prediction. This approach allows us to predict not only rarely used but also frequently used alternative splice sites. On a dataset extracted from the AltSplice database, our method correctly classified ∼70% of the splice sites into alternative and constitutive, as well as ∼80% of the locations of real competitors for alternative splice sites. It outperforms a method which only considers features extracted from the splice sites themselves. Furthermore, this approach can also predict the changes in activation level arising from mutations in flanking cryptic splice sites of a given splice site. Our approach might be useful for studying alternative splicing in both computational and molecular biology.
INTRODUCTION
Alternative splicing is emerging as an important mechanism contributing to the functional complexity of higher eukaryotes. It expands proteomic diversity and regulates developmental stages or tissue-specific processes by generating multiple transcripts from a single gene (1,2). Recent genome-wide studies have indicated that 40–60% of human genes undergo alternative splicing (3–5). Disruption of pre-mRNA splicing plays a role in human disease, so alternative splicing is highly relevant to numerous diseases and therapies (6,7). Thus, accurate prediction of alternative splice events is important in the study of gene function and disease therapy. However, detecting alternative splicing in the whole genome solely with traditional biological experiments is both time-consuming and expensive. Therefore, it is highly desirable to develop high throughput tools for quick identification of alternative splicing, especially tools whose predictions can provide useful guidance for further biological analysis.
Most recent large-scale studies have used expressed sequence tags (ESTs) or cDNAs for detection of alternative splicing (3–5,8). Usually, a pair of splice forms that match exactly at one splice site (donor/acceptor splice site, i.e. 5′/3′SS) and differ at the other (3′/5′SS) is required to identify an alternative splice event (4). Genomically aligned transcript sequences (ESTs and/or cDNAs) have also been integrated into ab initio gene structure prediction to provide alternative optimal predictions besides the classical optimal one (9). Using this method, each predicted alternative variant should be supported by transcript evidence. Although there are ∼7.9 million human ESTs in the latest release of dbEST (release 063006, June 30, 2006) (10), the full extent of splice variants is probably still far from being detected owing to the many inherent problems with ESTs, such as coverage limitations, bias of RT–PCR artifacts, EST fragmentation, etc. (5). Specifically designed microarrays have also been used for detection of alternative splice variants (11). However, even these high-throughput alternative splicing detections are not sufficient for the identification of all splice variants because probes are usually designed as spanning specific exon–exon junctions and it is difficult to test all combinations of tissues, developmental stages and physiological conditions.
Because of the limitations of these methods, several non-EST-based approaches have been proposed to predict alternative splicing. Some recent methods have tried to identify conserved skipped exons using features of their genomic sequences and comparative genomics (12–15), or to predict exon skipping and intron retention events by using the annotation of Pfam domains (16). By combining machine learning approaches and cross species conservation or protein domain annotations, these methods are able to predict partial alternative splice events which lead to entire exon skipping or entire intron retention. However, species-specific alternative splice events and events not including annotated Pfam domains are ignored by these methods, as exon extension/truncation (i.e. alternative 5′SS and alternative 3′SS) events, which are also prevalent in alternative splicing.
Several computational programs have been developed for the prediction of gene structure and splice sites based on the genomic sequences. These methods usually search for the optimal gene structure, and the splicing signals, such as splice sites, should fit the whole optimal gene structure well. Thus, most of these algorithms hardly detect any alternative splice event (17). Up to now, ab initio prediction of alternative splicing event based on one genomic sequence alone has been attempted only rarely (14), especially for splice events involving alternative 5′/3′SS. Recently, Wang and Marin (18) described an approach for prediction of alternative splice sites using splice site sequences. However, their method can only distinguish rarely used alternative splice sites from constitutive ones based on the features extracted from splice sites themselves. As alternative splice sites have various usage frequencies, and the sequence features of the most frequently used alternative splice sites are similar to those of constitutive ones, this method is only able to predict a fraction of human alternative splice sites.
The existing methods for splice site prediction usually use features of the splice sites themselves. However, it is difficult to predict alternative splice sites by using these features alone. Our current research shows that there is no essential distinction between constitutive and alternative splicing in terms of their splice site sequences. Instead, their differences are graded in nature and are correlated with the expression of the splice sites: the more frequently an alternative splice site is used, the more similar is its flanking sequence to that of constitutive splice sites (see Supplementary Data 1). Thus, discriminating all alternative splice sites from constitutive ones based on splice site sequences alone is a difficult task. Previous experiments have shown that the intrinsic strength of competing 5′SS is one of the factors involved in the choice of 5′SS (19). Roca et al. (20) further extended this selection model for constitutive versus alternative 5′SS selection for nearby 5′SS. Their experiments showed that mutations in flanking cryptic 5′SS could change the level of activation of constitutive 5′SS, suggesting that the choice of a splice site is not only related to its own intrinsic strength, but might also be influenced by its flanking competitors. Nearby alternative splice sites might be involved in a mutually exclusive competition for being spliced. This hypothesis of competition mechanism of splice sites selection, that is, alternative splice sites might compete with each other, might give a new insight to alternative splice site prediction. Therefore, alternative splice sites should not be predicted solely based on their own sequence features.
In this paper, we introduce the competition mechanism of splice sites selection into the field of alternative splice site prediction. First, we describe the application of support vector machine (SVM), a machine learning method, for predicting whether the relation between two candidate splice sites is competitive solely based on their genomic sequences. Then, we predict whether a given splice site is alternative or constitutive based on its relation to flanking potential splice sites. The results show that considering the involvement of splice sites competition in splice site selection provide useful information for alternative splice site recognition. The new method outperforms a method which only considers features extracted from splice sites themselves (18). Our method provides a novel approach for the detection of alternative splice sites based on the combination of sequence features and potential competition mechanism for splice sites selection which does not require additional data such as ESTs, etc. Furthermore, our method can also provide information for searching for potential competitors of a given splice site. It also provides useful clues to guide experimental analysis of alternative splicing, for instance towards detection of alternative splice events not covered by EST data or in evaluation of the effects on splice site activation of mutations in flanking sequences.
MATERIALS AND METHODS
Procedures for alternative splice site prediction
Based on the ‘competition hypothesis’ of splice site selection, we can divide the combination between a splice site and its flanking candidate splice sites into competitive splice site pairs (CSSPs) and non-competitive splice site pairs (NCSSPs). CSSPs refer to those pairs in which both splice sites are activated and compete with each other, such as alternative splice site pairs. Conversely, if a splice site pair has only one real spliced site and the other site in the pair is not spliced, such as an alternative-pseudo splice site pair or a constitutive-pseudo splice site pair, then the pair is an NCSSP. Thus, our approach for alternative splice sites recognition is implemented as follows:
Step 1: CSSP and NCSSP recognition. A machine learning method, SVM, is used for the detection of CSSPs and NCSSPs.
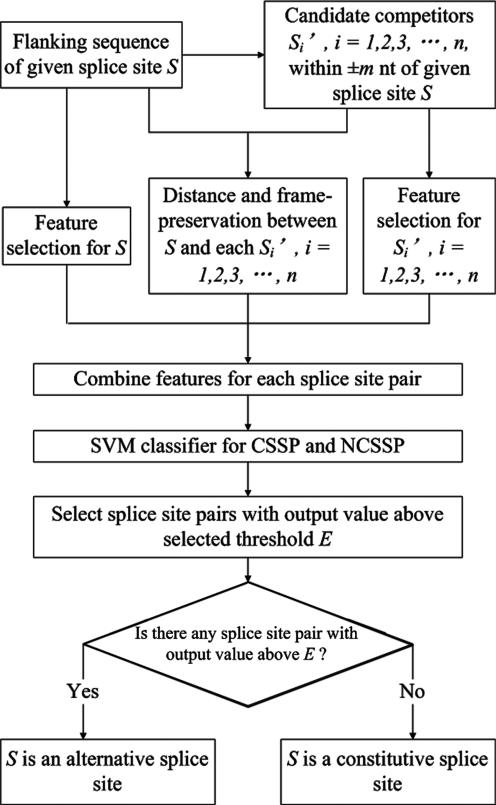
Step 2: Distinguishing alternative and constitutive splice sites. For each splice site, all GT (for 5′SSs) or AG (for 3′SSs) sites within ±m nt of that splice site are extracted as candidate competing splice sites. Each of these candidates is combined with the splice site in question, and a prediction is made to tell whether any of them represents a CSSP. If the answer is ‘yes’, then this splice site is an alternative one; otherwise, it is a constitutive one. A flow chart of our method is shown in Figure 1.
Figure 1.
Flow chart for our alternative splice site prediction method.
Dataset
Human sequences of alternative splice sites that obey the GT–AG rule were extracted from the AltSplice database (Human release 2) at http://www.ebi.ac.uk/asd/altsplice/index.html (21,22), together with the number of ESTs supporting them. Alternative 5′/3′SSs that have the same positions of upstream and downstream 3′/5′SSs as their competing sites were extracted, together with their flanking sequences. A total of 3383 alternative 5′SSs together with their 3550 competitive splice sites and 7236 alternative 3′SSs together with their 8036 competitive splice sites were collected. Constitutive splice sites were also extracted from the AltSplice database restricting to those ones whose flanking exons and introns do not show any alternative splice events. A total of 3359 constitutive 5′SSs and 7862 constitutive 3′SSs were randomly chosen.
The data was randomly divided into a training set and a testing set. The training set of 5′SSs includes 993 alternative 5′SSs and 1003 constitutive 5′SSs, with a total of 1040 pairs of alternative splice sites as well as 1974 randomly selected pairs of alternative/constitutive-pseudo splice site pairs. Our statistical analysis of the distance between two alternative splice sites shows that >90% of alternative 5′SSs and 3′SSs locate within 200 and 150 nt of their competitors, respectively (the length distribution of the alternative fragments are shown in Figure S4 in Supplementary Data 2). The 5′SS testing set includes 2390 alternative and 2356 constitutive 5′SSs, with a total of 2510 pairs of alternative splice sites as well as 72 988 pairs of alternative/constitutive-pseudo splice sites. The pseudo splice sites were extracted within a range from −200 nt of upstream exon to 200 nt of downstream intron of the 5′ splice site considered. The data extraction of training set and testing set for 3′SSs was similar (detailed information is shown in Table 1).
Table 1.
The datasets for identification of alternative splice sites
| Splice site (SS) | Splice site pair (SSP) | |||
|---|---|---|---|---|
| Alternative | Constitutive | Competitivea | Non-competitivea | |
| 5′SS | ||||
| Training set | 993 | 1003 | 1040 | 1974 |
| Testing set | 2390 | 2356 | 2510 | 72 988 |
| 3′SS | ||||
| Training set | 2136 | 2455 | 2357 | 4533 |
| Testing set | 5100 | 5407 | 5679 | 164 720b |
a‘Competitive’ refers to alternative splice site pairs and ‘non-competitive’ refers to alternative/constitutive-pseudo splice site pairs.
bFlanking pseudo splice sites were extracted within ±150 nt of the considered 3′SSs.
Support vector machine
Support vector machine (SVM) is a popular machine learning algorithm, which was initially proposed by Vapnik (23,24) based on statistical learning theory. It has been successfully applied to bioinformatics investigations, such as the identification of splice sites (25), and identification of skipped exons (13), etc. The basic idea of SVM is mapping data into a high-dimensional feature space, and then constructs a hyperplane as the decision surface between positive and negative data. The actual mapping is achieved through kernel functions, making it easy to implement and fast to compute. Popular kernel functions are:
| 1 |
| 2 |
radial basis function (RBF) kernel:
| 3 |
| 4 |
where xi, xj are input vectors, γ, r and d are kernel parameters.
In the present research, we used the software SVMlight (26) to implement SVM. This software can be downloaded from http://svmlight.joachims.org/.
Feature selection
Nucleotide composition is the basic feature of the splice site sequence. Each of the nucleotide, i.e. A, G, C and T, can be represented by a 4-bit string code as A-0001, G-0010, C-0100 and T-1000, respectively. For each real or pseudo splice site, regions of ±L nt around the splice site were examined. For donor splice sites, we set L = 20, and for acceptor splice sites, we set L = 30. Thus, each site of a splice site pair is represented by an 8L-D (dimension) feature vector.
Based on the splicing mechanism, we also included other features which might affect splice sites selection. We have previously found that the U1 snRNA binding free energy is a factor involved in the selection of 5′SSs (27). Thus, for each 5′SS in a pair, the free energy of U1 snRNA binding to 5′SS (positions −3 to +8) was calculated using the hybridization server on the Mfold web (http://www.bioinfo.rpi.edu/applications/hybrid/twostate.php) (28). For each 3′SS in a pair, several features of polypyrimidine tract (PPT) related region were considered. The PPT is important for splicing. It has been reported that mutations which change the pyrimidine composition of PPT may influence the selection of branch-site (BS) or cause the splicing system to abolish splicing altogether (29,30). BS which locates upstream of the PPT has a strong influence on the splicing result. An analysis of 19 experimentally proven BSs has shown that the average distance between the BS and the 3′ splice site is 33–34 nt and the minimal length of the PPT is 14 nt (31). We therefore calculated the number of pyrimidines in the last 35 nt upstream each 3′SS via a sliding window of 14 nt, and the window with the highest pyrimidine content was taken to represent the pyrimidine intensity of the PPT-related region for that site. The maximum number of continuous pyrimidines in that region was also calculated for each 3′SS. The distance between the region of maximum pyrimidine intensity or maximum number of continuous pyrimidines and the 3′SS was also calculated.
The features mentioned above can be used to represent the intrinsic strength of a splice site. The relationship between two sites in one pair (CSSP or NCSSP) depends on their relative strength comparison. In addition, we also included the distance and frame-preservation (an exact multiple of 3 nt in length) between a pair of splice sites that are also important features for alternative splicing in our method. We scaled each feature that is used in the range of [−1, +1].
Finally, all features were combined into one vector and an N-D feature vector for each pair of splice sites was obtained, where N = (8L + 1) × 2 + 2 = 324 for 5′SSs and N = (8L + 4) × 2 + 2 = 490 for 3′SSs.
Performance assessment
We used sensitivity (Sn), specificity (Sp), total accuracy (TA) and the Matthew's correlation coefficient (MCC) to evaluate the performance of our algorithm. We used True Positive (TP) and False Negative (FN) to denote the numbers of positive data (such as CSSPs or alternative splice sites) that were predicted as positive and negative, respectively. Similarly, True Negative (TN) and False Positive (FP) were used to denote the numbers of negative data (such as NCSSPs or constitutive splice sites) that were predicted as negative and positive, respectively. Then Sn and Sp were defined as:
| 5 |
| 6 |
That is, Sn and Sp are the proportion of positive and negative data, respectively, which were correctly predicted. TA and MCC were defined as:
| 7 |
| 8 |
In our study, a 5-fold cross-validation test was performed on the training set to validate the prediction performance. The training set was divided into five subsets of approximately equal size. We trained our algorithm based on four of these subsets, and then the remaining one was used to estimate the prediction accuracy of the trained classifier. This process was repeated until all subsets have been subjected to the cross-validation.
RESULTS
Recognition results of splice site pairs using SVM
The splice site pairs were divided into competitive and non-competitive splice site pairs. In our dataset, the alternative splice site pairs were considered as CSSPs, and the alternative-pseudo or constitutive-pseudo splice site pairs were considered as NCSSPs. In order to recognize CSSPs and NCSSPs, several commonly used kernel functions were tried: the linear, the polynomial of degree 2 and 3, the RBF and the sigmoid kernel function. We found that the RBF kernel performed better than the other kernels. The parameter γ was set to γ = 1/k for the RBF kernel where k is the number of features. We then performed a grid search over a range of values of the penalty parameter C ranging from 0.25 (2−2) to 128 (27). The performance was evaluated by a 5-fold cross-validation test. The best performance for 5′SSPs was achieved by an RBF kernel with parameter γ = 0.003 and C = 4, and the best result for 3′SSPs was obtained by an RBF kernel with γ = 0.002 and C = 16.
The results of using SVM to identify 5′SSPs and 3′SSPs in the testing set are shown in Table 2. Our SVM classifier was able to identify 84.94% of the 5′CSSPs and 78.34% of the 3′CSSPs in the test. These results indicate that our method can successfully estimate the relation between splice sites in pairs.
Table 2.
Performance of the SVM classifier for splice site pairs (SSPs) recognition on the testing set
| Sn (%) | Sp (%) | TA (%) | MCC | |
|---|---|---|---|---|
| 5′SSP | 84.94 | 89.35 | 89.21 | 0.395 |
| 3′SSP | 78.34 | 88.31 | 87.98 | 0.346 |
Prediction of alternative splice sites
The prediction of alternative splice sites was performed on the testing set according to the competition mechanism of splice sites selection. For a given splice site, we searched its flanking sequences for candidate competitors to identify CSSPs. A splice site pair with a prediction value above a selected threshold value E was considered a putative CSSP. The threshold value E grants flexibility in adjusting the algorithm's sensitivity and specificity. All splice sites involved in putative CSSPs were then considered as alternative.
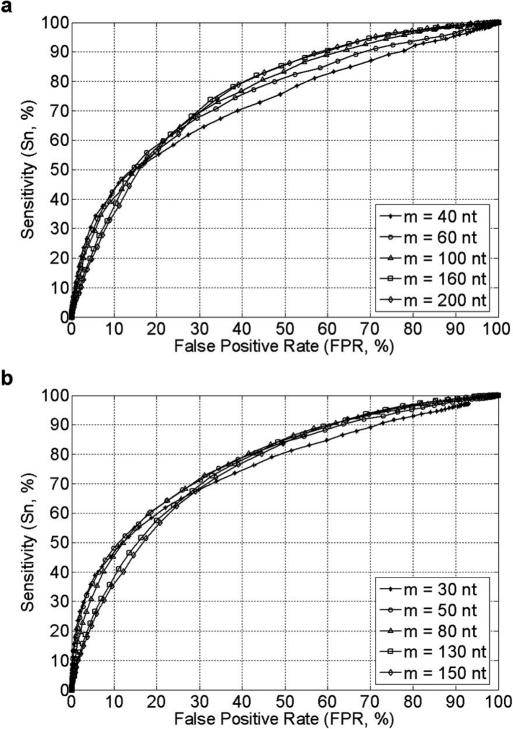
Flanking sequences of different lengths m were tested for searching candidate competitors of a given splice site, and Receiver Operating Characteristics (ROC) curves for alternative splice sites predictions under various values of m are shown in Figure 2. For a wide range of m, our method can correctly predict ∼70% of the alternative splice sites with a false positive rate ∼30%.
Figure 2.
ROC curves for prediction results on testing set with different m. The value of m is the length of flanking sequences for searching candidate competitors of a given splice site. False positive rate (FPR) = 1 − Sp. The algorithm's sensitivity and specificity could be adjusted by threshold value E. (a) Results of 5′SS prediction. (b) Results of 3′SS prediction.
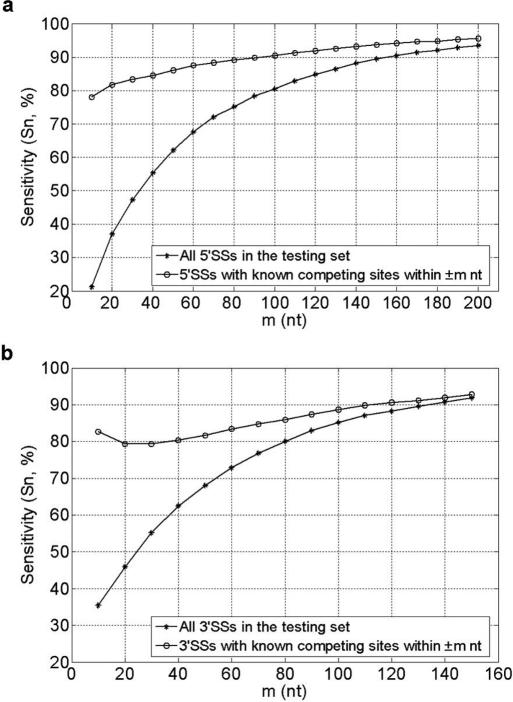
As the candidate competitors were extracted in the flanking regions of ±m nt of given splice sites, CSSPs that consist of competing sites lying beyond m nt could not be detected. Thus, alternative splice sites whose real spliced competitors lie only beyond m nt can hardly be detected. Thus, we further examined the performance for predicting the splice sites which have known spliced competitors in the range of ±m nt. Figure 3 shows the sensitivities of prediction under different values of m with threshold value E = 0 as an example (detailed results can be found in Tables S1 and S2 in Supplementary Data 3).
Figure 3.
The sensitivities of alternative splice site prediction with various lengths of flanking sequences for searching candidate competitors, threshold value E = 0. The x-axis represents the length (denoted by m) of flanking sequences. The lines marked with asterisks represent the prediction performance for all splice sites in testing set, and the lines marked with circles represent the prediction performance for splice sites which have real spliced competitors in considering range of sequences. (a) Results for 5′SSs. (b) Results for 3′SSs.
Generally speaking, our method can identify >80% of alternative 5′SSs or 3′SSs which have known spliced competitors within ±m nt under the restriction on flanking regions for candidate competitors searching. These results show that our method can successfully predict alternative splice sites, especially alternative splice sites with real spliced competitors within the investigated flanking regions. Moreover, as listed in Table 2, ∼80% of the CSSPs and near 90% of the NCSSPs can be correctly identified. From the relation between splice sites in pairs, our method could also identify the potential alternatives to a given splice site.
Comparison with existing methods
We compared the performance of our method with that of a published method named ASSP (18) on the testing set. ASSP is a web-application available at http://es.embnet.org/~mwang/assp.html for the prediction of alternative splice sites, and predicts alternative splice sites based on the features within the splice sites themselves. Pre-processing models are used by ASSP to scan the uploaded sequences for putative splice sites. If a splice site is recognized by the pre-processing models, i.e. its score is higher than a certain cut-off value, it can then be classified into alternative or constitutive splice site by ASSP. A total of 2199 constitutive 5′SSs, 2052 alternative 5′SSs, 5224 constitutive 3′SSs and 4307 alternative 3′SSs in our testing set were classified by ASSP, using the default cut-off values for 5′SS and 3′SS provided by the ASSP website. We call these data testing set I. We set m = 200 for 5′SSs and m = 150 for 3′SSs with a threshold value E = 0.7 in our method for comparison. The results of the comparison are listed in Table 3.
Table 3.
Summary of the performance of our method and ASSP on testing set I
| Sn (%) | Sp (%) | TA (%) | MCC | |
|---|---|---|---|---|
| Testing set I | ||||
| 5′SS | ||||
| Our method | 67.15 | 71.71 | 69.51 | 0.389 |
| ASSP | 56.63 | 62.66 | 59.75 | 0.193 |
| 3′SS | ||||
| Our method | 64.22 | 71.88 | 68.42 | 0.362 |
| ASSP | 58.16 | 65.10 | 61.97 | 0.233 |
Previous researches have used the fraction of total transcripts of a gene that supports an alternative splice event to measure its observed frequency (32,33). Similarly, we defined the splicing level of a splice site as its frequency of being used among all the competing sites in the gene (a detailed description can be found in Supplementary Data 1). We further compared the performance of our method and ASSP on identifying alternative splice sites with different splicing levels.
We estimated the splicing level of each alternative splice site in testing set I. Then all the alternative splice sites in testing set I were divided into two sub-testing sets labeled testing sets II and III according to their splicing levels, comprising alternative splice sites with splicing levels >0.7 (strong splice sites, SSSs) and <0.3 (weak splice sites, WSSs), respectively. Splice sites with intermediate splicing levels were not used. The results from the comparisons on testing sets II and III are listed in Table 4, and show that considering competitors in flanking sequences of given splice sites will improve the prediction performance. Our method outperforms ASSP, especially for frequently used alternative splice sites. This suggests that we can apply our method to any splice site, without the restriction to rarely spliced sites as ASSP does.
Table 4.
Prediction results of our method and ASSP on splice sites with different strengths
| Correctly predicted splice site (%) | ||
|---|---|---|
| Our method | ASSP | |
| Testing set II (strong splice site) | ||
| 5′SS | 60.08 | 42.97 |
| 3′SS | 53.27 | 44.56 |
| Testing set III (weak splice site) | ||
| 5′SS | 75.77 | 69.58 |
| 3′SS | 73.21 | 69.34 |
We also repeated the same analysis using the data extracted from AltExtron to further examine the performance of our method on distinguishing between constitutive and rarely used alternative splice sites. There are >20 000 constitutive exons, 698 alternative isoform 5′ splice sites and 1347 alternative isoform 3′ splice sites in the AltExtron database. The alternative isoform splice sites refer to those rarely recognized splice sites of extended or truncated exons (18,22). Wang and Marin (18) constructed a training set including 10 000 constitutive 5′SSs, 600 alternative isoform 5′SSs, 10 000 constitutive 3′SSs, and 1200 alternative isoform 3′SSs to train ASSP. The testing set they used included 1000 constitutive 5′SSs, 98 alternative isoform 5′SSs, 1000 constitutive 3′SSs and 147 alternative isoform 3′SSs. The accuracies of ASSP on this testing set were 79.12% for donors and 73.48% for acceptors (18). We randomly extracted a training set and a testing set from the AltExtron database with the same number of splice sites as for Wang and Marin (18). For each splice site in the training set, we extracted all CSSPs for each alternative splice site and randomly chose one NCSSP for each alternative or constitutive splice site, and trained our SVM classifier on this set. Whether the splice sites in the testing set were alternative or not were then predicted using our method. This procedure was repeated 10 times and the average prediction performance was calculated. On average, 88.19% of donor sites and 81.80% of acceptor sites were correctly identified by our method with m = 200 for donors, m = 150 for acceptors, and threshold E = 0. Thus, our method can achieve a satisfying performance on classifying constitutive and rarely used alternative splice sites.
Recently, several non-EST-based methods other than ASSP have been developed for predicting alternative splice events (12–16). We further compared our method with the previously published non-EST-based methods. Our method differs from these methods in both the goals of prediction and the data sources underlying the predictions. First, the method presented here was designed to predict alternative 5′SS and 3′SS which lead to exon extension/truncation, rather than entire exon skipping or intron retention. We extracted 937 internal exons from 100 randomly selected genes from the Ensembl genome annotation project (34) and tested our method and one of the previously published approaches [ACESCAN (15)] on these exons. Results showed that our method could predict near half exons which might be extended or truncated by alternative 5′SS/3′SS. However, our method cannot tell whether an exon will be skipped. ACESCAN, on the other hand, can be used to predict whether an exon is a conserved skipped exon both in human and mouse, but cannot predict alternative splice events involving exon extension/truncation. Second, all features used by our method can be derived from the pre-mRNA sequences, whereas methods that predict skipped exons or retained introns rely on cross-species sequence conservation or protein annotation. The comparison between our method and previously published approaches are listed in Tables S3 and S4 in Supplementary Data 4. Thus, our method and the published non-EST-based methods could complement each other in predicting different types of alternative splicing.
Predicting the influence of mutations in flanking sequence on splicing
Our approach was also adapted to mutational analysis of genome sequence flanking a given splice site, and can estimate the influence of mutations in cryptic splice sites flanking a given splice site on the activation level of the given site. Here, we use an example to illustrate this adaptability of our method.
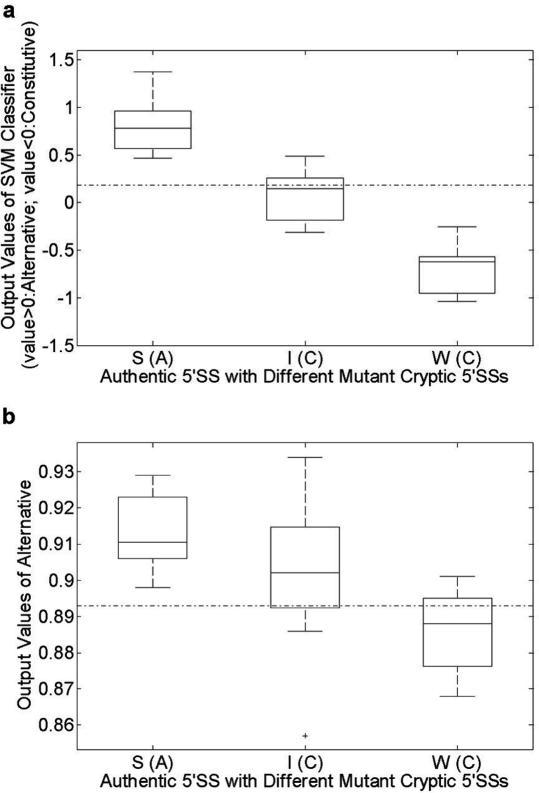
The mutational analysis of the cryptic 5′SS located 16 nt upstream of the authentic 5′SS of the first exon in the human β-globin gene has shown that mutations of the cryptic 5′SS can influence the selection of the authentic 5′SS (20). Based on the in vitro splicing efficiencies, 26 mutant cryptic 5′SSs were grouped into three functional subclasses: strong, intermediate and weak. Strong mutant cryptic 5′SSs cause the authentic splice site to be alternatively spliced while the intermediate and weak mutant splice sites did not influence the constitutive splicing of the authentic site.
We used our method to predict whether the authentic 5′SS would be turned into an alternative splice site or remain a constitutive site under each situation of mutation. The activation of the authentic 5′SS was only related to its combination with the mutant cryptic 5′SS, since all the combination of other possible splice sites within the upstream exon and downstream intron to the authentic 5′SS were predicted to be NCSSPs. The threshold value was set to E = 0. Results are shown in Figure 4. Our method could correctly predict the effect of all strong and weak mutations as well as the effect of near half of all the intermediate mutations. However, it could not predict the change in activation level of the authentic 5′SS if only the authentic splice site itself was considered (as with ASSP), because the mutations in the candidate competitor do not significantly change the flanking sequence characteristics of the authentic site. The results are also shown in Figure 4. Regardless of which mutant of the cryptic 5′SS was tested, ASSP always predicted the authentic 5′SS as an alternative splice site with confidence level >0.88, whereas experimental data showed that the authentic 5′SS was constitutively spliced in the majority of cases (20). The detailed results from the analyses with our method and ASSP are listed in Table S5 in Supplementary Data 5.
Figure 4.
Box plot of prediction values for authentic 5′SS with different groups of mutant cryptic 5′SSs. The dash-dotted lines in (a) and (b) represent the prediction values for wild-type authentic 5′SS with the wild-type cryptic 5′SS of our method and ASSP, respectively. The x-axis represents the authentic 5′SS with different groups of mutant cryptic 5′SSs, and the category labels on the x-axis represent different groups of mutation sites as followed: ‘S’, strong mutant sites; ‘I’, intermediate mutant sites; ‘W’, weak mutant sites; and the letter in parentheses represents the authentic 5′SS is alternative (A) or constitutive (C) spliced validated by experiments. (a) Output values of our SVM classifier on the splice site pair of authentic 5′SS and mutant cryptic 5′SS. A positive value indicates that the authentic 5′SS is predicted to be alternatively spliced and a negative value means the authentic 5′SS is predicted to be constitutively spliced. (b) Output values for splice sites assigned to be alternative by ASSP.
To further evaluate the methods, we calculated Pearson's correlation coefficient (r-value) between the prediction values and the experimentally determined activation levels of authentic 5′SS splicing in competition with the mutant sites. Results are shown in Table 5. Our method can fit the results of the splicing assays well (r = −0.69, p = 10−4), whereas the results with ASSP (r = −0.36, p = 0.07) cannot. This implies that when studying alternative splicing, we should consider splice sites and their flanking information, including possible competing sites as well as splicing regulators, rather than just the splice sites themselves. Doing so, our method not only achieves a satisfying performance on alternative splice site prediction, but also provides evidence for the influence of competition on the selection of alternative splice sites and facilitates further experimental work.
Table 5.
Correlations (Pearson's correlation coefficients) between prediction values and the experimentally validated percentage of activation (20) of authentic 5′SS
| Our method | ASSP | |||
|---|---|---|---|---|
| r | P-value | r | P-value | |
| Authentic 5′SS with all 26 mutants | −0.689 | 1.004 × 10−4 | −0.364 | 0.067 |
| Authentic 5′SS with strong mutants | −0.696 | 0.125 | −0.286 | 0.583 |
DISCUSSION
In this paper, we describe a novel approach that predicts alternative splice sites based on the competition mechanism of splice sites selection. Alternative splice sites were predicted according to their relation to their flanking potential splice sites. We used SVM to distinguish competitive from non-competitive splice site pairs based on features derived from their genomic sequences alone. These features might also be factors related to the splicing machinery. Data from other sources, such as ESTs and cross-species conservation, are not required by our method. Our method can predict >80% of alternative splice sites that have known competing sites within their flanking searching regions, as well as the locations of the potential competitors in these regions. These results might benefit further experimental analysis of alternative splicing.
The concept of competition has already been used by the optimal algorithms in other fields. For example, some computational programs predicting the gene structure of alternative isoform by using a suboptimal parse of a HMM gene model have considered competition between different splice patterns. Here, we introduce the competition hypothesis into alternative splice site prediction. The method that we propose is different from most other splice site predictors. The prediction of a splice site by using our method is not only based on its own intrinsic strength, but also related to the strength of its candidate competitors. The competition hypothesis for splice sites selection may shed light on the biological significance of alternative splice site usage, and is of importance for the prediction of alternative splice sites.
The results of our prediction are restricted to the regions searched for candidate competitors of a given splice site, and it is therefore difficult to detect alternative splice sites whose spliced competitors lie beyond the scanned regions. We have shown that for >90% of alternative 5′ and 3′ splice sites, the competing sites locate within 200 or 150 nt, respectively, allowing our method to predict the majority of alternative splice sites. The range of the investigated flanking regions can be flexibly adjusted according to application. To further reduce the false positive rate, the application-dependent threshold E can be used to eliminate possible NCSSPs.
The comparison with ASSP shows that the approach presented here has 6–10% higher sensitivity with substantially lower false positive rate. Particularly, our approach has much better performance on predicting strong splice sites than ASSP, and has 17.11% and 8.71% higher sensitivity than ASSP for predicting strong 5′SSs and 3′SSs, respectively. We have mentioned that frequently used alternative splice sites are similar to constitutive splice sites in terms of their flanking sequences. Thus, it is difficult to distinguish between these two types of splice sites by features extracted from the splice sites alone. A method considering splice sites alone, such as ASSP, can only distinguish constitutive and rarely used alternative splice sites. In contrast, our approach considers not only the features of splice sites themselves, but also their relation to competing sites. This allows our method to detect both strong and weak alternative splice sites. Furthermore, when we restricted our method on distinguishing between constitutive and rarely used alternative splice sites (i.e. we trained and tested our method on the data extracted from the AltExtron database), we got much better prediction performance than that of distinguishing between constitutive and all alternative splice sites. This is because the features of rarely used alternative splice sites are much more distinct from constitutive ones on both splice sites sequences and their relation to their competing sites. Recent reports have shown that there could be hundreds of exonic splicing silencers (ESSs) (35) and exonic splicing enhancers (ESEs) (36) that involved in regulating pre-mRNA splicing. Moreover, intronic splicing silencers (ISSs) and intronic splicing enhancers (ISEs) are also assumed to be involved in the regulation of many alternative splice events (37). All these evidences indicate that alternative splicing is regulated by a complex system of factors that spread not only in the vicinity of the splice sites, but also in the whole exon and intron regions. We believe that with an increased understanding of other splicing regulators and the mechanism governing alternative splice sites selection, the performance of our prediction approach can be further improved.
In addition, our method can predict changes in splice site activation level arising from mutations in its flanking sequences. This kind of mutations usually do not significantly change the splice site itself. It has been reported that the activation level of a splice site can be influenced by the strength of a flanking competitor, even though the splice site itself is not changed (20). We successfully used our method to predict the results of experimental splicing assays with strong and weak mutations (20). We have also shown that a method which considers splice site features alone cannot correctly predict such results. Thus, our approach represents a clear improvement over the previous method which considers splice site alone. It should be useful for investigating alternative splicing caused by mutations occurring not only in splice site but also outside the vicinity of splice site itself.
Accurate prediction of alternative splice sites is important both for experimental work and for disease therapy. The method presented here represents a first step towards ab initio alternative splice site prediction based on its genomic sequence alone by bringing the competition mechanism of splice sites selection into alternative splice site prediction. An alternative splice site which leads to exon extension/truncation can be predicted by using this method even in the absence of EST evidence, and the method will be a complement to previous non-EST-based methods used to identify alternative splice events. Moreover, several computer programs have been developed for the prediction of gene structure by integrating multiple sources of evidence, including output of gene finders and transcripts information (9,38). The use of genomically aligned transcript sequences allows computational method for gene prediction to identify alternative isoforms which are supported by transcript evidences (9). The method presented here can also be integrated into these methods in order to extend the prediction to also include alternative splice sites without supporting transcripts. The combination of splice site sequence features and potential competition mechanism of splice sites selection renders our method capable of predicting both alternative splice sites and the locations of their potential competitors. This will provide useful clues for biological analysis of alternative splicing and represents one step further towards computational discrimination between alternative and constitutive splice sites, that is to say, we should not only consider the splice sites alone but also take their potential competitors and flanking regulatory elements as a whole.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
Supplementary Material
Acknowledgments
We sincerely thank Prof. Xuegong Zhang for his helpful discussions and Dr Liang Ji for his valuable comments on this manuscript. We also thank Dr Geir Skogerbø for careful reading and correction of the manuscript and Prof. Runsheng Chen for his help on this work. This work is supported in part by National Natural Science Foundation of China (No. 60234020 and No. 60572086) and the National Basic Research Program of China (2004CB518605). Funding to pay the Open Access publication charges for this article was provided by National Natural Science Foundation of China.
Conflict of interest statement. None declared.
REFERENCES
- 1.Graveley B.R. Alternative splicing: increasing diversity in the proteomic world. Trends Genet. 2001;17:100–107. doi: 10.1016/s0168-9525(00)02176-4. [DOI] [PubMed] [Google Scholar]
- 2.Kazan K. Alternative splicing and proteome diversity in plants: the tip of the iceberg has just emerged. Trends Plant Sci. 2003;8:468–471. doi: 10.1016/j.tplants.2003.09.001. [DOI] [PubMed] [Google Scholar]
- 3.Kan Z., Rouchka E.C., Gish W.R., States D.J. Gene structure prediction and alternative splicing analysis using genomically aligned ESTs. Genome Res. 2001;11:889–900. doi: 10.1101/gr.155001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Modrek B., Resch A., Grasso C., Lee C. Genome-wide detection of alternative splicing in expressed sequences of human genes. Nucleic Acids Res. 2001;29:2850–2859. doi: 10.1093/nar/29.13.2850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Modrek B., Lee C. A genomic view of alternative splicing. Nature Genet. 2002;30:13–19. doi: 10.1038/ng0102-13. [DOI] [PubMed] [Google Scholar]
- 6.Faustino N.A., Cooper T.A. Pre-mRNA splicing and human disease. Genes Dev. 2003;17:419–437. doi: 10.1101/gad.1048803. [DOI] [PubMed] [Google Scholar]
- 7.Garcia-Blanco M.A., Baraniak A.P., Lasda E.L. Alternative splicing in disease and therapy. Nat. Biotechnol. 2004;22:535–546. doi: 10.1038/nbt964. [DOI] [PubMed] [Google Scholar]
- 8.Bonizzoni P., Rizzi R., Pesole G. ASPIC: a novel method to predict the exon-intron structure of a gene that is optimally compatible to a set of transcript sequences. BMC Bioinformatics. 2005;6:244. doi: 10.1186/1471-2105-6-244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Foissac S., Schiex T. Integrating alternative splicing detection into gene prediction. BMC Bioinformatics. 2005;6:25. doi: 10.1186/1471-2105-6-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Boguski M.S., Lowe T.M., Tolstoshev C.M. dbEST—database for ‘expressed sequence tags’. Nature Genet. 1993;4:332–333. doi: 10.1038/ng0893-332. [DOI] [PubMed] [Google Scholar]
- 11.Johnson J.M., Castle J., Garrett-Engele P., Kan Z., Loerch P.M., Armour C.D., Santos R., Schadt E.E., Stoughton R., Shoemaker D.D. Genome-wide survey of human alternative pre-mRNA splicing with exon junction microarrays. Science. 2003;302:2141–2144. doi: 10.1126/science.1090100. [DOI] [PubMed] [Google Scholar]
- 12.Sorek R., Shemesh R., Cohen Y., Basechess O., Ast G., Shamir R. A non-EST-based method for exon-skipping prediction. Genome Res. 2004;14:1617–1623. doi: 10.1101/gr.2572604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dror G., Sorek R., Shamir R. Accurate identification of alternatively spliced exons using support vector machine. Bioinformatics. 2005;21:897–901. doi: 10.1093/bioinformatics/bti132. [DOI] [PubMed] [Google Scholar]
- 14.Ohler U., Shomron N., Burge C.B. Recognition of unknown conserved alternatively spliced exons. PLoS Comput. Biol. 2005;1:113–122. doi: 10.1371/journal.pcbi.0010015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yeo G.W., Van Nostrand E., Holste D., Poggio T., Burge C.B. Identification and analysis of alternative splicing events conserved in human and mouse. Proc. Natl Acad. Sci. USA. 2005;102:2850–2855. doi: 10.1073/pnas.0409742102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hiller M., Huse K., Platzer M., Backofen R. Non-EST based prediction of exon skipping and intron retention events using Pfam information. Nucleic Acids Res. 2005;33:5611–5621. doi: 10.1093/nar/gki870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Florea L., Di Francesco V., Miller J., Turner R., Yao A., Harris M., Walenz B., Mobarry C., Merkulov G.V., Charlab R., et al. Gene and alternative splicing annotation with AIR. Genome Res. 2005;15:54–66. doi: 10.1101/gr.2889405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang M., Marin A. Characterization and prediction of alternative splice sites. Gene. 2006;366:219–227. doi: 10.1016/j.gene.2005.07.015. [DOI] [PubMed] [Google Scholar]
- 19.Eperon L.P., Estibeiro J.P., Eperon I.C. The role of nucleotide sequences in splice site selection in eukaryotic pre-messenger RNA. Nature. 1986;324:280–282. doi: 10.1038/324280a0. [DOI] [PubMed] [Google Scholar]
- 20.Roca X., Sachidanandam R., Krainer A.R. Determinants of the inherent strength of human 5′ splice sites. RNA. 2005;11:683–698. doi: 10.1261/rna.2040605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Clark F., Thanaraj T.A. Categorization and characterization of transcript-confirmed constitutively and alternatively spliced introns and exons from human. Hum. Mol. Genet. 2002;11:451–464. doi: 10.1093/hmg/11.4.451. [DOI] [PubMed] [Google Scholar]
- 22.Thanaraj T.A., Stamm S., Clark F., Riethoven J.J., Le Texier V., Muilu J. ASD: the Alternative Splicing Database. Nucleic Acids Res. 2004;32:D64–D69. doi: 10.1093/nar/gkh030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vapnik V.N. The Nature of Statistical Learning Theory. New York: Springer; 1995. [Google Scholar]
- 24.Vapnik V.N. Statistical Learning Theory. New York: Wiley; 1998. [Google Scholar]
- 25.Sun Y.F., Fan X.D., Li Y.D. Identifying splicing sites in eukaryotic RNA: support vector machine approach. Comput. Biol. Med. 2003;33:17–29. doi: 10.1016/s0010-4825(02)00057-4. [DOI] [PubMed] [Google Scholar]
- 26.Joachims T. Making large-scale SVM learning practical. In: Schölkopf B., Burges C., Smola A., editors. Advances in Kernel Methods—Support Vector Learning, Chapter 11. Cambridge, MA: MIT Press; 1999. pp. 169–184. [Google Scholar]
- 27.Bi J., Xia H., Li F., Zhang X., Li Y. The effect of U1 snRNA binding free energy on the selection of 5′ splice sites. Biochem. Biophys. Res. Commun. 2005;333:64–69. doi: 10.1016/j.bbrc.2005.05.078. [DOI] [PubMed] [Google Scholar]
- 28.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Norton P.A. Polypyrimidine tract sequences direct selection of alternative branch sites and influence protein binding. Nucleic Acids Res. 1994;22:3854–3860. doi: 10.1093/nar/22.19.3854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Buvoli M., Mayer S.A., Patton J.G. Functional crosstalk between exon enhancers, polypyrimidine tracts and branchpoint sequences. EMBO J. 1997;16:7174–7183. doi: 10.1093/emboj/16.23.7174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kol G., Lev-Maor G., Ast G. Human-mouse comparative analysis reveals that branch-site plasticity contributes to splicing regulation. Hum. Mol. Genet. 2005;14:1559–1568. doi: 10.1093/hmg/ddi164. [DOI] [PubMed] [Google Scholar]
- 32.Kan Z., States D., Gish W. Selecting for functional alternative splices in ESTs. Genome Res. 2002;12:1837–1845. doi: 10.1101/gr.764102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Modrek B., Lee C.J. Alternative splicing in the human, mouse and rat genomes is associated with an increased frequency of exon creation and/or loss. Nature Genet. 2003;34:177–180. doi: 10.1038/ng1159. [DOI] [PubMed] [Google Scholar]
- 34.Clamp M., Andrews D., Barker D., Bevan P., Cameron G., Chen Y., Clark L., Cox T., Cuff J., Curwen V., et al. Ensembl 2002: accommodating comparative genomics. Nucleic Acids Res. 2003;31:38–42. doi: 10.1093/nar/gkg083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang Z., Rolish M.E., Yeo G., Tung V., Mawson M., Burge C.B. Systematic identification and analysis of exonic splicing silencers. Cell. 2004;119:831–845. doi: 10.1016/j.cell.2004.11.010. [DOI] [PubMed] [Google Scholar]
- 36.Fairbrother W.G., Yeh R.F., Sharp P.A., Burge C.B. Predictive identification of exonic splicing enhancers in human genes. Science. 2002;297:1007–1013. doi: 10.1126/science.1073774. [DOI] [PubMed] [Google Scholar]
- 37.Fu X.D. Towards a splicing code. Cell. 2004;119:736–738. doi: 10.1016/j.cell.2004.11.039. [DOI] [PubMed] [Google Scholar]
- 38.Allen J.E., Salzberg S.L. JIGSAW: integration of multiple sources of evidence for gene prediction. Bioinformatics. 2005;21:3596–3603. doi: 10.1093/bioinformatics/bti609. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.