Systems biology aims to decipher the structure and dynamics of signaling networks (Kitano, 2002). An important unanswered question at the heart of such approaches is: Can simple mathematical models adequately describe signal integration in complex processes? Ideally, such models exist in a cycle where they are used to generate new experimental hypotheses that, once tested, are used to refine the model and lead to more sophisticated hypotheses. Ultimately, such knowledge can be used both to gain an in-depth understanding of a given process and to predict responses to complex stimuli.
To begin, one needs both an interesting biological process and a robust quantitative measure of response. Photomorphogenesis provides an excellent framework on both counts. In nature, seeds germinate in a wide range of light conditions. Light is perceived by a suite of photoreceptors, including the primarily red/far-red light-absorbing phytochromes (Wang and Deng, 2002). In low levels of light, seed-lings exhibit greatly elongated hypocotyls and small cotyledons tightly enclosing the apex. As light intensity increases, the rate of hypocotyl elongation decreases, cotyledons expand, and the shoot apical meristem initiates new leaves. Several hormones have been implicated in promoting or antagonizing light responses (Nemhauser and Chory, 2002). For example, mutants defective in brassinosteroid (BR) synthesis or perception exhibit strikingly light-grown morphology, up-regulation of light-induced transcripts when grown in the dark, and altered light responses (Friedrichsen and Chory, 2001; Luccioni et al., 2002). Several factors have been linked with light-dependent regulation of BR levels (Neff et al., 1999; Kang et al., 2001; Wang et al., 2002).
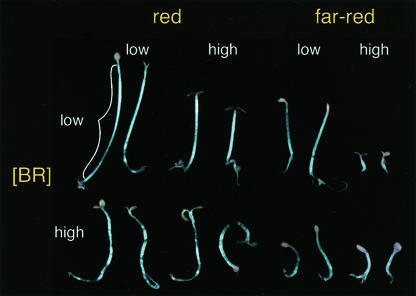
As a first step toward taking a systems approach to seedling growth, we created a matrix of light and hormone response, using hypocotyl length as a convenient quantitative measure. Plants of four genotypes (wild type, overexpressers of the BR receptor [BRI1], and mutants lacking photoreceptors phytochrome A or B) were exposed to five fluence rates of red or far-red light and five levels of exogenous brassinolide (BL), the most active BR. The dramatic range of wild-type seedling morphology observed under these conditions is shown in Figure 1. The response to each variable considered on its own was as described previously (Friedrichsen and Chory, 2001; Wang and Deng, 2002). Exposure to higher light intensities, whether red or far-red, resulted in reduced hypocotyl length. Illumination with far-red light caused a more dramatic inhibition of hypocotyl length than red light. The extent to which BL affected seedling growth depended upon the color and intensity of light to which the seedlings were exposed. Hypocotyls of seedlings grown in red light and exposed to high concentrations of BL exhibited a “kinked” growth habit, an effect that was more dramatic at lower fluence rates of light. This negative effect of BL on hypocotyl length observed in red light was quite different from what was observed in farred light. In low intensities of far-red light, BL had only a small effect on hypocotyl elongation, whereas in high intensities of far-red light, exposure to BL produced a substantial increase in hypocotyl length. We wanted to ask if the diversity of form achieved through such a matrix of different input factors could be modeled mathematically, and if so, what such a model would reveal about the light/hormone relationships underlying this response.
Figure 1.
Light and BRs have profound effects on seedling morphology. Pairs of wild-type seedlings are shown in conditions at the extremes of this analysis.
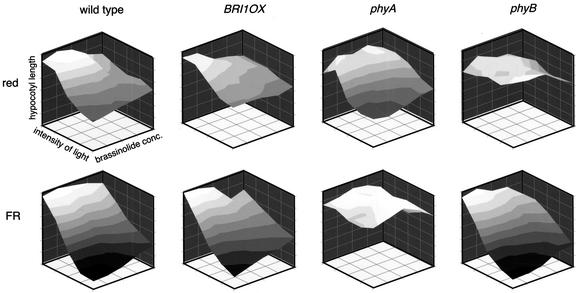
Hypocotyl length measurements resulting from this multidimensional grid of genetic and environmental factors were visualized as three-dimensional surface plots (Fig. 2). If the relationship between the two input factors, light and BL, was strictly additive, the three-dimensional graph would form a plane angled in space by the magnitude of the slope of each factor's effect. In contrast, the curved plots of wild-type hypocotyl lengths suggest interactions between light and hormone perception. Multiple regression analysis was used to test whether these putative interactions were statistically significant and to partition the observed variation in the output (hypocotyl length) into the different input factors (genotype, light intensity, light color, and hormone concentration) and the interactions between these factors (Pinheiro and Bates, 2000). The best model we identified can be stated as follows: The slope of the linear function describing hypocotyl length (h) can be expressed as the sum of genotype (g), color of illumination (c), fluence rate (f), BL concentration (b), and all possible two- and three-way interactions between these factors. Expressed mathematically, this statement would read as follows: h = g + c + f + b + (g × c) + (g × f) + (g × b) + (c × f) + (c × b) + (f × b) + (g × c × f) + (g × f × b) + (c × f × b). All factors included in the model were found to be significant (P < 0.05).
Figure 2.
Graphical representation of the mean hypocotyl lengths at given fluence rates and BL concentrations suggest an interaction between light and hormone perception. Red and far-red light are depicted separately, as are each genotype used in the study. As expected, far-red light shows a more dramatic shortening effect on hypocotyl length than red light, and the photoreceptor null mutants phyA and phyB are largely blind to far-red and red light, respectively.
The estimates of coefficients for each factor's effect are listed in Table I and are given in relation to the base state of wild type in far-red light at the lowest fluence rate of light and lowest concentration of BL. For example, the estimate of the main effect of fluence rate was negative, indicating that hypocotyl length decreased as fluence rate increased (Table I, fluence rate = –2.94). In addition, the model suggests that the effect of increasing fluence rate is stronger in far-red light than in red light. The positive estimate shown for the red × fluence rate interaction coefficient in Table I indicates that in red light, the fluence rate coefficient (–2.94) is modified by the addition of a red × fluence rate coefficient (+1.40), resulting in a less negative effect on hypocotyl length than what was observed in far-red light. Thus, we can conclude that intensity of light significantly affects hypocotyl length, an observation supported by a large number of previous studies (Wang and Deng, 2002). The same logic may be applied to the rest of the terms of the model.
Table I.
Hypocotyl lengths, within the conditions of this experiment, can be described by a linear function with main effect and interaction terms summing to define the slope of the line
Estimates of coefficients for significant factors and interaction terms derived from such a linear mixed effects model are shown here. Effects on hypocotyl length are given in relation to the base state of wild type in far-red light at the lowest fluence rate of light and lowest concentration of BL. Any significant differences in estimates resulting from differences in genotype are listed below each term. Terms directly addressing the relationship between light and brassinosteroid perception are shown in bold.
| Source of Variation | Coefficient | SE | P Value |
|---|---|---|---|
| Fluence rate | -2.94 | 0.08 | <0.0001 |
| Fluence rate × BRI1OX | 0.46 | 0.11 | <0.0001 |
| Fluence rate × phyA | 2.58 | 0.13 | <0.0001 |
| Fluence rate × phyB | 0.63 | 0.11 | <0.0001 |
| BL | -0.59 | 0.06 | <0.0001 |
| BL × phyB | 0.33 | 0.07 | <0.0001 |
| Red | -4.76 | 0.47 | <0.0001 |
| Red × BRI1OX | 1.18 | 0.51 | 0.0194 |
| Fluence rate × BL | 0.15 | 0.01 | <0.0001 |
| Fluence rate × BL × phyA | -0.08 | 0.02 | <0.0001 |
| Fluence rate × BL × phyB | -0.07 | 0.02 | <0.0001 |
| BL × red | 0.27 | 0.05 | <0.0001 |
| BL × red × BRI1OX | -0.15 | 0.05 | 0.0011 |
| BL × red × phyA | 0.39 | 0.06 | <0.0001 |
| BL × red × phyB | -0.31 | 0.05 | <0.0001 |
| Red × fluence rate | 1.40 | 0.09 | <0.0001 |
| Red × fluence rate × phyA | -2.08 | 0.11 | <0.0001 |
| Red × fluence rate × phyB | 0.98 | 0.08 | <0.0001 |
| Red × fluence rate × BL | -0.07 | 0.01 | <0.0001 |
The most striking finding is the strong impact on BL response of increasing light intensity. The BL response is somewhat complex. In the model, the base state effect on hypocotyl length of exogenous BL in dim light is negative (i.e. increasing levels of exogenous BL produced shorter hypocotyls; Table I, BL = –0.59). As light intensity was increased, the effects of BL became less negative (Table I, fluence rate × BL = 0.15). Upon exceeding an apparent threshold, BL increased hypocotyl length. This continuum of BL effect on hypocotyl lengths could result from light decreasing endogenous BR levels or response (Fig. 3). To clarify whether the complicated effects of BL on wild-type plants results from limitations of exogenous hormone application, hypocotyls from plants overexpressing the BR receptor, BRI1, were also measured in the same matrix of conditions. Previous studies showed that 10-fold overproduction of BRI1 in BRI1OX plants results in hypersensitivity to exogenous BRs and reduced sensitivity to the BR biosynthesis inhibitor, brassinazole (Wang et al., 2001) without altering endogenous BR levels (S. Mora-Garcia, S. Fujioka, and J. Chory, unpublished data). In our studies, BRI1 overexpression attenuated both red and far-red light response (Table I; fluence rate (wild type) = –2.94 versus fluence rate [BRI1OX] = –2.94 + 0.46 = –2.48) without significantly altering overall BL response. Thus, our model likely reflects physiologically relevant interactions between BR and light response pathways. Phytochromes likely mediate this interaction because loss of PHYA or PHYB reduced the positive effect of light on BL response (Table I; fluence rate × BL = 0.15 versus fluence rate × BL × phyA = 0.15 – 0.08 = 0.07 and fluence rate × BL × phyB = 0.15 – 0.07 = 0.08).
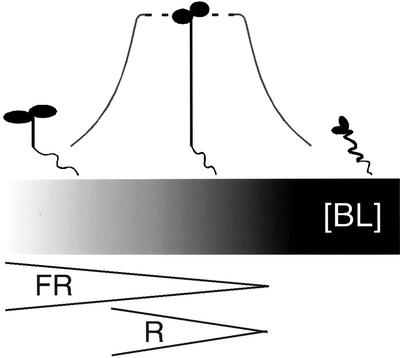
Figure 3.
Light quality and quantity regulate BR response. The range of seedling morphology observed in this study is depicted above a gradient representing predicted endogenous BR levels underlying this response. The gray curve connecting the seedlings reflects the noncontinuous nature of the BR response: areas of hyper-responsiveness flanking a zone where increased BR levels produce little effect. This reflects the finding that most light environments used in this study produced seedlings with little response to exogenous BL. Only seedlings grown in the extremes of light intensity showed robust BR responses. Wedges below the bar represent one model for spectrum-specific effects on BR response. The width of the wedge represents light intensity. In this model, less far-red (FR) than red (R) light is needed to reduce BR levels by a comparable amount. Thus, in addition to having shorter hypocotyls, seedlings grown in high-intensity far-red light would be more sensitive to exogenous BRs than seedlings grown in high-intensity red light. Dark is the point at the far right of both brackets.
Our data also indicate that light color significantly impacted both BL response and the interaction between light intensity and BL response. As mentioned previously, the BL response has three phases in its effect on hypocotyl length: negative, neutral, and positive. Red light was less effective at causing the transition from BL inhibition of hypocotyl elongation to BL promotion of it (Table I, fluence rate × BL (far-red) = 0.15 versus fluence rate × BL (red) = 0.15 – 0.07 = 0.08). At high concentrations of BL and low light, hypocotyl elongation was inhibited in red but not in far-red light (Fig. 2). High intensities of light also showed a color-specific effect, with far-red light producing a far more robust increase in hypocotyl length in response to exogenous BL than red light (Fig. 2). One model for a light color-specific effect is shown in Figure 3. Far-red light may inhibit hypocotyl length more effectively than red light by more efficient reduction of endogenous BR levels or response. This difference could be explained by a far-red light-specific BR pathway, perhaps mediated by factors such as BAS1 (Neff et al., 1999). Another possibility is that photoreceptor-specific effects on other response pathways acting in the hypocotyl may modify the BR response.
By using a combination of physiological, genetic, and mathematical approaches, we have begun to dissect the complex interactions regulating seedling photomorphogenesis. We were successful in fitting a relatively simple model to the data. This model enabled us to show that both light intensity and light quality determine the degree of BR response, and conversely, that increased BR response reduces sensitivity to light. This analysis provides strong evidence for a direct relationship between phytochromes and BR response in regulating hypocotyl elongation. Simple models were able to describe the observed variation in hypocotyl lengths and generate a testable model for future studies. New tools to manipulate endogenous hormone levels and provide temporal resolution will refine and test the model proposed here. By building a predictive model of hypocotyl growth, we have moved one step closer to answering fundamental questions of growth dynamics in biological contexts.
MATERIALS AND METHODS
Plant Material, Growth Conditions, and Measurements
Columbia (Col-0) was the wild-type reference for these experiments. Both phytochrome null mutants (phyA-211 and phyB-9) and the BRI1 overexpresser (BRI1OX) are in the Col-0 background (Reed et al., 1993; 1994; Friedrichsen et al., 2000). Seeds were sterilized for 15 min in 70% (v/v) ethanol and 0.01% (v/v) Triton X-100, followed by 10 min of 95% (v/v) ethanol. After sterilization, seeds were suspended in 0.1% (w/v) low-melting point agarose and spotted on plates containing one-half-strength Murashige Minimal Organics Medium (Invitrogen, Carlsbad, CA), 0.8% (w/v) Phytagar (Invitrogen), and one of five concentrations of BL (0.1, 1, 10, 100, and 1,000 nm). Seeds on plates were stratified in the dark at 4°C for 4 d. Plates were given a 1-h pulse of white light to initiate germination and then moved to appropriate growth conditions. Seedlings were grown in two identical Percival LED chambers (model no. E30LED, Percival Scientific, Inc., Perry, IA). Fluence rates of red and far-red light were measured with a LI-COR 1800 light meter (LI-COR, Lincoln, NE). Neutral density filters were employed to yield different fluence rates for each plate (red light: 0.1, 0.3, 0.6, 1.6, and 7.6 μmol m–2 s–1; and far-red light: 0.2, 0.5, 1.1, 4.2, and 13 μmol m–2s–1). Between six and 12 seedlings were removed on d 4 from one plate at a time and scanned between two transparencies on a flat-bed scanner. NIH Image 1.62 (National Institutes of Health, Bethesda, MD) was used to perform hypocotyl length measurements. The identical experiment was repeated for Col-0, BRI1OX and phyB-9 to allow for estimation of experimental variance (error) term. These two experiments gave a data set of approximately 3,500 measurements.
Statistical Analysis
Statistical analysis on hypocotyl length measurements was performed in R (Ihaka and Gentleman, 1996) using the nlme package (Pinheiro and Bates, 2000). A linear mixed-effects model was used with: genotype, color of light, log(fluence rate × 100), log(BL concentration × 100), and all two and three-way interactions modeled as fixed effects. For each of the two replicates of the experiment, a random effect (error) variable was included. The four-way interaction term was found to be significant but to only explain an extremely small amount of variance (<0.01%) and, therefore, was not included in the final model. The unexplained variance remaining in the model was found to be normally distributed, supporting the underlying assumptions required for performing regression analysis.
Acknowledgments
We thank Charles Berry for his guidance in all matters statistical; Meng Chen and Justin Borevitz for judicious advice about experimental design and careful reading of the manuscript; Matt Offenbacher, Åsa Strand, Dana Schroeder, Brian Burger, and Dave Wolyn for challenging and insightful discussions; Leslie Barden and Julie Tran for technical assistance; and Takeshi Nakano and Meng Chen for providing seeds.
Article, publication date, and citation information can be found www.plantphysiol.org/cgi/doi/10.1104/pp.102.017061.
This work was supported by the National Institutes of Health (grant no. GM52413 to J.C. and postdoctoral fellowship no. F32 GM20742 to J.L.N.). J.N.M. was a Helen Hay Whitney fellow, and J.C. is an Associate Investigator of the Howard Hughes Medical Institute.
References
- Friedrichsen DM, Chory J (2001) BioEssays 23: 1028–1036 [DOI] [PubMed] [Google Scholar]
- Friedrichsen DM, Joazeiro CA, Li J, Hunter T, Chory J (2000) Plant Physiol 123: 1247–1256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ihaka R, Gentleman R (1996) J Comput Graph Stat 5: 299–314 [Google Scholar]
- Kang JG, Yun J, Kim DH, Chung KS, Fujioka S, Kim JI, Dae HW, Yoshida S, Takatsuto S, Song PS et al. (2001) Cell 105: 625–636 [DOI] [PubMed] [Google Scholar]
- Kitano H (2002) Science 295: 1662–1664 [DOI] [PubMed] [Google Scholar]
- Luccioni LG, Oliverio KA, Yanovsky MJ, Boccalandro HE, Casal JJ (2002) Plant Physiol 128: 173–181 [PMC free article] [PubMed] [Google Scholar]
- Neff MM, Nguyen SM, Malancharuvil EJ, Fujioka S, Noguchi T, Seto H, Tsubuki M, Honda T, Takatsuto S, Yoshida S et al. (1999) Proc Natl Acad Sci USA 96: 15316–15323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nemhauser JL, Chory J (2002) In CR Somerville, EM Meyerowitz, eds, The Arabidopsis Book. American Society of Plant Biologists, Rockville, MD http://www.aspb.org/publications/arabidopsisdoi/10.1199/tab.0054
- Pinheiro JC, Bates DM (2000) Mixed-Effects Models in S and S-Plus. Springer-Verlag, New York
- Reed JW, Nagatani A, Elich TD, Fagan M, Chory J (1994) Plant Physiol 104: 1139–1149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed JW, Nagpal P, Poole DS, Furuya M, Chory J (1993) Plant Cell 5: 147–157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Deng X (2002) In CR Somerville, EM Meyerowitz, eds, The Arabidopsis Book. American Society of Plant Biologists, Rockville, MD http://www.aspb.org/publications/arabidopsis doi/10.1199/tab.0074
- Wang ZY, Nakano T, Gendron J, He J, Chen M, Vafeados D, Yang Y, Fujioka S, Yoshida S, Asami T et al. (2002) Dev Cell 2: 505–513 [DOI] [PubMed] [Google Scholar]
- Wang ZY, Seto H, Fujioka S, Yoshida S, Chory J (2001) Nature 410: 380–383. [DOI] [PubMed] [Google Scholar]