Toward elimination of discrepancies between theory and experiment: The rate constant of the atmospheric conversion of SO₃ to H₂SO₄

Abstract

The hydration rate constant of sulfur trioxide to sulfuric acid is shown to depend sensitively on water vapor pressure. In the 1:1 SO₃-H₂O complex, the rate is predicted to be slower by about 25 orders of magnitude compared with laboratory results [Lovejoy, E. R., Hanson, D. R. & Huey, L. G. (1996) J. Phys. Chem. 100, 19911–19916; Jayne, J. T., Pöschl, U., Chen, Y.-m., Dai, D., Molina, L. T., Worsnop, D. R., Kolb, C. E. & Molina, M. J. (1997) J. Phys. Chem. A 101, 10000–10011]. This discrepancy is removed mostly by allowing a second and third water molecule to participate. An asynchronous water-mediated double proton transfer concerted with the nucleophilic attack and a double proton transfer accompanied by a transient H₃O⁺ rotation are predicted to be the fastest reaction mechanisms. Comparison of the predicted negative apparent “activation” energies with the experimental finding indicates that in our atmosphere, different reaction paths involving two and three water molecules are taken in the process of forming sulfate aerosols and consequently acid rain.

The globally averaged negative climate forcing of 1–2 W/m² caused by sulfate aerosols in our atmosphere (1–5) is a major reason why it is very difficult to prove a climate warming induced by anthropogenic emissions. Changes of the sulfur cycle not only alter Earth's albedo but are also directly related to climate change, volcanism, and tectonics on Venus (6) and presumably also on the Jupiter moons Europa (7) and Io (8). A second effect accompanying the atmospheric clouds [especially because of the contained acidic aqueous sulfates (9)] is “acid rain” falling in large amounts on Earth's surface. The pH of rain is as low as 4 in certain areas, significantly lower than 50 years ago, and the most acidic fog in Los Angeles shows a pH of as low as 1.7 (10). This dramatic change has necessitated governmental Sulfur Protocols in the United States and Europe, which are now beginning to result in a recovery of surface waters (11, 12). The production rate and amount of the acidic compounds are quantities that would be required for a better understanding of the recovery process.

More than 100 million tons of sulfur are emitted per year, mainly in the form of dimethyl sulfide (DMS) (13–15) and sulfur dioxide (SO₂) (10, 16–17). DMS is oxidized subsequently to SO₂ at a model frequency of 0.7 × 10⁻⁵ s⁻¹, which by itself is oxidized following the Stockwell–Calvert mechanism (18) at a rate of 1.3 × 10⁻⁵ s⁻¹ to sulfur trioxide by reaction with the hydroxyl radical and O₂ (19–22). Next, SO₃ is hydrated to form sulfuric acid (H₂SO₄) and sulfates (SO₄²⁻), which play a major role in the process of cloud formation as good cloud condensation nuclei (23–25). Especially polar stratospheric clouds (PSC) form from such sulfate nuclei (21, 26–29). These PSC provide a catalytically active surface for reactions converting chlorine and bromine reservoir species to halogen radicals directly capable of attacking Earth's protecting ozone layer (30–37). The detailed mechanisms and reaction rate constants for these processes are keys for understanding the gas-to-particle conversion (21), which can be assessed from both the experimental and theoretical side (19).

In this report, we focus on the mechanism of the atmospheric hydration of SO₃ to H₂SO₄ and the corresponding reaction rate constant following the reaction scheme:

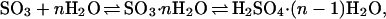1

where n is the length of the water bridge. It is now well established that the second part of the reaction, i.e., the unimolecular isomerization, has a substantial activation barrier, which is overcome by the preassociation reaction acting as a driving force (38). In molecular beam studies, the decay of SO₃ has been attributed mostly to the complexation of water and SO₃ rapidly isomerizing to H₂SO₄ (39, 40). The conversion time sets an upper limit of 13 kcal/mol on the reaction barrier to unimolecular isomerization (40, 41). The bimolecular hydration rate constant corresponding to this process was determined to be about 9.1 × 10⁻¹³cm³⋅s⁻¹ as early as 1975 (42). Newer studies carefully eliminating heterogeneous wall reactions have inferred upper limits of 2.4 × 10⁻¹⁵cm³⋅s⁻¹ and 5.7 × 10⁻¹⁵cm³⋅s⁻¹ for the homogenous reaction (43–45). All these studies assume a linear dependence of the SO₃ loss rate on water vapor pressure. More recent gas-phase studies yielded a second-order dependence of this rate with respect to water vapor pressure (43, 46), implying the involvement of water dimers (47). Experiments under both turbulent (47) and laminar (48) flow conditions yielded a nitrogen pressure independent conversion rate constant of SO₃ to sulfuric acid of 2.0–3.0 × 10⁻³¹cm⁶⋅s⁻¹ at 300 K.

From the theoretical side, it has been established that the reaction barrier in the 1:1 complex is rather high (23.2–29.0 kcal/mol) (49–52). Involvement of the water dimer instead of a single water molecule leads to a reduction of the predicted barrier to 7.4–12.4 kcal/mol (51, 52). The possibility that even higher hydrates are responsible for the reaction chamber results and/or the atmospheric reaction has not received much attention in the literature. A careful investigation of the reaction path and rate for the different hydrates taking into account quantum effects like tunneling is also missing in the literature to the best of our knowledge. Therefore, we here provide a calculation of the dynamics of this hydration in the presence of up to n = 3 water molecules by variational transition state theory and multidimensional tunneling methods.

Computational Methods

Stationary points were calculated at hybrid density functional level of theory [B3LYP/6–31+G(d)] (53) as implemented in gaussian98 (54). The nature of these stationary points was verified by diagonalization of the Hessian matrix. All transition states exhibit a single negative eigenvalue. Coupled clusters with single, double, and perturbational triple excitation energies at geometries found by application of second-order Møller Plesset perturbation theory (CCSD(T)/aug-cc-pVDZ//MP2/aug-cc-pVDZ) (55–57) served as verification of the generally high performance of hybrid density functional theory B3LYP for hydrogen-bonded clusters (58–61).

The path of steepest descent (minimum energy path, intrinsic reaction coordinate) (62, 63) was evaluated in a mass-scaled coordinate system (64) using a reduced mass of 1 amu starting from the transition state (TS) at B3LYP/6–31+G(d) level (53, 60, 65) with the aid of the path integrator of Page–McIver (66, 67) and a stepsize of Δs = 0.05 bohr (1 bohr = 5.3 × 10⁻¹¹ m). The Hessian was updated every third point in both directions. The reaction rate for the unimolecular isomerization step was obtained from classical variational transition state theory (CVTST) (68) corrected semiclassically to describe nonclassical barrier penetration, i.e., tunneling, and reflection (69–72). These nonclassical effects were quantified by the microcanonical optimized multidimensional tunneling method (μOMT) (73) as implemented in polyrate8.2 (74, 75).

The effect of the preequilibria on the reaction rates was taken into account by calculating the association constant of SO₃ and n = 1–3 water molecules (76). According to the experimental finding of second-order dependence on water vapor pressure and first-order dependence on SO₃ pressure, the formation rate of sulfuric acid can be written as third-order law

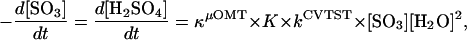2

where the product of the tunneling correction factor (κ^μOMT), the equilbrium constant for the preassociation (K), and the unimolecular rate constant (k^CVTST) correspond to the rate constants k depicted in Fig. 3. To compare our results with the experimentally determined rate constants, we assumed all four mechanisms to be second order in water pressure by converting the ΔG values calculated at B3LYP level for the preassociation to equilibrium constants of units atm⁻² (1 atm = 1.0 × 10⁵ Pa) instead of units atm⁻ⁿ, which are then converted to cm⁶ by multiplying with (1.363 × 10⁻²²T)² cm⁶⋅atm². Apparent activation energies E_a were then gained from the graphs in two different temperatures in Fig. 3

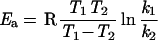3

instead of just summing the electronic energies at 0 K for the preassociation and the reaction barrier, as this additionally includes enthalpy and entropy effects as well as quantum effects like zero-point energy and tunneling. The activation energies in the temperature region investigated vary less than ±1 kcal/mol.

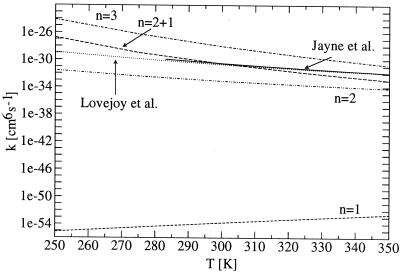
Figure 3.

Bimolecular reaction rate constant for the reaction SO₃ +nH₂O → SO₃·nH₂O → H₂SO₄·(n − 1)H₂O as a function of the temperature. Experimental data are taken directly from Jayne et al. (47) and Lovejoy et al. (48). Calculated values were obtained from B3LYP/6-31+G(d) hypersurfaces and single-level dynamics in the microcanonical optimized multidimensional tunneling framework of variational transition state theory. The preassociation was considered as described in the text.

Results

Stationary Points.

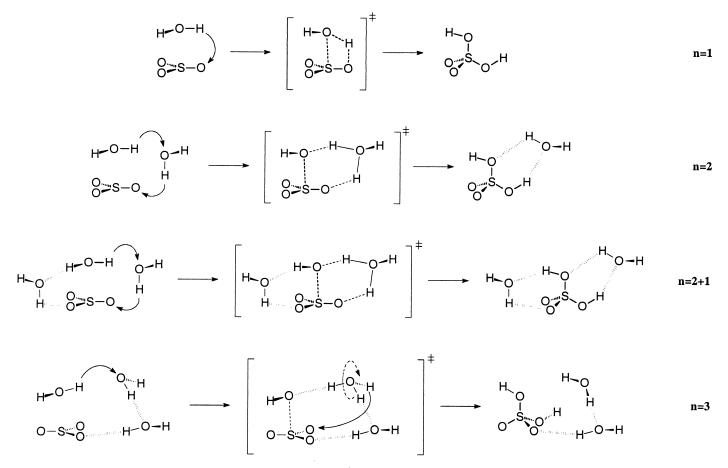
Altogether we localized four sets of stationary points (see Fig. 1), consisting of a preassociation complex between sulfur trioxide and water (“educts”), the transition states to the hydration coupled with proton transfer and the (hydrated) sulfuric acid species (“products”). The four sets differ in the number n of water molecules involved, which varies between one and three. For the case of three participating water molecules, we found two different isomers.

Figure 1.

Qualitative representation of the stationary points of the different unimolecular isomerization steps of SO₃ hydration. Water addition concerted with a single proton transfer in the presence of a single water molecule (n = 1), hydration concerted with water-mediated double proton transfer (n = 2), hydration concerted with water-mediated double proton transfer in the presence of a third microsolvating water molecule (n = 2 + 1), and hydration concerted with the sequence proton transfer/rotation of H₃O⁺/proton transfer in the presence of a third stabilizing water molecule (n = 3).

Some of these stationary point structures have been characterized by experimental and/or computational techniques (77–82). The IR spectrum of the 1:1 SO₃-H₂O complex predicted by hybrid density functional theory agrees with the results obtained by matrix isolation in nitrogen (77). Two bands above 3,500 cm⁻¹, the 1,340/1,326 cm⁻¹ doublet, the band at 1,018 cm⁻¹, and four bands between 460 and 560 cm⁻¹ can be correlated directly with the observed spectrum. The geometry is reminiscent of a donor-acceptor complex, which is consistent with microwave-spectroscopy results (78). The intermolecular S–O distance is predicted to be 2.395 Å instead of 2.432 Å, the out-of-plane distortion of the SO₃ part is 1.9° instead of 2.6°, and the angle between the C₂ axis of water and the intermolecular S–O axis is 108° instead of 103°. Also the reaction product sulfuric acid agrees well with microwave results (83). Concerning the global minimum of the 1:1 complex of sulfuric acid with water, we find that the water molecule is attached in a similar manner to sulfuric acid, as was found both from independent ab initio calculations (79–81) and IR matrix isolation studies (82). We did not find evidence for any ionic character of the 1:1 and also 1:2 sulfuric acid–water minima, which also agrees with the experimental (82) and theoretical findings (84). On the other hand, the global minimum we find for the 1:2 complex differs from the one assumed in the literature to be the global minimum (81). The cyclic arrangement of the two water molecules around sulfuric acid we find here is favorable by 3.28 kcal/mol over the double chain structure noted in the literature. Note that the sulfuric acid–water minima depicted in Fig. 1 correspond not to the global minima but rather to the local minima found as endpoint of the intrinsic reaction coordinate. After Reaction 1 proceeds to the products depicted in Fig. 1, the water molecules will reorient to the global minimum. However, the forward reaction rate constant is not affected by the nature of the sulfuric acid hydrates.

The Reaction Mechanism.

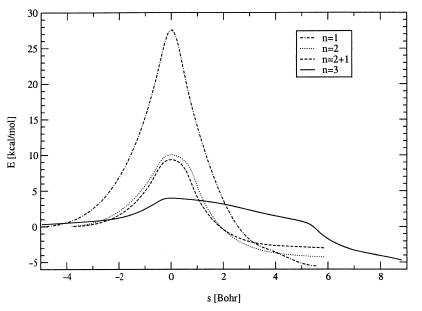
The reaction mechanism can be deduced from the classical minimum energy path (64), which is synonymous to the intrinsic reaction coordinate (62, 63). The energy along the reaction coordinate s for the four investigated cases is depicted in Fig. 2. The hydration involving just one molecule of water involves the nucleophilic attack of a water oxygen to the sulfur atom concerted with the transfer of the water proton to an oxygen atom of SO₃. The unfavorable four-member ring in the transition state causes the rather high hydration barrier of 28 kcal/mol (see Table 1). Introduction of a second water molecule reduces the sterical strain, so that the reaction barrier is reduced to 10–11 kcal/mol. The two proton transfer processes from the first water molecule to the second water molecule and from the second water molecule to the oxygen of sulfur trioxide occur not synchronously at the transition state but asynchronously. The first proton is transferred before reaching the TS and the second one after having passed the TS, which yields a hydronium ion (H₃O⁺) character of the transition state. Recently, we found that a similar mechanism applies to the hydration of carbon dioxide (85). In contrast to this mechanism, the tautomerization of the 7-azaindole dimer, which is also facilitated by the addition of water molecules, is likely to occur stepwisely (86, 87).

Figure 2.

Energy along the classical reaction coordinate (MEP, IRC) as found at B3LYP/6-31+G(d) level of theory for the reaction SO₃ + nH₂O →SO₃·nH₂O → H₂SO₄·(n − 1)H₂O.

Table 1.

Comparison of association energies (SO₃ + nH₂O → SO₃⋅nH₂O) and the reaction barrier to the unimolecular isomerization [SO₃⋅nH₂O → H₂SO₄⋅(n − 1)H₂O] at different levels of inclusion of electron correlation

n	Association energy, kcal/mol			Reaction barrier, kcal/mol
	B3LYP/6-31+G(d)	MP2/aug-cc-pVDZ	CCSD(T)/aug-cc-pVDZ	B3LYP/6-31+G(d)	MP2/aug-cc-pVDZ	CCSD(T)/aug-cc-pVDZ
1	−9.96	−8.72	−9.09	27.60	28.11	28.15
2	−22.48	−19.40	−19.81	10.03	11.61	11.34
2 + 1	−36.50	−31.39		9.35
3	−36.43	−31.12		3.99

CCSD(T) energies were calculated at the MP2 geometries. 

Allowing the participation of a third water molecule gives rise to at least three mechanistic possibilities: (i) a proton transfer along all three water molecules to SO₃; (ii) a proton transfer that is analogous to the two water case with one water molecule acting as spectator, i.e., microsolvent; or (iii) a double proton transfer that involves rotation of the transient hydronium ion bringing an attached hydrogen atom in a favorable position for the transfer to one oxygen atom of SO₃.

We were able to confirm mechanisms ii (n = 2 + 1) and iii (n = 3) from our calculations as depicted in Fig. 1. We could not verify mechanism i, because none of the first-order transition states is connected with the minima by a triple proton transfer, as demonstrated by the intrinsic reaction coordinate calculation.

In the case of mechanism ii, the microsolvating spectator water molecule reduces the reaction barrier by about 0.7 kcal/mol. Additionally, the third water molecule opens a second reaction channel of equal probability so that the reaction rate is increased by a factor of two. The other mechanistic features agree qualitatively well with the two-water case, as can be seen from a comparison of the curves in Fig. 2. A drastic reduction of the reaction barrier down to 4 kcal/mol results if the transient H₃O⁺ species rotates (mechanism iii). It seems that the microsolvating third-water molecule is the key factor that allows this rotation to take place, as we could find no such rotation in the two-water case. The rotation by itself makes the barrier rather broad, as can be seen from the broad bump between 0 bohr and 5 bohr in Fig. 2 for the n = 3 reaction.

Reaction Rate Constants.

It is evident that the reaction involving just one water molecule is too slow by about 23 orders of magnitude to account for the experimental behavior (see Fig. 3), as the unimolecular isomerization is as slow as 6 × 10⁻¹⁴ s⁻¹ even at 350 K.

The reaction involving two water molecules agrees better but is still slower by three orders of magnitude. Microsolvation of the two-water bridge by just one additional water molecule further accelerates the reaction, especially at low temperatures (around 250 K). At 350 K an order of magnitude is still missing in comparison to the reaction chamber results. The rotary mechanism involving three water molecules is predicted to be faster than the observed results. At low temperatures, the prediction is higher by five orders of magnitude, which might indicate that the association of the three-water molecules in a bridge cannot be accomplished before the unimolecular isomerization occurs. At high temperatures, the prediction is slightly too high, implying that this mechanism plays an important role in the homogeneous gas-phase conversion process of sulfur trioxide to sulfuric acid. Because of the broad barrier, quantum mechanical tunneling does not play a decisive role for the rotary mechanism down to temperatures of 200 K, where κ^μOMT is still lower than 1.2. The small “imaginary” frequency of 288i cm⁻¹ of the transition state also shows this broad nature of the barrier. In the case of water-mediated double proton transfer, tunneling accelerates the reaction by a factor of about 20 (n = 2 + 1) and 10 (n = 2) at 200 K. The corresponding “imaginary” frequencies are 582i cm⁻¹ and 564i cm⁻¹, respectively. Very low kinetic isotope effects on changing from H₂O to D₂O predicted for these three mechanisms are consistent with experiments (48), implying that they could indeed describe the experimental situation. A single proton transfer (n = 1) is accelerated by a factor of more than a million at 200 K and still more than 100 at 300 K because of tunneling. The narrow nature of this barrier can be seen from the “imaginary” frequency of 1663i cm⁻¹. Very large kinetic isotope effects for this mechanism are in strict disagreement with the reaction chamber results (48). In other words, the decreasing asynchronous nature of the molecular events increases the importance of quantum mechanical tunneling, but the dominant effect on the total rate is not tunneling but rather the rate constant of the unimolecular isomerization that is accelerated with increasing water content.

Discussion

Complexes with clusters of more than approximately 12 water molecules would be converted to sulfuric acid with nearly no energy barrier, i.e., ultrafast (88). However, the water content of our atmosphere precludes formation of complexes with very large clusters. In binary sulfuric acid–water vapors, the distribution of hydrates is such that at relative humidities of around 50% there are about 10¹⁰ hydrates with one to three water molecules but only 10⁸ with four and only 10⁶ with six water molecules (89). Relative humidities of over 300% are required so that also complexes of four water molecules can be found to an extent similar to the one- to three-water molecule complexes with sulfuric acid.

The barriers for the unimolecular reaction (see Table 1) for clusters with n > 1 water molecules are all lower than +13 kcal/mol, which is the upper limit for the actual unimolecular isomerization barrier from comparing Rice–Romsperger–Kossel–Marcus rate constants using various barriers with the collision deactivation of 5 × 10⁵ s⁻¹ of chemically activated sulfur trioxdide water complexes found by Hofmann-Sievert and Castleman (40). Our predictions for unimolecular rate constants for n = 3 varying between 1 × 10⁸ s⁻¹ (200 K) and 2 × 10⁹ s⁻¹ (350 K) demonstrate that our findings agree with the dominant reaction channel being isomerization rather than collision deactivation. Molecular beam results showing a ratio of 8:1 of water monomer to dimer, but only a ratio of 3:1 in the reaction products with SO₃, clearly underline that much faster reactions take place with n > 1 water molecules (40).

The preassociation equilibrium of SO₃ and n = 1–3 water molecules acts as a driving force to overcome the barrier to isomerization. The association energies, i.e., binding energies, of sulfur trioxide–water complexes presented in Table 1 are in reasonable agreement with experimental results (42). For n > 1, the gain in energy because of association is larger than the energy required to cross the transition state to the unimolecular step, i.e., the overall apparent “activation” energy becomes negative. The reaction rate constant is independent of the sequence of association, i.e., whether the H₂O⋅H₂O or the SO₃⋅H₂O adduct forms first. Comparing the experimentally determined apparent “activation” energies for the overall process of −13 kcal/mol (47, 48) between 283 and 370 K with the here-determined overall apparent “activation” energies of about +10 kcal/mol (n = 1), −8 kcal/mol (n = 2), −24 kcal/mol (n = 2 + 1), and −27 kcal/mol (n = 3), it is likely that the laboratory-determined rate constant is in fact an averaged value that emerges from mixed participation of the latter three mechanisms. The same conclusion arises when judging from predicted kinetic isotope effects.

In the troposphere, where the water content is rather high, most likely the fastest mechanism, namely the double-proton transfer with transient H₃O⁺ rotation, will play the dominant role. However, the rate-determining step under these water-rich conditions will be the oxidative step from SO₂ to SO₃ (47). Increasing the altitude to the stratosphere reduces the water content and the total pressure, which inhibits the formation of larger sulfur trioxide complexes with water. Therefore, the importance of water-mediated double-proton transfer increases. Additionally, heterogeneous processes on aerosol surfaces gain importance (47). The half life (76) of sulfur trioxide under upper stratospheric conditions (10, 47) (10⁻² atm, 250 K, 5 parts per million volume water vapor = 10¹² water molecules/cm³) is predicted to be between 15 min (100% rotary mechanism) and 8 days (100% water-mediated double-proton transfer). Colder temperatures and increased water vapor pressure additionally decrease this half life. This estimated homogeneous half life is similar in magnitude to the predictions by Jayne et al. (47) for heterogeneous processes. Therefore, we believe both homogeneous and heterogeneous reactions to be of equal importance as rate-determining steps in the upper stratosphere for the oxidative conversion of dimethyl sulfide and SO₂ to sulfates.

Abbreviation

TS

transition state