Multibody dynamic simulation of knee contact mechanics

Abstract

Multibody dynamic musculoskeletal models capable of predicting muscle forces and joint contact pressures simultaneously would be valuable for studying clinical issues related to knee joint degeneration and restoration. Current three-dimensional multi-body knee models are either quasi-static with deformable contact or dynamic with rigid contact. This study proposes a computationally efficient methodology for combining multibody dynamic simulation methods with a deformable contact knee model. The methodology requires preparation of the articular surface geometry, development of efficient methods to calculate distances between contact surfaces, implementation of an efficient contact solver that accounts for the unique characteristics of human joints, and specification of an application programming interface for integration with any multibody dynamic simulation environment. The current implementation accommodates natural or artificial tibiofemoral joint models, small or large strain contact models, and linear or nonlinear material models. Applications are presented for static analysis (via dynamic simulation) of a natural knee model created from MRI and CT data and dynamic simulation of an artificial knee model produced from manufacturer’s CAD data. Small and large strain natural knee static analyses required 1 min of CPU time and predicted similar contact conditions except for peak pressure, which was higher for the large strain model. Linear and nonlinear artificial knee dynamic simulations required 10 min of CPU time and predicted similar contact force and torque but different contact pressures, which were lower for the nonlinear model due to increased contact area. This methodology provides an important step toward the realization of dynamic musculoskeletal models that can predict in vivo knee joint motion and loading simultaneously.

1. Introduction

Mechanical loading, particularly dynamic loading, is believed to play a major role in the development and progression of knee joint osteoarthritis [1,2]. Furthermore, motion (i.e., kinematics) and loading (i.e., contact pressures) appear to have an interactive effect on disease progression [3,4]. Motion and loads are also important in artificial knees, influencing wear [5–8] which can lead to osteolysis and, ultimately, implant failure. Even for tissue engineering applications, understanding the mechanical environment to which the replacement or repair cells are subjected is crucial for optimizing the repair process [9]. Thus, knowledge of in vivo joint motion and loading during functional activities is needed to improve our understanding of knee joint degeneration and restoration.

While dynamic X-ray imaging advances now permit accurate measurement of in vivo knee joint motion [10–14], a non-invasive experimental approach does not exist for measuring in vivo knee joint loading. Thus, joint contact pressures must be predicted by computational methods. These predictions are influenced by muscle co-contractions [4] which in turn are affected by the amount of constraint present in the knee joint model used to estimate muscle forces [15,16]. Since the knee is statically indeterminate [17], the ideal computational environment would combine a multibody dynamic model to predict muscle forces with a deformable contact model of the articular surface geometry to predict contact pressures. However, a review of published three-dimensional multibody knee models (Table 1; [18–29]) reveals that only one was dynamic and utilized a full-body rather than knee-only model [24]. Though this model included muscle force predictions, it utilized rigid contact theory, which cannot calculate contact pressures. While most models used deformable contact theory, they were quasi-static and so incapable of predicting muscle forces and joint contact pressures simultaneously during dynamic simulations.

Table 1.

Survey of three-dimensional knee contact models where bone poses are determined using multibody rather than finite element methods. Bones are treated as rigid bodies possessing rigid or deformable contact surfaces. Only one study was dynamic and used a full-body rather than knee-only model, though this study used rigid rather than deformable contact theory.

Study	Model type	Multibody model	Contact model	Muscle forces
Wismans et al. [18]	Quasi-static	Knee	Rigid	Omitted
Blankevoort et al. [19]	Quasi-static	Knee	Deformable	Omitted
Pandy et al. [20,21]	Quasi-static	Knee	Deformable	Included
Abdel-Rahman and Hefzy [22]	Quasi-static	Knee	Rigid	Omitted
Kwak et al. [23]	Quasi-static	Knee	Deformable	Included
Piazza and Delp [24]	Dynamic	Full-body	Rigid	Included
Cohen et al. [25,26]	Quasi-static	Knee	Deformable	Included
Dhaher and Kahn [27]	Quasi-static	Knee	Rigid	Included
Chao [28]	Quasi-static	Knee	Deformable	Included
Elias et al. [29]	Quasi-static	Knee	Deformable	Included

To build on the valuable foundation provided by these previous studies, an approach is needed to incorporate deformable contact models of the knee into multibody dynamic simulations. Simulations of the musculoskeletal system can be generated using existing codes such as Software for Interactive Musculoskeletal Modeling (SIMM) and the Dynamics Pipeline (Motion Analysis Corporation, Santa Rosa, CA [30]), Musculoskeletal Modeling in Simulink (MMS) software (A.E. Mann Institute for Biomedical Engineering, Los Angeles, CA [31]), or commercial multibody dynamics software (e.g., ADAMS, MSC Software, Santa Ana, CA [32]; Autolev, Online Dynamics, Sunnyvale, CA [33]; DADS, LMS International, Leuven, Belgium [34]; SD/Fast, Parametric Technology Corporation, Waltham, MA [35]). Thus, a modular modeling approach that permits incorporation of a deformable knee model into any multibody dynamic simulation environment would have the widest possible applicability.

This study describes a computationally efficient methodology to achieve this goal. Applications are presented for a natural knee contact model created from MRI and CT data and an artificial knee contact model produced from manufacturer’s CAD data. The approach provides an important step toward the realization of dynamic musculoskeletal models that can predict in vivo knee joint motion and loading simultaneously.

2. Multibody knee contact methodology

We propose a four-step methodology for incorporating deformable contact models of the tibiofemoral joint into a multibody dynamics framework. The four steps involve (1) preparation of the articular surface geometry, (2) development of efficient methods to calculate distances between contact surfaces, (3) implementation of an efficient contact solver that accounts for the unique characteristics of human joints, and (4) specification of an application programming interface (API) that will work within any multibody dynamic simulation environment.

2.1. Contact surface preparation

Repeated distance evaluations between contacting surfaces are the primary computational bottleneck when incorporating elastic contact into a multibody dynamics framework. For elastic contact problems solved via numerical methods, distances between the undeformed contact surfaces are sampled for each relative pose of the contacting bodies specified by the numerical integrator, regardless of the method used for calculating contact pressures. From our experience, this typically requires about 80% of the total CPU time during the course of a dynamic simulation. Though distance calculations can be performed efficiently with tessellated surface approximations [24], we have chosen to work with nonuniform rational B-spline (NURBS) surfaces [36,37] to represent the contact geometry as accurately and smoothly as possible, thereby eliminating contact force discontinuities that can slow numerical integration [38,39].

The efficiency of distance calculations between NURBS surfaces depends on at least three factors: the number of parametric (i.e., u–v) spline curves used to represent each NURBS patch, whether the NURBS patches are trimmed (i.e., portions of the surfaces have been removed) or untrimmed, and the number of contiguous NURBS patches used to define a contact surface (Fig. 1). When first created, NURBS patches are untrimmed with a four-sided boundary. To define an irregularly shaped boundary (e.g., to fit existing CAD surfaces or point cloud data—see below), one can create either an “oversized” NURBS patch using simple surface creation techniques (e.g., revolve, extrude) followed by trimming, or a perfectly sized NURBS patch whose outer boundary is defined by an irregular network of four curves and inner contours by points to be fitted. Distance calculations are most efficient when each NURBS patch is untrimmed and uses as few u–v curves as possible. Whether a contact surface should be modeled with a single NURBS patch or multiple patches depends on the method used for calculating distances (see below). We use commercial software to create contact surfaces composed of single or multiple untrimmed NURBS patches with a minimum number of u–v curves to meet the desired surface accuracy (see Applications).

Fig. 1.

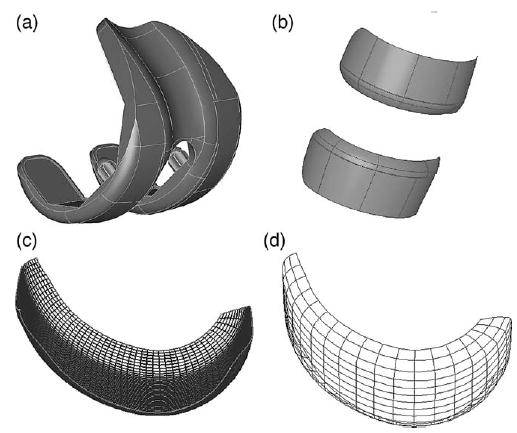
Contact surface preparation demonstrated for an artificial knee model. Starting from manufacturer’s CAD data (a), the trimmed NURBS contact surfaces (b) are removed from the model. Commercial software (see text) is used to fit untrimmed NURBS patches to the contact surfaces and then merge them into a single patch (c). Finally, other commercial software (see text) is used to minimize the number of parametric B-spline curves representing the surface (d) while maintaining a specified level of surface accuracy.

Once NURBS contact surfaces are generated, all geometries are transformed into an anatomical coordinate system to facilitate subsequent geometry calculations. For both natural and artificial knees, the positive y axis is superior, the positive z axis medial, and the positive x axis defined by y cross z (posterior for a right knee, anterior for a left knee). For a natural knee, an anatomic coordinate system is constructed for each bone using estimated joint centers and anatomic landmarks. For an artificial knee, the centroid of the bounding box for each component is used to define the coordinate system origin in the x and z directions. For the y direction, the bottom surface of the tibial insert and the bone box dimensions of the femoral component are used to define the origin.

2.2. Efficient distance calculations

The two primary goals for calculating distances between contacting surfaces are to minimize the number of calculations and to make each calculation as efficient as possible. An additional requirement is the development of a distance sampling method that works for conformal (i.e., one surface with positive curvature and the other with negative curvature) and nonconformal (i.e., both surfaces with positive curvature) situations equally well. Both situations exist in human joints and may even exist at different locations within the same joint (e.g., a patellofemoral joint model).

Given the relative pose of the two contacting bodies at any instant, we use four strategies to minimize the number of distance calculations. The first is to perform all CPU-intensive geometry initialization in a pre-processing phase prior to beginning the simulation. This includes reading in the contact surface geometry for both the tibia and femur, detecting connectivity between the NURBS patches defining each contact surface, constructing contact pairs and associated data structures, and determining whether the surfaces are from a natural knee or artificial knee. A natural knee will have twice as many surfaces as an artificial knee due to the inclusion of subchondral bone surfaces needed to calculate local cartilage thickness. Each contact pair consists of a “fixed” body (the tibia) and “moving” body (the femur) for calculating relative kinematics.

Three types of surfaces are analyzed in pre-processing to facilitate subsequent contact calculations: element surfaces, contact surfaces, and back surfaces (Fig. 2). Planar element surfaces are created at y = 0 on the fixed body. Rectangular element grids constructed on these surfaces are projected in the positive y direction onto the fixed body’s contact surfaces, thereby creating an approximately rectangular grid of contact elements [40]. With this method, each contact element can be assigned a two-dimensional index that facilities storage of the element thickness, area, and local coordinate system for later use. For artificial knees, the distance from the fixed body contact surface to the planar element surface defines the thickness of each contact element. For natural knees, the distance from the fixed body contact surface to the corresponding subchondral bone back surface defines the thickness of each element. The moving body also has contact surfaces. For artificial knees, the contact surfaces are treated as rigid, so no back surface or local thickness information is required. For natural knees, each NURBS patch in a contact surface is subdivided based on its u–v space, and the distance between the sampled points and the corresponding subchondral bone back surface calculated and stored in a separate data structure. During a simulation, once a u–v location is found on a particular NURBS patch of the moving body, bilinear interpolation is used to estimate the cartilage thickness at that location.

Fig. 2.

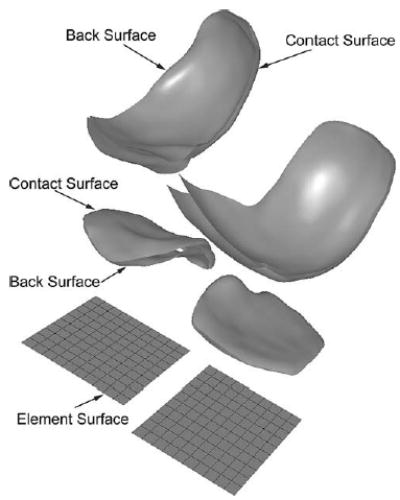
Classification of surface types analyzed during contact calculations. Element surfaces created on the tibia are used to construct a planar element grid on the medial and lateral sides. Contact surfaces on the tibia and femur represent the contacting articular geometry. Back surfaces only exist for natural knees and represent the subchondral bone surfaces on the tibia and femur needed to calculate local cartilage thickness. Projection of element boundaries from the element surfaces onto the tibial contact surfaces produces contact elements with unique normal directions, coordinate systems, thicknesses, and areas.

A second strategy to minimize number of distance calculations is to calculate distances from one contact surface directly to the other. In numerical contact models using elastic half-space theory, it is common to create a tangent plane (i.e., a special midsurface) defined by where the normals on the two contact surfaces are co-linear and anti-parallel [41] (Fig. 3a). Because all contact calculations are performed relative to this plane, two sets of distance calculations are required—one from the tangent plane to each contact surface. Finding the tangent plane requires solving a nonlinear root-finding problem that is sensitive to the initial guess and fails frequently for complex geometry, halting the entire dynamic simulation. Furthermore, a tangent plane does not work well for conformal joints such as the hip, since the contact midsurface is highly curved. A single tangent plane also works poorly in situations where multiple contacts occur between the same pair of surfaces.

Fig. 3.

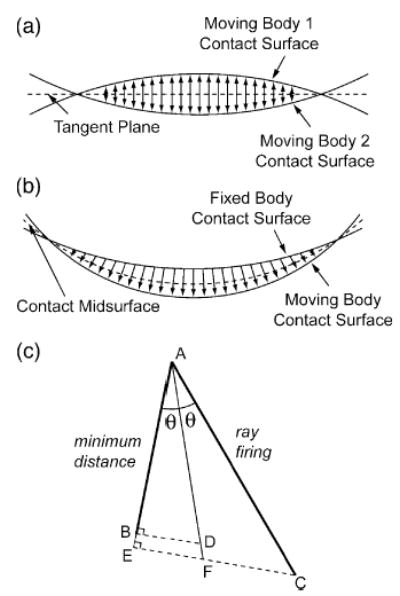
Distance evaluation methods for contact calculations. (a) The tangent plane commonly used for nonconformal contact situations requires two sets of distance calculations—one from the tangent plane to each moving body (tibia and femur). (b) The implicit midsurface proposed in our approach works for conformal and nonconformal contact situations and requires half the number of distance calculations. For each contact element on the fixed body (tibia), the distance to the corresponding moving body (femur) contact surface is calculated directly and then corrected. (c) The corrected distance vector is calculated from trigonometry based on knowledge of the minimum distance and ray firing directions. Either minimum distance or ray firing can be used to calculate distances. The minimum distance vector (AB) is perpendicular to the point found on the moving body, while the ray firing vector (AC) is perpendicular to the normal on the fixed body. If ray firing is used, the minimum distance direction can be well approximated from the normal of the point found on the moving body. The distance along the midsurface normal, defined from the bisector between the minimum distance and ray firing directions, is larger than the minimum distance result and smaller than the ray firing result. If minimum distance is used, the distance is grown slightly by calculating the distance (AD) that produces the minimum distance (AB) when projected onto the minimum distance direction. If ray firing is used, the distance is shrunk slightly by projecting it onto the minimum distance direction (AE) and then growing the distance (AF) using the same approach as for minimum distance. In practice, corrected distances from the two approaches are nearly identical given typical element sizes.

To eliminate these issues, we have developed a novel approach for calculating distances between two contact surfaces using an implicit rather then explicit midsurface (Fig. 3b). For any element on a fixed body contact surface, the distance to the corresponding moving body contact surface is calculated directly and then corrected, cutting the number of distance evaluations in half. The correction uses trigonometry to approximate the distance along the local midsurface normal regardless of the method used for calculating distances (Fig. 3c, see caption). If minimum distance is used (i.e., the distance vector is perpendicular to the point found on the moving body), the correction grows the distance slightly. If ray firing is used (i.e., the distance vector is perpendicular to the starting point on the fixed body), it shrinks the distance slightly. The results from the two approaches are nearly identical, with the corrected distances lying between the minimum distance and ray firing values. This approach implicitly creates an approximately planar midsurface for nonconformal contacts, similar to the tangent plane in half-space problems, and a curved midsurface for conformal contacts. It also accommodates contact surfaces that are conformal in some regions and nonconformal in others.

Another strategy for minimizing distance calculations is to copy previous contact solutions whenever the relative kinematics change little. Numerical integrators frequently place the contacting bodies in the same relative pose several times while performing trial steps. If the change in kinematic variables (i.e., generalized coordinates) is below a small user-defined tolerance, pressure results stored from the previous pass are copied to the current solution, thereby eliminating the need for new distance calculations.

A final strategy for minimizing distance calculations is to use the previous contact solution as an initial guess for the current solution. Searching all elements for interpenetration, as required during the initial pass, is extremely expensive computationally. Since numerical integration changes the relative pose of the contacting bodies by only small amounts from one integrator step to the next, the current contact area typically contains elements from the previous area. Thus, if the change in relative kinematics is considered too large to copy the previous solution, the new contact area is found starting from the previous contact area using an efficient Breadth-First search algorithm [42]. This algorithm starts by testing all of the previous contacting elements one at time. If a tested element is still active (i.e., in contact), all of its neighbors are searched systematically, with the search progressing outward until a ring of non-active elements is identified. Remaining elements on the previous active list that have not yet been evaluated are tested in a similar manner. In addition to minimizing the number of distance evaluations, this method is able to track multiple contact areas that form by the splitting of a single contact area. If no active elements are found by the Breadth-First search, all elements on the fixed body are tested to ensure that no contact is occurring elsewhere.

The most computationally efficient evaluation approach is to use minimum distance with a single NURBS patch for each femoral contact surface (Table 2; the complexity of the tibial contact surfaces is inconsequential since they are only analyzed in preprocessing). When distance sampling CPU times are computed using single-patch contact surfaces, minimum distance is five to nine times faster than ray firing. When multiple-patch contact surfaces are used instead, ray firing performance improves and minimum distance worsens. However, minimum distance using a single NURBS patch with minimized u–v space is still more than four times faster than ray firing with multiple patches.

Table 2.

Determination of the most computationally efficient approach for calculating distances between contact surfaces based on analysis of an artificial knee femoral component. Single and multiple NURBS contact surfaces were evaluated using ray firing and minimum distance methods implemented with the ACIS 3D Toolkit (Spatial Corporation, Westminster, CO). Difference ACIS minimum distance functions were required for single and multiple patches. Minimization of u–v space involved reduction of u–v lines until the maximum surface error approached 0.05 mm relative to the original single-patch surface. CPU times were determined using Rational Quantify software (IBM Corporation, White Plains, NY). A single-patch surface with minimum number of u–v lines combined with the minimum distance method yielded the best performance.

NURBS geometry		Tolerance statistics (mm)			CPU time (μs)
Patches	u–v space	Maximum error	Average error	Standard deviation	Ray firing	Minimum distance
1	Original	–	–	–	4,459,922	879,488
1	Minimized	0.0412	0.00448	0.00530	3,789,363	437,183
12	Minimized	0.0486	0.00148	0.00192	2,175,889	2,461,545
24	Minimized	0.0434	0.00202	0.00275	2,031,059	2,791,974
48	Minimized	0.0397	0.00163	0.00264	1,929,122	3,442,914
96	Minimized	0.0276	0.00134	0.00198	1,908,546	3,577,577

2.3. Contact model formulation

Once distances are sampled between the undeformed contact surfaces, a variety of elastic contact theories can be used to generate contact pressure results numerically. Elastic half-space theory, where the contacting bodies are assumed to be semi-infinite, approximately planar in the region of contact, and linearly elastic, is extremely well developed in the literature [40,41,43–45]. However, it violates important characteristics of natural and artificial joints, such as having an elastic layer of variable thickness covering one or both bodies, contact areas of comparable dimensions to those of the contacting bodies, curved or even wavy contact interfaces, and nonlinear material properties.

An alternate approach consistent with these characteristics is elastic foundation (or “bed of springs”) theory [19–21,46,47]. Derived from plane strain elasticity theory for an elastic layer bonded to a rigid substrate [41], this contact modeling approach scatters independent springs over the contact surfaces, where the springs represent an elastic layer of known thickness covering one or both bodies. Unlike elastic half-space theory, this simplified contact model does not account for how pressure applied at one surface location produces deformations at all locations, thereby eliminating the integral nature of contact problems. However, the benefits of this simplification are faster pressure calculations and facilitated analysis of conformal geometry, layered contact, and nonlinear materials.

We use different forms of the elastic foundation model depending on the magnitude of surface deformations. For small deformations as in artificial knees, the following equation is used to calculate the pressure p of any spring element on the tibial insert surface [19–21,46,47]:

$$p=\frac{(1-v)E}{(1+v)(1-2v)}\frac{d}{h}$$ (1)

where E is Young’s modulus of the elastic layer, ν is Poisson’s ratio of the layer, h is the layer thickness, and d is the spring deformation. Both h and d are calculated on an element-by-element basis, with d defined as the interpenetration of the undeformed contact surfaces in the direction of the approximated midsurface normal. If both bodies possess an elastic layer of the same material, then the two layers are treated as a single layer of combined thickness. Thus, for natural knees, the local thickness of the tibial and femoral articular cartilage are added to determine h for any element [19], while for an artificial knee, h is due to the local thickness of the tibial insert assuming the femoral component is rigid. For larger deformations as in natural knees, the stiffness of the elastic layer increases with surface deformation due to geometric nonlinear behavior so that Eq. (1) becomes [19]:

$$p=\frac{(1-v)E}{(1+v)(1-2v)}\cdot ln\left[1-\frac{d}{h}\right]$$ (2)

Due to the independent nature of the spring elements, both contact pressure models can be solved using linear or nonlinear material models. For nonlinear materials, E can be defined as a function of the pressure p [48], which we derive from a three-parameter nonlinear material model [34]:

$$\varepsilon =\frac{1}{2}{\varepsilon }_0\frac{p}{p_0}+\frac{1}{2}{\varepsilon }_0{\left(\frac{p}{p_0}\right)}^n$$ (3)

where ɛ is strain, p is contact pressure, and ɛ₀, p₀, and n are material parameters. This is a nonlinear power-law material model [41] with the addition of a linear term that produces a standard linear material model when n = 1. This material model with n = 3 has been shown to fit experimental data for polyethylene extremely well [39,49]. For an estimated value for p, E = dp/d∊ is calculated from Eq. (3):

$$E=1/\left\{\frac{1}{2}\frac{{\varepsilon }_0}{p_0}\left[1+n{\left(\frac{p}{p_0}\right)}^{n-1}\right]\right\}$$ (4)

Given the interpenetration d for any spring, Eq. (4) is substituted into Eq. (1) or (2) to produce a single nonlinear equation for p that is solved using standard root-finding methods.

Once p is known for every element, the net contact force and torque acting on the two bodies are computed using the principle of replacement [50]. The contact force on each element in the direction of the local midsurface normal is found by multiplying the element pressure by the element area. Then the calculated element forces are replaced with an equivalent contact force vector, defined as the vector sum of the individual element forces applied at the origin of the fixed body coordinate system, along with a contact torque vector, defined as the sum of the moments of the individual element forces about the fixed body coordinate system origin. In this way, the contact model looks like any other load in the multibody dynamic model as far as the numerical integrator is concerned.

2.4. Dynamic model construction

We have developed an API to allow our deformable contact knee model to function within any multibody dynamic simulation environment. The approach described above was coded in C++ and compiled as a dynamic link library (DLL), with all geometry evaluations performed by the ACIS 3D Toolkit (Spatial Corporation, Westminster, CO). In addition to model parameters (e.g., materials, number of elements) and model options (e.g., choice of contact model, material model, distance sampling method, output quantities), six generalized coordinates and their time derivatives are passed to the DLL by the multibody code. The generalized coordinates specify the relative pose of the moving body with respect to the fixed body, with the rotations defined using a body-three 1–2–3 sequence [51]. Outputs returned to the multibody code include a net contact force and torque vector applied to each body along with measured quantities of interest (e.g., peak and average contact pressures, contact forces, contact areas, and number of active elements). Output data files containing any desired internal information can also be generated depending on the setting of an output flag.

3. Applications

Two sample applications are provided to demonstrate how the model functions within a multibody dynamic simulation environment and to evaluate the influence of contact and material model choices on model predictions. The first application involves static analysis (via dynamic simulation) of a natural knee model and the second is a dynamic simulation of an artificial knee model. A commercial multibody dynamics simulation code (Pro/MECHANICA MOTION, Parametric Technology Corporation, Waltham, MA) was used as the test bed for both models, where the tibia was welded to ground and the femur connected to the tibia via a six degree-of-freedom joint. This joint provided the relative kinematic inputs required by the contact DLL, which was interfaced to the multibody code via a custom load. All simulations were performed on a 2.4 GHz Pentium IV workstation.

3.1. Static analysis of natural knee contact

A natural knee contact model was created from MRI and CT data collected from a single cadaver knee and used to compare contact predictions made with the large and small strain formulations. Institutional review board (IRB) approval was obtained for the data collection and subsequent modeling. Prior to scanning, the specimen was cut approximately 15 cm above and below the joint line. Sagittal plane MRI data were collected using a 3.0-T GE Signa Horizon LX scanner with a quadrature knee coil. A T2-weighted 3D Fast-GRE sequence was used with a 1 mm slice thickness, 256 × 256 image matrix, and 160 mm × 160 mm field of view. Axial CT data were collected from the same specimen using a GE LightSpeed QX/i scanner in helical mode. The scanning parameters were a 1.25 mm overlapping slice thickness, 512 × 512 image matrix, and 160 mm × 160 mm field of view. The tibia and femur in both data sets were segmented using commercial image processing software (SliceOmatic, Tomovision, Montreal, CA). Articular cartilage and subchondral bone surfaces were segmented manually from the MRI data, while cortical bone surfaces were segmented semi-automatically from the CT data using a watershed algorithm. The point clouds from both scans were exported for subsequent surface creation.

Commercial reverse engineering software (Geomagic Studio, Raindrop Geomagic, Research Triangle Park, NC) was used to convert the MRI and CT point cloud data into a combined geometric model for contact analysis. Point clouds from each bone and imaging modality were loaded separately and automatically converted to polygonal surface models. The subchondral bone surfaces from MRI were automatically registered to the corresponding cortical bone surfaces from CT, creating a composite geometric model with articular cartilage surfaces from MRI and cortical bone surfaces from CT. NURBS surfaces were fitted to the polygonal models and the articular cartilage surfaces from MRI merged into single NURBS patches for contact analysis. The number of u–v control points for the articular cartilage was minimized in commercial surface modeling software (Rhinoceros, Robert McNeel & Associates, Seattle, WA). The tolerance (mean ± standard deviation) between the original point clouds from MRI and the final NURBS surfaces was 0.18 ± 0.18 mm for the femur and 0.20 ± 0.29 mm for the tibia.

The articular cartilage and cortical bone surfaces for the tibia and femur were imported into Pro/MECHANICA MOTION to construct a multi-body model for static analysis. The articular cartilage contact and subchondral bone back surfaces needed by the DLL were read in separately. The meniscus was omitted in the model. Young’s modulus for articular cartilage was set to 4 MPa [26] and Poisson’s ratio to 0.45 [19] to represent a relatively short time-frame response. Minimum distance was used for the distance calculations, the femoral contact surface u–v space was 11 × 13, and the contact element grid set to 20 × 15 in the medial and lateral tibial compartments.

The static analysis was performed by numerically integrating the equations of motion using an implicit Euler integrator with loose error tolerances. This approach uses dynamic simulation with large numerical damping to settle the bodies together. For a static analysis without gravity, the mass properties do not affect the final solution and were set to sufficiently large values to permit dynamic simulation. The femur was fixed at 30° of flexion relative to the tibia and subjected to a 1000 N vertical load to bring it into contact [52]. To account for the lack of ligaments to constrain the motion, flexion–extension, internal–external rotation, and anterior–posterior translation of the femur were locked to values corresponding to in vitro experiments performed with the same cadaver knee. The remaining three degrees of freedom were adjusted by the dynamic simulation until the femur reached its final static configuration, as indicated by a maximum acceleration below a small user-defined tolerance.

The static analysis successfully settled the femur onto the tibia, adjusting the three free degrees of freedom as necessary to achieve the final pose (Fig. 4). The dynamic simulation was slow initially when the femur was out of contact, since all elements on the tibia were searched when no contact was occurring. Once both sides were in contact, the numerical integrator settled the femur into its final static pose within approximately 1 min of CPU time. Shorter CPU times were required if the initial pose was closer to the final static pose. The large and small strain models predicted similar contact conditions except for peak pressure, which was higher for the large strain model due to its inherent strain hardening (Table 3).

Fig. 4.

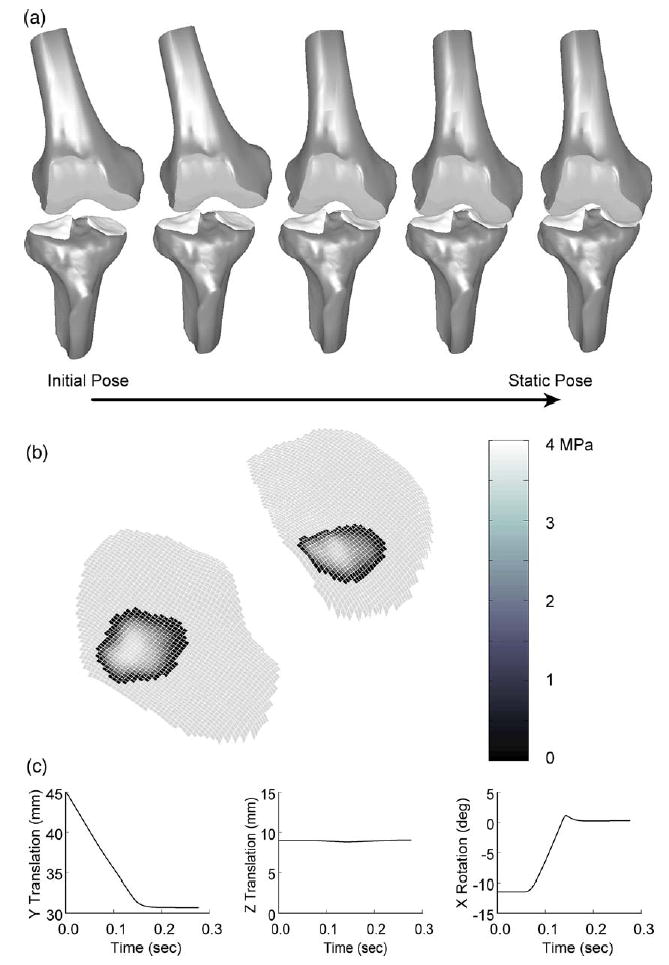
Static analysis results (via dynamic simulation) for the natural knee contact model using the large strain formulation. (a) Animation of dynamic simulation progression from initial pose to static pose. (b) Contact pressure contours on the tibial condyles at the final static pose. (c) Motions predicted by the dynamic simulation. Y translation is superior–inferior, Z translation is medial–lateral, and X rotation is varus–valgus.

Table 3.

Comparison of static analysis results for the natural knee model using large and small strain contact models.

	Large strain		Small strain
Quantity	Medial	Lateral	Medial	Lateral
Contact force (N)	565.6	513.7	565.5	513.1
Contact torque (N m)	14.17	7.145	14.27	7.146
Peak pressure (MPa)	4.216	4.225	3.893	3.854
Average pressure (MPa)	1.640	2.208	1.640	2.190
Contact area (mm2)	344.9	232.6	344.7	234.3

3.2. Dynamic simulation of artificial knee contact

An artificial knee contact model created from manufacturer CAD geometry of an Osteonics 7000 cruciate-retaining knee implant (Stryker Howmedica Osteonics, Inc., Allendale, NJ) was used to compare contact predictions using linear and nonlinear material models. The contact surfaces were extracted from the tibial insert and femoral component and imported into Geomagic Studio for resurfacing. After conversion to polygonal surface models, a new network of untrimmed NURBS patches was created and merged for each femoral contact surface. The number of u–v control points for the contact surfaces was minimized in Rhinoceros, with the tolerance between the original and resurfaced geometry being 0.002 ± 0.002 mm.

The original CAD geometry for the tibial insert, tibial tray, and femoral component were imported into Pro/MECHANICA MOTION to construct a multi-body model for dynamic simulation. The contact surfaces were read in separately by the DLL. For the linear material model, Young’s modulus of the ultra-high molecular weight polyethylene tibial insert was set to 463 MPa [53] and Poisson’s ratio to 0.46 [54]. For the nonlinear material model, the material parameters were set to ɛ₀ = 0.0597, σ₀ = 18.4, and n = 3 to represent polyethylene at 37 °C [39]. Minimum distance was used for the distance calculations, the femoral component contact surface u–v space was 15 × 20, and the contact element grid was set to 30 × 30 in both compartments. Mass properties for all bodies were calculated from their volumes assuming uniform mass density. To simulate gait, flexion–extension, internal–external rotation, and anterior–posterior translation of the femoral component were prescribed based on IRB-approved fluoroscopically measured kinematics from a patient with the identical implant [55]. The femoral component was loaded axially off-center to produce a 70% medial–30% lateral load split [56,57] using a vertical ground reaction force curve scaled to between 0.25 and 3.0 body weight [58–60]. Superior–inferior translation, medial–lateral translation, and varus–valgus rotation were predicted via dynamic simulation, with a preliminary static analysis performed to settle the femoral component onto the tibial insert. The dynamic simulation used the implicit integrator DASSL [61] to accommodate the numerical stiffness caused by deformable contact.

The dynamic simulation was able to predict the motion of the three free degrees of freedom (Fig. 5a), the contact forces in the medial and lateral compartments, and the net contact force and torque applied to both bodies. A subsequent inverse dynamics analysis driven by the predicted and prescribed motions from forward dynamics was used to calculate the contact area and pressure distribution throughout the gait cycle (Fig. 5b). The predicted medial–lateral translation and varus–valgus rotation were within the accuracy envelope of the fluoroscopically measured motion, while the predicted superior–inferior translation possessed the same general shape as the experimental curve but was shifted upward by about 0.5–1 mm (Fig. 5c). This off-set was likely due to thickness differences between the modeled and actual insert as well as imperfect superior–inferior positioning of the modeled insert relative to the tibial tray. A course element grid was used for forward dynamics and a finer grid of 50 × 50 for inverse dynamics since the contact forces and torques needed for forward dynamics are relatively insensitive to grid density while contact pressures and areas are more sensitive (Fig. 6). The forward dynamic simulations required approximately 10 min of CPU time to complete and the subsequent inverse dynamics analyses required less than 30 s. At the point of maximum load during stance phase, contact force and torque were similar for the two material models, while peak and average pressure were lower and contact area larger for the nonlinear material (Table 4). These differences were most pronounced on the medial side where the load was the largest. At other points in the cycle where the loads were smaller, the differences were less pronounced.

Fig. 5.

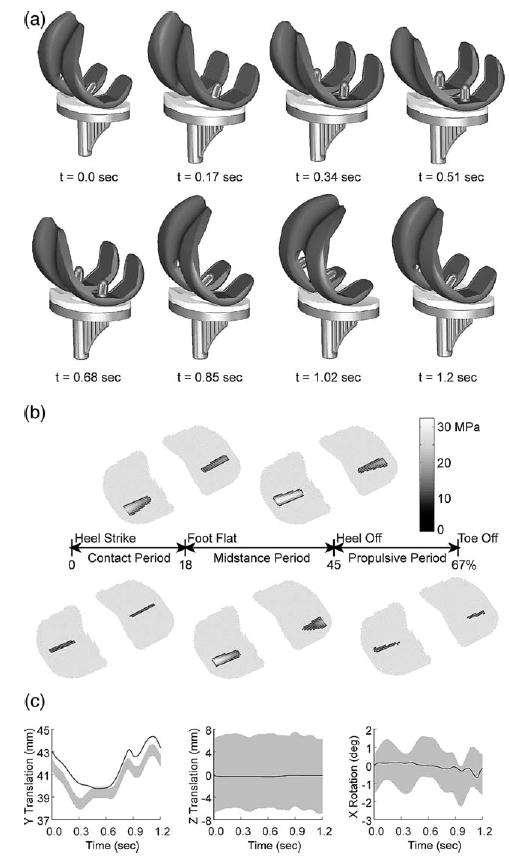
Dynamic simulation results for the artificial knee contact model using the linear material formulation. (a) Animation of dynamic simulation progression for one cycle of gait. (b) Contact pressure contours on the tibial insert at five locations in the gait cycle. (c) Motions predicted by the dynamic simulation (solid lines) compared to accuracy envelopes for the fluoroscopic measurements (gray bands) [10]. Y translation is superior–inferior, Z translation is medial–lateral, and X rotation is varus–valgus.

Fig. 6.

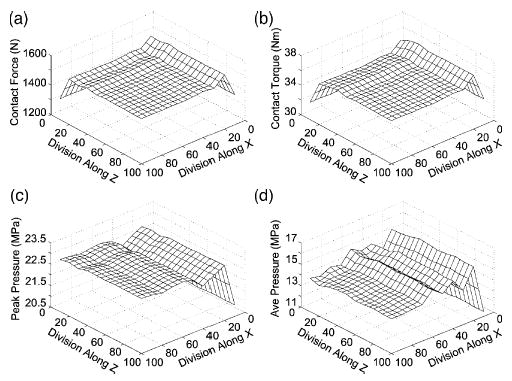
Sensitivity of contact predictions to the number of element divisions in the x and z directions for the artificial knee model. (a) Contact force. (b) Contact torque. (c) Peak pressure. (d) Average pressure. The sensitivity can be different in the two directions. Contact force and torque are much less sensitive to the element grid than are peak and average contact pressure. The high average pressure sensitivity is due to contact area sensitivity (not shown).

Table 4.

Comparison of dynamic simulation results for the artificial knee model using linear and nonlinear material models. Contact predictions are from the location in the gait cycle with maximum axial load.

	Linear material		Nonlinear material
Quantity	Medial	Lateral	Medial	Lateral
Contact force (N)	1467	623.3	1417	613.1
Contact torque (N m)	35.82	16.67	34.23	15.95
Peak pressure (MPa)	28.09	17.07	15.58	11.34
Average pressure (MPa)	16.60	9.030	12.50	8.017
Contact area (mm2)	88.37	69.02	113.4	76.47

4. Discussion

This paper has presented a new methodology for simulating deformable contact in human joints within a multibody dynamics environment. The approach requires use of specially prepared contact surfaces, efficient distance calculation methods, a contact solver selected for its applicability to human joints, and an API to tie the contact model into a larger multibody dynamic model. The methodology was successfully applied to static analysis (via dynamic simulation) of a natural knee contact model created from MRI and CT data and dynamic simulation of an artificial knee contact model created from manufacturer CAD data. These two applications demonstrate the computational efficiency of the approach, which can perform dynamic simulations in as little as 10 min of CPU time, and highlight important differences between the large versus small strain and linear versus nonlinear model formulations.

As with any modeling environment, the current formulation possesses several important limitations. The current contact models are elastic, the assumption being that the dynamics of the contact interface are significantly faster than those of the gross motion being simulated. Inclusion of viscoelastic effects would require adding states to track the element deformations over time. Alternatively, it may be possible to use equivalent elastic parameters to approximate specific dynamic loading situations such as 1 Hz gait motions [62]. While the material properties in the present model can be linear or nonlinear, the materials are still assumed to be isotropic and homogeneous, which are likely worse assumptions for natural knees than for artificial knees. Plasticity in artificial knees [63] could easily be added via a new material model. The other serious limitation for natural knee models is the lack of the menisci. The meniscus is difficult to model even in finite element software [64], and an approach that models the menisci as spring elements [16] could be used as a starting point.

Though validation of the methodology is beyond the scope of this paper, comparison with experimental data suggests that the current approach produces reasonable predictions. Static contact pressures predicted by the artificial knee contact model were recently compared with experimental measurements [39]. For the 16 experimental cases investigated (loads of 750, 1500, 2250, and 3000 N with flexion angles of 0°, 30°, 60°, and 90°), the linear material model was able to match peak and average contact pressures simultaneously using a single set of material parameters, while the nonlinear material model was only able to match the average pressure data well. The artificial knee contact model with linear material properties has also been used to predict damage on an Osteonics 7000 cruciate-retaining implant (Stryker Howmedica Osteonics, Allendale, NJ) [55]. Based on dynamic simulations of gait and stair activities derived from in vivo fluoroscopic data, damage predictions matched maximum damage depths measured from the post-mortem retrieval to within 0.1 mm, with good quantitative and qualitative agreement in damage areas and locations of maximum damage as well. The natural knee contact model without meniscus has been evaluated against static experimental pressure data measured with the Tekscan K-Scan system [65]. For a single load of 1000 N, the model can predict average pressures, contact areas, and contact forces extremely well (within ±10%) but peak pressures less accurately (within ±50%). These evaluations are valuable for determining the capabilities and limitations of the current contact models so that they can be refined and improved as new understanding is gained.

We have identified several areas for potential computational and functional enhancements. Addition of patellofemoral contact using the patella as the fixed body with a planar element surface would enhance the current model’s utility. Use of element surfaces besides planes (e.g., cylinders and spheres) would extend the applicability of the framework to joints such as the ankle and hip. Use of a fixed grid on each element surface limits the accuracy of contact force and torque solutions. The addition of an adaptive grid option during dynamic simulation would allow us to vary the size of the elements to accommodate the size of the contact area, thereby producing contact force and torque results that are insensitive to the element grid. Despite our efforts to minimize the CPU time required by distance calculations, they remain the primary computational bottleneck. Since contact pairs are independent during contact calculations, multithreading of distance calculations would allow full use of computational resources on multiprocessor machines.

Our ultimate goal is to incorporate deformable contact models of natural and artificial knees into full-body dynamic musculoskeletal models created with programs such as SIMM and the Dynamics Pipeline. Within this larger simulation environment, elements representing muscles, ligaments, neural controllers, and/or ground contact models can be included. By using optimization methods to tune the model’s kinematic structure [66–68] and MRI data to tune its musculoskeletal geometry [26,69,70], it may soon be possible to create patient-specific dynamic simulations that can be used to predict optimal surgical parameters or rehabilitation strategies for individual patients based on predicted functional outcome [26,28].

In summary, this paper has presented a detailed computational methodology for incorporating a deformable contact knee model into multibody dynamic simulation software. The current implementation works for the tibiofemoral joint of artificial knees or natural knees without the menisci and can accommodate small and large strain contact models with linear or nonlinear material properties. The methodology can predict contact forces, pressures, and areas and is sufficiently fast computationally to perform dynamic simulations of the tibiofemoral joint in as little as 10 min. The specified API allows the contact model to be incorporated into any multibody dynamics simulation code.