Abstract
A simple and rapid method is presented for solving the three-dimensional structures of protein–protein complexes in solution on the basis of experimental NMR restraints that provide the requisite translational (i.e., intermolecular nuclear Overhauser enhancement, NOE, data) and orientational (i.e., backbone 1H-15N dipolar couplings and intermolecular NOEs) information. Providing high-resolution structures of the proteins in the unbound state are available and no significant backbone conformational changes occur upon complexation (which can readily be assessed by analysis of dipolar couplings measured on the complex), accurate and rapid docking of the two proteins can be achieved. The method, which is demonstrated for the 40-kDa complex of enzyme I and the histidine phosphocarrier protein, involves the application of rigid body minimization using a target function comprising only three terms, namely experimental NOE-derived intermolecular interproton distance and dipolar coupling restraints, and a simple intermolecular van der Waals repulsion potential. This approach promises to dramatically reduce the amount of time and effort required to solve the structures of protein–protein complexes by NMR, and to extend the capabilities of NMR to larger protein–protein complexes, possibly up to molecular masses of 100 kDa or more.
Solving the three-dimensional solution structures of larger (≥30-kDa) macromolecular protein–protein complexes by NMR currently presents a highly challenging, complex, and time-consuming task (1). For example, the recently determined structure of the 40-kDa complex of the N-terminal domain of enzyme I (EIN) and the histidine phosphocarrier protein HPr required ≈3,500 h of experimental measurement time and ≈2 years to analyze the data (2). The most time-consuming portion of the analysis is the interpretation of the nuclear Overhauser enhancement (NOE) data, which yield approximate interproton distance restraints that provide the mainstay of any NMR structure determination (3, 4). Typically, however, the intermolecular NOEs comprise only a tiny fraction of the total number of NOEs used in the structure determination; in the case of the EIN–HPr complex, for example, approximately 100 intermolecular NOEs were assigned of over 3,000 used (i.e., ≈3% of the total) (2). Because intermolecular NOEs can be observed exclusively by making using of various isotope labeling strategies combined with appropriate isotope-edited and filtered NMR experiments (1), it follows that any approach that circumvents the need to assign the intramolecular NOEs would lead to a dramatic saving in time and effort. In the case of many protein–protein complexes, particularly those where the strength of the interaction is rather weak, the backbone conformation of the individual components does not change significantly upon complex formation. Moreover, if x-ray structures or very high quality NMR structures of the free proteins are available, any significant change in backbone conformation can be readily ascertained a priori by comparison of the observed one-bond 15N-H backbone residual dipolar couplings (1DNH) measured on the complex with those calculated from the free structures by optimization of the magnitude and orientation of the alignment tensor (5). Thus, if high-resolution structures of the free proteins are available and no significant changes in the backbone occur upon complexation, it should be feasible to dock two proteins by using restraints that provide the requisite translational and orientational information. Approximate NOE-derived intermolecular interproton distance restraints possess both translational and orientational content, while dipolar couplings measured in dilute liquid crystalline media provide highly accurate long-range orientational restraints (2, 5–9). In this paper I show that accurate docking can be achieved by rigid body minimization using a target function that comprises only three terms, consisting of intermolecular NOE and 1DNH dipolar coupling restraints, supplemented by an intermolecular van der Waals repulsive potential. I demonstrate the applicability of this approach, using the EIN–HPr complex as an example.
Methods
Coordinates for the NMR structure (restrained regularized mean) of the EIN–HPr complex (2) and the x-ray structures of free EIN (10) and HPr (11) were taken from the Research Collaboratory for Structural Bioinformatics (RCSB) Protein Data Bank (accession codes 3EZA, 1ZYM, and 1POH, respectively). Experimental 1DNH dipolar coupling and intermolecular NOE-derived interproton distance restraints were taken from ref. 2 (PDB accession code 3EZAMR). All calculations were carried out in xplor (12), modified to incorporate refinement against dipolar coupling restraints (13). Calculations using conventional Powell minimization in cartesian coordinate space in which only interfacial side chains are allowed to move also used a conformational database potential for the side-chain torsion angles (14), as well as restraints to maintain idealized covalent geometry.
Results and Discussion
In conventional cartesian coordinate minimization or simulated annealing there are (3N − 6) degrees of freedom, where N is the number of atoms. For NMR structure determinations, the experimentally derived NMR restraints are limited in number and the structure can be solved only by making use of prior knowledge of the covalent geometry (in terms of restraints for bond lengths, bond angles, planes, and chirality) and some sort of van der Waals term to prevent atoms from coming too close together (4, 8). In addition, minimization cannot circumvent the large energy barriers on the path toward the global minimum region, and consequently trapping in false local minima invariably occurs. For this reason, it is necessary to make use of more powerful optimization techniques such as simulated annealing to ensure that the global minimum region is reached (15). If the two proteins are treated as rigid bodies, however, and docking is guided by intermolecular distance restraints and dipolar couplings, the number of degrees of freedom is reduced to 9. Thus, one molecule is fixed, the second is allowed to undergo both translation and rotation (6 degrees of freedom), whereas the axis of the alignment tensor for the residual dipolar couplings only undergoes rotation (3 degrees of freedom). Hence, if there are sufficient experimental restraints that provide the requisite orientational and translational information, the two components of the complex can be accurately docked. The method I have used for docking involves the application of rigid body minimization.
Given that the intermolecular NOE data possess both orientational and translational content, one might suppose that the intermolecular NOEs alone could define the geometry of the complex. Under optimal conditions this is certainly true. In general, however, while the translational and orientational information contained within the intermolecular NOE data are usually sufficient to yield an approximate orientation of the two components of the complex, it may not be adequate to accurately dock the two proteins in the absence of dipolar couplings. This is due to a number of factors: (i) The intermolecular NOE restraints are limited to protons in close spatial proximity (<6 Å) so that accumulation of errors can readily occur when the intermolecular NOEs are required to determine long-range order. (ii) The intermolecular NOEs may be limited in number, particularly as it is often difficult to unambiguously assign many of the intermolecular NOEs during the early stages of a structure determination. (iii) The intermolecular NOE-derived interproton distances are limited in both accuracy and precision, particularly because these restraints are usually approximate and classified into several loose ranges; hence, accurate orientation of the two components of the complex can generally be achieved only in the presence of a large number of correlated intermolecular NOE restraints. Finally, (iv) the vast majority of intermolecular NOEs involve side chains, thereby introducing additional conformational freedom because many side chains can sample a range of possible torsion angle combinations.
In contrast to the intermolecular NOE-derived interproton distance restraints, the dipolar couplings can readily be measured with high accuracy and precision (5). The observed dipolar coupling for a backbone 15N-H vector is given by (13)
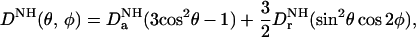 |
1 |
where DaNH and DrNH in units of Hz are the axial and rhombic components of the traceless second rank diagonal tensor DNH; θ is the angle between the N–H interatomic vector and the z axis of the tensor; and φ is the angle that describes the position of the projection of the N–H interatomic vector on the x–y plane, relative to the x axis. If the dipolar couplings have been measured for only a single alignment tensor (i.e., in one liquid crystalline medium), it follows from Eq. 1 that there are four possible orientations of one molecule relative to another that will be compatible with the measured dipolar couplings (16). This degeneracy is resolved by the intermolecular NOE data, since the resulting interproton distance restraints provide both translational and orientational information. Thus, in conjunction with intermolecular NOE data, the dipolar couplings provide a source of readily accessible orientational restraints with which to accurately define the relative orientation of the individual protein components within a complex.
To demonstrate the feasibility of accurately docking protein–protein complexes by rigid body minimization on the basis of intermolecular NOE and dipolar coupling data, I have used the EIN–HPr complex as an example. The experimental restraints comprise 231 residual 1DN-H dipolar couplings (153 for EIN and 78 for HPr) and 109 NOE-derived intermolecular interproton distance restraints (classified into the usual four distance ranges corresponding to strong, medium, weak, and very weak NOEs) (2). The values of the axial component (DaNH) of the alignment tensor and the rhombicity (DrNH/DaNH), obtained directly from the powder pattern distribution of the measured dipolar couplings (17), are −14.3 Hz and 0.4, respectively (2). The x-ray structures of free EIN (10) and HPr (11), solved at 2.5-Å and 1.5-Å resolution, respectively, both satisfy the residual dipolar couplings reasonably well with dipolar coupling R factors (18) of 26.6% and 15.8%, respectively, and display backbone (N, Cα, C′) atomic rms differences of 1.14 Å (residues 2–230) and 0.6 Å (residues 1–85), respectively, from the corresponding bound structures in the original EIN–HPr complex determined by NMR (2).
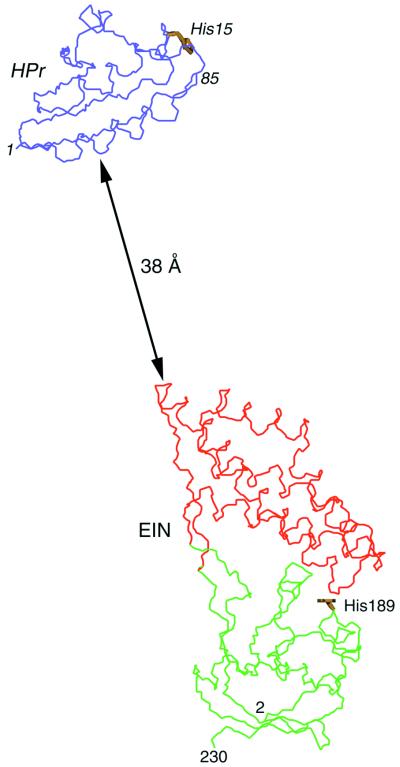
In the starting coordinate frame the distance of closest approach between EIN and HPr is ≈38 Å, with the Cα atoms of the two active-site histidines (His-189 of EIN and His-15 of HPr) separated by ≈92 Å (Fig. 1A). In addition, the orientation of the two proteins is completely different from that in the EIN–HPr complex and the two active sites are not opposed. The dipolar coupling R factor for EIN and HPr in the initial coordinate frame is 66%, the rms from the intermolecular distance restraints is 79 Å, and the backbone atomic rms difference from the original NMR structure of the complex is 29 Å (Table 1). The rigid body minimization protocol proceeds as follows: 500 steps of rigid body minimization with the force constants for the dipolar coupling (kdip), NOE-derived interproton distance (kNOE) and quartic repulsive van der Waals repulsion (kvdw) terms set to 0.1 kcal⋅mol−1⋅Hz−2, 0.01 kcal⋅mol−1⋅Å−2, and 4 kcal⋅mol−1⋅Å−4, respectively, and the van der Waals radii scaled to 0.8 times (svdw) their values in the CHARMM19/20 parameters. This is followed by 100 cycles of rigid body minimization (500 steps per cycle) in which kdip, kNOE, and kvdw are slowly increased from 0.1 to 0.5 kcal⋅mol−1⋅Hz−2, 0.01 to 30 kcal⋅mol−1⋅Å−2, and 0.004 to 1.0 kcal⋅mol−1⋅Å−4, respectively, and svdw is reduced from 0.9 to 0.75. This is finally followed by 500 steps of rigid body minimization with the values of kdip, kNOE, kvdw, and svdw set to 0.5 kcal⋅mol−1⋅Hz−2, 60 kcal⋅mol−1⋅Å−2, 3 kcal⋅mol−1⋅Å−4, and 0.75, respectively, and another 500 steps of rigid body minimization with svdw increased to 0.78 and the other force constants unaltered. The resulting structure is 1.18 Å away from the restrained minimized mean NMR structure solved in the conventional manner and has a dipolar coupling R factor of 29% (Table 1). The intermolecular van der Waals contacts, however, are very poor, because the side chains at the interface have not been allowed to move in any way and consequently some steric clash is inevitable (Table 1). To circumvent this problem, the structure is subjected to conventional cartesian coordinate Powell minimization in which all of the coordinates are held fixed with the exception of the side-chain atoms (from the γ position onwards) of those residues for which intermolecular NOEs are observed. These comprise 15 side chains for EIN and 14 for HPr. The target function now comprises terms for covalent geometry, nonbonded contacts [in the form of a quartic van der Waals repulsion term and a conformational database potential of side-chain torsion angles (8)], and the NOE and dipolar coupling restraints. The Powell minimization protocol involves 50 cycles (20 steps per cycle) in which kdip, kNOE, and kvdw are increased from 0.1 to 0.5 kcal⋅mol−1⋅Hz−2, 0.5 to 60 kcal⋅mol−1⋅Å−2, and 0.1 to 4 kcal⋅mol−1⋅Å−4, respectively, with svdw set to 0.8, and the force constant for the conformational database potential set to 1, followed by 500 steps of minimization with the force constants unchanged. The latter procedure results in a dramatic improvement in the van der Waals contacts without any alteration in the position of the backbone atoms (Table 1). The whole process of rigid body minimization, followed by conventional Powell minimization in which only the relevant side chains are allowed to move, (which takes ≈5 min of the central processing unit on a 1998 Dec Alpha 600-MHz workstation) can be then repeated for a second time. The final structure is 1.17 Å away from the original NMR structure (Fig. 2a), has a dipolar R factor of 28%, and exhibits a negative intermolecular Lennard–Jones energy, indicative of yet further improvements in the intermolecular nonbonded contacts (Table 1).
Figure 1.
The starting coordinates used in the rigid body minimization calculations. In the initial coordinate frame, the x-ray structures of EIN (α and α/β domains comprising residues 2–230, shown in red and green, respectively) and HPr (blue) are separated by ≈38 Å and their relative orientation is completely different from that in the EIN–HPr complex. The Cα–Cα distance between the active site histidines (shown in yellow) is ≈92 Å.
Table 1.
Structural statistics
| Structure | Dipolar coupling R factor, %* | rms from intermolecular distance restraints, Å | Intermolecular ELJ, kcal⋅mol−1† | Backbone atomic rms to original NMR structure of complex‡ |
|---|---|---|---|---|
| Free x-ray structures | ||||
| EIN | 26.6§ | 1.14¶ | ||
| HPr | 15.8§ | 0.60¶ | ||
| Starting EIN, HPr coordinate frame | 66.3§ | 79.4 | 0 | 28.8 |
| Rigid body docking with all intermolecular interproton distance restraints‖ | ||||
| Round 1 rigid body | 28.9 | 0.81 | 4.1 × 107 | 1.18 |
| Round 1 side chain | 28.9 | 0.42 | 4.5 × 101 | 1.18 |
| Round 2 rigid body | 28.8 | 0.37 | 2.1 × 101 | 1.17 |
| Round 2 side chain | 28.8 | 0.37 | −1.2 × 101 | 1.17 |
| Rigid body docking with nine intermolecular distance restraints‖** | ||||
| Round 1 rigid body | 28.8 | 1.34 | 1.5 × 107 | 1.46 |
| Round 1 side chain | 28.8 | 1.05 | 9.3 × 102 | 1.46 |
| Round 2 rigid body | 27.8 | 0.93 | 5.8 × 102 | 1.31 |
| Round 2 side chain | 27.8 | 0.92 | 6.8 × 102 | 1.31 |
The dipolar coupling factor is defined as the ratio of the measured rms to the expected rms if the N–H vectors were randomly distributed. The latter is given by {2Da2[4 + 3 (Dr/Da)2/5}1/2 (18).
ELJ is the Lennard–Jones van der Waals energy (computed only for the intermolecular contacts) from the CHARMM19/20 empirical energy function. This term is not included in any of the calculations.
Refers to N, Cα, and C′ backbone atoms of residues 2–230 of EIN and residues 1–85 of HPr.
The dipolar coupling R factor for the free proteins and for EIN and HPr in the initial coordinate frame are obtained by optimization of the orientation of the alignment tensor, keeping the values of Da (−14.3 Hz) and Dr/Da (0.4) fixed to their experimental values.
These values represent the backbone atomic rms difference between the NMR structure of EIN in the complex and the x-ray structure of free EIN, and between the NMR structure of HPr in the complex and the x-ray structure of free HPr.
The protocol of rigid body minimization followed by Powell minimization of the interfacial sidechains is given in the text.
The intermolecular distance restraints comprise eight approximate interproton distance restraints corresponding to all the observed intermolecular NH–methyl NOEs, supplemented by a distance restraint to ensure that the Cα–Cα distance between the active–site histidines is less than 12 Å.
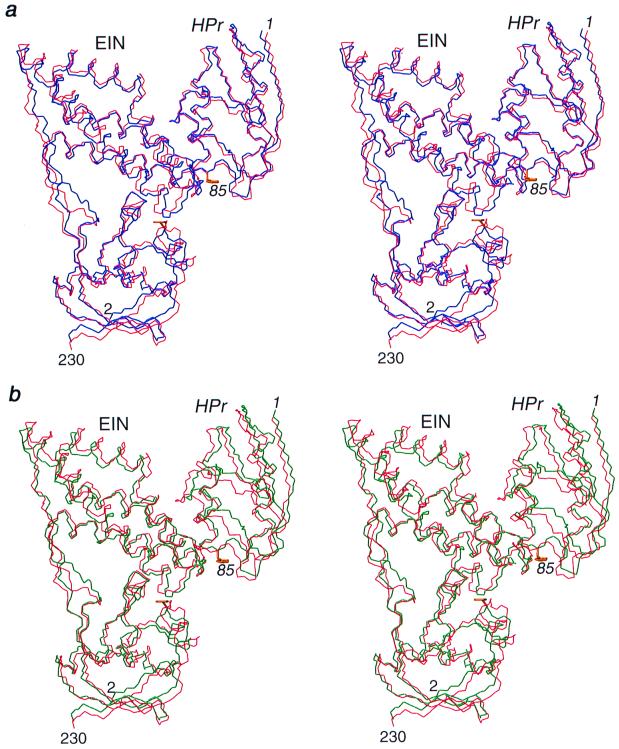
Figure 2.
Stereoviews providing a comparison of the results of rigid body minimization with the original NMR structure of the EIN–HPr complex. The original NMR structure is shown in red, and the structures calculated by rigid body docking of the free x-ray structures on the basis of 109 and 9 intermolecular distance restraints are shown in blue (a) and green (b), respectively. In addition to the experimental intermolecular interproton distance restraints, 231 experimental 1DNH dipolar couplings are used in the calculations. The active-site histidines (His-189 of EIN and His-15 of HPr) in the structures obtained by rigid body docking are shown in yellow. Only residues 2–230 of EIN comprising the α and α/β domains are shown.
If the above calculations are repeated using the complete set of intermolecular NOE restraints and no dipolar couplings (so that the problem is reduced to only six degrees of freedom because the three degrees of freedom for rotation of the axis of the alignment tensor are eliminated), the resulting structure is 1.22 Å away from the original NMR structure. Thus, the 109 approximate intermolecular interproton distance restraints are sufficiently correlated to provide the requisite translation and orientational information in their own right to accurately dock the two proteins. Although the introduction of dipolar couplings in this instance improves the accuracy by only a small degree, it does provide considerable increased confidence in the resulting structure, because the nature of the NOE and dipolar coupling data are so different and the number of restraints per degree of freedom is increased from ≈18 to ≈38.
In many instances it may not be possible to assign as many intermolecular NOE restraints as in the case of the EIN–HPr complex. I therefore carried out a second set of calculations using the identical protocol with only eight intermolecular NOE restraints between backbone amides and methyl groups involving 10 side chains (5 from EIN and 5 from HPr), supplemented by a distance restraint in which the Cα atoms of the active-site histidines (His-189 of EIN and His-15 of HPr) were restrained to be less than 12 Å apart. In this case, rigid body minimization of the basis of the 9 intermolecular distance restraints alone (i.e., 1.5 restraints per degree of freedom) yields a structure of the complex that is 2.6 Å away from the original NMR structure. The introduction of dipolar coupling restraints increases the number of restraints per degree of freedom to ≈27 and therefore, not surprisingly, produces a very large improvement in accuracy such that, even with so few intermolecular distance restraints, the final structure is only 1.3 Å away from the original NMR structure (Fig. 2b and Table 1). This result attests to the power of dipolar coupling restraints in providing orientational information and illustrates the complementarity of the intermolecular NOE and dipolar coupling data. The poor accuracy of the structure calculated in the absence of dipolar couplings is a reflection both of the low ratio of restraints per degree of freedom and of accumulation of errors that is inherent in the use of short-range (<6 Å) approximate distance restraints. Consequently, with dipolar couplings available one does not need to strive to interpret as many intermolecular NOEs as possible, making it much easier to accurately define the structure of a complex. Moreover, since the assignments of many of the intermolecular NOEs may be initially ambiguous, the inclusion of dipolar couplings in the rigid body minimization procedure permits accurate docking to be obtained at a much earlier stage of the structure determination, thereby obviating the need for extensive rounds of iterative refinement in which intermolecular NOEs are incrementally assigned and added to the restraints list in the light of each successive intermediate structure.
Concluding Remarks
In conclusion, if high-quality structures of the unbound state are available and there are no significant changes upon complexation (as assessed from the measured dipolar couplings), it is possible to solve the structure of a protein–protein complex on the basis of only intermolecular NOE and backbone 1DNH dipolar coupling restraints using rigid body minimization. Because only a few intermolecular NOE restraints are required to provide the necessary translational information and remove any ambiguities in the orientational information provided by the dipolar couplings, this technique should permit the structures of much larger complexes to be solved by NMR. Thus, resonance assignments can potentially be made on fully perdeuterated complexes up to ≈100 kDa by using triple-resonance transverse-relaxation optimized (TROSY) pulse sequences (19), possibly in combination with segmental isotope labeling schemes (20, 21), and intermolecular NOEs between backbone amide and methyl groups can be observed in samples in which one component is 15N-labeled and fully perdeuterated, while the second component is 13C-labeled and fully perdeuterated with the exception of the methyl groups (1, 22). Moreover, even for large systems 1DNH dipolar couplings can be accurately measured on fully perdeuterated proteins either in two dimensions by recording 1H-15N TROSY-heteronuclear single-quantum coherence (HSQC) and regular decoupled HSQC spectra, or in three dimensions by a combination of TROSY-1HN–15N–13C′ (HNCO) correlation and J-scaled TROSY-HNCO spectra (23). Finally, the same methodology should also be applicable to solving structures of complexes between proteins and conformationally rigid ligands.
Acknowledgments
I thank Drs. Ad Bax, Carole Bewley, and Attila Szabo for useful discussions. This work was supported in part by the AIDS Targeted Antiviral Program of the Office of the Director of the National Institutes of Health.
Abbreviations
- NOE
nuclear Overhauser enhancement
- EIN
N-terminal domain of enzyme I
- HPr
histidine phosphocarrier protein
References
- 1.Clore G M, Gronenborn A M. Nat Struct Biol. 1997;4, Suppl. S:849–853. [PubMed] [Google Scholar]
- 2.Garrett D S, Seok Y-J, Peterkofsky A, Gronenborn A M, Clore G M. Nat Struct Biol. 1999;6:166–173. doi: 10.1038/5854. [DOI] [PubMed] [Google Scholar]
- 3.Wüthrich K. NMR of Proteins and Nucleic Acids. New York: Wiley; 1986. [Google Scholar]
- 4.Clore G M, Gronenborn A M. CRC Crit Rev Biochem Mol Biol. 1989;24:479–564. doi: 10.3109/10409238909086962. [DOI] [PubMed] [Google Scholar]
- 5.Tjandra N, Bax A. Science. 1997;278:1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 6.Tjandra N, Omichinski J G, Gronenborn A M, Clore G M, Bax A. Nat Struct Biol. 1997;4:732–738. doi: 10.1038/nsb0997-732. [DOI] [PubMed] [Google Scholar]
- 7.Prestegard J H. Nat Struct Biol. 1998;5, Suppl. S:517–522. doi: 10.1038/756. [DOI] [PubMed] [Google Scholar]
- 8.Clore G M, Gronenborn A M. Proc Natl Acad Sci USA. 1998;95:5891–5898. doi: 10.1073/pnas.95.11.5891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Clore G M, Starich M R, Bewley C A, Cai M, Kuszewski J. J Am Chem Soc. 1999;121:6513–6514. [Google Scholar]
- 10.Liao D I, Silverton E, Seok Y-J, Lee B R, Peterkofsky A, Davies D R. Structure. 1996;4:861–872. doi: 10.1016/s0969-2126(96)00092-5. [DOI] [PubMed] [Google Scholar]
- 11.Jia Z, Quail J W, Waygodd E B, Delbaere L T. J Biol Chem. 1993;268:22490–22501. doi: 10.2210/pdb1poh/pdb. [DOI] [PubMed] [Google Scholar]
- 12.Brünger A T. xplor, A System for X-ray Crystallography and NMR. New Haven, CT: Yale Univ. Press; 1993. [Google Scholar]
- 13.Clore G M, Gronenborn A M, Tjandra N. J Magn Reson. 1998;131:159–162. doi: 10.1006/jmre.1997.1345. [DOI] [PubMed] [Google Scholar]
- 14.Kuszewski J, Gronenborn A M, Clore G M. J Magn Reson. 1997;125:171–177. doi: 10.1006/jmre.1997.1116. [DOI] [PubMed] [Google Scholar]
- 15.Nilges M, Gronenborn A M, Brünger A T, Clore G M. Protein Eng. 1988;2:27–38. doi: 10.1093/protein/2.1.27. [DOI] [PubMed] [Google Scholar]
- 16.Ramirez B E, Bax A. J Am Chem Soc. 1998;120:9106–9107. [Google Scholar]
- 17.Clore G M, Gronenborn A M, Bax A. J Magn Reson. 1998;133:216–221. doi: 10.1006/jmre.1998.1419. [DOI] [PubMed] [Google Scholar]
- 18.Clore G M, Garrett D S. J Am Chem Soc. 1999;121:9008–9012. [Google Scholar]
- 19.Wider G, Wüthrich K. Curr Opin Struct Biol. 1999;9:594–601. doi: 10.1016/s0959-440x(99)00011-1. [DOI] [PubMed] [Google Scholar]
- 20.Yamazaki T, Otomo T, Oda N, Kyogoku Y, Uegaka K, Ito N, Ishino Y, Nakamura H. J Am Chem Soc. 1998;120:5591–5592. [Google Scholar]
- 21.Xu R, Ayers B, Cowburn D, Muir T W. Proc Natl Acad Sci USA. 1999;96:388–393. doi: 10.1073/pnas.96.2.388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gardner K H, Kay L E. Annu Rev Biophys Biomol Struct. 1998;27:357–406. doi: 10.1146/annurev.biophys.27.1.357. [DOI] [PubMed] [Google Scholar]
- 23.Kontaxis G, Clore G M, Bax A. J Magn Reson. 2000;143:184–196. doi: 10.1006/jmre.1999.1979. [DOI] [PubMed] [Google Scholar]