Skip to main content
NCBI home page
Molecular Systems Biology logoLink to Molecular Systems Biology
. 2005 Mar 29;1:2005.0001. doi: 10.1038/msb4100004

A global view of pleiotropy and phenotypically derived gene function in yeast

Aimée Marie Dudley 1,*, Daniel Maarten Janse 1,*, Amos Tanay 2, Ron Shamir 2, George McDonald Church 1,a
PMCID: PMC1681449  PMID: 16729036

Abstract

Pleiotropy, the ability of a single mutant gene to cause multiple mutant phenotypes, is a relatively common but poorly understood phenomenon in biology. Perhaps the greatest challenge in the analysis of pleiotropic genes is determining whether phenotypes associated with a mutation result from the loss of a single function or of multiple functions encoded by the same gene. Here we estimate the degree of pleiotropy in yeast by measuring the phenotypes of 4710 mutants under 21 environmental conditions, finding that it is significantly higher than predicted by chance. We use a biclustering algorithm to group pleiotropic genes by common phenotype profiles. Comparisons of these clusters to biological process classifications, synthetic lethal interactions, and protein complex data support the hypothesis that this method can be used to genetically define cellular functions. Applying these functional classifications to pleiotropic genes, we are able to dissect phenotypes into groups associated with specific gene functions.

Keywords: bicluster, genetics, genomics, phenotype, yeast deletion

Introduction

Pleiotropy occurs when a mutation in a single gene produces effects on more than one characteristic, that is, causes multiple mutant phenotypes. In humans, this phenomenon is most obvious when mutations in single genes cause diseases with seemingly unrelated symptoms (Brunner and van Driel, 2004), including transcription factor TBX5 mutations that cause the cardiac and limb defects of Holt–Oram syndrome, glycosylation enzyme MPI mutations that produce the severe mental retardation and blood coagulation abnormalities of Type 1b congenital disorders of glycosylation, and DNA damage repair protein NBS1 mutations that lead to microcephaly, immunodeficiency, and cancer predisposition in Nijmegen breakage syndrome (http://www.ncbi.nlm.nih.gov/omim/). A major challenge in the analysis of pleiotropic genes is determining whether all of the phenotypes associated with a mutation result from the loss of a single function or of multiple functions encoded by the same gene. In addition to providing important information about gene function, distinguishing between these two models is important for devising effective treatments and analyzing drug side effects. Classical genetic analysis attempts to resolve such issues by isolating and characterizing multiple alleles of the same gene, with the goal of determining whether these phenotypically defined functions are genetically separable. Unfortunately, this type of approach is time consuming and often not feasible in a clinical setting, which relies on the identification of naturally occurring alleles.

Techniques and resources developed in the fields of functional genomics and computational biology have the potential to meet such challenges through the large-scale analysis of mutant phenotype data. Pioneering efforts in these areas have been carried out in model organisms, such as the yeast Saccharomyces cerevisiae. These include the construction of resources such as comprehensive, isogenic mutant collections (Giaever et al, 2002) and experimental methods for measuring the fitness effects conferred by mutations in individual genes (Winzeler et al, 1999) or synthetic interactions between multiple genes (Tong et al, 2001). Analysis of these data has also been enhanced by the application of a variety of computational methods for grouping genes by common attributes (Everitt et al, 2001). Despite such advances, only a few recent studies have begun to use these resources to examine the response of mutants to a relatively large number of environmental perturbations (Giaever et al, 2004; Lum et al, 2004; Parsons et al, 2004). Furthermore, these studies have focused on the analysis of condition-specific effects, that is, genes with phenotypes in only one of the conditions examined, largely ignoring the results obtained for pleiotropic genes. While useful in identifying major effector molecules active under a given condition, including possible drug targets, this approach fails to capture the full complexity of the network of cellular functions required for response to an environmental perturbation. Nonetheless, such genomic results and conventional genetic principles suggest that the strong relationship between mutant phenotype and cellular function can be captured by the use of large phenotype profiles and leveraged for the analysis of both condition-specific and highly pleiotropic genes.

In this study, we implement a system for obtaining and analyzing mutant phenotype data on a genome-wide scale to generate a comprehensive network of genetically defined gene functional classifications. We use this system to measure the growth phenotypes of 4710 yeast mutants under 21 experimental conditions. Then, using a combination of single-dimension analysis and biclustering algorithms, we group both condition-specific and highly pleiotropic genes by common phenotype profile. Results comparing these clusters to biological process classifications, synthetic lethal interactions, and protein complexes support the hypothesis that phenotype profiles generated by this high-throughput, unsupervised method can be used to discover genetically defined functional categories. By applying these phenotype classifications to the phenotype profiles of highly pleiotropic genes, we generate hypotheses about the number of functions carried out by these genes and the conditions under which they are required. We also use these data to make an initial estimate of the degree of pleiotropy in yeast, demonstrating that it is significantly higher than can be explained by random chance.

Results

Measuring mutant growth under 21 conditions

To facilitate the generation of large mutant phenotype profiles, we developed a simple, cost-effective method for measuring the growth of a comprehensive set of yeast mutants under a relatively large number of conditions. Our strategy uses commercial microarray software (GenePix, Axon Instruments) to derive spot size and intensity information from digital images of cells replica pinned on conventional agar plates. Data are processed and normalized using a series of freely available Perl and Visual Basic scripts (Supplementary information) that assign a growth value corresponding to no growth, slow growth, or full growth to each strain under each condition. To distinguish general slow growth from condition-specific growth defects, we normalize the growth values of each strain under an experimental condition by its value under the YPD control condition (Materials and methods). Using this system, we assayed the growth of the 4710 strain homozygous diploid yeast deletion set (Giaever et al, 2002) under 21 environmental conditions (Materials and methods) in duplicate, a total of >105 data points. The homozygous deletion set was chosen in an attempt to minimize the effects of unlinked mutations documented in the haploid deletion strains (Hughes et al, 2000b; Bianchi et al, 2001) that could confer unrelated phenotypes or suppress true phenotypes. Experimental conditions were selected to cover a variety of cellular processes that could be measured in the context of rich media, allowing the use of the same control condition and permitting the inclusion of auxotrophic mutants unable to grow on minimal media. Each measurement was performed twice and only phenotypes that were consistent between both replicates were studied further. Of the 4710 mutants screened, 767 displayed significant growth defects, with either a slow growth or no growth phenotype relative to the control, under at least one of the 21 conditions.

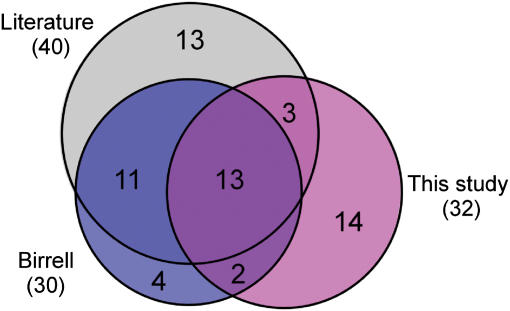
We assessed the accuracy of our results in two ways. First, we compared our data to published data sets generated using the homozygous diploid yeast deletion set that assayed similar experimental conditions by a competitive growth/Affymetrix bar-code hybridization method (Winzeler et al, 1999) (Supplementary information). Figure 1 shows a comparison with the results of Birrell et al (2001) in a screening of the same deletion collection for UV sensitivity. The comparison shows a high degree of overlap between our data, the Birrell et al results, and a set of UVS mutants described in the literature (Birrell et al, 2001). In the Birrell et al study, six of the UVS mutants not identified by our study were annotated as having mild UVS growth defects (Supplementary Table 1), consistent with the greater sensitivity proposed for the competitive growth assay (Winzeler et al, 1999). In contrast, our study identified three UV-sensitive mutants that the Birrell et al study failed to detect due to poor hybridization of the DNA barcodes to the Affymetrix chip (Supplementary Table 2), highlighting an advantage of the plate-based growth method. Neither our study nor the Birrell et al study detected UVS phenotypes for 13 mutants described in the literature (Supplementary Table 2), suggesting strain-dependent differences in phenotype or errors in the deletion set. Our study also identified an additional 14 UVS mutants not present in either set, including ctf4, rpb9, sgs1, and two genes of unknown function (Supplementary Table 4). To confirm the results of the high-throughput assay, we tested the UV sensitivity of each strain individually (Supplementary Figure 1). With the exception of one strain, cdc40, with growth defects too severe to permit a reliable assay, all strains showed a detectable UVs phenotype, including 10 strains that exhibited strong UV sensitivity. In addition, all strains, except mrpl3, contained the correct gene deletion as determined by PCR (Dutta, Dudley, and Church, unpublished results), a result that highlights errors that can be introduced as a result of tracking errors or contamination. We also assessed the accuracy of our data through a statistical analysis of experimental replicates (Supplementary Methods 1). From these estimations, we conclude that the probability of erroneously assigning a growth defect is 0.0037. Thus, growth defects observed in both replicates agree well with published results and are predicted to be highly accurate.

Figure 1. Comparison of UV-sensitive mutants identified in this study, published results from Birrell et al, and a set of UVS mutants collected from the literature.

Figure 1

Open in a new tab

The set of UVS mutants from this study only include those that showed UV sensitivity in both replicates. The inclusion of mutants that showed UV sensitivity in only one replicate in this study would increase the overlap with Birrell et al to 21 and the overlap with the literature to 23 mutants.

Grouping genes by common phenotype profile

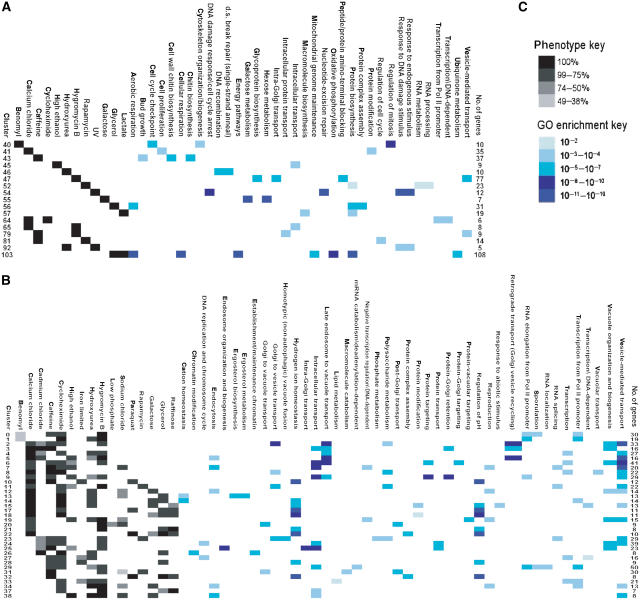
Analyses of RNA expression data (Golub et al, 1999; Hughes et al, 2000a; Ross et al, 2000; Segal et al, 2004), large-scale mutant phenotype data (Lum et al, 2004; Parsons et al, 2004), and large databases of clinical data for monogenic human diseases (Brunner and van Driel, 2004) have demonstrated that grouping genes based on their profiles across many conditions can be used to discover modules of genes with similar functions. To group our mutants by common phenotype profile, we first divided them into two classes. The first class, containing 551 mutants with growth defects in only one or two conditions, was clustered into 65 groups each encompassing a profile across all 21 conditions (Figure 2A). To group the remaining 216 highly pleiotropic genes with growth defects in 3–14 conditions (Figure 2B), we employed a biclustering algorithm (Materials and methods). Unlike the single-dimension clustering scheme used to group the low- pleiotropy mutants, biclustering methods (Cheng and Church, 2000; Getz et al, 2000; Segal et al, 2001; Tanay et al, 2002) use statistical parameters to select sets of genes that share common phenotypes across a subset of conditions in a profile. In this way, biclustering has the potential to reveal relationships that exist over only a subset of the data that may be obscured by clustering methods that rely on overall similarity metrics. Of the 216 highly pleiotropic mutants, 155 were grouped into at least one bicluster, with some belonging to more than one cluster.

Figure 2. Cluster profiles (gray scale) and GO functional category enrichment (blue scale).

Figure 2

Open in a new tab

For clusters derived from mutants with growth defects in (A) one or two conditions or (B) three or more conditions, the percentage of cluster members with a given growth defect, the P-values of enrichment in a given GO category, and the number of genes in each cluster are shown. (C) A key to the color code scheme is also shown. Only clusters with >4 members and significant enrichment in at least one GO category are presented. Only the conditions present in at least one of these clusters are shown. The full data set is available at our website (Supplementary information).

Phenotype profiles define functional classes

To test the hypothesis that grouping genes by common phenotype profile can be used to discover a set of genetically defined functional classes, we compared our results to independent data types. One method of determining the functional coherence of a group of genes is to measure the enrichment of independently derived functional categories (Tavazoie et al, 1999). We assessed the degree to which our clustering methods grouped genes of common function by testing the statistical significance of the overlap between our clusters and members of the Gene Ontology (GO) functional categories (Ashburner et al, 2000).

Phenotype profile clusters derived from the low-pleiotropy mutants showed statistically significant enrichment for a number of GO functional categories (Figure 2A). Some examples of well-characterized conditions and functions identified by this analysis include enrichment for galactose metabolism in the ‘galactose only' cluster (P=3.8 × 10−18), response to DNA damage in the ‘UV only' cluster (P=1.8 × 10−17), and cellular respiration in the glycerol and lactate cluster (P=2.1 × 10−18). For less well-characterized combinations of conditions, functional enrichment results offer insights into the manner in which the cell responds to these perturbations. Such results identified in this study include the enrichment transcription from RNA polymerase II (Pol II) promoters (P=6.7 × 10−4) in the calcium and cycloheximide cluster and enrichment of cell cycle regulation (P=1.2 × 10−3) in the caffeine and rapamycin cluster. Another set of clusters that offers potential for the discovery of new cellular functions is the set of clusters with no significant enrichment for any of the GO functional categories (Supplementary Figure 2). An interesting example is the cluster defined by a ‘cycloheximide only' phenotype, which contains 25 genes including eight of unknown function.

Biclustering the set of highly pleiotropic genes produced groups with more complex phenotype profiles (Figure 2B), but with equally specific functional enrichments as the gene sets constructed from low-pleiotropy mutants. Consistent with recently published results (Parsons et al, 2004), many of the clusters that include conditions with drugs added to the media are enriched for Golgi, vacuole, and intracellular transport functions. In fact our entire set of highly pleiotropic genes is significantly enriched for genes annotated with a vacuolar organization and biogenesis in the GO database (P=7 × 10−19 by hypergeometric distribution). In addition to its role in intracellular protein transport and degradation, the yeast vacuole serves to maintain intracellular pH through the transport of hydrogen and other cations (Jones et al, 1997). Several biclusters were enriched for this function exclusively (Figure 2B and Supplementary Figure 3). Within the set of highly pleiotropic genes, we also identified clusters enriched for functions unrelated to the vacuole and intracellular transport. One large class involved functions related to transcription by RNA Pol II, with several clusters enriched for transcriptional categories exclusively (Figure 2B and Supplementary Figure 4). Other functional categories included sporulation, ergosterol biosynthesis, phosphate metabolism, and DNA replication. Thus, similar to the grouping of genes required for growth in only a single condition, our biclustering of highly pleitropic genes was able to provide further information about general responses such as multidrug resistance and identify more specific responses that may be obscured by these large, general effects.

The functional enrichment results (Figure 2 and Supplementary information) also support the hypothesis that additional functions can be discovered for a group of genes that share one phenotype, by further clustering these members with respect to their phenotype profiles across many conditions. For example, the combination of sensitivity to benomyl, cycloheximide, hydroxyurea, and hygromycin B in cluster 1 (Figure 2B) groups genes enriched for two functional categories, transcription from RNA Pol II promoters (P=1.6 × 10−5) and RNA elongation from Pol II promoters (P=2.7 × 10−5). In contrast, clusters derived from profiles containing any of these phenotypes individually (Figure 2A) show enrichment for categories distinct from those of cluster 1 and from each other: the ‘benomyl only' cluster is enriched for functions related to the mitotic cell cycle and microtubule organization; the ‘hydroxyurea only' cluster is enriched for functions related to DNA recombination and repair; the ‘hygromycin B only' cluster is enriched for functions related to Golgi and vesicle transport; and the ‘cycloheximide only' cluster does not show significant enrichment for any GO functional category. Thus, clustering mutants with a wide range of pleiotropies by phenotype profile successfully groups genes with common biological functions.

The fact that both condition-specific and highly pleiotropic genes can be grouped by common phenotype profiles into gene sets that show significant enrichment for known biological processes suggests that such a method can be used to identify such functional classes de novo. To test this hypothesis further, we compared the results of our phenotypic clustering to other genetic and biochemical methods of assessing common gene function. These include synthetic lethal interactions, membership within the same protein complex, and associations between members of different protein complexes.

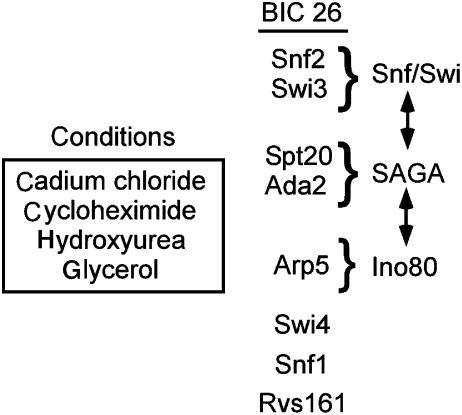
For example, bicluster 26 contains components of three large, multiprotein complexes, SAGA, Swi/Snf, and Ino80 (Figure 3). We hypothesized that these complexes, and more specifically these complex members, share functions required under the environmental conditions associated with bicluster 26 (cadmium, cycloheximide, hydroxyurea, and glycerol). This assertion is supported by several lines of genetic and biochemical evidence. First, these complexes are known to have similar biochemical activities, modifying chromatin structure to facilitate transcriptional activation. In addition, genetic data, including synthetic lethal interactions, have suggested common functions for several members of bicluster 26. Synthetic lethal interactions between SAGA components (including spt20) and Swi/Snf components (including snf2) were used to suggest common, parallel functions of those complexes (Roberts and Winston, 1997). Synthetic lethal interactions have also been reported between other members of cluster 26, including spt20–swi4 (Dror and Winston, unpublished results) and swi4–rsv161 (Tong et al, 2004). Thus, the common phenotype profile shared by members of bicluster 26 can be used to group together genes that share common functions as defined by other forms of genetic and biochemical evidence.

Figure 3. Information obtained from phenotypic profile clustering.

Figure 3

Open in a new tab

The members of bicluster 26, information about their protein complex membership, and the conditions used to assemble the bicluster are shown.

To compare our phenotypically defined functional classifications with other genetic and biochemical data in a more comprehensive manner, we examined our data in relation to protein complexes cataloged from the literature in the MIPS database (Mewes et al, 2004), complexes identified by TAP purification and mass spectrometry (Gavin et al, 2002), and synthetic lethal data available in the GRID database (Breitkreutz et al, 2003). Of the 266 complexes annotated in MIPS, 107 displayed a growth defect in at least one of our conditions, with 14 of these also containing synthetic lethal interactions between protein complex members. Similarly, 132 of the 232 protein complexes described by Gavin et al contained members with growth defects and 23 of these also contained members with synthetic lethal interactions. To visualize the results of this analysis, we graphed all genetic interactions (both membership in the same phenotypic cluster and synthetic lethality) observed within or between protein complex members (Materials and methods and Supplementary information).

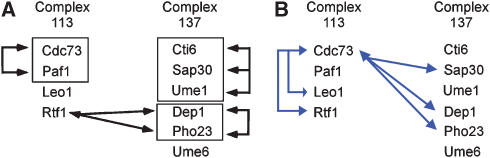
Figure 4A shows a sample result from this analysis, interactions defined using the common phenotype profile data for Gavin complex 113 (the Paf1/Cdc73 transcriptional elongation complex) and complex 137 (the Sap30 histone deacetylase complex). As expected, several members of the same complex, for example, Paf1 and Cdc73, have common phenotypic profiles, suggesting that these components share functions similar enough to produce a common effect across a large number of conditions. This analysis also highlights the fact that groups of proteins within a complex may belong to different phenotypic classes, for example, the Cti6–Sap30–Ume1 and Dep1–Pho23 groups, suggesting that the complexes also contain distinct groups of functions required under different sets of conditions. Interestingly, these results are complemented by synthetic lethal interactions (Figure 4B), which make distinct predictions about protein functions within and between complexes. For example, the cdc73–leo1 and cdc73–rtf1 synthetic lethal interactions support the hypothesis that Cdc73 has functions distinct from and parallel to those of Leo1 and Rtf1. In addition, cdc73 synthetic lethal interactions with members of the Sap30 complex, sap30, dep1, and pho23, suggest that components of these two complexes share common (parallel) functions. These results support the functional classes defined by phenotype cluster membership and underscore the value of both types of large-scale genetic analyses.

Figure 4. A comparison of the information derived from (A) phenotypic profile data and (B) synthetic lethal data.

Figure 4

Open in a new tab

Complex 113 (the PAF transcriptional complex) and 137 (the Sap30 histone deacetylase complex) were taken from the Gavin et al data set. Black arrows indicate genetic interactions derived from membership in the same phenotypic cluster; black boxes highlight these same interactions for members of the same complex. Blue arrows indicate synthetic lethal interactions between CDC73 and members of either complex. The figures include only the protein complex subunits that were members of a phenotype profile cluster.

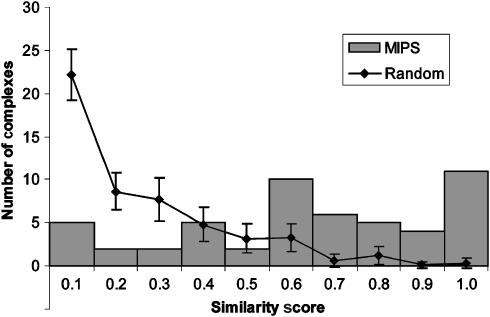
To assess the overlap between common phenotype and protein complex membership more quantitatively, we developed a simple measure of phenotype similarity between members of the same protein complex. Briefly, we measured the similarity of phenotypes by calculating the average distance between the phenotype profiles of all pairs of subunits within that complex (Materials and methods). Results for the 52 MIPS complexes with two or more members displaying phenotypes in our data set demonstrate that complexes span the range of similarity from homogeneous to heterogeneous, with two-thirds of the complexes scoring in the range of greater phenotype similarity (score >0.5) (Figure 5). These results are in sharp contrast to a randomly generated distribution, which is biased toward greater phenotypic heterogeneity. The fact that well-characterized multiprotein complexes contain members with a greater degree of phenotype similarity than would be predicted by chance provides evidence for the relationship between common phenotype and functional prediction at the level of protein–protein interaction. These results strengthen our assertion that phenotype profiles are suitable for use as functional classifier.

Figure 5. Phenotype similarity between members of the same protein complex.

Figure 5

Open in a new tab

Scores range from 0 (no phenotypes in common) to 1 (all phenotypes in common). Gray bars depict results for the 52 MIPS complexes in which two or more members with growth defects in at least one of the 21 conditions screened. The line depicts the averages and standard deviations of 1000 permutations of randomly generated complexes.

Classifying pleiotropic gene functions

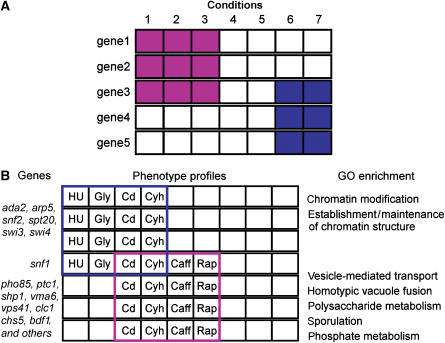
For a given pleiotropic gene, it is possible that all phenotypes observed result from the loss of a single function required under multiple conditions or that different sets of phenotypes result from the loss of separate functions, each required under different conditions. Conventional genetic analysis cannot distinguish between these two possibilities without identifying distinct mutant alleles that exhibit different subsets of phenotypes, demonstrating that the functions are genetically separable. Our phenotypically derived functional classes have the potential to provide such information from the analysis of a single mutant allele, such as the complete gene deletions examined in this study. In the theoretical example shown (Figure 6A), functional classes are assigned to each pleiotropic gene based on common phenotype profile. Genes belonging to a single profile cluster, for example, gene1, are hypothesized to carry out a single function under the conditions included in that profile, while genes with membership in multiple clusters, for example, gene3, are hypothesized to have multiple functions required under different subsets of conditions. Figure 6B shows an example from this study, the snf1 protein kinase mutant. In our data set, the snf1 mutant is assigned to two biclusters with partially overlapping sets of phenotypes. The hypothesis that these two biclusters define distinct functional classes is supported by the fact that these clusters contain different genes and are enriched for different GO functional categories (Figure 6B). Multiple functions of Snf1 are also consistent with information from the literature, demonstrating that the kinase can act interchangeably with any of three β-subunits (Sip1, Sip2, or Gal83) to target different substrates (Schmidt and McCartney, 2000) and has been implicated in a number of diverse cellular processes, including response to glucose depletion (Carlson, 1999), response to some genotoxic stresses (Dubacq et al, 2004), and regulation of filamentation and invasive growth (Cullen and Sprague, 2000; Kuchin et al, 2002). Our observations on the functions of pleiotropic genes may be validated and refined with direct experiments to enhance our understanding of important biological processes in yeast.

Figure 6. Using phenotype profiles to identify separable functions in pleiotropic genes.

Figure 6

Open in a new tab

(A) General principle. For a pleiotropic gene (gene3) with growth defects in five conditions (1–3, 6, and 7), it is possible to partition these phenotypes into two sets of functions (blue and purple) based on the results of biclustering. (B) SNF1 example. SNF1 belongs to two biclusters with the phenotypes (HU=hydroxyurea, Gly=glycerol, Cd=cadmium, Cyh=cycloheximide, Caff=caffeine, Rap=rapamycin) outlined in blue and purple. Subsets of the genes present and GO functional categories enriched in each bicluster are also listed.

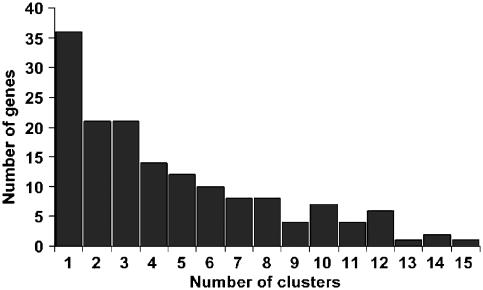
To examine the degree to which our functional classifications divided the phenotypes of pleiotropic genes into separate sets of phenotypes, we graphed the number of biclusters per gene (Figure 7). From this analysis, we find that 23% of the pleiotropic genes that could be assigned to a bicluster were assigned to only one functional classification, suggesting that all of the phenotypes associated with this mutant are associated with a single gene function. As more conditions are examined, it is possible that additional phenotypes will be added to this class of genes, producing one of two possible results. The addition of a new phenotype could divide the phenotypes assigned to a mutant into multiple functional categories by now assigning it to multiple biclusters. Alternatively, the gene may still remain in a single cluster defined by a larger number of phenotypes, suggesting a single functional classification. The remaining pleiotropic mutants were assigned between two and 15 functional classifications. The partial overlap between phenotypes associated with some of the biclusters (Figure 2B) has two possible implications for the genes assigned with more than one function. One possibility is that these sets of conditions do in fact define multiple functions that are each required under multiple conditions, for example, both functions proposed for SNF1 may be required for growth in cadmium and caffeine (Figure 6B). Alternatively, some of these significantly overlapping clusters, while passing the statistical criteria for distinct clusters, may be biologically redundant and therefore not sufficient to define separate biological functions. The use of additional information, such as the enrichment for distinct functional categories (Figure 6B), may help to distinguish between these two classes.

Figure 7. Distribution of the number of phenotypically defined functions (biclusters) assigned to the pleiotropic genes in this data set.

Figure 7

Open in a new tab

Estimating the degree of pleiotropy in yeast

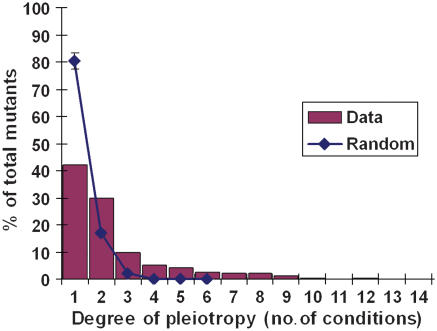
The availability of phenotype data generated under a large number of conditions also permits initial explorations of more global properties of the yeast genetic network, such as an estimation of the overall degree of pleiotropy in yeast. To assess the degree of pleiotropy in the set of 767 mutants that displayed a phenotype in at least one of our 21 conditions, we counted the number of phenotypes observed for each gene deletion. The results (Figure 8) show that most genes (∼70%) that display growth defects under these conditions have a relatively low degree of pleiotropy, with phenotypes in only one or two conditions. To test the statistical significance of this amount of pleiotropy, we generated a random distribution of phenotypes per gene such that the same properties of the original data set, that is, the same frequency of growth defects in each of the 21 conditions, were maintained (Materials and methods). This random distribution (Figure 8) was significantly different from the experimental distribution by Kolmogorov–Smirnov goodness-of-fit test (P=9 × 10−70), with double the percentage of genes assigned only a single phenotype and a maximum of six phenotypes per gene. Thus, the genes with phenotypes in this data set appear to have significantly more pleiotropy than would be predicted by chance.

Figure 8. Distribution of pleiotropy in our data and 1000 randomly generated sets.

Figure 8

Open in a new tab

Error bars represent ±1 standard deviation. These distributions are significantly different as assessed by the Kolmogorov–Smirnov test with a P-value of 9 × 10−70.

While the analysis based on the data collected in this study provides an initial estimate of the degree of pleiotropy in yeast, there are several other factors that could influence these results. One factor that could artificially inflate the difference observed between the experimental and random data sets is biological dependency between conditions. To address this issue, we repeated the analysis with a subset of conditions that are significantly different from each other, that is, conditions with relatively few genes in common, and found a similar difference between the experimental and random distributions (Supplementary Figures 5 and 6). Other factors that may affect our estimate for the degree of pleiotropy are limited coverage of the phenotype space and the reported aneuploidy and secondary mutations present in the mutant collection (Hughes et al, 2000b; Bianchi et al, 2001). We expect that as more phenotype data are generated, possibly with cleaner mutant libraries, our estimations may be revised.

Discussion

Large-scale mutant analyses provide a wealth of information about the effects of environmental stimuli on the cell. The experimental system employed in this study has several advantages over published methods that employ competitive growth followed by hybridization of labeled DNA to Affymetrix chips (Winzeler et al, 1999), which we hope will translate into an increased use of large-scale phenotype screens. First, the method is cost effective and, with the exception of the image analysis software, requires reagents and equipment available in most genetics/molecular biology laboratories. Also, because the method does not rely on molecular bar codes, it can be used with any set of strains and is not influenced by bar code hybridization efficiency or errors (Eason et al, 2004). In contrast, because our method relies on knowing the identity of each mutant at a given position in a grid, it is sensitive to tracking errors and contamination, which would not affect bar-coded strains to the same extent. Finally, although competitive growth assays may be better able to detect weaker phenotypes, independent growth assays are less affected by phenomena such as crossfeeding and are more easily translatable to growth rates across multiple experiments. Although this study used discrete measurements of growth obtained from single time points, the ease of the automated analysis would also facilitate higher resolution growth curves from the same agar plate-based system.

One difficulty encountered in the analysis of phenotypic profiles in yeast is the presence of a large number of highly pleiotropic genes (Parsons et al, 2004), which prevents many clustering algorithms from uncovering significant patterns that are biologically relevant (Dudley, Janse, and Church, unpublished results). We overcome this obstacle by employing a biclustering algorithm to focus on a subset of conditions determined by statistical significance. Such algorithms will be of even greater importance as data are generated for an increasing number of conditions. We have further extended the use of phenotype profiles by demonstrating that groups of phenotypes measured with high-throughput techniques and clustered by an unsupervised method can be used to define genetically new classes of in vivo functions. Interestingly, our results demonstrate that phenotypic classes provide information that is distinct from but complementary to complex mutant phenotypes, such as synthetic lethality, underscoring the importance of both methods.

In this study, we propose an additional use for these phenotypically defined functional categories, the classification of the phenotypes of highly pleiotropic genes. In addition to having the advantages of being a high-throughput and unsupervised method, our approach has the potential to accomplish a goal that cannot be achieved through conventional methods, determining the association between gene functions and mutant phenotypes based on a single mutant allele, such as a complete open reading frame (ORF) deletion. While extremely useful for analysis in yeast, such a method holds even greater promise for the analysis of pleiotropic genes in organisms that are less genetically tractable. For example, RNAi technology has been used to silence endogenous genes in worms, flies, and mammalian cell lines (Schutze, 2004), essentially accomplishing a gene knockdown akin to the gene deletions examined in this study. Large-scale analyses of phenotypes measured in such RNAi screens (Kiger et al, 2003; Boutros et al, 2004) or of naturally occurring monogenic disease alleles (Brunner and van Driel, 2004) hold the potential for discovering comparable functional classes for pleiotropic, human disease genes.

Pleiotropy, while frequently observed, is thought to pose evolutionary disadvantages for an organism, including limiting the rate of adaptation and reducing the level of adaptation for some traits in response to selection for others (Otto, 2004). Although our analysis of the overall amount of pleiotropy in yeast is a preliminary estimate, we believe that it will advance the study of genetic networks in two important ways. First, our observation of a greater degree of pleiotropy than can be explained by chance, even among the most dissimilar conditions tested, provides empirical evidence supporting the importance of pleiotropy in biological systems. As new data are added and the degree of pleiotropy is revised, it will be important to evaluate the relatedness of the environmental conditions examined. Because phenotypic pleiotropy implies that the phenotypes assessed are sufficiently different to be considered separate outcomes, results from highly related physiologic challenges, for example, UV sensitivity at different wavelengths, would not provide an accurate measure of pleiotropy. Second, our results provide an experimentally derived data set that may be used to inform and test predictions made by computational models of genetic networks and evolution that incorporate pleiotropy (for examples, see Wagner, 2000; Griswold and Whitlock, 2003).

Materials and methods

Large-scale phenotype measurement

Growth phenotypes of the 4710 strain homozygous diploid yeast deletion set (ResGen), containing precise ORF deletions for most nonessential genes in S. cerevisiae (Giaever et al, 2002), were measured under a control (YPD) and 21 experimental conditions. All conditions used rich media (YPD or YEP plus the indicated carbon source) (Rose et al, 1990). Unless noted, media are referenced in Hampsey (1997). Carbon source utilization conditions included 2% galactose/1 μg/ml antimycin A, 2% raffinose/1 μg/ml antimycin A, 3% glycerol, and 2% lactate. Nutrient-limiting conditions included low-phosphate YPD and iron-limited YPD (200 μM bathophenanthroline) (Askwith et al, 1996). General stress conditions included high ethanol concentrations (YPD+6% ethanol), low pH (pH 3.0), high salt (1.2 M sodium chloride), high sorbitol (1.2 M sorbitol), and oxidative stress (1 mM paraquat). Conditions associated with cellular functions included microtubule function (15 μg/ml benomyl), DNA replication/repair (100 J/m2 UV and 11.4 mg/ml hydroxyurea), transcriptional elongation (20 μg/ml mycophenolic acid) (Exinger and Lacroute, 1992), and protein synthesis (0.18 μg/ml cycloheximide and 0.1 μg/ml rapamycin) (Cardenas et al, 1999). Other conditions included divalent cations (0.7 M calcium chloride), heavy metals (55 μM cadmium chloride), aminoglycosides (50 μg/ml hygromycin B), and caffeine (2 mg/ml).

Yeast deletion strains were grown to saturation in liquid YPD in 96-well plates and transferred to 384-well plates using a BioMek FX (Beckman) liquid transfer robot. This rearraying step serves only to reduce the number of plates required per condition and can be accomplished without the use of a robot. Strains were then transferred to solid agar plates containing each of the 21 experimental media or YPD using a 384-well replica pin device. Following growth at 30°C, plates were digitally photographed using a GelDoc Station (Bio-Rad). Images were saved as eight-bit TIFF images and converted to 16-bit TIFFs for compatibility with the GenePix 4.0 Analysis Suite (Axon Instruments) using Adobe Photoshop. Images were then batch processed by GenePix, and data corresponding to the 384 spots per plate were saved as tab-delimited text files. Under the assumption that only a small number of strains per plate would deviate from wild-type levels, growth differences between plates and conditions were normalized by calculating the average diameter and intensity measurements of all spots on a plate. Spots differing from this average by empirically determined standard deviations were deemed slow growers or nongrowers (Supplementary information). To distinguish condition-specific growth defects from general slow growth, strain growth under each experimental condition was normalized to its growth on the YPD control plate. All conditions were tested in duplicate and only growth defects that replicated were used for further analysis. Additional information, including lower confidence results from growth defects in only one replicate, scripts, and digital plate images, is available at our website (Supplementary information).

Phenotype similarity in protein complexes

The phenotype profile of each member of a complex was represented as a vector, with each element assigned a ‘1' if the deletion strain did not grow on that particular condition, or a ‘0' if it did. The phenotype similarity between two members of the same complex was measured as the cosine of the angle between these phenotype vectors calculated according to the formula

graphic file with name msb4100004-i1.jpg

The average of these values for all pairwise combination is the phenotype similarity score, which ranges from 0 (no phenotypes in common) to 1 (identical phenotype profiles for all members). For comparison, the same calculations were repeated for 1000 randomly generated sets of complexes. The random sets preserved the overall structure of the experimental set, keeping constant the total number of complexes, subunits per complex, and the number of conditions showing no growth for each subunit. However, the identities of the conditions were permuted for all subunits over all complexes, thus generating random phenotype profiles. Differences between the experiment and randomly generated distributions were compared using the Kolmogorov–Smirnov test for goodness of fit (Sokal and Rohlf, 1995).

Randomized pleiotropy distribution analysis

To generate a random distribution for comparison with the degree of pleiotropy observed in our data set, we started with the experimental matrix of mutants × conditions. We then randomized the assignment of phenotypes in each condition, preserving the overall number of mutants with a phenotype in each condition, but randomizing any association between phenotypes (pleiotropy). An average pleiotropy distribution of 1000 such random sets was calculated. The observed frequencies from the experimental data were then compared against this expected distribution using the Kolmogorov–Smirnov test for goodness of fit (Sokal and Rohlf, 1995). Although initially developed for continuous data, the Kolmogorov–Smirnov test is also applicable to discrete data (Sokal and Rohlf, 1995).

Biclustering overview

To discover a comprehensive and nonredundant collection of genes with statistically significant combinations of growth defects within the set of highly pleiotropic mutants, we used a biclustering scheme designed to identify patterns that exist in only a subset of the data that may be obscured by clustering methods that rely on metrics measuring similarity across the entire profile. Here we present a general overview of our biclustering strategy written for the nonspecialist. The next section provides a more detailed description of the algorithm.

Given a matrix of mutants (genes) by conditions, the goal of biclustering is to order the rows and columns to find ‘dense' regions of the matrix, that is, groups of genes with growth defects in the same subset of conditions. The challenge in using such an approach lies in the fact that there are many possible submatrices, and thus many possible biclusters that may be highly redundant or not statistically significant. In this study, we adapted the SAMBA (statistical-algorithmic method for bicluster analysis) biclustering algorithm (Tanay et al, 2004) to exhaustively search the 216 gene × 21 condition matrix for all significant biclusters. In this method, we first used a branch and bound-like algorithm to find all high-scoring condition subsets (biclusters). The score of a bicluster is based on the probability of observing that bicluster against a random background model. These initial biclusters were then refined by finding genes that could be added or removed from the cluster to improve the score. For example, we could add genes that only dropped out in a subset of conditions defined in the bicluster, and remove genes that were highly pleiotropic and thus less statistically significant. Redundancies occurred when small biclusters were merely subsets of larger ones. We used a threshold-based redundancy filter to reduce the initial 280 biclusters to set of 40 nonredundant biclusters, choosing clusters with the largest condition sets such that each condition contributed significantly to the final score.

Biclustering algorithm

Assuming a binary matrix U of each gene's condition-specific sensitivities for a set of genes V and a set of conditions E, we define u ve =1 whenever the gene v is sensitive in the condition e. We denote by d v the number of conditions in which the gene v is sensitive and by d e the number of genes that are sensitive in the condition e and let N=Σ v d v =Σ e d e .

Our background probabilistic model assumes that all possible sensitivity matrices in which every gene v is sensitive in d v conditions and every condition has d e sensitive genes are equally likely. We define U rand as a random variable over that uniform distribution of matrices. A bicluster B=(E′,V′) is defined by a set of conditions E′={e 1 ,…,e l } and a set of genes (V′=v 1 ,…,v m ). We define

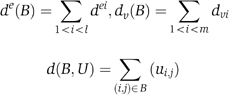
graphic file with name msb4100004-i2.jpg

Given a bicluster, we are interested in the probability of observing many sensitivities among its genes and conditions at random. This is formalized as Pr(d(B,U rand)⩾d(B,U)). In fact, this probability can be approximated as

graphic file with name msb4100004-i3.jpg

where h is the hypergeometric distribution. Expanded, it may be calculated as

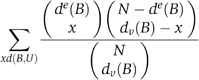
graphic file with name msb4100004-i4.jpg

The approximation is good whenever l or m is not too small. In what follows, we use Score(B)=−log(Pr(B)) as our bicluster scoring function.

Our exhaustive biclustering algorithm uses a branch and bound-like technique to find all condition subsets that induce a high-scoring bicluster. For each subset E′, we first compute the set V′ of genes that are sensitive in all the conditions in E′. The resulting bicluster (E′,V′) is called a complete bicluster and we compute its Score((E′,V′)). If the score does not exceed a given threshold T b , we disregard this bicluster. Furthermore, if the size of V′ is small, we can safely ignore all condition subsets that contain E′. This pruning procedure allows, in the typical data analyzed here, very rapid exhaustive analysis. For high-scoring, complete biclusters, we refine (E′,V′) by adding and removing genes to optimize the bicluster score. For example, we might remove a highly pleiotropic gene if the score of the bicluster without it exceeds the score of the original bicluster. Similarly, we may add genes that were not sensitive in just few of the bicluster's conditions. Our optimization terminates when additional score improvement is not possible.

The result of the exhaustive algorithm is a large collection of high-scoring biclusters, which may be highly redundant. We identified two types of redundancies. First, a bicluster defined by a set of conditions E′ and genes V′ may give rise to many other biclusters with additional conditions and smaller gene sets, even if the additional conditions are completely random (because the original bicluster is scoring highly). Conversely, subsets of E′ may induce gene sets that are very similar to V′. In this case, a better representation of the bicluster may be made from the larger conditions set.

Assuming that we are given two biclusters B 1=(E 1,V 1) and B 2=(E 2,V 2). We filter out redundancies by approximating the conditional probabilities:

graphic file with name msb4100004-i5.jpg

Assuming first that E 1=E 2+{e′} (one additional condition), we heuristically approximate P(B 1∣B 2), ignoring gene in degrees, as

graphic file with name msb4100004-i6.jpg

If, on the other hand, E 2=E 1+{e′}, we compute the probability of the bicluster built on the difference between V 1 and V 2:

graphic file with name msb4100004-i7.jpg

We say a bicluster B is dominated by a bicluster B′ if the approximated P(B∣B′) is larger than a threshold T r . To eliminate redundancies from our bicluster set, we mask out biclusters that have a dominating bicluster differing by exactly one condition (even if the dominating bicluster is itself masked out). This results in a set of biclusters that are significant with respect to our background model and to each other.

The implementation of our algorithm is efficient for a reasonable number of conditions (a few minutes on a standard desktop computer for our data set of 21 conditions). To gain statistical power, we used the genes that showed sensitivity in at least two conditions as the set V. For the matrix U, we set u ij to 1 only if the two replicates agreed the strain i was sensitive in the condition j. We used T b =5 and T r =1e−5. The algorithm discovered 280 biclusters with at least three conditions and reduced them to 40 nonredundant biclusters used in the subsequent biological analysis.

Functional enrichment

We annotated gene clusters sharing common phenotypic profiles using the SGD GO annotations (www.geneontology.org) and the standard hypergeometric functional enrichment test (Sokal and Rohlf, 1995). To correct for the extensive multiple testing resulting from testing enrichment on many different, yet highly dependent GO terms, we resampled random sets of genes that were the same size as our clusters and computed the maximum functional enrichment P-value for each GO term. In this way, we estimated the empirical probability of this maximum P-value and used it to determine a threshold for significant enrichment P-values on true clusters. Only results with P-values more significant than these thresholds are reported.

Genetic interactions of protein complexes

Protein complex data were taken from 232 complexes derived using a large-scale TAP tag purification and mass spectrometry identification (Gavin et al, 2002) and complexes cataloged in the MIPs database (Mewes et al, 2004). Synthetic lethal data were obtained from the yeast GRID database (Breitkreutz et al, 2003). Interactions between all protein complex pairs described above were examined, and only protein complexes with at least one subunit represented in a phenotype cluster profile were considered further. See Supplementary information for scripts, figures, and detailed methods.

Supplementary Material

Supplementary Figure 1

msb4100004-s1.pdf (168.7KB, pdf)

Supplementary Figure 2

msb4100004-s2.pdf (11.4KB, pdf)

Supplementary Figure 3

msb4100004-s3.pdf (16.7KB, pdf)

Supplementary Figure 4

msb4100004-s4.pdf (20.1KB, pdf)

Supplementary Figure 5

msb4100004-s5.pdf (49.9KB, pdf)

Supplementary Figure 6

msb4100004-s6.pdf (16.3KB, pdf)

Supplementary Figure 7

msb4100004-s7.pdf (45.3KB, pdf)

Supplementary Method

msb4100004-s8.pdf (19.6KB, pdf)

Supplemental Table 1

msb4100004-s9.pdf (16.7KB, pdf)

Supplemental Table 2

msb4100004-s10.pdf (15.9KB, pdf)

Supplemental Table 3

msb4100004-s11.pdf (14.7KB, pdf)

Supplemental Table 4

msb4100004-s12.pdf (13KB, pdf)

Acknowledgments

We thank John Aach, Barak Cohen, Daniel Segrè, and Fred Winston for valuable advice and helpful discussions; John Aach, Barak Cohen, and Dana Pe'er for critical reading of the manuscript; and Anupriya Dutta for technical assistance. AMD was supported by the Alexander Hollaender Distinguished Postdoctoral Fellowship Program (US Department of Energy) and the Genome Scholar/Faculty Transition Award (NIH/NHGRI). GMC was supported by the US Department of Energy, the Defense Advanced Research Projects Agency, and the PhRMA Foundation. AT was supported by a Horovitz fellowship. RS was supported by the Israel Science Foundation.

References

  1. Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G (2000) Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat Genet 25: 25–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Askwith CC, de Silva D, Kaplan J (1996) Molecular biology of iron acquisition in Saccharomyces cerevisiae . Mol Microbiol 20: 27–34 [DOI] [PubMed] [Google Scholar]
  3. Bianchi MM, Ngo S, Vandenbol M, Sartori G, Morlupi A, Ricci C, Stefani S, Morlino GB, Hilger F, Carignani G, Slonimski PP, Frontali L (2001) Large-scale phenotypic analysis reveals identical contributions to cell functions of known and unknown yeast genes. Yeast 18: 1397–1412 [DOI] [PubMed] [Google Scholar]
  4. Birrell GW, Giaever G, Chu AM, Davis RW, Brown JM (2001) A genome-wide screen in Saccharomyces cerevisiae for genes affecting UV radiation sensitivity. Proc Natl Acad Sci USA 98: 12608–12613 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Boutros M, Kiger AA, Armknecht S, Kerr K, Hild M, Koch B, Haas SA, Consortium HF, Paro R, Perrimon N (2004) Genome-wide RNAi analysis of growth and viability in Drosophila cells. Science 303: 832–835 [DOI] [PubMed] [Google Scholar]
  6. Breitkreutz BJ, Stark C, Tyers M (2003) The GRID: the general repository for interaction datasets. Genome Biol 4: R23 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brunner HG, van Driel MA (2004) From syndrome families to functional genomics. Nat Rev Genet 5: 545–551 [DOI] [PubMed] [Google Scholar]
  8. Cardenas ME, Cutler NS, Lorenz MC, Di Como CJ, Heitman J (1999) The TOR signaling cascade regulates gene expression in response to nutrients. Genes Dev 13: 3271–3279 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Carlson M (1999) Glucose repression in yeast. Curr Opin Microbiol 2: 202–207 [DOI] [PubMed] [Google Scholar]
  10. Cheng Y, Church GM (2000) Biclustering of expression data. Proc Int Conf Intell Syst Mol Biol 8: 93–103 [PubMed] [Google Scholar]
  11. Cullen PJ, Sprague GF Jr (2000) Glucose depletion causes haploid invasive growth in yeast. Proc Natl Acad Sci USA 97: 13619–13624 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dubacq C, Chevalier A, Mann C (2004) The protein kinase Snf1 is required for tolerance to the ribonucleotide reductase inhibitor hydroxyurea. Mol Cell Biol 24: 2560–2572 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Eason RG, Pourmand N, Tongprasit W, Herman ZS, Anthony K, Jejelowo O, Davis RW, Stolc V (2004) Characterization of synthetic DNA bar codes in Saccharomyces cerevisiae gene-deletion strains. Proc Natl Acad Sci USA 101: 11046–11051 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Everitt BS, Landau S, Lesse M (2001) Cluster Analysis. New York, NY: Oxford University Press Inc. [Google Scholar]
  15. Exinger F, Lacroute F (1992) 6-Azauracil inhibition of GTP biosynthesis in Saccharomyces cerevisiae . Curr Genet 22: 9–11 [DOI] [PubMed] [Google Scholar]
  16. Gavin AC, Bosche M, Krause R, Grandi P, Marzioch M, Bauer A, Schultz J, Rick JM, Michon AM, Cruciat CM, Remor M, Hofert C, Schelder M, Brajenovic M, Ruffner H, Merino A, Klein K, Hudak M, Dickson D, Rudi T, Gnau V, Bauch A, Bastuck S, Huhse B, Leutwein C, Heurtier MA, Copley RR, Edelmann A, Querfurth E, Rybin V, Drewes G, Raida M, Bouwmeester T, Bork P, Seraphin B, Kuster B, Neubauer G, Superti-Furga G (2002) Functional organization of the yeast proteome by systematic analysis of protein complexes. Nature 415: 141–147 [DOI] [PubMed] [Google Scholar]
  17. Getz G, Levine E, Domany E (2000) Coupled two-way clustering analysis of gene microarray data. Proc Natl Acad Sci USA 97: 12079–12084 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Giaever G, Chu AM, Ni L, Connelly C, Riles L, Veronneau S, Dow S, Lucau-Danila A, Anderson K, Andre B, Arkin AP, Astromoff A, El-Bakkoury M, Bangham R, Benito R, Brachat S, Campanaro S, Curtiss M, Davis K, Deutschbauer A, Entian KD, Flaherty P, Foury F, Garfinkel DJ, Gerstein M, Gotte D, Guldener U, Hegemann JH, Hempel S, Herman Z, Jaramillo DF, Kelly DE, Kelly SL, Kotter P, LaBonte D, Lamb DC, Lan N, Liang H, Liao H, Liu L, Luo C, Lussier M, Mao R, Menard P, Ooi SL, Revuelta JL, Roberts CJ, Rose M, Ross-Macdonald P, Scherens B, Schimmack G, Shafer B, Shoemaker DD, Sookhai-Mahadeo S, Storms RK, Strathern JN, Valle G, Voet M, Volckaert G, Wang CY, Ward TR, Wilhelmy J, Winzeler EA, Yang Y, Yen G, Youngman E, Yu K, Bussey H, Boeke JD, Snyder M, Philippsen P, Davis RW, Johnston M (2002) Functional profiling of the Saccharomyces cerevisiae genome. Nature 418: 387–391 [DOI] [PubMed] [Google Scholar]
  19. Giaever G, Flaherty P, Kumm J, Proctor M, Nislow C, Jaramillo DF, Chu AM, Jordan MI, Arkin AP, Davis RW (2004) Chemogenomic profiling: identifying the functional interactions of small molecules in yeast. Proc Natl Acad Sci USA 101: 793–798 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, Bloomfield CD, Lander ES (1999) Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286: 531–537 [DOI] [PubMed] [Google Scholar]
  21. Griswold CK, Whitlock MC (2003) The genetics of adaptation: the roles of pleiotropy, stabilizing selection and drift in shaping the distribution of bidirectional fixed mutational effects. Genetics 165: 2181–2192 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hampsey M (1997) A review of phenotypes in Saccharomyces cerevisiae . Yeast 13: 1099–1133 [DOI] [PubMed] [Google Scholar]
  23. Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, Kidd MJ, King AM, Meyer MR, Slade D, Lum PY, Stepaniants SB, Shoemaker DD, Gachotte D, Chakraburtty K, Simon J, Bard M, Friend SH (2000a) Functional discovery via a compendium of expression profiles. Cell 102: 109–126 [DOI] [PubMed] [Google Scholar]
  24. Hughes TR, Roberts CJ, Dai H, Jones AR, Meyer MR, Slade D, Burchard J, Dow S, Ward TR, Kidd MJ, Friend SH, Marton MJ (2000b) Widespread aneuploidy revealed by DNA microarray expression profiling. Nat Genet 25: 333–337 [DOI] [PubMed] [Google Scholar]
  25. Jones EW, Webb GC, Hiller MA (1997) Biogenesis and function of the yeast vacuole. In Molecular Biology of the Yeast Saccharomyces, Pringle JR, Broach JR, Jones EW (eds) Vol. III, pp 363–469. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press [Google Scholar]
  26. Kiger AA, Baum B, Jones S, Jones MR, Coulson A, Echeverri C, Perrimon N (2003) A functional genomic analysis of cell morphology using RNA interference. J Biol 2: 27 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kuchin S, Vyas VK, Carlson M (2002) Snf1 protein kinase and the repressors Nrg1 and Nrg2 regulate FLO11, haploid invasive growth, and diploid pseudohyphal differentiation. Mol Cell Biol 22: 3994–4000 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lum PY, Armour CD, Stepaniants SB, Cavet G, Wolf MK, Butler JS, Hinshaw JC, Garnier P, Prestwich GD, Leonardson A, Garrett-Engele P, Rush CM, Bard M, Schimmack G, Phillips JW, Roberts CJ, Shoemaker DD (2004) Discovering modes of action for therapeutic compounds using a genome-wide screen of yeast heterozygotes. Cell 116: 121–137 [DOI] [PubMed] [Google Scholar]
  29. Mewes HW, Amid C, Arnold R, Frishman D, Guldener U, Mannhaupt G, Munsterkotter M, Pagel P, Strack N, Stumpflen V, Warfsmann J, Ruepp A (2004) MIPS: analysis and annotation of proteins from whole genomes. Nucleic Acids Res 32 (Database issue): D41–D44 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Otto SP (2004) Two steps forward, one step back: the pleiotropic effects of favoured alleles. Proc R Soc London B 271: 705–714 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Parsons AB, Brost RL, Ding H, Li Z, Zhang C, Sheikh B, Brown GW, Kane PM, Hughes TR, Boone C (2004) Integration of chemical–genetic and genetic interaction data links bioactive compounds to cellular target pathways. Nat Biotechnol 22: 62–69 [DOI] [PubMed] [Google Scholar]
  32. Roberts SM, Winston F (1997) Essential functional interactions of SAGA, a Saccharomyces cerevisiae complex of Spt, Ada, and Gcn5 proteins, with the Snf/Swi and Srb/mediator complexes. Genetics 147: 451–465 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rose MD, Winston F, Hieter P (1990) Methods in Yeast Genetics: A Laboratory Course Manual. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press [Google Scholar]
  34. Ross DT, Scherf U, Eisen MB, Perou CM, Rees C, Spellman P, Iyer V, Jeffrey SS, Van de Rijn M, Waltham M, Pergamenschikov A, Lee JC, Lashkari D, Shalon D, Myers TG, Weinstein JN, Botstein D, Brown PO (2000) Systematic variation in gene expression patterns in human cancer cell lines. Nat Genet 24: 227–235 [DOI] [PubMed] [Google Scholar]
  35. Schmidt MC, McCartney RR (2000) beta-subunits of Snf1 kinase are required for kinase function and substrate definition. EMBO J 19: 4936–4943 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Schutze N (2004) siRNA technology. Mol Cell Endocrinol 213: 115–119 [DOI] [PubMed] [Google Scholar]
  37. Segal E, Friedman N, Koller D, Regev A (2004) A module map showing conditional activity of expression modules in cancer. Nat Genet 36: 1090–1098 [DOI] [PubMed] [Google Scholar]
  38. Segal E, Taskar B, Gasch A, Friedman N, Koller D (2001) Rich probabilistic models for gene expression. Bioinformatics 17 (Suppl 1): S243–S252 [DOI] [PubMed] [Google Scholar]
  39. Sokal RR, Rohlf FJ (1995) Biometry: The Principles and Practices of Statistics in Biological Research. New York: WH Freeman and Company [Google Scholar]
  40. Tanay A, Sharan R, Kupiec M, Shamir R (2004) Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data. Proc Natl Acad Sci USA 101: 2981–2986 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Tanay A, Sharan R, Shamir R (2002) Discovering statistically significant biclusters in gene expression data. Bioinformatics 18 (Suppl 1): S136–S144 [DOI] [PubMed] [Google Scholar]
  42. Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM (1999) Systematic determination of genetic network architecture. Nat Genet 22: 281–285 [DOI] [PubMed] [Google Scholar]
  43. Tong AH, Evangelista M, Parsons AB, Xu H, Bader GD, Page N, Robinson M, Raghibizadeh S, Hogue CW, Bussey H, Andrews B, Tyers M, Boone C (2001) Systematic genetic analysis with ordered arrays of yeast deletion mutants. Science 294: 2364–2368 [DOI] [PubMed] [Google Scholar]
  44. Tong AH, Lesage G, Bader GD, Ding H, Xu H, Xin X, Young J, Berriz GF, Brost RL, Chang M, Chen Y, Cheng X, Chua G, Friesen H, Goldberg DS, Haynes J, Humphries C, He G, Hussein S, Ke L, Krogan N, Li Z, Levinson JN, Lu H, Menard P, Munyana C, Parsons AB, Ryan O, Tonikian R, Roberts T, Sdicu AM, Shapiro J, Sheikh B, Suter B, Wong SL, Zhang LV, Zhu H, Burd CG, Munro S, Sander C, Rine J, Greenblatt J, Peter M, Bretscher A, Bell G, Roth FP, Brown GW, Andrews B, Bussey H, Boone C (2004) Global mapping of the yeast genetic interaction network. Science 303: 808–813 [DOI] [PubMed] [Google Scholar]
  45. Wagner A (2000) The role of population size, pleiotropy and fitness effects of mutations in the evolution of overlapping gene functions. Genetics 154: 1389–1401 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Winzeler EA, Shoemaker DD, Astromoff A, Liang H, Anderson K, Andre B, Bangham R, Benito R, Boeke JD, Bussey H, Chu AM, Connelly C, Davis K, Dietrich F, Dow SW, Bakkoury ME, Foury F, Friend SH, Gentalen E, Giaever G, Hegemann JH, Jones T, Laub M, Liao H, Liebundguth N, Lockhart DJ, Lucau-Danila A, Lussier M, M'Rabet N, Menard P, Mittmann M, Pai C, Rebischung C, Revuelta JL, Riles L, Roberts CJ, Ross-MacDonald P, Scherens B, Snyder M, Sookhai-Mahadeo S, Storms RK, Véronneau S, Voet M, Volckaert G, Ward TR, Wysocki R, Yen GS, Yu K, Zimmermann K, Philippsen P, Johnston M, Davis RW (1999) Functional characterization of the S- cerevisiae genome by gene deletion and parallel analysis. Science 285: 901–906 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure 1

msb4100004-s1.pdf (168.7KB, pdf)

Supplementary Figure 2

msb4100004-s2.pdf (11.4KB, pdf)

Supplementary Figure 3

msb4100004-s3.pdf (16.7KB, pdf)

Supplementary Figure 4

msb4100004-s4.pdf (20.1KB, pdf)

Supplementary Figure 5

msb4100004-s5.pdf (49.9KB, pdf)

Supplementary Figure 6

msb4100004-s6.pdf (16.3KB, pdf)

Supplementary Figure 7

msb4100004-s7.pdf (45.3KB, pdf)

Supplementary Method

msb4100004-s8.pdf (19.6KB, pdf)

Supplemental Table 1

msb4100004-s9.pdf (16.7KB, pdf)

Supplemental Table 2

msb4100004-s10.pdf (15.9KB, pdf)

Supplemental Table 3

msb4100004-s11.pdf (14.7KB, pdf)

Supplemental Table 4

msb4100004-s12.pdf (13KB, pdf)

Articles from Molecular Systems Biology are provided here courtesy of Nature Publishing Group

RESOURCES