Form follows function: the architecture of complex networks

The architectural tourist coming to Chicago for only a few days will have a hard time planning her visit. In any case, she is unlikely to skip such masterpieces as the Carson, Pirie, Scott and Co. building, by Louis Sullivan, or the SR Crown Hall, in the campus of the Illinois Institute of Technology, by Ludwig Mies van der Rohe. The philosophy of both architects revolved around the premise ‘form follows function,' which became a mantra for numerous other leading architects and industrial designers during a good part of the last century. In biology, evolution operates according to a similar premise because the form that provides better functionality is likely to be selected. With the advent of high-throughput technologies in molecular biology, such an observation has regained relevance. While data sets continue to grow and systems-level molecular information becomes available for more and more organisms, the hope is that we can obtain greater insight into cellular processes by analysing the architecture of complex biochemical networks (Wagner, 2005).

In a recent article, Ohtsuki et al (2006) discuss an interesting example of the interplay between form and function in complex evolutionary systems. Understanding how altruistic attitudes can be maintained in selective social and biological environments is a long-standing puzzle. Altruists are individuals that pay an evolutionary price to provide an evolutionary benefit to others; defectors do not pay any price and do not provide any benefits. In a perfectly mixed unstructured world, where every individual is equally likely to interact with every other individual, defectors are more fit because they benefit from altruists without paying any price. The fate of altruists is thus extinction, even though a world made of altruists is globally better than a world made of defectors.

But what happens if individuals do not live in a perfectly mixed world? This is the question that Ohtsuki and colleagues address, and their answer is remarkably simple and powerful: evolution will favour altruists provided that the average number of interactions per individual is small enough. In other words, they prove analytically that if a system is to sustain cooperation, then the average connectivity of individuals must be small enough: form must follow function. Other recent results provide further evidence of the intimate relationship between network architecture and evolutionary dynamics (Eguíluz et al, 2005; Lieberman et al, 2005).

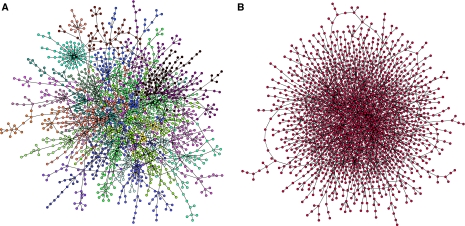
The implications of this relationship are far reaching. If form follows function, then we should be able to infer systems function and evolution, as well as their interplay, from the architecture of complex biochemical networks. But one needs to be extremely careful when drawing conclusions. Consider, for example, the network of physical interactions between proteins in yeast (Figure 1A), and ask what can we learn from the amount of interactions between hub proteins, that is, proteins with many interactions.

Figure 1.

Using the appropriate null model. (A) Network of protein interactions in yeast. (B) Randomization of the network of protein interactions in yeast. The randomization provides the appropriate null model to study the relationship between form and function in the real network. In the null model, hub proteins are more connected to each other than in the real network. Additionally, the randomization lacks the modular structure of the real network (represented by different colours in panel A).

Colliza et al (2006) have recently addressed this problem. Indeed, hub proteins do have many interactions with each other: whereas only 0.2% of all possible protein interactions in yeast are observed experimentally, this fraction goes up to about 40% if one considers only hub proteins. However, as Colizza and colleagues point out, there is little to be learned from this result. After all, any protein is more likely to interact with a hub protein than with the average protein, which has only six interactions. A sociological analogy helps illustrate the point: discovering that hub proteins have many interactions with each other is equivalent to discovering that two persons with many friends are more likely to be friends of each other than two persons with very few friends or, for that matter, with no friends at all; definitely, not much to be excited about.

Rather, if we are to learn anything about cellular behaviour, functional needs and evolution, the relevant question is not how many interactions hub proteins have with each other, but whether they have more or less interactions with each other than expected from chance alone. The solution suggested by Colizza et al is to compare the actual number of interactions between hub proteins to the number of interactions expected when all the structure of the interaction network is eliminated, but keeping the number of interactions of each protein intact (Figure 1B). In short, an appropriate null model is necessary before any conclusions can be drawn. Surprisingly, they find that hub proteins interact with each other less than expected. This is an important finding, which points to the need to investigate whether there are physical restrictions for hub proteins to interact with each other, or whether there is an evolutionary advantage for them not to interact.

The need to determine appropriate null models before jumping to conclusions is not restricted to the analysis of hubs in complex networks. The same caution is necessary, for example, when studying one of the most important properties of complex biochemical networks: their modular structure (Guimerà et al, 2004; Guimerà and Amaral, 2005). Most biochemical networks are organized into modules, regions with a high density of interactions; think, for example, of pathways within the metabolism. The problem is that, owing to fluctuations, even structure-less networks have sub-networks with a higher density of interactions than the network as a whole (Guimerà et al, 2004). The relevant question is, therefore, whether a given network has a significantly modular structure. The fact that all biochemical networks are significantly modular suggests the existence of evolutionary mechanisms responsible for modularity.

Which are these mechanisms? Why do hub proteins interact with each other less than expected? What is the interplay between form and function in biochemical networks? These are important questions that we need to answer.