Abstract
A classic example of ecophysiological adaptation is the observation that animals from hot arid environments have lower basal metabolic rates (BMRs, ml O2 min−1) than those from non-arid (luxuriant) ones. However, the term ‘arid’ conceals within it a multitude of characteristics including extreme ambient temperatures (Ta, °C) and low annual net primary productivities (NPPs, g C m−2), both of which have been shown to correlate with BMR. To assess the relationship between environmental characteristics and metabolic rate in birds, we collated BMR measurements for 92 populations representing 90 wild-caught species and examined the relationships between BMR and NPP, Ta, annual temperature range (Tr), precipitation and intra-annual coefficient of variation of precipitation (PCV). Using conventional non-phylogenetic and phylogenetic generalized least-squares approaches, we found no support for a relationship between BMR and NPP, despite including species captured throughout the world in environments spanning a 35-fold range in NPP. Instead, BMR was negatively associated with Ta and Tr, and positively associated with PCV.
Keywords: allometry, temperature, basal metabolic rate, productivity, precipitation, aridity
1. Introduction
Basal metabolic rate (BMR, measured by indirect calorimetry as ml O2 min−1) represents a significant component of animal energy budgets (Speakman 2000), and is correlated with a range of ecological, physiological and life-history variables, as well as phylogeny (e.g. McNab 2002; Blomberg et al. 2003; White & Seymour 2004; Lovegrove 2005). However, even after accounting for the effects of body mass (e.g. McKechnie & Wolf 2004a), considerable interspecific variation remains, and understanding the causes and consequences of this variation is key to understanding how animals function in the wild and the limits that are set on their physiological performance.
A classic adaptive explanation for variation in BMR derives from the observation that species from hot arid environments have lower BMRs than species from non-arid environments (McNab & Morrison 1963; Lovegrove 2000; Tieleman & Williams 2000; White 2003; Withers et al. 2006). This is postulated to result from the need to reduce (i) the rates of endogenous heat production in hot environments where evaporative water loss is restricted by water scarcity (McNab & Morrison 1963), and (ii) the food requirements and energy expenditure in environments where resources are sparse and widely distributed (Lovegrove 1986). Complementary to this, the high BMRs of species from temperate and polar latitudes (Weathers 1977; Ellis 1984) are associated with high maximal rates of thermogenesis and increased cold tolerance (Dutenhoffer & Swanson 1996; Swanson & Liknes 2006).
A link between low environmental productivity and animal metabolism in arid environments is intuitively appealing. However, a simple dichotomous distinction between hot- and non-arid environments conceals a suite of biotic and abiotic characteristics, any or all of which could account for the observation of lower BMRs with increasing aridity. Characteristics of hot arid environments include low primary productivity, low and temporally unpredictable precipitation, extreme ambient temperatures and high potential evapotranspiration, each of which has been shown to be related to BMR. For example, among birds, BMRs of falconiform species from hot climates are lower than those from colder climates (Wasser 1986), and the BMR of larks (Alaudidae) is negatively correlated with a continuous measure of aridity that incorporates ambient temperature and precipitation (Tieleman et al. 2003). Among mammals, BMR is positively correlated with net primary productivity (NPP) and rainfall, and negatively correlated with ambient temperature and rainfall variability (Mueller & Diamond 2001; Lovegrove 2003; Rezende et al. 2004; Withers et al. 2006).
The BMRs of birds from the wet tropics are also thought to be lower than those of temperate species (e.g. Hails 1983; Wikelski et al. 2003), but since wet tropical (luxuriant) environments are characterized by both high temperatures and high environmental productivities, a specific causal relationship between BMR, temperature and productivity has not been established. Previous studies have favoured single cause analyses, such as the classic arid–mesic dichotomy, and therefore failed to separate these variables as predictors (e.g. Tieleman & Williams 2000; White 2003). Other studies failed to include habitat productivity as a potential predictor of BMR (e.g. Lovegrove 2003; Withers et al. 2006), or they considered only a limited range of ambient temperature or environmental productivity (e.g. Mueller & Diamond 2001). It is therefore unclear which component of the ‘arid-luxuriant’ dimension (precipitation, ambient temperature, productivity or some combination) best accounts for broad-scale variation in metabolic rate. Here, we address this issue by examining the influence of NPP, precipitation, intra-annual variation in precipitation, mean annual ambient temperature and annual temperature range on BMR in wild birds captured at sites that span a broad range of these environmental parameters.
2. Material and methods
Body mass (M, g), BMR (ml O2 min−1) and source locality data for 149 populations (139 species) of wild-caught birds were compiled from the peer-reviewed literature. NPP (g C m−2) data (see below) were available for 93 of these populations (43 of the populations for which NPP data were unavailable represent only two locations), and data for Struthio camelus were excluded because the mass of this species (94.5 kg) is considerably greater than the remaining ones (range: 5.5–776 g). Thus, data for 92 populations (90 species) were included in the analysis (see electronic supplementary material). The dataset includes 61 sedentary species and 31 migratory or nomadic species captured at localities ranging from 43 °S to 66 °N. Data were accepted only if M, BMR and source locality data were provided in the same paper, individuals were captured as adults and BMR measurements were obtained under strictly defined conditions (McNab 1997; Frappell & Butler 2004; McKechnie & Wolf 2004a). Thus, all BMR and mass measurements were obtained for post-absorptive, adult, non-reproductive individuals in a thermoneutral environment during their inactive circadian phase. BMR measurements of 35 species were made within 24 h of capture, 11 species were measured within one week of capture and the remaining 46 species were measured after a longer period. BMR and mass were log-transformed for analysis.
Net primary productivity for the 0.5° longitude/latitude square in which each species was captured was obtained from www.pik-potsdam.de (Cramer et al. 1999). Habitat NPP values ranged from 32.4 to 1144 g C m−2. Ambient temperature (Ta, °C) and temperature range (Tr, °C) of capture sites were obtained at the same resolution from the Climate database v. 2.1 (W. Cramer, Potsdam, personal communication). Ta values were calculated by averaging mean monthly temperatures for January–December, and ranged from −0.8 to 27.0°C. Ta values were significantly correlated with latitude in the Northern (r=−0.92, n=71, p<0.0001) and Southern (r=−0.92, n=21, p<0.0001) Hemispheres, but not at low latitudes (less than 25°: r=−0.03, n=27, p>0.05) where Ta ranges from only 24 to 27°C. Across the globe, latitude is therefore not an ideal surrogate for Ta, despite demonstration of a significant relationship between latitude and BMR in other studies of environmental adaptation (e.g. Weathers 1979; Ellis 1984). Furthermore, since latitude integrates a range of variables (day length, seasonality, etc.), a priori hypotheses about the effect of latitude can only be generated with specific reference to these variables. Thus, because latitude cannot itself cause variation in BMR, but can only be a surrogate for the variable(s) that do, we elected not to include latitude as a potential correlate of BMR. Tr values ranged from 6.1 to 16.6°C and were calculated as the difference in mean monthly temperatures between the warmest and the coldest months. Precipitation (P, also downloaded from the Climate database) ranged between 0.4 and 272 mm month−1 and was log-transformed for analysis. Unfortunately, it was not possible to assess the relationship between inter-annual variation in precipitation and BMR because the Climate database does not provide annual estimates of precipitation. The intra-annual coefficient of variation of precipitation (PCV) was calculated by dividing mean monthly precipitation by the standard deviation of monthly precipitation, and ranged between 0.12 and 1.31. There was some multicollinearity between climate variables, in common with other studies (e.g. Withers et al. 2006). NPP was significantly correlated with log P (r=0.87, p<0.0001, Bonferroni corrected α=0.005), Ta (r=0.32, p=0.002) and Tr (r=−0.63, p<0.0001), and Tr was significantly correlated with log P (r=−0.68, p<0.0001). PCV was significantly correlated with log P (r=−0.56, p<0.0001), NPP (r=−0.63, p<0.0001) and Tr (r=0.49, p<0.0001). However, Ta was not correlated with log P (r=0.20, p=0.06) or Tr (r=0.01, p=0.93), and PCV was not correlated with Ta (r=0.23, p=0.03).
Data were analysed using both conventional and phylogenetically informed analyses. The method of phylogenetic generalized least squares (PGLS) was used to control for phylogenetic non-independence (Grafen 1989; Martins & Hansen 1997). This is necessary since metabolic rates for related species may not be statistically independent (e.g. Freckleton et al. 2002; Blomberg et al. 2003; Rezende et al. 2004). Such non-independence violates the assumption of standard statistics that errors are uncorrelated, and may result in biased parameter estimates and increased type I error rates if it is not taken into account (Harvey & Pagel 1991).
Phylogenetic generalized least squares explicitly incorporates the expected covariance among species into a statistical model fit by generalized least squares. The correlation between error terms is thus altered to reflect the degree of phylogenetic relatedness among species. PGLS can be shown to be exactly equivalent to the widely used method of independent contrasts for a completely resolved phylogeny and the assumption that traits evolve by a ‘Brownian motion’ model of evolution (Rohlf 2001). Under the assumption of Brownian motion, the expected trait covariance between any two species is directly proportional to the amount of shared evolutionary history, which equals the length of the branches connecting the root of the phylogenetic tree to their most recent common ancestor. If this assumption is incorrect (e.g. if closely related species are not more similar in traits than two randomly chosen species), then a statistical model incorporating phylogenetic information may not fit the data as well as a model assuming that traits evolved independently (phylogenetic independence).
However, the covariance matrix can be modified in PGLS to accommodate the degree to which trait evolution deviates from Brownian motion, using a measure of phylogenetic correlation, λ, derived by Pagel (1999; see also Freckleton et al. 2002). λ is a multiplier of the off-diagonal elements of the covariance matrix (i.e. those quantifying the degree of relatedness between species), with λ normally varying between 0 and 1. If the covariance matrix is constructed assuming a Brownian motion model of evolution, then λ=1 retains that model, while λ=0 specifies phylogenetic independence. Intermediate values of λ specify models in which trait evolution is phylogenetically correlated but to a lesser extent than expected under the Brownian motion model. The maximum-likelihood value of λ can be estimated by fitting PGLS models with different values of λ and finding the value that minimizes the log-likelihood. This best-fitting model can be used as a basis for inference (e.g. of the form of an allometric relationship), while the value of λ associated with it can be used as a metric of the degree of phylogenetic correlation in the data (Freckleton et al. 2002). The PGLS approach was implemented in R (Ihaka & Gentleman 1996) using the Analysis of Phylogenetics and Evolution package (Paradis et al. 2004) and code written by R. P. Duncan (for more details, see Halsey et al. 2006).
We assumed that the species in our dataset were related according to the phylogeny of Sibley & Ahlquist (1990), with genera assigned to higher taxa as described by Sibley & Monroe (1990). Since we do not know all the branch lengths in the phylogeny, we set all branches in the model to be equal. A copy of the phylogeny is available on request.
Burnham & Anderson's (2001) framework for model comparison was used to identify the most plausible model(s) of trait evolution based on the calculated value of Akaike's information criterion (AIC) as a measure of model fit (see also Burnham & Anderson 2002). AIC value was calculated as −2 times the log-likelihood of the model, +2 times the number of estimable parameters (Burnham & Anderson 2001). This addition penalizes superfluous parameters in the model, so that the best absolute model fit is not necessarily that with the highest AIC if some of the parameters explain little additional variance in the data (in the same way that adding additional parameters to a multiple regression always increases the r2, but not necessarily significantly so). The best out of all of the (evolutionary+statistical) models tested to explain BMR was that with the lowest AIC. The probability that any given model is actually the best fit out of those tested was measured by its Akaike weight (Burnham & Anderson 2001), the relative-likelihood of the model compared to all others (the likelihood of the model divided by the sum of the likelihoods of all other models).
Six different a priori statistical models for log BMR were initially tested and are listed in table 1. All these models include log body mass as a predictor, and the first model includes log mass alone (table 1). The next five models include each of NPP, Ta, Tr, log P and PCV as additional predictors. Many studies have shown that water availability and temperature together are important determinants of productivity and species richness (see review in Whittaker et al. 2003), and hence may also relate to variation in BMR. However, the number of possible models resulting from the various combinations of temperature and precipitation variables, plus their interaction terms, approaches the number of data points. To assess whether a model that combines the various environmental predictors of log BMR was a better fit to the data than any of the six models described above, we used a stepwise backwards elimination procedure to derive a minimum adequate model for log BMR from a full model that includes all the main predictor variables, plus interaction terms between the temperature and the rainfall variables. Variables were deleted from the models if their confidence intervals encompassed zero, starting with the variable with the widest confidence intervals. Main effects were not deleted if they were still present in an interaction term in the model. The simple and stepwise models were calculated both controlling for phylogenetic relatedness, and assuming all species are equally related (a conventional, non-phylogenetic analysis: λ=0).
Table 1.
Akaike's information criterion (AIC) values and Akaike weights (wi) for the 12 simple statistical and evolutionary models. (NPP, net primary productivity; Ta, ambient temperature; Tr, temperature range; P, log precipitation; PCV, coefficient of variation of precipitation; non-phylogenetic, conventional across species analysis; phylogenetic, GLS model incorporating information on phylogenetic relatedness, with equal branch lengths (see §2).)
| statistical model | evolutionary model | AIC | wi |
|---|---|---|---|
| log mass | non-phylogenetic | −120.7 | <0.001 |
| phylogenetic | −150.42 | <0.001 | |
| log mass+NPP | non-phylogenetic | −125.12 | <0.001 |
| phylogenetic | −149.68 | <0.001 | |
| log mass+Ta | non-phylogenetic | −137.32 | <0.001 |
| phylogenetic | −169.52 | 0.999 | |
| log mass+Tr | non-phylogenetic | −120.69 | <0.001 |
| phylogenetic | −150.2 | <0.001 | |
| log mass+P | non-phylogenetic | −121.67 | <0.001 |
| phylogenetic | −148.89 | <0.001 | |
| log mass+PCV | non-phylogenetic | −120.79 | <0.001 |
| phylogenetic | −148.53 | <0.001 |
It was not possible to calculate the average conditions experienced by migrant or nomadic species because latitude and longitude are not available for all locations occupied by the measured individuals, and this represents a potential limitation of the present analysis. As migrant or nomadic species are likely to be exposed to a range of environmental variables that may be poorly represented by the 0.5° latitude/longitude region in which they were captured, and owing to the probable acclimatization of captive birds to conditions not representative of the environments in which they were captured, the analysis was therefore repeated with these variables included. Mobility was coded as a binary variable (sedentary or migratory/nomadic); length of time in captivity was coded as overnight, up to a week or over a week.
3. Results
One of the simple models was found to be a better fit to the data, as judged by the model Akaike weights (wi), the probability that a model is the best out of all those compared (table 1). This best-fit model explained log BMR in terms of log M and Ta, controlling for phylogeny, with maximum-likelihood λ=1 and parameter estimates (±s.e.) for log M of 0.680±0.031 and for Ta of −0.007±0.002. The probability that this model is the best one of those listed in table 1, as judged by its Akaike weight, is 0.999 (table 1).
Table 2 shows the results of the stepwise elimination of variables from a full model. The resulting minimum adequate model is log BMR=log M+Ta+Tr+PCV, with positive parameter estimates for log M and PCV, and negative estimates for Ta and Tr. The minimum adequate model is the same whether or not the analysis is performed in a phylogenetic framework, and the parameter estimates for the best-fit non-phylogenetic model are similar to those for the best-fit phylogenetic one. Nevertheless, the likelihood ratio for these models (which can be considered nested with an extra parameter, λ, for the phylogenetic model) indicates that the phylogenetic model is the better fit to the data (χ12=11.8, p<0.001). The best simple model and the minimum adequate model both give allometric exponents for BMR that do not differ significantly from two-thirds, but do differ from three-quarters. The PGLS approach does not allow the calculation of coefficients of determination. However, for the non-phylogenetic analysis, r2=0.871 for the model log BMR=log M, r2=0.895 for the model log BMR=log M+Ta and r2=0.915 for the model log BMR=Ta+Tr+PCV. Thus, Ta alone accounts for 18% of the variation in mass-independent BMR (i.e. 18% of the variation not accounted for by mass), while Ta, Tr and PCV account for 34% of the variation in mass-independent BMR.
Table 2.
Parameters for the best-fit models for log BMR, as assessed by stepwise backwards elimination from a full model containing all the main effects and the interactions between temperature and precipitation variables. (For the phylogenetic model, λ=1 and AIC=−174.69. For the non-phylogenetic model, AIC=−153.07.)
| phylogenetic | non-phylogenetic | |||
|---|---|---|---|---|
| estimate | s.e. | estimate | s.e. | |
| intercept | −0.831 | 0.086 | −0.701 | 0.060 |
| log mass | 0.681 | 0.030 | 0.650 | 0.024 |
| Ta | −0.008 | 0.002 | −0.010 | 0.001 |
| Tr | −0.012 | 0.004 | −0.016 | 0.005 |
| PCV | 0.100 | 0.040 | 0.187 | 0.043 |
With mobility and time in captivity included in the full model, the stepwise elimination procedure still resulted in a best minimum adequate model that described BMR in terms of log mass, Ta, Tr and PCV. Adding movement and captivity variables increased the AIC value for the non-phylogenetic model over the value for the equivalent model without movement and captivity, and the regression estimates for the movement and captivity variables in the best model encompassed zero. For the phylogenetic model, movement and captivity lowered the model AIC value from −174.69 to −177.91, but the regression estimates for the movement and captivity variables in the best model again encompassed zero, and hence these variables were eliminated from the model by our stepwise procedure. Overall, neither mobility nor captivity duration alter the finding that the best model for BMR for the present sample of wild-caught species includes body mass, Ta, Tr and PCV.
4. Discussion
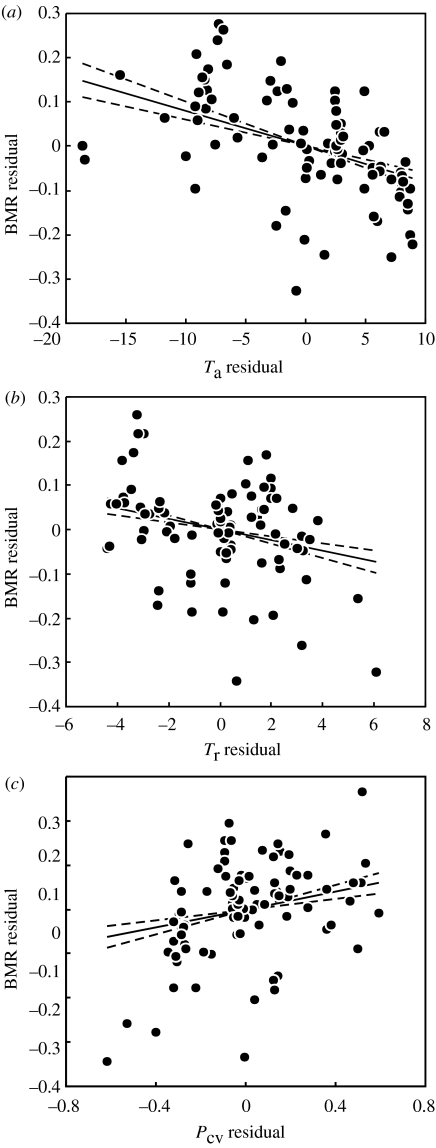
We set out to investigate the relationship between a range of environmental characteristics and BMR among birds. Our results show the following. (i) The models incorporating phylogeny are superior to non-phylogenetic models in fitting data on avian BMR (tables 1 and 2), and thus are to be preferred on statistical grounds. They are also to be preferred on biological grounds, as in all cases the maximum-likelihood value of phylogenetic correlation (λ) was 1, indicating strong phylogenetic correlation in these data. Nevertheless, phylogenetic and non-phylogenetic models produced essentially the same answers in the present study. (ii) BMR is strongly influenced by body mass. (iii) There is no support for including NPP as well as mass to model BMR (table 1). (iv) There is good support for including mean annual ambient temperature (Ta; figure 1a and table 1). (v) There is also support for including temperature range (Tr; figure 1b) and coefficient of variation in precipitation in a model that includes log mass and Ta (figure 1c and table 2).
Figure 1.
Relationship between BMR and (a) ambient temperature (Ta), (b) annual ambient temperature range (Tr) and (c) intra-annual coefficient of variation for precipitation (PCV). To remove the potential confounding effects of body mass and collinearity between environmental variables, residuals are presented. Residuals are calculated as the difference between measured and predicted values (i.e. BMR residuals in (a) are calculated as measured log BMR minus log BMR as predicted by log M, Tr and PCV; Ta residuals are calculated as Ta minus Ta as predicted by log M, Tr and PCV). Solid line is the phylogenetically correct and mass-independent correlation between BMR and the environmental variable, plotted through the bivariate mean and shown as ±1 s.e. of the coefficient from table 2 (dashed lines).
(a) Net primary productivity and basal metabolic rate
A priori, NPP would appear to be a good candidate for accounting for BMR variation. As NPP represents the rate of resource accumulation within an environment, it would seem reasonable to assume that the rate of resource demand (i.e. metabolic rate) would be matched to supply. Thus, it might be predicted that BMR and NPP among birds would be positively correlated, as has been demonstrated for Peromyscus mice (Mueller & Diamond 2001). However, across the range of five localities from which these Peromyscus species were sampled, NPP and Ta are highly correlated (r=−0.98, p=0.003; Ta values obtained as described in §2). Therefore, Ta could equally well explain the observed variation in BMR in that study. Indeed, in our analysis, models with Ta alone are more likely to provide the best fit to the data than models with NPP alone (table 1), despite a significant correlation between Ta and NPP (r=0.32, p=0.002). The relative weakness of NPP as a predictor of BMR among birds is not a consequence of a lack of variability in NPP, since NPP values in our data span a 35-fold range from 32.4 to 1144 g C m−2.
(b) Ambient temperature (Ta) and basal metabolic rate
The predominance of Ta in the simple models describing BMR in terms of mass and a single environmental variable (table 1) suggests that, after mass, avian BMR is most strongly related to Ta. Ta is also a significant predictor of avian BMR in a more complex model selected by stepwise backwards elimination from a full model containing all the main effects (log mass, NPP, Ta, Tr, log P and PCV) and the interactions between temperature and precipitation variables (table 2).
Although it is clear that Ta and BMR are negatively associated at both the population (Merola-Zwartjes & Ligon 2000; Broggi et al. 2004) and the species level (figure 1a), it remains to be determined whether BMR changes as a consequence of phenotypic acclimatization or genotypic adaptation to Ta. Many, but not all, birds increase BMR seasonally in apparent response to the low temperatures encountered during winter (Dawson et al. 1985; Cooper & Swanson 1994; Liknes et al. 2002) and in acclimation experiments (Williams & Tieleman 2000; Klaassen et al. 2004; McKechnie & Wolf 2004b), and phenotypic plasticity is a significant contributor to the scaling of avian BMR (McKechnie et al. 2006). Within species, geographically separate populations may differ in the degree of seasonal acclimatization (Dawson et al. 1983; O'Conner 1996), with acclimatization being more pronounced in populations from higher latitudes that show a greater seasonal temperature range (Weathers 1979). An increased BMR in cold conditions is associated with an increased thermogenic capacity and therefore cold tolerance (Dutenhoffer & Swanson 1996; Rezende et al. 2002; Swanson & Liknes 2006), but experimental acclimation studies are lacking for birds from low latitudes and it is not clear if the apparently limited acclimatization response of birds from the wet tropics is associated only with the narrow natural temperature range of those environments. In warm environments, where body temperature (Tb) must be defended against a temperature difference (Tb−Ta) that is smaller than in cold environments, reduced BMR reduces both energy expenditure and endogenous heat load (McNab & Morrison 1963). A reduction in endogenous heat load is advantageous, because evaporative cooling is often restricted either by water scarcity or high humidity in warm environments.
(c) Other environmental variables and basal metabolic rate
The negative association between BMR and Tr (figure 1b) suggests that birds from seasonally variable environments have low BMRs. This response is apparently different between mammals and birds. Lovegrove's (2003) slow–fast metabolic continuum model for mammals, for example, predicts low BMRs for species from environments with low seasonal fluctuations in day length and temperature, and high BMRs for species from seasonally variable environments. However, as noted by Rezende et al. (2004), Lovegrove (2003) identified significant correlations between BMR and both mean temperature and latitude (‘…which determined the magnitude of Ta fluctuations…’ (Lovegrove 2003, p. 94)), but did not report results of an analysis with both independent variables in the model. Our analysis shows that models incorporating all of Ta, Tr and PCV are superior to models including only one of these variables (table 2), so it is not clear if the apparent difference between birds and mammals is genuine, or if it arises as a consequence of different methods of analysis. Investigation of associations between environmental characteristics and BMR using a uniform approach for birds and mammals would establish which of these is the case.
Similarly, Withers et al. (2006) reported a negative correlation between marsupial BMR and PCV, whereas we find a positive relationship for birds (table 2 and figure 1c). Again, the reason for the difference between birds and mammals is unclear, but may also arise owing to different methods of analysis. Withers et al. (2006) suggested that the pattern of low BMR for marsupials in high PCV areas was related to reduced energy demands in areas with low and unpredictable primary productivity. However, we have shown that BMR is not related to NPP, at least in birds. A uniform approach to investigation of environmental correlates of BMR would establish the reason for the difference between birds and marsupials.
5. Conclusion
Our analysis of the relationship between avian BMR and environmental variables reveals a significant association between BMR and Ta, Tr and PCV, but not NPP. Thus, we can infer that the relatively low BMR of birds inhabiting hot arid environments arises as a consequence of generally high temperatures with seasonal extremes. In hot environments, low BMR presumably reduces endogenous heat load (McNab & Morrison 1963), and the low BMR of birds inhabiting luxuriant environments also arises as a consequence of the associated high temperatures.
Acknowledgments
We thank Lesley Alton, John Terblanche and three anonymous referees for providing comments about an earlier version of this manuscript, and Richard Duncan, Fritz Geiser, Jon Green, Lewis Halsey, Alex Kabat and Roger Seymour for helpful discussions. This work was supported by grant NER/A/2003/00542 from the Natural Environmental Research Council.
Supplementary Material
all of the data on which the analysis is based: Body mass (M, g), basal metabolic rate (BMR, ml O2 min-1), capture locality (latitude and longiture, °), habitat annual net primary productivity (NPP, g C m 2), mean monthly precipitation (P, mm), intra-annual coefficient of variation of precipitation (PCV), mean annual ambient temperature (Ta, °C), and annual temperature range (Tr, °C).
References
- Blomberg S.P, Garland T, Jr, Ives A.R. Testing for phylogenetic signal in comparative data: behavioral traits are more labile. Evolution. 2003;57:717–745. doi: 10.1111/j.0014-3820.2003.tb00285.x. doi:10.1554/0014-3820(2003)057[0717:TFPSIC]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- Broggi J, Orell M, Hohtola E, Nilson J.A. Metabolic response to temperature variation in the great tit: an interpopulation comparison. J. Anim. Ecol. 2004;73:967–972. doi:10.1111/j.0021-8790.2004.00872.x [Google Scholar]
- Burnham K.P, Anderson D.R. Kullback-Leibler information as a basis for strong inference in ecological studies. Wildlife Res. 2001;28:111–119. doi:10.1071/WR99107 [Google Scholar]
- Burnham K.P, Anderson D.R. Springer; New York, NY: 2002. Model selection and multimodel inference: a practical information-theoretic approach. [Google Scholar]
- Cooper S.J, Swanson D.L. Seasonal acclimatization of thermoregulation in the black-capped chickadee. Condor. 1994;96:638–646. [Google Scholar]
- Cramer W, Kicklighter D.W, Bondeau A, Moore B.I, Churkina G, Nemry B, Ruimy A, Schloss A.L. Comparing global models of net primary productivity (NPP): overview and key results. Global Change Biol. 1999;5(Suppl. 1):1–15. doi:10.1046/j.1365-2486.1999.00009.x [Google Scholar]
- Dawson W.R, Marsh R.L, Buttemer W.A, Carey C. Seasonal and geographic variation of cold resistance in house finches Carpodacus mexicanus. Physiol. Zool. 1983;56:353–369. [Google Scholar]
- Dawson W.R, Buttemer W.A, Carey C. A reexamination of the metabolic response of house finches to temperature. Condor. 1985;87:424–427. [Google Scholar]
- Dutenhoffer M.S, Swanson D.L. Relationship of basal to summit metabolic rate in passerine birds and the aerobic capacity model for the evolution of endothermy. Physiol. Zool. 1996;69:1232–1254. [Google Scholar]
- Ellis H.I. Energetics of free-ranging seabirds. In: Whittow G.C, Rahn H, editors. Seabird energetics. Plenum Press; New York, NY: 1984. [Google Scholar]
- Frappell P.B, Butler P.J. Minimal metabolic rate, what it is, its usefulness, and its relationship to the evolution of endothermy: a brief synopsis. Physiol. Biochem. Zool. 2004;77:865–868. doi: 10.1086/425191. doi:10.1086/425191 [DOI] [PubMed] [Google Scholar]
- Freckleton R.P, Harvey P.H, Pagel M. Phylogenetic analysis and comparative data: a test and review of evidence. Am. Nat. 2002;160:712–726. doi: 10.1086/343873. doi:10.1086/343873 [DOI] [PubMed] [Google Scholar]
- Grafen A. The phylogenetic regression. Phil. Trans. R. Soc. B. 1989;326:119–157. doi: 10.1098/rstb.1989.0106. [DOI] [PubMed] [Google Scholar]
- Hails C.J. The metabolic rate of tropical birds. Condor. 1983;85:61–65. [Google Scholar]
- Halsey L.G, Butler P.J, Blackburn T.M. A phylogenetic analysis of the allometry of diving. Am. Nat. 2006;167:276–287. doi: 10.1086/499439. doi:10.1086/499439 [DOI] [PubMed] [Google Scholar]
- Harvey P.H, Pagel M.D. Oxford series in ecology and evolution. Oxford University Press; New York, NY: 1991. The comparative method in evolutionary biology. [Google Scholar]
- Ihaka R, Gentleman R. R: a language for data analysis and graphics. J. Comput. Graph. Stat. 1996;5:299–314. doi:10.2307/1390807 [Google Scholar]
- Klaassen M, Oltrogge M, Trost L. Basal metabolic rate, food intake, and body mass in cold- and warm-acclimated Garden Warblers. Comp. Biochem. Physiol. A. 2004;137:639–647. doi: 10.1016/j.cbpb.2003.12.004. doi:10.1016/j.cbpb.2003.12.004 [DOI] [PubMed] [Google Scholar]
- Liknes E.T, Scott S.M, Swanson D.L. Seasonal acclimatization in the American Goldfinch revisited: to what extent do metabolic rates vary seasonally? Condor. 2002;104:548–557. doi:10.1650/0010-5422(2002)104[0548:SAITAG]2.0.CO;2 [Google Scholar]
- Lovegrove B.G. The metabolism of social subterranean rodents: adaptation to aridity. Oecologia. 1986;69:551–555. doi: 10.1007/BF00410361. doi:10.1007/BF00410361 [DOI] [PubMed] [Google Scholar]
- Lovegrove B.G. The zoogeography of mammalian basal metabolic rate. Am. Nat. 2000;156:201–219. doi: 10.1086/303383. doi:10.1086/303383 [DOI] [PubMed] [Google Scholar]
- Lovegrove B.G. The influence of climate on the basal metabolic rate of small mammals: a slow–fast metabolic continuum. J. Comp. Physiol. B. 2003;173:87–112. doi: 10.1007/s00360-002-0309-5. [DOI] [PubMed] [Google Scholar]
- Lovegrove B.G. Seasonal thermoregulation power in mammals. J. Comp. Physiol. B. 2005;175:234–247. doi: 10.1007/s00360-005-0477-1. doi:10.1007/s00360-005-0477-1 [DOI] [PubMed] [Google Scholar]
- Martins E.P, Hansen T.F. Phylogenies and the comparative method: a general approach to incorporating phylogenetic information into the analysis of interspecific data. Am. Nat. 1997;149:646–667. doi:10.1086/286013 [Google Scholar]
- McKechnie A.E, Wolf B.O. The allometry of avian basal metabolic rate: good predictions need good data. Physiol. Biochem. Zool. 2004;77:502–521. doi: 10.1086/383511. doi:10.1086/383511 [DOI] [PubMed] [Google Scholar]
- McKechnie A.E, Wolf B.O. Partitioning of evaporative water loss in white-winged doves: plasticity in response to short-term thermal acclimation. J. Exp. Biol. 2004b;207:203–210. doi: 10.1242/jeb.00757. doi:10.1242/jeb.00757 [DOI] [PubMed] [Google Scholar]
- McKechnie A.E, Freckleton R.P, Jetz W. Phenotypic plasticity in the scaling of avian basal metabolic rate. Proc. R. Soc. B. 2006;273:931–937. doi: 10.1098/rspb.2005.3415. doi:10.1098/rspb.2005.3415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNab B.K. On the utility of uniformity in the definition of basal rate of metabolism. Physiol. Zool. 1997;70:718–720. doi: 10.1086/515881. [DOI] [PubMed] [Google Scholar]
- McNab B.K. Comstock Cornell; Ithaca, NY: 2002. Physiological ecology of vertebrates. [Google Scholar]
- McNab B.K, Morrison P. Body temperature and metabolism in subspecies of Peromyscus from arid and mesic environments. Ecol. Monogr. 1963;33:63–82. doi:10.2307/1948477 [Google Scholar]
- Merola-Zwartjes M, Ligon J.D. Ecological energetics of the Puerto Rican tody: heterothermy, torpor, and intra-island variation. Ecology. 2000;81:990–1003. doi:10.2307/177173 [Google Scholar]
- Mueller P, Diamond J. Metabolic rate and environmental productivity: well-provisioned animals evolved to run and idle fast. Proc. Natl Acad. Sci. USA. 2001;98:12 551–12 554. doi: 10.1073/pnas.221456698. doi:10.1073/pnas.221456698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Conner T.P. Geographic variation in metabolic seasonal acclimatization in house finches. Condor. 1996;98:371–381. [Google Scholar]
- Pagel M. Inferring the historical patterns of biological evolution. Nature. 1999;401:877–884. doi: 10.1038/44766. doi:10.1038/44766 [DOI] [PubMed] [Google Scholar]
- Paradis E, Claude J, Strimmer K. APE: analyses of phylogenetics and evolution in R language. Bioinformatics. 2004;20:289–290. doi: 10.1093/bioinformatics/btg412. doi:10.1093/bioinformatics/btg412 [DOI] [PubMed] [Google Scholar]
- Rezende E.L, Swanson D.L, Novoa F.F, Bozinovic F. Passerines versus nonpasserines: so far, no statistical differences in the scaling of avian energetics. J. Exp. Biol. 2002;205:101–107. doi: 10.1242/jeb.205.1.101. [DOI] [PubMed] [Google Scholar]
- Rezende E.L, Bozinovic F, Garland T., Jr Climatic adaptation and the evolution of basal and maximum rates of metabolism in rodents. Evolution. 2004;58:1361–1374. doi: 10.1111/j.0014-3820.2004.tb01714.x. doi:10.1554/03-499 [DOI] [PubMed] [Google Scholar]
- Rohlf F.J. Comparative methods for the analysis of continuous variables: geometric interpretations. Evolution. 2001;55:2143–2160. doi: 10.1111/j.0014-3820.2001.tb00731.x. doi:10.1554/0014-3820(2001)055[2143:CMFTAO]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- Sibley C.G, Ahlquist J.E. Yale University Press; New Haven, CT: 1990. Phylogeny and classification of birds: a study in molecular evolution. [Google Scholar]
- Sibley C.G, Monroe B.L., Jr . Yale University Press; New Haven, CT: 1990. Distribution and taxonomy of birds of the world. [Google Scholar]
- Speakman J.R. The cost of living: field metabolic rates of small mammals. Adv. Ecol. Res. 2000;30:177–297. [Google Scholar]
- Swanson D.L, Liknes E.T. A comparative analysis of thermogenic capacity and cold tolerance in small birds. J. Exp. Biol. 2006;209:466–474. doi: 10.1242/jeb.02024. doi:10.1242/jeb.02024 [DOI] [PubMed] [Google Scholar]
- Tieleman B.I, Williams J.B. The adjustment of avian metabolic rates and water fluxes to desert environments. Physiol. Biochem. Zool. 2000;73:461–479. doi: 10.1086/317740. doi:10.1086/317740 [DOI] [PubMed] [Google Scholar]
- Tieleman B.I, Williams J.B, Bloomer P. Adaptation of metabolism and evaporative water loss along an aridity gradient. Proc. R. Soc. B. 2003;270:207–214. doi: 10.1098/rspb.2002.2205. doi:10.1098/rspb.2002.2205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wasser J.S. The relationship of energetics of falconiform birds to body mass and climate. Condor. 1986;88:57–62. [Google Scholar]
- Weathers W.W. Temperature regulation in the dusky munia, Lonchura fuscans (Cassin) (Estrildidae) Aust. J. Zool. 1977;25:193–199. doi:10.1071/ZO9770193 [Google Scholar]
- Weathers W.W. Climatic adaptation in avian standard metabolic rate. Oecologia. 1979;42:81–89. doi: 10.1007/BF00347620. [DOI] [PubMed] [Google Scholar]
- White C.R. The influence of foraging mode and arid adaptation on the basal metabolic rate of burrowing mammals. Physiol. Biochem. Zool. 2003;76:122–134. doi: 10.1086/367940. doi:10.1086/367940 [DOI] [PubMed] [Google Scholar]
- White C.R, Seymour R.S. Does BMR contain a useful signal? Mammalian BMR allometry and correlations with a selection of physiological, ecological and life-history variables. Physiol. Biochem. Zool. 2004;77:929–941. doi: 10.1086/425186. doi:10.1086/425186 [DOI] [PubMed] [Google Scholar]
- Whittaker R.J, Willis K.J, Field R. Climatic-energetic explanations of diversity: a macroscopic perspective. In: Blackburn T.M, Gaston K.J, editors. Macroecology: concepts and consequences. Blackwell Publishing; Oxford, UK: 2003. pp. 107–129. [Google Scholar]
- Wikelski M, Spinnery L, Schelsky W, Scheuerlein A, Gwinner E. Slow pace of life in tropical sedentary birds: a common-garden experiment on four stonechat populations from different latitudes. Proc. R. Soc. B. 2003;270:2383–2388. doi: 10.1098/rspb.2003.2500. doi:10.1098/rspb.2003.2500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams J.B, Tieleman B.I. Flexibility in basal metabolic rate and evaporative water loss among hoopoe larks exposed to different environmental temperatures. J. Exp. Biol. 2000;203:3153–3159. doi: 10.1242/jeb.203.20.3153. [DOI] [PubMed] [Google Scholar]
- Withers P.C, Cooper C.E, Larcombe A.N. Environmental correlates of physiological variables in marsupials. Physiol. Biochem. Zool. 2006;79:437–453. doi: 10.1086/501063. doi:10.1086/501063 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
all of the data on which the analysis is based: Body mass (M, g), basal metabolic rate (BMR, ml O2 min-1), capture locality (latitude and longiture, °), habitat annual net primary productivity (NPP, g C m 2), mean monthly precipitation (P, mm), intra-annual coefficient of variation of precipitation (PCV), mean annual ambient temperature (Ta, °C), and annual temperature range (Tr, °C).