Climate change and the optimal arrival of migratory birds

Abstract

Recent climate change has sparked an interest in the timing of biological events, which is a general problem in life-history evolution. Reproduction in many organisms breeding in seasonal environments, e.g. migratory birds, is dependent on the exploitation of a short but rich food supply. If the seasonal timing of the food peak advances owing to climate change, then one would expect the bird to track those changes, hence, initiate migration and breeding earlier. However, when there is competition for territories and a risk of pre-breeding mortality, the optimal response to a shifting food distribution is no longer obvious. We develop a theoretical model to study how the optimal arrival time depends on the mean and variance of the food distribution, the degree of competition for territories and the risk of mortality. In general, the optimal shift in arrival date should never be as extreme as the shift in food peak date. Our results also show that we should expect the high variation of trends in arrival date observed among migratory birds, even if migration and information about climate change were unconstrained.

1. Introduction

The timing of major events in an organism's life is a classical problem in life-history theory (Lack 1968; Iwasa & Levin 1995; Barta et al. 2006) and recent climate change (IPCC 2001) has sparked an interest in the study of climate-related changes in phenology (Harrington et al. 1999; Walther et al. 2002; Parmesan & Yohe 2003; Root et al. 2003; Visser & Both 2005). Over the past decades, there has been a positive trend in the advancement of spring across the Northern Hemisphere (Schwartz et al. 2006). Shifting seasonal patterns of abiotic conditions and resource availability affect the timing of phenological events, such as reproduction (Dunn 2004) and migration (Lehikoinen et al. 2004; Chadwick et al. 2006), in various organisms. However, the optimal timing of energetically demanding biological events, e.g. breeding, is often set by the seasonal patterns of other trophic levels, such as the availability of food (Lack 1968). If the phenology of different trophic levels responds differently to climate change, then there will be a temporal mismatch between resource requirement and availability with potential fitness consequences (Both et al. 2006). For instance, mistimed reproduction in birds may result in fewer and lighter offspring (Perrins & McCleery 1989; van Noordwijk et al. 1995) and, originally, the match–mismatch hypothesis (Cushing 1990) was formulated to explain the interannual variability in fish recruitment as a function of the timing of plankton production (Hjort 1914).

The interpretation of the observed changes in phenology shown by many organisms is facilitated by theory. It has been suggested that the shift in the phenology of a species' food abundance is, as a first approximation, an appropriate yardstick reflecting how much a species should shift its phenology to match the climatically induced environmental change (Visser & Both 2005). This yardstick is of course overly simplistic, as pointed out by Visser & Both (2005), as it focuses on one phenology event and food as the only selection agent. Furthermore, the match–mismatch hypothesis ignores the overall level of food abundance which might compensate small temporal mismatches (Durant et al. 2005).

In this paper, we develop a model to study how an organism (assumed to be a migratory bird) should adjust its timing of arrival to the breeding grounds after having over-wintered elsewhere in order to maximize the expected number of offspring produced, as a response to a change in (i) the resource peak date or (ii) the variance of the resource distribution. The model takes into account that competition for territories is a major driver of early arrival and the instantaneous mortality rate declines over the season and ultimately limits early arrival. There is a parallel theory for the optimal emergence date in insects explaining the occurrence of protandry (e.g. Wiklund & Fagerström 1977), which has also been studied in birds (e.g. Rubolini et al. 2004). Our model is similar in the respect that there is a trade-off between the benefits and the risks of early arrival. However, the main difference between the protandry models and the model presented here is that the reproductive success is also a function of the amount of food acquired during the limited breeding season.

2. Model

The probability of getting a territory, P_e, is given by the territory function and is a function of the time of arrival

$$P_{\text{e}}=\frac{{\text{e}}^{z\hat{t}}}{{\text{e}}^{z\hat{t}}+{\text{e}}^{zt}},$$ (2.1)

where $\hat{t}$ is the day of arrival corresponding to P_e=0.5 and z is a measure of competition for territories such that P_e approaches a step function (equal to intense competition) when z goes to infinity. There are situations when there is no single evolutionary stable optimal arrival date (see Iwasa & Levin 1995) and we should therefore expect a distribution of arrival dates. However, we are studying the optimal arrival of the average individual and our predictions can be confronted with empirical data on the average behaviour of a population. Distinguishing empirically between variance in arrival dates resulting from different optima within a population or different strengths of density-dependent competition across populations is difficult and requires very detailed data (e.g. Gunnarsson et al. 2006). Competition for territories can be seen as a game and there will be a strong selection for arriving early enough to get a territory (Kokko 1999). To mimic this selection, even though all individuals are assumed equal, we first find the optimal arrival date (t^*) for a given $\hat{t}$ (see below). We then decrease $\hat{t}$ and find the new t^* until $t^{*}=\hat{t}$, such that there will not be any benefit arriving earlier than $\hat{t}$.

When the bird arrives, it takes x₁ days before egg-laying can be initialized. One can think of x₁ as the time needed to find a mate, a territory, accumulate resources and/or recover from migration depending on the life-history characteristics of the species. During the time period x₁, there is a risk of mortality. The mortality cost modelled here is the extra cost of early arrival in the breeding area, and the longer the period x₁ the lower the probability of surviving to breeding. Furthermore, the instantaneous mortality rate goes down later in the season, so that it becomes easier to survive x₁ days later than early in the season. The probability of surviving from the day of arrival (t₀) to the start of breeding (initializing egg-laying), t₁=t₀+x₁, can be expressed as

$$P_{\text{s}}={\text{e}}^{({\lambda }_{\max }/b)({\text{e}}^{-b{t}_1}-{\text{e}}^{-b{t}_0})},$$ (2.2)

where λ_max is the maximum mortality rate and b measures the strength of the exponential decline rate over the season (see appendix A for the derivation of equation (2.2)). Throughout the paper, we will use a fixed value of λ_max and vary the mortality risk by changing b. To keep the model simple, we assume that there is no mortality risk during breeding (Sillet & Holmes 2002). However, the results would not be qualitatively different if we instead made the assumption of a low daily mortality rate throughout the breeding season.

Even though there are obvious fitness gains from arriving early, the onset of breeding has presumably evolved through natural selection to match offspring requirements and food availability (Lack 1968; Visser et al. 2004). The amount of food available over the season is described by a normal random variate, r_t, with mean μ and standard deviation σ. The amount of food available during breeding (R) is the integral of r_t between the start of breeding (t₁) and the end of breeding (t₂=t₁+x₂),

$$R={\int }_{t_1}^{t_2}{r}_t\text{d}t,$$ (2.3)

where x₂ is the fixed time to accomplish the breeding. We evaluated this integral numerically using the quad function in MatLab (The MathWorks 2000). One could, of course, think of various nonlinear relationships between the amount of food available and the number of offspring produced. However, as a first approximation we assume a linear relationship. Hence, the life-history problem is to find the day of arrival maximizing the expected number of offspring, hence, to maximize the product P_eP_sR.

(a) Climate change and life history

We consider two alternative climate change scenarios resulting in (i) a shift towards earlier resource peak date or (ii) an increase or decrease in the variance of the resource distribution. We contrasted two different life histories characterized by high/low degree of competition for territories. Furthermore, we studied the effect of pre-breeding mortality risk by varying the seasonal survival curve. For each life history and survival curve, we calculated the optimal arrival date under the climate change scenarios.

3. Results

Before evaluating the optimal response to a change in the resource's peak date or its width, we need to understand the factors influencing the optimal arrival date for a given resource function. It is always true that, everything else being equal, the stronger the competition for territories the earlier the optimal arrival date. Similarly, the lower the mortality rate after arrival the earlier the birds should arrive. There is a negative relationship between the optimal arrival date and the time needed for breeding (x₂). Depending on the strength of competition, the pre-breeding mortality risk and the width of the resource distribution, one can get various (e.g. decreasing or hump-shaped) relationships between the optimal arrival date and x₁, the time needed before start of egg-laying (e.g. finding a mate and building a nest) (not shown). However, the exact value is not critical for the qualitative results and below we let x₁=10, which seems reasonable for many passerine birds, in all the results below.

(a) The effect of shifting food peak date

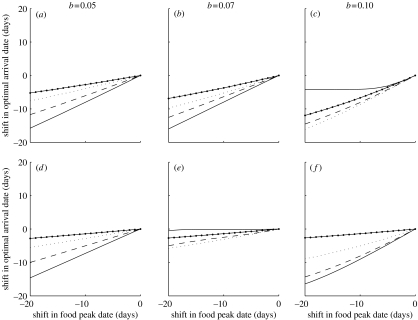
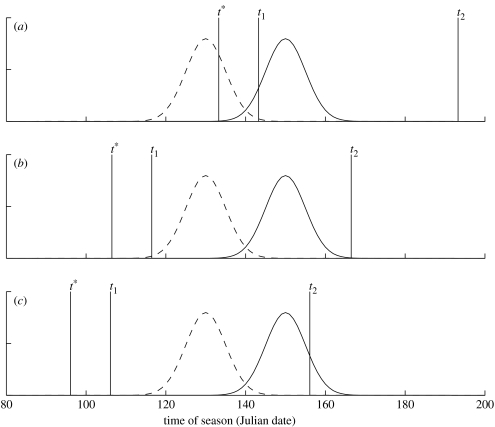
As long as the probability of surviving to the start of breeding is an increasing function of arrival date, the optimal shift in arrival date is always less than the shift in resource peak date (figure 1). This is a general result and independent of all other parameters in the model. However, the actual response will depend on the width of the resource distribution, the degree of competition for territories and the risk of mortality. The stronger the competition the weaker the response to a shift in food peak date (compare (a)–(c) and (d)–(f) in figure 1). The only exception is when the food distribution is narrow and the mortality risk low (figure 1c,f, solid lines). In general, the optimal response to an advanced resource distribution gets stronger when the resource distribution is narrow. However, there are exceptions (figure 1c,e) and these results can be understood by studying the time of arrival and breeding in relation to the resource function. In figure 2, we show the timing of arrival and breeding in relation to a narrow food distribution (σ=5) when the competition for territories is high. When the mortality risk is high, the birds arrive just in time to start breeding before the resource abundance peak (figure 2a). If the resource distribution is advanced, the optimal response is to advance the arrival date (cf. figure 1d). When the mortality risk is somewhat lower, the breeding starts well before the peak date and ends before the food is gone (figure 2b). If the food distribution is shifted, say, 10 days there should not be any response in arrival date (cf. figure 1e). However, if the mortality risk is low, the birds should arrive and breed very early but still need to make sure that they do not miss the food peak (figure 2c). If the resource distribution is shifted, then the arrival time should track the change owing to the survival and territory acquisition benefits of arriving early in the season.

Figure 1.

Optimal shift in arrival date as a response to an advancement of food peak date for different mortality risks. The standard deviation of the food distribution (σ) is 5 (solid line), 10 (dashed line), 20 (dotted line) or 40 (solid line with dots). In (a–c), the competition for territories is weak (z=0.01) and in (d–f) competition is strong (z=0.1). The value of μ before the shift in food peak date was 150. Other parameter values are x₁=10, x₂=50 and λ_max=170.

Figure 2.

The food distribution before (solid line) and after (dashed line) an advanced peak date. The vertical lines mark the optimal arrival date (t^*), the start of breeding (t₁) and the end of breeding (t₂) before the shift. The mortality risk is (a) high (b=0.05), (b) medium (b=0.07) or (c) low (b=0.1). Other parameter values are μ=150, σ=5, x₁=10, x₂=50, λ_max=170 and z=0.1.

In conclusion, when the birds arrive very early or late in relation to the food peak, they should respond to an advanced food distribution by shifting the arrival date. However, when they arrive well in time before the food peak and the breeding ends after the peak, the optimal response to an advanced food distribution is a weak shift (if any) in arrival date.

(b) The effect of shifting variance

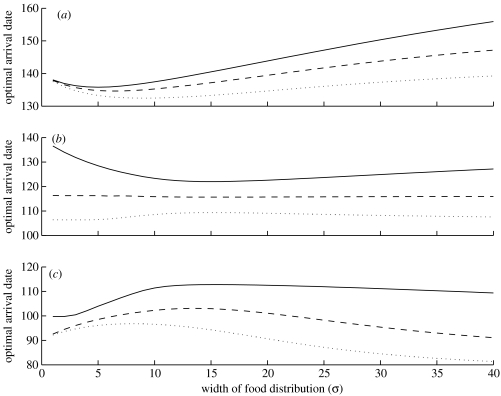
The effect of changing the width of the food distribution while keeping the peak date constant depends on the mortality risk as well as the degree of competition (figure 3). If the mortality risk is high, the relationship between optimal arrival date and the width of the food distribution will have a minimum. On the other hand, if the mortality risk is low, the relationship between the optimal arrival date and the width of the food distribution will have a maximum. For intermediate mortality risk, the shape of the curve will depend on the degree of competition (figure 3b). Again, the results can be understood by noting that high mortality risk and low competition yield later arrival compared to low mortality risk and high competition. Under high mortality risk arrival, the optimal arrival date is constrained to being relatively late. An increase in the width of the food distribution then allows the birds to further delay arrival in order to reduce mortality cost, although strong competition constrains these delays (cf. figure 2). Hence, birds arriving early or late in relation to the food distribution should respond differently to any change in the food distribution to balance the risk of mortality, the probability of getting a territory and the amount of food available during breeding.

Figure 3.

The optimal arrival date as a function of the standard deviation of the food distribution (σ) when the pre-breeding mortality risk is (a) high (b=0.05), (b) medium (b=0.07) or (c) low (b=0.1). The solid, dashed and dotted lines correspond to z=0.01, 0.05 and 0.1, respectively. The other parameter values are μ=150, x₁=10, x₂=50 and λ_max=170.

4. Discussion

Phenological adaptation in seasonal environments is a fundamental life-history problem (Roff 1983), for which importance has grown with recent climate change. Mistiming of phenological events as a result of climate change may be a widespread phenomenon (Both et al. 2006), but it is not clear how observed phenological shifts in, e.g. in arrival date of migratory birds (Lehikoinen et al. 2004) should be interpreted. It has recently been suggested that the shift in the phenology of a species' food abundance is, by a first approximation, an appropriate yardstick reflecting how much a species should shift its phenology to match the climatically induced environmental change (Visser & Both 2005).

We have shown that given a pre-breeding survival probability less than 1, the optimal arrival time should always advance less than the food peak advances. The expected change in arrival for a given change in food peak date depends not only on the change in food peak but also on when, in relation to the food peak, the birds arrived before the shift. This in turn is determined by the width of the resource distribution, the degree of competition for territories and the risk of mortality. These processes interact in intricate ways to generate a diversity of trends in arrival time in response to a given change in food peak date. This can be illustrated by contrasting two life histories. First, let us consider a species, which could be exemplified by the skylark (Alauda arvensis), that arrives early in spring at a time when the mortality risk owing to bad weather is relatively high. They still breed relatively late and the breeding season is prolonged (Donald 2004), which indicates that the food distribution is wide. The expected shift in optimal arrival date in response to a shift in food peak date should therefore be weak (figure 1a,d, solid line with dots), especially if the time from arrival to breeding is longer than the 10 days assumed above (not shown). An alternative life history is illustrated by, say, the pied flycatcher (Ficedula hypoleuca), a species where the competition for territories is high if nest holes are limiting and the food peak is relatively narrow (Both & Visser 2001). If the mortality risk is either high (figure 1d, solid line) or low (figure 1f, solid line), we would expect a relatively strong shift in optimal arrival date. However, for intermediate mortality risk, the optimal response is not to advance the arrival date. Hence, here it becomes critical to obtain an estimate of the survival rate from arrival to the start of breeding in order to predict the optimal response.

There are unfortunately very few empirical data available to study how a shift in phenology of a species (e.g. arrival date in migratory birds) can be coupled to a shifted food distribution (reviewed by Visser & Both 2005). However, one striking example is given by the pied flycatcher in The Netherlands. There is advancement in the emergence date of their main prey (caterpillars), but the birds still arrive at the same time. However, the flycatchers have advanced the start of breeding by decreasing the time from arrival to egg-laying (i.e. the parameter x₁ assumed to be fixed in our model). Assuming the pre-breeding mortality risk to be very low, our model suggests that the flycatchers should respond by advancing their arrival also. However, temperatures before the actual observed arrival of the flycatchers have not increased at all, which may indicate an increased risk of mortality earlier in the season (C. Both 2006, personal communication). It has been argued that the reason why we do not see an advanced arrival could be that the arrival date is constrained by the fact that, in long-distance migrants, the timing of migration is under endogenous control (Berthold 1996; Gwinner 1996) while still at the wintering grounds, and the cues needed to trigger the onset of migration are unlikely to be linked to the climate on their breeding grounds (e.g. Both & Visser 2001). However, adaptation to climate change in long-distance migrants may not be as constrained as previously suggested. For instance, it has recently been shown that long-distance migrants, including the pied flycatcher, have in fact advanced their migration more than short-distance migrants (Jonzén et al. 2006). Whether the observed changes are enough to avoid a population decline (Both et al. 2006) is a different question which is far from trivial (Ådahl et al. 2006).

In conclusion, we have shown that the optimal shift in arrival date should never be as extreme as the shift in food peak date. Furthermore, one could expect to find high variation of trends in arrival date observed among migratory birds, even if migration and information about climate change were unconstrained and the birds responded in some way to maximize the reproductive output. The reason is that the optimal timing of arrival depends not only on the peak date of food, as emphasized in previous studies (Visser & Both 2005), but also on the variance in the food availability. Furthermore, the trade-off between the probability of getting a territory and surviving to breeding affects when, in relation to a given food distribution, the birds should arrive. These are parameters that have not been previously discussed when interpreting phenology shifts in response to climate change.

Appendix A

From the time of arrival, t₀, to the time of breeding, t₁, there is a risk of mortality. The probability of surviving (P_s) the x₁ days from t₀ to t₁ can be written as

$$P_{\text{s}}=P(Y>x_1)=P(Y>t_1|Y>t_0)=\frac{P(Y>t_1\cap Y>t_0)}{P(Y>t_0)}=\frac{P(Y>t_1)}{P(Y>t_0)}=\frac{1-F_Y(t_1)}{1-F_Y(t_0)},$$ (A 1)

where F_Y(t), the distribution function of the stochastic variable γ, i.e. the probability of not being alive after day t, is

$$F_Y(t)=1-{\text{e}}^{-{\int }_0^t\lambda (u)\text{d}u}.$$ (A 2)

We let the instantaneous mortality rate decline exponentially over the season

$$\lambda (u)={\lambda }_{\text{max}}{\text{e}}^{-bu},$$ (A 3)

where λ_max is the maximum mortality rate and b measures the strength of the exponential decline rate over the season u.

Inserting equation (A 3) in (A 2) and simplifying we get

$$F_Y(t)=1-{\text{e}}^{-({\lambda }_{\text{max}}/b)(1-{\text{e}}^{-bt})}.$$ (A 4)

Using equation (A 4) in (A 1), it is straightforward to show that the probability of surviving from the day of arrival to the start of breeding can be expressed as

$$P_{\text{s}}={\text{e}}^{({\lambda }_{\text{max}}/b)({\text{e}}^{-b{t}_1}-{\text{e}}^{-b{t}_0})}.$$ (A5)