The cost of replication fidelity in human immunodeficiency virus type 1

Abstract

Mutation rates should be governed by at least three evolutionary factors: the need for beneficial mutations, the benefit of minimizing the mutational load and the cost of replication fidelity. RNA viruses show high mutation rates compared with DNA micro-organisms, and recent findings suggest that the cost of fidelity might play a role in the evolution of increased mutation rates. Here, by analysing previously published data from HIV-1 reverse transcriptase in vitro assays, we show a trade-off between enzymatic accuracy and the maximum rate of polymerization, thus providing a biochemical basis for the fitness cost of fidelity in HIV-1. This trade-off seems to be related to inefficient extension of mispairs, which increases fidelity at the expense of the polymerization rate. Since in RNA viruses fast replication is critical for survival, this could impose a high cost of fidelity and favour the evolution of high mutation rates.

1. Introduction

RNA viruses show mutation rates orders of magnitude higher than DNA micro-organisms (Drake et al. 1998). Although the lack of 3′ exonuclease activity provides a biochemical basis for this error-prone replication, this does not necessarily imply that RNA virus polymerases are intrinsically unable to improve fidelity to some extent. Variability in mutation rates, both within and between RNA virus species (Drake & Holland 1999; Pfeiffer & Kirkegaard 2003), extensive work with HIV-1 mutators and anti-mutators, and the presence of 3′ exonuclease activity in eukaryotic RNA polymerases (Thomas et al. 1998) suggest that high mutation rates cannot be merely attributed to biochemical restrictions. Since mutation rate is a heritable and variable characteristic, it becomes a target for natural selection. As stated by Drake et al. (p. 1683, 1998), ‘sometimes an organism's mutation rate is considered to be “determined” by the particular set of mechanisms it applies. It is more accurate, however, to view that organism's mutation rate as determined by deep evolutionary forces, by the life history it has adopted, and by accidents of their evolutionary history. The particular mechanisms employed and their efficiencies are merely devices to carry out the underlying necessity’.

Keeping this in mind, three evolutionary factors have to be considered to understand the origin and maintenance of high mutation rates in RNA viruses (Sniegowski et al. 2000). First, raising error rates provides the opportunity to explore more genotypes and, hence, to rapidly find adaptive mutations. Based on this, it has often been argued that elevated mutation rates are maintained in RNA viruses owing to the rapid adaptive capacity they bestow (Holland et al. 1982; Domingo & Holland 1997; Domingo 2002). Second, since deleterious mutations are more abundant than beneficial mutations, there is a selective pressure for reducing mutation rates towards whatever limit is imposed by biochemical restrictions (Kimura 1967). Third, increasing replication fidelity should come at an energetic or kinetic cost and hence have a negative impact on fitness.

Although the cost of replication fidelity has received some theoretical attention (Kimura 1967; Dawson 1998), only recently has it been suggested that it might be important for the evolution of mutation rates in RNA viruses. Using a series of vesicular stomatitis virus (VSV) mutants carrying single amino acid substitutions in the RNA polymerase gene, it was shown that changes leading to lower mutation rates also led to slower growth rates, indicating that fidelity paid a fitness cost (Furió et al. 2005). However, the biochemical basis of this cost remains unclear. To shed some light on this issue, we took advantage of the relatively high number of previously published in vitro experiments with HIV-1 reverse transcriptase (RT). After tabulating steady-state kinetic constants from different studies and standardizing the data, we observed a positive correlation between catalytic constants and mutation rates, thus providing a biochemical basis for the cost of replication fidelity in HIV-1.

2. Material and methods

(a) Biochemical data

We examined 11 publications containing data from steady-state kinetic experiments (table 1). These datasets included 26 different single amino acid RT mutants, most of which were involved in drug resistance. In all cases, the rate of polymerization (V) was measured for several nucleotide concentrations. Assuming a reaction scheme of the kind

$$\frac{\text{E}{\text{p}}_n}{t}+\text{dNTP}\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}\frac{\text{E}{\text{p}}_n}{t}\text{dNTP}\stackrel{k_{\text{cat}}}{⟶}\frac{\text{E}{\text{p}}_{n+1}}{t}+{\text{PP}}_{\text{i}},$$

where E p_n/t is the enzyme/template/primer complex, dNTP is any nucleotide, and PP_i is pyrophosphate; k_cat and K_m=k₋₁/k₁ were estimated from the Michaelis–Menten equation

$$V=\frac{k_{\text{cat}}\left[\text{E}{\text{p}}_n/t\right]}{1+K_{\text{m}}/\left[\text{dNTP}\right]}.$$ (2.1)

Table 1.

HIV-1 RT mutants, each carrying a single amino acid replacement, for which steady-sate fidelity assays were available. (A single study (Menéndez-Arias 1998), in which non-sense codons were introduced in the RNAase H domain, was not included. Each enumerated mutant was analysed on a single experiment unless the number of assays is indicated in parenthesis.)

experiments	mutants	references
misinsertion	Y183F	Bakhanashvili et al. (1996)
mispair extension	M184L and Y183F	Bakhanashvili et al. (1996)
misinsertion	Y115A, Y115F, Y115S and Y115W	Martín-Hernández et al. (1996)
misinsertion	M184A and M184V	Pandey et al. (1996)
mispair extension	Y115S (n=2), Y115V (n=2), Y115W (n=2), Y115A, Y115C, Y115F, Y115G, Y115H, Y115I, Y115L, Y115M and Y115N	Martín-Hernández et al. (1997)
misinsertion	F160W (n=2) and F160Y	Gutiérrez-Rivas et al. (1999)
mispair extension	F160W and F160Y	Gutiérrez-Rivas et al. (1999)
mispair extension	R72A	Lewis et al. (1999)
misinsertion	F227A and W229A (n=2)	Wisniewski et al. (1999)
misinsertion	Y115A and Y115V	Cases-González et al. (2000)
mispair extension	Y115A and Y115V	Cases-González et al. (2000)
misinsertion	Q151M (n=2) and Q151N (n=2)	Kaushik et al. (2000)
misinsertion	M230I (n=7) and Y115W	Gutiérrez-Rivas & Menéndez-Arias (2001)
mispair extension	M230I and Y115W	Gutiérrez-Rivas & Menéndez-Arias (2001)
misinsertion	A114G and A114S	Cases-González & Menéndez-Arias (2005)

The inverse of the Michaelis–Menten constant, $K_{\text{m}}^{-1}$, measures the affinity of the enzyme for dNTP, whereas the catalytic constant k_cat governs nucleotide incorporation and is proportional to the maximum rate of polymerization.

In vitro fidelity was estimated by misinsertion or mispair extension assays. In both kinds of experiments, the enzyme is initially incubated with a template and a primer to allow complex formation. In misinsertion assays, a single, incorrect, nucleotide is added to the reaction, hence forcing its polymerization. The control experiment is performed using only the correct nucleotide. In mispair extension assays, the polymerase is forced to extend a non-complementary 3′ end, and the control experiment is performed with a fully complementary primer. Since kinetic parameters for the 26 mutants were obtained in different conditions, they cannot be compared directly. For this reason, we expressed them as a ratio relative to the wild-type prior to statistical analyses.

(b) Mutation rate estimation

Mutation rates were calculated as

$$\mu =\frac{k_{\text{cat}}^{\text{i}}/K_m^{\text{i}}}{k_{\text{cat}}^{\text{c}}/K_m^{\text{c}}},$$ (2.2)

where super-indexes i and c refer to incorrect and correct nucleotides, respectively. The Michaelis–Menten model was used to obtain all four parameters as described earlier. This model does not introduce any cost of fidelity. By construction, equation (2.2) should guarantee some degree of correlation between μ and each of the four kinetic parameters. Specifically, mutation rates should positively correlate to $K_m^{\text{i}}$and $k_{\text{cat}}^{\text{i}}$, i.e. to the affinity for incorrect nucleotides and to their rate of incorporation, respectively, whereas mutation rates should negatively correlate to $K_m^{\text{c}}$ and $k_{\text{cat}}^{\text{c}}$, i.e. affinity and rate of incorporation for correct nucleotides. Therefore, observing any of these correlations would not be informative. A kinetic cost of fidelity, however, might change the sign of these correlations. Trying to detect kinetic costs in this way is a conservative approach because any unexpected trend might cancel out with the correlation expected from equation (2.2).

(c) Statistical analyses

For each study, all the values were corrected by the wild-type to account for differences in wild-type reference strains or in experimental procedures across studies. Since the relative mutation rate varied by approximately four orders of magnitude, we decided to work with log relative mutation rates. Consequently, we also log-transformed the four involved kinetic parameters. Parametric Pearson's correlations are reported throughout the text, but the analyses were also done using Spearman's non-parametric correlation to ensure that the results were not driven by the presence of outliers. All statistics were done with SPSS v. 12.0 (www.spss.com).

3. Results and discussion

(a) A kinetic cost of fidelity

Mutation rates, as calculated from equation (2.2), were typically close to 10⁻³ substitutions per nucleotide, but ranged several orders of magnitude. Trivially, equation (2.2) predicts that $k_{\text{cat}}^{\text{i}}$ and $K_m^{\text{c}}$ should positively correlate to mutation rate, whereas $K_m^{\text{i}}$ and $k_{\text{cat}}^{\text{c}}$ should negatively correlate to mutation rate. Using all 119 log-transformed data, the correlations between mutation rates and $\text{log}{k}_{\text{cat}}^{\text{i}}$ (Pearson's r=0.235, p=0.010), $\text{log}{K}_m^{\text{c}}$ (r=0.524, p<0.001) and $\text{log}{K}_m^{\text{i}}$ (r=−0.356, p<0.001) were as predicted by equation (2.2) and hence were not informative. However, there was an unexpected, highly significant, positive correlation between log mutation rates and $\text{log}{k}_{\text{cat}}^{\text{c}}$ (r=0.306, p<0.0001). Since $k_{\text{cat}}^{\text{c}}$ determines the maximum rate of polymerization, the latter correlation suggests that increasing the speed of the reaction comes at the cost of reducing its fidelity. This conclusion is based on a conservative approach because the trend was detected ignoring the bias introduced by equation (2.2).

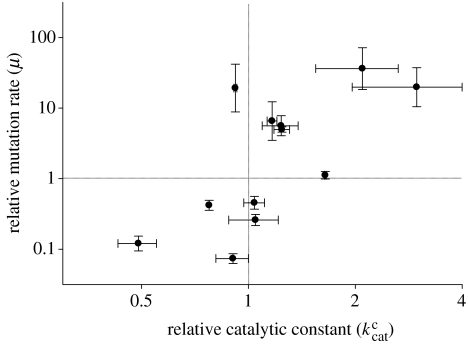
We then sought to explore the correlation between mutation rates and catalytic constants in further detail. In the above datasets, some mutants were represented by a larger amount of replicates than others and, in some cases, the assays were done using all the three possible incorrect nucleotides, whereas in other cases, only one or two incorrect nucleotides were tested. To minimize the effect of these heterogeneities, we focused only on mutants for which mutation rates and $k_{\text{cat}}^{\text{c}}$ values were drawn from at least two independent experiments, and we obtained average parameter values for each mutant. After doing so, among the 12 remaining genotypes, the positive correlation between log mutation rates and $\text{log}{k}_{\text{cat}}^{\text{c}}$ was confirmed (r=0.584, p=0.046; figure 1).

Figure 1.

Change in mutation rate as a function of the catalytic constant for 12 HIV-1 RT mutants, in log scale. Mean values and standard errors are shown.

The unexpected relationship between error rates and the catalytic constant implies that $k_{\text{cat}}^{\text{c}}$ shall indeed be dependent on some of the other three kinetic parameters, such that linear changes in $k_{\text{cat}}^{\text{c}}$ would produce faster than linear changes in $k_{\text{cat}}^{\text{i}}$, $K_m^{\text{c}}$ or $K_m^{\text{i}}$. These three possibilities were tested by performing linear regressions between the involved parameters in log-scale. Focusing on mutants with at least two independent experiments, we first performed a linear regression analysis between $\text{log}{k}_{\text{cat}}^{\text{i}}$ and $\text{log}{k}_{\text{cat}}^{\text{c}}$, including the two other kinetic parameters in the model to control for possible additional correlations. A multiple linear regression of the form $\text{log}{k}_{\text{cat}}^{\text{i}}=\alpha +{\beta }_1\text{log}{k}_{\text{cat}}^{\text{c}}+{\beta }_2\text{log}{K}_m^{\text{i}}+{\beta }_3\text{log}{K}_m^{\text{c}}$ provided no evidence for β₂>0 or β₃>0. In contrast, the estimated β₁ was not only significantly larger than zero (β₁=2.760, partial t-test, p=0.001), but also significantly larger than one (partial t-test, p=0.003), indicating that $k_{\text{cat}}^{\text{i}}$ increased faster than linearly with $k_{\text{cat}}^{\text{c}}$. In other words, increasing the polymerization rate of correct nucleotides triggers disproportionately larger increases in the polymerization rate of incorrect nucleotides and hence increases the mutation rate.

We also examined the relationship between $K_m^{\text{i}}$ and $k_{\text{cat}}^{\text{c}}$ using the multiple linear regression model, $\text{log}{K}_m^{\text{i}}=\alpha +{\beta }_1\text{log}{k}_{\text{cat}}^{\text{c}}+{\beta }_2\text{log}{k}_{\text{cat}}^{\text{i}}+{\beta }_3\text{log}{K}_m^{\text{c}}$. This provided no evidence for β₁>1. The same negative result was obtained when examining the relationship between $K_m^{\text{c}}$ and $k_{\text{cat}}^{\text{c}}$.

(b) Putative mechanisms underlying the cost of fidelity

If DNA polymerases followed the simple Michaelis–Menten reaction scheme, error rates would strictly depend on the relative affinity for incorrect and correct nucleotides, but it is well known that observed error rates are substantially lower than that (Showalter & Tsai 2002). Indeed, the reaction scheme of DNA polymerases includes various additional steps (Kunkel 2004). In HIV-1 RT, nucleotide binding to RT/template/primer complexes is believed to occur through a two-step mechanism, whereby after initial nucleotide binding, the catalysis complex transitions from an open conformation to a closed activated form, which tightens together the primer, the template and the nucleotide and triggers nucleotide incorporation (Kati et al. 1992; Rittinger et al. 1995). Both the conformational change step and the nucleotidyl transfer step might be rate limiting and might play an important role in HIV-1 replication fidelity (Showalter & Tsai 2002; Joyce & Benkovic 2004; Kunkel 2004).

Two-step reactions provide a possible mechanism for the cost of fidelity. For any given error fraction in the open conformation state determined by differences in affinity, during the second step, incorrect nucleotides should again dissociate more often than correct nucleotides owing to their higher off-rates, hence amplifying the discriminatory power. A double or multiple checkpoint mechanism could render nucleotide incorporation more specific but, on the other hand, it would impose an effective delay in the turning-on of the product formation, slowing down the rate of nucleotide incorporation (Hopfield 1974; Joyce & Benkovic 2004). Since this model deals with the incorporation of correct versus incorrect nucleotides, it predicts a positive correlation between mutation rates and catalytic constants for misinsertion assays, but not for mispair extension assays. However, using only the 71 log-transformed data obtained from misinsertion experiments, we failed to detect this correlation (r=0.127, p=0.293). The correlation remained non-significant after selecting only mutants for which estimates were obtained from at least two independent experiments (r=0.276, n=7, p=0.550). Therefore, the data did not support the possibility that a several-step mechanism imposes a kinetic cost for polymerization fidelity. However, we must recall that this is a conservative analysis, and a lack of positive correlation between log μ and $\text{log}{k}_{\text{cat}}^{\text{c}}$ could mean that either there is no cost of fidelity or this cost has been hidden by the negative correlation between log μ and $\text{log}{k}_{\text{cat}}^{\text{c}}$ determined by equation (2.2).

A second clue to the mechanism underlying the cost of fidelity in HIV-1 RT comes from observations indicating that, if an incorrect nucleotide is incorporated to the nascent chain, its extension occurs at a much slower rate than for the correct pair (Kunkel 2004). The more the extension is restricted by mispairs, the higher the fidelity but, at the same time, there will be some reduction in the overall rate of polymerization. This being true, there should be a positive correlation between the mutation rate and the catalytic constant for mispair extension assays, but not for misinsertion assays. In good agreement, after restricting the analysis to mispair extension assays, the correlation between log μ and $\text{log}{k}_{\text{cat}}^{\text{c}}$ turned out to be highly significant (r=0.499, n=48, p<0.001). This was confirmed after using only mutants with at least two independent experiments (r=0.956, n=5, p=0.011). Therefore, it seems likely that the observed cost of fidelity could be at least partially owing to inefficient mispair extension, which would minimize error rates at the expense of decreasing polymerization rates.

(c) In vivo relevance of steady-sate experiments

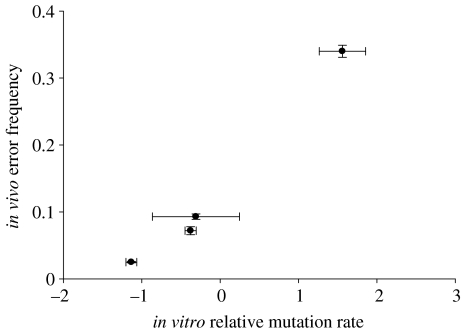
It is unclear whether fidelity assays from steady-state experiments accurately predict the in vivo mutation rate. Equation (2.2) provides the mutation rate as a direct function of catalytic constants, but it does not take into account additional factors, including the modulating effect of other HIV-1 genes (Mansky 1998), cellular factors that could influence HIV-1 RT fidelity or RNA editing. We partially addressed this question by looking at a study in which a panel of 16 single-residue HIV-1 RT mutants was assayed for in vivo fidelity using the lacZ reporter gene (Mansky et al. 2003). For four of these mutants (Y115A, Q151N, F227A and W229A), in vitro steady-state mutation rate estimations were also available. Despite the limited sample size, there was a strong association between in vitro and in vivo estimations (r=0.990, p=0.010; figure 2), indicating that steady-state experiments accurately predicted the in vivo mutation rate.

Figure 2.

In vivo error rate determinations from lacZ assays against in vitro mutation rates from steady-state experiments. The former are expressed as the ratio of white- and light-blue-stained colonies to total colonies. Mean values and standard errors are shown.

Then, it remains to be elucidated to what extent $k_{\text{cat}}$ influences the in vivo rate of DNA synthesis. The rate of polymerization does depend not only on $k_{\text{cat}}$, but also on $K_m$. When substrate concentration is low, relative to $K_m$, this rate is roughly proportional to the ratio $k_{\text{cat}}/K_m$, whereas at saturating substrate concentrations, $k_{\text{cat}}$ becomes the rate-limiting parameter. Recently, a highly sensitive method was developed to measure intracellular nucleotide content per cell (Diamond et al. 2004). Using this technique in combination with confocal microscopy, average nucleotide concentrations of 0.03 μM and 5.0 μM were estimated for macrophages and CD4⁺ T-cells, respectively. In the same study, an average $K_m^{\text{c}}$=0.07 μM was estimated from steady-state kinetic experiments, implying that in CD4⁺ T-cells $k_{\text{cat}}$ is clearly the rate-limiting parameter, whereas in macrophages, nucleotides are not at saturating concentrations, and hence, both parameters are important in determining the rate of polymerization. Direct experiments estimating the growth rates of HIV-1 RT mutants with different k_cat values would be helpful in further clarifying this point.

(d) Implications for the evolution of mutation rates in RNA viruses

In order to survive host defence mechanisms, parasites need to generate genetic variation. Thus, it seems reasonable to argue that selection should have favoured the evolution of high mutation rates in RNA viruses (Holland et al. 1982; Sasaki 1994; Domingo & Holland 1997; Domingo 2002). However, there are some problems with this argumentation. First, far from being exclusive to RNA viruses, parasitic lifestyles are common among many kinds of organisms. More specifically, DNA and RNA viruses face very similar environmental challenges and, if high mutation rates were advantageous to them, DNA viruses should have lost proofreading mechanisms and evolved error rates close to those of RNA genomes. Second, population genetics shows that in many situations, the adaptive advantage of mutators is far from being evolutionarily stable. In asexual species, modifier alleles that increase mutation rate are more likely to be associated with beneficial mutations and hence have a chance to get fixed in the population (Smith & Haigh 1974; Sniegowski et al. 1997; Taddei et al. 1997). However, in sexual species, linkage to beneficial mutations is rapidly dissipated by recombination (Kimura 1967; Drake et al. 1998) and, as a consequence, the adaptive advantage of mutators is too weak to overcome the short-term disadvantage of generating many deleterious mutations. Many RNA viruses, especially HIV-1, show high levels of recombination.

The cost of replication fidelity might be an important though previously neglected selective factor favouring the evolution of high mutation rates in RNA viruses (Furió et al. 2005). Being the trade-off between polymerization speed and accuracy, true selection could not simultaneously maximize both parameters. On one hand, selection for fast replication would promote the evolution of higher mutation rates but, on the other hand, the pressure for reducing the mutational load would favour lower mutation rates. The interplay between these opposing factors should determine an evolutionarily optimal mutation rate (Dawson 1998). HIV-1 in particular and RNA viruses in general are characterized by enormous burst sizes, small genomes with frequently overlapping reading frames, fluctuating population sizes, lack of redundancy and short generation times (Holland et al. 1982; Perelson et al. 1996). They thus represent an extreme form of r-selected populations, in which fast replication is strongly favoured (Pianka 1970; Krakauer & Plotkin 2002). For this reason, the interplay between the cost of fidelity and mutational load might produce different outcomes in RNA viruses and more complex organisms. It still remains to be elucidated why other rapidly replicating genomes, such as DNA viruses, did not evolve high mutation rates too. Some speculations can be made: first, RNA virus polymerases might be under stronger functional restrictions because they have to accomplish both replication and transcription; and second, some DNA viruses might benefit from cellular repair systems, hence freeing their polymerases from the trade-off between replication speed and accuracy, while others simply rely on the host polymerases to achieve their own replication. Although further research is required, it seems that the trade-off between replication fidelity and efficiency might contribute to determining the evolution of mutation rates.