Abstract
We present the LGA (Local-Global Alignment) method, designed to facilitate the comparison of protein structures or fragments of protein structures in sequence dependent and sequence independent modes. The LGA structure alignment program is available as an online service at http://PredictionCenter.llnl.gov/local/lga. Data generated by LGA can be successfully used in a scoring function to rank the level of similarity between two structures and to allow structure classification when many proteins are being analyzed. LGA also allows the clustering of similar fragments of protein structures.
INTRODUCTION
If one were to compare two slightly different conformations of the same protein, the overall root mean square deviation (RMSD) of all corresponding C-alpha atoms would give a useful impression of the similarity between the two structures. Unfortunately, a small perturbation in just one part of the protein (e.g. in a hinge joining two domains) can create a large RMSD and it would seem that the two structures are very different overall. Thus, it is desirable to also consider local regions of the proteins in assessing their similarity. In essence, the smaller such ‘deviant’ regions, the more similar the two structures are. If one compares two different proteins, where there is not a preassigned correspondence between amino acid residues, a sequence-independent alignment (residue correspondence) has to be generated first, adding another significant level of complexity.
We were thus motivated to develop a method that would take into account both local and global structure superpositions and also would be capable of working without a preassigned residue correspondence. We called this method ‘LGA’ for local/global alignment. Below we describe our algorithm and apply the LGA program to several test cases in order to highlight some of its features.
EVALUATING STRUCTURE SIMILARITY BETWEEN PROTEINS
Most structure comparison programs are built on the principle that a suitable scoring function can be defined with its optimum corresponding to the most significant structural match for a given protein. Many established comparison techniques evaluate structural similarity by two numbers, the RMSD between two superimposed structures together with the number of ‘equivalent’ (structurally aligned) residues. However, it is very difficult to optimize these two quantities simultaneously, since one can be optimized at the expense of the other. For example, the structural aligner, DALI (1), which is based on the alignment of distance matrices, solves the optimization problem by combining several numbers into a single quantity, called z-score. ProSup (2) maximizes the number of equivalent residues while RMSD is kept close to a constant value. An additional problem can arise when structures are similar in small, local regions. These regions of similarity can be overlooked when one global superposition is applied. In general, in many cases there is no ‘best’ superposition that reveals all regions of similarity between compared proteins.
To resolve these problems while comparing two structures, the LGA program generates many different local superpositions to detect regions where proteins are similar. The LGA scoring function has two components, LCS (longest continuous segments) and GDT (global distance test), established for the detection of regions of local and global structure similarities between proteins. These two measures were extensively tested during the last three successive rounds of CASP [Critical Assessment of Techniques for Protein Structure Prediction (3–7)] providing constructive ranking of evaluated 3D models. In comparing two protein structures, the LCS procedure is able to localize and superimpose the longest segments of residues that can fit under a selected RMSD cutoff. The GDT algorithm is designed to complement evaluations made with LCS searching for the largest (not necessary continuous) set of ‘equivalent’ residues that deviate by no more than a specified distance cutoff.
Data generated by the LCS and GDT algorithms
In an attempt to generate detailed information about regions of local similarity between two protein structures (Molecule1 and Molecule2) or segments thereof, each residue from Molecule2 is assigned to the largest set of residue pairs (C-alpha atoms from Molecule1 and Molecule2) provided it is a part of that set and can be fit under a selected RMSD (LCS algorithm) or distance (GDT algorithm) cutoff. If an analysis of two structures is based only on the superpositions limited to one selected RMSD or distance cutoff then it would not give full information on similarity between the two structures; some similarities would be detected, some would not. To avoid such limitations, LCS results are generated for a set of increasing RMSD cutoffs [1 Å (Ångstrom), 2 Å and 5 Å], and in the GDT analysis, two structures are scanned every 0.5 Å, starting from 0.5 Å up to a 10.0 Å distance cutoff. This approach allows us to gather very detailed information on local similarities between two structures. The results of such calculations are reported in the format as shown in Table 1.
Table 1. Example of data generated by LCS and GDT analyses.
| Column # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | … |
| Cutoffs: | 1 Å | 2 Å | 5 Å | 0.5 Å | 1.0 Å | 1.5 Å | 2.0 Å | 2.5 Å | 3.0 Å | 3.5 Å | 4.0 Å | 4.5 Å | … | ||||
| LCS_GDT | Molecule-1 | Molecule-2 | Length_of_the continuous | ||||||||||||||
| LCS_GDT | Residue | Residue | |||||||||||||||
| LCS_GDT | Name | Number | Name | Number | Segment | Global distance test data | |||||||||||
| LCS_GDT | V | 40 | A | 29 | 23 | 26 | 90 | 10 | 18 | 22 | 23 | 24 | 24 | 27 | 33 | 49 | … |
| LCS_GDT | A | 41 | Q | 30 | 23 | 26 | 90 | 10 | 18 | 22 | 23 | 24 | 25 | 27 | 42 | 55 | … |
| LCS_GDT | L | 42 | L | 31 | 23 | 26 | 90 | 4 | 7 | 20 | 23 | 24 | 25 | 36 | 46 | 55 | … |
| LCS_GDT | E | 43 | E | 32 | 8 | 26 | 90 | 4 | 7 | 15 | 23 | 24 | 25 | 35 | 46 | 55 | … |
| LCS_GDT | Q | 44 | V | 33 | 8 | 26 | 90 | 4 | 6 | 9 | 18 | 24 | 26 | 37 | 46 | 55 | … |
| LCS_GDT | T | 45 | T | 34 | 8 | 26 | 90 | 4 | 7 | 9 | 13 | 22 | 25 | 36 | 46 | 55 | … |
| LCS_GDT | G | 46 | G | 35 | 8 | 14 | 90 | 3 | 7 | 9 | 12 | 17 | 22 | 35 | 46 | 55 | … |
In the output shown in Table 1, columns 2–5 provide information on residues from two compared structures, and columns 6, 7 and 8 show the results from LCS analyses under 1 Å, 2 Å and 5 Å RMSD cutoffs, respectively. For example, residue L-31 from Molecule2 is a member of a 23-residue long continuous segment that can be superimposed with corresponding residues from Molecule1 under a 1 Å RMSD cutoff, but residue E-32 is an element of a segment consisting of just eight residues at an RMSD cutoff of 1 Å. In columns 9–28 the results of GDT analysis under 0.5 Å through 10.0 Å distance cutoffs are reported. For example, residue E-32 belongs to a set of four residues (not necessarily continuous) that can fit under a 0.5 Å distance cutoff, a set of seven residues under a 1.0 Å and a 25-residue set under 3.0 Å.
The GDT algorithm
In the GDT procedure, the search for an optimal superposition between two structures is performed as follows. For each selected pair of three, five and seven residue-long segments from both structures, an RMSD and a superposition are calculated. Each calculated superposition is used as a starting point to give an initial list of equivalent residues (C-alpha atom pairs from Molecule1 and Molecule2). The list of such equivalences is iteratively extended to collect the largest set of residues that can fit under a given distance cutoff. The goal of the iterative procedure is to exclude atoms that are more distant than a threshold (distance cutoff ) between Molecule1 and Molecule2 after the transform is applied. Starting from the initial set of atom pairs, the algorithm is as follows: (a) obtain the transform; (b) apply the transform; (c) identify all atom pairs for which the distance is larger than the threshold; (d) re-obtain the transform, excluding those atoms; (e) repeat steps (b)–(d) until the set of atoms used in calculations is the same for two cycles running.
The LCS and GDT algorithms are complementary
Results of the LCS algorithm identify local regions of similarity between proteins, while residues identified by GDT arise from anywhere in the structure (i.e. sequence continuity need not be maintained). From this point of view, GDT detects global, as opposed to local, similarity. Using GDT we focus on distance rather than RMSD. Using LCS, however, we can optimize (minimize) RMSD on the selected residues. So from this point of view, LCS gives complete and optimal information. Working with distance analysis (maximum norm) an optimal method for finding the ‘best superposition’, which will minimize the distances between all selected residues, is not known. Results can only be approximated. So to find the ‘best’ global structural match, GDT uses many distance cutoffs and superpositions. The GDT algorithm ‘tests’ each residue one by one from Molecule2, trying to assign it to the largest set of residues possible (not necessarily continuous) deviating from Molecule1 by no more than a specified distance cutoff. GDT evaluates a selected but large number of superpositions, in effect yielding consistently reliable results.
Description of the LGA scoring function
By combining these two techniques (RMSD based and distance based), LGA not only calculates a ‘best’ superposition between two proteins (meaning ‘under certain RMSD and distance cutoffs’), but also identifies the regions of local similarity between compared structures. In the structure alignment search procedure, for each generated list of equivalent residues, the following values are calculated: LCS_vi—percent of residues (continuous set) that can fit under an RMSD cutoff of vi Å (for vi=1.0, 2.0,…) and GDT_vi—an estimation of the percent of residues (largest set) that can fit under the distance cutoff of vi Å (for vi=0.5, 1.0,…). A scoring function (LGA_S) can be defined as a combination of these values and can be used to evaluate the level of structure similarity of selected regions. For a given parameter w (0.0≤w≤1.0), representing a weighting factor, we calculate LGA_S by the formula: LGA_S=w * S(GDT)+(1−w) * S(LCS) where S(F) function is defined as follows:
foreach vi (v1, v2,…,vk) {
Y=(k−i+1) /k; X=X+Y * F_vi;
}
S(F)=X/((1+k)* k/2);
The same scoring function is applied by the LGA program to perform the selection and ranking of the regions of structure similarities in the sequence dependent mode of analysis as well as in the sequence independent mode.
Graphical presentation of results from structure comparison of NMR models
How can the results of a multiple superposition (Table 1) between two structures be visualized? Let us compare an NMR average model, 1m2e_A, of the N-terminal domain of Synechococcus elongatus kaia (KAIA135N) with its 25-member family of low energy (designated 1m2f_A_n). In Table 2, NMR models are sorted by GDT_TS values.
Table 2. NMR models 1m2f_A_1–1m2f_A_25 compared to an average model 1m2e_A and sorted by GDT_TS value where GDT_TS = (P1+P2+ P4+P8)/4, and Pd is a percent of residues from 1m2e_A that can be superimposed with corresponding residues from 1m2f_A_n under selected distance cutoffs d=1, 2, 4, 8.
| Model | N1 | N2 | DIST | N | RMSD | GDT_TS |
|---|---|---|---|---|---|---|
| 1m2f_A_8 | 135 | 135 | 3.0 | 135 | 0.79 | 97.037 |
| 1m2f_A_16 | 135 | 135 | 3.0 | 133 | 0.70 | 96.296 |
| 1m2f_A_17 | 135 | 135 | 3.0 | 133 | 0.80 | 96.296 |
| 1m2f_A_2 | 135 | 135 | 3.0 | 135 | 0.91 | 96.296 |
| 1m2f_A_1 | 135 | 135 | 3.0 | 133 | 0.93 | 96.111 |
| 1m2f_A_19 | 135 | 135 | 3.0 | 134 | 0.95 | 96.111 |
| 1m2f_A_11 | 135 | 135 | 3.0 | 134 | 0.84 | 95.926 |
| 1m2f_A_14 | 135 | 135 | 3.0 | 133 | 0.91 | 95.926 |
| 1m2f_A_20 | 135 | 135 | 3.0 | 133 | 0.94 | 95.926 |
| 1m2f_A_7 | 135 | 135 | 3.0 | 131 | 0.85 | 95.741 |
| 1m2f_A_21 | 135 | 135 | 3.0 | 130 | 0.80 | 95.556 |
| 1m2f_A_5 | 135 | 135 | 3.0 | 134 | 1.04 | 95.556 |
| 1m2f_A_10 | 135 | 135 | 3.0 | 135 | 1.09 | 95.556 |
| 1m2f_A_18 | 135 | 135 | 3.0 | 134 | 0.89 | 95.370 |
| 1m2f_A_12 | 135 | 135 | 3.0 | 133 | 0.92 | 95.370 |
| 1m2f_A_13 | 135 | 135 | 3.0 | 131 | 0.95 | 95.370 |
| 1m2f_A_15 | 135 | 135 | 3.0 | 130 | 0.80 | 95.185 |
| 1m2f_A_24 | 135 | 135 | 3.0 | 133 | 0.89 | 95.185 |
| 1m2f_A_22 | 135 | 135 | 3.0 | 131 | 0.85 | 95.000 |
| 1m2f_A_25 | 135 | 135 | 3.0 | 134 | 0.94 | 95.000 |
| 1m2f_A_9 | 135 | 135 | 3.0 | 132 | 1.14 | 95.000 |
| 1m2f_A_4 | 135 | 135 | 3.0 | 130 | 1.01 | 94.444 |
| 1m2f_A_3 | 135 | 135 | 3.0 | 129 | 0.74 | 94.074 |
| 1m2f_A_23 | 135 | 135 | 3.0 | 132 | 1.00 | 93.704 |
| 1m2f_A_6 | 135 | 135 | 3.0 | 130 | 1.05 | 92.963 |
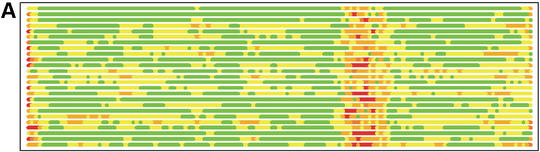
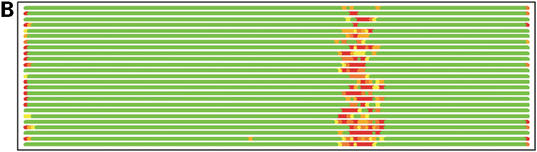
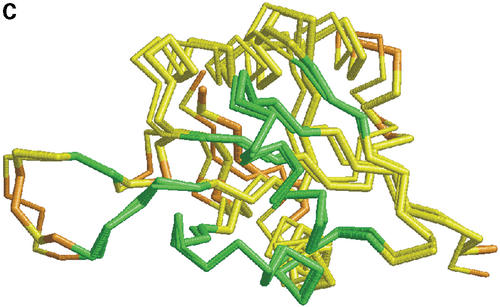
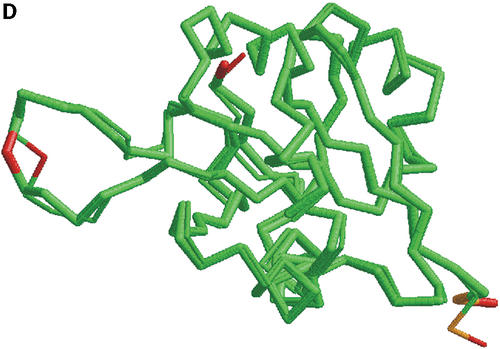
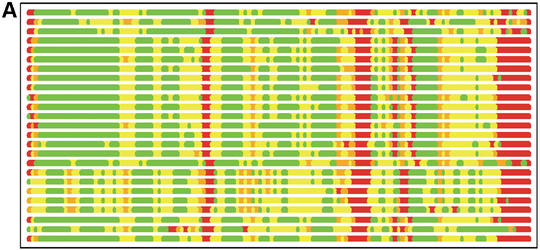
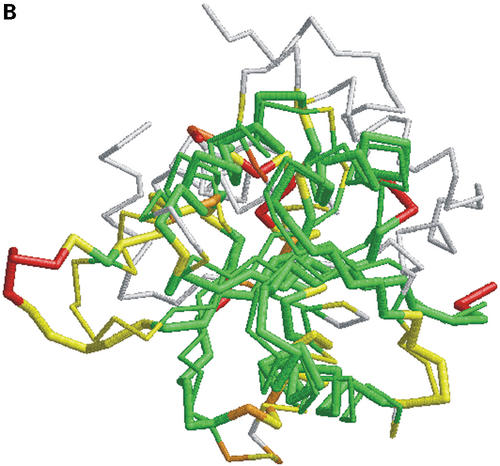
In Figure 1 we show how colored strip charts can be used to plot output from the LGA program (data from Tables 1 and 2). Each bar from Figure 1A or B corresponds to one pair of analyzed structures. The ordering of bars is the same as in Table 2. Rasmol plots (Fig. 1C and D) are provided only for one model, 1m2f_A_2 (fourth in Table 2 and bar charts).
Figure 1.
(A) C-alpha–C-alpha distance deviation bars from one LGA superposition under a 3.0 Å distance cutoff. Residues superimposed below 1.0 Å are in green, below 2.0 Å in yellow, below 3.0 Å in orange, below 4.0 Å in brown and residues at or above 4.0 Å in red. (C) RasMol plot of two superimposed structures: 1m2f_A_2 and 1m2e_A. Colors correspond to the fourth bar from (A). (B) C-alpha–C-alpha deviation bars for multiple LGA superpositions. (D) RasMol plot of superimposed structures 1m2f_A_2 and 1m2e_A corresponding to fourth bar representation from (B) where >85.0% of equivalent residues under distance cutoff=1.5 Å are in green, >70.0%: yellow, >50.0%: orange, >20.0%: brown and ≤20.0%: red.
Figure 1B shows that the results of multi-superposition LGA analysis as reported in Table 1 can be used to detect regions of similarity between proteins from those where the structures differ. Analysis based on a single superposition (Fig. 1A) does not distinguish the regions of similarity so clearly.
Graphical presentation of results from sequence independent database searches
The greatest utility of structure alignment programs, such as LGA, lies in their ability to superimpose protein structures regardless of sequence identity and to detect regions of structural similarity. In Table 3 we provide a list of 10 of the closest PDB structural matches to the already mentioned NMR average model 1m2e_A (CASP5 target T0138). The PDB database search was performed with the use of the LGA program working in sequence independent mode. The level of sequence identity (Seq_Id) to other structurally similar PDB entries was very low, on the order of 12%.
Table 3. List of the 10 of the closest PDB structures to 1m2e_A found by the LGA program. Proteins are sorted by N—the number of superimposed residues under a distance cutoff 5.0 Å.
| Name | N1 | N2 | DIST | N | RMSD | Seq_Id | LGA_S |
|---|---|---|---|---|---|---|---|
| 1a04_B | 205 | 135 | 5.0 | 118 | 2.36 | 11.86 | 63.707 |
| 1a2o_B | 347 | 135 | 5.0 | 117 | 2.47 | 11.97 | 62.598 |
| 1rnl | 200 | 135 | 5.0 | 116 | 2.14 | 12.07 | 69.416 |
| 1e6m_A | 128 | 135 | 5.0 | 116 | 2.23 | 10.34 | 64.587 |
| 6chy_A | 128 | 135 | 5.0 | 116 | 2.25 | 10.34 | 63.363 |
| 6chy_B | 128 | 135 | 5.0 | 116 | 2.26 | 10.34 | 64.196 |
| 2che | 128 | 135 | 5.0 | 116 | 2.28 | 9.48 | 64.372 |
| 1a0o_C | 128 | 135 | 5.0 | 116 | 2.29 | 10.34 | 63.826 |
| 1ffg_C | 128 | 135 | 5.0 | 116 | 2.29 | 10.34 | 63.161 |
| 1ffw_A | 128 | 135 | 5.0 | 116 | 2.32 | 9.48 | 62.522 |
Graphical presentation of the results from the LGA database search is given in Figure 2. Each bar corresponds to one hit to a protein from the PDB database. The bars are ordered as in Table 3. Figure 2A shows regions of structural similarity (in green) between the reference structure, 1m2e_A and each PDB database hit from Table 3. Regions of high structural diversity are shown in red. A RasMol plot (Fig. 2B) is given for the best database match, PDB protein, 1a04_B.
Figure 2.
Bar representation of the results from sequence independent LGA superpositions, and a RasMol plot of superimposed first template 1a04_B and T0138. Residues superimposed below 2.0 Å are in green, below 4.0 Å in yellow, below 6.0 Å in orange and residues at or above 6.0 Å or not superimposed are in red (target) and in white (template).
LGA IN COMPARISON WITH OTHER PROGRAMS
An important requirement for any structure comparison method is its ability to detect weak structural similarity. In the Table 4 we compare results of LGA to those of four methods available as web services and which are frequently used by the scientific community: VAST (8), DALI (1), CE (9) and ProSup (10). This identical dataset was used in a comparison of ProSup to other structural alignment programs [Table III in reference (10)].
Table 4. Comparison of structure alignments for 10 ‘difficult’ structures (11). For each protein pair the N and RMSD results from different methods are provided where N is a number of equivalent residues with the corresponding RMSD.
| Proteins | VAST | DALI | CE | ProSup | LGA | |
|---|---|---|---|---|---|---|
| 1bge-B | 2gmf-A | 71/2.3 | 94/3.3 | 107/3.9 | 87/2.4 | 91/2.5 |
| 1cew-I | 1mol-A | 75/2.0 | 81/2.3 | 81/2.3 | 76/1.9 | 79/2.0 |
| 1cid | 2rhe | 78/2.0 | 96/3.1 | 97/2.9 | 84/2.3 | 93/2.3 |
| 1crl | 1ede | 186/3.7 | 212/3.6 | 219/3.8 | 161/2.6 | 182/2.6 |
| 1fxi-A | 1ubq | 48/2.1 | 52/2.5 | 64/3.8 | 54/2.6 | 61/2.6 |
| 1ten | 3hhr-B | 76/1.5 | 86/1.9 | 87/1.9 | 85/1.7 | 87/1.9 |
| 1tie | 4fgf | 76/1.6 | 114/3.1 | 116/2.9 | 101/2.4 | 104/2.3 |
| 2sim | 1nsb-A | 299/4.2 | 289/3.2 | 275/3.0 | 248/2.6 | 269/2.6 |
| 2aza-A | 1paz | 70/2.1 | 82/3.0 | 84/2.9 | 82/2.6 | 80/2.2 |
| 3hla-B | 2rhe | 58/2.3 | 74/3.0 | 83/3.3 | 71/2.7 | 74/2.5 |
The number N of structurally equivalent residues differs considerably for several protein pairs. One would expect that a higher number of equivalent residues would indicate better performance of a particular method in the detection of structural similarity. However, comparing the number of equivalent residues is insufficient without taking RMSD into account. RMSD reported by LGA is fairly constant in all cases. Our program can keep the smallest range of RMSD 1.9–2.6 while providing a high number of aligned residues. In a comparison to ProSup, in some cases LGA superimposes more residues under the same distance cutoff (sometimes with a slightly higher value of RMSD). During the CASP4 competition, both programs were used for evaluation of structure predictions and to perform PDB searches showing similar results.
CONCLUSION
Optimizing the number of equivalent residues while keeping the RMSD constant provides a simple and intuitive measure of structure similarity (as concluded in 10). Such a measure can be used effectively for ranking in database searches. We show that in LGA an additional requirement of fulfilling distance restrictions combined with extensive analysis of regions of local similarities (from searches with multiple distance and RMSD cutoffs) was successfully implemented. Our approach can generate data that provide detailed information not only about the degree of global similarity but also about regions of local similarity in protein structures. It allows the clustering of similar fragments of structures, and the use of such clusters to identify sequence patterns that would represent local structural motifs.
Accessibility, limitations and further development of the program
An online LGA service is accessible at http://PredictionCenter.llnl.gov/local/lga. The required input consists of two sets of protein structure coordinates in PDB format. For calculations, a user can specify chains, residue segments or select isolated residues. As a result of LGA processing the user will get the translation/rotation matrices, the rotated coordinates of the first structure and (optionally) the coordinates of the second structure (target, unchanged). Depending on need, the user can choose between several options described in detail in the ‘help’ file. For example, there are four options: -1, -2, -3, -4 that allow the user to select the calculation method. Option-1 is a standard RMSD calculation performed on all selected residues in both structures. Option-2 allows the selection of a user specified distance cutoff (-d:f.f ), and only the residues within this distance cutoff will be superimposed using an iterative procedure as described in the section ‘The GDT algorithm’. Option-3 is used to generate detailed LCS and GDT information about regions of local and global similarity as shown in Table 1 (see section ‘Data generated by the LCS and GDT algorithms’). And finally, option-4 is used to perform the structure alignment search (structure comparison of proteins without a preassigned residue correspondence). With option ‘-d:f.f’, which specifies a distance cutoff in Ångstroms, the user may force LGA to calculate tighter or more relaxed superpositions for a selected region. The possible ranges for distance cutoff are from 0.1 to 10.0 Å. The default value is 5 Å. For a description of more advanced options please consult the online documentation.
The program reports a single, final superposition and no alternative alignments are provided. In the current version of the LGA server, a text-only output is available. A future release of the service will contain a graphical presentation package to generate plots as shown in Figures 1 and 2.
Acknowledgments
ACKNOWLEDGEMENTS
The author thanks John Moult for establishing the CASP experiment during which the LGA program was extensively tested. The CASP assessors have contributed valuable comments on the use of the results from LGA for CASP evaluations. The author also wishes to thank Michael Levitt for his valuable suggestions on the LGA program and its performance. Finally, the author thanks his colleagues from LLNL: Tom Slezak for his continuous help and support, Ceslovas Venclovas and Daniel Barsky for their comments in using the program and Carol Zhou and Dorota Sawicka for critical reading of the manuscript. This work was performed under the auspices of the US Department of Energy by the University of California, Lawrence Livermore National Laboratory under Contract No. W-7405-Eng-48.
REFERENCES
- 1.Holm L. and Sander,C. (1993) Protein structure comparison by alignment of distance matrices. J. Mol. Biol., 233, 123–138. [DOI] [PubMed] [Google Scholar]
- 2.Feng Z.K. and Sippl,M.J. (1996) Optimum superimposition of protein structures: ambiguities and implications. Fold Des., 1, 123–132. [DOI] [PubMed] [Google Scholar]
- 3.Zemla A., Venclovas,C., Reinhardt,A., Fidelis,K. and Hubbard,T.J. (1997) Numerical criteria for the evaluation of ab initio predictions of protein structure. Proteins, S1, 140–150. [DOI] [PubMed] [Google Scholar]
- 4.Zemla A., Venclovas,C., Moult,J. and Fidelis,K. (1999) Processing and analysis of CASP3 protein structure predictions. Proteins, S3, 22–29. [DOI] [PubMed] [Google Scholar]
- 5.Orengo C.A., Bray,J.E., Hubbard,T., LoConte,L. and Sillitoe,I. (1999) Analysis and assessment of ab initio three-dimensional prediction, secondary structure, and contacts prediction. Proteins, S3, 149–170. [DOI] [PubMed] [Google Scholar]
- 6.Zemla A., Venclovas,C., Moult,J. and Fidelis,K. (2001) Processing and evaluation of predictions in CASP4. Proteins, 45 (Suppl. 5), 13–21. [DOI] [PubMed] [Google Scholar]
- 7.Tramontano A., Leplae,R. and Morea,V. (2001) Analysis and assessment of comparative modeling predictions in CASP4. Proteins, 45 (Suppl. 5), 22–38. [DOI] [PubMed] [Google Scholar]
- 8.Gibrat J-F., Madej,T. and Bryant,S.H. (1996) Surprising similarities in structure comparison. Curr. Opin. Struct. Biol., 6, 377–385. [DOI] [PubMed] [Google Scholar]
- 9.Shindyalov I.N. and Bourne,P.E. (1998) Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng., 11, 739–747. [DOI] [PubMed] [Google Scholar]
- 10.Lackner P., Koppensteiner,W.A., Sippl,M.J. and Domingues,F.S. (2000) ProSup: a refined tool for protein structure alignment. Protein Eng., 13, 745–752. [DOI] [PubMed] [Google Scholar]
- 11.Fischer D., Eloffson,A., Rice,D.W. and Eisenberg,D. (1996) Proceedings of the 1st Pacific Symposium on Biocomputing. In Hunter,L. and Klein,T. (eds), World Scientific Publishing Company, Singapore, pp. 300–318. [Google Scholar]