Geno2pheno: estimating phenotypic drug resistance from HIV-1 genotypes

Abstract

Therapeutic success of anti-HIV therapies is limited by the development of drug resistant viruses. These genetic variants display complex mutational patterns in their pol gene, which codes for protease and reverse transcriptase, the molecular targets of current antiretroviral therapy. Genotypic resistance testing depends on the ability to interpret such sequence data, whereas phenotypic resistance testing directly measures relative in vitro susceptibility to a drug. From a set of 650 matched genotype–phenotype pairs we construct regression models for the prediction of phenotypic drug resistance from genotypes. Since the range of resistance factors varies considerably between different drugs, two scoring functions are derived from different sets of predicted phenotypes. Firstly, we compare predicted values to those of samples derived from 178 treatment-naive patients and report the relative deviance. Secondly, estimation of the probability density of 2000 predicted phenotypes gives rise to an intrinsic definition of a susceptible and a resistant subpopulation. Thus, for a predicted phenotype, we calculate the probability of membership in the resistant subpopulation. Both scores provide standardized measures of resistance that can be calculated from the genotype and are comparable between drugs. The geno2pheno system makes these genotype interpretations available via the Internet (http://www.genafor.org/).

INTRODUCTION

A panel of 17 approved antiretroviral agents is currently available for treating infections with human immunodeficiency virus type 1 (HIV-1). Each of these drugs targets one of the two viral enzymes protease or reverse transcriptase (RT). Despite the introduction of combination therapies, treatment success is limited due to the evolution of drug resistant variants (1). Thus, resistance testing has become an important diagnostic tool in the management of HIV infections (2,3).

Resistance testing can be performed either by measuring viral activity in the presence and absence of a drug [phenotypic resistance testing (4)] or by scanning the viral genome for resistance-associated mutations (genotypic resistance testing). Direct sequencing of the HIV pol gene, which codes for protease and RT, produces genomic data of ∼1200 bp, while phenotypic test results are usually reported as resistance factors, defined as the fold-change in susceptibility to the drug relative to a susceptible reference virus. It has been shown that patients can benefit from both genotypic and phenotypic testing (5), but genotyping is faster and cheaper, whereas phenotypic results, represented by a single number for each drug, are easier to handle. In principle, the DNA sequence should determine the resistance phenotype. However, it is challenging to retrieve phenotypic information from the genotype due to complex mutational patterns.

Several expert groups have approached this problem by extracting classification rules from the scientific literature. Links between genetic variations and resistance have been established by site directed mutagenesis experiments, by observing genetic changes under continuous drug pressure in cell culture or by analysis of clinical samples derived from patients after failing (mono-)therapy (6). These rule sets classify genotypes into two or more categories ranging from ‘susceptible’ to ‘resistant’. Some of them aim at predicting not only phenotypic resistance, but also therapy response by considering data on clinical outcomes. Besides these knowledge-based systems, statistical and machine learning approaches have been applied successfully to matched genotype–phenotype pairs in order to solve this classification problem (7–9). After defining certain phenotypic cut-off values, classification models are learned from labelled sequences. In some cases these data-driven approaches lead to parsimonious models, but in general they produce models that are harder to interpret. However, unlike with rules-based systems, model construction and update can be automated and model parameters such as sensitivity or specificity can be controlled explicitly.

In the geno2pheno system two machine learning approaches, decision trees and support vector machines (SVM), have been implemented for a range of different cut-offs (8,9). On submitting an HIV-1 pol gene sequence, users of this web service can obtain classification results for each of the 17 drugs and a selected cut-off value. Because of the difficulty of finding appropriate cut-off values, we here extend the data analysis approach to quantitative phenotype predictions by using support vector machines (SVM). This machine learning technique appears appropriate for a regression problem with many free variables (sequence positions) and a target variable (resistance factor) subject to considerable noise. We present SVM regression models that can predict the fold-change in susceptibility from the genotype. These predicted resistance factors are then compared with predictions obtained from genotypes from untreated patients and with the distribution of predicted resistance factors over a large set of clinical samples. The resulting scores provide continuous measures of resistance that are comparable between different drugs. In particular, we will derive definitions of susceptibility and resistance based on the statistics of all predictions and derive a probability score that allows for discriminating between these two classes.

METHODS

Arevir database

The Arevir database is a multi-center clinical database containing patient data, therapies, clinical and virological markers, as well as genotypic and phenotypic resistance test results. The experimental setup for genotyping and the phenotypic recombinant virus assay have been described elsewhere (4,9). Subtypes have been determined as the most significant hits in a BLAST search against the 93 pol gene reference sequences provided by the Los Alamos HIV Sequence Database (http://hiv-web.lanl.gov/content/hiv-db/SUBTYPE_REF/Table1.html). For the present study we use three different sets of sequences: the first set consists of 652 genotypes, including 604 subtype B and 48 (7.4%) non-B sequences, that have also been phenotyped. The majority of these sequences have been deposited in GenBank (accession numbers AF347117 to AF347605). The second set comprises 184 sequences, which have been identified from patients that have not been treated with any antiretroviral drug before (therapy-naive patients). Six sequences with obvious indications of transmission of a drug resistant virus have been removed from this set. The remaining 178 sequences [124 subtype B, 54 (30.3%) non-B] are used for assessing the natural variation of predicted phenotypes among therapy naive patients. The third set consists of 2000 sequences [1695 B, 305 (15.3%) non-B], including samples from the first two sets, that have been selected randomly from the database in order to estimate the unconditional probability density of predicted phenotypes found in clinical isolates. All calculations involving resistance factors are performed on logarithmized values to base 10 and are reported as such.

Support vector regression

For developing a regression model, sequences have been aligned to the reference strain HXB2 and each sequence position gives rise to 20 indicator variables, one for each amino acid. We use all 99 sequence positions of the protease and the first 220 positions of the RT. A further attribute indicating the presence of the 69SS insertion complex is added for the RT. Thus, the input space dimensions are 1980 and 4401 for protease and RT, respectively. These high-dimensional regression problems are solved with a linear support vector machine (SVM) with an epsilon-insensitive loss function (10). For all drugs, epsilon is fixed at 0.1 such that prediction errors of <0.1 log₁₀-resistance factors are not penalized in the training phase. The regularization parameter C that controls the trade-off between minimizing training error and model complexity is determined by cross-validation for each drug separately. We use the LIBSVM software library for solving the SVM optimization problem (Chang,C.-C. and Lin,C.-J., 2001, http://www.csie.ntu.edu.tw/~cjlin/libsvm). For each drug, a linear regression function represented as a weighted sum over all sequence positions is learned from the data.

Density estimation

Standard procedures are used for fitting the parameters of a normal distribution. Bimodal distributions of resistance factors (RF) are fitted to a two-component mixture model. The density of x=log₁₀RF is modelled as α · φ(x; μ₁, σ₁) +(1−α) · φ(x; μ₂, σ₂), where we denote by φ(x;μ,σ) the density of the normal distribution with mean μ and standard deviation σ, and the mixing parameter by α. Parameters are estimated from the data by applying the EM algorithm (11). The solutions obtained from this iterative fitting procedure are virtually independent of variations in the starting solution.

Class probabilities

In the generative two-component mixture model we can assume μ₁<μ₂ and refer to samples originating from the left Gaussian bump as ‘susceptible’ and to the others as ‘resistant’. Within this model we consider the log-likelihood function that decides whether a given resistance factor is more likely to belong to the resistant than to the susceptible group. This quantity is approximated by a linear function L in order to obtain the monotonic function (1+e^−L(x))⁻¹, which can be shown to approximate the conditional class probability prob(resistant|x) of membership in the resistant subpopulation.

Although the mixture model has five free parameters, the probability scoring function has only two due to the linear approximation of the log-likelihood. Thus, as a measure of confidence in the fitted function, we report confidence intervals for the location of the inflection point and the gradient in this point estimated from 1000 bootstrap samples.

RESULTS

Regression analysis

For each drug, a regression model is generated from matched genotype–phenotype pairs. The ability of these models to generalize from the training data was assessed by 10-fold cross-validation and is reported as the mean squared error and as the squared correlation coefficient between predicted and observed log₁₀ resistance factors (Table 1). Since the range of observed resistance factors differs substantially among drugs, only the latter measure of performance allows for comparisons between drugs. Estimated squared correlation coefficients vary between 0.3 and 0.79 with an average of 0.6 (±0.14) indicating that the models account for 30–79% of phenotypic variance.

Table 1. Results from regression analysis.

Drug	N	MSE (SE)	r2
ZDV	649	0.554 (0.040)	0.62
ddI	649	0.101 (0.009)	0.42
ddC	534	0.122 (0.013)	0.30
d4T	649	0.145 (0.015)	0.33
3TC	648	0.332 (0.019)	0.72
ABC	637	0.075 (0.011)	0.60
TDF	321	0.091 (0.005)	0.50
NVP	649	0.638 (0.056)	0.55
DLV	648	0.476 (0.033)	0.55
EFV	634	0.354 (0.026)	0.60
SQV	652	0.204 (0.022)	0.71
IDV	652	0.197 (0.017)	0.73
RTV	652	0.176 (0.017)	0.79
NFV	651	0.207 (0.011)	0.71
APV	464	0.173 (0.013)	0.65
LPV	307	0.169 (0.016)	0.73
ATV	305	0.262 (0.034)	0.61

Drugs are encoded in three-letter code, nucleoside inhibitors of the RT: zidovudine (ZDV), zalcitabine (ddC), didanosine (ddI), stavudine (d4T), lamivudine (3TC), abacavir (ABC) and tenofovir disoproxil fumarate (TDF); non-nucleoside RT inhibitors: nevirapine (NVP), delavirdine (DLV) and efavirenz (EFV); and protease inhibitors: saquinavir (SQV), indinavir (IDV), ritonavir (RTV), nelfinavir (NFV), amprenavir (APV), lopinavir (LPV) and atazanavir (ATV). Predictive performance was estimated from 10-fold cross-validation and is reported as the mean squared error (MSE), its standard error (SE) and the squared correlation coefficient (r²) between predicted and observed log₁₀-resistance factors.

Variation among drug-naive patients

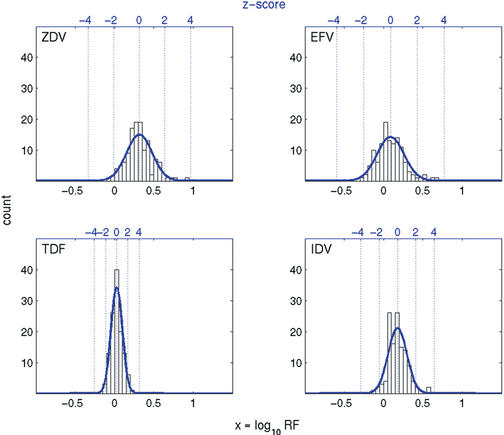
In order to quantify natural variation of predicted resistance factors among patients that have not received any antiretroviral medication before, we predict phenotypes from a set of genotypes derived from untreated patients. We observe significant differences in predictions between subtype B and non-B sequences for zalcitabine, nevirapine, delavirdine and nelfinavir (rank sum tests, adjusted for multiple testing at a false discovery rate of 1%). However, since the prediction models have been trained on a set of matched genotype–phenotype pairs containing <8% of non-B sequences, we cannot rule out the possibility that this finding is an artifact of the regression function. Therefore, we restrict the analysis of samples from treatment-naive patients to the 124 subtype B sequences. For all drugs, the resistance factors predicted from this set follow a normal distribution. Table 2 reports estimates for the mean and the standard deviation. We observe considerable differences between drugs for both parameters. In Figure 1, four representative examples are displayed (see Supplementary Material for all drugs). Once we know these distributions, we can report for each predicted phenotype how many standard deviations it is away from the mean among drug-naive patients. This z-score provides a standardized and comparable measure of deviation from the expected value for the untreated subtype B subpopulation.

Table 2. Results from density estimations.

Drug	Distribution parameter estimates
	Drug-naive subpopulation (N=124)		Whole population (N=2000)					Probability score parameter estimates
	mean RF [95% CI]	std [95% CI]	α	μ1	σ1	μ2	σ2	xi [95% CI]	grad [95% CI]
ZDV	0.315 [0.286; 0.344]	0.163 [0.144; 0.186]	0.433	0.260	0.188	1.827	0.651	0.682 [0.648; 0.717]	14.655 [13.736; 15.613]
ddI	0.096 [0.085; 0.108]	0.065 [0.058; 0.074]	0.686	0.241	0.165	0.588	0.334	0.500 [0.332; 0.652]	10.525 [4.525; 12.675]
ddC	0.050 [0.041; 0.058]	0.046 [0.041; 0.053]	0.283	0.069	0.056	0.369	0.215	0.146 [0.136; 0.157]	29.652 [26.291; 33.180]
D4T	0.081 [0.071; 0.091]	0.057 [0.051; 0.066]	0.481	0.091	0.075	0.411	0.246	0.217 [0.197; 0.239]	25.860 [23.240; 28.715]
3TC	0.186 [0.166; 0.207]	0.114 [0.101; 0.131]	0.564	0.399	0.303	2.117	0.301	1.275 [1.226; 1.320]	18.880 [17.776; 20.020]
ABC	0.098 [0.088; 0.107]	0.054 [0.048; 0.061]	0.272	0.084	0.053	0.631	0.281	0.189 [0.178; 0.200]	42.319 [38.796; 46.374]
TDF	0.027 [0.014; 0.040]	0.071 [0.063; 0.081]	0.394	0.002	0.078	0.420	0.229	0.134 [0.120; 0.149]	27.307 [25.342; 29.391]
NVP	0.306 [0.270; 0.342]	0.201 [0.179; 0.230]	0.549	0.259	0.269	1.742	0.624	0.815 [0.776; 0.854]	10.105 [9.447; 10.734]
DLV	0.235 [0.212; 0.258]	0.130 [0.116; 0.149]	0.569	0.183	0.192	1.260	0.592	0.576 [0.528; 0.641]	12.654 [11.861; 13.494]
EFV	0.088 [0.057; 0.119]	0.171 [0.152; 0.196]	0.558	0.056	0.215	1.280	0.573	0.501 [0.443; 0.563]	12.073 [11.234; 12.973]
SQV	0.084 [0.064; 0.103]	0.110 [0.098; 0.126]	0.546	0.070	0.119	1.142	0.619	0.345 [0.325; 0.366]	21.406 [20.154; 22.643]
IDV	0.177 [0.156; 0.198]	0.117 [0.104; 0.134]	0.575	0.164	0.141	1.271	0.520	0.494 [0.472; 0.516]	19.383 [18.405; 20.380]
RTV	0.124 [0.104; 0.144]	0.112 [0.100; 0.128]	0.564	0.115	0.121	1.370	0.635	0.414 [0.390; 0.439]	22.828 [21.620; 24.155]
NFV	0.134 [0.105; 0.162]	0.161 [0.143; 0.184]	0.534	0.135	0.174	1.262	0.511	0.509 [0.482; 0.537]	15.228 [14.398; 16.144]
APV	0.066 [0.039; 0.093]	0.152 [0.135; 0.174]	0.585	0.067	0.142	0.851	0.504	0.358 [0.340; 0.376]	16.295 [15.444; 17.173]
LPV	0.074 [0.052; 0.096]	0.123 [0.109; 0.140]	0.576	0.046	0.136	1.060	0.598	0.351 [0.328; 0.376]	18.353 [17.362; 19.433]
ATV	0.164 [0.142; 0.186]	0.124 [0.111; 0.142]	0.544	0.166	0.132	1.061	0.480	0.448 [0.416; 0.479]	18.899 [17.841; 20.102]

Three-letter drug codes are given in the legend of Table 1. Mean and standard deviation (std) of the normal distributions found for samples from drug-naive patients are given together with 95% confidence intervals (CI). Parameters of the mixture model α·φ(x; μ₁, σ₁)+(1−α)·φ(x; μ₂, σ₂) were estimated from 2000 random samples. Confidence intervals at the 95% level for the location of the inflection point (x_i) and its gradient (grad) provide a measure of dependence of the fitted probability score on the data.

Figure 1.

Histogram data and fitted normal density for predicted resistance factors from subtype B genotypes derived from 124 treatment-naive patients. The bottom x-axes refer to log₁₀ resistance factors (RF), whereas the top x-axes denote z-scores (numbers of standard deviations from the mean).

Density estimation

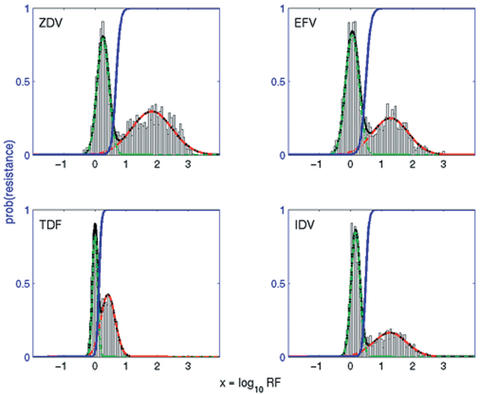
We can gain more information on the meaning of a predicted resistance factor by studying the distribution of predictions over all genotypes. Analysis of a random sample of 2000 sequences shows large differences in range, location and deviation of modes, but also reveals the bimodal nature of the distribution common to all drugs (Fig. 2 and Supplementary Material). Thus, the probability density is approximated with a two-component Gaussian mixture model. Table 2 shows the parameter estimates of this model for all drugs and Figure 2 displays the fitted density curves for the four drugs from Figure 1 (see Supplementary Material for all drugs). Since bimodality is less pronounced for zalcitabine and didanosine, the modes intersect more heavily for these drugs. Restriction to subtype B sequences does not lead to significantly different estimates (data not shown).

Figure 2.

Histogram data and Gaussian mixture model fit for predicted resistance factors for 2000 samples drawn randomly from the population. Displayed are the bimodal mixture density (black line) and the densities for the suscepatible (dashed green line) and resistant (dashed red line) subpopulations. The conditional class probability of belonging to the resistant subpopulation given the predicted phenotype is plotted as a blue line.

The two Gaussian components give rise to an intrinsic definition of susceptibility and resistance. Thus, we can calculate the probability of belonging to the resistant subpopulation given a predicted resistance factor. In Figure 2 the cumulative density of this probability is plotted as a function of the predicted phenotype (cf. also Supplementary Material). Table 2 summarizes the parameter estimates. Different curve shapes and locations reflect differences in the transition from susceptibility to resistance. The probability score provides a normalized and comparable measure of resistance for all antiretroviral drugs.

Geno2pheno

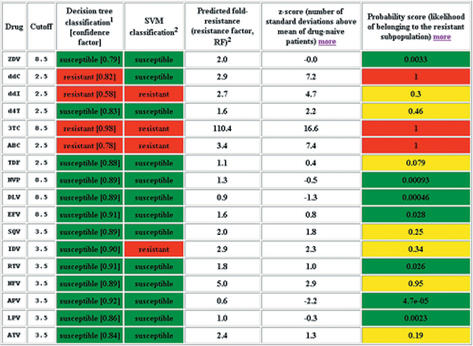
For a submitted pol gene sequence the geno2pheno system returns an alignment to the reference strain HXB2, classification results according to the preset cutoffs, the predicted resistance factors, z-scores relative to treatment-naives and probability scores for all drugs. Figure 3 shows a sample output of these measures of resistance. The geno2pheno web service is freely available at http://www.genafor.org/.

Figure 3.

Screenshot showing part of the output of the geno2pheno web service. Three-letter drug codes are given in the caption of Table 1. The table contains classification results [columns three and four, discussed in (3,4)], predicted phenotypes (column five), z-scores (column six) and probability scores (column seven). Only classification results are affected by the choice of cut-offs.

DISCUSSION

Genotypic resistance testing has become part of routine diagnostics in the treatment of HIV infected patients. However, its clinical benefit is limited in practice by the complex relationship between genotypic variations on the one hand and phenotypic resistance in vitro and treatment response in vivo on the other hand. The geno2pheno system has been designed to support the interpretation of sequence data resulting from genotypic resistance tests. Here we have presented regression models that can predict the fold-change in susceptibility to a drug from the genotype. These models translate complex mutational patterns into a single resistance factor for each drug. Since the range of this quantity differs considerably between the various antiretroviral agents, we propose two transformations.

Firstly, we report the deviation of a predicted resistance factor from the mean value for samples from treatment-naive patients. Similar to results for experimentally determined phenotypes in drug-naive patients (12), the distribution of predicted phenotypes also shows substantial variation between drugs, but follows a normal distribution in every case. Thus, the z-score that denotes how many standard deviations the predicted resistance factor for a given sample and drug is away from the mean for treatment-naive patients provides a measure of drug resistance that is better comparable between drugs than the absolute predicted resistance factors. We have excluded from this analysis subtype non-B sequences, because the small number of phenotyped non-B sequences does not allow for a definite conclusion about non-B baseline resistance profiles.

Secondly, we propose a score that quantifies the probability of a sample to originate from the resistant rather than the susceptible subpopulation given the predicted resistance factor. Thus, the notion of resistance arises only from the distribution of predicted phenotypes that were estimated from a large random clinical sample. The bimodal nature of these distributions suggests a ‘two-state model’ of the virus: a susceptible (wild type) state that is attained preferably in the absence of drug and a resistant state that is advantageous and hence more frequently observed under drug pressure. Unlike z-scores with respect to drug-naive patients, the probability score exploits information on location and variance of both the susceptible and the resistant subpopulation. As a probability, this score is normalized to the interval [0; 1] and interpretable without predetermined cut-off values.

Both scores are based on test statistics that are derived from predicted phenotypes. Thus, we fit the distribution parameters to predicted rather than experimentally determined phenotypes, because prediction introduces an additional source of noise and systematic biases are accounted for.

The ultimate goal of genotype interpretation is to provide a direct estimate of expected treatment response. This task is much more difficult than drug-wise resistance predictions, because complex clinical data have to be included and the in vivo effect of a therapy depends on additional factors such as patients adherence and drug pharmacokinetics. Moreover, mono-therapies are obsolete and there is a large number of possible combination therapies. Nevertheless, the problem could be approached in a similar fashion albeit based on substantially larger datasets (13). Another promising approach is to use the individual phenotype predictions as building blocks for a scoring function that is defined on any drug combination (14). Towards this end, it has been shown that the SVM based phenotype predictions can be integrated into a scoring scheme that is predictive of virological response (15). We plan to integrate such services into the geno2pheno system in the future when they have reached an adequate level of quality and after careful statistical validation and practical testing.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.