Comprehensive quantitative analyses of the effects of promoter sequence elements on mRNA transcription

Abstract

We have generated a WWW interface for automated comprehensive analyses of promoter regulatory motifs and the effect they exert on mRNA expression profiles. The server provides a wide spectrum of analysis tools that allow de novo discovery of regulatory motifs, along with refinement and in-depth investigation of fully or partially characterized motifs. The presented discovery and analysis tools are fundamentally different from existing tools in their basic rational, statistical background and specificity and sensitivity towards true regulatory elements. We thus anticipate that the service will be of great importance to the experimental and computational biology communities alike. The motif discovery and diagnosis workbench is available at http://longitude.weizmann.ac.il/rMotif/.

INTRODUCTION

In recent years, genomic technological advancements have transformed the study of gene regulatory networks (1). While traditional studies in the field were usually designed to address individual genes and small networks, the combination of genomic sequence information with transcriptome-wide mRNA abundance monitoring has made it possible to deduce the structure of gene regulatory networks at an unprecedented throughput. A major focus of current computational methods that utilize such genome-wide data is the identification of promoter elements, short oligonucleotides, of ∼6–20 nt, that usually affect expression through specific interactions with transcription factor proteins. A popular and successful paradigm is based on clustering of mRNAs according to expression profiles, followed by the application of motif finding algorithms that look for shared motifs in the promoter sequences of co-expressed genes (2–4). Complementary methods perform such motif finding searches on the promoters of orthologous genes, assuming that functional regulatory sites should display particularly high conservation among diverging species (5–7). Common to all such methods is the search for motifs whose extent of representation in the analyzed data significantly exceeds that anticipated by chance given an appropriate background random model.

These efforts were useful in successful reconstruction of known regulatory motifs and they also resulted in numerous testable predictions, some of which were proven experimentally (8–10). However, such methodologies are prone to a considerable amount of both false-positive and false-negative motif predictions. Many false-positive predictions are motifs that occur also in the promoters of many genes outside of the mRNA expression cluster from which they were derived. These motifs are usually not sufficient to determine particular expression patterns. On the other hand, such over representation-based methods are, by definition, of limited scope, their false-negatives are motifs that occur in sets of genes that are smaller than the size threshold required for their detection with sufficient statistical significance.

We propose an alternative motif discovery and analysis tool that will meet these two opposing challenges at once. This is based on our previously introduced notion of expression coherence (EC), a measure of the extent to which a set of genes (e.g. genes that contain a given motif in their promoter) display expression profiles similar to each other at a given set of conditions (11,12). Formally, the EC score of a set of N genes is defined as the number p of pairs of genes in the set for which the Euclidean distance between the mean and variance normalized expression profiles falls below a threshold, D, divided by the total number of pairs of genes in the set EC=p/[0.5 * N * (N−1)] (11). While in previous analyses we have mainly used a corollary of this definition to detect functional interactions between different motifs (11,12), we devote the current effort to using this measure for the discovery, refinement and in-depth analyses of individual motifs, the building blocks of subsequent combinatorial motif reconstructions. Scoring motifs according to the EC of the genes under their regulation ensures that only motifs that occur among tightly co-expressed genes would score highly. In addition, by introducing an appropriate alternative statistical model (see below) it also alleviates the need that detectable motifs will appear at a particularly high number of genes. Our expression pattern-based statistical model, that computes probabilities of obtaining the observed or higher EC scores by chance, relaxes the requirement that motifs will be particularly abundant and thus provides us with enhanced sensitivity towards promoter motifs that regulate very small transcriptional networks.

MATERIALS AND METHODS

Our WWW server is implemented with Perl CGI scripts. Computations and graph drawings are performed with Matlab (Mathworks, MA) code invoked from Perl. All yeast mRNA expression data were taken from ExpressDB (http://arep.med.harvard.edu/ExpressDB/). Regulatory motifs were obtained from TRANSFAC (http://transfac.gbf.de/TRANSFAC/) and from our motif combination supplementary WWW page (http://genetics.med.harvard.edu/~tpilpel/MotCoOc/MotCoOc.html). The TFBS (13) Perl module (http://forkhead.cgb.ki.se/TFBS) was utilized for multiple tasks, mainly for manipulation of position specific weight matrices for promoter scanning, calculation of information content of matrices and drawing of sequence logos, in addition to interfacing with TRANSFAC.

THE REGULATORY MOTIF WWW SERVER

We have developed a WWW server that provides the experimental and computational biology communities a comprehensive rigorous and easy-to-use interface to our wide set of motif discovery and analysis algorithms, statistical inference models and graphical representations.

A detailed exploration of regulatory motifs usually amounts to the considerable experimental effort of mutating individual nucleotide positions in the motifs, or entire sites, followed by connecting such mutated promoters to reporter genes for readout of the effect that various mutations exert on expression (14). This may be important for understanding DNA–protein interaction, for engineering of novel promoter elements and for understanding functional differences among alternative forms of motifs (15–18). Yet, for high throughput analyses of multiple candidate motifs, a fast computational method may be crucial. Interestingly it seems that evolution ‘performed’ some of the desired experiments—given a regulatory motif, one can typically find in the genome promoter elements that contain the motif of interest, yet, with various extents of deviation from its consensus. In addition, numerous whole genome mRNA expression measurements, combined with genomic sequence information, allow the measurements of expression profiles of genes that carry in their promoters particular motifs or variations on them. Such computational experiments constitute a recurring theme common to most of the motif discovery and analysis algorithms implemented in this WWW service.

The service is composed of several modules that correspond to different levels of prior knowledge about regulatory motifs.

Motif characterization

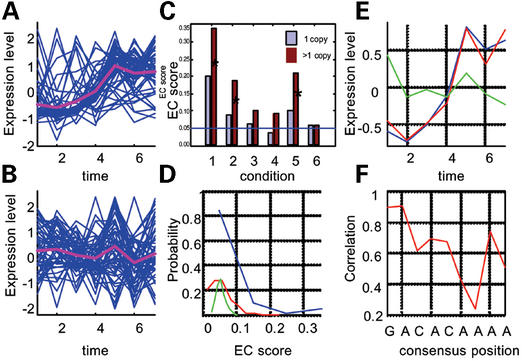
This module should be used when a solid hypothesis about the identity of a regulatory motif exists. The sources for such hypotheses may include phylogenetic footprinting (5–7) or experimental data (17,19). Given a genome sequence, mRNA expression dataset and a known or putative motif of interest, this module provides a quantitative ‘diagnosis’ of the effect that the motif exerts on expression patterns, calculated in terms of the EC score of the genes in which it occurs. Figure 1A–F demonstrates some of the available features. Figure 1A and B shows the expression profiles of yeast genes that contain in their promoter the sporulation transcription factor Ndt80, during sporulation and during MAPK signaling experiments (20,21). Clearly, the EC score of this same set of genes is particularly high for the sporulation time series and is much lower in the MAPK signaling experiment. Since Ndt80 is a sporulation factor, with no known involvement in MAPK signaling, this example demonstrates our ability to identify correctly the conditions to which regulatory motifs are relevant—the conditions in which their EC scores are significantly high. The user may thus scan a motif of interest against all available conditions and reveal subsets of conditions relevant to their motif.

Figure 1.

mRNA expression profiles of genes that contain the yeast sporulation motif Ndt80 measured during sporulation (A) (20) and during signaling through the MAPK pathway (B) (21). (C) The effect of multiple copies of a motif in promoters as demonstrated by the yeast cell cycle regulator, MCB. EC score was measured in six conditions: (1) cell cycle (26); (2) sporulation (20); (3) diauxic shift (27); (4) heat-shock (28); (5) MAPK signaling (21); and (6) DNA-damage response (29); for the genes that have one copy of the motif and for genes that have two or more copies of the motif in their promoters. The MCB position specific weight matrix (http://genetics.med.harvard.edu/~tpilpel/MotifList.html) was used to assign the motif to promoters using ScanACE (25) as reported previously (5). Conditions in which the EC score of the genes that have multiple copies is significantly higher than that of the genes that have a single copy are marked with ‘*’. The P-values on these hypotheses were calculated as before (11). (D) An example of three probability distributions of EC scores for random sets of genes of size 10 (blue), 30 (red) and 100 (green), obtained for the heat-shock experiment. (E and F) The effect of nucleotide substitutions at different positions within the motif on expression coherence. Shown in (E) are the averaged expression profiles, during sporulation, of genes that have the consensus Ndt80 motif (blue) and genes that have an A→T substitution relative to the consensus at the second position (red) and genes that have an A→G substitution relative to the consensus at the seventh position (green). (F) The averaged tolerance to substitution for each nucleotide position within the motif was defined as the averaged correlation coefficient between the averaged expression profiles of the genes that have a perfect match to the consensus motif and the averaged expression profiles of the genes that have each of the three possible substitutions relative to the consensus in that position.

Another feature that may be captured by our analyses is the effect of multiple copies of the same motif on mRNA expression. Previous reports have shown that often motifs may occur in multiple copies in the promoters of the genes under their regulation (22–24). Here we wish to provide the community with a computational means to easily further investigate the potential functional consequence of such multiple occurrences of motifs, through analysis of the effect that motif copy number may exert on mRNA expression profiles. We demonstrate the utility of the tool in Figure 1C that shows the EC scores, in multiple conditions, of genes that have a single copy of the yeast cell cycle regulatory motif, MCB, and the EC scores of genes that have two or more copies of that motif in their promoter. In three out of the six conditions examined, the EC score of genes that have multiple copies of the motif were significantly (<0.01) higher than the EC scores of genes that have a single copy of that site (see legend).

Figure 1D demonstrates the way we calculate the P-value on the hypothesis that a given EC score or higher, obtained with a gene set of a given size at a particular time course/set of conditions, may be observed by chance by a random set of genes of the same size in the same condition. This is done by a pre-computation of a set of distributions of the EC scores, each obtained for 1000 random sets of genes for various values of gene sizes, at each of the analyzed conditions. The estimated P-value for a given motif is simply the fraction of random samples of the same size that had at the same condition the same EC score or higher. In cases where that fraction equals zero, a lower bound (<0.001) on the significance is reported. Note that the P-values for EC scores are inversely proportional to the size of the gene set. Thus EC scores that are even only slightly higher than the score expected by chance (0.05) may be highly significant if they are obtained with large enough gene sets. For instance the P-value for an EC score of 0.07, obtained for a motif occurring in >100 genes would be estimated to be <0.001 (see the server for detailed relationship between EC score, gene set size and P-values).

Figure 1E demonstrates the additional mode of analysis provided by the server that allows a more in-depth examination of the significance of individual nucleotide positions within motifs. In this figure, we have examined the expression profiles of genes that have two alternative substituted forms of the sporulation factor Ndt80. The first gene set has a promoter element that deviates from the consensus at positions 2 while the second set deviates at position 7. While deviation from the consensus at the second position did not result in considerably altered expression profiles, the seventh position showed much higher sensitivity to variation on the motif. Figure 1F provides such quantitative analysis for all nucleotide positions in the motif in the form of a profile of tolerance to substitutions at each nucleotide position. While the first and second positions in the example show relatively high tolerance to substitutions, the seventh shows the highest sensitivity to substitutions.

Motif refinement

This module should be used when the user has a good knowledge about the identity of a regulatory motif, yet they consider potential local modifications of the motif. The WWW server provides two complementary modules for such refinements. The first module systematically attempts to extend the motif by additional nucleotides at both its ends. The second module performs systematic single nucleotide ‘substitutions’ at all nucleotide positions within the motif, as done in Figure 1F, yet this time not for characterizing the motif but for its refinement. In both cases we use improvement in EC scores of the modified motifs as a refinement engine.

Table 1 summarizes a test of the first module in which we asked whether a truncated version of a motif could be extended such that the original motif will be reconstructed. This is useful in the frequent cases in which prior knowledge provides only the ‘core’ of a motif. For benchmarking we used the sporulation factor Ndt80's binding site GACACAAAA. As an input we used the central seven nucleotides from that site, namely ACACAAA. The server generated 56 motifs by adding up to two nucleotides at one or both ends of the input motif. Each potential extended candidate was evaluated by its EC score and by a p-value on that score. Table 1 shows the top 10 scoring candidates, ranked by their EC scores. The EC score of GACACAAAA ranks at the top of this list and indeed to the best of our knowledge this is the correct binding site for that transcription factor (http://genetics.med.harvard.edu/~tpilpel/MotifList.html).

Table 1. Refinement of a core motif using an EC criterion.

P-value	No. of genes	EC score	Motif	Rank
<0.001	55	0.34	GACACAAAA	1
<0.001	21	0.34	CGACACAAA	2
<0.001	44	0.28	TGACACAAA	3
<0.001	23	0.21	GACACAAAC	4
<0.001	31	0.18	ACACAAACT	5
0.002	21	0.18	GACACAAAT	6
<0.001	38	0.17	ACACAAATT	7
<0.001	36	0.16	AGACACAAA	8
<0.001	45	0.15	CTACACAAA	9
<0.001	106	0.15	ACACAAAAA	10
0.003	130	0.1	ACACAAA	Original

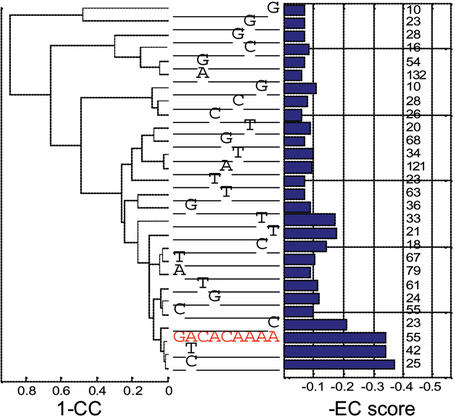
The ‘Motif Landscape’ module is an additional refinement and in-depth characterization tool for regulatory motifs. Here we allow the user to examine alternative substitutions relative to the input motif. For a systematic analysis and graphical depiction of the effect of alternative nucleotide positions in regulatory motifs on the expression patterns of downstream genes, we have modified our Combinogram workbench tool (11,12) to allow dissection of single motifs with a range of their substituted versions (see Fig. 2 for an example). For each consensus input motif of length L we examine the expression profiles of all sets of genes in the genome each containing one of the possible 3 * L single nucleotide substitutions relative to the consensus. Each gene set that contains a unique version of the motif is characterized by the expression profiles of all its genes and by their average. The graphic display shows the EC score in each such gene set and the similarity of their averaged expression profiles.

Figure 2.

A modified version of the Combinogram display designed to capture the effect of single nucleotide substitutions in regulatory regions on gene expression patterns. In this display, as in the original Combinograms, we represent the similarity of expression profiles between gene sets (1-correlation coefficients of their expression profiles, left side of the display) and within sets of genes (the EC score, right side of the display). The middle section displays the different promoter sequence elements shared among all the genes that are represented by each row of the display. The red motif is the consensus sequence and it represents all the genes that have a perfect match to it. The rest of the rows represent genes that have single substitutions relative to the consensus, with a ‘-’ indicating same nucleotide as the consensus, e.g. the bottom row represents the genes that have a GCCACAAAA motif instead of the consensus. The numbers next to the EC bars represent the number of genes that correspond to each row.

In the particular case shown in Figure 2 a slight improvement relative to the input motif (red sequence) is obtained in the EC score upon substituting the A at the second position with C. Yet the increase in the EC score is insignificant and, as shown in the dendrogram on the left part, it does not result in a considerable change in the overall expression profile. However, the current tool should be able to detect such changes when significant. Also, future versions of the server will allow the introduction of multiple substitutions at once that will allow the detection of potential interactions between sites (15,16).

De novo motif discovery

In cases where no motifs that regulate gene expression are known in a given organism at a particular condition or when users seek to identify new motif(s) relevant to the condition studied, the server provides an algorithm for the automated detection of novel motifs with significantly high EC scores. Given a genome sequence and mRNA expression dataset we perform de novo motif discovery using our new discovery algorithm (to be fully described elsewhere, Lapidot and Pilpel, in preparation). This is a stochastic algorithm that optimizes the EC score of an initial set of motifs. Briefly, this is a genetic algorithm with potential simulated annealing components that is initialized with a set of (potentially random) motifs. The algorithm iterates over stochastic optimization steps in which it performs ‘mutations’ in the motif sequences in addition to ‘crossovers’ between randomly selected pairs of motifs. The EC score, calculated for each motif, serves as a fitness function that determines the rate of reproduction of each candidate motif solution in the next generation. Typically after an order of 50 generations the algorithm converges upon a rather homogeneous population of motifs with particularly high EC scores, comparable to scores obtained in some experimentally known yeast motifs (http://genetics.med.harvard.edu/~tpilpel/MotComb.html). Such motifs may thus serve as excellent targets for further experimental explorations. The server allows running the algorithm on multiple choices of expression data and, in the near future, on new expression data that may be uploaded by users.

Additionally we provide a means for biased motif discovery. This option addresses the case where a user has some initial guess about motifs that may be involved in the regulation of the analyzed conditions, yet this initial guess may be considerably remote from the best solution in its vicinity, such that the exhaustive refinement described above may fail to identify that local optimum. In such cases, we propose an alternative to initializing the optimization algorithm with a set of random motifs. Users may choose to seed the algorithm with one or more motif candidates that may serve as their ‘educated guesses’. In such cases the algorithm will converge with a high probability onto a high scoring motif if it is similar enough to one of the input motifs or else it is likely to drift away to alternative motifs (more rigorous analyses of the convergence probabilities as a function of deviation of the seed from a close high scoring motif will be published elsewhere, Lapidot and Pilpel, in prepration).

The output from this algorithm is a set of motifs in the final population, along with their EC scores and graphs that depict the dynamics of the ‘evolutionary’ process. We also provide automated comparison of the motifs to known yeast regulatory motifs, using the CompareACE formalism (25) to evaluate whether new motifs have been found. See the home page of the server for additional figures with the typical dynamics of the optimization process.

SUMMARY

The various modes of regulatory motif analysis presented in this WWW server should help users in obtaining a good causal mapping between regulatory promoter elements and mRNA expression—a pressing need in many current functional genomic studies. Some of the computational analyses available in this service are equivalent in their scope to experiments for motif characterizations that usually amount to preparations of site specific mutated promoter constructs and measurements of activity of reporter genes under their regulation. Yet, it remains to be emphasized that in terms of accuracy the above experimental procedure is still likely to be considerably more accurate, especially since it can appropriately eliminate other potential functional elements in the control regions. The conclusions derived from our service should thus be considered as a highly efficient means to generate rigorously prioritized functional predictions that need to be experimentally tested.

Finally, currently our server supports analyses of the yeast Saccharomyces cerevisiae genome only. The next immediate enhancement of our service will be the inclusion of additional species, including human, for which both genomic sequence and mRNA expression data is available. This will allow the most valuable means to test hypothesis about the function of a motif across different genomes.