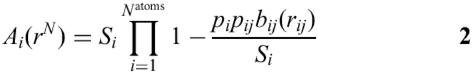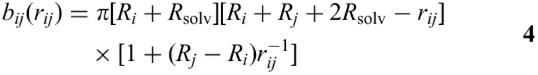POPS: a fast algorithm for solvent accessible surface areas at atomic and residue level

Abstract

POPS (Parameter OPtimsed Surfaces) is a new method to calculate solvent accessible surface areas, which is based on an empirically parameterisable analytical formula and fast to compute. Atomic and residue areas (the latter represented by a single sphere centered on the C^α atom of amino acids and at the P atom of nucleotides) have been optimised versus accurate all-atom methods. The parameterisation has been derived from a selected dataset of proteins and nucleic acids of different sizes and topologies. The residue based approach POPS-R, has been devised as a useful tool for the analysis of large macromolecular assemblies like the ribosome and it is specially suited for the refinement of low resolution structures. POPS-R also allows for estimates of the loss of free energy of solvation upon complex formation, which should be particularly useful for the design of new protein–protein and protein–nucleic acid complexes. The program POPS is available at http://mathbio.nimr.mrc.ac.uk/~ffranca/POPS and at the mirror site http://www.cs.vu.nl/~ibivu/programs/popswww.

INTRODUCTION

Solvent accessible surface areas (SASAs) are often used as an analysis tool by structural biologists. The idea that an important component of the driving force for protein folding is to be found in the burial of hydrophobic groups dates back to the sixties (1) and to the early seventies when Lee and Richards (2) introduced the concept of solvent-accessible surface defined by a probe rolling over the protein surface. Since then, many methods have been proposed for the calculation of solvent accessibilities. One of the most accurate algorithms was introduced by Richmond (3), which is based on an analytical formula and quite expensive to calculate. Wodak and Janin (4) proposed a very simple formula based on a probabilistic method that is fast to compute and easily derivable. The formula was tested and parameter-optimised on a number of small solutes and proteins. In order to improve the performance of the formula, we have recently re-parameterised it to reproduce accurate atomic (POPS-A) and residue (POPS-R) SASAs (5). The versatility of this approach has allowed us to implement POPS areas for implicit solvent models in MD programs and as a weighting factor in structural alignment, threading and structural refinement packages. The residue level approach is particularly useful for the analysis of large structural assemblies, in order to filter key interactions between molecules due to the burial of surface area. Moreover, it has been designed to characterise the hydrophobic or hydrophilic nature of exposed and buried surfaces and can be used to estimate the loss of solvation free energy upon complex formation. The recently solved structure of the Thermus thermophilus 70S ribosome at residue level (C^α and P only for proteins and RNAs) (6) represented the ideal candidate to demonstrate the efficiency and the predictive power of POPS-R (5).

POPS ANALYTICAL FORMULA

The total SASA of a molecule composed of N atoms is given by:

where A_i is the SASA of the ith atom.

The algorithm we used to approximate the A_i is based on the analytical expression proposed by Still and co-workers (7,8) and on the probabilistic method of Wodak and Janin (4). The original formula is:

where S_i=4π(R_i+R_solv)² is the SASA of the isolated atom i with radius R_i and a solvent probe with radius R_solv.

The term b_ij (r_ij) represents the SASA removed from S_i by the overlap of the atoms i and j at a distance r_ij=|r_i−r_j|.

If r_ij>R_i+R_j+2R_solv

while if r_ij<R_i+R_j+2R_solv

The empirical parameter p_i depends on the atom type, while the empirical parameter p_ij serves as an additional discriminating factor that distinguishes between first and next covalently bound neighbour atoms (p_1,2 and p_1,3, respectively) and non-covalently bound atoms (p_≥1,4). These parameters were optimised by Hasel et al. (7), reproducing the exact SASAs of a large number of small molecules.

We chose to make the parameters p_i dependent on the type of atom in a given residue (e.g. one p_i for the C^β of each standard amino acid or one p_i for the N1 of each nucleotide, for a total of about 250 parameters) and to split the p_≥1,4 connectivity parameter into two parameters, namely p_1,4 and p_≥1,4. Moreover, we applied the same algorithm to approximate the A_i at residue level, which means that each amino acid and nucleotide is represented by a single sphere centred on the C^α atom for amino acids and at the P atom for nucleotides. In this case each parameter p_i corresponds to one amino acid or nucleotide and R_i is the radius of the sphere that simulates the entire residue.

Both the POPS-A and POPS-R empirical parameters were optimised over the atomic or residue SASAs (for POPS-A and POPS-R, respectively) of a database of 89 specifically chosen biological molecules (proteins, nucleic acids and protein–nucleic acid complexes). The SASAs of the atoms of these molecules were evaluated with the program Naccess, NACS in the following (9) and constitute the POPS-A training dataset of about 120 000 atoms. The residue NACS SASAs were obtained by adding up the atomic NACS areas and these constitute the POPS-R dataset of about 12 000 residues.

POPS-A SASAs of the atoms in the atomic dataset were fitted to the NACS SASAs through a minimisation of the σ² variance of POPS-A from NACS areas with respect to the empirical parameters p_i and p_ij. The atom radii proposed by Hasel (7) were adopted. For the POPS-R parameterisation the same procedure was applied by using the areas in the residue dataset. Besides the parameter p_i, for each residue the radius R_i of the sphere used to simulate the whole amino acid or nucleotide was also optimised in the fitting procedure.

Examples of the performances of POPS-A and POPS-R are reported in Table 1. This small set of different classes of molecules (for a larger set see 5) indicates that usually both POPS-A and POPS-R total SASAs are well within 10% from NACS SASAs (9). However, we have to underline that some of the good performances of POPS-R are often due to error compensation. For this reason, we believe that better descriptors of POPS-A and POPS-R are the average errors at atomic and residue levels.

Table 1. NACS SASAs in Ų and percentual errors with POPS-A and POPS-R approaches. CPU time for POPS execution in seconds.

PDB code	Descriptiona	NACS SASA	POPS-A % error	POPS-R % error	POPS-Ab CPU time	POPS-Rb CPU time
1bfmA	α-Prot	5896	−5	−15	0.36	0.01
1lrv	α-Prot	12811	4	2	3.66	0.08
1htm	αβ-Prot	9220	−8	−8	0.98	0.04
2hgf	αβ-Prot	6087	0	4	0.78	0.03
1dlc	β-Prot	10185	10	9	2.63	0.07
5hir	β-Prot	3389	8	−2	0.19	0.01
1aaf	irr-Prot	6306	6	3	0.24	0.01
1gid	RNA	46789	0	0	46.93	1.40
103d	DNA	4294	−2	2	0.32	0.01
1hdw	Prot/RNA	29659	3	−3	11.54	0.98
1hcr	Prot/DNA	6738	−5	7	0.34	0.01

^aα-Prot, mainly α protein; β-Prot, mainly β protein; irr-Prot, mainly irregular protein, according to CATH's definition; Prot/RNA, protein/RNA complex; Prot/DNA, protein/DNA complex.

^bCPU times on a Pentium IV 2.4 GHz processor under Linux RedHat 7.1, POPS compiled with Portland Fortran.

The cross-validation re-sampling procedure we followed indicated that POPS-A predicts atomic SASAs with an average absolute error of 2.6 Ų, while POPS-R predicts residue SASAs with an average absolute error of 23 Ų (5). The execution CPU times for POPS-A and POPS-R are also reported in Table 1.

DESCRIPTION OF THE WEB INTERFACE

The general appearance of the POPS web interface is shown in Figure 1. In order to execute the calculation on our system the user is asked to register or to give an email address for identification. The complete registration procedure offers the advantage of keeping track of generated outputs, which will be stored in user accessible form on our system for about 6 weeks.

Figure 1.

Web interface for the calculation of POPS areas.

Input

The SASA calculation can be performed on any structure of the PDB database. In this case, the user is required to enter the PDB code identifier in the ‘Enter a PDB Identifier’ window. Alternatively, the SASA calculation can be performed on a structure provided by the user. In this case, the user is requested to upload the PDB file on which the SASA calculation has to be performed.

If the PDB file (in the database or uploaded) contains more than one structure (model), POPS will consider only the first structure by default. POPS calculation of all the structures can be switched on by using the ‘Multiple Models’ button.

By default, the all-atom SASA (POPS-A) will be calculated. To perform a SASA calculation at residue level (POPS-R), the button ‘Coarse Grained Calculation’ must be activated.

Output

Besides the total SASA of the targeted systems, the user may choose to obtain the detailed atomic and residue SASAs as well. These two options can be activated by switching on the ‘Output Atomic Areas’ and/or the ‘Output Residue Areas’ buttons, respectively. The total and residue SASAs are also partitioned into hydrophobic and hydrophilic contributions. Finally, the POPS-A and POPS-R parameters are accessible through the ‘All atoms’ and ‘Coarse grained’ links on the web interface. POPS outputs will usually appear on the screen with access to all relevant data.

Outlook

Future developments will include the possibility of uploading a PDB file with several structures (models), like for large macromolecular assemblies, and to analyse the amount of buried SASA owing to overlaps between different sub-structures or molecules. A table containing a summary of the buried SASAs will be included. Additionally, estimates of the free energy of hydration lost in the interaction of two structures will be evaluated.