GeneFizz: a web tool to compare genetic (coding/non-coding) and physical (helix/coil) segmentations of DNA sequences. Gene discovery and evolutionary perspectives

Abstract

The GeneFizz (http://pbga.pasteur.fr/GeneFizz) web tool permits the direct comparison between two types of segmentations for DNA sequences (possibly annotated): the coding/non-coding segmentation associated with genomic annotations (simple genes or exons in split genes) and the physics-based structural segmentation between helix and coil domains (as provided by the classical helix-coil model). There appears to be a varying degree of coincidence for different genomes between the two types of segmentations, from almost perfect to non-relevant. Following these two extremes, GeneFizz can be used for two purposes: ab initio physics-based identification of new genes (as recently shown for Plasmodium falciparum) or the exploration of possible evolutionary signals revealed by the discrepancies observed between the two types of information.

INTRODUCTION AND BACKGROUND

The GeneFizz web tool presented here implements the classical model of helix-coil transitions (1–3) for given DNA sequences. The output of the program plots the probability of opening of the double-helix for various temperatures along the sequence. The tool permits the convenient superposition of this physics-based segmentation with the genetic segmentation (coding/non-coding regions), as provided by annotation files.

The helix-coil model is inherently associated with the model of DNA double-helix (4). Indeed, the double-helix must open to provide access to the genetic information stored in the double-helix. Based on this close association between double-helix and helix-coil there are two important issues in the backround of the GeneFizz tool. The first issue is relevant to the methodological possibility of implementing large-scale structural models and the second issue is relevant to physics-based genomic analyses.

Large-scale models

Large-scale models treat biological macromolecules as a single entity. At such scales atomistic details are not relevant; instead simplified representations must be adopted with discrete numbers of accessible states for elements such as base pairs or amino acids. Realistic, large-scale models must take into account long-range effects, necessary for bringing into close ‘contact’ elements which are distant on the primary sequences. This requirement leads, in most cases, to computational untractability [in terms of algorithmic complexities O( f (n)), following the models, with n the length of the sequence].

An appropriate methodological solution was proposed in 1977 for the helix-coil model, in linear molecules, with the so-called Poland-Fixman-Freire (PFF) algorithm (5). In this case, the long-range effect in the model is relevant to the physical representation of the denaturation ‘bubbles’. Following classical polymer physics (6,7), power-law representations ( j^−α, with j the length of the loop) must be adopted for the loop-entropies. With this long-range effect, the evaluation of the partition function (in statistical mechanics) is in O(n²) [instead of O(n) for a nearest-neighbour model, if the length-dependence in loop-entropies is neglected]. PFF algorithm (5) permitted reduction of the algorithmic complexity from n² to I×n, by adopting a multiexponential representation for the long-range effect (with I exponential components).

The PFF algorithm has not been generalised to models more complex than the linear helix-coil model. However, revisiting ideas in the PFF (3,8) suggests that the representation of long-range effects as multiexponential functions is conceptually the unique solution which can drastically reduce algorithmic complexities. Extending the ideas to higher-order models, such as helix-coil transitions in circularly closed and topologically constrained molecules, algorithmic complexities can be reduced by several orders of magnitude, with million fold reductions in the calculation times (8). This generalised formulation was called SIMEX [SIMulation with EXponentials (8)]. The Padé-Laplace method (9,10) in signal analysis can be used to obtain appropriate numerical representations of long-range effects as multiexponential functions. The [SIMEX]-[Padé-Laplace] methodological toolbox provides new perspectives for implementing large-scale models. Here the implementation concerns the classical linear helix-coil model.

Physics-based genomic analyses

It seemed natural, at the start of the genomic era, to analyse DNA sequences according to the structural properties. Such physics-based genomic analyses were, however, progressively superseded by more textual-oriented string-based analyses, such as the pattern-recognition procedures, often involving ‘training sets’, which are used today. Possible relations between helix/coil and coding/non-coding segmentations of DNA sequences were first examined in the late seventies and early eighties when the first genomes, phages and plasmids became available. However such analyses (see, for example, 11–13, and 14 for more detailed discussions) did not provide clear-cut answers. Even though these results concerned only a small set of genomic data, physics-based analyses have infrequently been made on the large genomic sequences available today. Our analyses of a series of complete genomes showed that correspondences between the helix/coil and coding/non-coding types of segmentations could not be described as simple all-or-none answers (14). Rather, an overlap between the two segmentations was demonstrated with very different levels of correspondence in different genomes and organisms (14). This variability ranges from an almost perfect match to complete unrelatedness and raises several interesting evolutionary questions which lead to intriguing hypotheses (14).

Practically, in the most favourable cases (with a high overlap between the segmentations), the physics-based signal should permit ab initio gene predictions (15). Overall, the closest correspondences occur in complex eucaryotic genomes, such as that of Plasmodium falciparum (15), which includes many split genes. An exhaustive study of the known, cloned genes (15) revealed for this genome a detailed correspondence between coding regions (simple genes or exons in split genes) and DNA regions of relative high thermal stability (with sharp delimitations provided by the helix-coil model). The physics-based study of this genome represented an interesting, supposedly difficult, test case for ab initio gene identifications. Indeed chromosomes 2 (16) and 3 (17) were annotated by different groups, before the complete genome was published, using different gene identification programs and methods (such as the Glimmer program). These original results were also cross-annotated (18,19) and several possibly missed genes were reported (reanalysis by the TIGR group of the chromosome 3, originally annotated by the Sanger group). In this context it was especially interesting to test physics-based ab initio gene identification for this genome. This alternative approach (20), confirmed details of a series of genes predicted by the physics scheme (15), which were missed with the different gene identification methods.

The correspondence observed for P.falciparum is not limited to this genome and does not depend on its skewed GC content. Complete pre-calculated maps of the superpositions of genetic and physics segmentations for different eucaryotic genomes will be presented elsewhere. Here we present the GeneFizz web tool which allows an interactive exploration of physics-genetics correspondences for user-provided sequences. This tool should be useful in two areas: (i) gene identification and annotation and (ii) the exploration of possible evolutionary information associated with discrepancies between physics and genetics signals.

MODELS, ALGORITHMS, OUTPUTS AND SETTINGS

A large literature has described helix-coil transitions in linear DNAs in much detail (1–3). The basic model is recalled diagrammatically in Figure 1. Based on the SIMEX algorithm for linear molecules, GeneFizz plots the probability that the double-helix opens, along a user-provided sequence, for various temperatures. In this output, the probability ‘0’ corresponds to the helical state and the probability ‘1’ to the coiled state. The parameters used are described in detail elsewhere (14,21). Notably, for the thermodynamic description of the stacking of bases in the helical state, the 10 dinucleotide stability constants of Gotoh and Tagashira (22) were used. For the loop-entropy factor, the value α in the power-law was set to 1.95. This law was represented as a sum of 14 exponentials (for denaturation bubbles extending, theoretically, up to about 5000 bp) with the Padé-Laplace method (followed by a least-squares refinement). With this implementation of the model the only ‘free-parameters’ are the temperatures and these are set by the gross GC content of the considered sequences.

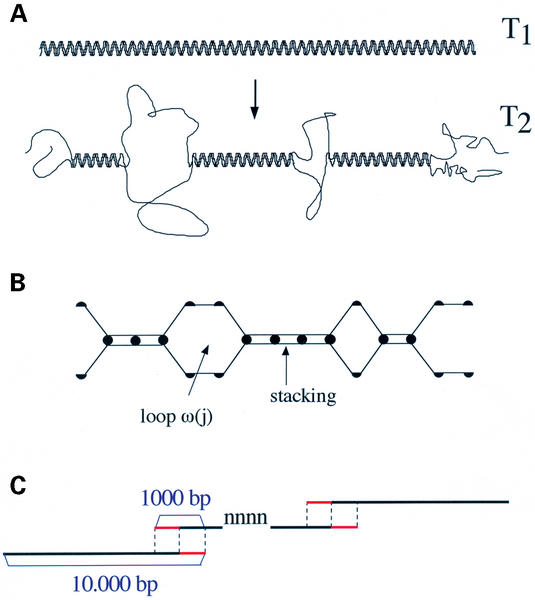
Figure 1.

Schematic representation of the helix-coil model. (A) With increasing temperatures, disruptions occur in the double-helix and specific regions (following the sequence) switch from the helical state to the coiled state. For a linear molecule, in addition to internal loops, the disruptions lead to single-stranded free-ends. (B) For the statistical mechanics calculations, simplified representations are adopted following which a base pair is either in the closed (helical) state or open (coiled) state. For a sequence of length n, the partition function is the sum of the weights associated with the 2ⁿ possible configurations. From the partition function, various quantities of interest (such as the opening probability along the sequence) are readily calculated. The weight attributed to a given configuration, such as the one represented diagramatically, corresponds to the equilibrium constant for its formation (from two single strands). For base pairs in the helical state, the weight corresponds to the sequence-dependent stacking energies. For denaturation bubbles, the weight corresponds to loop-entropies (power laws in j^−α, depending on the length j of the loop; with a penalty σ₀ for loop opening in the range 10⁻⁵–10⁻⁶). (C) Calculation scheme for long genomic sequences, sliced into stretches of length 10 000 bp. The stretches are chosen with an overlapping window of length 1000 bp. For a given stretch, the probabilities for the last 500 bp (represented in red) are discarded and replaced by the probabilities calculated for the same base pairs in the next stretch (with the 500 first probabilities being discarded). This scheme avoids end-effects for the linear helix-coil model calculations. Whenever ‘nnnnn’ or ‘NNNNNN’ stretches are encountered, end-effects cannot be avoided at both extremities of such stretches.

In addition to the acceleration due to the SIMEX formulation, calculation times can be further reduced by slicing very long genomic sequences into a number of shorter sequences of length L. In GeneFizz L was set to 10 000 bp. For the linear helix-coil model, in contrast to the helix-coil model in supercoiled DNA, slicing does not influence long-range effects from one stretch to the next one (for the considered length L). Remaining boundary problems were treated with an appropriate scheme of overlapping-windows calculations. This calculation is represented schematically in Figure 2C: with an overlapping window of length l=1000 bp, the probabilities obtained for the last 500 bp of a given stretch were discarded and replaced by the corresponding probabilities for the next stretch. Similarly, the probabilities for the first 500 bp of the next stretch were discarded. We verified that this overlapping window treatment for linear model calculations completely avoided edge effect problems. It is important to note however that such end-effects cannot be avoided for stretches of uncompleted sequences (boundaries of ‘nnnnnnnn’ or ‘NNNNNNNN’ stretches). In the outputs, such interruptions are shown as a continuous horizontal line of constant value 0.5 over the length of the corresponding stretches.

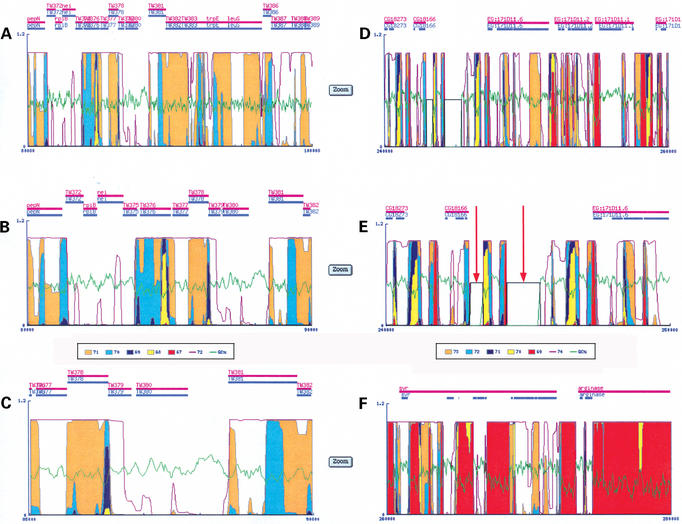
Figure 2.

Outputs of GeneFizz and basic features. (A–C) GeneFizz outputs for T.whipplei TW08/27 (accession: BX251411). (A) Corresponds to a 20 kb stretch. The GC% is plotted in green, in addition to the probability of helix opening curves (for the GC% curve the scale [0_100%] corresponds to the scale [0_1] for the probabilities). Probability curves, corresponding to increasing temperatures [following the colour legend below the panel in (B)], are superimposed. The zoom button at the right-side of each panel allows a 2× zooming for the output [thus in (A) the sequence extends from 80 000 to 100 000 bp; with the zooming in (B) the sequence extends from 80 000 to 90 000 bp; with the zooming in (C) the sequence extends from 85 000 to 90 000 bp]. Genes (with names as in the annotation) are represented as horizontal bars, above the probability curves. (D–F) GeneFizz outputs for D.melanogaster (accession: AE003417). (E) Corresponds to a 2× zoom of (D). The red arrows in (E) indicate the occurrence of ‘nnnnnn’ stretches in the sequence (represented in the GeneFizz output as constant horizontal plots, at the value 0.5 throughout the lengths of the stretches). For split genes, the ‘gene’ and ‘CDS’ features are represented respectively as continuous horizontal bars in magenta (with the names of the genes) and split horizontal bars in blue (associated with the exons, as detailed in the ‘CDS’ feature of the annotation).

For a GeneFizz analysis, a user must provide a genomic sequence with or without annotations, following various formats: fasta, EMBL, GenBank, NCBI (entered either by browsing or copy/pasting). The program proposes a default set of temperature values, based empirically on the gross GC content. This set can be modified by the user (up to six temperatures at a time).

The output plots the probabilities of DNA opening, calculated every 20 bp, along the sequence, with the probability curves associated with different temperatures plotted in different colours as indicated by the legend. With increasing temperatures, regions which were in the closed (helical) state open progressively. Accordingly, the various probability curves can be superimposed, from the lowest temperature curve in the foreground to the highest temperature curve, in the background, with no visually hidden information. In addition to the probability curves, the output plots along the sequence the GC% curve as well as any provided genetic annotations. Genes—which may be simple genes, split genes, tRNAs, etc—are reported as horizontal bars, above the probability curves, with the names of the genes as annotated. Bars are naturally positioned after the coordinates of the corresponding annotated genes. By default, the outputs are provided for stretches of 20 000 bp. Typically, a complete output for a sequence of 200 000 bp (with six temperatures) is obtained within minutes (the internet address of the output is sent by email to the user). A zooming tool facilitates detailed inspection of the results: for any given elementary panel of the output (associated with a sequence of length 20 000 bp) a button displays the output as two panels of length 10 000 bp each. Up to three successive zoomings of the panels provide output panels for sequences of length 2500 bp. Raw data associated with the probability curves can also be downloaded for other treatments.

These features are illustrated in detail in Figure 2 which shows outputs for one procaryotic and one eucaryotic genome. The procaryotic genome (Fig. 2A–C) is Tropheryma whipplei TW08/27. Figure 2B is one of the two panels obtained by a 2× zooming of the panel in Figure 2A. Similarly, Figure 2C is a panel obtained by a 2× zooming of the panel in Figure 2B. As usual in bacteria, the annotation concerns simple genes and the horizontal bars reporting the genes display the same information for ‘gene’ and for ‘CDS’ (as in NCBI file with accession number BX251411). As usually observed for procaryotes (14), the physics and genetics segmentations are not clearly related. The eucaryotic sequence (Fig. 2D–F) is from chromosome X (accession AE003417) of the Drosophila melanogaster genome. The two stretches in panels D and F are contiguous, from base pairs 240 000 to 260 000 and base pairs 260 000 to 280 000. In this case, the genes are of course essentially split with exons. Accordingly, the ‘gene’ feature (such as for ‘svr’ in Fig. 2F, uninterrupted magenta horizontal bar) indicates the overall extension of the gene, whereas the individual exons (as detailed in the ‘CDS’ feature) are represented separately (blue, split, horizontal bars, below the uninterrupted gene bar). The panel in Figure 2E (a 2× zoom of the panel in Fig. 2D) illustrates the occurrence of ‘nnnnnn’ stretches in the sequence (plotted by horizontal lines at value 0.5; see red arrows). The comparison between the panels in Figure 2D and F illustrates the close correspondence between the genes, notably in terms of exon density, and the segmentation of the sequence by the physics signal.

Uses of the information provided by the physics for gene analyses are described below in greater detail.

EXAMPLES OF GENOMIC ANALYSES WITH GeneFizz

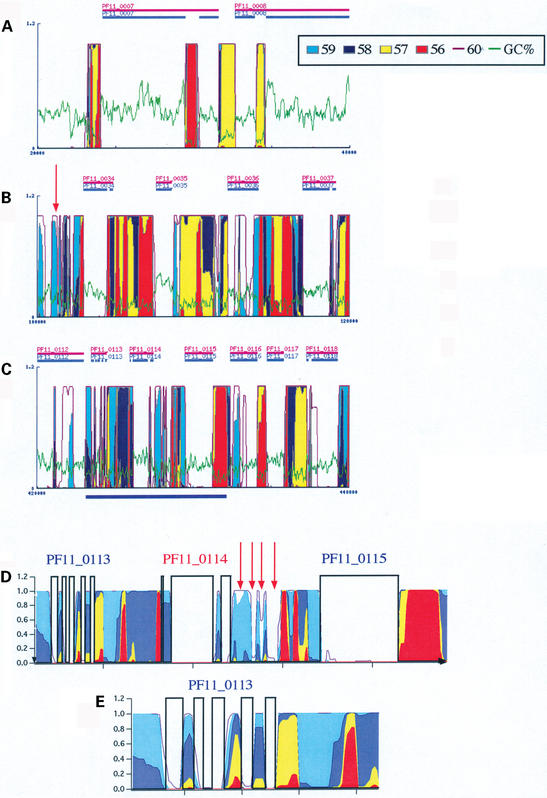
Possible analyses with GeneFizz are presented in Figures 3 and 4 with examples from the P.falciparum and D.melanogaster genomes. In Figure 3 (A, B and C) three snapshots of GeneFizz outputs are presented for the chromosome 11 of P. falciparum [as part of the complete genome (23)]. This output demonstrates close correspondence between physics and genetics for this genome. Further detail and discussion on the ‘discrepancies’ have been published (15,20). The GeneFizz analyses suggest that the annotation of the complete P.falciparum genome is of an exceptional quality. This annotation was based on the combination of a series of different gene identification methods (see www.PlasmoDB.org; a global analysis for the complete genome based on the physics properties will be presented elsewhere). Despite this annotation quality, the physics analysis suggests that many individual exons may have been missed (exons belonging to identified genes), as well as a number of split genes. Two such potentially missed genes are indicated in Figure 3B (red arrow, a gene at the left side of PF11_0034) and Figure 3C (a gene between PF11_0114 and PF11_0115; a close-up view of this region is presented in Fig. 3D, with red arrows pointing to the individual exons). The close-up view in Figure 3D, permits detailed verification of the good correspondence between gene annotation and physics segmentation for the genes PF11_0113 (with still a further close-up view in Fig. 3E) to PF11_0115.

Figure 3.

GeneFizz analyses for the P.falciparum genome. (A–C) GeneFizz outputs for the chromosome 11 (accession: NC_004315). Each output corresponds to a 20 kb stretch. The GC% is plotted in green, in addition to the probability of helix opening curves (temperatures, following the colours, as indicated in the legend). The genes (following the annotations in NC_004315) are indicated as horizontal bars, with the interruptions corresponding to the exons in split genes. (D and E), close-up views plotted with the ‘results file’ downloaded from the GeneFizz output (text files for the probability curves, at the different temperatures). The region in (D) corresponds to the region underlined in blue in (C). Red arrows show putative missed exons.

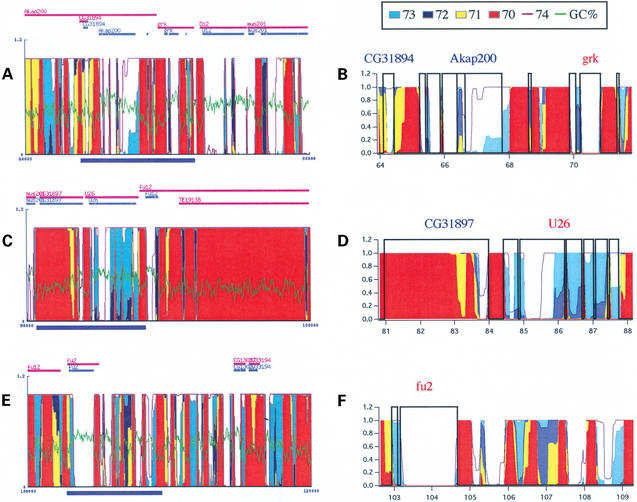
Figure 4.

GeneFizz analyses for the D.melanogaster genome. (A, C and E) GeneFizz outputs for the chromosome 2L (accession: AE003621, version: 14-FEB-2003). Conventions are as in Figure 3. (B, D and F) Close-up views for regions underlined in blue in (A), (C) and (E), respectively. These views were plotted with the ‘results file’ downloaded from the GeneFizz output.

Figure 4 shows similar GeneFizz outputs for D.melanogaster genomic sequences. The snapshots in Figure 4A, C and E correspond to contiguous (by stretches of 20 kb) sequences from the chromosome 2L of the complete genome [accession number: AE003621; 14-FEB-2003 (24)]. They show a similar situation to that of P.falciparum, with a significant shift in the set of temperatures used because of the GC content (70–74°C, instead of 56–60°C for P.falciparum, with the thermodynamic parameters used). This observation will be extended to the complete genome elsewhere. Correspondences between the genes and physics-based segmentation can be checked in the close-up views in Figure 4B (to A), D (to C) and F (to E) (in each case the corresponding regions are represented underlined in blue in Fig. 4A, C and E). As a preliminary example of potential analyses with GeneFizz, we note that a putative gene such as CG31897 (Fig. 4D) could not be confirmed by the physics analysis. In contrast, a significant number of exons, and possibly a gene, may have been missed at the right-hand side of the gene fu2 (Fig. 4E and F). An extensive application of the GeneFizz tool may lead to a significant number of corrections to the annotations (both in terms of suppressing putative genes or adding new ones), which should be tested experimentally.

FUTURE IMPROVMENTS TO GeneFizz

Continuing improvements to GeneFizz will be reported in a ‘what's new’ section of the web site (with the possibility of receiving news from updates through mail, by subscription). Planned improvements to GeneFizz are as follows:

1. At present the helix-coil model is implemented with the described set of thermodynamic and physical parameters. It did not seem important to offer a choice between various sets of parameters as available in the literature, since the model appears to be very robust with respect to these parameters. Various sets (obtained for different conditions, such as ions, pH, etc.) may be needed to account in detail for melting curves obtained under different experimental conditions. Here, such considerations are not really relevant since our interest lies in the probability maps as structural ‘descriptors’ of the sequences. Surprisingly, the extreme robustness of the model with respect to these parameters seems not to have been described in the vast literature devoted to the helix-coil model. However, this robustness becomes apparent only when the complete physical model is implemented, taking into account the long-range physical representation of loops. This is no longer true when only the nearest-neighbour stackings are considered. Similarly, with physically reasonable values for the magnitude of the loop opening penalty, the choice of the precise value for the power law (α in j^−α, following the lengths of the loops, with α>1; set to 1.95 in GeneFizz) is not relevant. Despite these observations, future versions of GeneFizz will offer the choice between various sets of parameters. This option will be intended for users specifically interested in comparisons with experimental data. In this direction, in addition to the probability maps, outputs for ‘melting curves’ and Tm calculations will also be provided (design of primers, etc.).

2. The capacity to retrieve annotation features will be extended for comparisons between physics and genetics segmentations: in addition to the default features, the user will be able to plot annotation features of particular interest.

3. For gene discovery, progressively more automated physics-based analyses will be provided permitting combination of results from sequence analyses—open reading frames, etc.—with the segmentation information provided by the physics.

4. From questions of genomic evolution, attempts will be made to relate physics-based signals to other known features for genomes with no correspondence between physics and genetics segmentations. In this direction, analyses of the P.falciparum genome suggest meaningful interpretations may exist (15) for some of the observed ‘discrepancies’ (genes with alternative expressions, etc.).

PERSPECTIVES AND CONCLUSIONS

The GeneFizz tool is the first of a series of physics-based genomic analyses (PBGA), which will be available at the pbga.pasteur.fr web site. As well as methodological tools, pre-calculated maps for various complete genomes are planned. While the examples discussed here were biased towards the gene-identification side, physics-based genomic analyses seem likely also to help in shaping new evolutionary pictures for the making of genomes. In contrast to pattern-recognition methods involving training steps, the signal analysed in GeneFizz reveals structural features intrinsic to the sequences. Training rules could not be used to ‘enhance’ gene identification when the physics signal diverged from the genetic segmentation. Several evolutionary-oriented analyses of informations emerging from the physics analysis have been performed (14,15). Systematic exploration of the physical properties of genomes should permit rigorous testing of hypotheses on the basis of correspondences and discrepancies between the physics and the genetics.