Single-Leaf Resolution of the Temporal Population Dynamics of Aureobasidium pullulans on Apple Leaves

Abstract

The abundance of phylloplane microorganisms typically varies over several orders of magnitude among leaves sampled concurrently. Because the methods traditionally used to sample leaves are destructive, it has remained unclear whether this high variability is due to fixed differences in habitat quality among leaves or to asynchronous temporal variation in the microbial population density on individual leaves. We developed a novel semidestructive assay to repeatedly sample the same apple leaves from orchard trees over time by removing progressively more proximal ∼1-cm-wide transverse segments. Aureobasidium pullulans densities were determined by standard leaf homogenization and plating procedures and were expressed as CFU per square centimeter of segment. The A. pullulans population densities among leaves were lognormally distributed. The variability in A. pullulans population densities among subsections of a given leaf was one-third to one-ninth the variability among whole leaves harvested concurrently. Sequential harvesting of leaf segments did not result in detectable changes in A. pullulans density on residual leaf surfaces. These findings implied that we could infer whole-leaf A. pullulans densities over time by using partial leaves. When this successive sampling regimen was applied over the course of multiple 7- to 8-day experiments, the among-leaf effects were virtually always the predominant source of variance in A. pullulans density estimates. Changes in A. pullulans density tended to be synchronous among leaves, such that the rank order of leaves arrayed with respect to A. pullulans density was largely maintained through time. Occasional periods of asynchrony were observed, but idiosyncratic changes in A. pullulans density did not contribute appreciably to variation in the distribution of populations among leaves. This suggests that persistent differences in habitat (leaf) quality are primarily responsible for the variation in A. pullulans density among leaves in nature.

The population density of phylloplane microorganisms represents the cumulative outcome of concurrent biological and physical processes that affect the leaf habitat (1, 9). Given the superficial similarity of leaves of similar size and position in a uniform canopy and their exposure to a common pool of airborne inoculum and environmental conditions, microbial abundance could be predicted to be approximately the same for all leaves assayed concurrently. However, the abundance of a particular species or class of microbes can vary over a range of several orders of magnitude (7, 9). The reason for such high variation has remained obscure. Perhaps the wide range of population densities is indicative of a highly dynamic system in which substantial demographic shifts occur independently within individual leaves over time. Alternatively, the densities of individual populations may be essentially stable but vary widely among leaves, perhaps due to differences in habitat quality.

Destructive sampling techniques commonly used in phyllosphere demographic studies cannot distinguish between these alternative explanations (5, 10). The inability to resample the microbial population on the same leaf through time obviously makes it impossible to track events on a given leaf. This limitation also complicates assessing the change in the average density of microbes in a population of leaves through time. High leaf-to-leaf variability makes it difficult to obtain precise estimates of the average density of microbes among leaves, and the precision needed for a given experiment may require very large sample sizes. The ability to repeatedly assay the density on a leaf may overcome many of the problems, making it possible to factor out leaf-to-leaf variability in density, thereby allowing stronger inferences about temporal variability.

An alternative for dealing with high leaf-to-leaf variability is bulk sampling, in which multiple leaves are pooled and processed in the same assay, which permits analysis of a larger number of leaves at each time point. This approach, however, has two drawbacks. First, if it is not known how microbial densities are distributed among leaves, it is impossible to obtain an accurate descriptor of mean population densities. For example, if densities are normally distributed among leaves, a pooled sample gives the correct average density for leaves. On the other hand, if densities are lognormally distributed among leaves, it would be most informative to determine the geometric average of densities for leaves, but this quantity cannot be obtained from a pooled sample. The second drawback of the bulk sampling approach (which is also shared by a massively replicated experiment with single leaves) is that it reveals only the average temporal variation among leaves. There could be large differences in the microbial population dynamics among individual leaves.

Here we investigated the possibility of monitoring changes in the microbial population densities of individual leaves by using a semidestructive approach. Previous results obtained by fluorescence in situ hybridization indicated that populations of the epiphytic yeast-like fungus Aureobasidium pullulans did not vary appreciably or systematically among 1-cm-wide segments across adaxial surfaces (3) of apple leaves harvested from trees in an orchard. While there is heterogeneity in the spatial distribution of A. pullulans cells at a microscopic scale (A. pullulans population densities are significantly greater on cuticular surfaces overlying veinal tissues than on interveinal surfaces), the bilateral symmetry and extensive reticulation of the apple leaf venation pattern results in a relatively uniform distribution of A. pullulans cells at a macroscopic (whole-leaf or leaf segment) level. The high density of trichomes precluded a similar assessment of A. pullulans distribution on abaxial surfaces, but leaf imprint assays suggested that the distributions of A. pullulans propagules are comparable on adaxial and abaxial leaf surfaces (Woody, unpublished data). Based on these observations, we hypothesized that whole-leaf A. pullulans density could be estimated by harvesting and analyzing small leaf portions. Furthermore, we hypothesized that the injury to leaves caused by successive harvesting of distal tissues would not adversely affect the remaining A. pullulans habitat. If these two hypotheses are correct, then the temporal dynamics of A. pullulans populations on individual leaves can be determined by periodic sampling of leaf segments.

The results of experiments described here support both the hypotheses described above. Furthermore, using this technique to track A. pullulans densities on individual leaves through time, we found that the rank order of densities of A. pullulans among field leaves is largely maintained, even during periods in which average per-leaf A. pullulans abundance changes substantially. This suggests that persistent differences in habitat (leaf) quality are the principal cause of variation in A. pullulans abundance among leaves.

MATERIALS AND METHODS

Leaf samples.

All experiments were conducted in the summer of 2002 by using apple leaves (Malus domestica cv. Liberty scions grafted to M26 rootstock) harvested from relatively small (ca. 2- to 2.5-m-high) 8-year-old trees that were maintained untreated with fungicide in an orchard at the West Madison Agricultural Research Station (Madison, Wis.). Table 1 shows the harvest dates, numbers of source trees, and numbers of leaves used for different experiments. The leaves selected for analysis originated primarily from spur clusters, although in some cases basal leaves that were approximately the same age were obtained from terminal shoots. The leaves were taken from clusters located 1 to 2 m above the orchard floor and at arbitrary canopy positions with respect to inner and outer branches. In each experiment that required sampling through time, a number of leaves that exceeded the number required for the analysis by 25 to 33% were preselected from candidate pools derived in equal proportions from the four directional quadrants of each tree. The criteria used for preselection included leaf size and physical condition; the sizes of qualified leaves were representative of the size of other leaves in the canopy, and leaves that had obvious wounds (caused by insect predation or environmental circumstances, for example) were excluded from the candidate pools.

TABLE 1.

Sampling schedule

Harvest date	No. of source trees	No. of leaves or leaf segments harvested for the following exptl objectivesa:
		WhLf	IL	TC	NS
1 July	2	12	12
5 July	4	12		12
8 July	4	12	12	12
10 July	4	12		12
12 July	4	12		12
16 July	1	7
24 July	4	15		15	15b
26 July	4	15		15	15
29 July	4	15		15	15
31 July	4	15		15	15
26 August	4			15
27 August	4			15
30 August	4			15
3 September	4			15
16 September	4			10
17 September	4			10
21 September	4			10
24 September	4			10

^aWhLF, whole-leaf A. pullulans density determination; IL, within-leaf (segment) A. pullulans density distribution assays; TC, time course experiment; NS, naïve segment A. pullulans density distribution assays.

^bNaïve segments were used to determine the initial A. pullulans densities in the time course experiment.

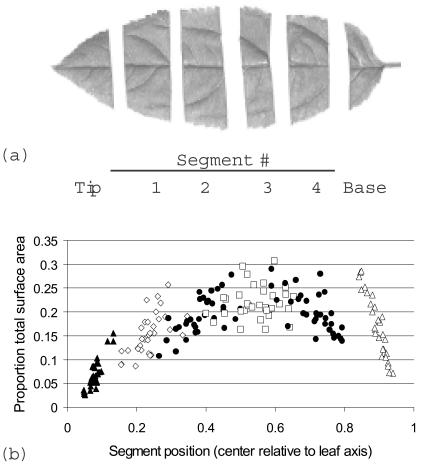
Whole leaves were harvested by using scissors to cut the petiole. Leaf segments were obtained by cutting transversely across leaves (Fig. 1a). Our goal was to generate leaf segments that contained approximately equal portions of total leaf surface area and of the primary (main) vein. Leaf tip and basal segments were not considered in our analyses. Because apple leaves are often sharply tapered near their tips, the total surface areas of tip segments were substantially smaller and more variable than the areas of interior segments (Fig. 1b). Basal segments were similarly more variable in terms of relative size; also, broadening of the primary vein near the petiole presented potential complications. As noted above, A. pullulans densities are significantly greater on leaf surfaces that overlie veins (3). Preliminary experiments (see below) in which we determined the segment-specific A. pullulans density of all leaf segments indicated that density was sometimes lower on tip segments and higher on basal segments, perhaps because of the changing proportions of surface area located above veins (Woody, unpublished data). Internal segments 1 to 4 collectively comprised 77% of the total leaf surface area on average.

FIG. 1.

Description of apple leaf segments. (a) Representative segmented leaf. The designations for leaf regions are indicated below the segments. (b) Variation in leaf surface area among segments and relative segment position. The different symbols indicate data points representing the proportion of total leaf area included in each segment versus the position (measured on center) of each segment relative to the corresponding leaf tip-petiole axis. The data are from measurements for 38 leaves harvested on five dates in the summer of 2002.

Leaves or leaf segments harvested from orchard trees were placed individually into sterile plastic bags (Whirl-pacs) and transported on ice to the laboratory for subsequent manipulations.

Enumeration of leaf-associated fungi.

An electronic image of each leaf sample was generated by using a Sony charge-coupled device camera; the total leaf surface area was determined by using the area morphometry module of the Optimas image analysis software package (MediaCybernetics, Carlsbad, Calif.). Individual leaves or leaf segments were subdivided with scissors into ∼1- to 2-cm² fragments and added to a homogenizer cup containing 50 ml of sterile 0.01% Tween 20 and then minced for 45 s at maximal speed in a Sorvall OmniMixer. Quadruplicate 0.2-ml aliquots of the resulting suspension were plated on cYPD medium (5 g of yeast extract per liter, 5 g of dextrose per liter, and 5 g of Bacto Peptone [Difco] per liter, solidified with 2% Bacto Agar [Difco] and amended with 25 μg of chloramphenicol per ml); dilutions were prepared as necessary with sterile water. The plates were incubated at room temperature (21 to 25°C) for 2 days and inspected with a dissecting microscope at a magnification of ×6 to ×12, and the numbers of colonies were expressed as CFU of A. pullulans and CFU of all other fungi. A. pullulans colonies were distinguishable from other yeast-like fungi on the basis of colony color, morphology, and growth characteristics. The other fungi included non-A. pullulans yeasts and filamentous fungi that formed discrete colonies or foci during the incubation period. The titers of A. pullulans and of the other culturable fungi in each 50-ml suspension were normalized to the total leaf surface area (accounting for both adaxial and abaxial leaf surfaces) for each tissue sample. The results are therefore expressed below in CFU per square centimeter.

Semidestructive sampling.

In three of the four experiments conducted to track A. pullulans density on individual leaves through time, the initial manipulations included removal of tip segments 3 days prior to harvest and determination of densities for segment 1 samples. These procedures were included in early experiments (2 to 12 July) to accommodate parallel assays performed to determine whether the act of removing segments might have artifactually altered the A. pullulans density on residual leaf portions. Prior tip removal was not included in experiments conducted on 24 to 31 July, in which we also compared the A. pullulans density on repeatedly sampled leaves with the density on corresponding naïve segments excised from previously untreated leaves. However, for consistency, prior removal of tip segments was included as a part of the standard procedures in experiments conducted from 23 August to 3 September and from 13 to 24 September.

Initial A. pullulans densities were determined by harvesting segment 1 samples at zero time, and densities at later times were determined by successive removal of segments 2 to 4 at 1- to 4-day intervals. All segments were processed essentially as described above for whole-leaf samples, except that transverse sections that were ∼3 mm wide were removed to exclude marginal tissues adjoining previously cut edges. Andrews et al. (3) found that local A. pullulans densities were higher on leaf surfaces that had experienced piercing wounds, probably as a result of insect predation. Although we did not systematically address the question, we were concerned that wounds caused by previous removal of leaf segments might similarly lead to localized increases in A. pullulans density, and we therefore omitted the wounded tissues from our analyses. The peripheral areas removed typically accounted for ∼10% of the total segment surface area (data not shown).

For each time point, the instantaneous A. pullulans density on leaves was estimated directly from the density determined for the corresponding segments. As part of the methodological development, we assessed the density distribution of A. pullulans among internal leaf segments 1 to 4. There was a limited tendency for the sizes of A. pullulans populations to be larger on proximal (basal) segments and smaller on distal (apical) segments. However, the associated R² value of a regression of relative density on segment position was only 0.06. This indicates that if there was a positional bias in A. pullulans distribution among segments, it was very small relative to the noise in the data. Furthermore, we tested at length various estimating procedures to account for such possible consistent differences in A. pullulans densities. These weighting schemes could potentially provide a more accurate means of inferring A. pullulans density on leaves based on segment-specific density determinations. Ultimately, however, we found no alternative method that increased the estimation precision sufficiently to justify the added effort in applying the procedure.

Statistical methods.

The Shapiro-Wilk test for normal distribution (13) was used to determine whether a normal or lognormal model adequately described the distribution of A. pullulans populations among leaves. Normal probability plots (data not shown) were generated by using normal quantile values on the ordinate and A. pullulans density or log₁₀ A. pullulans density estimates on the abscissa. The primary output statistic of the Shapiro-Wilk test is W, a quantity whose magnitude describes the degree to which data plotted by using alternative scales conform to a normal distribution. W can range from 0 to 1, where values close to 1.0 support normality and values far from 1.0 indicate nonnormality. Use of W allowed a formal test of the hypothesis that A. pullulans or log₁₀ A. pullulans density estimates were normally distributed. W values computed from both scales were compared to the appropriate threshold value, W_α, which depended on sample size. Values of W that were less than W_α indicated rejection of the null hypothesis that the input values were consistent with a normal distribution at α = 0.05. Additionally, R², the coefficient of determination based on regression of the ordinate on the abscissa of normal probability plots, was used descriptively to compare the untransformed densities with the densities obtained from log₁₀-transformed estimates to assess which scale produced values that more closely approximated a normal distribution.

Analysis of variance (ANOVA) calculations comparing means and Levene's test for homogeneity of variance (14) were conducted by using log₁₀-transformed density estimates as input values for SAS (Cary, N.C.) statistical analysis software licensed to the University of Wisconsin-Madison (12). All P values were compared to α = 0.05. Two-factor (leaf × time) ANOVA was used to analyze time course data obtained by semidestructive sampling. The total sum of squares in each experiment was partitioned into leaf effects, time effects, and an error term. The error term included leaf × time interaction effects, as well as measurement error. For the purposes of this analysis, the sum of squares for error could be thought of as an upper boundary for the sum of squares due to interaction.

RESULTS

Variation in A. pullulans density among leaves.

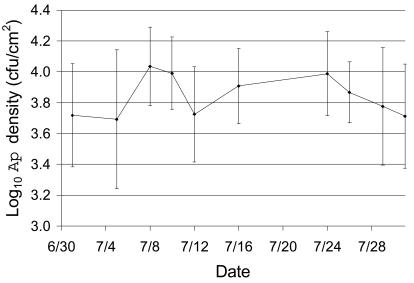
Analysis of the mean A. pullulans density and analysis of the distribution of A. pullulans populations among leaves were based on data from leaves harvested on 10 occasions during July 2002 (Fig. 2). The average A. pullulans density for leaves varied over a relatively narrow 2.5-fold range during that period (∼4.5 × 10³ to 1.2 × 10⁴ CFU/cm²). In contrast, the variation in A. pullulans density among leaves sampled on any single date was considerably greater. For example, the minimum range of densities was 4-fold for 15 leaves harvested on 26 July (3.8 × 10³ to 1.5 × 10⁴ CFU/cm²), and the maximum range was >26-fold for 12 leaves harvested on 1 July (8 × 10² to 2.1 × 10⁴ CFU/cm²). The average range, weighted according to the number of leaves sampled on each date, was ∼12-fold.

FIG. 2.

Mean A. pullulans abundance for collections of whole leaves harvested on 10 dates during July 2002. The error bars indicate standard deviations. The number of leaves sampled on each date is shown in Table 1. Ap, A. pullulans.

We used the Shapiro-Wilk test to determine the appropriate scale for expression of A. pullulans population density estimates (Table 2). In three experiments the Shapiro-Wilk test explicitly rejected the hypothesis that untransformed values were normally distributed (α = 0.05), whereas all log-transformed data sets were consistent with the predictions of a normal distribution. For 9 of 10 experiments the W (and R²) values were larger for the log-transformed data than for the raw data. We concluded that a lognormal distribution describes the distribution of A. pullulans populations among leaves well, and therefore we used log₁₀-transformed units in the experiments whose results are shown Fig. 2 and thereafter to express and analyze A. pullulans density.

TABLE 2.

Shapiro-Wilk test of normal distribution of A. pullulans population density estimates

Date	No. of whole leaves sampled	Wαa	A. pullulans				Other fungi
			Wb		R2c		W		R2
			Raw	Log10	Raw	Log10	Raw	Log10	Raw	Log10
1 July	12	0.859	0.747	0.889	0.701	0.836	0.915	0.910	0.924	0.894
5 July	12		0.883	0.897	0.916	0.936	0.896	0.951	0.920	0.970
8 July	12		0.964	0.929	0.972	0.927	0.955	0.899	0.966	0.888
10 July	12		0.713	0.859	0.693	0.860	0.816	0.960	0.792	0.953
12 July	12		0.772	0.952	0.748	0.944	0.673	0.908	0.643	0.909
16 July	7	0.803	0.837	0.952	0.815	0.946	0.770	0.921	0.731	0.881
24 July	15	0.881	0.908	0.969	0.909	0.966	0.760	0.908	0.790	0.939
26 July	15		0.884	0.942	0.906	0.967	0.885	0.935	0.894	0.960
29 July	15		0.902	0.906	0.931	0.935	0.841	0.946	0.865	0.973
31 July	15		0.881	0.982	0.867	0.971	0.835	0.924	0.836	0.940

^a95% confidence limit threshold value for the sample size used.

^bOutput statistic of the Shapiro-Wilk test, where 1.0 is a perfect fit (normality). The boldface values indicate rejection of the null hypothesis of normal distribution.

^cObtained by linear least-squares regression on normal probability plots (data not shown).

Correlation between A. pullulans density and the aggregate population density of other fungi on leaves.

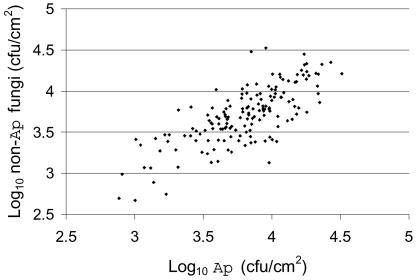
A. pullulans was the predominant fungal species recovered from apple leaves during July, accounting for ≥50% of the total number of propagules isolated from 86 of 127 leaves (68%). Consistent with previous results (2), leaves harbored numerous additional yeast-like and filamentous fungi, but any single species or morphotype was far less abundant than A. pullulans. The average ratio of A. pullulans density to the aggregate density of cocultured fungi was 1.24:1. Leaves that supported high-density A. pullulans populations also tended to support high densities of other fungi (Fig. 3). The correlation coefficient (r) relating A. pullulans density to the aggregate density of other fungi was 0.75 for all leaves.

FIG. 3.

Correlation of density of A. pullulans and density of non-A. pullulans fungi on individual whole leaves. The density of A. pullulans (Ap) and the density of other fungi (collectively) are plotted for each of the 158 leaves represented in Fig. 2. R² = 0.56.

Like the distribution of A. pullulans, the distribution among leaves of non-A. pullulans fungi, as a class, was well described by a lognormal distribution (Table 2). The R² values of the log-transformed data related to the distribution of non-A. pullulans fungi were greater than those obtained by using the corresponding untransformed data on 8 of 10 occasions. Furthermore, whereas all sets of log-transformed estimates were consistent with a normal distribution, the Shapiro-Wilk test rejected the hypothesis that the corresponding untransformed values were normally distributed in 6 of 10 data sets.

Comparison of within-leaf variation and among-leaf variation in A. pullulans density.

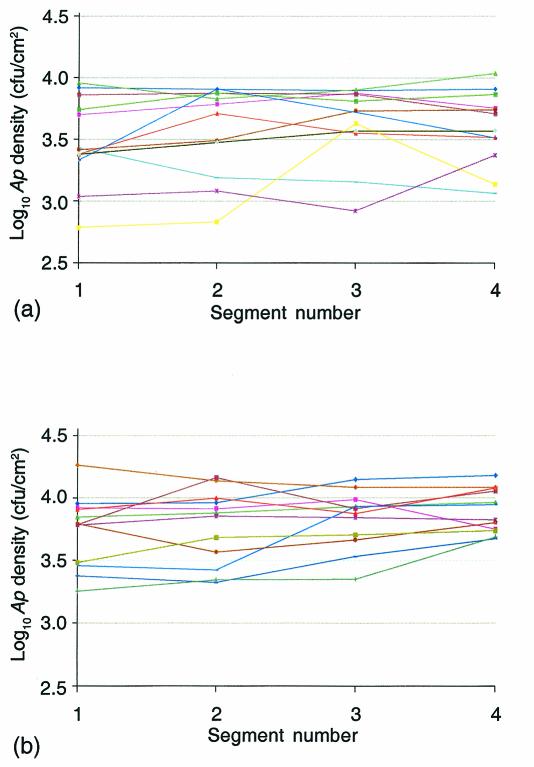
The within-leaf variation in A. pullulans distribution was determined by concurrent but separate assays of A. pullulans densities on the four internal segments of individual leaves (Fig. 1). The results of replicate experiments conducted on 1 July and on 8 July (Fig. 4) and the corresponding summary statistics of two-factor (leaf × segment) ANOVA (Table 3) show that the within-leaf variation in the distribution of A. pullulans propagules was much smaller than the among-leaf variation. The total sum of squares in each experiment was partitioned into among-leaf effects, within-leaf (segment-to-segment) effects, and an error term. The error term included variation from leaf × segment interactions and from measurement error. The within-leaf variation for leaves harvested on 1 July was not statistically distinguishable from zero (P = 0.23); the within-leaf variation for leaves sampled on 8 July was statistically greater than zero (P = 0.019) but nonetheless constituted only ∼6% of the total sum of squares. The predominant variability in A. pullulans density distribution on each date was attributable to among-leaf effects.

FIG. 4.

Within-leaf distribution of A. pullulans density. A. pullulans (Ap) densities for internal segments 1 to 4 of 12 leaves identified by color were determined concurrently in replicate experiments conducted on 1 July (a) and on 8 July (b).

TABLE 3.

Two-factor ANOVA comparison of within-leaf and among-leaf variation in A. pullulans density distribution

Date	No. of leaves sampled	Source of variation	Sum of squares	df	MS	F	P
1 July	12	Leaves	3.99	11	0.36	12.97	<0.01
		Segments	0.13	3	0.04	1.52	0.227
		Error	0.92	33	0.03
		Total	5.04	47
8 July	12	Leaves	2.25	11	0.21	12.65	<0.01
		Segments	0.18	3	0.06	3.79	0.019
		Error	0.53	33	0.02
		Total	2.97	47

Impact of successive sampling on the residual A. pullulans habitat.

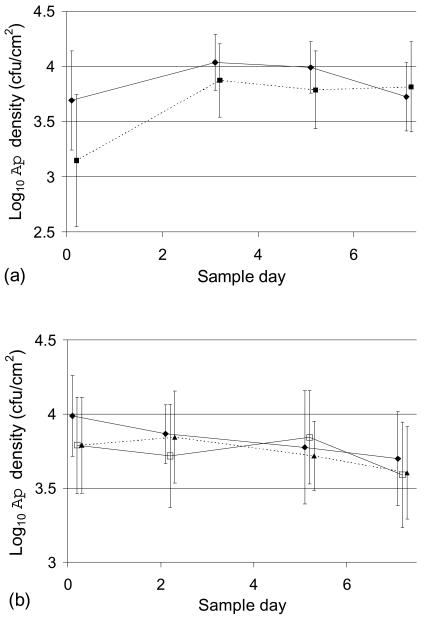
To test whether removal of distal leaf segments induced a leaf response that noticeably altered the remaining A. pullulans habitat and, concurrently, whether the whole-leaf density could be adequately estimated from a single segment, we compared the means of A. pullulans density estimates obtained for segments of leaves that had been repeatedly sampled to the estimates for untreated whole leaves harvested on the same dates. In experiments conducted on 2 to 12 July (Fig. 5a), the mean A. pullulans density on segment 1 (harvested from leaves that had been wounded 3 days previously by removal of tip segments) was significantly lower than the mean density on whole (untreated) leaves (P = 0.019, as determined by ANOVA). However, the means converged on subsequent sampling dates, on which segments were taken from leaves that had experienced a total of two to four prior wounding events, and the differences were not significant (0.11 ≤ P ≤ 0.56, as determined by ANOVA).

FIG. 5.

Effect of prior wounding on A. pullulans densities in the residual leaf habitat. Mean A. pullulans (Ap) densities for segments taken from successively sampled leaves (dotted lines), untreated whole leaves (♦), and naïve segments (□) are plotted versus time (sample day, where zero time was the day on which segment 1 samples were analyzed). The error bars indicate standard deviations. (a) Sampling performed on 5 to 12 July. Data were obtained by analysis of 12 whole leaves on each date and of segments taken in succession from 12 additional leaves; data were obtained from 11 of the 12 repeatedly sampled leaves on sample day 3 (segment 2) and from 10 of the 12 repeatedly sampled leaves on sample day 7 (segment 4). (b) Sampling conducted on 24 to 31 July. The results on each date were obtained by analysis of 15 whole leaves, naïve segments excised from 15 previously untreated leaves (14 leaves on day 2), and segments taken in succession from 15 additional leaves (14 leaves on day 2).

Similar results were obtained in experiments conducted on 24 to 31 July (Fig. 5b), in which the tips of leaves that were going to be repeatedly sampled were not removed prior to harvesting of segment 1 samples. Omission of the tip removal step allowed comparison (by ANOVA) of the mean A. pullulans density on segments taken from previously sampled leaves to the mean density on the corresponding segments excised from previously untreated leaves (naïve segments). Thus, at zero time, the mean A. pullulans density for naïve segment 1 samples was not significantly different from the mean density for whole leaves (P = 0.08). On sample day 2, the mean A. pullulans density for segment 2 samples harvested from leaves previously sampled at zero time was not significantly different from either the mean density for whole leaves (P = 0.82) or the mean density for naïve segment 2 samples (P = 0.32). Similarly, on sample days 5 and 7, there was not a significant difference between the mean A. pullulans density for segments obtained from previously wounded leaves and the average A. pullulans density for whole leaves (P = 0.62 and P = 0.42, respectively) or for naïve segments (P = 0.22 and P = 0.91, respectively). Levene's test for homogeneity of variance (data not shown) indicated that the variance in the A. pullulans density distribution among internal leaf segments of repeatedly sampled leaves was not significantly different from the variance among concurrently sampled whole leaves on any date in either experiment (Fig. 5) or from the variance in A. pullulans density distribution among naïve segments (Fig. 5b).

In overview, for seven of eight dates the difference between the means for whole leaves and the means for segments was not significant. Moreover, the differences were very small compared to the differences among leaves. For segment 1 on 5 July the magnitude of the difference was still modest compared to the among-leaf variability, notwithstanding the fact that significance was found. This could have resulted from the occasional low segment 1 density found in the preliminary tests of the system.

Temporal dynamics of A. pullulans populations on repeatedly sampled individual leaves.

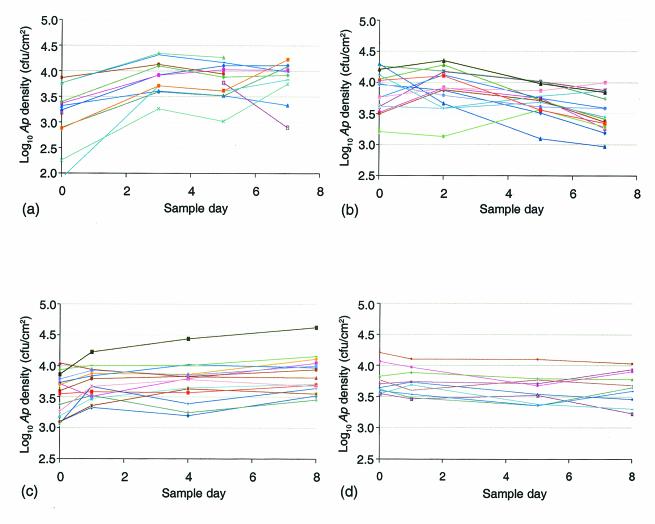
Semidestructive sampling was used to track the instantaneous density of A. pullulans on individual leaves through time (Fig. 6). The A. pullulans population densities on individual leaves were remarkably stable over time compared to the leaf-to-leaf variations in density. Although substantial changes in density were observed occasionally, such changes tended to be synchronous among leaves. Thus, leaves arrayed on the basis of A. pullulans density maintained approximately the same rank order through time.

FIG. 6.

Temporal variation in A. pullulans density on individual leaves. The lines indicate changes in A. pullulans (Ap) density that occurred on individual leaves over time; each color shows the data for a different leaf. Sampling was performed on 5 to 12 July (a), 24 to 31 July (b), 26 August to 3 September (c), and 16 to 24 September (d).

The proportion of the total sum of squares attributed to time effects (reflecting synchronous changes) was greatest during the experiment performed on 5 to 12 July, in which all leaves exhibited a notable and fairly consistent increase in A. pullulans density within the first 3 days (Fig. 6a and Table 4). Conversely, time effects were negligible (∼1.5% of the total variance) from 16 to 24 September. The average density inferred for leaves in the latter experiment did not change significantly during any interval over the 8 days on which we tracked A. pullulans density (Fig. 6d).

TABLE 4.

Two-factor (leaf × time) ANOVA A. pullulans time course data^a

Tracking period	No. of leaves analyzed	Source of variation	Sum of squares	Proportion of total sum of squares		df	MS	F	P
				All sources	Excluding timeb
5-12 July	9	Leaf	3.19	0.32	0.61	8	0.40	4.72	<0.01
		Time	4.65	0.47		3	1.55	18.33	<0.01
		Leaf × time	2.03	0.21	0.39	24	0.08
		Total	9.86			35
24-31 July	14	Leaf	2.04	0.4	0.45	13	0.16	2.44	0.02
		Time	0.51	0.1		3	0.17	2.67	0.06
		Leaf × time	2.50	0.49	0.55	39	0.06
		Total	5.05			55
26 August-3 September	15	Leaf	4.34	0.73	0.84	14	0.31	15.83	<0.01
		Time	0.82	0.14		3	0.27	13.96	<0.01
		Leaf × time	0.82	0.14	0.16	42	0.02
		Total	5.98			59
16-24 September	10	Leaf	1.67	0.82	0.83	9	0.19	14.72	<0.01
		Time	0.03	0.02		3	0.01	0.85	0.48
		Leaf × time	0.34	0.17	0.17	27	0.01
		Total	2.04			39

^aExcludes leaves for which data from less than four time points were collected. See Fig. 6.

^bExcluding sum of squares time.

If the sum of squares attributable to time effects is disregarded, the remainder can be expressed as the ratio of leaf effects to leaf effects plus the leaf × time interaction. The value for this ratio is a measure of the extent to which the relative A. pullulans densities among leaves were maintained through time. Thus, after the sum of squares attributable to synchronous changes through time was excluded, >80% of the remaining sum of squares for A. pullulans density could be assigned to leaf effects in both the experiment performed on 26 August to 3 September and the experiment performed on 16 to 24 September (Table 4). Although the mean A. pullulans density increased slightly for leaves monitored between 27 August and 3 September, all leaves displayed similar increases and therefore maintained approximately the same rank order with respect to A. pullulans density. A synchronous increase of slightly greater magnitude occurred for leaves sampled from 5 to 8 July; however, the changes in the A. pullulans density on individual leaves were less uniform during subsequent intervals (Fig. 6a). Finally, the lowest proportion of the total sum of squares attributable to leaf effects, 0.45, was observed on 24 to 31 July (Fig. 6b). The changes in A. pullulans densities were almost entirely independent between 24 July and 26 July, although more synchronous movements toward lower densities were observed thereafter.

DISCUSSION

Our results apparently provide the first assessment of the dynamics of microbial populations on individual leaves sampled through time. This was possible because two key experimental prerequisites were met. First, compared to the great variation (lognormal distribution) in A. pullulans densities among leaves, the densities were similar for regions of a leaf. Second, removal of distal leaf segments had no apparent effect on the A. pullulans habitat provided by the remaining proximal leaf portions. Thus, overall A. pullulans density could be extrapolated reliably from an analysis of leaf segments. The evidence for this conclusion is restricted formally to the results of two field experiments performed in one summer in a single orchard, together with three smaller-scale pilot trials performed in June and July. Our goal in this paper is to present the method so that other researchers can try it with their systems. We make no claim that it will work under all conditions and for all systems. Thus, the general utility of this new technique in phyllosphere microbial ecology remains to be established, but it is likely to have broad applicability.

It seems unlikely that our A. pullulans-apple leaf system is somehow uniquely suitable for a semidestructive sampling approach, although there are several features that may have facilitated its development. First, consistent with previous studies (2), A. pullulans was typically the most abundant fungal species cultured from apple leaves, which are a convenient size and shape for subdivision. Semidestructive sampling may not be useful for studying low-abundance microbe species whose populations are more difficult to measure precisely on less-than-entire leaves or on plants with very small leaves. We selected a segment size arbitrarily to allow for several harvest times. Clearly, the number of repeated samples that can be taken from a given leaf and hence the duration of experiments are finite. The lower boundaries of segment size depend on damage from wounding and the area size required to reflect the population size on the entire leaf. The size of the leaf and the number of desired experimental time points should set the upper boundaries. Leaves of some plant species, such as the finely pinnately compound Acacia spp. or honey locust (Gleditsia spp.), may have inherently suitable subunits (leaflets) that require little or no subdivision. As alluded to above, the degree of variation in the microbe population of interest among leaflets or other subunits will have to be determined in preliminary experiments for each microbe-plant system.

Second, we found that A. pullulans densities were similar across leaf surfaces. This reinforces conclusions from our previous intensive, multiyear study of A. pullulans distributions on adaxial surfaces by microscopy (3). Clearly, a relatively even or otherwise predictable distribution is a prerequisite of this approach. Third, apple leaves seemed to behave neutrally overall to wounding events, at least with respect to maintenance of the residual A. pullulans habitat and given the scale of this study and the fact that we did not process the perimeter tissue adjoining the previously cut surfaces. Finally, the A. pullulans populations which we studied were populations on mature leaves that emerged weeks or months before sampling. It seems likely that the fungal community structure of individual leaves had approached something resembling an equilibrium state. Heterochronic changes in leaf morphology or physiology were unlikely to have perturbed the A. pullulans habitat during the periods in which we tracked population density. An individual leaf may change significantly as a microbial substratum during periods of active growth in its life cycle from emergence to senescence and abscission.

Compared to more traditional replicate or bulk sampling methods, a significant practical advantage of using semidestructive sampling is that substantially fewer individual experimental assays are required to obtain statistically valid estimates of mean population density through time. This advantage is due to the fact that the number of independent assays required to adequately describe mean population density at any moment is scaled according to the variance among samples taken over time. The within-leaf variability in the distribution of A. pullulans propagules was one-third to one-ninth of the variability among leaves, and so determination of changes in A. pullulans density over time by repeated sampling of individual leaves required similarly reduced sample sizes.

We used semidestructive sampling to investigate the relative importance of temporal variability among the alternative sources of variation in A. pullulans abundance among leaves. By sampling leaf segments at 1- to 4-day intervals, we observed occasional periods in which the A. pullulans densities on individual leaves changed in a direction and with a magnitude that was largely independent of other populations monitored over the same periods. However, these occasions were relatively infrequent. Usually, changes in A. pullulans density associated with a given leaf occurred in unison with population changes on other leaves.

Excluding the variation due to synchronous changes in A. pullulans density, fixed among-leaf effects were the predominant source of variation among A. pullulans populations under the conditions of our experiments. The remaining variation was incorporated in an error term representing leaf × time interaction effects, along with measurement error. Genuine asynchronous changes in A. pullulans density among leaves were at least one of the sources that contributed to variation in the error term; however, it seems likely that measurement error, primarily due to segment-to-segment variation in A. pullulans distribution within leaves, was the primary source of residual variation. It was not possible to explicitly account for within-leaf variation in the analysis of time course data, but some sense of its contribution can be gleaned by comparison of the time course plots (Fig. 6) to the segment-specific density plots (Fig. 4). Although the leaves whose A. pullulans populations were tracked through time were necessarily different from those used to examine within-leaf variation, the most important difference between the experiments is the passage of time. The apparent synchrony of A. pullulans populations through time is all the more striking in light of this comparison.

The predominance of leaf effects among the sources of variation, as well as the correlation between the abundance of A. pullulans and the abundance of other fungal species, may indicate that the availability or quality of shared habitat features was growth rate limiting for phyllosphere fungi. For example, the rate of photosynthesis may vary among leaves due to positional effects (e.g., shading, age, surface orientation relative to ambient light) or other factors that affect leaf physiology (6). Alternatively, photosynthate production may be similar among leaves, but the leakiness of leaf surfaces may vary. The amounts of sugars varied about 25-fold among seemingly identical, uncolonized leaves of bean plants grown under favorable, controlled conditions (11). The structure of individual leaf surfaces could also be an important determinant of fungal density by limiting the availability of possible protected sites (4) or other preferred niches (8).

Why is the discovery that a given leaf has a demonstrable impact on the population biology of its epiphytic inhabitants exciting? First, we now have a clear indication that there is a biologically meaningful signal behind the seemingly immense stochastic leaf-to-leaf variability in microbe population density. This striking variation is a general phenomenon that has been observed but has not been explained since the inception of phyllosphere microbiology a century ago. Second, our work confirms that the individual leaf is a key determinant in microbe population dynamics. Finally, there is a clear need for further study of leaf systems and other habitats to understand the source of variation in densities among microbe populations sampled at the same time.