Abstract
Scan statistics are applied to combine information on multiple contiguous genetic markers used in a genome screen for susceptibility loci. This information may be, for example, allele sharing proportions for sib pairs or logarithm of odds (lod) scores in general small families. We focus on a dichotomous outcome variable, for example, case and control individuals or affected-affected versus affected-unaffected siblings, and suitable single-marker statistics. A significant scan statistic based on the single-marker statistics represents evidence of the presence of a susceptibility gene. For a given length of the scan statistic, we assess its significance by Monte Carlo permutation tests. Comparing P values for varying lengths of scan statistics, we treat the smallest observed P value as our statistic of interest and determine its overall significance level. We applied this method to a genome screen with autism families. The result was informative and surprising: A susceptibility region was found (genome-wide significance level, P = 0.038), which is missed with conventional approaches.
Much progress has been made in the localization of susceptibility genes. Methods implemented in programs such as aspex (1), genehunter (2, 3) and allegro (4) can make use of all marker loci on a chromosome and render any point along the chromosome as informative as possible. On the other hand, once that information has been obtained, it is applied in rather traditional ways. In this paper, we embark on approaches to gene mapping by jointly analyzing information at a number of marker loci covering a contiguous area of the genome.
In genome screens, logarithms of likelihood ratios (so-called lod scores) are computed for many points on the genome, where the likelihood in the numerator refers to the presence of a susceptibility locus at a given position, and the likelihood in the denominator assumes absence of that locus. True peaks of such lod score curves are known to be wider than false peaks (5). Consequently, higher positive lod scores and a larger number of them are expected around true rather than around false peaks. This property of lod scores generally is not taken into account in the search for susceptibility loci, but ad hoc approaches have suggested increased power when information from a small number of neighboring markers is combined (6, 7). In this paper, we propose a way of testing for disease association/linkage that combines the information from marker loci clustering around a local peak and assesses its genome-wide significance by permutation tests. The use of this method is illustrated on a real data set in which our approach furnishes greatly enhanced significance as compared with conventional analysis.
Scan Statistics and Permutation Tests
Consider a sequence of random variables, X1, . . . XN. For 1 ≤ L ≤ N, let YL(t) = Σi=tt+L−1 Xi be a moving sum of L consecutive observations. The linear (unconditional) scan statistic then is defined as
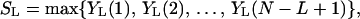 |
1 |
that is, as the largest moving sum of length L (8). Scan statistics have been used in epidemiology, molecular biology, and many other areas of science and engineering to detect clustering, for example, in DNA sequence analysis (9).
Here, Xi is an observation or a statistic based on the genotypes at the ith marker, and the sum YL(t) refers to the combined information of ordered markers, moving along the chromosomes. For example, Xi might be the number of alleles shared identically by descent (IBD) by an affected sib pair at the ith marker locus in a genome screen. Alternatively, there is precedent for using log likelihood ratios as “observations”—correlations between lod scores (10) or allele sharing proportions (11) at specific loci have been interpreted as evidence for genetic interaction between these loci. It is clear that a scan statistic based on lod scores captures the particular feature of true peaks being wider than false peaks (see the Introduction). Therefore, scan statistics are expected to be more powerful for detection of susceptibility loci than is a statistic focused only on a single marker locus.
The major developments of this paper are the simultaneous investigation of several scan statistics with different numbers of clustered loci and the choice of the smallest associated significance level as our test statistic. The corresponding test is mathematically intractable but can be achieved by computer-based methods, bootstrap, or permutation, which have been proven effective (12). Below, we employ Monte Carlo permutation tests to search for clusters of consecutive markers that point to a gene underlying the trait studied.
Global Significance Levels
We focus on data in which the phenotype is dichotomous, for example, observations on cases and controls, or affected-affected (AA) versus affected-unaffected (AU) sib pairs. Consider a scan statistic of fixed length L, for example, L = 5. Under the null hypothesis of no disease association or linkage, any set of marker genotypes in an individual is equally likely to occur with a binary outcome. This finding implies that data matrices with any permutation of the n binary outcomes have equal probabilities of occurrence. We make use of this fact to numerically calculate the significance level associated with an observed scan statistic, SL. For each permutation sample, we compute the scan statistic (irrespective of where in the sequence of observations it occurs); the proportion, PL, of permutation samples with a scan statistic at least as large as SL represents the significance level associated with SL.
The PL value so computed represents the global significance level, as opposed to a locus-specific significance level (13), for a given value of L. However, there may be no a priori reason for choosing any particular value for L. Rather, one would like to try any one of the values from 1 through, say, Lmax = 10 and focus on the smallest PL value obtained. This minimum PL value, Pmin, then represents the statistic whose significance level is to be determined. It is obtained from the permutation samples as follows. We view the statistics, S1, S2, . . . SLmax, as multiple (correlated) measurements. In each permutation sample, a minimum significance level, Pmin*, is obtained in analogy to the one observed in the real data. Then, the overall significance level, Pglobal, associated with Pmin is given by the proportion of permutation samples with Pmin* < Pmin (14).
Application to Autism Genome Screen
In a genome screen for autism, independent sib pairs were genotyped for a total of 324 microsatellites (J. J. Liu, unpublished observations). With a broad disease definition, 86 AA and 91 AU sib pairs were available. At each marker locus, the allegro program (4) determined the lod score associated with the allele sharing proportion in each sib pair. The statistic used for the ith marker was the difference, Xi = uAA − uAU, where uAA and uAU are total lod scores in AA and AU sib pairs, respectively. Scan statistics of lengths 1 through 10 were tried. In 100,000 permutations, P values were obtained as shown in Table 1.
Table 1.
Scan statistics of varying lengths L for autism genome screen resulting in a statistic of Pmin = 0.015
| L | Var. no. | SL | P value |
|---|---|---|---|
| 1 | 159 | 3.50 | 0.131 |
| 2 | 159 | 6.91 | 0.050 |
| 3 | 158 | 9.69 | 0.034 |
| 4 | 158 | 11.85 | 0.030 |
| 5 | 156 | 14.27 | 0.021 |
| 6 | 156 | 16.42 | 0.015 |
| 7 | 155 | 17.76 | 0.016 |
| 8 | 155 | 18.58 | 0.020 |
| 9 | 154 | 19.17 | 0.024 |
| 10 | 153 | 18.94 | 0.040 |
Var. no. indicates the first element of SL. Overall significance level is P = 0.047 for Lmax = 10 and P = 0.038 for Lmax = 6.
For marker number 159, the total lod score observed in AA pairs was 1.21 and the score for AU pairs was −2.29. Neither lod score is remarkable. The difference in lod scores, 3.50, is the largest such difference observed in the data and, in our Monte Carlo permutation test, is associated with a genome-wide significance level of 0.131. This finding does not indicate significant presence of a disease susceptibility gene anywhere in the genome. With an associated significance level of Pmin = 0.015, the most significant scan statistic is that of length 6. Because we are searching for the scan statistic with the smallest P value, we have to compute the genome-wide significance level associated with Pmin. The result, Pglobal = 0.038, still is statistically significant (at the 5% level). For a dense map of markers in an allele sharing study, a genome-wide significance level of Pglobal = 0.05 corresponds to a locus-specific significance level of P = 0.000022 or a lod score of 3.6 (13). Similarly, Pglobal = 0.038 translates into P = 0.0000163 or a lod score of 3.8.
Discussion
The example data shown above strikingly demonstrate the usefulness of our approach. For the same data, it reduces the significance level from 0.131 to 0.038. In our experience, this is not an isolated result. Other data that is not shown here furnished similar improvements. We expect that our method will become particularly useful, for example, when thousands of dense single nucleotide polymorphism markers are tested for association with a disease. Our result of a genome-wide significance level of P = 0.038 for the autism data is remarkable—for complex traits, it has been difficult to find global significance levels smaller than 0.05 (15).
Trying out a large number of scan statistics of different lengths will result in an increased global significance level. As shown in Table 1, for lengths of the scan statistic from 1 through 10, the associated overall significance level is P = 0.047. We recommend one of the following three possibilities to make this approach as efficient as possible: (i) testing only one length, (ii) testing all lengths until the scan statistic starts decreasing, or (iii) testing all lengths until the P value starts increasing.
(i) In linkage analysis, the genetic distance between marker loci determines the correlation of the lod scores between them. Very tightly linked markers are expected to furnish identical lod scores. In the autism genome screen quoted above, the average marker spacing was approximately 10 centimorgans (cM). Thus, the scan statistics performing best in these data covered a region of 50–60 cM. It may be useful for investigators to apply a scan statistic of fixed length covering approximately 60 cM. The resulting P value will then be global, without any need for correction for multiple testing.
(ii) For increasing lengths, L, the associated scan statistics SL tend to increase in size, at least initially. Eventually, SL < SL − 1 will occur. In our data, a drop of the scan statistic occurs in the step from length 9 to length 10. Presumably, a negative value, SL − SL − 1, indicates that L − 1 should be taken as the maximum length of the scan statistic. If we do this, the overall significance level of P = 0.047 for Lmax = 10 drops to P = 0.041 for Lmax = 9. In other instances, the change in significance level may be more pronounced.
(iii) An appealing choice for Lmax is an increase in length-specific P value, which in the autism data occurs from step 6 to 7. For Lmax = 6, the overall significance level turns out to be P = 0.038.
The largest difference in total lod scores between AA and AU pairs is equal to 3.50 (marker 159). A maximum positive lod score of this magnitude is generally associated with a genome-wide significance level of approximately 0.05 (13). Our result of a much higher significance level shows that the difference in lod scores between AA and AU pairs may not be interpreted in the same manner as a lod score observed in one type of family data.
Statistics may have unequal properties for different variables (genetic markers in our case). For example, if markers have different numbers of alleles, and allele frequencies are compared between cases and controls, a suitable statistic is the χ2 for a 2 × n table, with n being the number of alleles. Markers with different numbers of alleles will yield statistics with different numbers of degrees of freedom. It is then recommended, for example, to convert these statistics to empirical significance levels, P, and use log[−log(P)] as the statistics of interest, which now are all on an equal scale.
Once the scan statistic has identified an interesting genomic region on a chromosome, the procedure may be applied on a chromosome-by-chromosome basis. This approach may find additional, weaker susceptibility loci.
lod scores derived from a multilocus linkage analysis refer to the strength of linkage to a particular location on a genetic map, where a local maximum of the lod-score curve identifies the estimated position of a susceptibility locus. The scan statistics developed here provide additional support for linkage above and beyond what is conveyed by the maximum lod score. They are powerful when a susceptibility locus exerts an effect over multiple marker loci, which is generally the case for genetic linkage in today's genome screens. It also is expected to be true for disequilibrium mapping in special populations, where disequilibrium extends over multiple loci. In large outbred populations, disequilibrium is not expected to extend over more than 1/3 cM (16) so that marker loci must be very densely spaced for scan statistics to show their full potential. Thus, depending on the population investigated and/or the type of analysis carried out, scan statistics may have useful lengths extending over rather large (linkage) or only short (association) genomic regions.
The increased power provided by scan statistics has the effect that smaller numbers of observations (or families) may yield as strong a result as do conventional statistics based on larger numbers of observations. Conversely, with a given number of observations, conventional methods will detect susceptibility loci of some minimum effect (“signal strength”) but scan statistics will detect loci of smaller effects. However, scan statistics as proposed in this paper are not useful for narrowing a candidate region once linkage has been established.
Computer programs carrying out the calculations described in this paper are available from the authors.
Acknowledgments
We thank Dr. Conrad Gilliam for making the autism data available to us and Dr. Dale Nyholt for carrying out the lod-score calculations. This work was supported by Grants HG00008 and MH44292 from the National Institutes of Health.
Abbreviations
- lod
logarithm of odds
- AA
affected-affected
- AU
affected-unaffected
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.170179197.
Article and publication date are at www.pnas.org/cgi/doi/10.1073/pnas.170179197
References
- 1.Schwab S G, Albus M, Hallmayer J, Honig S, Borrmann M, Lichtermann D, Ebstein R P, Ackenheil M, Lerer B, Risch N, et al. Nat Genet. 1995;11:325–327. doi: 10.1038/ng1195-325. [DOI] [PubMed] [Google Scholar]
- 2.Friddle C, Koskela R, Ranade K, Hebert J, Cargill M, Clark C D, McInnis M, Simpson S, McMahon F, Stine O C, et al. Am J Hum Genet. 2000;66:205–215. doi: 10.1086/302697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kruglyak L, Daly M J, Reeve-Daly M P, Lander E S. Am J Hum Genet. 1996;58:1347–1363. [PMC free article] [PubMed] [Google Scholar]
- 4.Gudbjartsson D F, Jonasson K, Frigge M L, Kong C A. Nat Genet. 1999;25:12–13. doi: 10.1038/75514. [DOI] [PubMed] [Google Scholar]
- 5.Terwilliger J D, Shannon W D, Lathrop G M, Nolan J P, Goldin L R, Chase G A, Weeks D E. Am J Hum Genet. 1997;61:430–438. doi: 10.1086/514855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goldin L R, Chase G A. Genet Epidemiol. 1997;14:785–789. doi: 10.1002/(SICI)1098-2272(1997)14:6<785::AID-GEPI37>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 7.Goldin L R, Chase G A, Wilson A F. Genet Epidemiol. 1999;17:157–164. doi: 10.1002/(SICI)1098-2272(1999)17:3<157::AID-GEPI1>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- 8.Glaz J, Balakrishnan N, editors. Scan Statistics and Applications. Basel: Birkhauser; 1999. pp. 3–24. [Google Scholar]
- 9.Karlin S, Brendel V. Science. 1992;257:39–49. doi: 10.1126/science.1621093. [DOI] [PubMed] [Google Scholar]
- 10.MacLean C J, Sham P C, Kendler K S. Am J Hum Genet. 1993;53:353–366. [PMC free article] [PubMed] [Google Scholar]
- 11.Cox N J, Frigge M, Nicolae D L, Concannon P, Hanis C L, Bell G I, Kong A. Nat Genet. 1999;21:213–215. doi: 10.1038/6002. [DOI] [PubMed] [Google Scholar]
- 12.Efron B, Tibshirani R. Science. 1991;253:390–395. doi: 10.1126/science.253.5018.390. [DOI] [PubMed] [Google Scholar]
- 13.Lander E, Kruglyak L. Nat Genet. 1995;11:241–247. doi: 10.1038/ng1195-241. [DOI] [PubMed] [Google Scholar]
- 14.Manly B F J. Randomization, Bootstrap, and Monte Carlo Methods in Biology. New York: Chapman & Hall; 1998. [Google Scholar]
- 15.Moldin S O. Genet Epidemiol. 1997;14:1023–1028. doi: 10.1002/(SICI)1098-2272(1997)14:6<1023::AID-GEPI77>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 16.Collins A, Lonjou C, Morton N E. Proc Natl Acad Sci USA. 1999;96:15173–15177. doi: 10.1073/pnas.96.26.15173. [DOI] [PMC free article] [PubMed] [Google Scholar]


