Multiple valence superatoms

Abstract

We recently demonstrated that, in gas phase clusters containing aluminum and iodine atoms, an Al₁₃ cluster behaves like a halogen atom, whereas an Al₁₄ cluster exhibits properties analogous to an alkaline earth atom. These observations, together with our findings that Al₁₃⁻ is inert like a rare gas atom, have reinforced the idea that chosen clusters can exhibit chemical behaviors reminiscent of atoms in the periodic table, offering the exciting prospect of a new dimension of the periodic table formed by cluster elements, called superatoms. As the behavior of clusters can be controlled by size and composition, the superatoms offer the potential to create unique compounds with tailored properties. In this article, we provide evidence of an additional class of superatoms, namely Al₇⁻, that exhibit multiple valences, like some of the elements in the periodic table, and hence have the potential to form stable compounds when combined with other atoms. These findings support the contention that there should be no limitation in finding clusters, which mimic virtually all members of the periodic table.

The formation of materials with properties different from those of the constituent atoms is a known phenomenon in nature. For example, the formation of NaCl molecules/solid with characteristics different from its constituent elements, Na and Cl, is a classic example. One of the objectives of the research on superatoms (1–3) is to explore if one can carry out, what nature does, in a more facile and controlled manner. Developing an understanding of the factors governing the chemical behavior of clusters (4–10) and demonstrating that this knowledge can be used to design stable building blocks for new materials is critical for translating this concept into practice. For metal clusters, a simple electronic shell model called jellium (11) is routinely used to describe the global features of the electronic structure. In this model, the nuclei together with the innermost electrons form a positive-charged background, whereupon the valence electrons coming from individual atoms are then subjected to this potential. For pure metal clusters, within a spherical jellium background, this approach results in a shell structure where the electrons are arranged in electronic shells 1s², 1p⁶, 1d¹⁰, 2s², 1f¹⁴, 2p⁶ … compared with 1s², 2s², 2p⁶, 3s², 3p⁶, 4s², 3d¹⁰ … in individual atoms. Similar shell structure is also obtained for square well and harmonic forms of background potential (12), indicating that the shells derived within a jellium picture represent generic features of electronic states in a confined free electron gas. Clusters containing 2, 8, 18, 20, 34, 40 … electrons correspond to filled electronic shells and exhibit enhanced stability as seen via abundances in mass spectra of simple metal clusters, higher ionization potential, lower electron affinity, and chemical inertness seen in reactivity experiments. In this respect, an Al₁₃ cluster with 39 valence electrons and an electronic structure of 1s², 1p⁶, 1d¹⁰, 2s², 1f¹⁴, 2p⁵ lacks a single electron as do halogen atoms, which, upon addition of a single electron, acquire a filled shell status (13). Indeed, previous studies (14, 15) have shown that Al₁₃ has an electron affinity comparable to halogen atoms, indicating a chemical behavior reminiscent of halogen atoms. In a similar vein, we had recently shown that in cluster compounds with iodine, an Al₁₄ cluster exhibits behavior analogous to alkaline earth atoms (3). We had shown that Al₁₄I₃⁻ is a stable species and that its stability can be reconciled by considering Al₁₄ in a + 2 valence state (3). The electronic shell structure, outlined above, does become modified (16) for compound clusters as the combination of atoms with different electronegativities can rearrange their geometry and influence the electronic shells. In particular, the shell closings at 18 and 20 are sensitive to the nature of the compound cluster.

Although the above developments bring out a close analogy between atoms and superatoms, one of the most important features characterizing atoms is that numerous elements in the periodic table exhibit multiple valence states. For example, carbon exhibits both divalent and tetravalent characteristics and, strongly binds with O or Si atoms forming CO and SiC, both of which are highly stable. Are there superatoms that share this commonality to atoms?

In this article we present the results of a synergistic effort that combines first-principles' theoretical calculations and the reactive stability of selected clusters to demonstrate an additional member of the superatom family, namely Al₇⁻. What is truly remarkable is that unlike previous members, this superatom exhibits multiple valence states, enabling it to form stable compound clusters when combined with diverse atoms. In particular, we first demonstrate (8) the exceptional stability of Al₇C⁻ through the production of Al_nC⁻ clusters in reactions of aluminum clusters with benzene, and subsequent reactions of the clusters with oxygen to identify the stable species. The mass spectra show the Al₇C⁻ peak to be even more pronounced than Al₁₃⁻, another member of the superatom family, which we have previously identified, and studied extensively (1–3). Theoretical considerations indicate that a superatom concept enables one to understand the electronic origin of the exceptional stability often observed for these species. The same considerations also predict stability of other species such as Al₇O⁻, Al₇S⁻, Al₇I₂⁻, and Al₇⁺. Unlike Al₇C⁻, however, the stability of Al₇O⁻, Al₇S⁻, and Al₇I₂⁻ cannot be ascertained by O₂ etching experiments. The Al₇O⁻ and Al₇S⁻ clusters are not stable toward the formation of AlO₂⁻ or Al₂O₂; Al₇I₂⁻ is unstable toward the formation of Al₂O₂. Consequently, their stability has to be verified by a reactant less harsh than O₂. Experimental mass spectra, however, do show the stability of Al₇⁺ in oxygen-etching experiments. The present investigations provide further extensive support to the general nature of the superatom concept and show Al₇⁻ to be a member of the multivalent superatom family.

Results and Discussion

In brief, the clusters are produced by vaporizing a rotating and translating aluminum rod in a helium atmosphere. The production of mixed clusters is then accomplished by mixing the ablation species with a small percentage of the carrier gas containing the desired precursor. For example, Al_nC⁻ clusters are produced by adding benzene. To identify the stable species, the generated clusters are subsequently exposed to increasing amounts of etching gas introduced into the flow reactor in which the clusters are transported. In this way, the reactive anions are oxidized and often etched into smaller more stable fragments. The reacted species are mass-analyzed, thus spectra contain the stable species generated in the original mass distribution and the stable products generated in the oxidation and etching reactions. In this way, the peaks in the mass spectra of the reacted species identify the stable species.

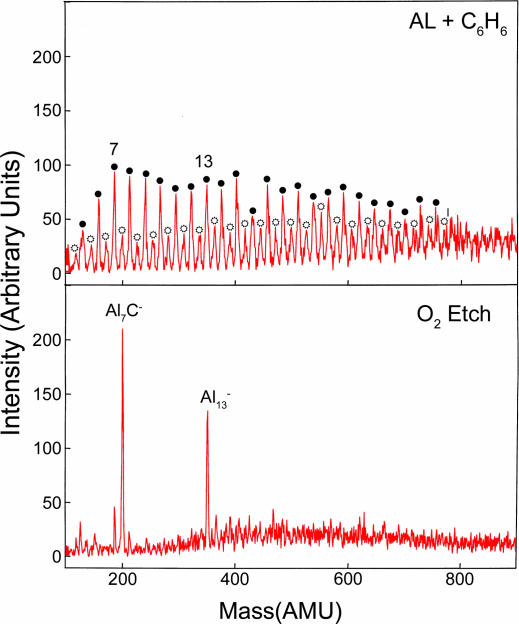
Fig. 1 shows the mass spectra of Al_nC⁻ clusters obtained by reacting the aluminum plasma with benzene and subsequently exposing the generated Al_nC⁻ clusters to >200 standard cubic centimeters per minute of oxygen. Fig. 1 shows that Al₇C⁻ is the only cluster containing one C atom (at small sizes) that survives in the mass spectra. The peak at Al₇C⁻ is conspicuously large and even more prominent than Al₁₃⁻, known to be resistant to oxygen because of its closed shell structure. It was suggested earlier (17) that the stability of Al₇C⁻ could be reconciled within a jellium model framework where the cluster could be looked upon as a compound jellium formed out of an Al₆, with a closed shell of 18 electrons and AlC⁻ with a closed shell of 8 electrons. Such a picture does have difficulties. The electron affinity of AlC (1.1 eV) is less than that of Al₆ (2.5 eV). Our calculations show that, whereas it takes only 3.76 eV to remove an Al atom from Al₇C⁻, it will take 9.09 eV to break it into Al₆ and AlC⁻. The C atom in Al₇C⁻ is located inside the Al₇ cage bonded to all of the Al sites, whereas one would expect it to bind to a single Al atom if it were a combination of Al₆ and AlC⁻.

Fig. 1.

Benzene is introduced in the source aluminum plasma to produce Al_n⁻ (●) and Al_nC⁻ (). The clusters are subsequently reacted with molecular oxygen at thermal energy.

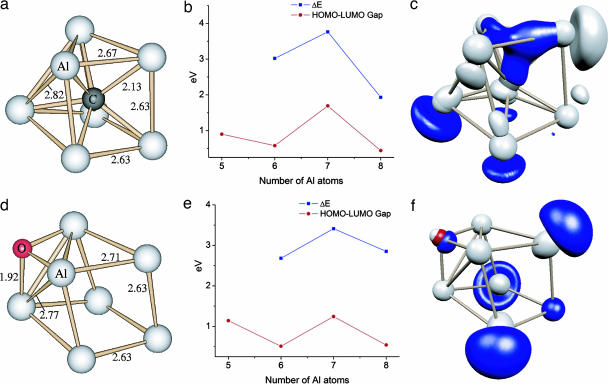
We begin by demonstrating that the true reason for the stability of Al₇C⁻ lies in the multiplet nature of Al₇⁻. Fig. 2 shows the geometry deduced for Al₇C⁻. Note that the cluster features an endohedral C atom as obtained in earlier studies. To examine the stability, we calculated the gain in energy, ΔE,

as a function of size as successive Al atoms are added to the preceding size Al_n−1C⁻. Here E is the total energy of the cluster. The results are shown in Fig. 2b. A peak in ΔE is a signature of stability as it implies a larger gain in energy in forming the stable species from the preceding size and lower energy in breaking the higher size to form the stable species. Note that there is a peak at Al₇C⁻ indicating its preferred formation from the growth of Al₆C⁻ and from the fragmentation of Al₈C⁻. Fig. 2b also shows the gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). In metallic clusters, the gap is generally indicative of stability and chemical inertness. Note that Al₇C⁻ has the highest HOMO–LUMO gap.

Fig. 2.

Structure and energetics of aluminum compound clusters. (a) Al₇C⁻-optimized geometry. (b) Energy gained by adding an Al atom to Al_n-1C⁻ species and HOMO–LUMO gap for the Al_nC⁻ clusters. (c) Electron charge density of the HOMO in Al₇C⁻ clusters. (d) Al₇O⁻-optimized geometry. (e) Energy gained by adding an Al atom to Al_n-1O⁻ species and HOMO–LUMO gap for the Al_nO⁻ clusters. (f) Electron charge density of the HOMO in Al₇O⁻.

We now discuss the stability of Al₇C⁻ and other aluminum-based clusters toward etching by O₂ more quantitatively. The possible fragmentation pathways involve the formation of AlO₂, AlO₂⁻, or Al₂O₂. Note that because the clusters are first thermalized, then exposed to molecular O₂, the OO bond is protected by a barrier and remains intact in the formation of AlO₂, AlO₂⁻, or Al₂O₂. Our calculations show that the binding energy (BE) of AlO₂ and AlO₂⁻ with OO bond intact is 2.83 and 5.72, eV respectively, whereas the energy required for breaking an Al₂O₂ into two Al atoms and an O₂ molecule is 6.75 eV. These calculations show that those aluminum-based clusters, where it takes (i) <2.83 eV to remove a single Al, (ii) <5.72 eV to remove an Al⁻, or (iii) <6.75 eV to remove two Al atoms, will be energetically unstable toward etching by O₂. In this way, the stability of clusters can be tested, as less stable clusters are oxidized and often etched into smaller more stable fragments. In the case of Al₇C⁻, the removal of an Al atom requires 3.76 eV, and the removal of an Al⁻ requires 6.40 eV, whereas the removal of two Al atoms requires 6.78 eV of energy. The corresponding studies based on the Naval Research Laboratory Molecular Orbital Library (NRLMOL) show that the energy required to remove two Al atoms is 7.04 eV, whereas the BE of Al₂O₂ toward breaking into two Al atoms and an O₂ is 6.92 eV. Al₇C⁻ is therefore stable toward these fragmentation pathways and hence is not etched by O₂. The same considerations also explain the observation of Al₇⁺ in etching of the pure Al_n⁺ cations by oxygen. In this case, whereas it takes 4.32 eV to remove an Al atom, it takes 7.22 eV to remove two Al atoms. Why is Al₇C⁻ so stable? Can Al₇⁻ combine with other atoms to create stable species?

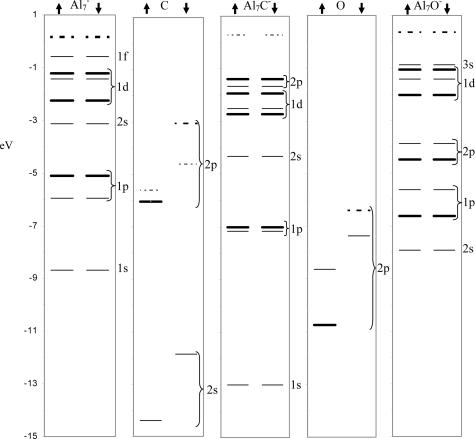
To answer the above questions, we outline the mechanism by which the Al₇⁻ cluster combines with other atoms to form stable compounds. An Al atom has a valence electronic configuration of 3s² 3p¹, and it has been proposed that Al_n clusters undergo a transition (18) from monovalent to trivalent starting around n = 6. The trivalent character in Al₇ is further established (19) by the mass spectra of the reacted Al_n⁺ cations that exhibit a sharp peak at Al₇⁺, indicative of a shell closing at 20 electrons within a jellium picture of the confined free electron gas. If instead, it was monovalent in character, it would display prominence as an eight-electron system, which it does not (13). An Al₇⁻, on the other hand, has 22 valence electrons. Within the jellium picture, the cluster has an electronic configuration of 1s², 1p⁶, 1d¹⁰, 2s², 1f², and Fig. 3 shows the one-electron levels in the free cluster. The molecular orbitals have been labeled by using the jellium classification (the levels roughly correspond to the overall shape of the molecular orbitals). A carbon atom has a valence structure of 2s², 2p² with four vacancies in the p-shell, and Fig. 3 shows the one-electron levels in carbon. To discuss the formation of Al₇C⁻, let us start with the one-electron levels in Al₇C⁻ also shown in Fig. 3. The 2s filled state of carbon is far below the manifold of Al₇⁻ and becomes the 1s state of Al₇C⁻. Consequently, the 1s and 2s states of pure Al₇⁻ become the 2s and 3s states of the combined system and are pushed up in energies (the resulting 3s is high in energy and is not shown). The partially filled p-states of carbon are around the same energy as 1p states of Al₇⁻ and form the bonding and antibonding combinations. The bonding combination leads to the 1p state of Al₇C⁻, whereas the antibonding combination leads to the 2p state that characterizes the group of highest occupied molecular states in Al₇C⁻. Because a carbon atom has four unfilled p-states, the occupation of the p-states can be looked on as the transition of four electrons from the 1f and the 2s states of Al₇⁻ to these unfilled states. The 1f unfilled states are pushed up in energy, and Fig. 3 shows the revised level structure in Al₇C⁻. Note that the p-states of C form bonding orbitals with Al₇⁻ states; hence it is not a charge transfer but a population of these bonding states. A better description is the transition of Al₇⁻ toward a + 4 valence state, which is similar to the transition of Al₁₄ toward a + 2 state reported previously (3). Obviously such a transition cannot be identified through Mulliken or other charge analysis, as recently undertaken by some authors (20). Fig. 2c shows the electron charge density in the HOMO orbital. As the bonding states are deep in energy, the occupation of bonding states stabilizes the cluster whereas the movement of unoccupied states opens a large HOMO–LUMO gap of 1.69 eV consistent with the stability and inertness of Al₇C⁻. A similar model would also account for the previously known (21, 22) enhanced stability of neutral Al₇N because Al₇ has 21 electrons, and the N states can be filled by occupation of three bonding orbitals.

Fig. 3.

One-electron levels in Al₇⁻, C, Al₇C⁻, O, and Al₇O⁻. The continuous thin lines represent single occupied levels, the continuous thicker lines represent double occupied levels, the dotted thin lines correspond to single unfilled states, the dotted thicker lines correspond to double unfilled states, and the arrows indicate the majority (up) and minority (down) spin states.

The key issue is whether such simple electronic counting rules and shell filling can be used to describe the stability of other members of the second row of the periodic table. Because the confined free electron gas exhibits shell closing at 18 and 20 electrons, the above arguments would suggest that Al₇M⁻ clusters should exhibit enhanced stability for cases where the M atom would require two or four electrons to fill the deep p-bonding orbitals. This criterion would indicate that Al₇O⁻ should also be quite stable, and Fig. 3 shows the levels in this cluster and an O atom (2s state of oxygen is deep in energy and is not shown). The bonding then proceeds as for Al₇C⁻, with the only difference being that only 1f electrons of Al₇⁻ are transferred to bonding states between Al₇⁻ and O. To examine quantitatively the stability, we investigated the Al_nO⁻ clusters containing five to eight Al atoms and computed ΔE and the HOMO–LUMO gap (shown in Fig. 2 d and e). Note that ΔE peaks at Al₇O⁻, indicating enhanced stability. Fig. 2f also shows the HOMO orbital. Although Al₇O⁻ is stable, it is not resistant to etching by O₂ because it takes 6.10 eV to remove two Al atoms.

It is now interesting to inquire as to whether the above considerations could be extended to other elements. In particular, could one use the above model to understand the bonding of Al₇⁻ to other elements in the second, third, and fourth row of the periodic table. To this end, we have calculated the BE of all of the atoms in the second, third, and fourth rows with Al₇⁻ using the equation

Here E(Al₇⁻), E(M), and E(Al₇M⁻) are the total energies of the Al₇⁻, M, and Al₇M⁻ species, respectively. For cases where M is a halogen atom, the BE was calculated by breaking into Al₇ and M⁻ fragments. In these calculations, the atoms were initially located at different positions around the Al₇ motif. The geometry was optimized by moving atoms in the direction of forces until the forces dropped below a threshold value of 3 × 10⁻⁴ a.u. Several spin multiplicities were tried to locate the ground state. Three different types of geometries were obtained. For B, C, and N we obtain an endohedral structure (Fig. 2a). For Li, Be, O, F, Na, Mg, Al, P, S, Cl, Cu, Zn, Ga, Ge, As, Se, and Br we obtain an external geometry (Fig. 2d), and for Si we obtained a capped geometry where the Al₇ opens up to accommodate the additional atom.

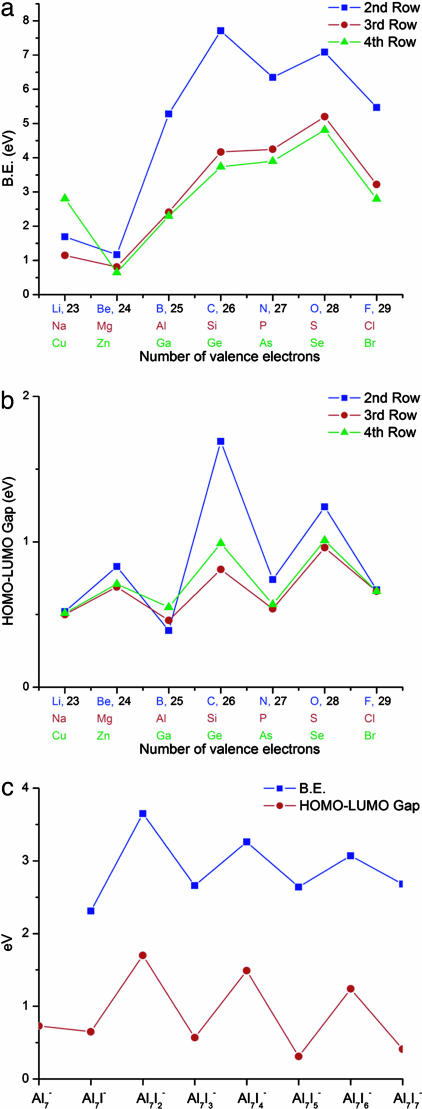
In Fig. 4a, we show the variation of BE for all of the anionic clusters. In each case, we have marked the total number of valence electrons. Note that Al₇C⁻ and Al₇O⁻ are not only stable with respect to addition of Al atoms, as discussed earlier, they also have the highest BE across the entire second row of the periodic table. What is quite amazing is that the same trend continues for the anions of the third-row and fourth-row elements. S in the third row and Se in the fourth row exhibit larger gain in BE than previous sizes, again indicative of their stability. In addition to the BE, we examined the variation of the HOMO–LUMO gap (Fig. 4b). Significantly, the HOMO–LUMO gap follows the stability trend, indicating a chemical inertness. For Si and Ge that correspond to a shell filling at 18, the BE only exhibits a shoulder whereas the HOMO–LUMO gap exhibit minor peaks. This behavior could be caused by the highly directional nature of the bonds from these atoms. To further confirm this extensive nature of the multivalence concept and reiterate the theoretical picture, Al_nS⁻ clusters were generated by reacting Al_n clusters with SO₂. The mass spectra of the resulting clusters contained Al₇S⁻ clusters, including other sulfur-containing clusters as well. When the clusters were exposed to O₂, however, all of the clusters, including Al₇S⁻, were etched away. The etching of Al₇S⁻ is understandable, noting that the energy required to remove two Al atoms is only 5.78 eV whereas energy gain in forming Al₂O₂ is 6.75 eV. Further, it will take 5.73 eV to remove an Al⁻ atom, making the formation for AlO₂⁻ a resonant reaction. The corresponding studies based on the NRLMOL, however, indicate that it will take 5.68 eV to remove an Al⁻ atom, whereas the gain in energy in forming AlO₂⁻ is 6.07 eV, opening this channel for fragmentation. In either case, Al₇S⁻ is unstable toward oxidation. We further calculated the electron affinity of the Al₇M⁻ clusters for M covering all of the third-row and fourth-row atoms. Al₇S⁻ and Al₇Se⁻ had the highest electron affinity, attesting to their closed electronic shell character.

Fig. 4.

Energetics of the Al₇M clusters. (a) BE of Al₇M⁻ clusters, M is an atom of the second, third, and fourth row of the periodic table. (b) HOMO–LUMO gap for the Al₇M⁻ clusters. (c) BE and HOMO–LUMO gap of the Al₇I_m⁻ clusters.

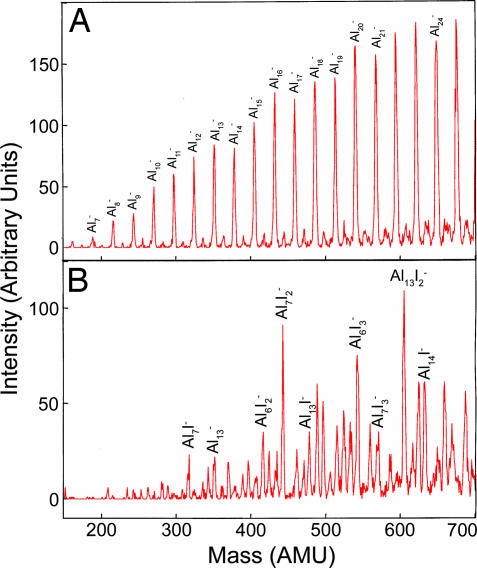
A critical test of the multiple valence would be to combine Al₇⁻ with atoms that have only one vacancy in the p-level (3) and a high electron affinity. The formation of the bonding states would then remove one electron at a time whereupon the effect of the 2f and 2s depopulation could be mapped out with the number of atoms. To carry out this important test, we considered anionic Al₇I_m⁻ clusters. An I atom has an electron affinity of 3.06 eV that is considerably higher than the measured electron affinity (15) of 2.43 for Al₇. One would therefore expect each additional I atom to combine with one electron from the Al₇ core. In Fig. 4c we show the variation of the BE and HOMO–LUMO gap as successive I atoms are added to the cluster. Note that Al₇I₂⁻ leading to a core of 20 electrons is particularly prominent compared with other sizes, again verifying the shell closures discussed above. More importantly, the corresponding HOMO–LUMO gap shows the same trend. The chemical features together with the BE again point to the valence status. To examine whether the stability of Al₇I₂⁻ is borne out by experiments, the aluminum clusters anions were reacted with iodine gas. Fig. 5 shows the mass spectra of the bare and reacted species. Note that the mass spectra indeed exhibits a peak at Al₇I₂⁻, confirming the theoretical prediction. We note that the variations in BE and HOMO–LUMO gap in Fig. 4c indicate Al₇I₄⁻ to be more stable than neighboring sizes, consistent with a shell closure at 18 electrons; however, it is not seen in Fig. 5. The reason is that it is energetically unstable toward the reaction

by 0.31 eV. Although Al₇I⁻ and Al₇I₃⁻ are less stable than Al₇I₄⁻, as discussed in a previous paper (23), their observation is linked to the enhanced stability of the corresponding neutral species. Al₇I₂⁻ is, however, unstable toward etching by O₂ as it takes 6.76 eV to remove two Al atoms, making the formation of Al₂O₂ a resonant reaction. Corresponding studies based on the NRLMOL indicate the formation of Al₂O₂ to be exothermic by 0.03 eV.

Fig. 5.

Mass spectra of Al_n⁻ clusters (A) reacted with I₂⁻ (B).

To summarize, we have demonstrated that bonding patterns of Al₇⁻ can be understood by regarding it as a superatom that exhibits multiple valence. The valence of 2 and 4 would make it analogous to C or Si. The stability of Al₇C⁻ on the one hand and that predicted for Al₇O⁻ and Al₇S⁻ on the other hand could then be correlated with the stability of SiC and CO, respectively. In the past we have shown that Al₁₃ and Al₁₄ could be regarded as superhalogen and alkaline earth superatoms. Importantly, unlike Al₁₃⁻ and Al₁₄, Al₇⁻ exhibits multiple valence, thus adding an additional dimension to the chemistry of superatoms.

Materials/Methods

Experimental Methods.

Al₇C⁻ species were created by ablating an aluminum rod in a flow of 8,000 standard cubic centimeters per minute of high-purity helium. Benzene vapor was added restrictively to the source to maximize the population of Al_nC⁻ species. The clusters and helium carrier gas merged into a laminar flow regime where they became thermalized. The clusters were then reacted with molecular oxygen, and products were extracted, mass-analyzed by a quadrupole mass filter, and detected by a channel electron multiplier. The Al₇I₂⁻ species were created by ablating an aluminum rod in a flow of 8,000 standard cubic centimeters per minute of high-purity helium. Molecular iodine was added externally to the source by flowing a small amount of helium through a sublimation cell containing molecular iodine.

Theoretical Methods.

The theoretical studies were carried out by using first-principles electronic structure calculations performed within a density functional formalism (24) that incorporates exchange and correlation using the generalized gradient approximation functional proposed by Perdew, Burke, and Ernzerhof (25). In particular, Gaussian basis sets were used to construct the atomic wave function, whereas the cluster wave function was formed from a linear combination of atomic orbitals. All calculations were performed with deMon2k software (26). Here, an auxiliary basis set was used for the variational fitting of the Coulomb potential (27, 28). The numerical integration of the exchange-correlation energy and potential were performed on an adaptive grid (29). The minimum structures were fully optimized in delocalized internal coordinates without constraints using the rational function optimization method and the Broyden, Fletcher, Goldfarb, and Shanno update (30). The double zeta valence polarized and the GEN-A2 auxiliary basis sets were used (31). To eliminate any uncertainty from the basis set or the numerical procedure, in selected cases we carried out supplementary calculations by using the NRLMOL developed by Pederson and coworkers (32–34) using the same density functional. For details, see refs. 3 and 32–34.

Abbreviations

HOMO

highest occupied molecular orbital

LUMO

lowest unoccupied molecular orbital

BE

binding energy

NRLMOL

Naval Research Laboratory Molecular Orbital Library.