Four-dimensional ultrafast electron microscopy of phase transitions

Abstract

Reported here is direct imaging (and diffraction) by using 4D ultrafast electron microscopy (UEM) with combined spatial and temporal resolutions. In the first phase of UEM, it was possible to obtain snapshot images by using timed, single-electron packets; each packet is free of space–charge effects. Here, we demonstrate the ability to obtain sequences of snapshots (“movies”) with atomic-scale spatial resolution and ultrashort temporal resolution. Specifically, it is shown that ultrafast metal–insulator phase transitions can be studied with these achieved spatial and temporal resolutions. The diffraction (atomic scale) and images (nanometer scale) we obtained manifest the structural phase transition with its characteristic hysteresis, and the time scale involved (100 fs) is now studied by directly monitoring coordinates of the atoms themselves.

Electron microscopy has become a pivotal tool in numerous fields of study, from materials to biological imaging. In a previous publication (1), we introduced the concept of single-electron imaging for the development of 4D ultrafast electron microscopy (UEM). The potential of UEM was demonstrated by obtaining images and diffraction patterns of materials and biological cells (1), and the scope of future applications has been highlighted in recent commentaries and reviews (refs. 2 and 3; see also ref. 4 and references therein). Because single-electron packets have no significant space–charge broadening, images and diffraction patterns are observed with atomic-scale spatial resolution and with the time resolution being fundamentally determined by the ultrashort duration of the optical pulse introduced to generate the photoelectrons in the microscope.

The images and diffraction patterns reported (1) were “snapshots” at a particular point in time. However, as shown in Fig. 1, by delaying a second initiating optical pulse to arrive at the sample in the microscope with controlled time steps, it is possible to obtain a series of such snapshots with a well defined frame time. Unlike optical pump–probe experiments, this experimental task, for the microscope, is technically nontrivial for a number of reasons. To determine the zero time point, the clocking of the electron packet and optical pulse at the sample must be made with femtosecond time precision. Moreover, in contrast to these all-optical experiments, the cross-correlation between electron and photon pulses requires a new methodology. In addition, for 120-keV electrons, the group velocity of electron packets in the microscope is two-thirds the speed of light, and care has to be taken to account for this group velocity mismatch. Overcoming these hurdles in conjunction with attaining high quality, nanometer-scale samples in the microscope provides the capability of observing the dynamical changes of systems in the far-from-equilibrium state with the combined resolutions mentioned above.

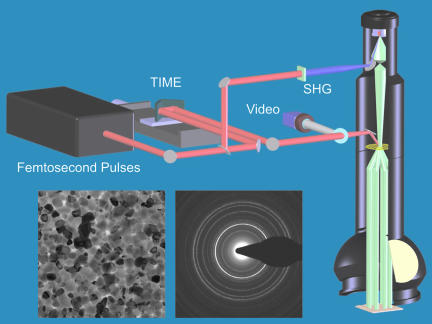
Fig. 1.

A schematic of UEM at California Institute of Technology. Shown are the femtosecond laser system and the transmission electron column. The temporal resolution is determined by the time between the single-electron packets and the initiating heat or excitation pulses. Typical images (real space) and diffraction patterns obtained by UEM are also show (for details see the text).

With the 4D UEM arrangement shown in Fig. 1, we demonstrate such studies of imaging and diffraction for the metal–insulator phase transition in vanadium dioxide (VO₂). Based on the difference in conductivity the transition is termed metal–insulator, but when considering other properties it is referred to as a metal–semiconductor transition. The dioxide exhibits an ultrafast transition and is an archetypical candidate for UEM study. Moreover, it is a strongly correlated system, and the interplay of electron correlations and nuclear motion is critical to the global dynamics of the phase transition. The material VO₂ undergoes a first-order phase transition from a low-temperature monoclinic (M) phase to a high-temperature tetragonal rutile (R) phase at ≈67°C (5, 6). Since its discovery almost half a century ago, this phase transition has been the subject of intense study (6–8).

A widely accepted picture of the energy band diagram of the electronic structure was presented early by Goodenough (9) and is based on an orbital description. In the monoclinic phase (space group P2₁/c), the formation of V–V pairs and the tilting of these dimers with respect to the rutile c axis completely destroys the symmetry of the VO₆ octahedron, which results in the splitting of the d_‖ manifold into a lower-energy, filled bonding (3d_‖) and higher-energy, empty antibonding (3d*_‖) state. The antibonding π* orbitals are pushed higher in energy because of the antiferroelectric tilting of the V dimers, which increases the overlap with the O 2p states. As a result, a band gap emerges, and a single 3d electron of V occupies the bonding d_‖ combination (9). In the rutile phase (space group P4₂/mnm), VO₆ octahedra form an edge-sharing chain along the c axis. The important feature here is the degeneracy of the 3d_‖ states and the lowering of the π* orbitals to be partly filled below the Fermi level.

There are a number of issues that remain unclear and require direct knowledge of structural dynamics. One issue is the exact nature of the energy gap, Peierls (9–11), or Mott–Hubbard (12, 13) type; in other words, the role of electron correlations must be elucidated in the description of the band structure. The actual electron–nuclear forces responsible for the change of structure from one phase to another must account for the ultrafast transformation. Recent studies considered both electron correlations within the V–V pairs and structural effects and successfully reproduced experimental data of photoemission and near-edge x-ray absorption fine structure spectra (14, 15). The phase transition is described as a correlation-assisted Peierls transition. In other words, the M phase can be described as a renormalized Peierls insulator at low energies and a Mott–Hubbard insulator at high energy (14).

Results and Discussion

Fig. 2 shows UEM real-space images obtained for the two phases of the transition: metallic (R) and insulator (M). With the microscope operating in the selected-area electron diffraction mode, we acquired the patterns in Fig. 3 before and after the transition. These images and diffraction patterns were obtained when the VO₂ films were driven through the transition by the heat deposited from the ramped, initiating (near infrared) laser pulses at 776 nm. Equivalently, we obtained the same images and patterns in UEM by ramping the sample temperature through the phase transition. This equivalence together with the observed hysteresis is shown in Figs. 4 and 5. Below we shall discuss these imaging and diffraction experiments as a function of time as the system undergoes the transition. The laser power required to induce the phase transition is a function of absorption and the ability of the sample to cool down between laser pulses. For the samples in the present study, an average power of ≈1 mW was sufficient to drive the transition. The thickness of these samples was estimated to be 50–200 nm from the observed polycrystalline grain sizes in the microscope (Fig. 2). The micrographs showed drastic changes when passing through the phase transition.

Fig. 2.

UEM images obtained before the phase transition (Left) and after the phase transition (Right). The magnification is ×42,000. (Scale bars: 100 nm.) It should be noted that these images would not be observed if the femtosecond pulses for photoelectron generation were blocked from the microscope.

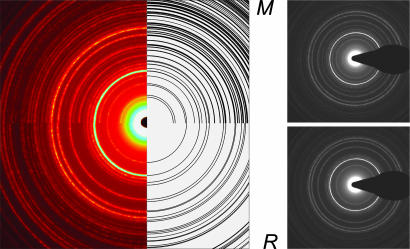
Fig. 3.

UEM diffraction patterns. (Right) patterns obtained before and after the phase transition. (Left) The composite diffraction pattern of the two phases observed experimentally and assigned theoretically by the black rings. The analysis was done as described in the text.

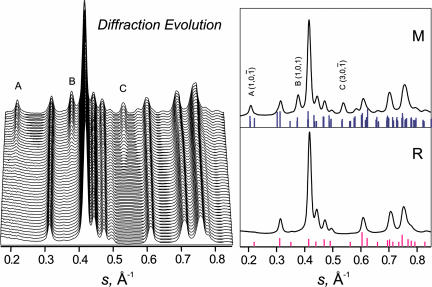
Fig. 4.

Diffraction evolution through the phase transition. The evolution was observed by ramping either the temperature of the sample or the average power. Shown here are the characteristic changes in the diffraction peaks as the system undergoes the transition from the rutile structure to the monoclinic structure. (Left) Of particular interest are the peaks labeled A, B, and C, which characterize the monoclinic phase. (Right) The diffraction peaks together with the theoretical assignments indicated by the bars.

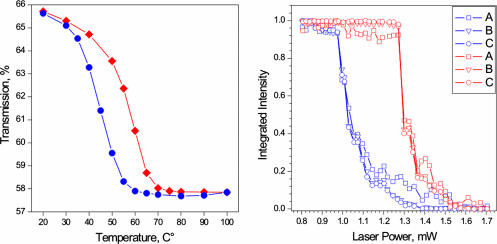
Fig. 5.

Phase transition hysteresis. The reported behavior was from experiments varying the temperature of the sample at steady state (Left) and varying the average power (Right). The transmission was measured in a window between 1,300 and 1,400 nm. The phase transition occurs in the range of 55°C (forward ramp) and at ≈1.2 mW of average power. We note that, at a given temperature (e.g., 45°C), the structures allowed are determined by the vertical positions between blue and red curves.

To quantify the structural changes with atomic-scale resolution, electron diffraction patterns were recorded while raising the sample temperature through the phase transition. Large changes in diffraction patterns were observed in the temperature region of 55–70°C (Fig. 3). The M and R phase share most of their diffraction peaks, but the M phase has several distinct peaks because of the broken symmetry originating from cell doubling. In Figs. 3 and 4, we can assign all diffraction peaks to these structures. The theoretical diffraction patterns (Figs. 3 and 4) of the polycrystalline materials for the R and M structures were generated by considering the crystal symmetry; similar patterns were constructed with JCEP/PCED software (16). The agreement between the simulated and experimental diffraction patterns is satisfactory and provides conclusive evidence that the correct phase of VO₂ films was fabricated. The electron diffraction data also demonstrate a characteristic heating/cooling hysteresis of the phase transition similar to that shown in Fig. 5. The width of the hysteresis loop, ≈15°C, is close to that reported for other films of VO₂ (17).

In Fig. 4, we display phase changes in the diffraction as the power was ramped. We also studied these changes as a function of increased temperature, and the behavior is similar. As shown below, the changes of diffraction peaks with time are indicative of this same phase change. Clearly, peaks A (101), B (101), and C (301) are characteristic of the monoclinic structure, and we focused our probing of structural dynamics on these peaks. For recording the temporal change, the electron and optical pulses were spatially and temporally coincident at the sample, and the time delay between them was controlled in steps of varying duration, 100 fs or longer. Knowing the transition temperature and shape of hysteresis (Fig. 5), instead of driving the entire phase transition with a single laser pulse, the average power was set such that the sample temperature was kept constant in the middle of the temperature range of the phase transition (≈45°C); some crystallites were in the R phase, whereas others were in the M phase.

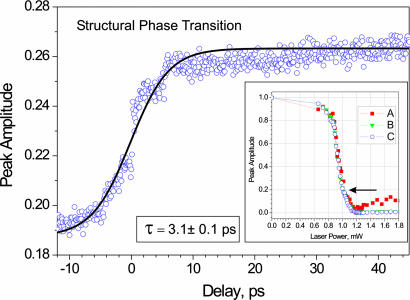
The frames were recorded in real time by continuously stepping the delay time between the electron and photon pulses. These frames were combined to make movies for images (Fig. 2) and diffraction (Fig. 3). The temporal behavior is presented in Fig. 6. Here, the integrated area, which is equivalent to the amplitude because the width remains constant, of the (301) M diffraction peak is plotted against time. The transient response shows the increase in the fraction of the monoclinic structure while the average power during the scan was maintained at ≈45°C. We note that if we shift the average power to temperatures outside the transition region (e.g., 80°C or 20°C), we do not see the temporal change. From the best fit we obtained a characteristic transition time for the dynamics of 3.1 ± 0.1 ps. In contrast to the static diffraction patterns, where the diffraction peak diminishes as the system temperature was increased, here we observed the opposite effect.

Fig. 6.

Observed ultrafast structural phase transition by UEM. The time scale was scanned from −15 to +45 ps and with steps of 100 fs. The rise with the best fit (3.1 ± 0.1 ps) represents the increase in the contribution percentage of the monoclinic structure at the temperature around the middle of the phase change (indicated by the arrow in Inset). When the rise was fit over a shorter range to highlight the step at longer time, the rise time became 2.1 ps. When the experiments were repeated between −150 ps and +1.15 ns with steps of 5 ps, we observed the same change but the rise was within a single step.

The above results indicate that the transition occurs as a result of nonthermal excitation and that both the electron and optical pulses must be coincident for the transition to occur. After adding energy to the system, we would have naively expected from the hysteresis behavior (Fig. 4) that the transition would shift more toward the high-temperature R phase; instead, the contribution of the low-temperature M phase is enhanced. This trend is further supported by the fact that, in a given pulse, the energy fluence is not sufficient to cause a large thermal gradient. In addition, the recovery of the system in the time between pulses (12.5 ns) is not complete. Finally, the observed large change requires the passage through the region of time zero and was not observed when the delay time was set at negative or positive times or when the step size greatly exceeded the observed rise time.

The ultrafast temporal change is the result of dynamical response in the phase transition region and must occur when the electron packet and optical pulse are within the observed window of time (Fig. 6). Optical studies of the M–R transition with femtosecond time resolution have indicated from reflectivity measurements that the transition occurs in ≈100 fs in thin samples (50 nm) (18). However, when the sample thickness was increased (200 nm film), a rise time of 2.9 ps was observed, remarkably in close agreement with our reported rise time of 3.1 ps. As mentioned above, we are observing the transition when the femtosecond optical and electron pulses are coincident.

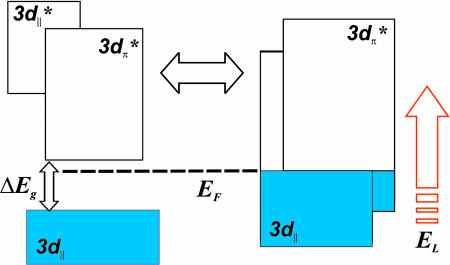
The following picture of structural changes on the ultrashort time scale is proposed. From the band structure (Fig. 7), the M phase has a band gap defined primarily by the splitting of the 3d manifold, and this gap is absent in the R phase. The initiating pulse electron packet on the ultrashort time scale induces, by momentum conservation, a transient stress in the nanometer-scale sample and as such leads to a nonequilibrium structure compatible with the M phase in its electronic configuration. The ultrashort optical pulse assists the transition through excitation to the antibonding band manifold and phase transformation occurs in 100 fs. Accordingly, the observed 3-ps rise time is the transit time for the nonequilibrium structure.

Fig. 7.

Schematic of the band structure for the insulator and metallic phases.

The stress is a “pressure-type” wave that survives for a few picoseconds and its effect is either kinematical (elastic), by expansion, or possibly by Jahn–Teller distortion (19). It is known that VO₂ structure is sensitive to changes of pressure and composition (20). However, it is also possible that some stress is caused by acoustic wave generation by the photon (with the electron packet assisting the transition). The stress wave in materials and in the presence of dislocations will have to be formed in an ≈3-nm slab, given the known sound velocity in the material and the rise in ≈3 ps. We note that the excitation of carriers from below the Fermi level to the antibonding 3d*_π band is significant for electron correlation effects.

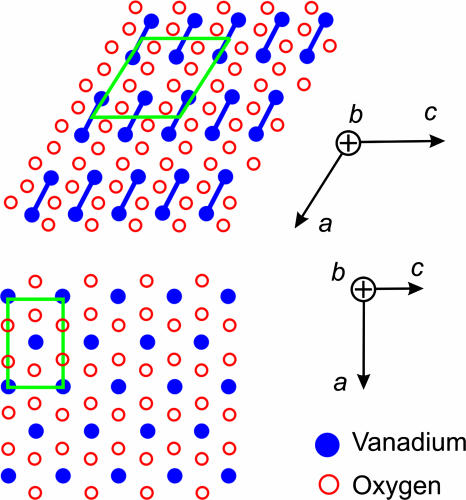
Because the transition is first-order in nature, we observed in the images some crystallites that completed the transition when others had not. This finding is consistent with the description of a first-order phase transition being the result of a latent heat; equilibrium with the surroundings is not instantaneous. The distribution of crystallite sizes plays an important role, especially for the thermally induced transition. In the diffraction patterns, the temporal changes reported here were for peaks indexed by (hkl), with k = 0; indeed, the structural changes (Fig. 8) are most pronounced perpendicular to the b axis, consistent with the observations made. The structure of the low-temperature monoclinic phase has the following unit cell dimensions: a = 5.75 Å, b = 4.53 Å, c = 5.38 Å, and β = 122.60°C. Unique to this structure is the V⁴⁺–V⁴⁺ pairing (21) along the a axis with alternating distances of 2.65 and 3.12 Å. For the high-temperature, rutile structure the cell parameters are a = 4.55 Å and c = 2.86 Å, with equivalent vanadium distances of 2.86 Å in the chains of edge sharing VO₂ octahedra. Through the phase transition, the (100) plane in the monoclinic plane shifts by 0.43 Å parallel to the (001) plane.

Fig. 8.

The structures involved in the phase transition. Shown are the two structures, with blue indicating the position of the vanadium ions (V⁴⁺) and red indicating the positions of oxygen ions (O²⁻), in the M (Upper) and R (Lower) phases.

Conclusion

The results reported here demonstrate the ability of the single-electron, ultrafast electron microscope (1, 22) to record images and diffraction patterns with combined temporal and spatial resolutions. We demonstrated the application in the study of metal–insulator phase transitions. The observed temporal change is evidence of a structural change from one phase to the other in a transition characterized by hysteresis. The temporal changes of the images illustrate the size selectivity of the first-order phase transition on the nanometer-scale, whereas the changes in the diffraction patterns provide the atomic-scale structural determination. By increasing the fluence and time between pulses we should be able to map out the transition in different regions of the hysteresis and phases. We will also compare our UEM results with those obtained by using x-ray diffraction and optical studies (18, 25) and with those obtained for different composition materials.

Materials and Methods

Polycrystalline VO₂ films were fabricated via a sol–gel method (23). The procedure was modified to provide an enhanced film quality and more uniform composition. The precursor vanadyl acetyl-acetonate (99.99% purity) (Sigma–Aldrich, St. Louis, MO) was dissolved in methanol and spin-coated onto a freshly cleaved mica substrate at 4,000 rpm for 20 s. The substrate was subsequently heated to 80°C on a hot plate for 20 min to remove excess solvent. At this point, an amorphous VO₂ thin film had formed on the substrate. To form the desired thermochromic phase, the samples were annealed for 2 h at 600°C in an N₂ environment. This step removed the remaining organics and transformed the films into a polycrystalline aggregate of the VO₂ rutile structure. The films were then slowly cooled in an N₂ environment, yielding polycrystalline VO₂ in the stable monoclinic M phase.

The VO₂ thin films were subsequently lifted off the mica substrate in deionized water, placed onto a 300-mesh molybdenum grid and then immediately inserted into the UEM for characterization. Before the film liftoff, the thermochromic activity and composition of the films were verified by optical transmission spectroscopy, and the transmission spectra of the films were measured as a function of temperature (Fig. 4). As was expected, the transmission sharply decreased in the near-infrared spectral region when passing through the insulator–metal phase transition between 50–70°C (24).

The conceptual design of the UEM is shown in Fig. 1 with a typical image and diffraction pattern obtained in this mode. The single-electron packets were generated from a femtosecond optical laser system entering the microscope through a set of optical elements and focused on the cathode. Another train of pulses was directed through another set of optical elements directly toward the sample. The laser system consists of a diode-pumped mode-locked Ti:sapphire laser oscillator that generates 120-fs pulses at 776 nm with a repetition rate of 80 MHz and an average power of 3.2 W. Part of the beam (2 W) is frequency-doubled in a nonlinear crystal β-BaB₂O₄ (BBO) to yield 388-nm pulses for generating the electron pulse train, and the rest was used as the initiation pulse to heat or excite the sample. Precise control of the amount of power directed onto the sample was accomplished by the use of a half-wave plate (λ/2) and a Glan–Thomson polarizer.

The microscope is a modified 120-kV G2 12 TWIN Tecnai transmission electron microscope (FEI Company, Hillsboro, OR), as described in ref 1. The light pulses were carefully steered with a computer-controlled mirror assembly and focused to an ≈50-μm spot on both the sample and the photocathode. To circumvent space–charge-induced broadening and the concomitant decrease in the ability of the microscope optics to focus these electrons, the energy was reduced so that electron pulses traveling along the microscope axis comprise on average a single (or a few) electron(s). Precision of alignment of electron and optical pulses was better than 10 μm.

Abbreviations

UEM

ultrafast election microscopy

M

monoclinic

R

rutile.