Exploring atomistic details of pH-dependent peptide folding

Abstract

Modeling pH-coupled conformational dynamics allows one to probe many important pH-dependent biological processes, ranging from ATP synthesis, enzyme catalysis, and membrane fusion to protein folding/misfolding and amyloid formation. This work illustrates the strengths and capabilities of continuous constant pH molecular dynamics in exploring pH-dependent conformational transitions in proteins by revisiting an experimentally well studied model protein fragment, the C peptide from ribonuclease A. The simulation data reveal a bell-shaped pH profile for the total helix content, in agreement with experiment, and several pairs of electrostatic interactions that control the relative populations of unfolded and partially folded states of various helical lengths. The latter information greatly complements and extends that attainable by current experimental techniques. The present work paves the way for new and exciting applications, such as the study of pH-dependent molecular mechanism in the formation of amyloid comprising peptides from Alzheimer's and Parkinson's diseases.

Many important biological phenomena, including ATP synthesis, enzyme catalysis, membrane fusion, protein folding/misfolding and aggregation involve pH-dependent conformational dynamics. To enable the exploration of these processes through computer simulation, a continuous constant pH molecular dynamics (CPHMD) method has been developed to effect a direct coupling between protonation and conformational dynamics in a macroscopic continuum solvent (1, 2). The CPHMD method introduces a direct coupling of solution pH conditions into molecular dynamics simulations, whereby the protonation states of protein ionizable side chains are not fixed but fluctuate in response to pH and the polypeptides local conformational state. It can be applied not only to the first-principles prediction of protein pKa values, which we have demonstrated in recent work (3), but also to the exploration of pH-coupled protein folding processes, an area where the traditional simulation methods employing preassigned fixed protonation states may break down (4). Here, we illustrate the utility of CPHMD simulations in studying pH-dependent peptide folding of the experimentally well characterized model peptide from the N terminus of ribonuclease A, the C peptide (5–8). A main objective of the paper is to demonstrate that CPHMD simulations can quantify the pH-modulated conformational populations and reveal direct correlations between electrostatic interactions and the pH-induced helix–coil transitions. Using a peptide with abundant experimental data, we show that the atomistic details arising from our simulation study not only complement but also extend the information attainable by current experimental techniques.

The 13-residue N-terminal fragment from ribonuclease A, commonly known as the C peptide, is the shortest amino acid sequence that displays pH-dependent partial α-helix formation in water. Extensive experimental studies using CD and NMR techniques (5–8) have provided strong evidence for two pairs of side chain–side chain interactions, Glu-2–Arg-10 and Phe-8–His-12, contributing to increased helix content at pH 5, where both Glu and His residues are ionized. Nevertheless, several important questions and controversies regarding the nature of the conformational distribution of this peptide remain. First, what states comprise the conformational equilibrium, which was proposed to contain full-length helix, partial helix, and unfolded states based on the NMR data of a C peptide analog RN24 (6)? Second, how are the electrostatic interactions, Glu-2–Arg-10 and Phe-8–His-12, related to the aforementioned conformational species? Do they contribute to the stability of the partial or full-length helix? Third, what is the exact nature of the interaction between Phe-8 and His-12? Is there a weak hydrogen bond between the amino group of His-12 and the aromatic ring of Phe-8 (8, 9)? Does Phe-8 interact with His-12 via an electrostatic interaction between the backbone carbonyl of Phe-8 and the amino group of His-12 (10)? These detailed questions are difficult, if not impossible, to address with the current experimental techniques.

Here, we examine the pH-dependent conformational equilibrium of the C peptide by coupling the protonation equilibrium at experimental salt concentrations to the atomistic folding dynamics. We attempt to answer questions regarding the exact nature and role of the electrostatic interactions, e.g., the competing salt-bridge pairs, Glu-2–Arg-10 and Lys-1–Glu-9, as well as those pertaining to the two modes of interaction between Phe-8 and His-12, on the stability of partial helical species that coexist with random coil states in the conformational equilibrium of the C peptide.

Results and Discussion

Total Helix Content.

The computed total helix content and mean residue ellipticity [θ]₂₂₂ of the C peptide exhibit a bell-shaped pH profile, in agreement with the measured CD data (5) (Fig. 1). The intermediate pH values (3.5, 5, 6.5) show the highest helix content or largest magnitude of [θ]₂₂₂, whereas low and high pH values (2, 8) display the lowest helix content or smallest magnitude of [θ]₂₂₂. Overall, the computed [θ]₂₂₂ are shifted up by ≈500–3,000 deg·cm²·dmol⁻¹ relative to the experimental values. These deviations can be largely attributed to the uncertainty in the minimum detectable helical length in the CD experiment and the neglect of backbone conformational dependence in the calculation of mean residue ellipticity (see Methods) (11). However, this systematic shift does not affect the change in helicity nor the underlying electrostatic interactions and conformational substates that occur in response to the change in environmental pH. Furthermore, the magnitude of the pH-induced change in helix content shown here is much greater than the sampling uncertainty (≈2%) estimated from independent simulations initiated from a folded conformation (Methods), suggesting that the computed pH-dependence of helicity is statistically significant.

Fig. 1.

Computed total helix content (Left) and mean residue ellipticity at 222 nm (Right) for the C peptide as a function of simulation pH. The solid lines with open symbols represent the simulation data obtained at 0.1 M ionic strength, whereas the dashed lines represent the data obtained in pure water. The black lines with filled symbols represent the experimental [θ]₂₂₂ values estimated from the work of Bierzynski et al. (5). The computed helix content is based on the ratio between the number of helical residues and total number of residues. The uncertainty in helix content is estimated to be 2% (see Methods). The computed mean residue ellipticity for all pH values is shifted down by 2,000 deg·cm²·dmol⁻¹ to facilitate the comparison of the pH-induced changes in mean residue ellipticity with experiment.

It is interesting to see that the inclusion of 0.1 M ionic strength leads to a decrease in the helix content at pH 5 and 8 by ≈4% and 10%, respectively, but an increase of ≈4% at pH 1. This trend is consistent with the CD data in ion screening tests using the analog peptide RN24 (K1A/E9L, acetylated at the N terminus) at pH 2 and 5.3 (7) as well as pH 9.5 (8). We discuss the ion screening effects in a later section.

Helix Location in the Partially Folded States.

To examine the nature of the conformational ensemble formed by the C peptide, we computed the probability distribution of the helix starting position (the first residue from the N-terminal direction) and the length of partial helices. There are ≈10%, 5%, and 40% fully unfolded states at pH 1, 5, and 8, respectively, in equilibrium with partial helical structures at 0.1 M ionic strength (Fig. 2). Apparently, the difference in the relative populations of unfolded states gives rise to the pH-dependent helix content observed in the CD experiment. Fig. 2 also reveals that the most favorable helix initiation site is Ala-6 at pH 1 and pH 5 and Ala-4 at pH 8. These two residues are favored by 10% relative to the second most probable starting residue at pH 1 and 5, but only 5% at pH 8. The majority of partial helices are of four or seven residues in length. With increasing pH, the population of seven-residue helices increases. The dominant helical length is 4 at pH 1, both 4 and 7 at pH 5, but 7 at pH 8.

Fig. 2.

Probability distribution of the helix starting (N-terminal side) position (Left) and length (Right) at pH 1 (Top), 5 (Middle), and 8 (Bottom) for the C peptide simulated at 0.1 M ionic strength (dotted bars) and in pure water (solid bars) as well as for RN24′ at pH 5 (Middle, dashed bars). The values at 0 correspond to the unfolded states.

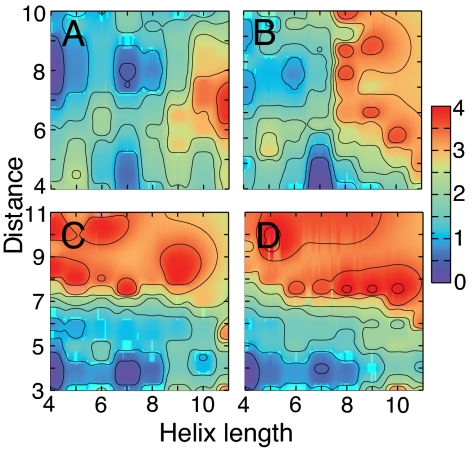
The distribution of various partial helical states formed by the C peptide can also be quantitatively examined by computing the two-dimensional potential of mean force (PMF), or the relative free energy (ΔG), as a function of the helix starting position and length. This quantity can help identify the most populated states, those with the lowest ΔG, in the conformational equilibrium. Consistent with the one-dimensional probability distribution (Fig. 2), Fig. 3 shows that pH indeed has quite a distinct signature on the helix location in the C peptide. At pH 1 and 5, the most populated conformer contains the four-residue helical segment Ala-6–Glu-9, whereas at pH 8 it contains the seven-residue helical stretch Ala-6–His-12.

Fig. 3.

Relative free energy (in kcal/mol) as a function of the helix starting (N-terminal side) position (x axis) and length (y axis) for the C peptide simulated at 0.1 M ionic strength and pH 1 (A), 8 (B), and 5 (C), and the relative free energy for RN24′ at 0.1 M ionic strength and pH 5 (D).

Although the total helix content of the analog peptide RN24′ (K1A/E9L) is almost identical to that of the C peptide (3% lower, data not shown) under the same simulation conditions (0.1 M ionic strength and pH 5), their distributions of conformational states differ (gray lines in Fig. 2 and lower right plot in Fig. 3). RN24′ favors partial helices with a four-residue helical segment starting from Ala-4, Ala-6, or Lys-7 as well as those with a five-residue helical segment starting from Lys-7. Moreover, there is a significant population of longer helices (lengths 8 and 9) initiating at Ala-4. Thus, the amino acid substitution (K1A/E9L) shifts the relative populations of partial helical states in the conformational equilibrium despite having very little effect on the relative population of unfolded states. The NOE and ³JHN_α data from a ¹H NMR study of the analog peptide RN24, which differs from RN24′ only in the N terminus, indicates an abrupt change in the conformation at Ala-4, suggesting that the first three residues are nonhelical (6). These data are consistent with our results, which show that Ala-4 and Ala-6 are the most probable helix initiation sites.

Interactions Glu-2–Arg-10 and Lys-1–Glu-9.

Amino acid substitution studies suggested that the Glu-2–Arg-10 salt bridge is responsible for the increased helix content at pH 5, relative to a lower pH where Glu-2 is protonated (7, 12). This salt bridge exists in the intact ribonuclease A (13) and was observed in the analog peptide RN24 in a ¹H NMR study (6). To understand the correlation between the salt-bridge interaction and helix stability, we computed the free energy as a function of helix length and the ion-pair distance in the C peptide. To our surprise, the Glu-2–Arg-10 salt bridge is only found among some of the four-residue partial helix states (data not shown). In contrast, the Lys-1–Glu-9 salt bridge dominates partial helices of length 7 (Fig. 4C). In fact, the probability distribution of the ion-pair distance shows that Glu-2 and Arg-10 are mostly not interacting (Fig. 4A, dashed curve), whereas Lys-1 and Glu-9 form a salt bridge (Fig. 4A, solid curve).

Fig. 4.

The simulation results for the C peptide and RN24′ at 0.1 M ionic strength and pH 5. (A) Probability distribution of r(Lys-1–Glu-9), the minimum distance (Å) between the amino nitrogen atom of Lys-1 and carboxyl oxygen atom of Glu-9 (solid lines) and r(Glu-2–Arg-10), the minimum distance between the carboxyl oxygen atom of Glu-2 and the amino nitrogen atom of Arg-10 (dashed lines). (B) The probability distribution of r(Glu-2–Arg-10). (C) Relative free energy (in kcal/mol) as a function of helix length and r(Lys-1–Glu-9). (D) Relative free energy as a function of helix length and r(Glu-2–Arg-10).

The correlation of the salt bridge Lys-1–Glu-9 but not Glu-2–Arg-10 with the formation of partial helices seems to contradict the substitution experiments, which ruled out Glu-9 and suggested that the latter interaction is the major contributor to the increased helix stability at pH 5 relative to pH 2 (7, 12). However, all of the substitution experiments were conducted based on the analog peptides (RN series) in the absence of the Lys-1 and Glu-9. To test the hypothesis of competition between Lys-1–Glu-9 and Glu-2–Arg-10, we performed a simulation for RN24′ (K1A/E9L), which resulted in a total helix content almost identical to that of the C peptide. Moreover, Glu-2 and Arg-10 form a salt-bridge interaction (Fig. 4B), which has the largest population in the states of helical length 8 and 9 and is also present among partial helices of length 4 (Fig. 4D). Thus, the electrostatic interaction Glu-2–Arg-10 is in direct competition and cannot coexist with Lys-1–Glu-9. The conditions of the experiments that were designed to explore the role of Glu-9 and salt bridge Glu-2–Arg-10 on the helix stability incidentally made the latter interaction more favorable.

Interaction Between Phe-8 and His-12.

Amino acid replacement experiments suggested that the aromatic ring contact between Phe-8 and the charged His-12 residues is responsible for the increased helix stability at pH 5 relative to a higher pH where His-12 becomes neutral (8). Supported by the edge-to-face configuration of Phe-8–His-12 in the crystal structure of ribonuclease A and the observation of weak ionic screening, the authors proposed a weak hydrogen bond between the charged donor, the amino group of His-12, and acceptor, the aromatic ring of Phe-8 (8, 9). However, this finding is in contradiction with the ¹H NMR experiment, which showed that the contact between Phe-8 and His-12 exists at both pH 5 and 8 (10). Combined with simple energy calculations, these authors proposed that an alternative interaction, the electrostatic interaction between the partially charged backbone carbonyl group of Phe-8 and the amino group of His-12, is responsible for the increased helix stability at pH 5 relative to pH 8.

We explore the nature of the interaction between Phe-8 and His-12 and examine its correlation with helix stability by computing the relative free energy of the C peptide as a function of partial helix length and three types of distances, which represent weak amino-aromatic hydrogen bonding (14), a nonspecific electrostatic and van der Waals interaction between aromatic rings, as observed at the (i, i + 4) positions in many helical proteins (15), and an electrostatic contact between the backbone carbonyl of Phe-8 and the amino group of His-12. Our findings are as follows. There is no Phe-8–His-12 hydrogen bonding at pH 5. The nonspecific aromatic ring contact between Phe-8 and His-12 is not favored in partial helix populations at pH 5 (Fig. 5A). However, it is strongly favored at pH 8 among the seven-residue helices (Fig. 5B). In contrast, the electrostatic interaction between the carbonyl of Phe-8 and amino of His-12 clearly dominates in both the four- and seven-residue helix populations at pH 5 (Fig. 5C) and also in the four-residue helix population at pH 1 (Fig. 5D). Thus, our simulation data supports the hypothesis that the Phe-8–His-12 backbone to side chain electrostatic interaction is the major contributor to the increased helix stability at pH 5 relative to pH 8.

Fig. 5.

Relative free energy (in kcal/mol) of the C peptide at 0.1 M ionic strength as a function of the helix length and the minimum distance between the aromatic ring atoms of both Phe-8 and His-12 (A, pH 5; B, pH 8), or between the backbone carbonyl oxygen atom of Phe-8 and the amino nitrogen atom of His-12 (C, pH 5; D, pH 1).

Representative Conformations of Partial Helices.

To obtain representative structures of the C peptide and its analog RN24′, we performed clustering of the MD trajectories. The resulting cluster center structures of the most populated clusters confirm the helix location data shown in Figs. 2 and 3. We examine the side-chain orientations of these partial helical structures. A representative structure from the simulation at pH 1 is the four-residue partial helix Ala-6–Glu-9, which displays the Phe-8–His-12 backbone to side-chain salt bridge (Fig. 6A). This four-residue partial helix, which is also the most populated in the pH 5 simulation is stabilized by the same salt bridge (not shown). The seven-residue partial helices Ala-6–His-12, which comprise the second most populated conformational cluster in the pH 5 simulation, is additionally stabilized by the Lys-1–Glu-9 salt bridge and a nonspecific aromatic ring contact between Phe-8 and His-12 (Fig. 6C), which is the only side-chain interaction seen in the dominant partial helix Ala-6–His-12 in the pH 8 simulation (Fig. 6B). The conformational equilibrium of the analog peptide RN24′ at pH 5 is more heterogeneous (Figs. 2 and 3). The dominant conformation shown here contains the nine-residue partial helix Ala-4–His-12, which is stabilized by all three sets of interactions as in the C peptide except that the Lys-1–Glu-9 salt bridge is now replaced by the Glu-2–Arg-10 salt bridge (Fig. 6D).

Fig. 6.

Representative conformations of the C peptide (A, pH 1; B, pH 8; C:, pH 5) and RN24′ (D, pH 5) from the simulations at 0.1 M ionic strength. The interacting side chains, Lys-1, Glu-2, Phe-8, Glu-9, and Arg-10, are shown in the licorice representation.

Ion Screening Effect.

Ion-screening experiments offer an indirect probe into the effect of electrostatic interactions on helix stability. We compare the results of the C peptide simulated at 0.1 M ionic strength with those in pure water at pH 1, 5, and 8. As discussed earlier, inclusion of 0.1 M ionic strength does not have a significant effect on the total helix content at pH 1 and 5 (Fig. 1). From Fig. 2 it is also clear that it does not significantly affect the distribution of conformational species in the equilibria at these two pH values. However, at pH 8, 0.1 M ion screening results in an increase in the random coil population from 20% to 40% and a decrease in the seven-residue partial helix population from 40% to 20%. Moreover, residue Ala-4 becomes more favored as the helix starting position in salt solution.

Combined amino acid interchange and ion screening experiments revealed that the Phe-8–His-12 interaction is not significantly screened by ions at pH 5 (8). Indeed, the probability distribution of the backbone to side chain electrostatic interaction between Phe-8 and His-12 does not change upon inclusion of 0.1 M ionic strength in the simulation at pH 5 (Fig. 7Left), which accounts for the Debye–Hückel screening effect. In contrast, the nonspecific electrostatic interaction between Phe-8 and His-12 is significantly weakened (Fig. 7 Right). The salt-screening behavior of these interactions is consistent with that of the total helix content of the peptide, reinforcing the roles of these two types of Phe-8–His-12 interactions as the major contributors to the helix stability and also explaining the small ion-screening effect on the total helix content at pH 1.

Fig. 7.

Probability distribution of the minimum distance between the backbone carbonyl oxygen atom of Phe-8 and amino nitrogen atom of His-12 (Left) at pH 5 and the minimum distance (Å) between the aromatic rings of Phe-8 and His-12 at pH 8 (Right) for the C peptide at 0.1 M ionic strength (solid lines) and in pure water (dashed lines).

Conclusion

We illustrated the application of CPHMD to explore atomistic details of the pH-dependent conformational equilibrium of a model peptide, the C peptide from ribonuclease A. In addition to reproducing a bell-shaped pH profile for the total helix content as obtained with CD spectroscopy (5), the simulation results provided information regarding the pH-dependent distribution of partial helical states that comprise the conformational equilibrium of the C peptide. Specifically, the conformational equilibrium of the C peptide consists of unfolded and partial helical states that are dominated by helical segments of lengths 4 and 7. Increasing pH lengthens the helical segments. At pH 1 and pH 5, the dominant conformers are partial helices, from Ala-6 to Glu-9, whereas at pH 8, the partial helices, from Ala-6 to His-12, are most populated. Simulation of the analog peptide RN24′ (K1A/E9L) revealed a more heterogeneous conformational ensemble, including mostly four-residue partial helices initiating at Ala-4 and Ala-6 but also some five- and nine-residue partial helices. Although a close comparison may not be meaningful due to the sensitivity of the distribution of conformational states to the amino acid sequence and charge state of the terminal group, these results are consistent with the NMR study of RN24 (K1A/E9L, succinyl terminus), which indicated that the first three residues are in a random coil state (6).

We examined the effects of the electrostatic interactions, Lys-1–Glu-9, Glu-2–Arg-10, and Phe-8–His-12, on helix stability. Instead of the Glu-2–Arg-10 salt bridge, as suggested by the substitution experiments (7, 12), Lys-1 and Glu-9 form a salt-bridge contact in the simulation at pH 5, which contributes to the stability of seven-residue partial helices, increasing the helix content relative to pH 1. The seemingly contradictory data are reconciled by considering RN24′, which lacks the possible interaction between Lys-1 and Glu-9. In this case, Glu-2 interacts with Arg-10, contributing to the stability of eight- or nine-residue partial helices initiating at Ala-4, which is in full agreement with the NMR data, suggesting that the Glu-2–Arg-10 salt bridge gives rise to the random coil states of the N-terminal residues of the peptide (6). In contrast to the amino-aromatic hydrogen bonding, as proposed by the substitution and ion-screening experiments (8, 9), the simulation revealed two modes of interaction between Phe-8 and His-12, a nonspecific aromatic ring contact at pH 8, and a backbone to side chain electrostatic interaction at pH 5, which was first proposed from the analysis of a NMR experiment (10). The latter interaction was found to stabilize four-residue partial helical states at pH 5, contributing to the increased helix content relative to pH 8. Finally, the Debye–Hückel screening behavior of the Phe-8–His-12 interactions explains the enhanced loss of helix content upon inclusion of salt at pH 8 relative to pH 5, which is consistent with the CD data (8).

The work we presented here demonstrates that CPHMD can offer atomistic insights into the pH-dependent folding of peptides and proteins, with the potential to greatly extend the information attainable by current experimental techniques. Limitations of the CPHMD simulation methods are directly linked to those of the underlying generalized Born (GB) implicit solvent model. For small proteins and peptides, where specific water–peptide or ion–peptide interactions seldom play a significant role in conformation equilibria (16), the balance between solvation and intramolecular interactions can be largely captured by a careful parameterization of GB input radii that targets the protein side chain–side chain interaction energies in explicit solvent. The reparameterization of the GBSW (generalized Born with a simple switching function) solvent model (17) combined with the adjustment of protein force field, as shown in our recent work (18), has enabled quantitative agreement with experimental conformational equilibria for a range of helical and β-hairpin peptides. Aided by the growing speed of computers and advancements in sampling algorithms, CPHMD may soon be applied to explore a variety of pH-driven conformational processes of biological significance, ranging from the proton gradient driven ATP synthesis to the disease-related amyloid formation.

Methods

Simulation Details.

The CPHMD method is an extended Hamiltonian approach, where a set of titration coordinates with fictitious masses is propagated simultaneously with the spatial coordinates at a specified external pH (1, 2). The coupling between conformational and protonation states is enabled through the attenuation of electrostatic and van der Waals interactions by the titration coordinates in an implicit GB solvent model (17, 18). Replica exchange (REX) is a sampling protocol that assists an increased rate of barrier crossing on the potential energy surface by performing random walk in temperature space (19). In a REX–CPHMD simulation, the CPHMD method is combined with the REX protocol to enhance the conformational and protonation state sampling (3). By exploiting the REX enhanced sampling protocol and the newly improved parameterization of GB force field (18), which better captures the balance between solvation and intramolecular forces, our recent work showed that the ionization equilibria of protein side chains can be predicted to quantitative accuracy (3).

All REX–CPHMD simulations were performed with 16 replicas, in the exponentially spaced temperature windows between 260 and 450 K. Exchanges were attempted every 2 ps with an average acceptance ratio of ≈45%. The simulation length per replica was 30–35 ns, resulting in a total simulation time of 480–560 ns. Our previous REX folding simulations for a range of small helical and β-hairpin peptides of similar length demonstrated good convergence (18). To further verify conformational convergence of the current simulations, we carried out a REX–CPHMD simulation in water at pH 1, starting from a fully helical conformation. The resulting total helix content is 40%, in good agreement with the 38% from the simulation starting from a fully extended conformation. The titration occurred at the side chains of α-amino, Glu, Lys, and His residues with the respective standard pK_a values of 7.5, 4.4, 10.4, and 6.5. Unless otherwise stated, we followed the simulation protocol in our previous work (3).

Structure Preparation.

All simulations were initiated from the fully extended conformation. The C peptide has the sequence, KETAAAKFERGHM, with a free N terminus and the C-terminal group blocked by N-methylamide. Although the related CD and NMR experiments (5, 7, 8) were conducted by using the C peptide homoserine lactone, we do not expect any significant difference in the conformational equilibrium between these two forms. To facilitate comparisons, the same terminal groups were used for the analog peptide RN24′ (K1A/E9L), although the NMR data were obtained with RN24 (K1A/E9L) that had a N-terminal succinyl group (6). Thus, the different charge on the N-terminal groups may result in somewhat different conformational equilibrium in RN24 and RN24′. We conducted simulations at an ionic strength of 0.1 M, as was used in the CD and NMR experiments (5–8). The pH conditions were 1, 2, 3.5, 5, 6.5, 8, and 10 for the C peptide and 5 for RN24′. An additional set of simulations of the C peptide was performed at pH 1, 5, and 8 in pure water.

Data Analysis.

Helix folding of the C peptide and RN24′ reached equilibrium after ≈10 ns of REX–CPHMD simulation, after which snapshots were recorded from the 280 K window after each REX attempt, resulting in a total of 15,000–17,500 structures. Conformational clustering of the trajectory was performed using a hierarchical clustering method as implemented in the GROMACS molecular dynamics software package (20) with a rms cutoff of 1 Å.

The mean residue ellipticity at 222 nm [θ]₂₂₂ was computed by using the following relationship (21):

where N_r is the number of residues in the peptide, N_h is the number of helices, and r_i is the number of residues that are in a helical conformation according to the DSSP algorithm (22). k, which represents the minimum number of helical residues required to produce the CD signal, is an empirically determined constant that ranges from 3 to 4.3 (23, 24). We adopted the value of 3 (23). [θ]_helix, which represents the mean residue ellipticity of a complete helix, is given by −42,500(1− 3/N_r) (23).

Abbreviations

CPHMD

constant pH molecular dynamics

GB

generalized Born

REX

replica exchange.