Abstract
One generally has the impression that one feels one's hand at the same location as one sees it. However, because our brain deals with possibly conflicting visual and proprioceptive information about hand position by combining it into an optimal estimate of the hand's location, mutual calibration is not necessary to achieve such a coherent percept. Does sensory integration nevertheless entail sensory calibration? We asked subjects to move their hand between visual targets. Blocks of trials without any visual feedback about their hand's position were alternated with blocks with veridical visual feedback. Whenever vision was removed, individual subjects' hands slowly drifted toward the same position to which they had drifted on previous blocks without visual feedback. The time course of the observed drift depended in a predictable manner (assuming optimal sensory combination) on the variable errors in the blocks with and without visual feedback. We conclude that the optimal use of unaligned sensory information, rather than changes within either of the senses or an accumulation of execution errors, is the cause of the frequently observed movement drift. The conclusion that seeing one's hand does not lead to an alignment between vision and proprioception has important consequences for the interpretation of previous work on visuomotor adaptation.
Keywords: adaptation, motor control, vision, proprioception, drift
One generally has the impression that one feels one's hand at the same location as one sees it. This impression has formed the basis for many theories about the calibration of our senses (1, 2), about how movements are controlled (3), and about the formation of body schema (4). The visual estimate of the position of one's hand (relative to oneself) is based on the retinal position of the hand's image and the orientation of the eyes. The proprioceptive estimate is based on joint or limb angles. When information is available in both modalities, we combine these sources of information into one coherent idea of where our hand is relative to ourselves (5), as has been modeled successfully assuming an optimal combination of sensory information (6–8) (Fig. 1A). The optimal combination of information from multiple sensors is a weighted average, with weights based on the precision (the inverse of the variance, see Eq. 1 in Materials and Methods). Although this optimal combination gives the most precise estimate of the position of our hand, it does not remove systematic errors (biases). If such biases exist (9), the optimal combination has an interesting consequence: the perceived (egocentric) position of our hand should change in a reproducible way whenever the hand moves out of sight.
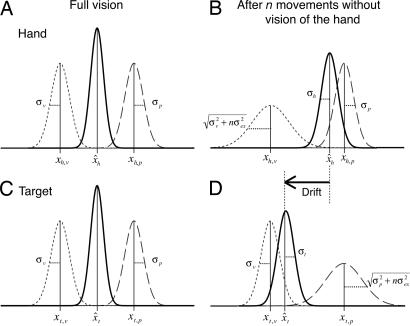
Fig. 1.
The model. The Gaussian curves represent the hypothesized probability density functions of proprioceptive (dashed), visual (dotted), and combined (continuous) estimates of position. (A and C) When the hand is at the target with full vision, the positions of both the hand (A) and target (C) are based on the optimal combination of proprioceptive and visual estimates. (B) We propose that if the hand disappears from view, the visual estimate of its position gradually becomes less precise with each movement that is made. The combined estimate of the location of the hand will therefore rely less on vision, so that the combined estimate shifts toward the proprioceptive estimate, with a reduction in precision. (D) At the same time, the proprioceptive estimate of target location becomes less precise. The combined estimate of the target location will therefore rely less on proprioception, so that the combined estimate shifts toward the visual estimate, with a reduction in precision. To keep the perceived position of the hand on target, the hand will drift over a distance equal to the difference between the two combined estimates (black arrow).
We think that such changes occur, but they are never noticed because they are not instantaneous. We propose that the visual estimate of hand position does not disappear as soon as the hand disappears from view (much as the approximate position of whatever you were looking at is still evident when you close your eyes). The visual estimate persists, and it is updated with efferent information about the hand's (intended) movements. However, each movement of the unseen hand adds uncertainty to this visual estimate because the actual movement can differ from the intended one. Considering this increasing uncertainty means that the combined (optimal) estimate will rely less and less on visual information about the hand, and it will therefore drift toward the proprioceptive estimate (Fig. 1B).
When our hand touches an object in our environment, we know that the object and our hand are at the same location. Consequently, not only our hand but also that object can be localized by the optimal combination of proprioception and vision. The proprioceptive estimate of an object's position must be as reliable as that of the hand (Fig. 1C) when one knows (visually or haptically) that they are at the same location because otherwise they would not be perceived at the same location (assuming optimal cue combination). For proprioception to contribute to the (egocentric) localization of the object, it is not necessary that the object contacts the hand, as long as the object's position relative to the hand is known (e.g., visually). This description of how humans combine information about the location of objects relative to their moving arm is similar to the algorithms that have been proposed to process location information of sensors in mobile robots (10, 11).
In the preceding paragraph, we argued that proprioception contributes to the (egocentric) localization of an object that we are not touching in a similar way as vision contributes to the localization of the unseen hand. Knowledge of the object's position relative to the hand is essential for these estimates. Even if the hand disappears from view, the proprioceptive estimate of an object's position does not change because the relative position does not change as long as the hand does not move. However, when the unseen hand moves, the information about the object's position relative to the hand (and thus the proprioceptive estimate of the object's location) becomes less precise because of the uncertainty about the correct movement execution. Because each movement of the unseen hand adds uncertainty to the proprioceptive estimate of the object's position, the combined estimate of that position will rely less and less on it, and it will drift toward the visual estimate (Fig. 1D). Thus after the hand is removed from view, the perceived location of hand and object will drift apart (the horizontal arrow in Fig. 1). A quantitative model of this reasoning is derived in Materials and Methods.
The hypothesis outlined above does not involve any mutual calibration between vision and proprioception. Using a paradigm that we used before to study adaptation (12, 13), we will directly test the prediction that no such calibration occurs. In this paradigm, subjects move a cube between four positions in a virtual environment, alternating between blocks of trials without any visual feedback about their hand's position and ones with visual feedback during the movements (Fig. 2). We start the experiment with a block without visual feedback. In this initial block, subjects make movements without having seen their hand in the virtual environment. They will make errors corresponding to the mismatch between vision and proprioception. The purpose of the visual feedback in subsequent blocks was to examine whether subjects mutually calibrated vision and proprioception when veridical feedback was given to them. We consider an absence of calibration to veridical feedback as an even stronger evidence for our theory than an absence of calibration to an arbitrary feedback. We predict that during these blocks with feedback subjects do not mutually calibrate vision and proprioception but only combine them in the same way for both hand and target. This combination results in the same bias for hand and target and thus in movements without a systematic error. After removing visual feedback, subjects' movement endpoints will gradually drift away from the targets until they make the same errors as in the initial block.
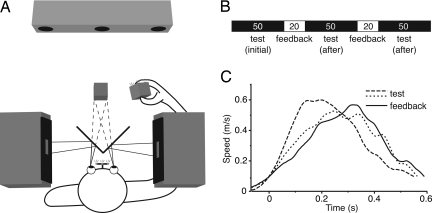
Fig. 2.
Experimental setup and design. (A) Subjects viewed a simple scene consisting of a three-dimensional cube floating in total darkness, and they held a similar-sized real cube in their unseen hand. They had to move the real cube to the position of the virtual cube in five successive blocks (B) either without (test) or with visual feedback of the movement of the real cube. The numbers of trials within each block are indicated. (C) The velocity profiles of a single subject's first movements in each of the last three blocks illustrate that subjects made normal movements with approximately bell-shaped velocity profiles.
Results
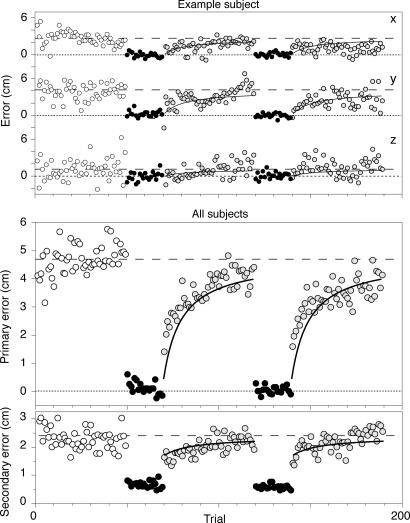
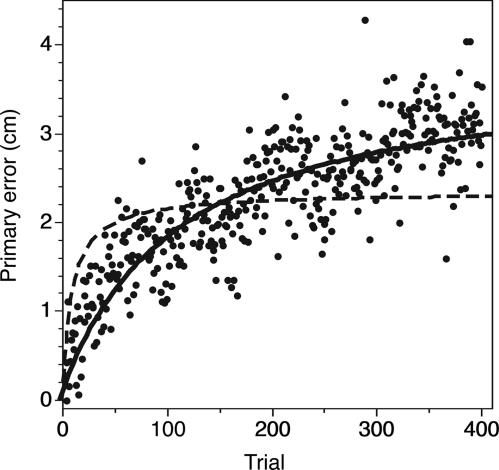
Any mismatch between vision and proprioception will lead to a bias in the initial block without visual feedback. Such biases were indeed clearly visible for all subjects (see, e.g., Fig. 3Upper). In the first block of trials in which subjects received no visual feedback about the position of their hand, subjects on average had a bias of 4.7 (range 2.8–9.7) cm, with a variable error () of 3.3 cm. To be able to determine the bias and variability on a trial-by-trial basis, we introduce two error measures. The primary error is the component of the error (in each trial) in the direction of the (average) bias in the initial block. On average, this error was obviously 4.7 cm in the first block. The secondary error (our measure for the variable error) is the component of the error (in each trial) that is perpendicular to the direction of the bias in the first block. This error was 2.3 (range 1.4–2.9) cm in the first block (see Fig. 3 Lower). These two errors were not correlated across subjects (r2 = 0.05; P > 0.5); subjects with a large bias were thus not more variable than subjects with a small bias. With visual feedback of the hand, the primary error was on average reduced to 0.1 (range −0.3–0.5) cm and the secondary error to 0.6 (range 0.4–1.2) cm. After removing the feedback, both the primary error and the secondary error increased.
Fig. 3.
The error in the hand's end position during the five consecutive blocks of trials. White disks, trials in the first test block in which the subjects only saw the target cube. Black disks, trials in the feedback blocks in which subjects saw both the target cube and the cube in their hand. Yellow disks, trials in the test blocks after a feedback block. The continuous curves are the model predictions based on the bias and variable error in the first two blocks (they are identical for the third and fifth blocks). (Upper) The three orthogonal components of the error during a typical session. (Lower) The primary and secondary error averaged over the two repetitions of all 10 subjects.
Comparison with Model.
The model (see Materials and Methods) predicts that the increase of (both primary and secondary) error per movement depends on the ratio between the perceptual variance (σv2 + σp2) and the execution variance (σex2). Substituting the measured bias and variances in Eqs. 4 and 5, we obtain a ratio of 9. This ratio, in combination with the average bias of 4.7 cm, predicts the continuous curves in Fig. 3. These curves are thus based on the blocks indicated by the white and black data points, and they predict the behavior shown by the yellow data points.
The prediction for the primary error (Eq. 4) starts at 0 for the last trial with feedback and increases to 4.0 cm after 50 trials without feedback. The experimentally observed time course of errors matches this prediction rather adequately, although the increase of errors is slightly faster than predicted.
We can also make a prediction for the secondary error by using Eq. 5. After a block of movements with visual feedback, the variance should be halved (because both hand and target are now localized by using two senses instead of one) so that the secondary error should be a factor smaller than in the initial block. This error should gradually increase to the level of the first block (Fig. 3 Lower, continuous curve). The measured secondary error follows the predictions rather well.
Subject Specificity.
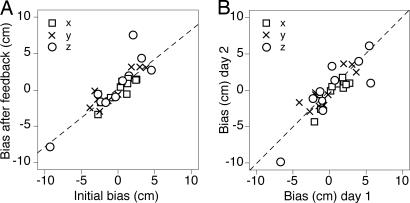
The bias differed considerably among subjects, both in amplitude and in direction. If this bias is really caused by a systematic mismatch between vision and proprioception, it should always have the same direction and amplitude for each subject. As predicted by Eq. 3, the three components of the individual subject's biases in the second half of the blocks in which veridical feedback was removed were in the same direction, but they were slightly smaller than those in the initial block (Fig. 4A). The limited number of trials within a block is the reason for these slightly smaller errors. The subject's biases were even reproducible across days (Fig. 4B).
Fig. 4.
The bias (systematic error) in individual subjects' performance in three orthogonal directions (x, horizontal; y, vertical; z, depth). Dashed lines indicate model predictions. (A) The error in the second half of the third and fifth blocks compared with the error in the first block. The model (Eq. 4) predicts a slope of 0.79. (B) The error in the second half of the blocks without feedback on the 2nd day compared with that on the 1st day. The model predicts equal errors (unity slope).
Additional Experimentally Confirmed Predictions.
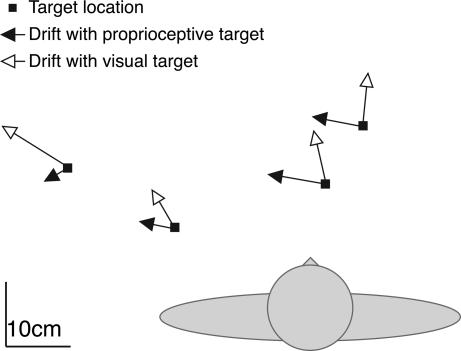
One important aspect of the model is that the drift is caused by the mismatch between two sensory sources of information, which means that if targets are presented in another modality (e.g., proprioceptively), the mismatch is likely to be different, so the drift will be in a different direction. This result is not what one would expect if drift were caused by execution errors only. To test this prediction, we reanalyzed data from an earlier experiment in which subjects moved their right hand over a horizontal surface to targets that were either defined visually or by proprioception of their left hand (ref. 14; for details, see Drift and Sensory Modality, which is published as supporting information on the PNAS web site). For both type of targets, movement endpoints of the right hand drifted considerably during the experiment. As predicted, the drift for proprioceptively defined targets was in a different direction than for visually defined targets (Fig. 5).
Fig. 5.
Top view of the total drift in the experiment by van Beers et al. (14). Data are averaged over all subjects. The length of the arrows equals 2.5 times the total drift. Subjects moved repeatedly with the right hand to the same target, leading to a gradual drift away from the target position. This drift was in a clearly different direction if the target was the left arm (filled arrows) than if the target was a visual marker (open arrows).
The model predicts that the drift should be slower if the execution error is smaller. Subjects are generally more precise if they can use the friction with a surface to stop their movement. We therefore also analyzed an experiment in which subjects moved a pen between four positions on a graphic tablet (ref. 15; for details, see Effect of Movement Precision on Drift Speed, which is published as supporting information on the PNAS web site). In a condition with visual feedback, the subjects' variances were 100 times smaller than in the trials with feedback of the present study. Without feedback, the variances were ≈9 times smaller. The ratio between the variances in perception and execution is thus >10 times larger than in the present study, which means that our model predicts a considerably slower drift (Fig. 6). We fit Eq. 4 to the data with the sensory mismatch as a single-fit parameter (because we have no independent measure of the mismatch in that study). Using the measured ratio of variances to determine the speed of the drift (continuous curve), the model fit the data very well; the systematic sensory mismatch is 3.6 cm according to this fit. Assuming the same ratio of variances (and thus speed of drift) as in Fig. 4 resulted in a much poorer fit (dashed curve). Thus, the relationship between the variability and the speed of drift is in accordance with our hypothesis.
Fig. 6.
The primary error in the experiment of de Grave et al. (15). The black dots are the measured errors (averaged over all subjects). The model (4) can fit these data well if we use the measured variances to calculate the speed of drift (continuous curve). If we assume that the drift speed is the same as in the present experiment (Fig. 4), the best fit (dashed curve) does not follow the data very well.
Discussion
As predicted, we found that subjects always drift back to the same error when visual feedback is removed (Fig. 3). This bias was different for different subjects, but it remained stable across days (Fig. 4), which shows that proprioception and vision are systematically misaligned in a stable, subject-specific way. Using the measured variances, we could predict the speed of the drift reasonably well. This good prediction was not a coincidence; we showed that in an experiment in which the variances were different, the speed of drift differed according to the model's predictions (Fig. 6). The drift can therefore be regarded as being caused by optimally combining inconsistent sources of information.
One might question whether the large systematic misalignment between vision and proprioception could not be an artifact because of errors in the alignment of our setup. There are two reasons why such misalignment cannot explain our results. First, there are indeed imperfections in the alignment of the setup (see Materials and Methods), for instance because the cathode ray tubes (CRTs) are not completely flat. However, these alignment errors are the same for all subjects, and much smaller than the subject-specific misalignment that we found. Secondly, we found a similar range of values for the systematic misalignment in the analysis of two experiments that were performed by using a two-dimensional set-up with a LCD projector (14, 15). Because the calibration of such a setup is very easy and does not involve any subject specific step, we can conclude that the subject-specific systematic misalignment that we found is not a technical but a physiological phenomenon.
The drift was slightly faster than predicted. Several of the various simplifying assumptions that we made may be responsible for this finding. For instance, we assumed that the increased uncertainty after removal of vision is only because of the expected execution errors. It seems very plausible that the abrupt disappearance of vision itself also adds uncertainty. Second, we assumed that the discrepancy between vision and proprioception could be described as a uniform translation, which ignores the deformations that have been reported (9). Third, subjects might have made more on-line corrections to their movements in the blocks with visual feedback than in those without, which would mean that we underestimated the execution variance by using σex2, and thus we underestimated the speed of drift (Eq. 4). Furthermore, in our calculations we neglected the fact that both the perceptual precision and the execution errors are direction-dependent (7, 16). If we take all of these simplifications into account, we are not surprised that our predictions differ slightly from the observed time course.
Movement Drift.
The drift in movement endpoints that we observed when removing visual feedback has been reported before (17–20), without noticing that the direction and amplitude of the drift are characteristic for a subject. Previous studies tried to explain the observed drift in terms of execution errors, sensory adaptation, or drifting sensory maps. Accumulation of random execution errors cannot explain why the drift repeatedly goes in the same direction. One could argue that the execution errors are systematic, for instance because of misjudgment of the interaction torques during the movement (18). However, accumulation of execution errors cannot explain why the direction of the drift depends on the sensory modality in which the target is presented (Fig. 5). Furthermore, neither accumulation of execution errors nor drift of sensory maps can explain why the same bias that was observed after a period of drift was immediately present (and constant) in the first block. This initial mismatch, which is reproducible across days, is the key for our claim that vision and proprioception are not aligned.
The important conclusion that follows from the present model is that one can see drift in performance without any drift in sensory information. The model is therefore compatible with the experimental finding that the proprioceptive information required for controlling movement direction is not affected by movement drift (18). The model is also compatible with various other regularities that have been observed. For instance, our model predicts that the amount of drift depends on the number of movements made and not on the time the hand is out of view, which is in line with the results of Desmurget et al. (19). The well established finding that faster movements are more variable than slow ones (21) leads to another prediction of our model. The larger variance in execution (thus larger σex2) of fast movements should lead to faster drift, which has indeed been observed (17), and it is the converse of our analysis of the experiment of de Grave et al. (15; see Fig. 6), which showed that with precise movements the speed of drift can be very low.
Adaptation.
The drift in performance that we observe resembles the decay observed in the test phase after adaptation to prism goggles (22, 23). At least part of that decay (and adaptation) might therefore also be the result of changing weights instead of recalibration of the senses. Such a change of weights without mutual calibration has been observed when haptic slant information helps to resolve the conflict between different visual slant cues (24). The change of weights without recalibration that we propose is between modalities. It might solve some problems in interpreting the experimental results of prism adaptation studies (25) because a change in the weights of visual and proprioceptive information about the hand's location might be the cause of effects that have been attributed to recalibration of the senses. The results of this experiment also have a more general lesson for data analysis. It is customary to remove unexplained drift and variability as the first step in data analysis, as we did in previous work on visuomotor behavior (13, 26). Our study shows that this removal might conceal important information about the processes under study.
Neural Implementation.
The presence of two separate estimates of both hand and target position seems to suggest that these estimates might be represented by different neurons. One group of neurons could represent the positions of both the hand and the target in visual coordinates, which seems to correspond to our knowledge about information processing in the posterior parietal cortex (27, 28). Following this line of reasoning, our model implies that there should also be neurons that represent the positions of both the hand and the target in proprioceptive coordinates. This proprioceptive coding of target position might seem implausible, but we previously provided evidence that an object that is as detached from the hand as a mouse cursor can be related to the proprioception of the hand (29). This proprioceptive coding of objects outside our body may be performed by cells located in the premotor cortex, whose visual receptive field shifts with arm position (30). However, different neurons are not necessary for representing two estimates; it could also be accomplished by neurons whose reference frame depends on the stimulus modality, as have been found in the ventral intraparietal area (31).
Conclusion.
Our model of optimal sensory integration (without any recalibration) describes the systematic drift in movement endpoints and the changes in the variable error very well, without any parameter fitting. Thus, we conclude that combining the information of vision and proprioception does not lead to mutual calibration.
Materials and Methods
Experiment.
Subjects were seated in a totally dark room, and they viewed two CRT displays (48 × 31 cm, viewing distance ≈40 cm; resolution 1,096 × 686 pixels, 160 Hz) by mirrors (Fig. 2A). Infrared markers mounted on a bite board and on the cube allowed us to track the movements of the subjects' heads and hands at 300 Hz with an Optotrak motion analysis system (NDI, Waterloo, ON). Before the experiment, we determined the positions of the nodal point of each of the subjects' eyes relative to the bite board by asking the subjects to look at targets located in various directions (relative to the head) through a pinhole in a disk held in front of the eye. The intersection between the lines through the targets and the pinhole defines the eyes' position relative to the head. Knowing these relative positions allowed us to draw an adequate image of the scene for each eye with a latency of <25 ms, without having to constrain the subjects' heads completely. The mirrors were half-silvered, which allowed us to check the quality of the simulation of the hand-held cube by moving the cube while the real cube was also visible and check the spatial discrepancies between the real cube and the simulated feedback cube. The discrepancies depended on the position of the cube (1.5 cm at most) because we did not correct for factors such as the slight curvature of the CRT screens, and they were similar for all subjects.
At the start of the experiment, the 10 subjects were instructed to align an invisible 5-cm cube that they held in their hand with a visual simulation of a red cube of the same dimensions. On each trial, the location of the target cube was chosen at random from one of the four corners of an imaginary 20-cm tetrahedron in front of the subject. Thus, the movements were not simple back-and-forth movements but a random sequence of movements in 12 different directions in three-dimensional space. As soon as a movement to a target was finished (i.e., when the speed dropped below 10 cm/s), a new target was presented. Using this velocity threshold, subjects had the feeling that the new target appeared at the moment that they thought they had finished their movement. The threshold level made it impossible to use a slow-velocity phase at the end to correct possible errors. No further instructions on speed or accuracy were given, but all subjects chose movement times of about 0.5 s. Typical velocity profiles are shown in Fig. 2C.
The experiment started with an initial block of 50 test trials without any visual feedback to determine whether the subject showed a systematic mismatch between visual and proprioceptive localization. Subsequently, we gave subjects the possibility to align vision and proprioception. To do so, we showed a yellow simulated cube that moved with the cube in the subject's hand during a block of 20 feedback trials. Subsequently, we tested whether subjects had aligned vision and proprioception in a second block of 50 trials without visual feedback. To see whether we could further improve the alignment, we presented another block of 20 trials with feedback and a final block of 50 test trials without feedback (Fig. 2B). The total duration of a session was ≈3–5 min. Each subject performed this set of five blocks twice, on different days.
Data Analysis.
We analyzed the three-dimensional errors in the endpoints of the movements separately for each subject. Different subjects might have different systematic mismatches between vision and proprioception. To be able to average over different subjects, we split the error in each trial into two components. One component was the component of the error in the direction of the bias in the initial block (primary error), which is a signed measure and is expected to be 0 in the trials with visual feedback. The other component (secondary error) is the absolute value of the remaining error (i.e., the component of the error that is perpendicular to the bias in the initial block). This measure is unsigned. Our hypothesis implies that the drift after removal of visual feedback will be in the direction of the bias in the initial block and thus captured by the primary error. If so, the remaining errors (as captured by the secondary error) are variable errors.
Our hypothesis predicted that subjects would show a bias that remains constant in the initial block, that there would be no bias in the block with visual feedback, and that the subjects' errors would increase asymptotically to errors having the same magnitude and direction as in the initial block in subsequent blocks without visual feedback. We know of no other hypothesis that makes a similar qualitative prediction. Moreover, we can quantify these predictions with a model based on Bayesian reasoning.
Model.
To quantify the predictions, we must make an assumption about how the perceived positions (x) of the hand (h) and target (t) are based on their proprioceptive (p) and visual (v) estimates. According to Bayesian inference, the combination leading to the most reliable estimate is a weighted average with weights determined by the reliability of each source of information, which can be estimated from the inverse of the variance of estimates based on that source of information (32, 33). We assume that our subjects use this optimal combination of information. For the estimated location x̌h of a visible hand, the optimal weighted average of the proprioceptive estimate xh,p (with variance σp2) and visual estimate xh,v (with variance σv2) is:
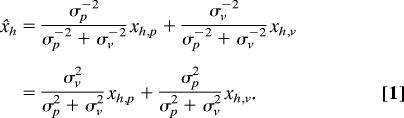 |
As argued in the introduction, the location of a target is given by an equivalent combination of visual and proprioceptive estimates. To predict what happens when the hand moves out of view, we have to make an assumption about the subjects' estimate of their variability in motor performance because this estimate determines the amount of positional uncertainty that each movement adds. We assume that subjects judge it correctly, so we assess it from the movement endpoints under normal, full-vision conditions (the blocks with full-visual feedback). We will refer to this estimate as the execution variance (σex2).
Bias.
Using these two assumptions, we can estimate the perceived position of the hand x̌h and target x̌t after n movements without visual feedback:
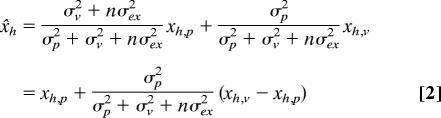 |
and
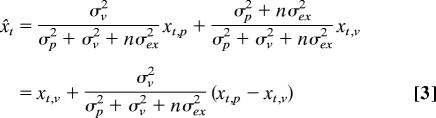 |
The consequence for the bias can best be seen by considering what happens when the unseen hand is at the target (xh,p = xt,p = xp; xh,v = xt,v = xv). In that case, one will perceive a difference between the position of the hand and the target that increases with the number of movements that one has made without seeing ones hand or feeling the target (assuming that proprioception and vision differ systematically: xp ≠ xv):
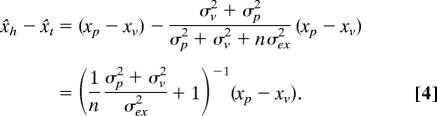 |
We can determine the parameters in Eq. 4 from our experiment in which subjects moved their hand repeatedly among several targets. In the initial block of trials (before any feedback), we assume that the bias was constant and equal to xp − xv. We furthermore assume that the variance in this initial block is because of visual, proprioceptive, and execution errors (σv2 + σp2 + σex2). With visual feedback of the hand (the second and fourth block of trials), we assume that the presence of relative visual information (providing direct information about the distance between hand and target) ensured that no bias was present (x̌h = x̌t) and that the variance was caused by execution errors only (σex2). In the subsequent blocks in which visual feedback is removed, the bias should gradually return to the value before any feedback following Eq. 4. The primary error in a trial is the best estimate that we have for the bias in that trial, so we compare the primary error with the prediction of Eq. 4.
Variable Error.
We can also make predictions for the measured variance in the movement endpoints. To do so, we need to know the relative contributions of vision and proprioception. We did not determine these contributions experimentally, but we assume that vision and proprioception are equally precise (σp = σv, which is a good approximation for some positions; ref. 34). For the localization of either the hand or the target, the predicted variance after the nth movement after removal of feedback is:
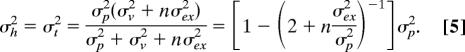 |
This equation predicts that the perceptual variance (σh2, σt2) directly after visual feedback (n = 0) will be half the variance without previous feedback (n = ∞). If we assume unequal weights for proprioception and vision, the reduction in variance will be smaller. As the reduction in variance does not seem to be smaller than predicted (Fig. 3 Lower), our assumption of equal variances seems justified. The prediction for the measured variance in the endpoints of a given trial is the sum of the two perceptual variances at that moment and the execution variance (σh2 + σt2 + σex2). We cannot measure directly the variance on each trial, but the (absolute) secondary error is proportional to the standard deviation. The average absolute deviation from the mean for a circular two-dimensional Gaussian distribution equals σ, so the secondary error is ≈1.25 times the standard deviation in one dimension.
Supplementary Material
Acknowledgments
This work was supported by Netherlands Organisation for Scientific Research Grants 452-02-073, 410-203-02, and 402-01-017 (to J.B.J.S.), 451-02-013 (to R.J.v.B), and 452-02-007 (to E.B.).
Abbreviation
- CRT
cathode ray tube.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS direct submission.
References
- 1.Lackner JR, DiZio PA. Trends Cognitive Sci. 2000;4:279–288. doi: 10.1016/s1364-6613(00)01493-5. [DOI] [PubMed] [Google Scholar]
- 2.Bedford FL. Trends Cognitive Sci. 1999;3:4–11. doi: 10.1016/s1364-6613(98)01266-2. [DOI] [PubMed] [Google Scholar]
- 3.Desmurget M, Pelisson D, Rossetti Y, Prablanc C. Neurosci Biobehav Rev. 1998;22:761–788. doi: 10.1016/s0149-7634(98)00004-9. [DOI] [PubMed] [Google Scholar]
- 4.Maravita A, Spence C, Driver J. Curr Biol. 2003;13:R531–R539. doi: 10.1016/s0960-9822(03)00449-4. [DOI] [PubMed] [Google Scholar]
- 5.Carrozzo M, McIntyre J, Zago M, Lacquaniti F. Exp Brain Res. 1999;129:201–210. doi: 10.1007/s002210050890. [DOI] [PubMed] [Google Scholar]
- 6.Knill DC, Pouget A. Trends Neurosci. 2004;27:712–719. doi: 10.1016/j.tins.2004.10.007. [DOI] [PubMed] [Google Scholar]
- 7.van Beers RJ, Sittig AC, Denier van der Gon JJ. J Neurophysiol. 1999;81:1355–1364. doi: 10.1152/jn.1999.81.3.1355. [DOI] [PubMed] [Google Scholar]
- 8.Sober SJ, Sabes PN. Nat Neurosci. 2005;8:490–497. doi: 10.1038/nn1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cuijpers RH, Kappers AML, Koenderink JJ. J MathPsychol. 2003;47:278–291. [Google Scholar]
- 10.Smith RC, Cheeseman P. Int J Robotics Res. 1986;5:56–69. [Google Scholar]
- 11.Fox D, Hightower J, Liao L, Schulz D, Borriello G. IEEE Pervasive Comput. 2003;2:24–33. [Google Scholar]
- 12.van den Dobbelsteen JJ, Brenner E, Smeets JBJ. Exp Brain Res. 2003;148:471–481. doi: 10.1007/s00221-002-1321-4. [DOI] [PubMed] [Google Scholar]
- 13.van den Dobbelsteen JJ, Brenner E, Smeets JBJ. J Neurophysiol. 2004;92:416–423. doi: 10.1152/jn.00764.2003. [DOI] [PubMed] [Google Scholar]
- 14.van Beers RJ, Sittig AC, Denier van der Gon JJ. Exp Brain Res. 1996;111:253–261. doi: 10.1007/BF00227302. [DOI] [PubMed] [Google Scholar]
- 15.de Grave DDJ, Brenner E, Smeets JBJ. Exp Brain Res. 2004;155:56–62. doi: 10.1007/s00221-003-1708-x. [DOI] [PubMed] [Google Scholar]
- 16.van Beers RJ, Haggard P, Wolpert DM. J Neurophysiol. 2004;91:1050–1063. doi: 10.1152/jn.00652.2003. [DOI] [PubMed] [Google Scholar]
- 17.Brown LE, Rosenbaum DA, Sainburg RL. Exp Brain Res. 2003;153:266–274. doi: 10.1007/s00221-003-1601-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brown LE, Rosenbaum DA, Sainburg RL. J Neurophysiol. 2003;90:3105–3118. doi: 10.1152/jn.00013.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Desmurget M, Vindras P, Grea H, Viviani P, Grafton ST. Exp Brain Res. 2000;134:363–377. doi: 10.1007/s002210000473. [DOI] [PubMed] [Google Scholar]
- 20.Wann JP, Ibrahim SF. Exp Brain Res. 1992;91:162–166. doi: 10.1007/BF00230024. [DOI] [PubMed] [Google Scholar]
- 21.Fitts PM. J Exp Psychol. 1954;47:381–391. [PubMed] [Google Scholar]
- 22.Clower DM, Boussaoud D. J Neurophysiol. 2000;84:2703–2708. doi: 10.1152/jn.2000.84.5.2703. [DOI] [PubMed] [Google Scholar]
- 23.Choe CS, Welch RB. J Exp Psychol. 1974;102:1076–1084. doi: 10.1037/h0036325. [DOI] [PubMed] [Google Scholar]
- 24.Ernst MO, Banks MS, Bulthoff HH. Nat Neurosci. 2000;3:69–73. doi: 10.1038/71140. [DOI] [PubMed] [Google Scholar]
- 25.Redding GM, Rossetti Y, Wallace B. Neurosci Biobehav Rev. 2005;29:431–444. doi: 10.1016/j.neubiorev.2004.12.004. [DOI] [PubMed] [Google Scholar]
- 26.van Beers RJ, Sittig AC, Denier van der Gon JJ. Exp Brain Res. 1998;122:367–377. doi: 10.1007/s002210050525. [DOI] [PubMed] [Google Scholar]
- 27.Cohen YE, Andersen RA. Nat Rev Neurosci. 2002;3:553–562. doi: 10.1038/nrn873. [DOI] [PubMed] [Google Scholar]
- 28.Medendorp WP, Goltz HC, Crawford JD, Vilis T. J Neurophysiol. 2005;93:954–962. doi: 10.1152/jn.00725.2004. [DOI] [PubMed] [Google Scholar]
- 29.Brenner E, Smeets JBJ. Spatial Vision. 2003;16:365–376. doi: 10.1163/156856803322467581. [DOI] [PubMed] [Google Scholar]
- 30.Graziano MSA. Proc Natl Acad Sci USA. 1999;96:10418–10421. doi: 10.1073/pnas.96.18.10418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Avillac M, Deneve S, Olivier E, Pouget A, Duhamel JR. Nat Neurosci. 2005;8:941–949. doi: 10.1038/nn1480. [DOI] [PubMed] [Google Scholar]
- 32.Jacobs R. Trends Cognitive Sci. 2002;6:345–350. doi: 10.1016/s1364-6613(02)01948-4. [DOI] [PubMed] [Google Scholar]
- 33.Deneve S, Pouget A. J Physiol (Paris) 2004;98:249–258. doi: 10.1016/j.jphysparis.2004.03.011. [DOI] [PubMed] [Google Scholar]
- 34.van Beers RJ, Wolpert DM, Haggard P. Curr Biol. 2002;12:834–837. doi: 10.1016/s0960-9822(02)00836-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.