Rainfall-Induced Release of Fecal Coliforms and Other Manure Constituents: Comparison and Modeling

Abstract

Modeling release of fecal coliforms is an important component of fate and transport simulations related to environmental water quality. Manure constituents other than fecal coliforms may serve as natural tracers of fecal contamination provided that their release from manure to runoff is similar to the fecal coliform release. The objectives of this work were to compare release of fecal coliforms (FC), chloride (Cl⁻), organic carbon (OC), and water-soluble phosphorus (P) from dissolving manure and to assess the performance of three models in describing the observed release. Bovine manure was applied on 0.5- by 0.3-m bare and vegetated subplots with 20% slope on sandy loam and clay loam soils. Concentrations of Cl⁻, FC, OC, and P were measured in runoff collected from troughs at the edges of the subplots at 5-min intervals during 1-h rainfall simulations. The one-parametric exponential model and two-parametric Vadas-Kleinman-Sharpley model and Bradford-Schijven model were fitted to the data. The Bradford-Schijven model had uncorrelated parameters, one of which was linearly related to the irrigation rate, and another parameter reflected the presence or the absence of vegetation. Kinetics of the FC release from manure was similar to the release kinetics of P and OC. The Bradford-Schijven model is recommended to simulate the release of manure constituents.

Manure is the primary source of pollution from animal feeding operations. According to a U.S. Environmental Protection Agency report from 1999 (32), an estimated 940 million tons of manure were generated from livestock and poultry operations (on a wet-weight basis) in the United States. Beef and dairy manure accounted for approximately 80% of the total amount. Manures are typically applied as solid or liquid slurries as fertilizers to land used for silage, grazing, or crops (9, 17, 36).

Manures have been documented to contain a variety of pathogenic microorganisms, which may be released into the environment in large numbers (6, 8, 23, 31). Since detection and quantitation of specific pathogens are difficult, fecal coliform (FC) bacteria are widely used as an indicator of fecal contamination of soil and water (30). FCs typically account for about 98% of the coliforms found in warm-blooded animal feces (5). Numerous studies have addressed the surface and vertical transport of FCs (3, 4, 10, 16, 21, 22, 28, 34, 35).

The surface transport of FCs is contingent upon their release from surface-applied manures, yet few studies have documented FC release rates or the factors which control their release. Springer et al. (28) and Thelin and Gifford (29) studied the effect of the manure age on FC release from bovine fecal deposits under simulated rainfall. Their findings revealed that FC concentrations in runoff decreased with manure age, presumably due to mortality. Thelin and Gifford (29) also observed a 5-min delay in FC release from old manure, which they interpreted as the time necessary for manure to hydrate. Springer et al. (28) and Kress and Gifford (14) studied FC release from 2-, 10-, and 20-day-old “standard cow pies” at rainfall intensities of 23, 51, and 69 mm h⁻¹. The increase in rainfall intensity did not significantly impact FC release from 2-day-old manure and significantly accelerated release from 10- and 20-day-old manure within 20 min from the initiation of rainfall. The authors concluded that rainfall intensity was only significant after the fecal deposits were completely air-dried.

A better understanding of FC release from surface-applied manures is needed to more appropriately simulate manure-borne bacterial transport with runoff. Different approaches have been proposed to simulate FC release from surface-applied or topsoil-incorporated manure. The Utah State model (28) uses a piece-wise linear relationship between the FC release rate and time. The MWASTE model (18, 19) uses the percent reduction method. The COLI model (35) evaluates the bacteria yield as the product of the mass of manure or soil eroded, a cell density factor, and a first-order die-off factor. In the runoff component of the Hydrological Simulation Program-FORTRAN model (1), the release of bacteria from manure increases nonlinearly with an increase in runoff. The SWAT/Microbial Sub-Model (25) estimates the transport of bacteria from the soil surface as the product of the bacteria content in 0.01 m of the surface soil layer, the bacteria partition coefficient in manure, and the depth of runoff water.

This disparity in modeling approaches reflects the limited information available on the factors affecting manure dissolution rates and release of microorganisms in runoff. Bradford and Schijven (2) analyzed the runoff water obtained by sprinkling different aqueous solutions over a disk filled with dairy calf manure and analyzed it for Cryptosporidium and Giardia (oo)cysts. They showed that the electrical conductivity of applied solution affected release rates. Schijven et al. (26) studied the effects of temperature, manure type, water application method (mist or drip), and flow rate of Cryptosporidium and Giardia (oo)cyst release from dairy cattle manure using a similar technique. Manure and (oo)cyst release rates did not vary with temperature. However, (oo)cyst release rates increased with higher irrigation rates and decreased with the increasing content of cow manure in a calf-cow manure mixture.

Phosphorus release from manure has also been the topic of several studies (11, 12, 13, 27, 34). Sharpley and Moyer (27) studied the effect of manure type on release of dissolved inorganic and organic P during simulated rainfall in laboratory columns. The decrease in leachate concentration of dissolved organic P over five consecutive rainfalls was lower for poultry manure, intermediate for swine slurry, and higher for dairy manure. In comparison, the pool of organic P that leached during rainfall was more rapidly depleted than the inorganic P pool. Kleinman et al. (12) used the National Phosphorus Research Project indoor runoff box protocol (20) to study the effect of the manure application method on P concentrations in runoff. They showed that runoff P losses were lower when manure was incorporated in the soil than when it was applied to the surface. Kleinman and Sharpley (13) used the same protocol to study the timing and sequence of runoff events on runoff P losses. They concluded that differences in runoff P concentrations related to manure type and application rate were diminished by repeated rainfall events as a result of manure P translocation into the soil and removal of applied P by runoff. Vadas et al. (33) have summarized the cited studies and developed a model to predict dissolved inorganic and organic P release from manures during simulated rainfall.

We are unaware of any studies comparing the performance of the different models with respect to the release rates of FCs and other manure constituents. The objectives of the present work were (i) to compare the kinetics of chloride (Cl⁻), FC, organic carbon (OC), and water-soluble P release from bovine manure applied on slopes with different soil textures and surface covers under simulated rainfall and (ii) to assess the applicability of recent models to describe the kinetics of Cl ⁻, FC, OC, and P release.

MATERIALS AND METHODS

Experimental.

Manure dissolution studies were conducted on a two-sided lysimeter, 21.34 m long and 13.2 m wide, located at the Patuxent Wildlife Research Refuge (Beltsville, Md.) during October 2003. The surface slope of the lysimeter was 20%. A detailed description of the lysimeter is given in Roodsari et al. (24). The soil was clay loam on one side of the lysimeter and sandy loam on the other side. Approximately half of each side was planted with a blue fescue (Festuca ovina “Glauca”) and white clover (Trifolium repens) mixture while the remainder was maintained bare. Eight subplots 0.50 m wide and 0.30 m long were established on two sides of the lysimeter in the bare and vegetated areas, resulting in four treatments: bare clay loam, vegetated clay loam, bare sandy loam, and vegetated sandy loam. All subplots were isolated to prevent cross-contamination. Rainfall was applied at a water pressure of 100 kPa using a rainfall simulator equipped with a TeeJetTM 1/4 HH SS 14 WSQ nozzle (Spraying Systems Co., Wheaton, IL) at 3 m above the soil surface. Plots were positioned at different distances from the nozzle to provide for variations in rainfall intensity during simulations. Grass was mowed 1 week prior to the experiment to maintain uniform grass height of about 5 cm. Subplots were irrigated for 30 min with simulated rainfall 1 day prior to the experiment at the same rate as in the runoff experiment. FC content varied from 56 to 135 CFU/ml in the runoff collected from plots in the prior irrigation. Manure slurry was collected from the dairy barn at the Dairy Research Unit of the USDA/ARS-Beltsville Agricultural Research Center, Beltsville, Md. Chloride, FC, OC, and P contents of the applied manure are shown in Table 1. Soil water content was measured gravimetrically in triplicates at depths of 0 to 5, 5 to 10, 10 to 15, and 15 to 20 cm prior to the manure application (Table 1). The manure slurry was uniformly applied at the top of the subplots at the rate of 11.7 liters m⁻². The uniformity was ensured by placing a wire mesh on top of subplots and pouring the predetermined amount of the manure onto each of the 5- by 10-cm mesh cells. Irrigation was started immediately after the manure application. Rainfall was simulated for 1 h after the initiation of runoff. Rainfall rates were measured with rain gauges installed adjacent to each subplot (Table 1). Runoff was collected in troughs located at the bottom of subplots for 2 min at 5-min intervals. Sample volumes varied between 140 and 380 ml among the subplots. The combination of soil properties and slope at the subplots ensured the unobstructed removal of the released manure constituents to the troughs.

TABLE 1.

Selected properties of the manure, volumetric soil water contents at depths of 0 to 20 cm prior to irrigation, and irrigation times and rates used in the study

Plot	Solid/liquid ratio (g/g)	Cl− (mg/liter)	FC (106 CFU/ml)	OC (mg/liter)	Water-soluble P (mg/liter)	Soil water content (cm3/cm3)a	Irrigation time (h)	Irrigation rate (cm/h)
								Subplot 1	Subplot 2
1	0.158	2,375	1.70	4,905	148.2	0.280 ± 0.035	1.217	2.90	3.38
2	0.082		1.71	4,381	158.5	0.227 ± 0.036	0.950	6.11	5.53
3	0.079	2,340	0.67	8,794	142.7	0.234 ± 0.029	1.267	5.37	7.49
4	0.075	4,254	2.05	15,919	169.9	0.243 ± 0.014	1.029	3.57	6.41

^aData are estimates of the average value ± standard error.

Runoff volume and Cl⁻, FC, OC, and P concentrations were measured in each runoff sample from each subplot. Chloride content was measured with a model 94178 chloride electrode (Thermo Electron Corp., Beverly, MA) with the detection range from 1.8 to 35,500 mg liter⁻¹. FC concentrations were determined by plating 50-μl subsamples of runoff, after centrifugation at 100 × g to remove sediment, onto MacConkey agar using an Autoplate 4000 spiral platter (Spiral Biotech, Bethesda, MD). After overnight incubation at 44.5°C, pink to red colonies typical of FC were counted using a Protocol plate reader (Synoptics, Cambridge, United Kingdom). FC data are expressed as the number of CFU. To measure P and OC, runoff samples were centrifuged and filtered through a 0.45-μm-pore-size filter. Soluble P was measured using Lachat Method 10-115-01-1-A, while total organic carbon was measured using a Phoenix 8000 TOC analyzer (Tekmar-Dohrman, Cincinnati, OH).

Release models. (i) Model I.

Vadas et al. (33) applied the equation

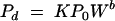(1)

to describe dissolved inorganic phosphorus loss in runoff from surface-applied dairy, poultry, and swine manure. Here P_d is the amount of P (mg of P kg⁻¹ of soil) desorbed in time t (min) at a water-to-soil ratio of W (ml of water g⁻¹ of soil), P₀ is the initial amount of desorbable P present in the soil (mg of P kg⁻¹ of soil), K and b are constants for a given soil, and the value of W is the volume of rainfall (cm³) divided by the dry weight (g) of applied manure M_d. This model can be transformed into:

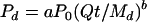(2)

or in terms of the P amount per volume of liquid manure:

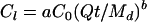(3)

where C_l is the amount of P (g of P cm⁻³ of liquid manure) released from manure in time t (h), C₀ is the initial amount of P (g of P cm⁻³ of liquid manure) in applied manure, Q is the aqueous phase flow rate (cm³ h⁻¹), and a and b are unitless parameters defining the shape of the release curve.

The aqueous P concentration follows from the temporal derivative of equation 3:

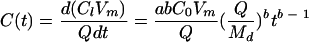(4)

where V_m is the volume of applied manure (cm³), C(t) is the concentration of P that has been released to the aqueous phase at time t.

(ii) Model II.

This exponential release model is used in the Hydrological Simulation Program-FORTRAN model to describe the release of FCs from storage on the land surface (1). The equation is written as follows:

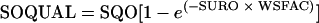(5)

where SOQUAL is the amount of FC bacteria washed off from the land surface (number of colonies/acre/time interval), SQO is surface storage of FC bacteria (number of colonies/acre), SURO is the total amount of surface runoff (in/time interval), and WSFAC is susceptibility of FC bacteria to wash-off (per inch). Equation 5 can be further summarized to:

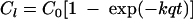(6)

where C_l is the amount of FC in CFU (CFU cm⁻³ of liquid manure) released from the manure in time t (h), C₀ is the initial amount of FC in the manure that can be released (CFU cm⁻³ of liquid manure), k is the rate constant equivalent to WSFAC but measured cm⁻¹, and q is the precipitation rate (cm h⁻¹). The time derivative of equation 6 results the concentration in runoff C(t) as:

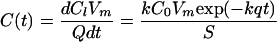(7)

where V_m is the initial manure volume (cm³) and S is applied area (cm²).

(iii) Model III.

This power-rational model (2) was developed to describe dairy calf manure release dissolving under a sprinkler in a laboratory study. The manure release is described with the following equation:

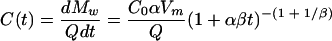(8)

where M_w is the cumulative manure mass released into the aqueous phase (g), Q is the aqueous phase flow rate (cm³ h⁻¹), V_m is the manure volume (cm³), and α(h⁻¹) and β are the fitting parameters defining the shape of the release curve.

The applicability of models I, II, and III was assessed separately for each of the Cl⁻, FC, OC and P release rates. Equations 4, 7, and 8 were fitted to each of the observed dependence release rates for Cl⁻, FC, OC, and P concentrations in the subplot runoff with time. The goodness-of-fit for model application was assessed by estimating the root mean square error (RMSE) as follows:

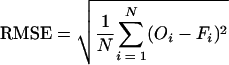(9)

where O_i and F_i are observed and fitted values, respectively, for the same manure component, and N is the number of observations.

To compare the kinetics of FC release from the manure at subplots with the release kinetics of Cl⁻, OC, and P, the observation data were presented in terms of the relative concentration (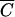 = C/Co), where C is the concentration in runoff and Co is the concentration in the applied manure. Coefficients of linear regression b₀ and b₁ were evaluated as follows:

(10)

where 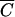_i is the relative Cl⁻, OC, or P concentration in runoff and 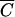_FC is the relative FC concentration in runoff. The determination coefficients, R², were computed for each regression. Statistical computations were done with Microsoft Excel and SigmaPlot 8.0 software (SigmaPlot version 8.0 user's manual, SPSS, Inc., Chicago, Ill.). Analysis of variance (ANOVA) was performed to evaluate the effect of vegetation, manure constituents, and soil texture on the values of model parameters using SPLUS software (15).

RESULTS

Kinetics of Cl⁻, OC, P and FC release.

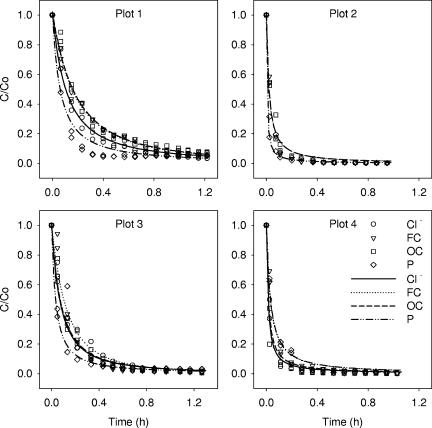
The kinetics of Cl⁻, FC, OC, and P release for all plots are shown in Fig. 1. All curves are characterized by a fast decrease in release rate followed by a gradual flattening. The decrease was more pronounced for the bare soil plots (plots 2 and 4) than the vegetated plots (plots 1 and 3). Release rates for Cl⁻, FC, OC, and P were different for each plot, with the largest difference observed for the vegetated clay loam plot (plot 1). The time required for release rates to fall below 0.1 h⁻¹ was 0.8, 0.9, 1.1, and 0.5 h for Cl⁻, FC, OC, and P, respectively, for plot 1.

FIG. 1.

Data measured (symbols) and fitted (lines) with equation 8 (model III) for release of Cl⁻, FC, OC, and P from manure on plots. Symbols are defined in plot 4.

Comparisons of relative FC concentrations versus Cl⁻, OC, and P concentrations are shown in Fig. 2. Statistical tests were performed to determine if the regression lines for 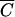_Cl versus 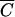_FC, 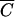_OC versus 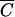_FC, and 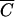_P versus _FC deviated from the 1:1 line (15). The coefficients b₀ and b₁ of the linear regression (10), coefficients of determination (R²) and F-statistics are presented in Table 2. Fecal coliforms were released more slowly than Cl⁻ and soluble P when b₁ was less than 1. Maximum values of R² were obtained for relationships between 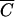_FC and 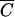_OC for plots 1 to 3 and between 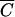_FC and 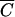_P for plot 4. R² values were equal to 0.983, 0.996, 0.980, and 0.989, respectively, for plots 1, 2, 3, and 4. The values of F-statistics indicated that there was no significant difference between FC and OC release from plots 1 and 2 or between FC and P release from plot 4.

FIG. 2.

Relationships between relative concentrations (C/Co) of chloride (Cl⁻), organic carbon (OC), water-soluble phosphorus (P), and fecal coliforms (FC) in runoff. Symbols are defined in plot 4.

TABLE 2.

Coefficients of linear regression b₀ and b₁ in equation 10, R² for this equation, and F-statistics of the linear regression identity to 1:1

Component	Parameter	Value for the indicated plota
		Plot 1	Plot 2	Plot 3	Plot 4
Cl−	b0	−0.050 ± 0.012		0.018 ± 0.011	−0.015 ± 0.013
	b1	0.995 ± 0.033		0.882 ± 0.030	0.910 ± 0.039
	R2	0.969		0.969	0.954
	F	11.15		6.12	4.69
OC	b0	0.007 ± 0.009	0.009 ± 0.004	0.015 ± 0.009	−0.022 ± 0.017
	b1	1.030 ± 0.025	0.978 ± 0.013	0.897 ± 0.024	0.871 ± 0.053
	R2	0.983	0.996	0.98	0.911
	F	2.97b	2.37b	6.94	5.10
P	b0	−0.076 ± 0.025	−0.012 ± 0.019	0.016 ± 0.026	0.011 ± 0.007
	b1	0.886 ± 0.066	0.875 ± 0.057	0.749 ± 0.069	0.983 ± 0.021
	R2	0.856	0.911	0.814	0.989
	F	12.00	3.38	6.23	1.33b

^aData are the estimates of the average value ± standard error.

^bNot significantly different from one at the 0.05 significance level.

Model comparison.

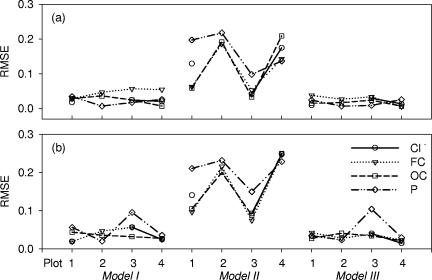
Model parameters were fit to the measured release rates of Cl⁻, FC, OC, and P and are shown with lines in Fig. 1. Model III described fast decline and flattening in release curves well. The goodness-of-fit for the application of the models to the experimental release curves was different for models I, II, and III. Figure 3 presents RMSE values for each of the plots. In general, the largest RMSEs were obtained with model II, and the smallest RMSEs (better fit) were obtained for models I and III. Furthermore, in model II applications to Cl⁻, FC, and OC release from the manure, the RMSE values were even larger at bare plots 2 and 4 than at vegetated plots 1 and 3. For FCs, for example, the minimum RMSE was equal to 0.186 and 0.143 at vegetated plots 2 and 4, respectively, whereas the lowest RMSE values equaled 0.063 and 0.053 at bare plots 1 and 3, respectively. The RMSE values for models I and III were similar for Cl⁻, FC, OC, and P release at all plots.

FIG. 3.

RMSEs of models fitted to the measured releases of Cl⁻, FC, OC, and P from manure on subplot 1 (a) and subplot 2 (b).

Model parameters.

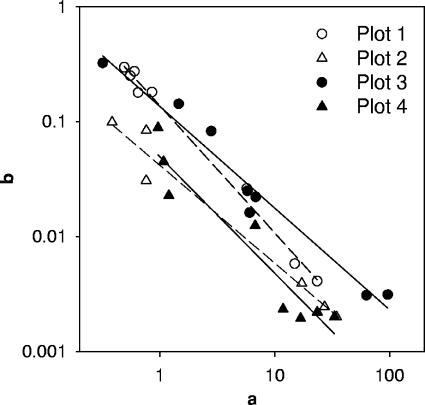
Estimated model I parameter values along with their standard errors are presented in Table 3. Parameters a and b were very different for two subplots of the same plot. The difference between minimum and maximum values was up to 2 orders of magnitude for both parameters (Table 3). Estimated standard errors of a and b were from 22 to 28 times larger than the estimated average values of these parameters for FC at subplot 1 of plots 2, 3, and 4. Such large standard errors of the parameters indicated substantial uncertainty in parameter estimation. No relationship was found between parameters of this model and soil texture, vegetation, or rate of irrigation (data not shown). An explanation of such uncertainty in parameter estimation was found when parameters a and b were split into two-plot data sets and plotted against each other (Fig. 4). Data showed that parameters of model I were highly correlated. The coefficient of determination (R²) values for regression of log(b) versus log(a) equaled 0.992, 0.968, 0.962, and 0.911 for plots 1, 2, 3, and 4, respectively. High values of standard errors for a and b resulted from a high correlation between these parameters. A similarity was also observed in paired regression lines of the vegetated plots (plots 1 and 3) and the bare plots (plots 2 and 4) (Fig. 4). This indicated the effect of vegetation on relationships between a and b.

TABLE 3.

Values of parameters a and b obtained by fitting equation 4 to the measured release of Cl⁻, FC, OC, and P from the manure (model I)

Parameter and component	Subplot	Value (± SE) at the indicated plot
		Plot 1	Plot 2	Plot 3	Plot 4
Parameter a
Cl−	1	0.643 ± 0.195		5.766 ± 15.66	11.78 ± 344.3
	2	5.688 ± 3.408		1.452 ± 0.762	33.04 ± 929.4
FC	1	0.551 ± 0.109	17.10 ± 405.1	62.77 ± 1,357.0	23.40 ± 658.8
	2	0.487 ± 0.098	27.04 ± 1,094.0	95.94 ± 1,644.0	6.725 ± 9.709
OC	1	0.849 ± 0.087	34.44 ± 927.2	6.819 ± 16.09	16.77 ± 596.2
	2	0.599 ± 0.076	0.760 ± 1.010	2.794 ± 2.109	1.191 ± 3.152
P	1	23.37 ± 449.0	0.756 ± 1.518	6.028 ± 11.46	1.072 ± 1.887
	2	14.93 ± 182.9	0.383 ± 0.404	0.317 ± 0.302	0.958 ± 0.729
Parameter b
Cl−	1	0.179 ± 0.050		0.025 ± 0.065	0.002 ± 0.068
	2	0.026 ± 0.015		0.142 ± 0.059	0.002 ± 0.056
FC	1	0.250 ± 0.042	0.004 ± 0.092	0.003 ± 0.066	0.002 ± 0.062
	2	0.296 ± 0.047	0.002 ± 0.099	0.003 ± 0.053	0.012 ± 0.018
OC	1	0.180 ± 0.017	0.002 ± 0.054	0.022 ± 0.051	0.002 ± 0.069
	2	0.273 ± 0.028	0.084 ± 0.106	0.082 ± 0.054	0.023 ± 0.059
P	1	0.004 ± 0.078	0.031 ± 0.060	0.016 ± 0.030	0.045 ± 0.079
	2	0.006 ± 0.071	0.099 ± 0.098	0.323 ± 0.182	0.089 ± 0.063

FIG. 4.

Relationship between parameters a and b in equation 4 (model I). Circles indicate vegetation plots and triangles indicate bare plots.

Average values for parameter k in model II were ranged from 0.257 to 0.922 cm⁻¹ (Table 4). The ANOVA was performed to evaluate the effect of vegetation, manure constituents (i.e., Cl⁻, FC, OC, and P), and soil texture (i.e., clay loam and sandy loam) on the values of parameter k. The vegetation (P < 0.000018), irrigation rate (P < 0.026), and the manure constituents (P < 0.034) appeared to be the significant contributing factors in the variability of parameter k. The soil texture effect was insignificant (P < 0.177).

TABLE 4.

Values of parameter k obtained by fitting equation 7 to the measured release of Cl⁻, FC, OC, and P from the manure (model II)

Component	Subplot	Value (± SE) of k (cm−1) at the indicated plot
		Plot 1	Plot 2	Plot 3	Plot 4
Cl−	1	0.690 ± 0.085		0.778 ± 0.066	0.257 ± 0.111
	2	0.763 ± 0.084		0.838 ± 0.032	0.648 ± 0.114
FC	1	0.762 ± 0.060	0.530 ± 0.124	0.879 ± 0.054	0.532 ± 0.136
	2	0.767 ± 0.041	0.673 ± 0.120	0.922 ± 0.042	0.713 ± 0.095
OC	1	0.803 ± 0.066	0.540 ± 0.115	0.786 ± 0.062	0.306 ± 0.118
	2	0.809 ± 0.039	0.558 ± 0.108	0.855 ± 0.026	0.485 ± 0.128
P	1	0.521 ± 0.118	0.310 ± 0.116	0.652 ± 0.101	0.542 ± 0.127
	2	0.508 ± 0.115	0.401 ± 0.113	0.747 ± 0.074	0.741 ± 0.092

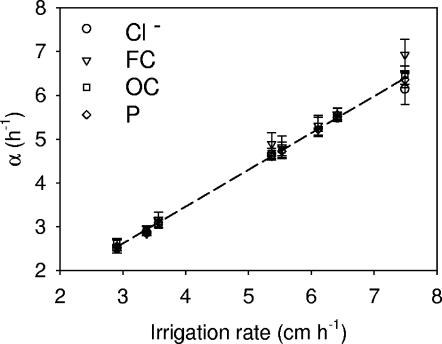
Variations observed in estimating parameters α and β in model III (equation 8) were less than those for model I. The value of α increased linearly from 2.51 to 6.93 h⁻¹ with the increasing irrigation rate for all plots and all monitored manure constituents (Fig. 5). The linear regression equation explaining the relationships for that plot was

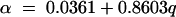(11)

where q is the irrigation rate (cm h⁻¹) (R² = 0.9882).

FIG. 5.

Relationship between parameters α in equation 8 (model III) and irrigation rate.

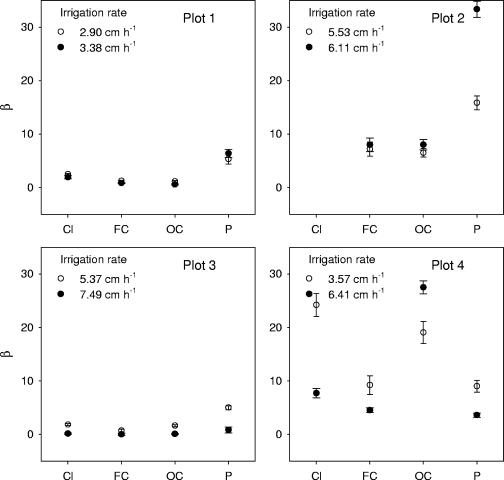
The variability of β was higher for bare plots 2 and 4 than for vegetated plots 1 and 3 (Fig. 6). The values for β varied from 0.56 to 6.38 in plot 1, from 2.77 × 10⁻⁸ to 5.01 in plot 3, from 7.18 to 33.36 at plot 2, and from 3.6 to 27.52 at plot 4. Small values for β (from 2.77 × 10⁻⁸ to 1.65) were obtained for FC and OC release, but β was relatively high (from 0.85 to 6.38) for P release at plots 1 and 3. The highest values for β were obtained for P release in plots 1, 2, and 3 and for Cl⁻ and for OC release in plot 4.

FIG. 6.

The values of parameter β obtained by fitting equation 8 (model III) to Cl⁻, FC, OC, and P release curves at plots.

Significant correlations between α and β were not observed in this study. Data in Fig. 6 show that, in general, smaller values for β corresponded to larger irrigation rates in plots 1, 3, and 4. We tested the statistical hypothesis that the increase in irrigation rate does not affect the value of β using the statistical sign test (7). The hypothesis could be rejected with the probability of 0.981.

Patterns of relationships between β values and the manure constituents were similar for vegetated plots 1 and 3 (Fig. 6). On average, the β values were higher for soluble P, smaller for FC and OC, and intermediate for Cl⁻ release from the manure. No similarity in relationship between β values and the manure constituents was observed for the bare plots (plots 2 and 4). Minimum values for β were obtained for OC, and maximums were obtained for P in plot 2, whereas β was higher for OC than for P at plot 4.

We then hypothesized that parameter β reflected a combined effect of irrigation rate, vegetation, and properties of the manure constituents in this study. ANOVA was applied to estimate the effect of vegetation, manure constituents, and soil texture on β values. The vegetation appeared to be a significant factor (P < 0.00009) of the variations of β. The manure constituents (P < 0.33) and the soil texture (P < 0.86) had no significant effect on the variations of β.

DISCUSSION

Manure is a heterogeneous matrix containing macro- and microscopic dietary fiber, microbial colloids, various biopolymers, and soluble components. Consequently, the observed release rates and transport of various manure constituents are likely to be inherently different and also to vary with environmental conditions. For example, soluble components should dissolve and be transported more rapidly than biopolymers or colloidal particles. However, sorption of constituents to macroscopic particles, which are transported more slowly (if at all), may affect apparent release rates.

Release rates of FCs from bovine manure versus other manure constituents were similar but not identical in this work. Slopes b₁ were significantly less than 1 where intercepts were not significantly different from 0 for Cl⁻ in plots 3 and 4, OC in plots 3 and 4, and P in plots 1, 2, and 3 (Table 1). In these cases FCs were relatively abundant in slowly released parts of manure compared with P, OC, and Cl⁻. The release rates would be completely identical if the proportions of concentrations of FC, P, OC, and Cl⁻ in released manure material were the same during the whole observation period. The faster release of Cl⁻ implies that Cl⁻ is present mostly in the easily released, probably liquid, part of manure. Later, the colloidal manure components dominate the released material, and Cl⁻ is almost absent in this material. The differences in the release of P, OC, and FCs can be attributed to the differences in proportions of these constituents in slowly released parts of manure.

Values of RMSE were higher with a one-parameter model (model II) than with two-parameter models (models I and III). The RMSE values for model II were larger in bare plots (plots 2 and 4), for which the decline in release curves was steeper (Fig. 2). This reflects the increased surface transport of macroscopic particles containing attached FC on bare versus vegetated plots. As only the slowly soluble manure material remains at the application site at late stages of dissolution, the relative importance of the two release mechanisms may change. The single parameter k in equation 7 obviously cannot account for two different release mechanisms, and that may explain the poor performance of model II compared with the two-parametric models I and III.

The decrease in values of parameter α and an increase in values of parameter β with the increase in irrigation rate were documented by the authors of model III in the laboratory study in which they conducted experiments by sprinkling various solutions over a manure disk and collecting the wash-off water. The value of α was five times lower, and β was eight times higher at a mist irrigation rate of 2.9 ml min⁻¹ than that of 10.5 ml min⁻¹. Our results show that in field conditions, the dependence of parameter α on the irrigation rate is very strong (equation 11), whereas the dependence of the β value on runoff rate is also present but is less pronounced.

At least two effects might cause the difference between manure release in the vegetated and bare plots. The vegetation shielded manure from direct rainfall impact and decreased physical (mechanical) forces on manure compared with the bare plot. Schijven et al. (26) observed similar effects using mist and drip irrigation. Mist irrigation resulted in less manure release compared with drip irrigation in their study. Plants and litter decrease the runoff rate and could retain FCs, manure, and colloid particles on the surface. Thus, vegetation could accumulate manure constituents at an earlier stage of runoff and serve as a source later. Both effects resulted in prolonged release of manure constituents on vegetated plots.

Overall, results of this study indicate that the kinetics of FC release are similar to the release kinetics of P and OC constituents but different from Cl⁻ release kinetics. FCs tended to be released at a similar rate or a slightly slower rate than P and OC in the vegetated plots. Model I (33) and model III (2) had similar accuracy in fitting to the kinetics of Cl ⁻, FC, OC, and P release. Model III, however, had uncorrelated parameters. Values of these parameters reflected differences in irrigation rate and vegetation. The Bradford-Schijven model is recommended as having more stable parameters related to the irrigation rate and vegetation.