A Molecular View of Melting in Anhydrous Phospholipidic Membranes

Abstract

A high-flux backscattering spectrometer and a time-of-flight disk chopper spectrometer are used to probe the molecular mobility of model freeze-dried phospholipid liposomes at a range of temperatures surrounding the main melting transition. Using specific deuteration, quasielastic neutron scattering provides evidence that, in contrast to the hydrocarbon chains, the headgroups of the phospholipid molecules do not exhibit a sharp melting transition. The onset of motion in the tails is located at temperatures far below the calorimetric transition. Long-range motion is achieved through the onset of whole-lipid translation at the melting temperature. Atomistic simulations are performed on a multibilayer model at conditions corresponding to the scattering experiments. The model provides a good description of the dynamics of the system, with predictions of the scattering functions that agree with experimental results. The analysis of both experimental data and results of simulations supports a picture of a gradual melting of the heterogeneous hydrophobic domain, with part of the chains spanning increasingly larger volumes and part of them remaining effectively immobile until the thermodynamic phase transition occurs.

INTRODUCTION

While biological function is primarily associated with the fully hydrated form of lipidic membranes, the dehydrated state is of considerable scientific and technological importance. A wide variety of organisms can survive over extended periods of time under anhydrobiotic conditions; the behavior of anhydrous cell membranes in such organisms is key to their ability to withstand desiccation, and is of enormous biological interest (1–3). From a technological point of view, the long-term storage of certain types of cells, for which liposomes serve as a simple model, can be achieved by freeze-drying in the presence of disaccharides (4). Liposomes, spherical assemblies of phospholipid bilayers, constitute a model system for biological membranes. Liposomes can mimic many of the thermophysical properties of cell membranes, and are therefore ideally suited to advance our fundamental understanding of biological systems. Liposomes are useful in their own right as carriers for drug delivery, gene therapy and immunization (5,6), and food products. The preparation of these liposomal carriers, many of which use synthetic products of natural phospholipids such as dipalmitoyl-phosphatidylcholine (DPPC), requires drying and rehydration (4).

Lipid membranes exhibit a melting transition between a solid (or gel) phase and a liquid phase (7). This transition has been studied extensively in hydrated systems, where considerable challenges arise (“ripple” phase formation, anomalous swelling, and hydration forces) (8,9). In contrast to the state of affairs for hydrated bilayers, comparatively few studies have examined the phase behavior of dry bilayer membranes. It is generally presumed that, in the absence of water, the headgroup spacing can decrease; this process facilitates the packing of the tails and raises the transition temperature well beyond that of fully hydrated bilayer membranes. This elevation of the main transition temperature can be avoided if freeze-drying is performed in the presence of sugars. Trehalose, a disaccharide of glucose, has a particularly profound stabilizing effect and leads to a significant depression of the main transition in freeze-dried liposomes to temperatures well below those of fully hydrated samples (4). This depression of the main transition temperature has been linked to the ability of some sugars to impart desiccation tolerance to living organisms and synthetic structures. To understand the mechanism through which sugars stabilize liposomes or cells, it is essential that we first develop a thorough understanding of the melting process of pure bilayer membranes under anhydrous conditions. The aim of this study is to provide a detailed view of melting in these systems through the concerted use of quasielastic neutron scattering experiments (QENS) and atomistic simulations.

To provide a context in which to discuss the data presented in this work, we provide a brief discussion of the findings of prior QENS studies of hydrated bilayers. It is important to emphasize that, out of necessity, such studies have resorted to uncontrolled assumptions and approximations. Data must often be manipulated extensively to extract useful information from the acquired spectra. A study of highly oriented lipid multilayers using QENS was conducted by König et al. (10). The effect of orientation and the role of water were considered separately using either a time-of-flight spectrometer (TOF, which probes mobility in the picosecond regime) or a backscattering spectrometer (which probes timescales from hundreds of picoseconds to nanoseconds). Multilayer samples of protonated dipalmitoyl-phosphatidylcholine (DPPC, significant scattering by all atoms) or tail-deuterated DPPC (reduced scattering from the tails) were examined at 5–20% water content. Note that, at 5% water content, a bilayer membrane could be viewed as partially to fully hydrated; only at water contents below 2.5% do membranes show significantly different behavior (11). Hydration levels were controlled through the use of salt solutions. The data were analyzed using a sum of Lorentzian functions and coarse analytical models to extract the fraction of elastic intensity simply referred to as the elastic incoherent structure factor (EISF). Significant differences were inferred between the mobility detected by each instrument from the fitted values of various parameters. In the TOF spectroscopy, the motion was found to be essentially isotropic with an EISF that did not vanish at the largest observed momentum transfers Q. Data from the backscattering spectrometer instrument exhibited a significant dependence on orientation and an EISF that rapidly vanished to zero. In addition to the above differences, the TOF measurements showed evidence of mobility below the melting transition. This result was interpreted as a continuous melting of the tails with increasing temperature. A more elaborate model was later employed to describe the data (12). A recent study of oriented hydrated dimyristoyl-phosphatidylcholine multilayers using the neutron backscattering technique (13) reported a second transition, which the authors attributed to a freezing of the water of hydration. Clearly, the study of hydrated bilayers presents challenges and questions that remain unresolved.

In this work, we consider the melting transition of anhydrous liposomes. The system under study is representative of lipid membranes under very low hydration conditions. Lipid molecules are associated at most to one water molecule (lipid monohydrate). The results and analysis presented in what follows constitute a first step in our efforts to understand the melting transitions of systems and formulations being designed for the desiccation and long-term storage of pharmaceutical products and cells. While water content is negligible, thereby facilitating analysis of our data, we chose to perform our experiments using liposomes, rather than oriented multilayers. This approach builds on the knowledge of these systems that we have accumulated over the past few years (14–16). A second reason for avoiding multilayer samples in our work stems from the difficulty of preparing well-characterized samples in the presence of sugars for future experiments (note that bilayer membranes are impermeable to disaccharides). Unlike previous QENS studies of bilayers, we fully exploit the ability of neutrons to preferentially probe the motion of specific protons in the sample: by considering DPPC with deuterated headgroups (dh-DPPC), we probe tail mobility; and by deuterating the tails (hd-DPPC), we probe headgroup mobility. Samples of dh-DPPC provide an improved means of studying tail mobility relative to the fully protonated or tail-deuterated DPPC.

In contrast to prior QENS work on bilayers, we avoid the use of approximate models and uncontrolled approximations by interpreting experimental data with the aid of atomistic molecular simulations. Note that the temporal (picoseconds to nanoseconds) and spatial (a few Ångstroms) resolution of QENS is such that atomistic molecular dynamics simulations are ideally suited for interpretation of QENS spectra. There is precedent in the polymer and protein literature for the use of molecular dynamics simulations for analysis of QENS data (17–20). For lipid membranes, however, a direct comparison of the results of simulations and QENS data has not been performed. In this work, simulations are used both to validate our model and to extract a precise view of the dynamic processes that give rise to the scattering spectra measured in our experiments.

The picture that emerges from this study is that of a highly inhomogeneous melting process, in which headgroups and tails exhibit different and distinct behaviors. Phospholipid headgroups in freeze-dried liposomes undergo a melting with no pronounced transition. Substantial mobility of the hydrophilic part is observed only above the transition; in contrast, the hydrophobic tails of the molecules exhibit considerable mobility even below the transition. The lipid tail mobility below the transition consists of several distinct physical processes, whose significance depends on location along the molecule. The precise molecular view of melting in dry bilayers that emerges from our experiments represents a significant contribution to our knowledge of melting dynamics in lipidic membranes.

METHODOLOGY

QENS experiments

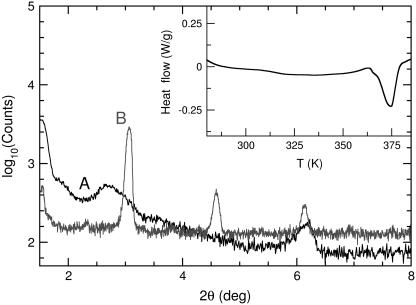
1,2-Dipalmitoyl-sn-glycero-3-phosphocholine (protonated lipid, referred to as hh-DPPC), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine-1,1,2,2D4-n,n, n-trimethyl-D9 (head deuterated, dh-DPPC), and 1,2-dipalmitoyl-D62-sn-glycero-3-phosphocholine (tail deuterated, hd-DPPC) were purchased from Avanti Polar Lipids (Alabaster, AL). The lipids were suspended at 323 K in a D₂O solution and then extruded 19 times through two 100-nm membrane filters. The extruded solutions were freeze-dried for 48 h in a Virtis Genesis model No. 12EL freeze-dryer (Virtis, Gardiner, NY) at a pressure of 30 mTorr and a condenser temperature of 193 K. Samples were loaded into Al cans in a dry nitrogen atmosphere for subsequent QENS measurements, to eliminate the uptake of water. Residual water measurements for dehydrated samples were performed using a Coulometer Metrohm, model No. 737 (Karl Fischer, Buckingham, UK); the water content was determined to be 2.0 to 2.5 wt %. Differential scanning calorimetry (DSC) was performed on the dehydrated samples from 253 K to 423 K at 10 K/min using a TA model No. Q100 differential scanning calorimeter (TA Instruments, New Castle, DE). Additional x-ray diffraction experiments were performed with a PANalytical's X'Pert PRO instrument (PANanalytical, Natick, MA). The diffraction peaks shown in Fig. 1 resemble those obtained for a hydrated system at low temperature in the subgel phase (22). To increase the quality of the recorded spectra, data were collected for highly oriented freeze-dried lipid multilayers prepared as described in König et al. (10). Our x-ray diffraction measurements on dry samples correspond to an isomorphous phase; there is no evidence of coexisting domains of different phases, as reported for hydrated systems (22). The DSC scans of the same samples only show a single melting transition, and should be contrasted with scans on systems where domain formations are present (23).

FIGURE 1.

Low-angle x-ray diffraction peaks on freeze-dried liposomes (A) and highly oriented freeze-dried lipid multilayers (B). Reflections shown, correspond to a constant lamellar repeat distance and are indicative of isomorphous packing. The inset presents a DSC scan on freeze-dried liposomes at 10 K/min. A single melting transition is evident.

Quasielastic neutron scattering experiments were performed using two spectrometers at the National Institute of Standards and Technology Center for Neutron Research in Gaithersburg, MD: the high-flux backscattering spectrometer (HFBS) (24) and the time-of-flight disk chopper spectrometer (DCS) (25). Freeze-dried powder samples were contained in a thin annular aluminum can that achieves 90% neutron beam transmission and avoids multiple scattering effects. The can was sealed with an indium O-ring and enclosed in a closed-cycle refrigerator.

In standard mode of operation of the HFBS instrument, the incident neutron wavelength is varied by Doppler shifting at approximately its nominal value of 6.271 Å (E = 2.08 meV). After scattering from the sample, only those neutrons having a final energy of 2.08 meV are collected by the detectors as ensured by Bragg reflection from Si(1,1,1) analyzer crystals. A dynamic range of ±17 μeV was chosen, which provided an energy resolution of 0.86 μeV as measured with a vanadium standard. In the alternative mode of operation (elastic scan), the Doppler drive is at rest and only the elastic intensity is collected as the temperature is ramped between 70 K and 400 K at a rate of 2 K/min. In both modes, the data are collected for wavevectors ranging between 0.62 Å⁻¹ and 1.75 Å⁻¹. The time-of-flight disk chopper spectrometer (DCS) was used with incident wavelengths of 4.2 Å and 5.6 Å and medium and low-resolution settings, both providing an energy resolution of ≈80 μeV (full width at half-maximum) as measured with a vanadium standard. The data were analyzed for momentum transfers between 0.5 Å⁻¹ and 2.8 Å⁻¹. The measured neutron intensities were corrected using the DAVE software developed by the National Institute of Standards and Technology Center for Neutron Research (http://www.ncnr.nist.gov/dave) for detector efficiency (comparison with a vanadium standard), for scattering from the empty annular can and for time-independent background.

Fixed window scans (elastic scans) were performed as a function of temperature on the HFBS instrument. The elastic scans probe the fraction of the protons having significant mobility (up to 5 ns for HFBS) over distances specified by Q (roughly 3 to 11 Å). Sufficiently high incoherent scattering from the labeled phospholipid groups is desirable to isolate their individual dynamics. The fractions of incoherent scattering for each sample are shown in Table 1, as estimated from the atomic scattering cross sections.

TABLE 1.

Estimated contributions to scattering from head and tail groups of DPPC

	hh-DPPC	hd-DPPC	dh-DPPC
Total incoherent* %	93.8	71.3	92.0
Total coherent %	6.0	28.1	7.8
Labeled incoherent %	93.8	51.4	80.8

^*Contributions from residual water were also taken into account.

The quasielastic scans (either with DCS or HFBS) provide the full dynamic structure factor S(q, ω) within the time and spatial resolution of each instrument. The intermediate scattering function (correlation in the time domain) is obtained from each of the two spectrometers after Fourier transformation using the procedure described in Sakai et al. (27). Deconvolution with the respective resolution function in the time domain reduces to a simple division. Data from each instrument were recorded at temperatures ranging from 310 K to 395 K. These measurements using both the DCS and the HBFS spectrometers offer a unique view of the dynamics of the protons in the sample from 0.5 ps to 5 ns over distances 3 to 11 Å.

Molecular simulations

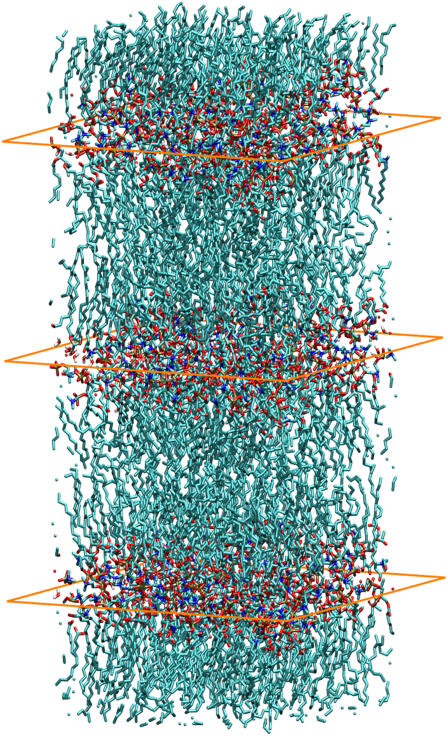
The modeling of lipid membranes in anhydrous conditions faces significant challenges imposed by both the detailed level of description that is required to address neutron scattering experiments and the characteristic timescales associated with relevant relaxation processes. While a number of studies have examined in full atomistic detail the behavior of hydrated bilayer membranes (28), simulations of bilayers at low hydration levels have been scarce. The simulations presented in this work were conducted on a multibilayer system (see Fig. 2) consisting of three different membranes in close proximity of each other. The multibilayer configuration is preferable to a single bilayer system due to the reduced coupling along the membrane normal direction imposed by periodic boundary conditions.

FIGURE 2.

Configuration of the multibilayer system studied. The rectangles are drawn to indicate the interfaces between the three different bilayers. Periodic boundary conditions were considered in the simulations in all three directions. (Graphical representations made with VMD (51).)

Consistent with our previous studies of lipid bilayers exposed to trehalose (29,30), the interaction parameters for the lipids were assembled from the GROMOS force field (31) for the headgroups of DPPC and the NERD force field (32–34) for the aliphatic tails. The SPC model was adopted for the residual water (35).

Simulations were performed using the GROMACS molecular dynamics software (36,37). A leap-frog integration algorithm with a time-step of 1 femtosecond was employed. Nonbonded interactions were accounted for using a twin-range cutoff scheme. Within 10 Å, interactions were evaluated at every time step based on a pair list recalculated every 10 steps. Intermediate-range interactions from 10 to 12 Å were calculated simultaneously with each pair-list update and assumed constant in between. Lennard-Jones interactions were cut off at 12 Å, where long-range electrostatics were handled using the smooth particle-mesh Ewald method (38) with a grid spacing of 1 Å, a real space cutoff at 10 Å, and a Gaussian width of 0.312 Å⁻¹.

The temperature and the pressure were kept constant using the weak coupling technique (39), with correlation times τ_T = 0.1 ps and τ_P = 2.0 ps for temperature and pressure, respectively. Pressure was independently coupled in three directions to an ambient pressure of 1 bar with a compressibility of 0.46 × 10⁻⁴ bar⁻¹, thereby allowing the area of the bilayer and the distance between the interfaces to fluctuate independently.

The initial configuration was taken from our previous work on hydrated DPPC lipid membranes (30). A configuration of 128 DPPC and 4336 water molecules was replicated along the membrane normal. Short molecular dynamics cycles of 0.5 ns were performed at 350 K removing 100 randomly chosen water molecules from each of the three water domains at the end of each cycle. The final configuration that resulted from this procedure consisted of 384 DPPC molecules and 300 water molecules; these numbers correspond to a residual water concentration of ∼2 wt %, consistent with our experimental samples. Fig. 2 depicts a representative multibilayer configuration, where the three rectangles have been drawn to delineate the interfaces between the membranes.

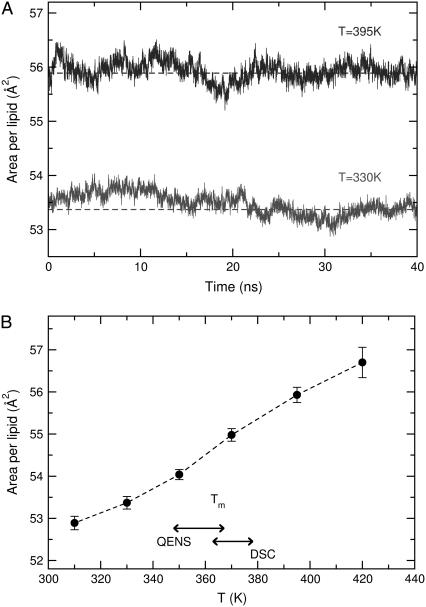
The multibilayer system was simulated for 40 ns at six different temperatures, namely 310, 330, 350, 370, 395, and 420 K. As shown in Fig. 3 a, the lateral area per headgroup fluctuates around an average value after an equilibration period of ∼10 ns. The average area per lipid (Fig. 3 b) changes appreciably in the region around the experimental melting transition. As discussed in the next section, the actual melting transitions of our samples are indicated by the horizontal arrows. While the reduction of the lateral area in this temperature range is clearly evident in our model system, the melting transition cannot be viewed as sharp. The smooth decrease could be either a result of computational limitations (small system size and short simulation times), or an expression of the actual thermodynamics of membranes under anhydrous conditions. We will examine the effect of temperature on membrane properties as probed by QENS in the next section, specifically through the elastic scans performed with HFBS.

FIGURE 3.

(a) Evolution of lateral area per lipid during the molecular dynamics simulations at 395 K and 330 K. The dashed line corresponds to the average extracted from the last 30 ns of the simulations. (b) Average area per lipid from the multibilayer model as a function of temperature. The horizontal arrows indicate the melting transition as probed by QENS and DSC on different samples (values listed in Table 2).

The last step of our simulation methodology includes the analysis of simulated trajectories to calculate the properties probed by QENS experiments. First, hydrogen positions are estimated using a standard tetrahedral representation and the trajectories of the united atoms that are used to represent the lipid tails (to compare to experiments with dh-DPPC). The self-part of the Van Hove correlation function G_s(r, t) describing the proton diffusion is calculated as (40)

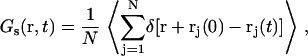(1)

where δ is the Dirac delta function, r_j is the position vector of particle (hydrogen nucleus) j, and N is the total number of particles tracked. This represents the conditional probability to find a particle that has experienced a displacement vector r within time t.

The intermediate incoherent scattering function I(q, t) is the space Fourier transform of the self-part of the Van Hove correlation function (40), namely

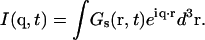(2)

Assuming that the displacements are isotropic, G_s(r, t) = G(r, t) and I(q, t) = I(q, t). Molecular simulations can probe the intermediate incoherent scattering function explicitly for different hydrogen atoms in the lipid molecules by calculating the respective Van Hove correlation functions. This selective calculation is performed by following the mobility of specific protons in the system. The results of simulations are compared to the experimental data by calculating the corresponding functions using only the positions of the protons that scatter significantly in the sample (e.g., hydrogens in the tails for the dh-DPPC sample). To complement the information provided by experiments, the scattering functions were calculated separately for each position along the lipid tails of DPPC (starting from the carbonyl group).

Special note: The identification of commercial instruments and materials in this article does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that they are necessarily the best available for the purpose.

RESULTS

Elastic scattering experiments

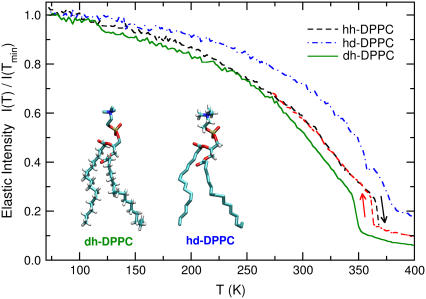
As discussed in Methodology, the fixed-window or elastic scans probe the mobility in the samples by determining the amount of elastic scattering (within the resolution of the HFBS instrument) as a function of temperature, starting from a state where no significant motion is present. Fig. 4 shows the fixed window scans (sum of all detectors, Q) for all three samples, normalized by the intensity at T_min = 70 K. For hh-DPPC, we show heating and cooling scans, in which a small degree of hysteresis can be observed. It is also evident that the sharp portion of the transition occurs mainly in the lipid tails. The elastic intensity of the headgroups does not exhibit a sharp decrease and is reminiscent of an amorphous solid undergoing softening (or solidification). The transition temperatures from scattering for hh-DPPC and dh-DPPC are listed in Table 2: they are somewhat displaced downward from the DSC values. The intensity of dh-DPPC decreases with temperature to a larger extent than that of hd-DPPC, indicating that there is more mobility in the tail region, particularly as the transition is approached. The behavior of hh-DPPC is similar to that of dh-DPPC at low temperatures. This result is expected, because the majority of the protons belong to the tail region, as illustrated by the structures of dh-DPPC and hd-DPPC in the inset of Fig. 4. While the amount of headgroup incoherent scattering is not particularly high, it is clear that the sharp transition observed in the tails is absent in the headgroups, and that the drop in elastic intensity is less. Note that any major contribution from the tails would translate into a sharp decay at the melting temperature.

FIGURE 4.

Average elastic intensity (normalized to T = 70 K) over Q = 0.62 Å⁻¹ to 1.75 Å⁻¹ as a function of temperature. The dashed lines represent heating and cooling curves for the fully protonated lipid. The loss of intensity due to headgroup motion is represented by dash-dotted lines and that due to tail motion by continuous lines. Errors in the average over Q intensity are minimal. The scattering originates mainly by the protons depicted in the inset by white bonds in each molecule. These molecular representations illustrate the specific labeling used in the experiments by showing only proton atoms and not deuterium.

TABLE 2.

Effect of deuteration on main transition as probed by DSC and QENS

Sample	DSC	QENS
Protonated lipid (hh-DPPC)	378 K	363–367 K
Heads deuterated lipid (dh-DPPC)	366 K	—
Tails deuterated lipid (hd-DPPC)	367 K	348 K

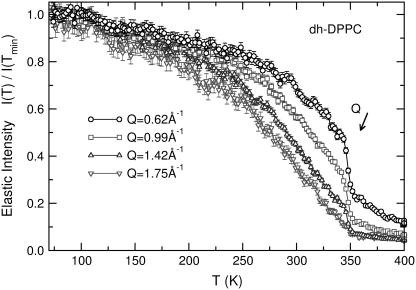
We now focus on the sharp portion of the transition by considering the spatial dependence of the elastic intensity for dh-DPPC (Fig. 5). The transfer of momentum in a neutron scattering experiment, Q = 2π/r, defines the spatial extent over which motion is observed. In Fig. 5, we examine the mobility for four different spatial scales: two are above the average lipid lateral spacing (d_lipid ≈ 4 to 5 Å) in the fluid phase, and the other two are below. Several remarks can be made. First, the shape of the curve at low temperatures is different in these two cases. Second, only spatial scales greater than d_lipid exhibit a sharp transition. Lastly, a residual gain in mobility after the transition occurs only above d_lipid. From these observations, we conclude that if the spatial scale of the measurement is less than d_lipid, as the temperature is raised all protons along the hydrophobic chains are able to gain mobility at a rate that is almost uniform (compare Q = 1.42 Å⁻¹ and 1.75 Å⁻¹ in Fig. 5). At the transition, all protons move freely and the intensity of elastic scattering reaches a constant plateau value. On the other hand, at spatial scales greater than d_lipid, only some of the protons are able to gain mobility before the transition; the rest become mobile simultaneously at the transition. The rate of intensity decrease depends on the spatial extent of the motion, as indicated by different momentum transfers. Above the transition, there are still protons that cannot move over the prescribed distance and continue to gain mobility with further increases in temperature. The most likely picture emerging from these data is that, since whole-lipid motion (diffusion and rotation) is expected to be relatively slow at low temperatures, it is the ends of the hydrophobic chains that can span increasingly larger volumes, somewhat independently from the main lipid motion. Increasing the temperature has both the effect of enhancing the mobility of the lower parts of the tails and that of introducing more protons from the higher parts of the tails (those closer to the headgroups) into the energy window of the instrument.

FIGURE 5.

Elastic intensity loss for as a function of temperature for dh-DPPC at different Q values corresponding to proton diffusion over short distances (high Q-values) and long distances (low Q-values).

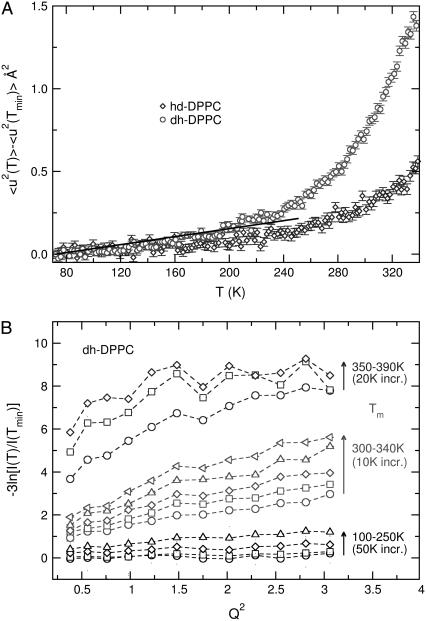
From fixed window scans, it is possible to extract a mean displacement 〈u²〉 of the proton positions about a fixed position (40). When translational motion is absent, the scattering intensity can be described by 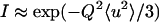, in which case the mean displacement can be obtained from the slope of a plot of 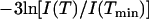vs. Q². Such a plot is shown in Fig. 6 b, with the extracted mean displacements in Fig. 6 a. Mean-square displacements are presented only for temperatures in the linear range of Fig. 6 b. Three temperature regimes can be identified in the mean-square displacements. Up to ≈220 K (the “vibrational regime”), the mean displacements are linear in temperature, indicating vibrational motion. Between 220 K and 250 K, another process appears, which is not vibrational in nature, but is still consistent with mean displacements about a fixed position: we refer to this as the localized regime. At temperatures above 340 K the transition occurs, and the spatial dependence of the intensity loss ceases to be linear (see Fig. 6 b).

FIGURE 6.

(a) Mean-square displacement of protons as extracted from the loss of intensity using the DAVE data analysis software (26). A line is drawn to indicate a linear regime up to ≈200–250 K. Data are drawn up to the melting transition due to deviations from linearity of ln I vs. Q² above 340 K. (b) Loss of intensity as a function of Q² for three separate temperature regimes. Errors are within the symbol size.

In the vibrational regime, changes with temperature are minimal. In contrast, the localized regime is characterized by a significant gain of mobility (Fig. 6 b), where the temperature dependence of the data is much more pronounced. Such dependence leads to the rapid increase in mean-square displacements evident in Fig. 6 a, and is consistent with the view that protons near the tail ends are able to gain mobility before the actual melting transition, where the onset of translational motion is observed. In keeping with this idea, it is apparent that the localized area accessible to the tail protons grows more rapidly with temperature than that of the head protons, which are not able to explore large localized areas. We thus expect that below the transition the headgroup protons (and the protons closest to them) move over much shorter distances than those in the lower part of the tails.

In the transition regime, a shift in intensity is observed, followed by a spatial dependence that can be roughly classified into two behaviors: at small spatial scales (high Q), the Q dependence of the intensity is flat; and at large spatial scales (low Q), the Q dependence is again roughly linear. The spatial scale dividing these two regions is consistent with d_lipid. At any given Q in the flat region, the scattering intensity changes little with temperature, since all motion is faster than the instrument's resolution. The range of Q values in the flat region indicates the range of spatial scales where this is the case: spatial scales less than d_lipid are flat at any temperature above T_m, indicating that no further gain in mobility occurs after the transition at spatial scales less than the intertail spacing.

These results suggest that the sharp transition associated with melting in dehydrated lipid bilayers arises from a sudden gain in mobility of only a portion of the lipid tails. Previous dynamic neutron scattering measurements of lipid systems at moderate levels of hydration presumed a linear variation of spatial diffusion along the tails that increases uniformly with temperature, together with lipid rotational diffusion (10). A subsequent study explored the concept of kink diffusion along the lipid tails, although the transition probabilities were assumed to be equal for all positions along the lipid tails (12). As discussed below, we believe that both of these views are unnecessarily approximate. To resolve the precise nature of lipid tail dynamics faster than 5 ns, as probed by the elastic scans by HFBS, in the following section we construct quasielastic scans that combine information from the two instruments.

Quasielastic scattering experiments

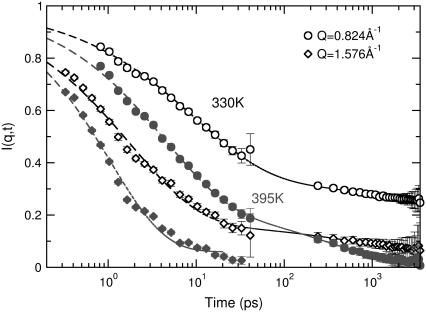
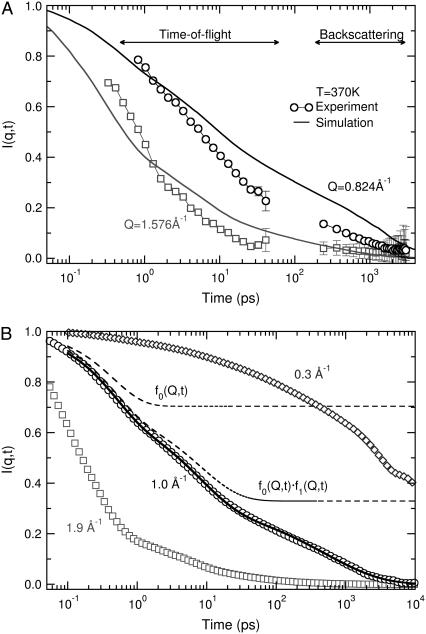
The lipid tail dynamics exhibit a complex character and consist of a superposition of different processes that contribute to the observed mobility. By measuring the full dynamic structure factor over a relatively wide time interval and longer spatial scales, we can gain insight into the molecular-level details of the dynamics of the bilayer. Fig. 7 presents the results of the DCS (time < 40 ps) and the HFBS (time > 200 ps) experiments. Data are shown at two different temperatures, 310 K and 395 K, i.e., above and below the melting transition.

FIGURE 7.

Incoherent intermediate scattering functions for dh-DPPC as extracted using the two different spectrometers. Solid points correspond to measurements at 395 K and open points at 330 K. Circles represent data at Q = 0.824 Å⁻¹ (mobility over large distances) while diamonds represent data at Q = 1.576 Å⁻¹ (short distances). The dashed lines represent fits of the combined data with Eq. 3.

The data from the DCS spectrometer exhibit a significant decay both at temperatures above and below the melting transition, as evidenced by the points in the figure for times shorter than 40 ps. This effect is observed at all length scales, although at longer distances the decay is less pronounced. Analysis of the data from the HFBS spectrometer requires additional treatment. Since a significant decay occurs out of the experimental window of the backscattering instrument, the collected data must be rescaled to present them in conjunction with the DCS data. Such a “merging” process was implemented by using data from the DCS spectrometer as received from the inverse Fourier transformation, and a combination of two processes described by a stretched exponential and a plateau constant,

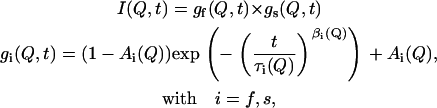(3)

where τ(Q) provides an estimate of the correlation time of the process and β(Q) the deviation from a single exponential. The HFBS data were then rescaled for presentation with the DCS data. It is important to note that the parameters describing the merged data are identical to those derived from the original data. An important quantity extracted from the fits is the plateau value A_i(Q), which is frequently referred to as the elastic incoherent structure factor (EISF). The EISF provides a measure of the fraction of the protons that are not mobile at a specific value of momentum transfer. The dependence of A_i on Q for different geometries of motion has been derived theoretically (40). As shown by the dashed lines in Fig. 7, the above equation provides an excellent description of our data. A constant β_s(Q) = 0.6 was chosen for all temperatures and momentum transfers for the experimental data; this value provided a satisfactory fit, and the quality of the spectra does not justify any variation. For the fast process, β_f(Q) was a free variable in the fitting procedure and varied between 0.45 and 0.64 at different Q-values, increasing with temperature. Correlation times τ_f(Q) varied between 0.75 ps and 6.0 ps at 395 K and increased to 3 to 18 ps at 310 K, depending on the Q considered. These values are in good agreement with segmental dynamics observed in polyethylene oligomers by QENS experiments and molecular dynamics simulations (19,41).

Fig. 7 provides evidence of significant mobility in the lipid tails at temperatures below the melting transition. While I(Q, t) exhibits a considerable decay in the picosecond time domain, even at low temperatures, this is not the case for the slower dynamics. The slow process is suppressed to a great extent when the temperature is reduced. At 310 K, the dynamic structure factor in the frequency domain, as measured by HFBS, is close to the resolution function of the instrument. Such a finding indicates that there is almost no motion present in the experimental window of the backscattering instrument. However, the elastic intensity probed by the same instrument decreases significantly as a function of temperature (Figs. 4 and 5). We therefore conclude that the mobility gained below the transition is mainly associated with the fast process observed by the DCS instrument, and remains mostly out of the experimental window of the HFBS instrument (but still decreases the elastic scattering).

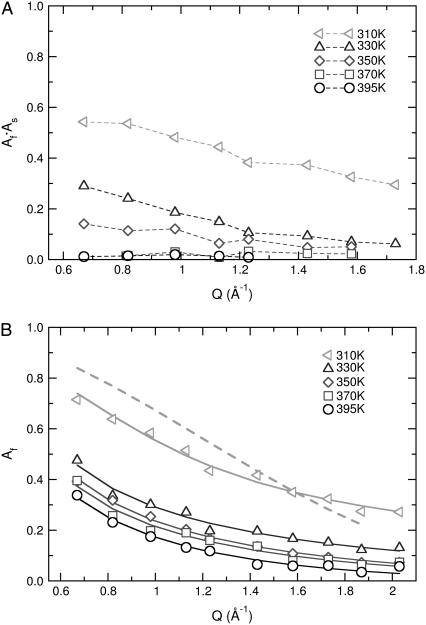
While mobility is present at low temperatures in the picosecond time domain, the fraction of protons that participate in the process (at a specific Q-value) varies with temperature. Equation 3 allows for an estimate of the fraction of atoms (EISF) that contributes to the decay of I(Q, t) through the values of A_f(Q) and A_s(Q). For the superposition of the two processes, the EISF is provided by the product A_f × A_s, as plotted in Fig. 8 a, which is almost inversely proportional to the amount of elastic loss intensity (although in the fitting procedure no time window is considered, in contrast to the scans where only atoms faster than 5-ns scatter). At high temperatures and above the melting transition, it is seen that all protons exhibit significant mobility at times shorter than a few nanoseconds over distances that correspond to Q > 0.8 Å. This is consistent with literature data for the EISF dependence of Q measured by backscattering spectroscopy (10). A distinct change is observed at the melting transition, which alters both the values and the qualitative shape of this dependence.

FIGURE 8.

(a) Elastic incoherent structure factor as a function of momentum transfer at different temperatures. The parameter is extracted from fitting the data with the product of two processes as described in Eq. 3. (b) Fraction of protons participating in the first process as expressed by the parameter A_f. The dashed line is the best fit with the model of diffusion in a sphere at 310 K (Eq. 4). The continuous lines are models using a linear sum of spheres as expressed in Eq. 5.

In contrast to the slow process, the mobility at short times (TOF spectroscopy) has been reported to be isotropic (10). Furthermore, the EISF from the fast process displays qualitatively similar behavior above and below the main transition (10). The variation of A_f with Q extracted by our analysis is plotted in Fig. 8 b and is shown by the open symbols. It is evident that the behavior above and below the melting transition is similar. The EISF dependence on Q has been explored extensively in the past with the goal of constructing analytical models that describe the physics of the motion probed by QENS. Apart from the character of the process, useful parameters such as the spatial extent of proton diffusion can be derived. A model that is often used to fit neutron scattering data is provided by the analytical description of diffusion in a sphere of radius R (42),

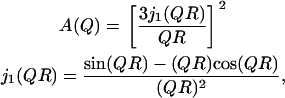(4)

where A(Q) is the EISF of the process and j₁(QR) is the first-order spherical Bessel function. It is unrealistic to expect such a simple model to describe the mobility of the protons in the lipid tails. This limitation is evident in Fig. 8 b, where the dashed line represents the best fit of the above equation at 310 K. A major argument against such description is that different protons along the lipid tails could experience mobilities over significantly different spatial extents. Such dynamic behavior could be described by using a sum of spheres with different sizes, corresponding to the motion of each proton along the lipid tails; such an approach was originally proposed by Carpentier et al. (43) to interpret experimental data on dicopper tetrapalmitate. Mathematically, the sum-of-spheres process can be expressed as

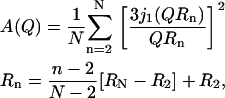(5)

where the free parameters are the radius of diffusion at the first position after the carbonyl group (R₂), the second-to-last carbon atom group (R_N, where N = 15, since the samples used in (43) had a deuterated terminal methyl group). This approach was also used in the multibilayer DPPC systems that König et al. (10) studied as a function of orientation and hydration; in that work, however, the samples were protonated (scattering from all atoms) or tail deuterated (significantly less scattering from the tails). Within the experimental error, no differences were found between different samples or orientations for the fast dynamics probed by the time-of-flight spectroscopy. Our samples with head-deuterated lipids provide a higher intensity emanating from the tail dynamics. By ignoring the contribution from the three protons in the glycerol backbone (it is expected to be negligible), we fit our data with the expression in Eq. 5 (where in our case N = 16, since the terminal methyl is not deuterated). The continuous lines in Fig. 8 b present the results of the sum-of-spheres model. It is clear that, within the experimental error, this model offers an excellent description of the spatial extent of dynamics probed by our experiments. The values extracted from our fit of the data, together with literature values from the dynamics of related systems, are presented in Table 3. Remarkably, given the assumptions made to arrive at this simple analytical model, our results are completely consistent with literature data for very different samples.

TABLE 3.

Parameters of best fit for the model of diffusion inside a sphere using a sum of spheres distributed linearly along the lipidic tails (n = 2, 3, …, 16)

	Temperature (K)	Rmin (Å)	Rmax (Å)
Experiments	310	0.14 ± 0.05	3.20 ± 0.09
	330	0.47 ± 0.12	5.59 ± 0.24
	350	0.79 ± 0.03	5.85 ± 0.16
	370	0.86 ± 0.08	6.19 ± 0.45
	395	1.15 ± 0.07	6.44 ± 0.37
	308*	0.18 ± 0.08	2.75 ± 0.10
	333*	0.72 ± 0.09	4.44 ± 0.20
	370†	1.3	4.2
	390†	1.6	4.7
Simulations	310	0.45 ± 0.02	3.79 ± 0.07
	330	0.54 ± 0.06	3.91 ± 0.17
	350	0.71 ± 0.05	3.83 ± 0.08
	370	0.66 ± 0.07	4.56 ± 0.23
	395	0.77 ± 0.11	4.86 ± 0.23

Results from literature QENS studies probing alkyl tail mobility are also shown.

^*Oriented multilayers of fully protonated DPPC with 12 wt % water. Data from König et al. (10).

^†Dicopper alkanoate complexes with deuterated terminal methyl groups (R_max corresponds to n = 15). Data from Carpentier et al. (43).

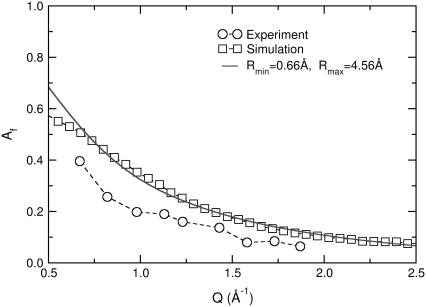
The simple model of diffusion in a sphere is capable of providing information about the spatial variation of proton diffusion as a function of position in the hydrophobic chains. One important hypothesis is that the nature of the elementary fast process can be described as diffusion in a sphere (isotropic motion with unrestricted displacements inside the radius). As alluded to earlier, the question of isotropy (or lack thereof) was addressed by König et al. (10) using oriented multilayers of DPPC; these authors did not find significant differences as a function of orientation using a time-of-flight spectrometer. A different-sized sphere for each position along the tails is assigned, assuming a linear change. This hypothesis of linear dependence was in fact questioned in the study where the model was first proposed (43). Additional experiments were performed with palmitic tails having a deuterated lower half of the tails. The value for the last atom scattering in this case (n = 8) did not conform to the one predicted by using whole protonated tails, suggesting that a complex nonlinear dependence should be considered. The apparent problem in the data treatment is that a more complex approach (e.g., two different linear dependencies for the top and lower part of the tails) did not yield better results, as reported in König et al. (10) and Carpentier et al. (43). The same finding is true for our data, since the linear dependence already describes the experimental data with no significant deviations (as shown in Fig. 8 b). To resolve this issue, we turn to atomistic simulations.

For completeness, we note that a subsequent study analyzed the dynamics of fully protonated lipid multilayers using the concept of chain defects and kink diffusion (12). The latter concept offers a more elaborate physical picture of the dynamics, since it does not assume distinct protons to be dynamically uncoupled. It actually invokes specific, discrete displacements that are induced through the creation and diffusion of kinks along the tails. The assumption of discrete jumps is highly idealized; in a fully flexible molecule, proton displacements are not discrete. Second, note the important hypothesis that transition probabilities for the diffusion or creation of a kink are uniform along the lipid chains. We view such approximations as unjustified, and in the remainder of our work we focus on interpreting the data only in terms of the sum-of-spheres model with significant input from atomistic simulations.

Atomistic simulations

The local dynamics of lipid molecules are directly associated with important membrane properties (e.g., permeability (44)). Direct comparison of atomistic simulations to experiments designed to probe molecular motions has only been attempted in a limited set of cases. QENS data offer an opportunity for a stringent comparison between experimental methods and simulations due to the two-dimensional (Q and t) character of the extracted scattering functions; not only is the temporal evolution considered (in the time or frequency domain), but the spatial extent of the mobility is also examined. Fig. 9 a displays the experimental data as measured by the two instruments (open symbols) and the results of simulations (shown by the continuous lines for two different momentum transfers at 370 K). Overall, the simulations offer a satisfactory description of the dynamics, particularly when we consider the complexity of the dynamics (the number and character of processes involved) over distances below and above the expected lipid-to-lipid distance. All major features of the experimental spectra are reproduced by the simulations. A quantitative comparison of theory and experiment reveals that the simulated dynamics are generally slower, except in the subpicosecond regime. Note that the discrepancy at very short times is expected; united-atom models provide faster dynamics due to the absence of explicit protonic motion in the simulation (45).

FIGURE 9.

(a) Incoherent intermediate structure factor for dh-DPPC as measured by QENS with two instruments (open symbols) and predicted by the simulations (continuous lines). Data are shown for two different momentum transfers Q at 370 K. (b) Incoherent intermediate structure factor at three different Q-values at 370 K (open symbols) as extracted from molecular dynamics. The continuous solid line is a best fit using Eq. 6 while the dashed lines are partial representations of the processes involved in the full scattering function.

Through the use of atomistic simulations we can clearly identify the presence of three major processes, two of which arise in the time-of-flight experimental window. The experimental data were insufficient to support this separation, but in the case of simulations, Eq. 3 had to be revised by separating the fast dynamics into two distinct processes,

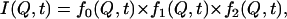(6)

where f_i(t) is a stretched exponential with a limiting plateau value as in Eq. 3. Equation 6 provides an excellent description of the simulation predictions, as shown in Fig. 9 b. Open symbols represent the collected results while the continuous line is a best fit for momentum transfer 1.0 Å⁻¹. The contributions of different processes are shown by the dashed lines. Before discussing the results of the fitting procedure, it must be emphasized that the separation into three different dynamic processes is not feasible at all Q-values since, as shown in the figure, at high and low Q-values the processes appear to merge. Such a feature originates from the physical picture of the dynamics of the tails. The diffusion over different distances is achieved through the superposition of processes, with the relative weight of each of them varying according to the Q examined. The slow dynamics contribute mostly to diffusion over large distances; in contrast, for large Q-values the fast processes are the major mechanism leading to displacements. Since the simulations are clearly capable of providing at least a realistic picture of the experimental data, we can proceed to assign specific processes to the data collected in our scattering experiments.

The slower nanosecond dynamics originate from whole-lipid motion, which is expected to be a molecular rotation over the principal axes. This process has been suggested in previous QENS studies (10) for hydrated oriented multilayers; the correlation times observed in our measurements and simulations are consistent with literature data. The experimental study of rotational dynamics requires assignment of diffusion coefficients in two directions. A full investigation would have to involve measurements of oriented multilayer membranes as a function of orientation rather than the liposomes used in our study. Due to insufficient data from the experiments, we therefore remain at the qualitative level, and conclude that rotational diffusion is present in the window of the backscattering instrument at 370 K and 395 K, and that this dynamic mode is rendered too slow to be observed by HFBS at temperatures lower than the melting temperature. As shown in Fig. 6 b, this conclusion is in agreement with the elastic scans performed with the backscattering instrument. The loss of intensity (mobility faster than 5 ns) above the melting transition has a significantly different Q dependence—a sign of a different process now present in the sample.

The fast dynamics probed by the time-of-flight instrument exhibit several interesting features at various temperatures. As stated earlier, there is a gradual “softening” of the tails, which is also supported by the decay of the curves at low temperatures (Fig. 7). The predictions of the simulation allow us to identify two different processes at times shorter than 100 ps. The fast dynamics are expected to be associated with conformational transitions occurring in the lipid tails. A preliminary estimate of the rate of these transitions can be generated by dividing the dihedral angles into three different intervals of 60°, centered at the maximum of the torsional populations (e.g., trans angles are defined from 150° to 210° and gauche⁺ from 270° to 330°). The rate of jumps from one domain to another was calculated for each dihedral along the lipid tail, and separately for each tail of DPPC (sn-1 and sn-2). The extracted estimates are in good agreement with the early computations of Venable et al. (46) at lower temperatures. Conformational transitions occur at ≈10 to 20 ps at 370 K, and correspond to the second fast process observed in Fig. 9 b (f₁(Q, t)). The first process, f₀(Q, t), can be attributed to torsional vibrations probed at high momentum transfers. These two processes (torsional vibrations around mean values and conformational jumps between these values) are a common characteristic of alkane dynamics and their separation has been addressed by a previous study of short polyethylene chains (47). While experiments do suggest this separation, it is only through the simulations that we can gain sufficient statistical accuracy to clearly identify this feature.

The local mobility expressed by torsion-vibrations and conformational jumps is likely related to the local environment of the lipid tails. A question remains as to how to relate the modeling predictions with the actual experimental data, so that we can extract the best estimate of the spatial extent of lipid tail mobility. In contrast to previous theoretical approaches (e.g., the kink-diffusion model), it is more difficult to dissect the spatial components of mobility directly from the conformational transition rates observed in a fully flexible simulation. Furthermore, torsional vibrations (and all faster modes such as angle bending) contribute significantly to the decay of the curves at high momentum transfer. We therefore choose to follow the same approach that was followed with the analysis of the experimental data. The elastic incoherent structure factor of the experimental data for the fast process can be compared to the plateau value of the superposition of the first two processes in Eq. 6, assuming g_f(Q, t) = f₀(Q, t) × f₁(Q, t). The values extracted are compared to the experimental results at 370 K in Fig. 10. The first finding is that the simulation results are in good agreement with experiments. While a constant deviation is apparent, the shape of the simulated curve follows closely the dependence on momentum transfer of our experimental data. As discussed earlier, the decomposition into three processes is valid only in a certain Q range, but within this range the simulation offers excellent resolution, thereby providing a test of the theoretical models assumed in the experimental analysis. We proceed by fitting the simulated data to a sum of spheres, with a linear variation of radius along the lipid tails as modeled by Eq. 5. The continuous line plotted in the figure represents this model; the resulting parameters are presented in Table 3. The parameters determined by this procedure, decrease with temperature, and follow a trend similar to that observed in the experiments. The agreement of the extracted R_min and R_max between experimental and simulation data is not quantitative; this was anticipated from the direct comparison of the actual EISF values (e.g., shown in Fig. 10 at 370 K).

FIGURE 10.

Elastic incoherent structure factor corresponding to the fast dynamics of lipid tails. Open circles are experimental data at 370 K as in Fig. 8 b. Open squares are calculated simulation data using Eq. 6 and the plateau value of the first two processes (f₀(Q, t) × f₁(Q, t)). The continuous line is a best fit using a sum of spheres of radius that varies linearly along the lipid tails (Eq. 5).

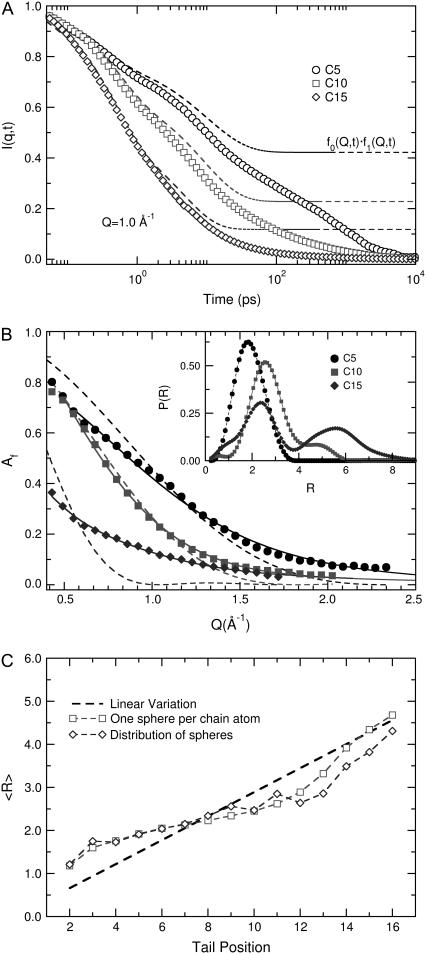
To determine if a distribution of sphere sizes arises from a variation in tail position, we analyzed separately the incoherent intermediate scattering functions for protons connected to different positions along the lipid tails (N = 2, …, 16). Fig. 11 a presents the predicted decays at Q = 1.0 Å⁻¹ by open symbols for the 5th, 10th, and 15th methylene positions. Several important differences can be identified and serve to demonstrate that protons at different positions of the tail diffuse over the same distance at significantly different rates. The average displacement induced by the fast local motions can be again extracted by the plateau parameter of the superposition of the first two processes (A_f = A₀ × A₁, Eq. 6). The dashed lines in the figure are plotted to visualize these dynamics at short times for different protons. The estimated plateau values are presented by the solid symbols in Fig. 11 b. The dashed lines in the Fig. 11 b represent best fits with Eq. 4, the model for diffusion in a sphere. Clearly the description of the local mobility of protons at a specific tail position, by diffusion in a sphere of radius R, is not particularly accurate. The source of the deviations could be that: 1), the differences between the two tails (sn-1 and sn-2) are not accounted for in the sphere analysis; 2), the molecular motions responsible for the displacements induce a diffusion over different specific distances (e.g., the kink diffusion model as described in (12)); and 3), each methylene at the same tail position of different lipids experiences a distinct mobility due to variations in the local environment.

FIGURE 11.

Dynamics of protons as function of position along the lipid tails as predicted by simulations. (a) Incoherent intermediate structure factor at Q = 1.0 Å. Dashed lines represent the fitting of the fast dynamics (Eq. 6). (b) EISF with fits by Eq. 4 (dashed lines) and Eq. 7 (solid lines). The distributions corresponding to the lines are shown in the inset. (c) Diffusion over spheres as extracted by Eq. 5 (dashed lines), Eq. 4 (open squares), and Eq. 7 (average of distribution shown with open diamonds).

To improve the description of the spatial extent of proton mobility, a model consisting of a distribution of spheres at each tail position was implemented. This model has been used before to interpret the motion of a globular protein (20). We consider a set of spheres {R_i} that differ in size by a small amount (e.g., ΔR = 0.1 Å). The elastic incoherent structure factor is provided by a sum of contributions α_i(Q) from each sphere, weighted by a probability P(R_i),

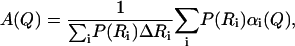where

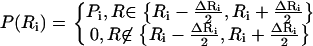and

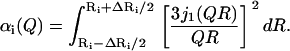(7)

With the above equations, we can decompose the EISF into contributions by a distribution of α_i(Q) that arises from diffusion over spheres of different sizes. The mathematical problem provided by such a transformation is similar to that encountered when fitting a dynamic decorrelation curve with a distribution of exponential functions. Following methods from the literature, we used a simulated annealing Monte Carlo optimization algorithm to extract the best distribution of spheres that describes our data, as described in Bello et al. (48). Since multiple solutions can provide equally satisfactory fits, we applied a regularizator as described in Provencher (49,50) to select the simplest one (fewer peaks in the distribution) that remains satisfactory. The continuous lines in Fig. 11 present the best estimates, with a distribution of spheres for different positions along the lipid tail. The improved description is apparent and the resulting distributions of spheres are shown in the inset. For the first position, a single peak at 0.5–1 Å was found. Subsequent protons along the tail diffuse over spheres with a distribution centered at ≈2 Å to 3 Å. A significant change is observed from the 8th to 10th position (depending on temperature). A single peak can no longer approximate the data, and a second peak at larger distances was needed.

While the model of diffusion in a sphere (or distribution of spheres) invokes considerable assumptions, an important feature can be extracted from such analysis. Both approximations, either that of a single diameter or that of a distribution of diameters for each position in the lipid tail, reveal a change of the spatial extent of dynamics. Fig. 11 c displays the linear distribution (obtained by approximating the EISF with Eq. 5) that was applied in the previous data analysis (10,43). The dashed line connects the minimum and maximum radius at 370 K from simulations as reported also in Table 3. The square and diamond symbols are the results at each tail position, using either a single sphere or a distribution of spheres, respectively (the average of the distribution is plotted). The two different approximations of the EISF are in agreement with respect to the average spatial extent of mobility along the tails. Both provide evidence that the dynamics are heterogeneous. The top part of the tails, although subject to conformational transitions, experiences diffusion over short distances, characteristic of cooperative dynamics through the appearance of kinks (coupled conformational transitions) (12). This is not the case for the bottom part of the tails, where a significant, gradual increase of the radius of the spheres is observed. An independent conformational transition at a certain part of the tail is expected to induce a displacement for all subsequent atoms. Such displacements will increase considerably toward the end of the chains, and are only encountered in the lower part of the molecules.

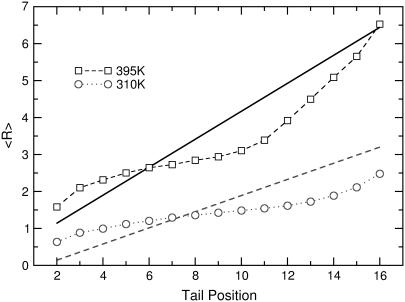
Fig. 10 shows that simulations can provide a good qualitative prediction of the EISF dependence on momentum transfer. Thus, we expect that tail protons display dynamics with a similar variation along the tail but quantitatively the spatial extent of the motion is different (which would result to a shift as observed in Fig. 10). To account for this difference, we calculated the ratios R_N/R₂ of each average sphere relative to the first sphere (N = 2) from the simulations. Using the radius of the minimum sphere R₂ as a free parameter, and extracting the ratios of the other spheres to R₂ from the simulations, we fitted the experimental EISF values shown in Fig. 8 b. While deviations between the fit and the actual data do exist, we believe that the resulting values offer a more realistic description of the spatial extent of mobility. The extracted values for the average radius of diffusion for each position along the tail are plotted in Fig. 12. The lines display the values presented in Table 3 and the points represent the values extracted using the sphere radii ratios from the simulations at the corresponding temperature. The plotted data, while based on a simple theoretical model, emerge from the combined use of simulations and experiments. The presence of local dynamics before the melting transition and their heterogeneous character are strongly supported by the above methodology, which provides a significant addition to our understanding of melting in anhydrous phospholipidic membranes.

FIGURE 12.

Diffusion over spheres of radius R using two different models for the dependence on lipid tail position at 310 K and 395 K. The lines are the data shown in Table 3 and assume a linear variation with two free parameters as described by Eq. 5. The symbols are values extracted using one free parameter (minimum sphere at N = 2) and the relative ratios to this parameter as extracted from the simulations at the corresponding temperature.

CONCLUSIONS

We have investigated the melting of anhydrous phospholipid membranes by means of experiments and computational methods. Neutron scattering elastic scans were performed as a function of temperature and momentum transfer with varying schemes of specific deuteration. Quasielastic neutron scattering experiments as a function of frequency and momentum transfer provided the dynamics of lipid tail protons at a specific temperature. Atomistic simulations of a multibilayer membrane model were performed to supplement our experimental results. All methods employed in this work provide a consistent molecular view of melting of these membrane systems.

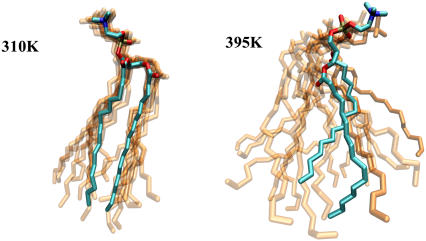
We summarize our findings with a simple graphical illustration of the dynamics as predicted by the simulations. Fig. 13 displays a single lipid extracted from the multibilayer model in anhydrous conditions. Different snapshots (every 400 ps) over a period of 4 ns are superimposed to demonstrate the mobility of various segments. This time-frame is approximately equivalent to the energy resolution of the neutron scattering instruments used in this study. At a low temperature, it is clear that the headgroup and a portion of the tails exhibit limited mobility. At this “upper” part of DPPC chains, the only significant motions are vibrations and, to a small extent, conformational transitions. While the rate of the transitions is not necessarily negligible, the physics of this process is highly cooperative in nature. Displacements are experienced through coupled transitions; they occur mostly over short distances and are not observable in the momentum transfer resolution of the instruments. Effectively, the upper part of the tail is rendered immobile. In the “lower” parts of the hydrocarbon chains, however, conformational transitions can displace the rest of the chain over longer distances. Both elastic and quasielastic experiments confirm such displacements over significant distances, at high frequencies but low temperatures. The extent of this heterogeneous character of tail dynamics is highly sensitive to temperature. As temperature increases, the lateral expansion of the membrane allows a larger set of protons to participate in these motions.

FIGURE 13.

Motion of individual lipids in a dry DPPC bilayer as modeled by computer simulations of an atomistic model. Starting with one configuration, snapshots from conformations sampled through a period of 4 ns are shown (shaded).

At high temperatures, the headgroups of the lipids melt with no signature of a distinct transition. This is evidenced by the elastic scans of tail deuterated samples. Lipid tail mobility due to the fast dynamics is significantly increased through a larger number of conformational transitions induced by the larger available volume. In addition to the fast dynamics, molecular rotations evolve in the experimental window of the instruments, thereby offering a complex picture of the dynamic behavior of lipid tails.

The softening of the headgroups and the effect of the increased lateral area of the membrane on the tail dynamics (and eventually the main transition) suggests that melting could be controlled by regulating the mobility of the phospholipid headgroups. In fact, it is believed that it is through this mechanism that the addition of lyoprotectant molecules, such as disaccharides, leads to depression of the melting temperature. This is also proposed to be responsible for the stabilizing role of agents such as trehalose. Having acquired a better understanding of how melting proceeds in anhydrous membranes, in the future we plan to study the unique properties of such protectant molecules on freeze-dried liposomes.